Synthesizing Disparate LiDAR and Satellite Datasets through Deep Learning to Generate Wall-to-Wall Regional Inventories for the Complex, Mixed-Species Forests of the Eastern United States
Abstract
:1. Introduction
1.1. Overview
1.2. The Current Approach
1.3. Deep Learning
1.4. Objectives
2. Materials and Methods
2.1. Forest Attributes
2.2. Training Data
2.3. Remote Sensing Data
2.3.1. LiDAR
2.3.2. Satellite Variables
2.4. Deep Learning Modeling
2.4.1. Data Preparation
2.4.2. Deep Learning Model Architecture
2.4.3. Deep Learning Model Training
2.5. Traditional Modeling
2.6. Validation
3. Results
3.1. Phase One Validation and Model Comparison
3.2. Phase Two Validation (CNN Model Only)
3.3. County-Level Comparisons
4. Discussion
4.1. Model Comparison
4.2. Assessing Performance
- Although we incorporated satellite spectral indices useful for species estimation, the model architecture may not have made full use of them.
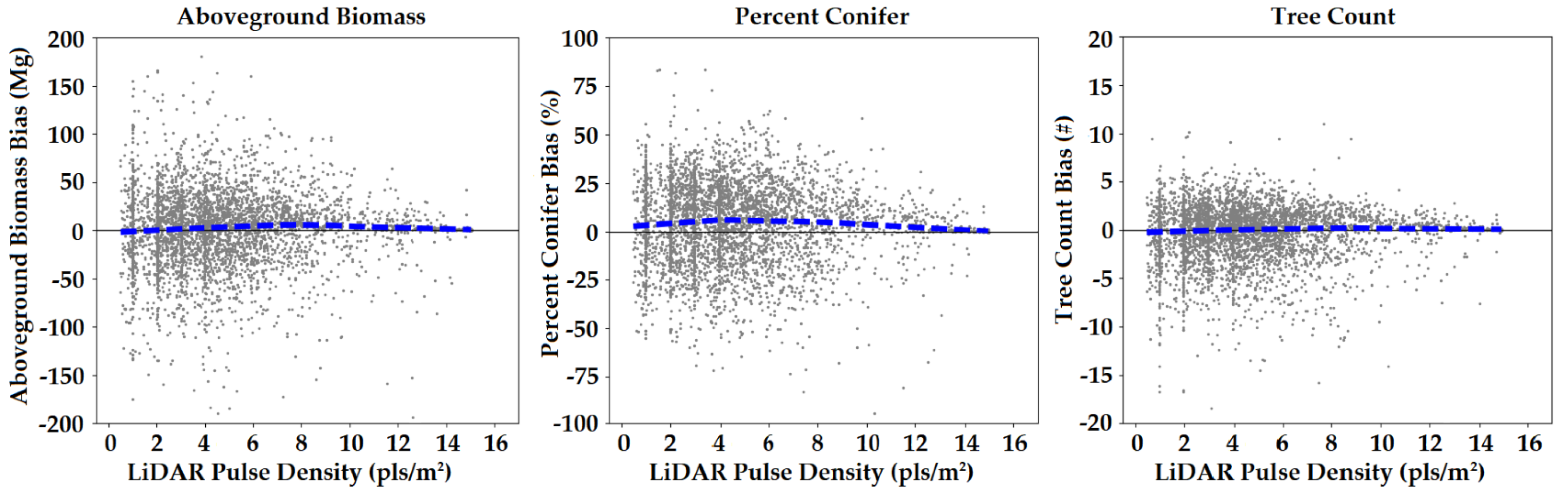
- Stem density was often underestimated in high density stands, but qualitatively, the maps seemed to suffer from banding in areas with low pulse density LiDAR (<3 pls/m2). The model may have made use of horizontal structural features in the canopy that could not be resolved in low density LIDAR. Ayrey and Hayes [1] determined that 3-D CNNs make use of the horizontal canopy structure, such as the edges of tree crowns.
- In re-examining our loss function, we find that half of our forest attributes were in some way related to tree size, while only one attribute estimated stem density. Thus, our unweighted loss function may have inadvertently favored attributes estimating tree size, resulting in a model that identified features in the LiDAR data that were more predictive of size, rather than density or species.
4.3. Mapping Errors
4.4. Our Results in Context
4.5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Inventory | Sites | Location (s) | Area (km2) | Number of Plots | LiDAR Acquisitions | Seasonality | Mean Pulse Densities (pls m−2) | Temporal Field/LiDAR Discrepancy (Years) |
|---|---|---|---|---|---|---|---|---|
| Acadia National Park | Mount Desert Isle au Haut Schoodic Point | −68.294, 44.339 −68.627, 44.032 −68.065, 44.351 | 671 | 128 | 2 | Leaf on/off | 1.5, 12 | 0 to +2 −2 to +2 |
| Baxter State Park | Scientific Forest Management Area | −69.000, 46.176 | 87 | 882 | 1 | Leaf off | 5 | −3 |
| Bartlett Experimental Forest Echidna | −71.286, 44.064 | 0.1 | 46 | 1 | Leaf on | 4 | −7 | |
| Cooperative Forestry Research Unit | Austin Pond Alder Stream Dow Road Golden Road Harlow Road Katahdin Ironworks Lazy Tom Lake Macwahoc Penobscot Experimental Forest Ronco Cove Rump Road Sarah Road Schoolbus Road St. Aurelie Summit Week’s Brook Weymouth Point | −69.705, 45.193 −69.798, 45.369 −69.609, 45.996 −68.675, 45.719 −67.842, 45.646 −69.367, 45.489 −69.456, 45.726 −68.286, 45.798 −68.608, 44.844 −69.634, 45.680 −71.018, 45.193 −70.911, 44.817 −70.778, 44.841 −70.161, 46.259 −68.480, 45.096 −68.522, 46.217 −69.308, 45.947 | 30,000 | 935 | 3 | Leaf on/off | 1.5,6, 12 | +2, +1, 0 |
| Carbon Monitoring System | −69.764, 45.589 | 4645 | 414 | 3 | Leaf on/off | 8, 5, 15 | −2, −4, −5 | |
| University of Maine Forests | Demeritt Forest Penobscot Experimental Forest | −68.678, 44.933 −68.608, 44.844 | 55 | 912 | 3 | Leaf on/off | 1.5, 12, 6 | −8 to +2 −9 to +2 −10 to +2 |
| Fox Forest | −71.911, 43.138 | 9 | 581 | 1 | Leaf off | 6 | −5 | |
| Harvard Forest Megaplot | −72.176, 42.538 | 0.4 | 6646 | 2 | Leaf on/off | 5, 12 | +1, +2 | |
| Harvard Forest Echidna | −72.182, 42.531 | 0.1 | 90 | 2 | Leaf on/off | 5, 12 | +6, +7 | |
| Holt Experimental Forest | −69.772, 43.871 | 0.1 | 1001 | 3 | Leaf on/off | 2, 12, 15 | −3, −5, −8 | |
| Howland Experimental Forest | −68.742, 45.206 | 2 | 556 | 2 | Leaf on/off | 5, 12 | +1, +2 | |
| Howland Echidna | −68.742, 45.206 | 0.1 | 80 | 2 | Leaf on/off | 5, 12 | −9, −5 | |
| Noonan Research Forest | −66.439, 45.977 | 0.1 | 25 | 1 | Leaf on | 5 | 0 | |
| Penobscot Experimental Forest | −68.608, 44.844 | 4 | 409 | 3 | Leaf on/off | 1.15, 12, 6 | −8 to +2 −10 to +2 −10 to +2 | |
| Null Plots | Regional | 500 | 1 | Leaf on/off | 1.5 to 15 | 0 |
References
- Ayrey, E.; Hayes, D.J. The Use of Three-Dimensional Convolutional Neural Networks to Interpret LiDAR for Forest Inventory. Remote Sens. 2018, 10, 649. [Google Scholar] [CrossRef] [Green Version]
- Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting forest stand characteristics with airborne scanning lidar. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1372. [Google Scholar]
- Jensen, J.L.R.; Humes, K.S.; Conner, T.; Williams, C.J.; DeGroot, J. Estimation of biophysical characteristics for highly variable mixed-conifer stands using small-footprint lidar. Can. J. For. Res. 2006, 36, 1129–1138. [Google Scholar] [CrossRef]
- Lim, K.S.; Treitz, P.M. Estimation of above ground forest biomass from airborne discrete return laser scanner data using canopy-based quantile estimators. Scand. J. For. Res. 2004, 19, 558–570. [Google Scholar] [CrossRef] [Green Version]
- Patenaude, G.; Hill, R.; Milne, R.; Gaveau, D.; Briggs, B.; Dawson, T. Quantifying forest above ground carbon content using LiDAR remote sensing. Remote Sens. Environ. 2004, 93, 368–380. [Google Scholar] [CrossRef]
- Woods, M.; Pitt, D.; Penner, M.; Lim, K.; Nesbitt, D.; Etheridge, D.; Treitz, P. Operational implementation of a LiDAR inventory in Boreal Ontario. For. Chron. 2011, 87, 512–528. [Google Scholar] [CrossRef]
- Wulder, M.A.; Bater, C.W.; Coops, N.C.; Hilker, T.; White, J.C. The role of LiDAR in sustainable forest management. For. Chron. 2008, 84, 807–826. [Google Scholar] [CrossRef] [Green Version]
- García-Feced, C.; Tempel, D.J.; Kelly, M. LiDAR as a tool to characterize wildlife habitat: California spotted owl nesting habitat as an example. J. For. 2011, 109, 436–443. [Google Scholar]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airborne laser scanning data using an area-based approach. For. Chron. 2013, 89, 722–723. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, R.; Weiskittel, A.; Kershaw, J.A., Jr. Influence of prediction cell size on LiDAR-derived area-based estimates of total volume in mixed-species and multicohort forests in northeastern North America. Can. J. Remote Sens. 2016, 42, 473–488. [Google Scholar] [CrossRef]
- Hayashi, R.; Kershaw, J.A.; Weiskittel, A. Evaluation of alternative methods for using LiDAR to predict aboveground biomass in mixed species and structurally complex forests in northeastern North America. Math. Comput. For. Nat. Resour. Sci. 2015, 7, 49–65. [Google Scholar]
- Hauglin, M.; Rahlf, J.; Schumacher, J.; Astrup, R.; Breidenbach, J. Large scale mapping of forest attributes using heterogeneous sets of airborne laser scanning and National Forest Inventory data. For. Ecosyst. 2021, 8, 1–5. [Google Scholar] [CrossRef]
- Nilsson, M.; Nordkvist, K.; Jonzén, J.; Lindgren, N.; Axensten, P.; Wallerman, J.; Egberth, M.; Larsson, S.; Nilsson, L.; Eriksson, J. A nationwide forest attribute map of Sweden predicted using airborne laser scanning data and field data from the National Forest Inventory. Remote Sens. Environ. 2017, 194, 447–454. [Google Scholar] [CrossRef]
- Kangas, A.; Astrup, R.; Breidenbach, J.; Fridman, J.; Gobakken, T.; Korhonen, K.T.; Maltamo, M.; Nilsson, M.; Nord-Larsen, T.; Næsset, E. Remote sensing and forest inventories in Nordic countries–roadmap for the future. Scand. J. For. Res. 2018, 33, 397–412. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Coops, N.C.; Tompalski, P.; Nielsen, S.E.; Bater, C.W.; Stadt, J.J. Regional mapping of vegetation structure for biodiversity monitoring using airborne lidar data. Ecol. Inform. 2017, 38, 50–61. [Google Scholar] [CrossRef]
- Dick, A. Enhanced Forest Inventory (EFI) Adoption in New Brunswick: Progress to Date and Future Directions; Report; Natural Resources Canada: Mattawa, ON, Canada, 2019.
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Seattle, WA, USA, 2009; Volume 123.
- Silva, C.A.; Crookston, N.L.; Hudak, A.T.; Vierling, L.A.; Klauberg, C.; Silva, M.C.A. Package ‘rLiDAR’. 2017. Available online: https://cran.r-project.org/web/packages/rLiDAR/index.html (accessed on 1 June 2019).
- Ayrey, E.; Hayes, D.J.; Fraver, S.; Kershaw, J.A., Jr.; Weiskittel, A.R. Ecologically-based metrics for assessing structure in developing area-based, enhanced forest inventories from LiDAR. Can. J. Remote Sens. 2019, 45, 88–112. [Google Scholar] [CrossRef]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.S.; Bourdon, J.F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Junttila, V.; Kauranne, T.; Finley, A.O.; Bradford, J.B. Linear Models for Airborne-Laser-Scanning-Based Operational Forest Inventory with Small Field Sample Size and Highly Correlated LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5600–5612. [Google Scholar] [CrossRef]
- Næsset, E. Assessing sensor effects and effects of leaf-off and leaf-on canopy conditions on biophysical stand properties derived from small-footprint airborne laser data. Remote Sens. Environ. 2005, 98, 356–370. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Assessing effects of laser point density, ground sampling intensity, and field sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2008, 38, 1095–1109. [Google Scholar] [CrossRef]
- Hansen, C.F. Lidar Remote Sensing of Forest Canopy Structure: An Assessment of the Accuracy of Lidar and Its Relationship to Higher Trophic Levels. Master’s Thesis, University of Vermont, Burlington, VT, USA, 2015. [Google Scholar]
- Næsset, E. Effects of different sensors, flying altitudes, and pulse repetition frequencies on forest canopy metrics and biophysical stand properties derived from small-footprint airborne laser data. Remote Sens. Environ. 2009, 113, 148–159. [Google Scholar] [CrossRef]
- Goodwin, N.R.; Coops, N.C.; Culvenor, D.S. Assessment of forest structure with airborne LiDAR and the effects of platform altitude. Remote Sens. Environ. 2006, 103, 140–152. [Google Scholar] [CrossRef]
- White, J.C.; Arnett, J.T.; Wulder, M.A.; Tompalski, P.; Coops, N.C. Evaluating the impact of leaf-on and leaf-off airborne laser scanning data on the estimation of forest inventory attributes with the area-based approach. Can. J. For. Res. 2015, 45, 1498–1513. [Google Scholar] [CrossRef] [Green Version]
- Villikka, M.; Packalén, P.; Maltamo, M. The suitability of leaf-off airborne laser scanning data in an area-based forest inventory of coniferous and deciduous trees. Silva Fenn. 2012, 46. [Google Scholar] [CrossRef] [Green Version]
- Ørka, H.O.; Næsset, E.; Bollandsås, O.M. Effects of different sensors and leaf-on and leaf-off canopy conditions on echo distributions and individual tree properties derived from airborne laser scanning. Remote Sens. Environ. 2010, 114, 1445–1461. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7 –12 June 2015; pp. 1–9. [Google Scholar]
- Taigman, Y.; Yang, M.; Ranzato, M.; Wolf, L. Deepface: Closing the gap to human-level performance in face verification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1701–1708. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Rizaldy, A.; Persello, C.; Gevaert, C.; Oude Elberink, S.; Vosselman, G. Ground and Multi-Class Classification of Airborne Laser Scanner Point Clouds Using Fully Convolutional Networks. Remote Sens. 2018, 10, 1723. [Google Scholar] [CrossRef] [Green Version]
- Ghamisi, P.; Höfle, B.; Zhu, X.X. Hyperspectral and LiDAR data fusion using extinction profiles and deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3011–3024. [Google Scholar] [CrossRef]
- Castelluccio, M.; Poggi, G.; Sansone, C.; Verdoliva, L. Land use classification in remote sensing images by convolutional neural networks. arXiv 2015, arXiv:1508.00092. [Google Scholar]
- Guan, H.; Yu, Y.; Ji, Z.; Li, J.; Zhang, Q. Deep learning-based tree classification using mobile LiDAR data. Remote Sens. Lett. 2015, 6, 864–873. [Google Scholar] [CrossRef]
- Ko, C.; Kang, J.; Sohn, G. Deep Multi-task Learning for Tree Genera Classification. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci 2018, 153–159. [Google Scholar] [CrossRef] [Green Version]
- Weinstein, B.; Marconi, S.; Bohlman, S.; Zare, A.; White, E. Individual tree-crown detection in RGB imagery using self-supervised deep learning neural networks. Remote Sens. 2019, 11, 1309. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Fu, H.; Yu, L.; Cracknell, A. Deep learning based oil palm tree detection and counting for high-resolution remote sensing images. Remote Sens. 2016, 9, 22. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Tang, H.; Lin, Y.; Han, S. Point-voxel cnn for efficient 3d deep learning. arXiv 2019, arXiv:1907.03739. [Google Scholar]
- Maturana, D.; Scherer, S. 3d convolutional neural networks for landing zone detection from lidar. Robotics and Automation (ICRA). In Proceedings of the 2015 IEEE International Conference on Fuzzy Systems, Istanbul, Turkey, 2–5 August 2015; pp. 3471–3478. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; Volume 1, p. 4. [Google Scholar]
- Ciuti, S.; Tripke, H.; Antkowiak, P.; Gonzalez, R.S.; Dormann, C.F.; Heurich, M. An efficient method to exploit LiDAR data in animal ecology. Methods Ecol. Evol. 2018, 9, 893–904. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef] [Green Version]
- MacPhee, C.; Kershaw, J.A.; Weiskittel, A.R.; Golding, J.; Lavigne, M.B. Comparison of approaches for estimating individual tree height–diameter relationships in the Acadian forest region. For. Int. J. For. Res. 2018, 91, 132–146. [Google Scholar] [CrossRef]
- Weiskittel, A.; Kershaw, J.; Crookston, N.; Hennigar, C. The Acadian variant of the Forest Vegetation Simulator: Continued development and evaluation. e-Gen. In Proceedings of the 2017 Forest Vegetation Simulator (FVS) e-Conference, Asheville, NC, USA, 28 February–2 March 2017; Keyser, C.E., Keyser, T.L., Eds.; USDA Forest Service, Southern Research Station: Asheville, NC, USA, 2017; pp. 10–13. [Google Scholar]
- Li, R.; Weiskittel, A.; Dick, A.R.; Kershaw, J.A., Jr.; Seymour, R.S. Regional stem taper equations for eleven conifer species in the Acadian region of North America: Development and assessment. North. J. Appl. For. 2012, 29, 5–14. [Google Scholar] [CrossRef] [Green Version]
- Woodall, C.W.; Heath, L.S.; Domke, G.M.; Nichols, M.C. Methods and Equations for Estimating Aboveground Volume, Biomass, and Carbon for Trees in the U.S. Forest Inventory, 2010; Gen. Tech. Rep. NRS-88; U.S. Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2011; 30p. [CrossRef] [Green Version]
- Russell, M.B.; Weiskittel, A.R. Maximum and largest crown width equations for 15 tree species in Maine. North. J. Appl. For. 2011, 28, 84–91. [Google Scholar] [CrossRef] [Green Version]
- Taylor, L.; Nitschke, G. Improving deep learning with generic data augmentation. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1542–1547. [Google Scholar]
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the conterminous United States–representing a decade of land cover change information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Zheng, D.; Rademacher, J.; Chen, J.; Crow, T.; Bresee, M.; Le Moine, J.; Ryu, S.R. Estimating aboveground biomass using Landsat 7 ETM+ data across a managed landscape in northern Wisconsin, USA. Remote Sens. Environ. 2004, 93, 402–411. [Google Scholar] [CrossRef]
- Pflugmacher, D.; Cohen, W.B.; Kennedy, R.E. Using Landsat-derived disturbance history (1972–2010) to predict current forest structure. Remote Sens. Environ. 2012, 122, 146–165. [Google Scholar] [CrossRef]
- Kilbride, J.B. Forest Disturbance Detection and Aboveground Biomass Modeling Using Moderate-Resolution, Time-Series Satellite Imagery. Master’s Thesis, University of Maine, Orono, ME, USA, 2018. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Key, C.H.; Benson, N.C. The Normalized Burn Ratio (NBR): A Landsat TM Radiometric Measure of Burn Severity; United States Geological Survey, Northern Rocky Mountain Science Center: Bozeman, MT, USA, 1999.
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Cibula, W.; Zetka, E.; Rickman, D. Response of thematic mapper bands to plant water stress. Int. J. Remote Sens. 1992, 13, 1869–1880. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Verma, S.B.; Rundquist, D.C.; Arkebauer, T.J.; Keydan, G.; Leavitt, B.; Ciganda, V.; Burba, G.G.; Suyker, A.E. Relationship between gross primary production and chlorophyll content in crops: Implications for the synoptic monitoring of vegetation productivity. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Hunt, E.R.; Daughtry, C.; Eitel, J.U.; Long, D.S. Remote Sensing Leaf Chlorophyll Content Using a Visible Band Index. J. Agron 2011, 103, 1090–1099. [Google Scholar] [CrossRef] [Green Version]
- Crist, E.P.; Cicone, R.C. A physically-based transformation of Thematic Mapper data—The TM Tasseled Cap. IEEE Trans. Geosci. Remote Sens. 1984, 256–263. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Friedl, M.; Gray, J.; Sulla-Menashe, D. MCD12Q2 MODIS/Terra+ Aqua Land Cover Dynamics Yearly L3 Global 500 m SIN Grid V006 [Data Set]; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2019. [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Zhou, Y.; Hauser, K. Incorporating side-channel information into convolutional neural networks for robotic tasks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2177–2183. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; Volume 16, pp. 265–283. [Google Scholar]
- Hayashi, R.; Weiskittel, A.; Sader, S. Assessing the feasibility of low-density LiDAR for stand inventory attribute predictions in complex and managed forests of northern Maine, USA. Forests 2014, 5, 363–383. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. VSURF: An R package for variable selection using random forests. R J. 2015, 7, 19–33. [Google Scholar] [CrossRef] [Green Version]
- Woudenberg, S.W.; Conkling, B.L.; O’Connell, B.M.; LaPoint, E.B.; Turner, J.A.; Waddell, K.L. The Forest Inventory and Analysis Database: Database Description and Users Manual Version 4.0 for Phase 2; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2010; Volume 245, 336p.
- Team, B.M. Microsoft Releases 125 million Building Footprints in the US as Open Data. 2018. Available online: https://github.com/microsoft/USBuildingFootprints (accessed on 1 June 2019).
- Legaard, K.; Simons-Legaard, E.; Weiskittel, A. Multi-Objective Support Vector Regression Reduces Systematic Error in Moderate Resolution Maps of Tree Species Abundance. Remote Sens. 2020, 12, 1739. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Næsset, E.; McRoberts, R.E.; Ståhl, G.; Andersen, H.E.; Gobakken, T.; Ene, L.; Nelson, R. Statistical rigor in LiDAR-assisted estimation of aboveground forest biomass. Remote Sens. Environ. 2016, 173, 98–108. [Google Scholar] [CrossRef]
- Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Hall, D.E.; Falkowski, M.J. Nearest neighbor imputation of species-level, plot-scale forest structure attributes from LiDAR data. Remote Sens. Environ. 2008, 112, 2232–2245. [Google Scholar] [CrossRef] [Green Version]
- Packalen, P.; Temesgen, H.; Maltamo, M. Variable selection strategies for nearest neighbor imputation methods used in remote sensing based forest inventory. Can. J. Remote Sens. 2012, 38, 557–569. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Shin, H.C.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoppus, M.; Lister, A. The status of accurately locating forest inventory and analysis plots using the Global Positioning System. In Proceedings of the Seventh Annual Forest Inventory and Analysis Symposium, Portland, OR, USA, 3–6 October 2005; McRoberts, R.E., Reams, G.A., Van Deusen, P.C., McWilliams, W.H., Eds.; US Department of Agriculture, Forest Service: Washington, DC, USA; Volume 77, pp. 179–184. [Google Scholar]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining spectral reflectance saturation in Landsat imagery and corresponding solutions to improve forest aboveground biomass estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, J.; Shataee Joibary, S.; Yaghmaee, F.; Mahiny, A. Modelling forest stand volume and tree density using Landsat ETM+ data. Int. J. Remote Sens. 2010, 31, 2959–2975. [Google Scholar] [CrossRef]
- Treitz, P.; Lim, K.; Woods, M.; Pitt, D.; Nesbitt, D.; Etheridge, D. LiDAR sampling density for forest resource inventories in Ontario, Canada. Remote Sens. 2012, 4, 830–848. [Google Scholar] [CrossRef] [Green Version]
- Shang, C.; Treitz, P.; Caspersen, J.; Jones, T. Estimating stem diameter distributions in a management context for a tolerant hardwood forest using ALS height and intensity data. Can. J. Remote Sens. 2017, 43, 79–94. [Google Scholar]
- Almeida, D.R.A.d.; Stark, S.C.; Shao, G.; Schietti, J.; Nelson, B.W.; Silva, C.A.; Gorgens, E.B.; Valbuena, R.; Papa, D.d.A.; Brancalion, P.H.S. Optimizing the remote detection of tropical rainforest structure with airborne lidar: Leaf area profile sensitivity to pulse density and spatial sampling. Remote Sens. 2019, 11, 92. [Google Scholar] [CrossRef] [Green Version]
- Blackard, J.; Finco, M.; Helmer, E.; Holden, G.; Hoppus, M.; Jacobs, D.; Lister, A.; Moisen, G.; Nelson, M.; Riemann, R. Mapping US forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping forest aboveground biomass in the Northeastern United States with ALOS PALSAR dual-polarization L-band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
- Ahmed, R.; Siqueira, P.; Bergen, K.; Chapman, B.; Hensley, S. A biomass estimate over the harvard forest using field measurements with radar and lidar data. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 4768–4771. [Google Scholar]
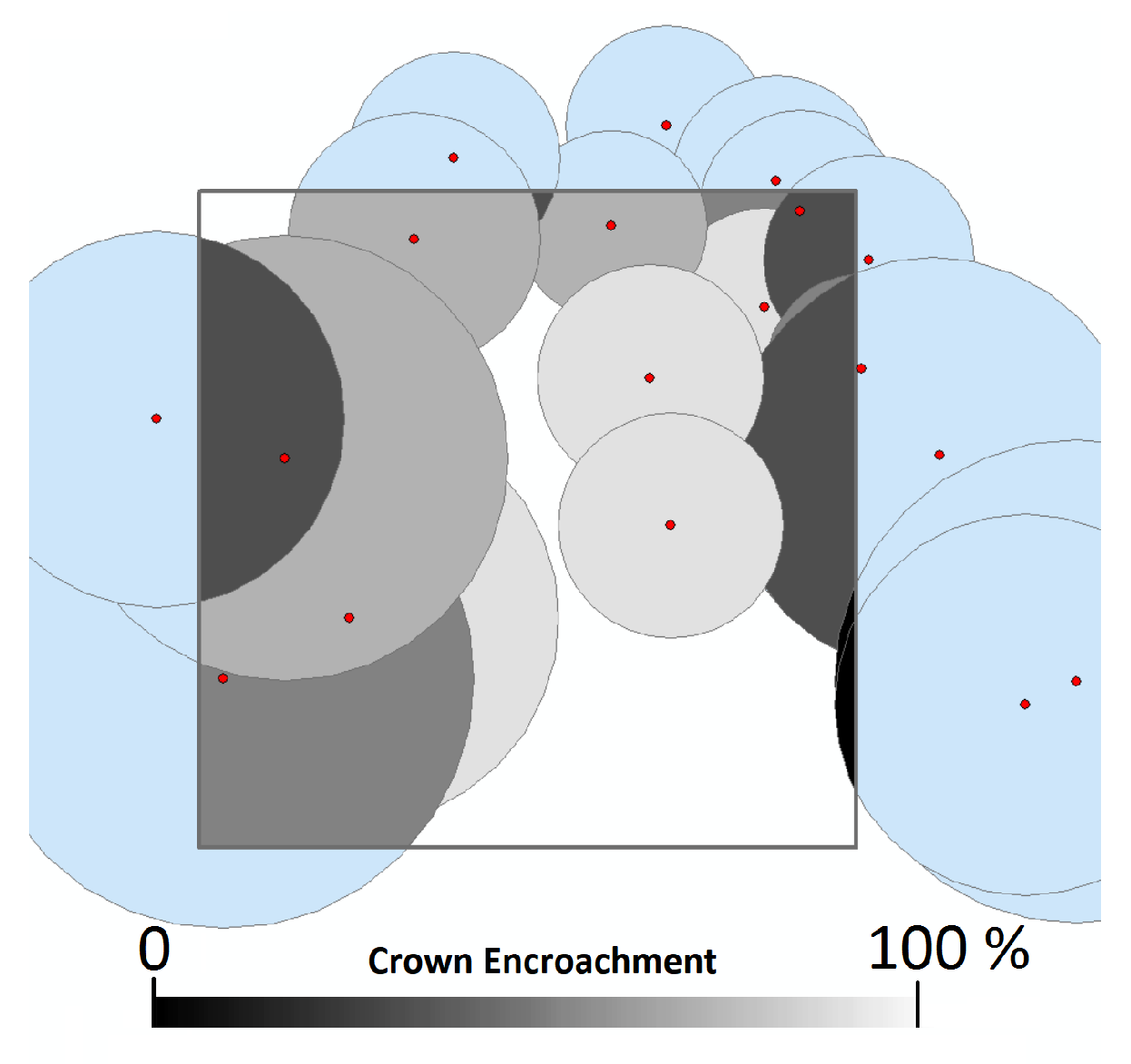
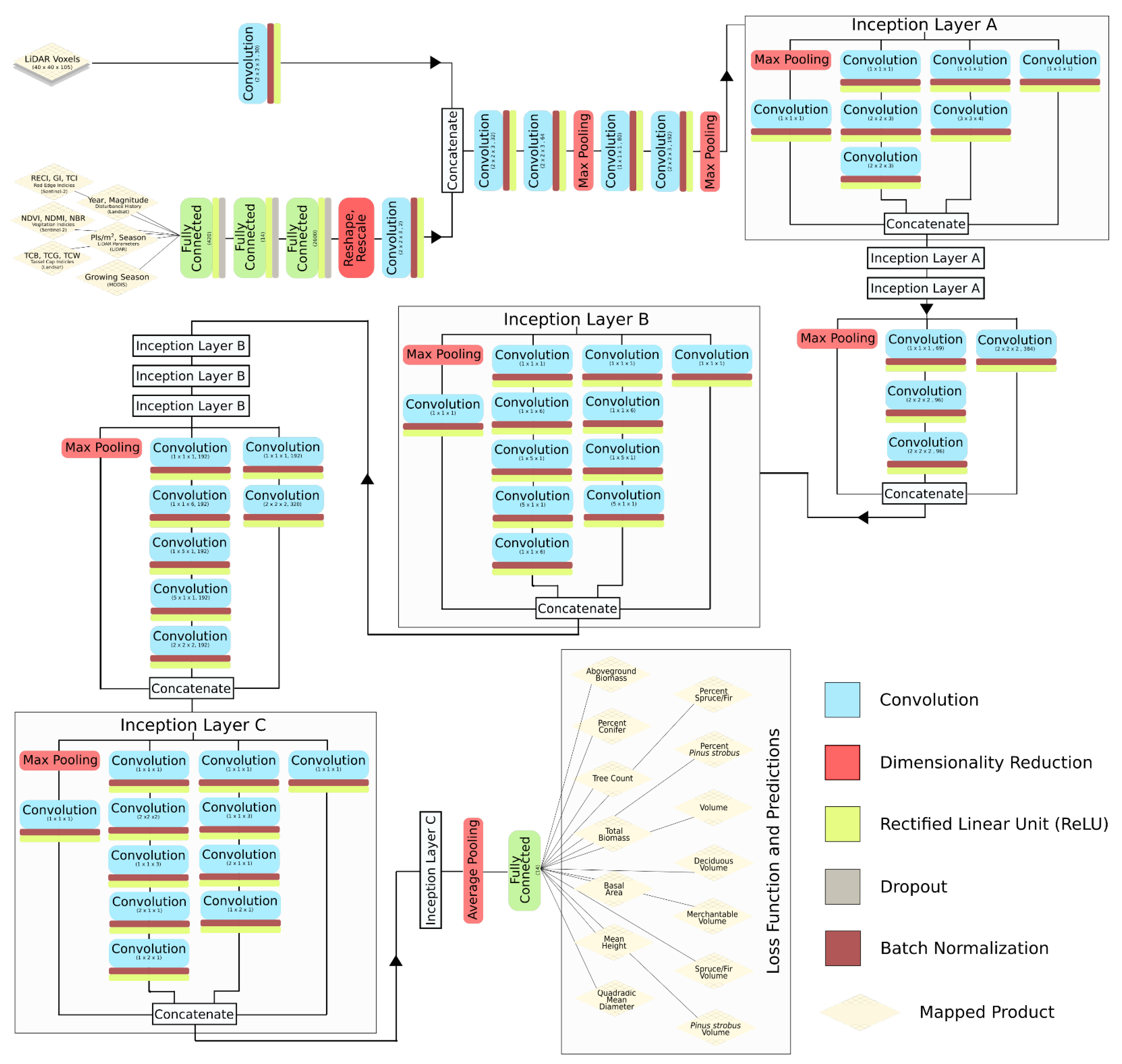
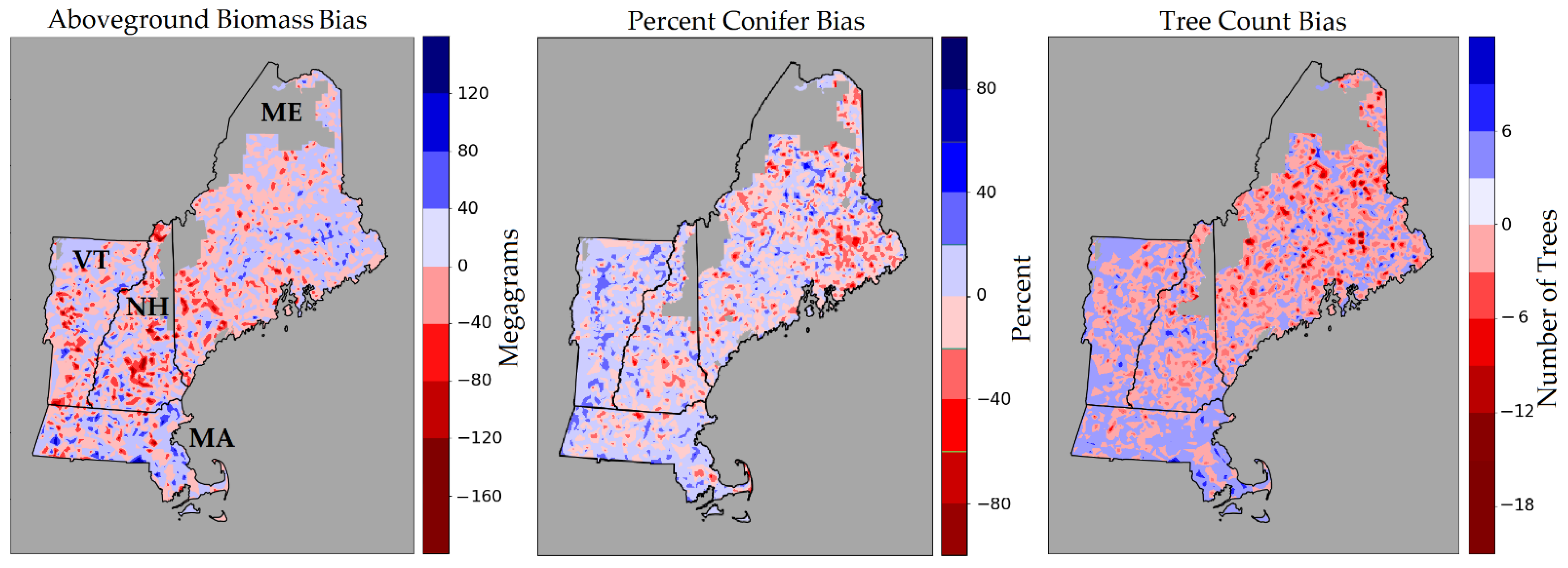
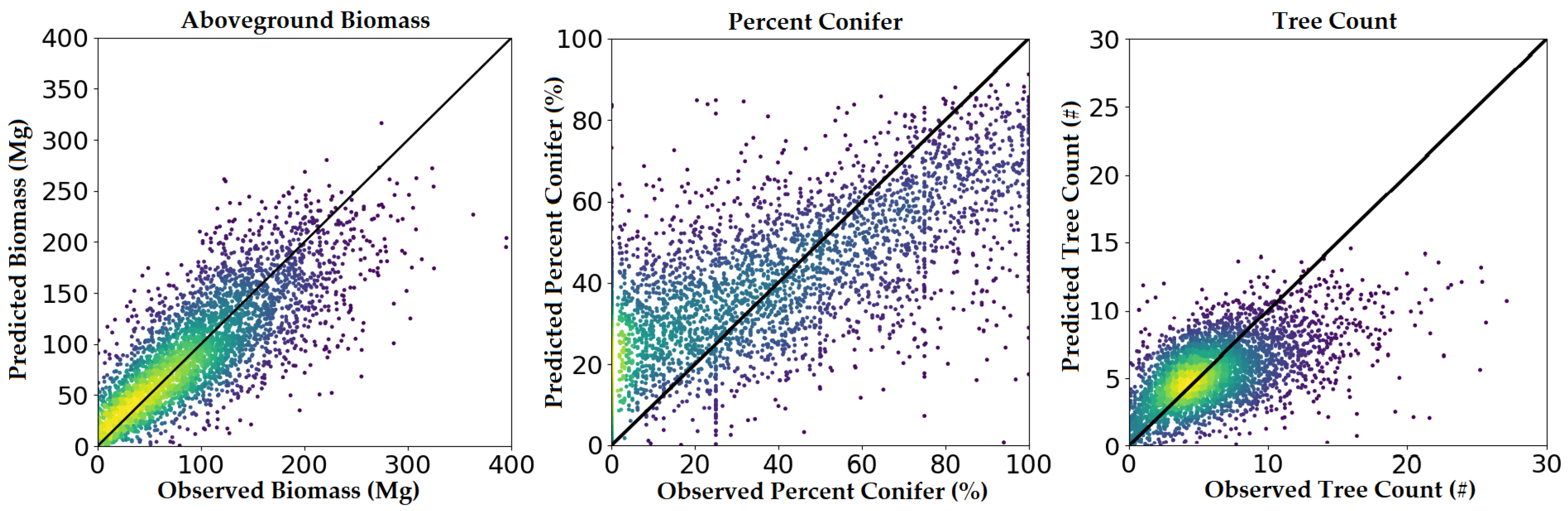


| Forest Attribute | Units | Description |
|---|---|---|
| Aboveground Biomass (AGB) | kg | Aboveground biomass as calculated by the USFS’s FIA component ratio method. |
| Total Biomass | kg | Total woody biomass as calculated by the USFS’s FIA component ratio method. |
| Basal Area | m2 | Basal area at breast height. |
| Mean Tree Height | m | Mean height of the trees’ apices. Not a measure of mean overall canopy height. |
| Quadratic Mean Diameter | cm | Quadratic mean of diameter at breast height. |
| Volume, Total | m3 | Total inner bark volume of each tree’s bole. |
| Volume, Merchantable | m3 | Total merchantable inner bark volume of each tree’s bole; starting at 10 cm above ground and ending at a height of 10 cm in diameter. |
| Tree Count (TC) | # | Total number of trees. |
| Percent conifer stems (PC) | % | Percentage of conifer stems. |
| Percent spruce-fir (Abies-Picea) | % | Percentage of spruce or fir species stems. |
| Percent Pinus strobus | % | Percentage of spruce or fir species stems. |
| Volume of deciduous | m3 | Total inner bark volume of deciduous tree boles. |
| Volume of spruce/fir (Abies-Picea) | m3 | Total inner bark volume of spruce or fir tree boles. |
| Volume of Pinus strobus | m3 | Total inner bark volume of white pine (Pinus strobus) tree boles. |
| Traditional Modeling | CNN without | CNN with | ||||
|---|---|---|---|---|---|---|
| with Satellite Metrics | Satellite Metrics | Satellite Metrics | ||||
| RMSE (%) | Bias (%) | RMSE (%) | Bias (%) | RMSE (%) | Bias (%) | |
| AGB * (Mg ha−1) | 48.5 29.4) | −1.2 | 34.5 (20.9) | 1.3 | 33.2 (20.1) | −1.5 |
| PC (%) | 13.3 – | −0.1 | 15.7 – | −2.3 | 14.2 – | −1.7 |
| TC (#) | 2.51 (37.2) | −0.01 | 2.10 (31.1) | −0.6 | 1.75 (26.1) | −0.03 |
| BIOTOT (Mg ha−1) | 58.2 (29.1) | 1.4 | 41.5 (20.8) | 1.2 | 40.0 (18.6) | −2.58 |
| BA (m−2) | 0.083 (24.5) | −0.001 | 0.065 (19.3) | −0.004 | 0.063 (20.0) | −0.009 |
| HT (m) | 2.6 (15.2) | 0.2 | 2.1 (12.0) | 0.6 | 1.5 (9.1) | −0.07 |
| QMD (cm) | 5.9 (23.9) | 0.14 | 4.3 (17.2) | 0.2 | 3.8 (15.3) | 0.1 |
| PSF % | 8.3 – | 0.1 | 10.8 – | −3.6 | 9.5 – | −0.2 |
| PWP % | 8.6 – | −0.1 | 6.7 – | 0.1 | 6.6 – | −0.3 |
| VOL (m−3) | 0.81 (27.5) | −0.019 | 0.580 (19.7) | −0.013 | 0.558 (18.9) | −0.022 |
| VOLM (m−3) | 0.751 (27.8) | −0.016 | 0.460 (20.1) | −0.012 | 0.524 (19.3) | −0.033 |
| VOLD (m−3) | 0.756 (60.6) | 0.002 | 0.460 (36.9) | −0.023 | 0.446 (35.8) | −0.017 |
| VOLSF (m−3) | 0.31 (91.4) | 0.007 | 0.227 (67.1) | 0.016 | 0.238 (70.2) | −0.017 |
| VOLWP (m−3) | 0.483 (94.2) | −0.016 | 0.388 (67.1) | −0.075 | 0.383 (74.6) | −0.039 |
| AGB * | PC | TC | BIOTOT | BA | HT | QMD | PSF | PWP | VOL | VOLM | VOLD | VOLSF | VOLWP | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Mg ha−1) | (%) | (#) | (Mg ha−1) | (m−2) | (m) | (cm) | (%) | (%) | (m−3) | (m−3) | (m−3) | (m−3) | (m−3) | |||
| Northern New England (MA, ME, NH, and VT) | FIA Plot- Level Assessment | RMSE | 36.9 | 19.2 | 3.0 | 44.5 | 0.08 | 3.3 | 5.2 | 17.0 | 13.2 | 0.625 | 0.578 | 0.416 | 0.298 | 0.454 |
| (%) | 46 | – | 57 | 46 | 45 | 30 | 31 | – | – | 46 | 48 | 58 | 123 | 235 | ||
| Bias | 1.18 | 1.89 | −0.541 | 2.26 | 0.03 | 1.35 | 0.38 | −1.96 | −4.25 | 0.069 | 0.094 | 0.006 | −0.035 | 0.034 | ||
| FIA Subplot- Level Assessment | RMSE | 57.0 | 25.6 | 4.67 | 68.6 | 0.12 | 4.4 | 7.7 | 21.8 | 15.0 | 0.994 | 0.922 | 0.622 | 0.389 | 0.587 | |
| (%) | 71 | – | 89 | 71 | 67 | 41 | 46 | – | – | 76 | 79 | 87 | 161 | 365 | ||
| Southern New England (CT and RI) | FIA Plot- Level Assessment | RMSE | 44.3 | 19.2 | 3.0 | 53.1 | 0.07 | 2.8 | 10.0 | 7.8 | 0.557 | 0.602 | 0.416 | 0.274 | 0.796 | 514 |
| (%) | 39 | – | 58 | 39 | 37 | 37 | 23 | – | – | 49 | 52 | 58 | 5326 | |||
| Bias | −3.46 | 1.89 | −0.54 | −3.42 | 0.013 | 1.33 | 4.4 | 0.48 | 0.235 | 0.09 | 0.006 | 0.114 | 0.231 |
| State | County | FIA AGB | CNN AGB | FIA PC | CNN PC | FIA TC | CNN TC |
|---|---|---|---|---|---|---|---|
| (Petagrams) | (Petagrams) | (%) | (%) | (Millions) | (Millions) | ||
| Maine | Cumberland | 18.8 | 26.7 | 89.8 | |||
| Maine | Hancock | 29.6 | 43.3 | 244.2 | |||
| Maine | Kennebec | 16.7 | 28.9 | 92.9 | |||
| Maine | Knox | 5.5 | 30.7 | 35.1 | |||
| Maine | Lincoln | 8.3 | 32.4 | 48.6 | |||
| Maine | Penobscot | 56.2 | 43.3 | 452.1 | |||
| Maine | Piscataquis | 61.1 | 46.3 | 528.0 | |||
| Maine | Sagadahoc | 5.18 | 33.5 | 29.7 | |||
| Maine | Waldo | 11.3 | 33.9 | 71.1 | |||
| Maine | Washington | 43.1 | 46.5 | 404.3 | |||
| Maine | York | 22.3 | 27.5 | 105.1 | |||
| Massachusetts | Barnstable | 4.4 | 24.0 | 41.3 | |||
| Massachusetts | Berkshire | 32.6 | 28.7 | 126.3 | |||
| Massachusetts | Bristol | 11.9 | 23.9 | 56.4 | |||
| Massachusetts | Dukes | 0.85 | 18.9 | 8.7 | |||
| Massachusetts | Essex | 11.2 | 18.4 | 39.3 | |||
| Massachusetts | Franklin | 27.3 | 30.0 | 93.1 | |||
| Massachusetts | Middlesex | 17.7 | 21.6 | 65.82 | |||
| Massachusetts | Nantucket | 0.1 | 0.0 | 7.0 | 0.8 | ||
| Massachusetts | Norfolk | 7.9 | 21.8 | 33.7 | |||
| Massachusetts | Plymouth | 14.4 | 27.2 | 67.3 | |||
| Massachusetts | Suffolk | NO PLOTS | 0.3 | NO PLOTS | 10.7 | NO PLOTS | 2.1 |
| Massachusetts | Worcester | 41.2 | 24.0 | 154.4 | |||
| New Hampshire | Belknap | 11.1 | 25.5 | 45.4 | |||
| New Hampshire | Cheshire | 25.6 | 31.8 | 98.3 | |||
| New Hampshire | Hillsborough | 23.5 | 27.3 | 92.3 | |||
| New Hampshire | Merrimack | 24.6 | 27.7 | 99.8 | |||
| New Hampshire | Rockingham | 17.9 | 22.3 | 72.7 | |||
| New Hampshire | Strafford | 9.8 | 27.5 | 42.4 | |||
| New Hampshire | Sullivan | 17.0 | 33.6 | 72.3 | |||
| Vermont | Caledonia | 14.8 | 33.1 | 76.0 | |||
| Vermont | Essex | 14.0 | 39.5 | 93.0 | |||
| Vermont | Lamoille | 12.4 | 35.6 | 62.4 | |||
| Vermont | Orange | 19.2 | 30.8 | 79.2 | |||
| Vermont | Rutland | 25.7 | 26.7 | 110.8 | |||
| Vermont | Washington | 19.6 | 33.6 | 91.0 | |||
| Vermont | Windham | 27.6 | 33.1 | 103.7 | |||
| Vermont | Windsor | 30.9 | 30.0 | 117.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayrey, E.; Hayes, D.J.; Kilbride, J.B.; Fraver, S.; Kershaw, J.A., Jr.; Cook, B.D.; Weiskittel, A.R. Synthesizing Disparate LiDAR and Satellite Datasets through Deep Learning to Generate Wall-to-Wall Regional Inventories for the Complex, Mixed-Species Forests of the Eastern United States. Remote Sens. 2021, 13, 5113. https://doi.org/10.3390/rs13245113
Ayrey E, Hayes DJ, Kilbride JB, Fraver S, Kershaw JA Jr., Cook BD, Weiskittel AR. Synthesizing Disparate LiDAR and Satellite Datasets through Deep Learning to Generate Wall-to-Wall Regional Inventories for the Complex, Mixed-Species Forests of the Eastern United States. Remote Sensing. 2021; 13(24):5113. https://doi.org/10.3390/rs13245113
Chicago/Turabian StyleAyrey, Elias, Daniel J. Hayes, John B. Kilbride, Shawn Fraver, John A. Kershaw, Jr., Bruce D. Cook, and Aaron R. Weiskittel. 2021. "Synthesizing Disparate LiDAR and Satellite Datasets through Deep Learning to Generate Wall-to-Wall Regional Inventories for the Complex, Mixed-Species Forests of the Eastern United States" Remote Sensing 13, no. 24: 5113. https://doi.org/10.3390/rs13245113
APA StyleAyrey, E., Hayes, D. J., Kilbride, J. B., Fraver, S., Kershaw, J. A., Jr., Cook, B. D., & Weiskittel, A. R. (2021). Synthesizing Disparate LiDAR and Satellite Datasets through Deep Learning to Generate Wall-to-Wall Regional Inventories for the Complex, Mixed-Species Forests of the Eastern United States. Remote Sensing, 13(24), 5113. https://doi.org/10.3390/rs13245113






