Revisited Estimation of Moderate Resolution Sargassum Fractional Coverage Using Decametric Satellite Data (S2-MSI)

Abstract

Since 2011, massive stranding of the brown algae Sargassum has regularly affected the coastal waters of the West Caribbean, Brazil and West Africa, leading to significant environmental and socio-economic impacts. The AFAI algal index (Alternative Floating Algae Index) is often used with remote sensing data in order to estimate the Sargassum coverage, and more precisely the AFAI deviation, which consists of the difference between AFAI and AFAI of the Sargassum-free background. In this study, the AFAI deviation is computed using NASA’s 1 km Terra/MODIS (Moderate-Resolution Imaging Spectroradiometer) and ESA/Copernicus’s 20 m Sentinel-2/MSI (Multi Spectral Instrument) for the same sites and at the same time. Both MODIS and MSI AFAI deviations are compared to confirm the relevance of AFAI deviation technique for two very different spatial resolutions. A high coefficient of determination was found, thus confirming a satisfactory downsampling from 20 m (MSI) to 1 km (MODIS). Then, AFAI deviations are used to estimate the fractional coverage of Sargassum (noted FC). A new linear relationship between the MODIS AFAI deviation and FC is established using the dense Sargassum aggregations observed by MSI data. The AFAI deviation is proportional to FC with a factor of proportionality close to 0.08. Finally, it is shown that the factor is dependent on the Sargassum spectral reflectance, submersion or physiological state.

1. Introduction

Since 2011, unprecedented massive stranding of the brown floating macro-algae Sargassum has been observed along the coastline of French Guyana, the Antilles Islands and the Caribbean Sea. Sargassum algal patterns look like large aggregations transported by currents over long distances across the Atlantic Ocean. Satellite data are thus highly suitable to monitor Sargassum spatial distribution. A first spectral index was defined in 2006 using ESA/Copernicus’s Envisat/MERIS (Medium Resolution Imaging Spectrometer) satellite sensor (300 m resolution), the so-called Maximum Chlorophyll Index (MCI), which is based on the water leaving radiance peak induced by Sargassum optical signature at 709 nm [1,2]. It has been shown that this peak reveals the presence of a high concentration of chlorophyll a at the surface, hence allowing the detection of extensive areas of pelagic vegetation (Sargassum spp.) [2]). The MCI index was used to determine the spatial distribution of Sargassum aggregations in the Gulf of Mexico and in the western Atlantic waters [3,4]. Following the MERIS era, ESA/Copernicus’s Sentinel-3/OLCI (Ocean and Land Colour Instrument) was launched on board Sentinel-3 in 2016. OLCI was designed to provide similar spatial resolution and spectral bands to MERIS, thus ensuring a continuity in the satellite data sets for Sargassum detection purposes [5].

Hu [6] proposed a Floating Algae Index (FAI) using data acquired by NASA’s Terra/MODIS (Moderate-Resolution Imaging Spectroradiometer) and Aqua/MODIS sensors to detect and trace blooms of Ulva prolifera macroalgae species in the Yellow Sea near Qingdao, China ([7,8]). Because FAI was defined using the vegetation red-edge reflectance, observable between 675 and 750 nm, it could be used to detect any floating vegetation including Sargassum [9]. However, because there was no effective cloud-masking method for FAI, both Sargassum and clouds showed high FAI values. To overcome this difficulty, Wang and Hu [10] defined the Alternative Floating Algae Index (AFAI) using data measured at relevant spectral bands such as 667 nm, 748 nm and 869 nm, which are less sensitive to the cloud contamination than the FAI.

Highly spatially resolved sensors such as ESA/Copernicus’s Sentinel-2/MSI (Multi Spectral Instrument), offering a typical spatial resolution between 10 m and 60 m, can also be relevant to detect Sargassum species. Ody et al. [11] recently defined the Modified Floating Algae Index (MFAI) by adjusting the AFAI index to the MSI spectral features using the bands at 665 nm, 833 nm and 940 nm.

In addition to Sargassum species detection, algae indices are required to quantify their fractional coverage, noted FC, within a pixel and ultimately the resulting biomass per unit area. The fractional coverage was defined in Wang and Hu [10] as the proportion of a pixel area occupied by “pure” Sargassum mats representative of their study area. Wang and Hu [10] proposed a linear relationship between the fraction of pixels covered by Sargassum species and the AFAI. To estimate the AFAI value for a pixel covered by 100% of Sargassum species, they used the average spectrum of in situ measurements of Sargassum mats combined with radiative transfer simulations. Wang et al. [12] extended that approach to estimate biomass amount using field measurements.

This study focuses on the methodological aspects for improving the detection of Sargassum presence and coverage over oceanic waters. The first objective of the current study is to verify that Sargassum could be accurately detected with MODIS and confirm the relevance of the AFAI for various spatial scales, namely between 1 km resolution (MODIS) and 20 m resolution (MSI), using data from both satellite sensors acquired at the same location and at the same time. Note that high resolution data are required to further investigate the influence of Sargassum on coastal ecosystems (e.g., stranding, invasion). A new relationship between the AFAI deviation and the Sargassum fractional coverage FC is then proposed based on satellite observations of large Sargassum aggregations using MSI sensors and using radiative transfer simulations. Finally, this study not only investigates floating algae coverage but provides insights on the influence of the Sargassum reflectance spectrum and the Sargassum submersion using an original adaptation of a radiative transfer model.

The paper is organized as follows. The study areas, the data and the methodology are outlined in Section 2. The feasibility of downsampling the detection of Sargassum from higher to lower satellite sensor spatial resolution is examined in Section 3 based on the comparison between AFAI derived from MODIS and MSI sensors. The consistency between AFAI and the fractional coverage is also studied in Section 3. The influence of various parameters (such as Sargassum immersion depth, Sargassum physiological state and water turbidity) on the relationship between AFAI and FC is discussed in Section 4.

2. Materials and Methods

2.1. Study Area

Various study areas in the Atlantic Ocean containing a significant coverage of Sargassum were selected from the Caribbean to the Ivory Coast (Africa) (Figure 1). The three sites of study show a bathymetry higher than 2000 m such that the seabed has no influence on the sea surface reflectance.

2.2. Satellite Data

Sentinel-2 is an Earth observation mission from the Copernicus European Program [13] that acquires optical imagery at high spatial resolutions (10 m, 20 m and 60 m) over land and coastal waters. The mission is characterized by a constellation of two twin satellites, Sentinel-2A and Sentinel-2B, which were launched by the European Space Agency (ESA) in 2015 and 2017, both carrying the MSI. The spatial resolution used in this study is 20 m. MSI acquires multi-spectral data for 13 bands in the visible, near infrared, and short-wave infrared parts of the spectrum.

Table 1. Band number, central wavelength, bandwidth and spatial resolution of MODIS [15] and MSI [16]. In bold the triplet that will be used for the AFAI calculation.

Sensor	Band Number	Central Wavelength (nm)	Bandwidth (nm)	Spatial Resolution (m)
MODIS	8	412	15	1000
	9	443	10	1000
	2	469	20	500
	10	488	10	1000
	11	531	10	1000
	12	551	10	1000
	4	555	20	500
	1	645	50	250
	13	667	10	1000
	14	678	10	1000
	15	748	10	1000
	2	859	35	250
	16	869	15	1000
	17	905	30	1000
	18	936	10	1000
	19	940	50	1000
MSI	1	443	20	60
	2	490	65	10
	2	560	35	10
	4	665	30	10
	5	705	15	20
	6	740	15	20
	7	783	20	20
	8	842	115	10
	8a	865	20	20
	9	945	20	60
	10	1375	30	60
	11	1610	90	20
	12	2190	180	20

provides the spectral bands and their spatial resolution in the [400–1000 nm] spectral range. The revisit period is 5 days under the same viewing angles. Both MSI instruments (on S2A and S2B) fly 180-degrees apart on the same orbit to optimize the revisit rate and the overall coverage.

MODIS is an imaging sensor that was launched by NASA in 1999 on board the Terra satellite, and in 2002 on board the Aqua satellite [14]. Each instrument acquires data at various spatial resolutions (2 bands at 250 m, 5 bands at 500 m and 29 bands at 1 km) for a total number of 36 spectral bands ranging from 0.4 to 14.4 μm. Table 1 provides the spectral bands and their spatial resolution. The MODIS spatial resolution used in this study is 1 km. Each instrument allows the entire Earth coverage every 1 to 2 days, a few hours apart from each other. Here, only the spectral bands at 667 nm, 748 nm and 869 nm of MODIS are required to calculate the AFAI.

The sole Terra platform is used for the comparison with Sentinel-2 observations because both platforms have the same overpass time, namely 10:30 a.m. local time at the equator, which is not the case for Aqua platform. The MODIS and Sentinel-2 acquisitions are concomitant within 50 min depending on the geographic location and the date (for our case the maximum time offset is 35 min). This time lag between the overpass of MODIS and MSI is not a critical issue for the purpose of investigating the feasibility of downsampling the detection of Sargassum from remotely sensed data. Indeed the potential drift of the Sargassum over 35 min is weak, typically lower than 1–2 km [17], owing to the low speed the Sargassum transport (i.e., lower than 1 m.s⁻¹). This transport distance is not significant in relation to the size of the study areas (50 to 150 km).

Table 2. Date of acquisition of MODIS and MSI satellite data used over each study area. Terra is the MODIS platform. Sentinel-2 platforms “A” and “B” are designated as S2A and S2B, respectively.

#	Study Area	Date of Acquisition	MODIS/Time (UTC)	MSI/Time (UTC)
1	Guadeloupe (Caribbean)	21 June 2018	Terra/14:35	S2B/14:47
2	Gulf of Guinea (Africa)	20 October 2018	Terra/11:15	S2B/10:40
3	Grenadines (Caribbean)	29 January 2019	Terra/14:50	S2A/14:37

reports the dates of satellite data acquisition over the study areas.

2.3. Data Preprocessing

2.3.1. Processing of MODIS Data for Deriving 1 km AFAI

This section is organized as follows: first the computation of AFAI is described; then the methodology used to determine the AFAI background and the AFAI deviation is detailed; finally, the Sargassum detection process is explained.

Level-1B MODIS data (i.e., top-of-the-atmosphere radiance) were obtained from NASA [14] and used to compute the AFAI following Wang and Hu’s method [10] (Equations (1) and (2)):

$$\mathrm{AFAI}=\mathrm{R}\left({\mathsf{\lambda }}_2\right)-\mathrm{R}\left({\mathsf{\lambda }}_1\right)-\left[\mathrm{R}\left({\mathsf{\lambda }}_3\right)-\mathrm{R}\left({\mathsf{\lambda }}_2\right)\right])\times \frac{{\mathsf{\lambda }}_2-{\mathsf{\lambda }}_1}{{\mathsf{\lambda }}_3-{\mathsf{\lambda }}_1}$$

(1)

Equation (1) can be re-written as follows (Equation (2)):

$$\mathrm{AFAI}=\mathrm{R}\left({\mathsf{\lambda }}_2\right)-\left(1-\mathrm{C}\right)\ast \mathrm{R}\left({\mathsf{\lambda }}_1\right)-\mathrm{C}\times \mathrm{R}\left({\mathsf{\lambda }}_3\right)$$

(2)

where $\mathrm{C}=\frac{{\mathsf{\lambda }}_2-{\mathsf{\lambda }}_1}{{\mathsf{\lambda }}_3-{\mathsf{\lambda }}_1}$and where λ₁ = 667 nm, λ₂ = 748 nm and λ₃ = 869 nm. R(λ) is the normalized reflectance above the sea surface derived from MODIS observations. The top-of-the-atmosphere radiance was corrected for molecular (Rayleigh) scattering and gaseous absorption using NASA’s Ocean Color Science Software (OCSSW-SeaDAS) package to derive R(λ). The correction of the top-of-the-atmosphere radiance for the aerosol effects was not performed because the aerosol correction procedure relies on black pixel assumptions that do not hold in presence of Sargassum, which thus could lead to overestimate the atmospheric contribution. Clouds were masked using the OCSSW mask (standard product from SeaDAS), which relies on the spectral band at 2130 nm and a threshold value of 0.030. Additional screening for clouds, sunglint and cloud shadows was performed following Wang and Hu [10].

Because AFAI is sensitive to various factors other than the presence of Sargassum, such as the water (i.e., Sargassum-free) spectral reflectance, the potential residual sunglint contamination and the presence of aerosols, the detection of Sargassum occurrence cannot just be determined using a constant threshold value on AFAI. Instead, the deviation of AFAI with respect to the surrounding Sargassum-free water (this surrounding is called the background) is examined. The AFAI background (${\mathrm{AFAI}}_{\mathrm{bg}}$) can be represented as a sum of three components:

$${\mathrm{AFAI}}_{\mathrm{bg}}={\mathrm{AFAI}}_0+{\mathrm{dAFAI}}_{\mathrm{w}}+{\mathrm{dAFAI}}_{\mathrm{geom}}$$

(3)

where ${\mathrm{AFAI}}_0$ retains the large-scale variation of AFAI (including potential residual atmospheric effects), ${\mathrm{dAFAI}}_{\mathrm{w}}$ is the local deviation of ${\mathrm{AFAI}}_{\mathrm{bg}}$ from ${\mathrm{AFAI}}_0$ due to small-scale variation of Sargassum-free ocean reflectance, and ${\mathrm{dAFAI}}_{\mathrm{geom}}$ is the deviation induced by the local variation of viewing geometry within a scan. Indeed, since each MODIS scan footprint is 10 km wide along-track (i.e., ten detectors having each a 1 km footprint), a detector-to-detector variability can be observed across the along-track angular aperture (ca. 0.8 degree) of the scan. As a result, scan-to-scan discontinuities appear over non-lambertian surfaces (e.g., water contaminated by sunglint signal) and leads to generate a 10 km cross-track striping effect in the MODIS observations.

While Wang and Hu [10] used a four-degree polynomial surface-fitting technique to determine ${\mathrm{AFAI}}_0$, we found that a median filter characterized by a 401 × 401 window (i.e., ~400 × 400 km at the center of the MODIS swath) was more robust when the ocean pixels remaining after the screening process are sparsely or unevenly distributed across the MODIS field-of-view; this median filter is able to provide artifact-free results. In addition, the median filter was applied to the AFAI image in the MODIS viewing geometry using a 10-row step along-track, which allows capturing ${\mathrm{dAFAI}}_{\mathrm{geom}}$. Practically, the median filtering yields ${\mathrm{AFAI}}_0+{\mathrm{dAFAI}}_{\mathrm{geom}}$. Following Wang and Hu [10], the pixels showing $\mathrm{AFAI}-\left({\mathrm{AFAI}}_0+{\mathrm{dAFAI}}_{\mathrm{geom}}\right)$greater than a threshold value ${\mathrm{T}}_{\mathrm{S}}$= 2.55 × 10⁻⁴ were considered as likely to contain Sargassum; those pixels were thus discarded from the background estimation. Because small-scale natural variability is expected in the remaining observations, including the variability induced by residual Sargassum contamination, a subsequent small-scale median filtering is applied to the expression $\mathrm{AFAI}-\left({\mathrm{AFAI}}_0+{\mathrm{dAFAI}}_{\mathrm{geom}}\right)$, using a 51 × 51 window (i.e., ~50 × 50 km at the center of the swath) to determine the ${\mathrm{dAFAI}}_{\mathrm{w}}$ component, yielding to an estimate of ${\mathrm{AFAI}}_{\mathrm{bg}}$ for all valid observations. Expectedly, the presence of Sargassum is the main cause for a positive deviation of AFAI from ${\mathrm{AFAI}}_{\mathrm{bg}}$. All pixels showing an AFAI deviation $\mathsf{\delta }\mathrm{AFAI}=\mathrm{AFAI}-{\mathrm{AFAI}}_{\mathrm{bg}}$ greater than a threshold value ${\mathrm{T}}_0$of 1.79 × 10⁻⁴ are identified as pixels containing Sargassum. That threshold was determined by Wang and Hu [10] using several MODIS $\mathsf{\delta }\mathrm{AFAI}$ histograms and manual validation. Such a threshold allows 95% of the Sargassum containing pixels to be captured.

2.3.2. Processing of MSI Data for Deriving 20 m AFAI

Several triplets of spectral bands were tested to generate FAI or AFAI using MSI sensor, namely the triplets (665 nm, 740 nm, 842 nm), (665 nm, 842 nm, 1610 nm), (665 nm, 865 nm, 1610 nm) and (665 nm, 740 nm, 865 nm). Since the MSI instrument is affected by a camera striping effect due to a difference of observation geometries across the instrument detectors, each band triplet leads to an index (FAI or AFAI) that is altered by that striping effect in a different way. The last band triplet, namely [665 nm, 740 nm, 865 nm], was finally adopted for this study because the derived AFAI was found to be the least sensitive to the striping effect (

Table 3. Tested triplets of MSI spectral bands and the impact of the striping (“+” means low striping and “++” means high striping).

Central Wavelength (nm)	665	740	842	865	1610	Impact of Striping
1st triplet	X	X	X			++
2nd triplet	X		X		X	++
3rd triplet	X			X	X	++
4th triplet	X	X		X		+

).

The MSI data processing was performed for the spatial resolution value of 20 m since it is the highest spatial resolution that is common to all the spectral bands composing the adopted triplet. The 665 nm spectral band was downsampled to 20 m resolution averaging over 2 × 2 pixel blocks. The MSI top-of-the-atmosphere reflectance provided by Copernicus Open Access Hub [13] was first corrected for both the Rayleigh scattering reflectance and the sunglint reflectance using the POLYMER algorithm [18]; the sunglint reflectance was estimated based on the wind speed provided by the ERA5 reanalysis dataset from ECMWF. The AFAI was then derived. Following the procedure applied for MODIS, the AFAI background was estimated using a local median filter applied for a window of 500 × 500 pixels (10 km). The AFAI background was subtracted from raw AFAI values to provide the AFAI deviation $\mathsf{\delta }\mathrm{AFAI}$. This step was carried out for both MODIS and MSI data (Figure 2).

2.4. Methodology

One transect (AB) of δAFAI was defined for the site #1 in MODIS (Figure 3a) and MSI (Figure 3b) images. Figure 3c shows the MODIS/δAFAI and MSI/δAFAI values along this transect. It is observed that each MODIS pixel containing Sargassum is highly heterogeneous, composed of a mix of Sargassum aggregations and Sargassum-free water. Even the largest aggregations hardly cover an entire MODIS pixel. On the contrary, MSI captures large aggregations with high δAFAI values that cover several contiguous pixels and sharply contrast from the background. That indicates that MSI is able to capture homogeneous pixels entirely covered with “pure” Sargassum.

In this study, the values of MSI/δAFAI pixels are re-projected and averaged for the closest MODIS/δAFAI pixels to perform a pixel-by-pixel comparison of the values of δAFAI provided by each sensor. δAFAI derived for MODIS and MSI are then compared. Given the high scatter of the observations, the confidence interval for slopes of the regression line was computed for each site using a bootstrap technique (N = 1000).

2.4.1. Relationship between δAFAI and Fractional Coverage

The above-surface reflectance $\mathrm{R}\left(\mathsf{\lambda }\right)$ of a given MODIS pixel containing Sargassum can be modeled as the sum of one Sargassum component and one Sargassum-free component (Equation (4)):

$$\mathrm{R}\left(\mathsf{\lambda }\right)=\mathrm{FC}\times {\mathrm{R}}_{\mathrm{sarg}}\left(\mathsf{\lambda }\right)+\left(1-\mathrm{FC}\right)\times {\mathrm{R}}_{\mathrm{w}}\left(\mathsf{\lambda }\right)$$

(4)

where ${\mathrm{R}}_{\mathrm{sarg}}$ is the Sargassum reflectance, ${\mathrm{R}}_{\mathrm{w}}$ is the water reflectance of the Sargassum-free fraction and FC is the Sargassum fractional coverage within the pixel. Note that ${\mathrm{R}}_{\mathrm{sarg}}$ is directly related to the Sargassum intrinsic reflectance, to its degree of dispersion and to its submersion in the ocean surface layer.

Based on Equations (2) and (4), ${\mathrm{AFAI}}_{\mathrm{bg}}$ can be written as a function of ${\mathrm{R}}_{\mathrm{w}}$ as follows (Equation (5)):

$${\mathrm{AFAI}}_{\mathrm{bg}}={\mathrm{R}}_{\mathrm{w}}\left({\mathsf{\lambda }}_2\right)-\left(1-\mathrm{C}\right)\times {\mathrm{R}}_{\mathrm{w}}\left({\mathsf{\lambda }}_1\right)-\mathrm{C}\times {\mathrm{R}}_{\mathrm{w}}\left({\mathsf{\lambda }}_3\right)$$

(5)

where C was defined in Equation (2).

The deviation of AFAI from the background can be established as proportional to the Sargassum fractional coverage FC (Equation (6)):

$$\mathsf{\delta }\mathrm{AFAI}\left(\mathrm{FC}\right)=\mathrm{K}\times \mathrm{FC}$$

(6)

K is the coefficient of proportionality between $\mathsf{\delta }\mathrm{AFAI}$ and FC and can be analytically calculated using Equation (7).

$$\mathrm{K}={\mathrm{R}}_{\mathrm{sarg}}\left({\mathsf{\lambda }}_2\right)-{\mathrm{R}}_{\mathrm{w}}\left({\mathsf{\lambda }}_2\right)-\left(1-\mathrm{C}\right)\times \left[{\mathrm{R}}_{\mathrm{sarg}}\left({\mathsf{\lambda }}_1\right)-{\mathrm{R}}_{\mathrm{w}}\left({\mathsf{\lambda }}_1\right)\right]-\mathrm{C}\times \left[{\mathrm{R}}_{\mathrm{sarg}}\left({\mathsf{\lambda }}_3\right)-{\mathrm{R}}_{\mathrm{w}}\left({\mathsf{\lambda }}_3\right)\right]$$

(7)

The slope K only depends on the local deviation of Sargassum reflectance from ocean Sargassum-free water reflectance.

The theoretical value of the slope K can be calculated from simulations (Section 2.4.3) using different intrinsic Sargassum reflectance spectra, for various FC values and by calculating the AFAI deviation from the above surface reflectance. For this calculation, “pure” Sargassum reflectance as measured by Ody et al. [11] at 0.01 m depth based on a mesocosm acquisition system was used (Figure 4). These two spectra exhibit an increase in reflectance in the green region (550 nm) and a strong increase in the reflectance around 700 nm corresponding to the red edge characteristic of the vegetation reflectance spectrum.

The value of the slope K of the linear relationship between $\mathsf{\delta }\mathrm{AFAI}$ and FC (Equation (6)) can also be empirically estimated from MSI images by focusing the analysis of the data on the dense Sargassum aggregation pixels. This is because K is the AFAI deviation value δAFAI of a “pure” Sargassum pixel (FC = 1), i.e., with no contribution from Sargassum-free water to the upward radiation. Such a pixel is unlikely to be found in natural conditions since processes such as dispersion (or at least expansion) and submersion of Sargassum could occur. However, one can assume that large dense aggregations contain a few pixels where the Sargassum mat is sufficiently dense, thick, and close to the surface to make the Sargassum-free water contribution negligible relative to that of the sole Sargassum component; thus, FC can be considered very close to 1 for such conditions. The distribution of δAFAI values observed across such a Sargassum aggregation varies from 0 (FC = 0) to K (FC = 1). This assumption is particularly reliable when dealing with MSI high spatial resolution. Therefore, K can be empirically estimated by determining the maximum value of the MSI/δAFAI distribution over the Sargassum aggregations. A kernel density estimation technique was used to smooth the observed distributions using a bandwidth equal to the standard deviation of δAFAI in the aggregation. The δAFAI value corresponding to the 99th percentile of the distribution was defined as the maximum value, yielding an approximation for K.

2.4.2. Flowchart of the Overall Methodology

The flow chart of the overall methodology used in this study is shown in Figure 5.

2.4.3. Radiative Transfer Model Taking into Account the Immersion Depth and the Fractional Coverage of Sargassum Aggregations

Radiative transfer simulations were carried out to investigate the influence of Sargassum aggregations that are located at a given depth in the water column, so-called immersion depth, on the above water reflectance. The immersion depth can be interpreted as an average depth over the ensemble of Sargassum fragments present in an aggregation. It should be highlighted that the influence of submersed Sargassum on the above water reflectance has not been studied to our knowledge since only floating algae were investigated by previous studies (Section 1). The fractional coverage FC of Sargassum aggregations located in the water column and the immersion depth are used as input parameters of the simulations. The semi-analytical formulation of the radiative transfer equation proposed by Lee et al. [19] was used for that purpose. Lee’s model simulates the sea surface reflectance using the water column bio-optical parameters, the depth and the seabed composition as inputs. The water bio-optical parameters consist of the chlorophyll concentration (chl), the Non-Algal Particles (NAP) concentration, and the Colored Dissolved Organic Matter (CDOM) absorption coefficient. Such parameters enable to determine the Inherent Optical Properties that include the absorption a(λ) and backscattering b_b(λ) coefficients, which are required to compute the deep-water reflectance ${\mathrm{r}}_{\mathrm{rs}}^{\mathrm{dp}}\left(\mathsf{\lambda }\right)$. The model also takes into account the seabed reflectance (${\mathrm{R}}_{\mathrm{b}}(\mathsf{\lambda }\left)\right)$ and the depth of the seabed (z), the z-axis convention is defined as positive in downward direction.

As mentioned in Equation (4), the surface reflectance is a linear combination of water reflectance and Sargassum reflectance. This decomposition is based on the assumption that Sargassum are located at the sea surface level. However, Sargassum aggregations can also be covered by a layer of water, at a given immersion depth. To examine the influence of Sargassum aggregation depth on the reflectance above the surface$\mathrm{R}\left(\mathsf{\lambda }\right)$, an infinite seabed depth is considered as input of the Lee’s model while Sargassum aggregations are modeled as an opaque layer located at a given immersion depth (z) (Figure 6). For such a configuration, the opaque Sargassum layer could be optically considered as a seafloor exclusively composed by Sargassum. The Sargassum in-depth aggregation is thus characterized by its fractional coverage FC = S₁/S₂ where S₁ is the projected area covered by the Sargassum aggregation and S₂ is the total surface of a given pixel. The seabed reflectance ${\mathrm{R}}_{\mathrm{b}}(\mathsf{\lambda })$ of Lee’s model is then replaced by the composite reflectance of the submersed Sargassum aggregation noted R_c$(\mathsf{\lambda })$ (Equation (8)):

$${\mathrm{R}}_{\mathrm{c}}(\mathsf{\lambda })=\mathrm{FC}\times {\mathrm{R}}_{\mathrm{sarg}}\left(\mathsf{\lambda }\right)+\left(1-\mathrm{FC}\right)\times {\mathrm{R}}_{\mathrm{w}}\left(\mathsf{\lambda }\right)$$

(8)

The Sargassum-free water column reflectance induced by the optical layer between the sea surface and the Sargassum aggregation depth, noted r_rsW and the reflectance induced by the Sargassum aggregation located at depth z, noted r_rsC, could be expressed through Equations (9) and (10), respectively:

$${\mathrm{r}}_{\mathrm{rs}}\mathrm{W}\left(0^{-},\mathsf{\lambda }\right)={\mathrm{r}}_{\mathrm{rs}}^{\mathrm{dp}}\left(\mathsf{\lambda }\right)\left(1-{\mathrm{e}}^{-\left(\frac{1}{\cos \left({\mathsf{\theta }}_{\mathrm{w}}\right)}+\frac{{\mathrm{D}}_{\mathrm{u}}^{\mathrm{W}}\left(\mathsf{\lambda }\right)}{\cos \left({\mathsf{\theta }}_{\mathrm{v}}\right)}\right){\mathrm{K}}_{\mathrm{d}}\left(\mathsf{\lambda }\right)\mathrm{z}}\right)$$

(9)

$${\mathrm{r}}_{\mathrm{rs}}\mathrm{C}(0^{-},\mathsf{\lambda })=\frac{1}{\mathsf{\pi }}{\mathrm{R}}_{\mathrm{c}}\left(\mathsf{\lambda }\right).{\mathrm{e}}^{-\left(\frac{1}{\cos \left({\mathsf{\theta }}_{\mathrm{w}}\right)}+\frac{{\mathrm{D}}_{\mathrm{u}}^{\mathrm{C}}\left(\mathsf{\lambda }\right)}{\cos \left({\mathsf{\theta }}_{\mathrm{v}}\right)}\right){\mathrm{K}}_{\mathrm{d}}\left(\mathsf{\lambda }\right)\mathrm{z}}$$

(10)

where θ_w and θ_v are the in-water solar zenith angle and viewing zenith angle, respectively, K_d is the diffuse attenuation coefficient, ${\mathrm{r}}_{\mathrm{rs}}^{\mathrm{dp}}$ the deep water reflectance under the sea surface$,$Du^W and Du^C are the optical path-elongation factors for photons scattered, respectively by the water column and by the composite Sargassum aggregation [19]. The remote sensing reflectance just beneath the sea surface, r_rs(0⁻$,\mathsf{\lambda }$) is the sum of the water column and the composite components (Equation (11)).

$${\mathrm{r}}_{\mathrm{r}\mathrm{s}}\left(0^{-},\mathsf{\lambda }\right)={\mathrm{r}}_{\mathrm{r}\mathrm{s}}\mathrm{W}\left(0^{-},\mathsf{\lambda }\right)+{\mathrm{r}}_{\mathrm{r}\mathrm{s}}\mathrm{C}\left(0^{-},\mathsf{\lambda }\right)$$

(11)

Finally, the reflectance just above the sea surface R($\mathsf{\lambda }$) is derived from r_rs(0⁻$,\mathsf{\lambda }$) in (Equation (12))$.$

$$\mathrm{R}\left(\mathsf{\lambda }\right)=\frac{0.52{\mathrm{r}}_{\mathrm{rs}}\left(0^{-},\mathsf{\lambda }\right)}{1-1.56{\mathrm{r}}_{\mathrm{rs}}\left(0^{-},\mathsf{\lambda }\right)}\times \mathsf{\pi }$$

(12)

The implementation of an opaque layer of Sargassum aggregation at a given depth in the Lee’s model, which is one original feature of the methodology proposed in the current study, enables to simulate the above-water reflectance using the following parameters as inputs: the bio-optical properties of the hydrosols (chl, NAP and CDOM), the Sargassum fractional coverage (FC) and the immersion depth of the Sargassum aggregations. R_w can be simulated for a given set of water column parameter values (chl, NAP and CDOM) for Sargassum free waters.

3. Results

3.1. Correlation between MODIS/δAFAI and MSI/δAFAI

High values of the coefficient of determination were found between MODIS/δAFAI and MSI/δAFAI for each study area (Figure 7). The linear regression slopes obtained by bootstrap had confidence intervals of 0.69 to 1.19. As unity is contained in the intervals, the values are not significantly different from 1. Thus, there is a satisfactory agreement between MODIS/δAFAI and MSI/δAFAI although both sensors have different spatial and spectral resolutions. Therefore, the relationship between δAFAI and FC that will be further investigated using MSI/δAFAI could be fairly applied to retrieve FC from MODIS/δAFAI.

3.2. Relationship between δAFAI and the Fractional Coverage FC

Based on the floating Sargassum reflectance spectrum (Figure 4) and Equation (7), the theoretical value of the slope K is 0.0874.

Following the methodology outlined in Section 2 (e.g., Figure 5), K was also estimated empirically from MSI data. For each of the three study areas shown in Figure 1 and Figure 2, a large dense Sargassum aggregation was selected (Figure 8a–c). δAFAI varies between a minimum and a maximum value that can be quantified using a histogram. Since the MSI pixel size is smaller than the large Sargassum aggregations, FC is supposed to vary from 0 to 1. The maximum value of the δAFAI distribution was determined (Figure 8), yielding an estimate of K (i.e., when FC = 1).

Table 4. Values of K corresponding to the maximum value of δAFAI for each site. Note that the theoretical value of K derived from Equation (7) is 0.0874.

Site Number	K (Dimensionless)
Site #1	0.0828
Site #2	0.0658
Site #3	0.0824

provides the estimates of K values for each site.

For Sites #1 and #3, K is consistent with the theoretical value (0.0874), which is satisfactory. For Site #2, K is 25% lower than the theoretical value, although the conditions that guarantee the presence of “pure” Sargassum pixels seem to be equally verified. That sample of Sargassum from West Africa may have morphological and physiological characteristics that are different from the other two Caribbean samples, which could explain the difference in δAFAI distribution. Other invasive species than Sargassum could have been considered. However, in situ sampling carried out across the Atlantic Ocean in previous studies did not reveal evidence of the occurrence of any other invasive species competitive with Sargassum [11,20,21,22]. Thus, although it might theoretically be possible, it should not be the case here. Note that the wind speed was lower for Site #2 (3 m.s⁻¹) than for Sites #1 and #3 (8 m/s), thus the aggregation on Site #2 could be less compact than the others.

3.3. Variability in the Regression Slope between δAFAI and FC (K Value)

The theoretical value of the slope K between δAFAI and FC (i.e., 0.0874), which was calculated using the floating Sargassum reflectance spectrum, was compared with the empirical value of K estimated using MSI data (Table 4). Empirical K values are systematically lower than the theoretical value because “pure” Sargassum cannot be rigorously observed in the field. Therefore, the maximum value of K is not reached since the slope K decreases with both the dispersion and submersion of Sargassum. In the field, the K value can be influenced by several parameters, namely, the physiological state of Sargassum, the water turbidity and depth. Russel and Heidi [23] measured two reflectance spectra of Sargassum. One spectrum corresponds to “healthy” Sargassum while the other spectrum corresponds to “senescent” Sargassum. The above water reflectance and the K values were simulated here based on these measured spectra for Sargassum located at 0.01 m beneath the sea surface.

Table 5. Coefficients of proportionality between δAFAI and FC, noted K (Equation (7)). The values were calculated by simulation (see text in Section 2.4.3) using different Sargassum reflectance spectra measured by several authors in the literature.

Sargassum Reflectance Spectrum	K
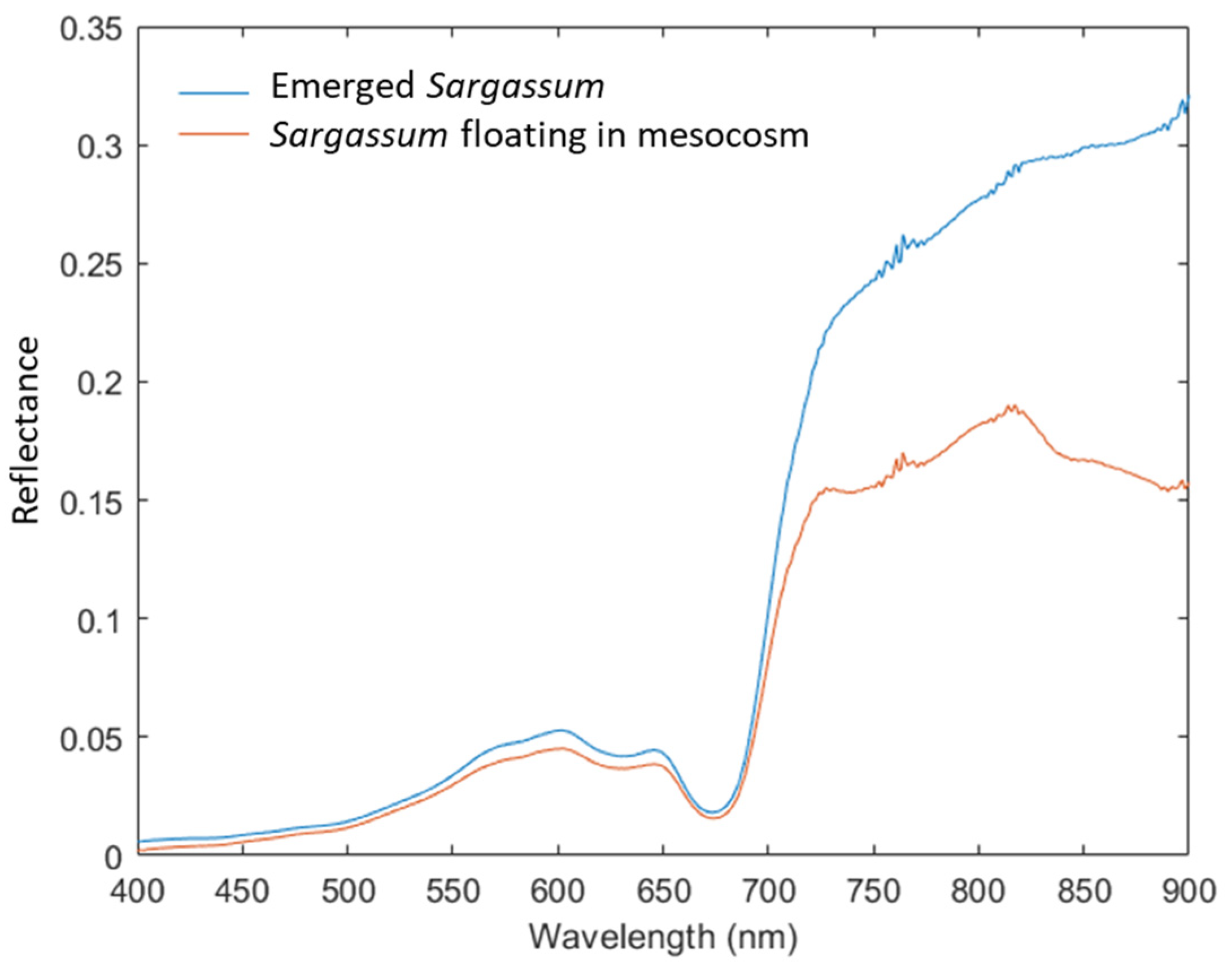
Pure Sargassum measured in the mesocosm [11]	0.1162
Floating (0.01 m) Sargassum measured in the mesocosm [11] (this study)	0.0874
Healthy Sargassum (0.01 m) [23]	0.0849
Senescent Sargassum (0.01 m) [23]	0.0568
Minimum Sargassum reflectance measured by Wang et Hu [10]	0.0257
Average Sargassum reflectance measured by Wang et Hu [10]	0.0441
Maximum Sargassum reflectance measured by Wang et Hu [10]	0.0724

reports the K values calculated from simulations.

The K values derived for a Sargassum depth of 0.01 m when using Sargassum re-flectance spectra measured in the mesocosm [11] and “healthy” Sargassum [23] are fairly similar (0.086). The degradation of Sargassum physiological state (senescent Sargassum) leads to a significant decrease in K (about 35%). Note that senescent Sargassum may also show a lower buoyancy.

4. Discussion

This study shows two important results and findings: (i) the Sargassum detection based on AFAI can be downsampled from 20 m to 1 km, allowing Sargassum monitoring with moderate resolution sensors such as MODIS; (ii) the variability of the coefficient of proportionality K to derive Sargassum coverage from AFAI could be significant, thus showing that a unique/invariant value should not be used.

Finding (i) could be consolidated using more data. However, since the theoretical analysis established that both MODIS/δAFAI and MSI/δAFAI are proportional to the Sargassum fractional coverage, finding (i) corroborates theory. Furthermore, the lack of MODIS-MSI concomitant observations makes it highly difficult to conduct the full statistical analysis that would be required to rigorously examine the time variability of Sargassum over seasonal cycles. Since their orbits are very different, the concomitance of MODIS and MSI observations of the same areas at the same time are rare. Thus, very few concomitant Sargassum detections are available for a direct comparison, bearing in mind that MSI time series is much shorter than MODIS, and MSI geographic coverage much smaller.

Regarding finding (ii), the intent of this study is to highlight a methodological issue when deriving Sargassum coverage from δAFAI using a “universal” (i.e., unique) value of coefficient K, as is commonly the case. This study proposes an empirical method to determine K.

Deeper statistical analysis dealing with the K values derived empirically will need to be carried out based on massive data processing. However, the methodology proposed in this study is not suited for performing such an extensive statistical analysis because it requires selecting specific Sargassum aggregations that are large enough to yield a distribution of δAFAI sufficiently sampled and relies on the hypothesis that those aggregations contain at least a few MSI pixels with fractional coverage close to 100% to derive K with the kernel density estimation technique. In addition to the poor geographic coverage of MSI, especially over open ocean waters, those requirements considerably limit the amount of exploitable data, hence the feasibility of deriving statistical trends for K.

The consistency between AFAI derived from MODIS and MSI sensors using satellite data acquired above scenes that are influenced by Sargassum was demonstrated in Section 3 although the spatial resolution of these sensors differs by almost two orders of magnitude. The MSI spatial resolution (20 m) provides pixels that can be entirely covered with “pure” Sargassum (large aggregations of type 5 in Ody et al. [11]) while the MODIS spatial resolution (1 km) can only provide pixels with a lesser coverage of Sargassum. Consequently, MODIS can hardly provide satisfactory conditions to make sure the cover of Sargassum is maximum.

The variability in K values with physiological state is significant as shown in Section 3. Other variables such as the water turbidity or the Sargassum depth could potentially have an influence on δAFAI and thus, on the K values (

Table 6. Influence of water turbidity (for Sargassum at 0.01 m depth) and Sargassum depth on the K value.

Water Turbidity	K	Sargassum Depth (m)	K
Clear water	0.0797	0 m	0.0871
Mid turbid waters	0.0871	0.10 m	0.0406
Turbid waters	0.1009	0.20 m	0.0275

). Typically, K increases with turbidity (because the water reflectance increases in Equation (7)). K decreases with the immersion depth because of the strong absorption of the radiation by pure seawater molecules in the near infrared. Such variations of K with depth corroborate the observations made by Ody et al. [11] who highlighted that the sea state could have a direct influence on Sargassum submersion and subsequently on the fractional coverage.

In this study, it was also verified through simulations that the sunglint has no influence on K. This is because the sunglint reflectance is spectrally flat, thus it does not alter the calculation of AFAI; hence, K remains pretty insensitive to the sunglint.

The current study calculated and empirically derived a slope K twice higher than the theoretical value proposed by Wang and Hu [10]. The value estimated by Wang and Hu (0.0441) is derived from the Sargassum reflectance spectrum based on the average of more than 50 spectra measured in the Gulf of Mexico and off Bermuda using a hand-held spectrometer. Consequently, they derived a value of K that relates the measured δAFAI to the fractional coverage of Sargassum mats that are typical of their study area, i.e., with average Sargassum density, not maximum density; hence the value of K they derived cannot be used to derive a fractional coverage of “pure” Sargassum.

On the contrary, the value of K retrieved in the current study, using the Sargassum spectrum measured in mesocosm (Figure 4) and MSI satellite data, relates the measured δAFAI to the fractional coverage of “pure” Sargassum. A decrease by a factor of 2 of the K value can lead to an overestimation of the fractional cover of Sargassum by a factor of 2 as well because of the linear relationship between δAFAI and K. Therefore, the selection and the use of a “pure” Sargassum reflectance spectrum are crucial to accurately estimate the fractional coverage and further the biomass. However, the retrieved value of K is only representative of the study area.

5. Conclusions

The feasibility of downsampling the detection of Sargassum from higher to lower satellite sensor spatial resolutions, namely, 20 m (Sentinel-2/MSI) and 1 km (MODIS) was demonstrated. The slope value of the linear relationship between δAFAI and the Sargassum fractional coverage, noted as K in this paper, was calculated from theory and empirically checked using remotely sensed data from MSI. One original feature of the study was to adapt a radiative transfer model, namely the Lee’s model, to take into account Sargassum aggregations located at a given depth while previous studies only consider aggregations floating at the sea surface. The adaption of Lee’s model is also relevant for analyzing the influence of various parameters such as the water turbidity, the submersion and the Sargassum physiological state (e.g., healthy or senescent) on the K value. It was shown that the use of a unique K value to calculate the fractional coverage, as previously proposed by Wang and Hu [10], is not relevant since it could lead to a wrong estimate of the Sargassum fractional coverage (typically by a factor of 2 as shown here) and the associated Sargassum biomass. This study does have a large-scale impact on the estimate of Sargassum coverage and thus biomass in the Atlantic Ocean. Further work could consist in investigating the influence of the sea state and of the Sargassum physiological state on the Sargassum depth to improve estimates of Sargassum fractional coverage and biomass. The relation between δAFAI and FC could also be applied in other regions (Gulf of Mexico, Yellow Sea, and East China Sea) and could be extended to other types of similar floating algae such as Enteromorpha prolifera or Porphyra yezoensis.