How Well Do We Know Europa’s Topography? An Evaluation of the Variability in Digital Terrain Models of Europa
Abstract
1. Introduction
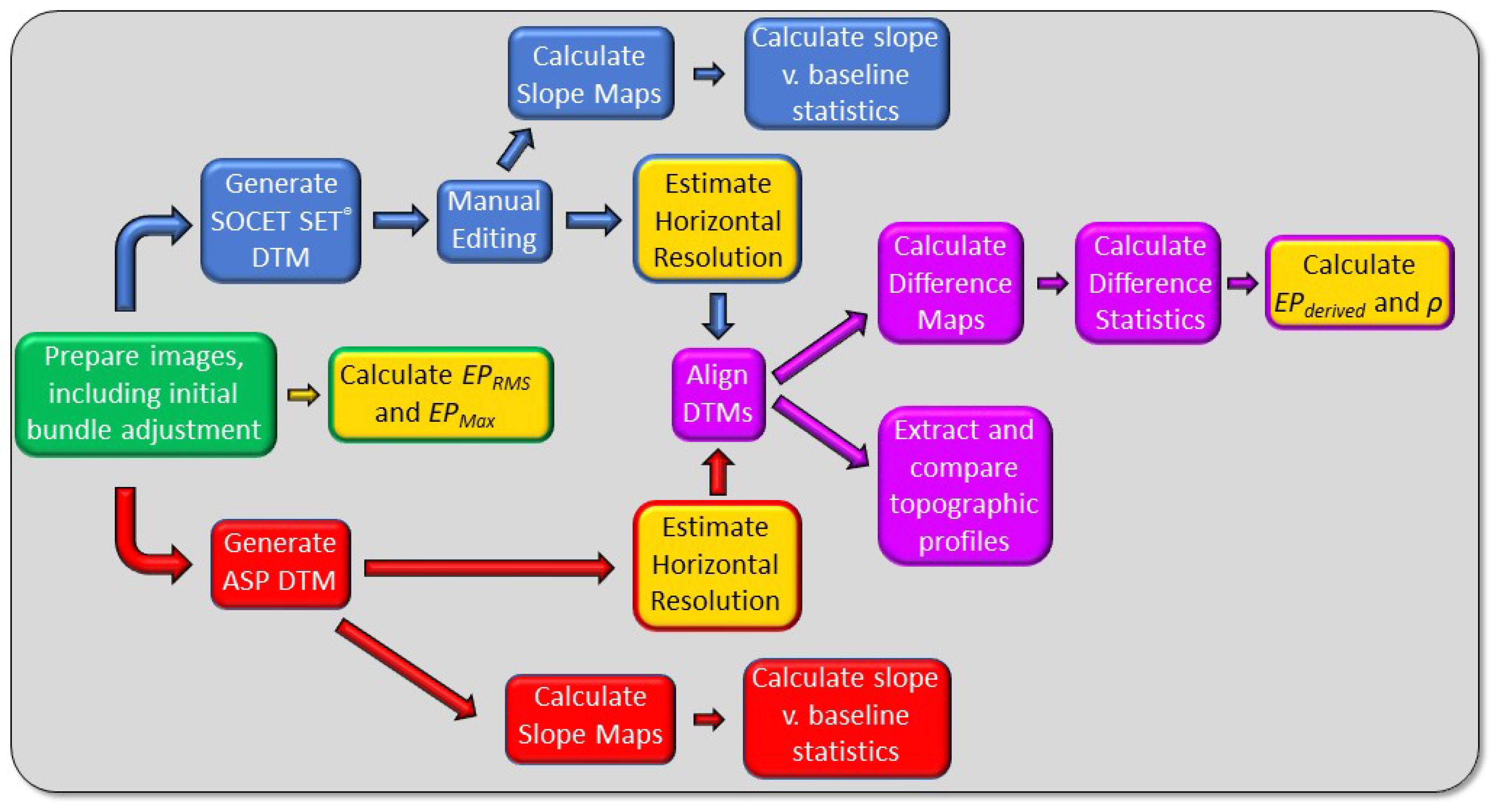
2. Materials and Methods
2.1. Assessing DTM Quality
2.2. Overview of Stereo Criteria
2.3. General Technical Approach to DTM Generation
2.4. Producing DTMs Using SOCET SET®
2.5. Producing DTMs Using the Ames Stereo Pipeline
2.6. Methods of Comparing DTMs
2.6.1. Visual Inspection of the DTMs and Identification of Small-Scale Topography
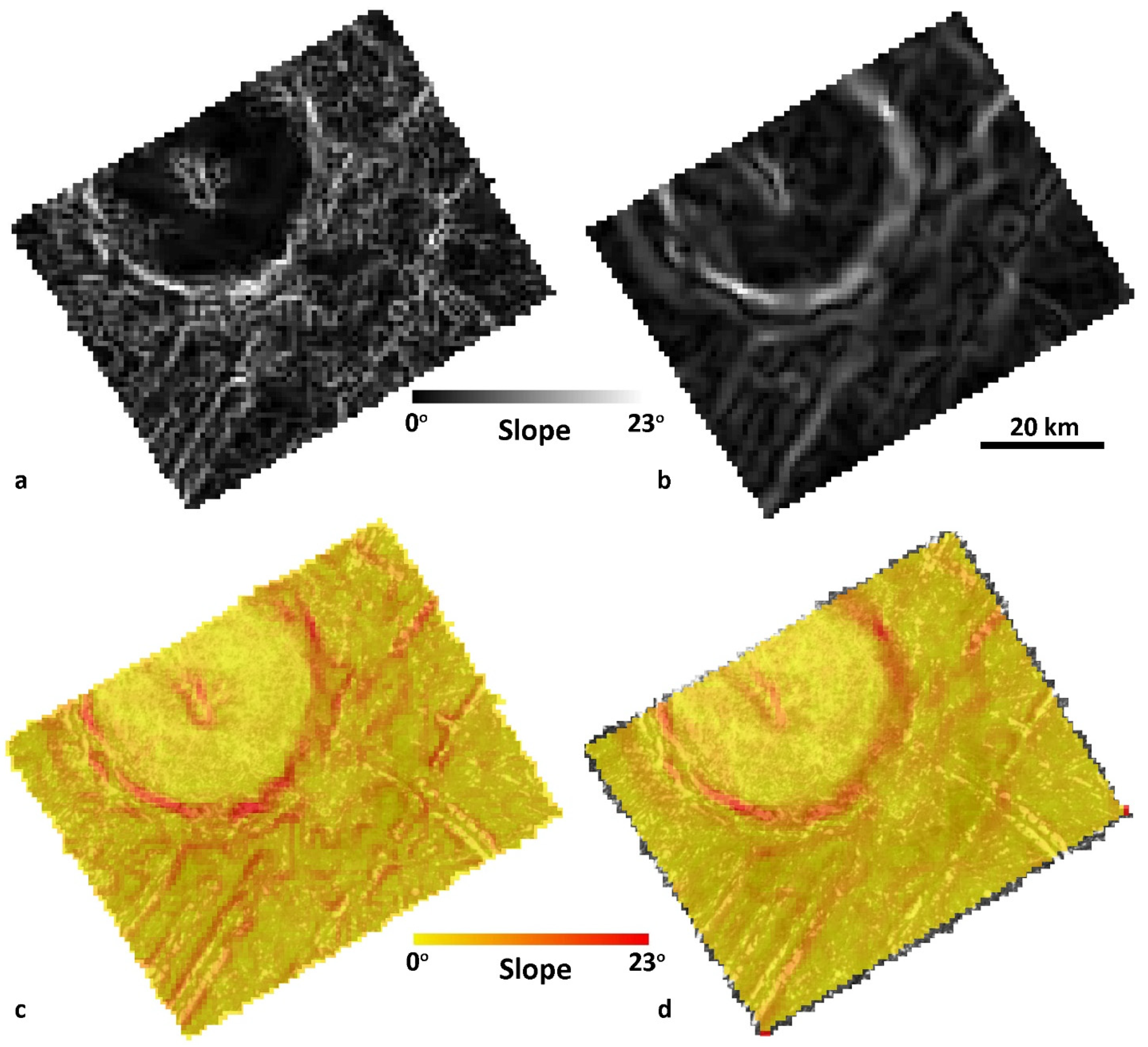
2.6.2. Generation and Evaluation of Hillshades
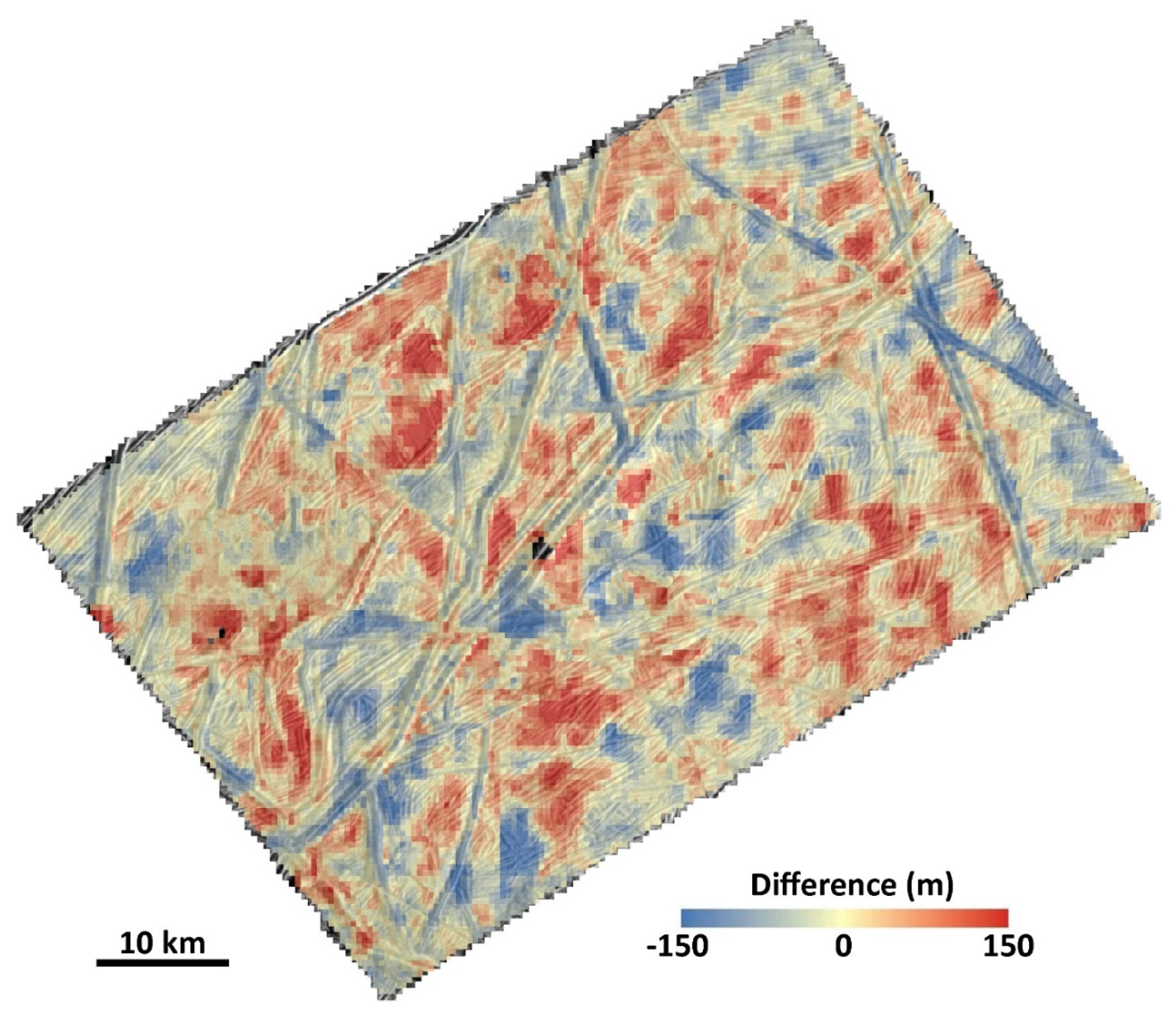
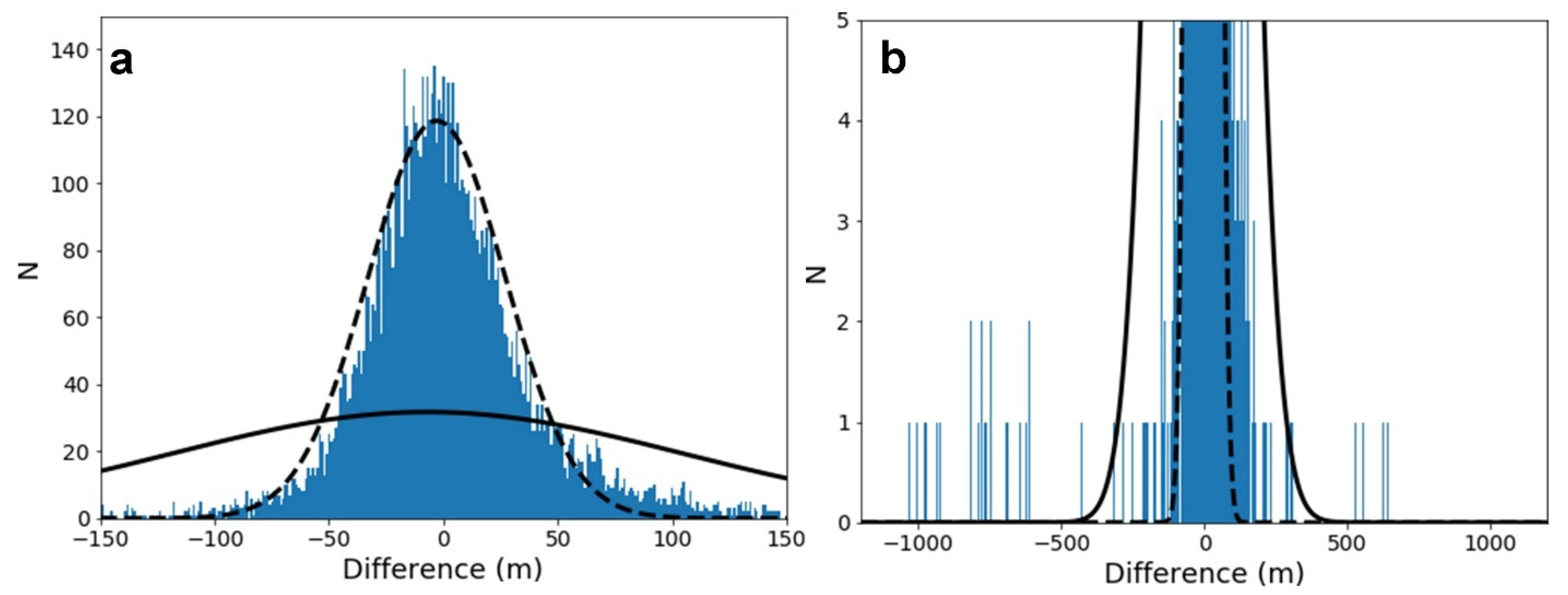
2.6.3. Differencing DTMs
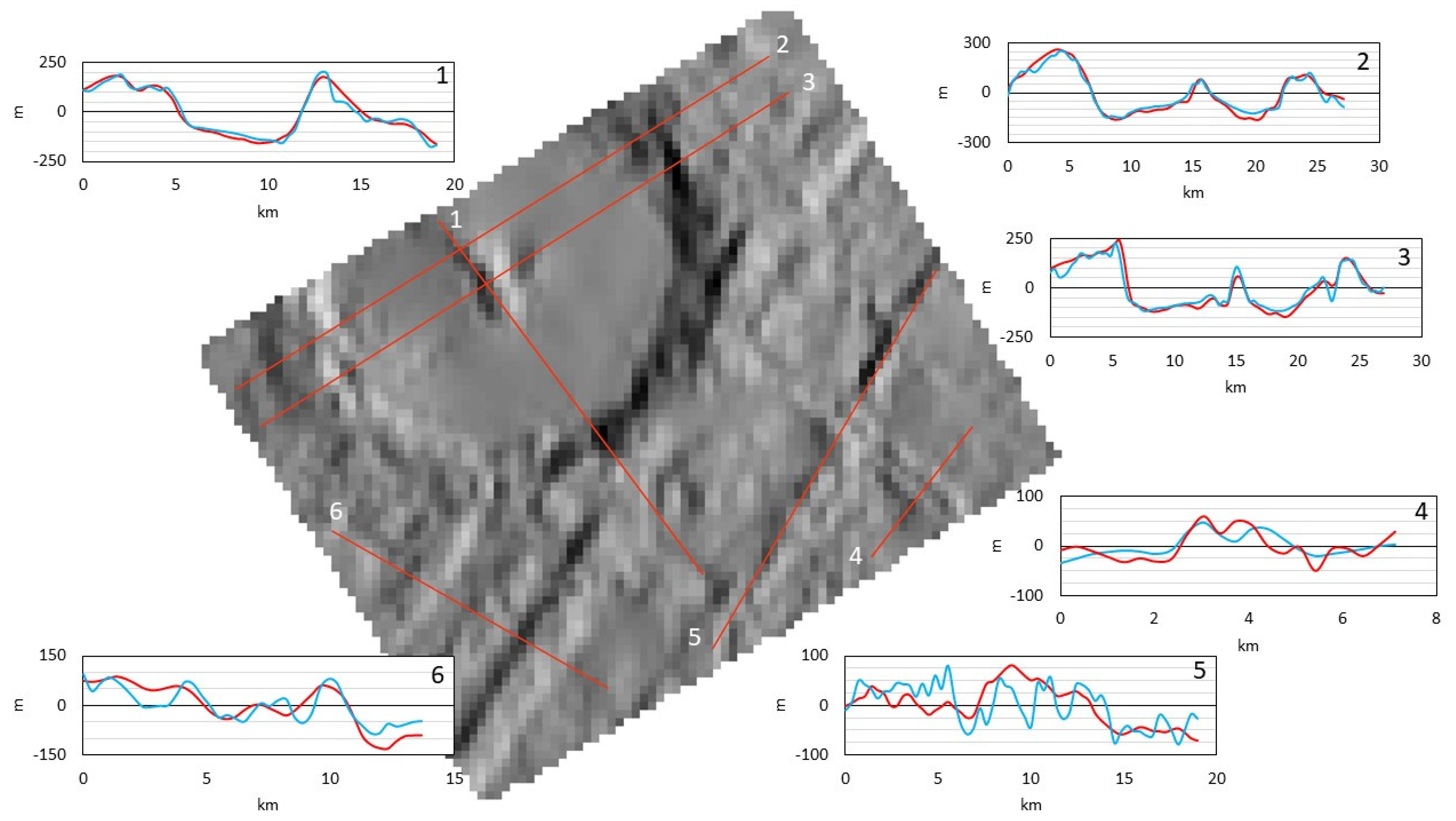
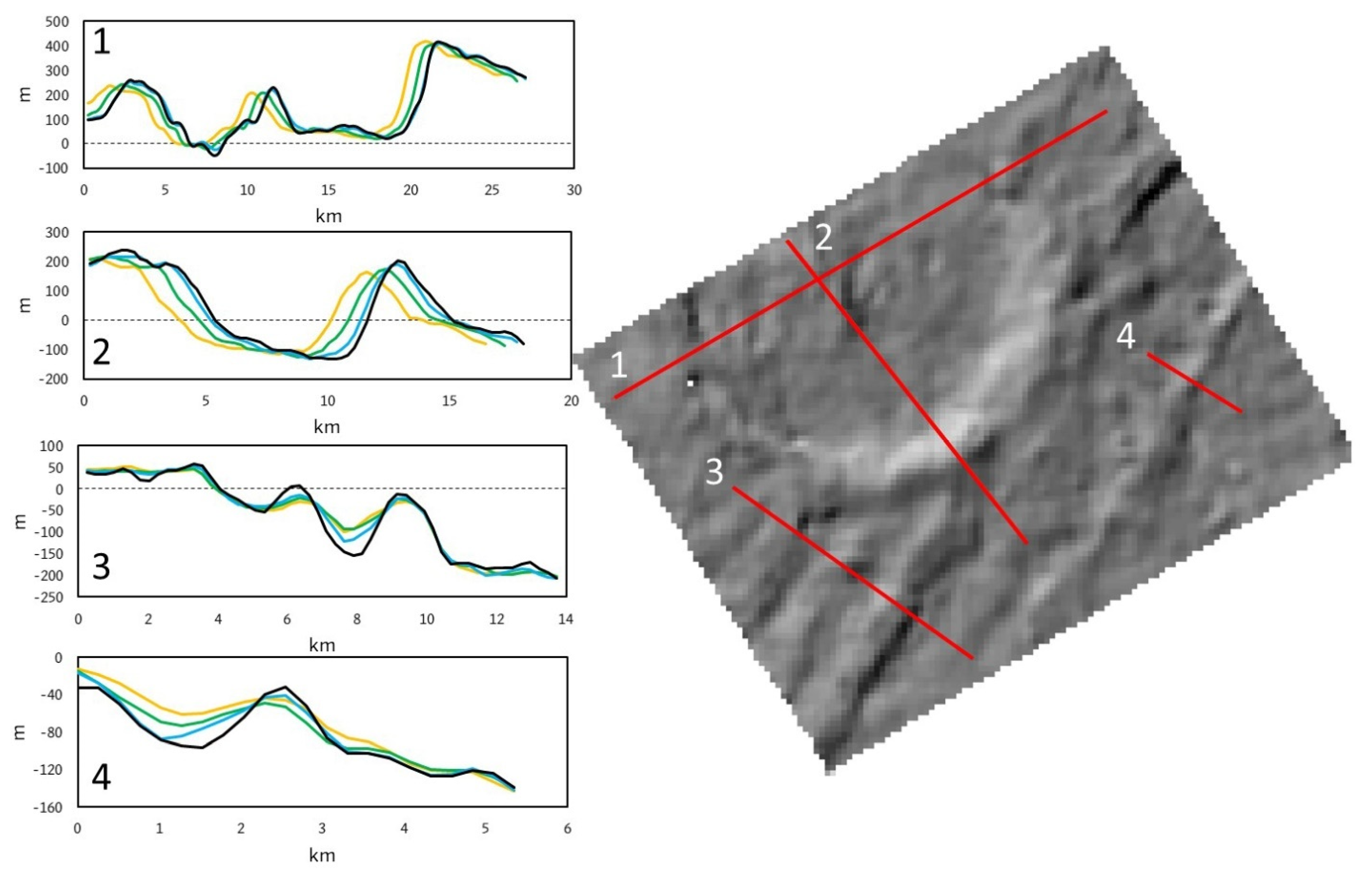
2.6.4. Topographic Profile Comparison
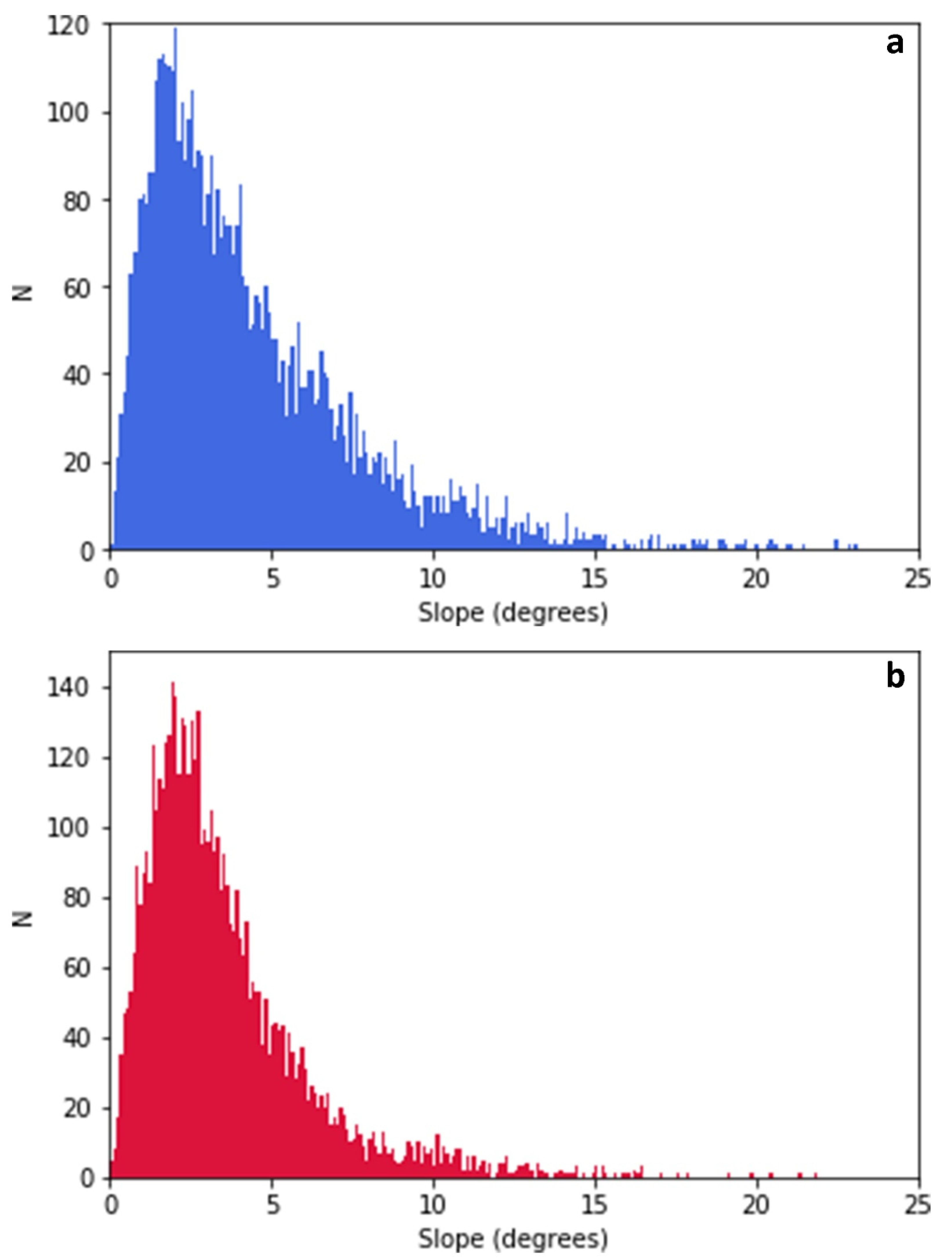
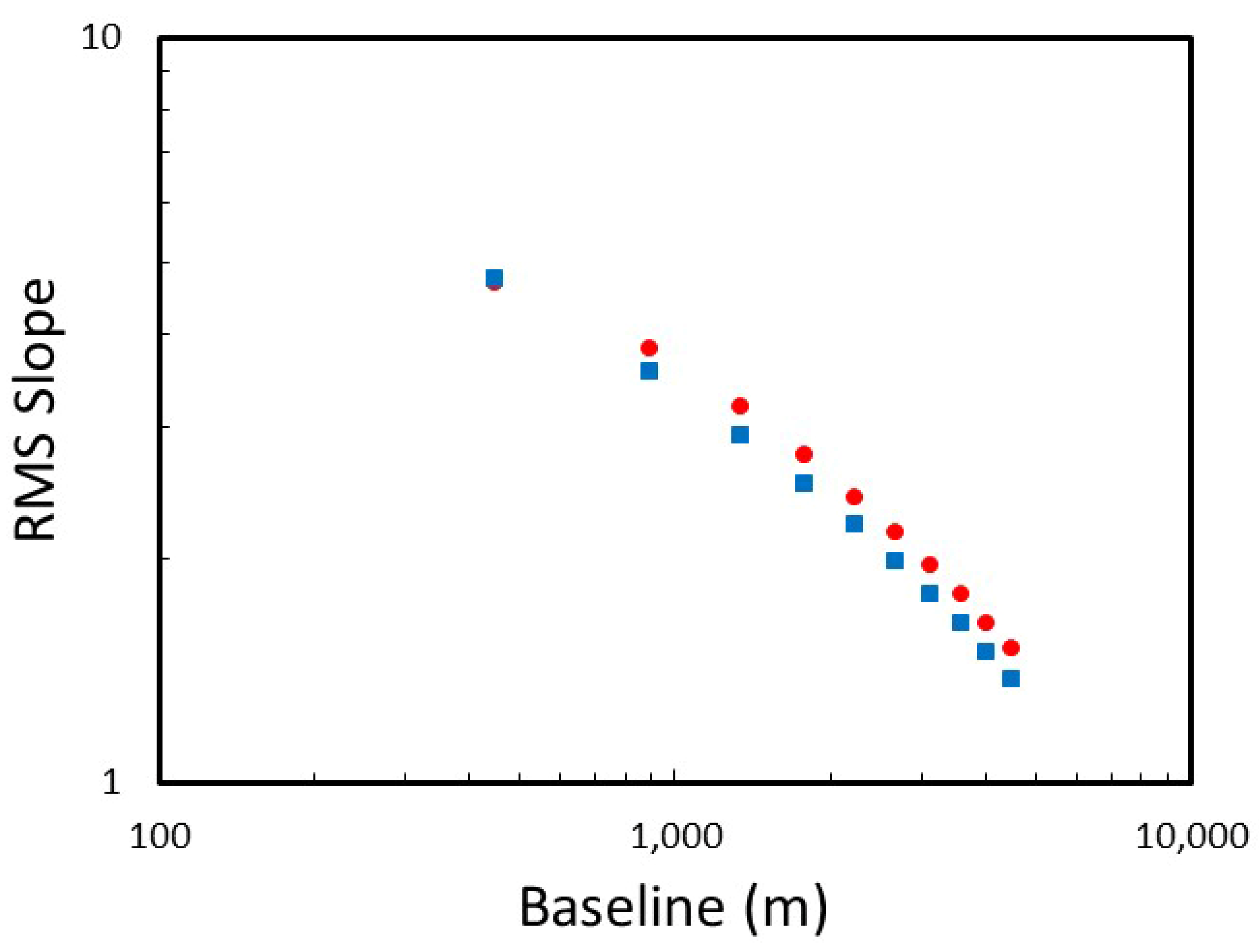
2.6.5. Slopes and Slope Statistics

2.7. Overview of Galileo Data for Europa
3. Results
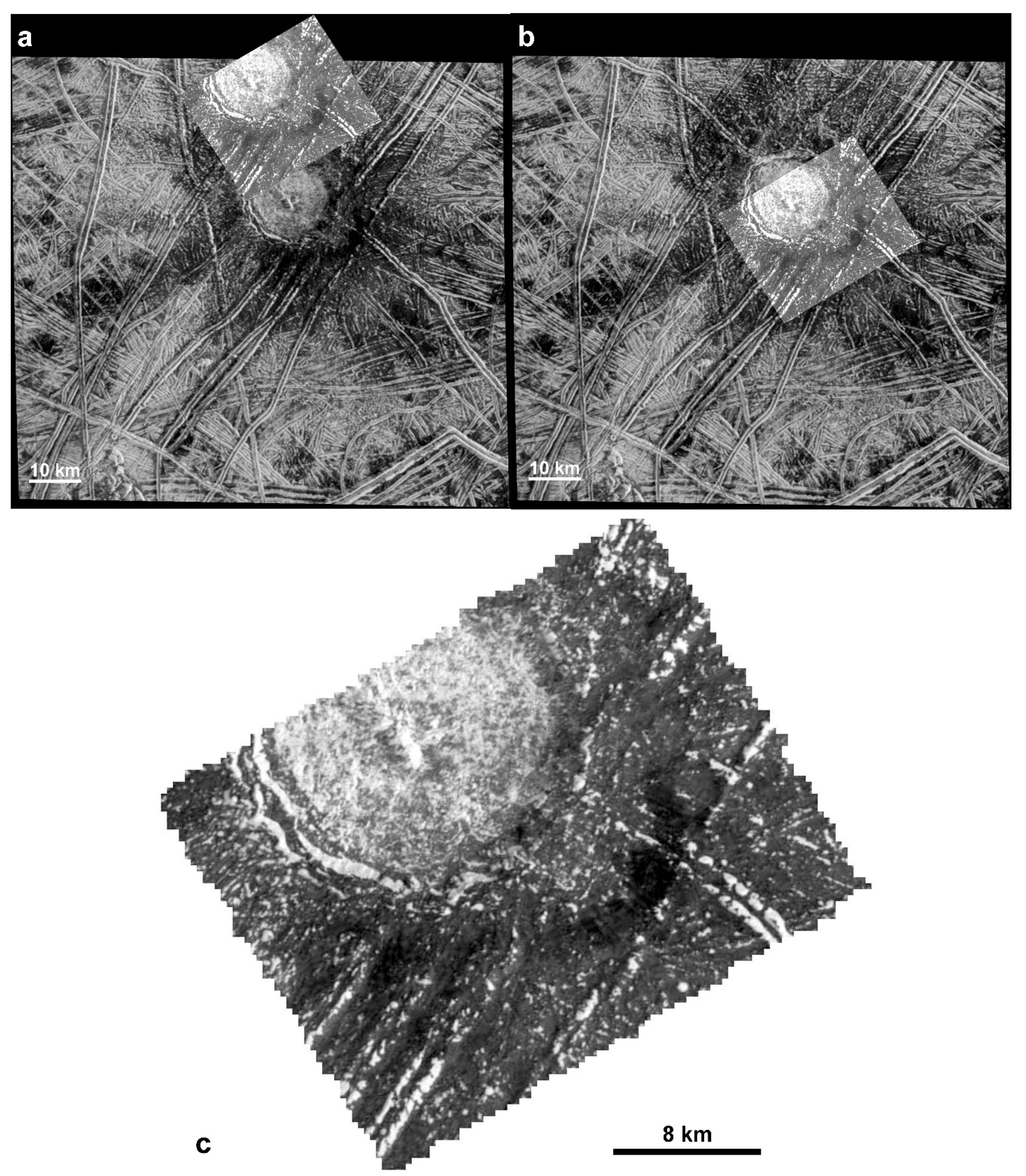
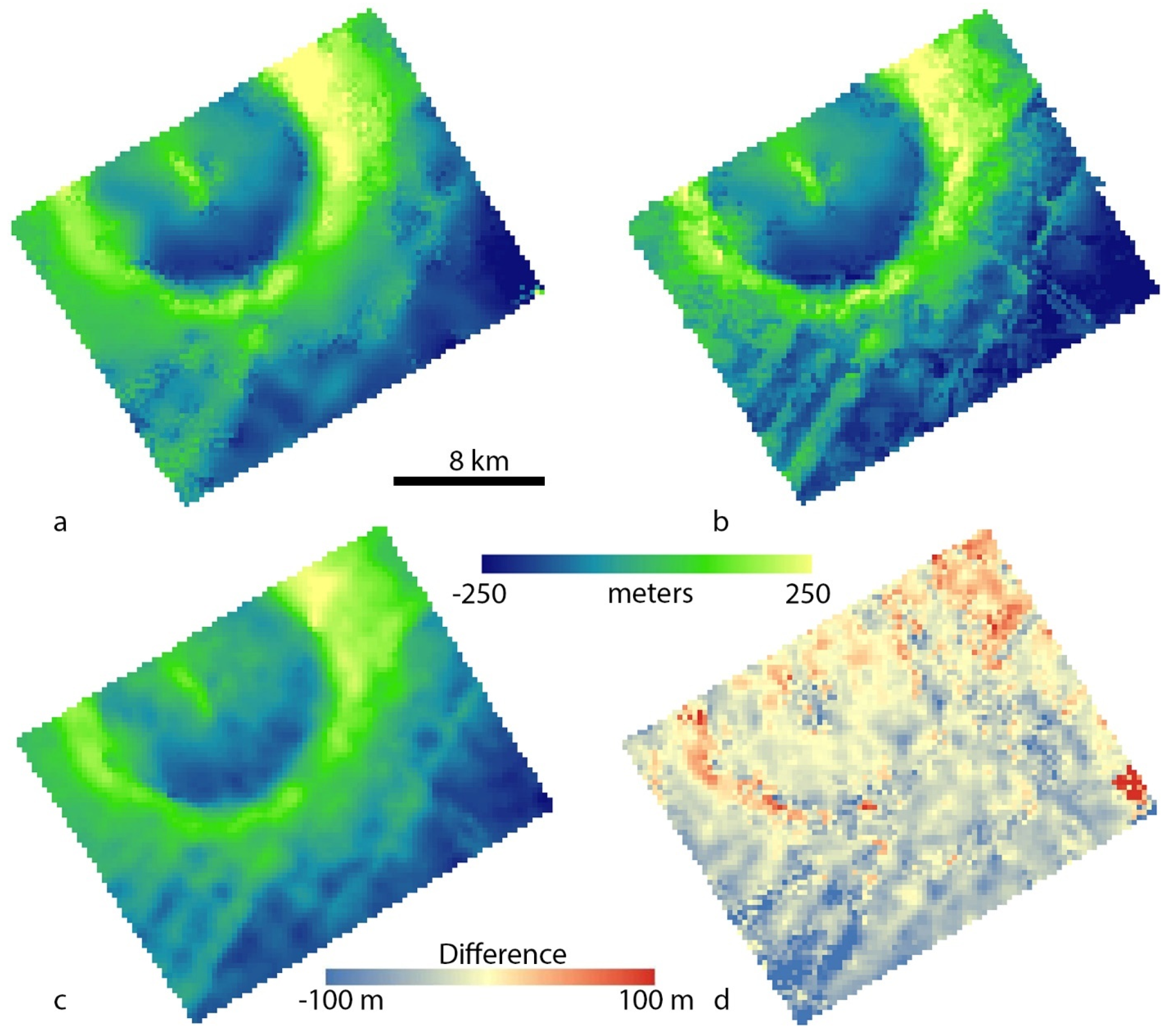
3.1. Detailed Case Study 1: Cilix Crater
| Image a | GSD (m/pixel) | ΔGSD b | i | e | GSDRMS (m/pixel) | DSTc | (p/h)d | EPRMSe | EPmaxf | |
|---|---|---|---|---|---|---|---|---|---|---|
| Cilix crater | s0449965000 s0449967535 | 110.1 63.2 | 1.7 | 31.8° 36.8° | 25.9° 29.9° | 90 | 0.044 | 1.18 | 23 m | 28 m |
| Chaos and pits | s0449961826 s0484888726 | 232.1 63.3 | 3.7 | 79.8° 79.9° | 38.8° 47.6° | 170 | 0.14 | 1.32 | 39 m | 53 m |
| Pwyll crater | s0383715500 s0383715504 s0426268700 | 243.8 244.7 125.8 | 1.9 | 76.2° 80.0° 57.9° | 40.3° 43.9° 48.3° | 194 | 4.1 | 1.8 | 32 m | 41 m |
| Ridged Plains | s0426272642 s0426272646 s0426272821 | 14.0 14.0 25.6 | 1.8 | 29.8° 29.8° 29.9° | 37.8° 37.8° 47.7° | 21 | 0.004 | 0.55 | 11 m | 14 m |
| Agenor Linea | s0466669500 s0466669578 | 50.0 210–223 | 4.3 | 75–80° 71–80° | 37–39° 31–40° | 156 | 2.2 | 0.88 | 52 m | 74 m |
| s0466664665 s0466664326 |
3.1.1. Visual Inspection of DTMs and Hillshades: Smallest Observable Features, Blunders and Artifacts
| DTM Pixel Scale (m/Post) | SOCET Res. (DTM Posts) | SOCET Res. (Meters) | SOCET Res. (RMS Image Pixels) | SOCET Res. (Max Image Pixels) | ASP Res. (DTM Posts) | ASP Res. (Meters) | ASP Res. (RMS Image Pixels) | ASP Res. (Max Image Pixels) | |
|---|---|---|---|---|---|---|---|---|---|
| Cilix crater | 350 | 3 | 1.1 km | 11.1 | 9.1 | 4 | 1.4 km | 15.5 | 12.7 |
| Chaos and pits | 450 | 4 | 1.8 km | 10.6 | 7.8 | 5 | 2.3 km | 13.2 | 9.7 |
| Pwyll crater | 750 | 2 | 1.5 km | 7.7 | 6.1 | 3 | 2.3 km | 11.5 | 9.2 |
| Ridged Plains | 60 | 3 | 180 m | 8.6 | 7.0 | 4 | 240 m | 11.4 | 9.4 |
| Agenor Linea | 750 | 4 | 3.0 km | 19.2 | 13.8 | – | – | – | – |
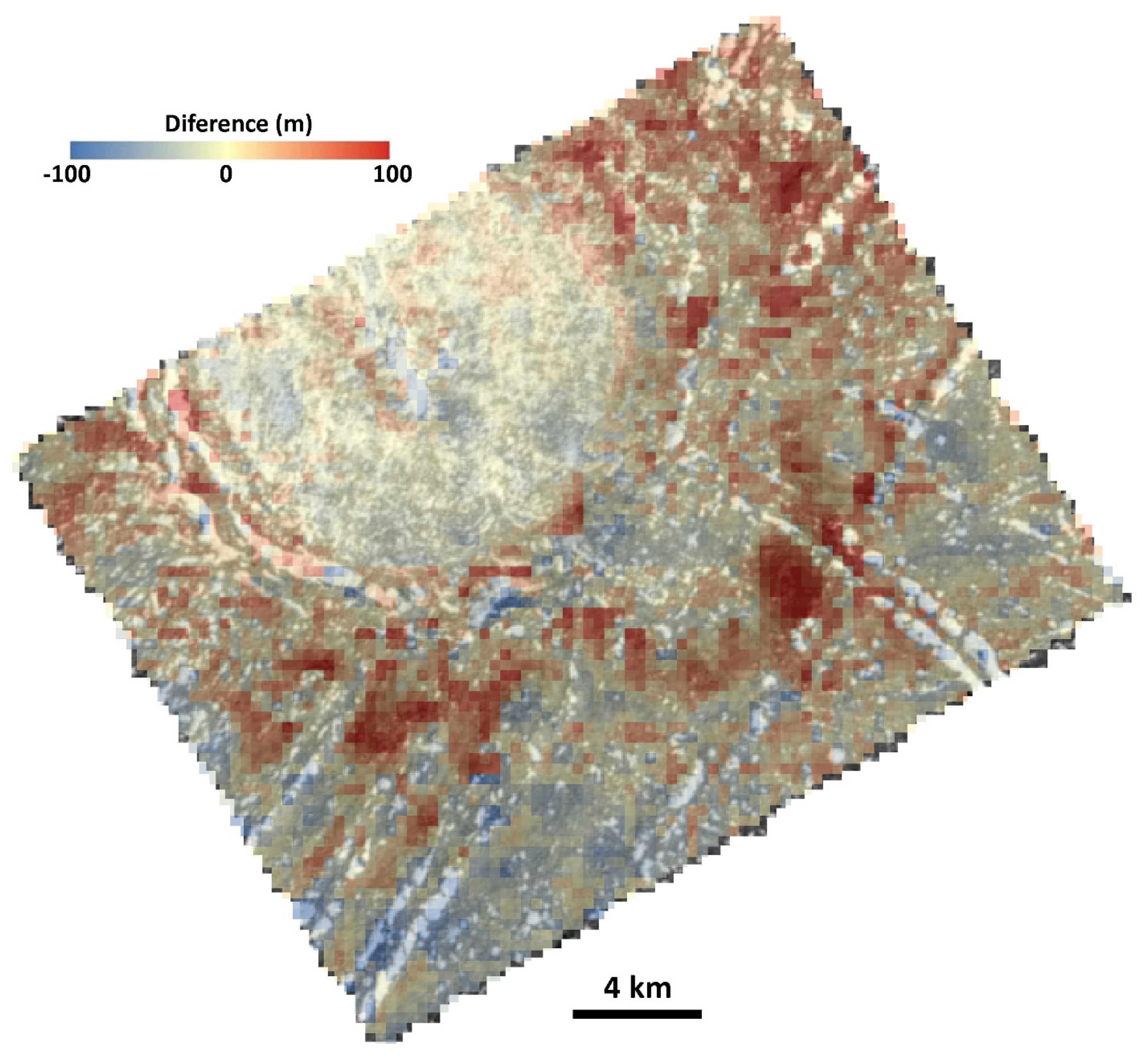
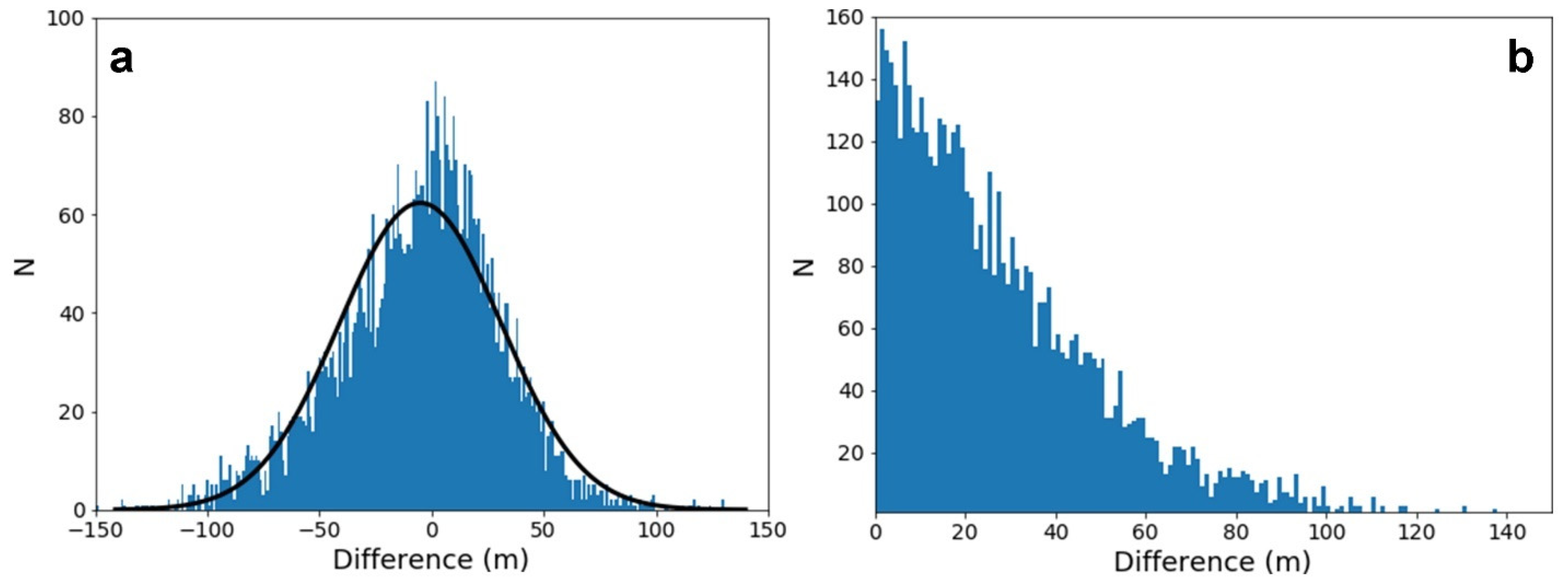
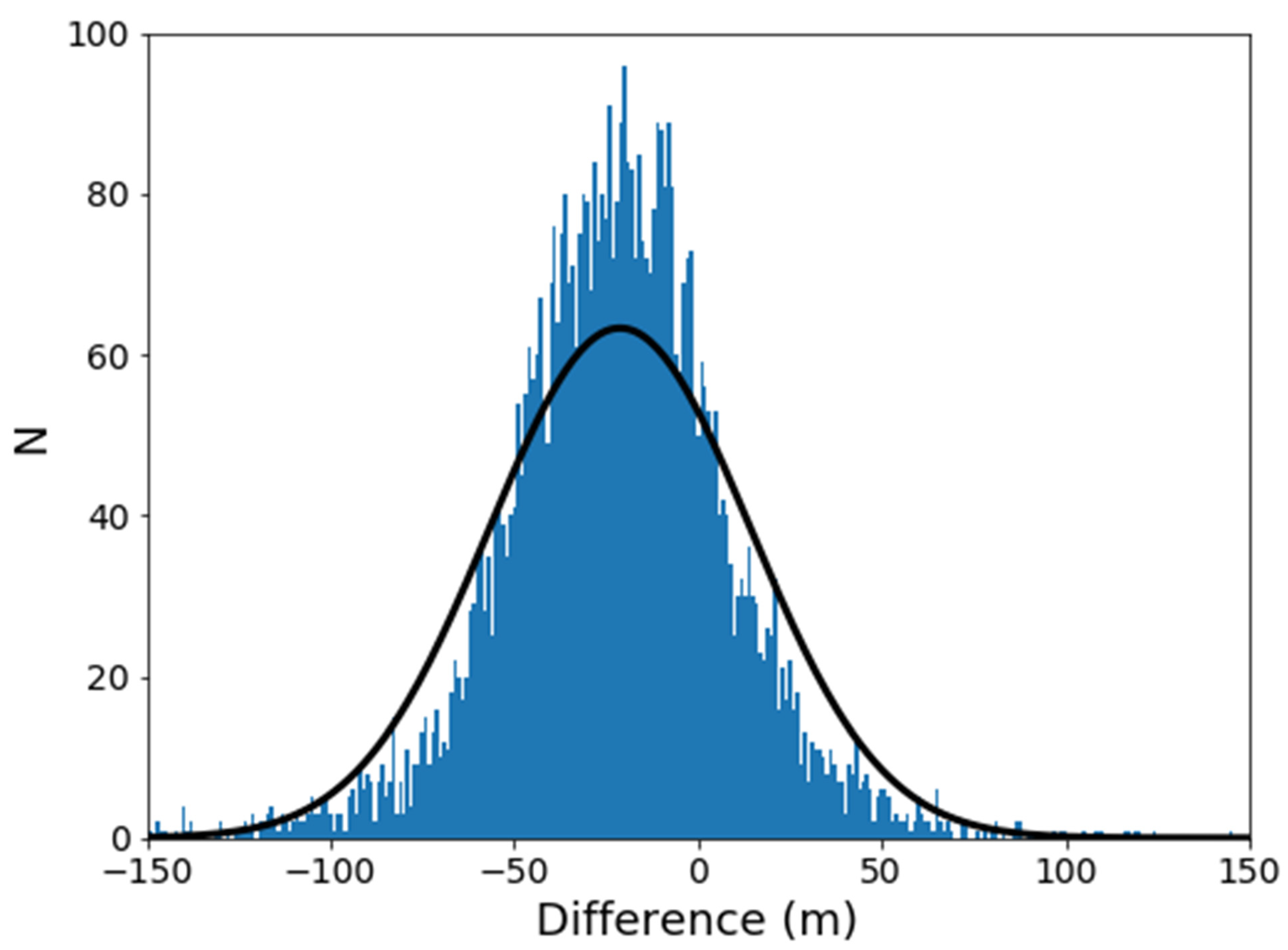
3.1.2. Difference Map and Statistics
| EPderived | ρRMS (Pixels) | ρmax (Pixels) | SOCET Res × ρRMS (Pixels2) | SOCET Res. × ρmax (Pixels2) | ASP Res. × ρRMS (Pixels2) | ASP Res. × ρmax (Pixels2) | |
|---|---|---|---|---|---|---|---|
| Cilix crater | 36 m | 0.5 | 0.4 | 5.6 | 3.6 | 7.8 | 5.1 |
| Chaos and pits | 66 m | 0.5 | 0.4 | 5.3 | 3.1 | 6.6 | 3.8 |
| Pwyll crater | 112 m | 1 * | 0.8 * | 7.7 * | 4.9 * | 11.5 * | 7.4 * |
| Ridged Plains † | 21 m 14 m | 0.6 0.4 | 0.5 0.3 | 5.2 3.4 | 3.5 2.1 | 6.8 4.6 | 4.7 2.8 |
| Agenor Linea | ~100 m | 0.6 | 0.4 | 11.5 | 5.5 | – | – |
3.1.3. Topographic Profiles
3.1.4. Slopes and Slope Statistics
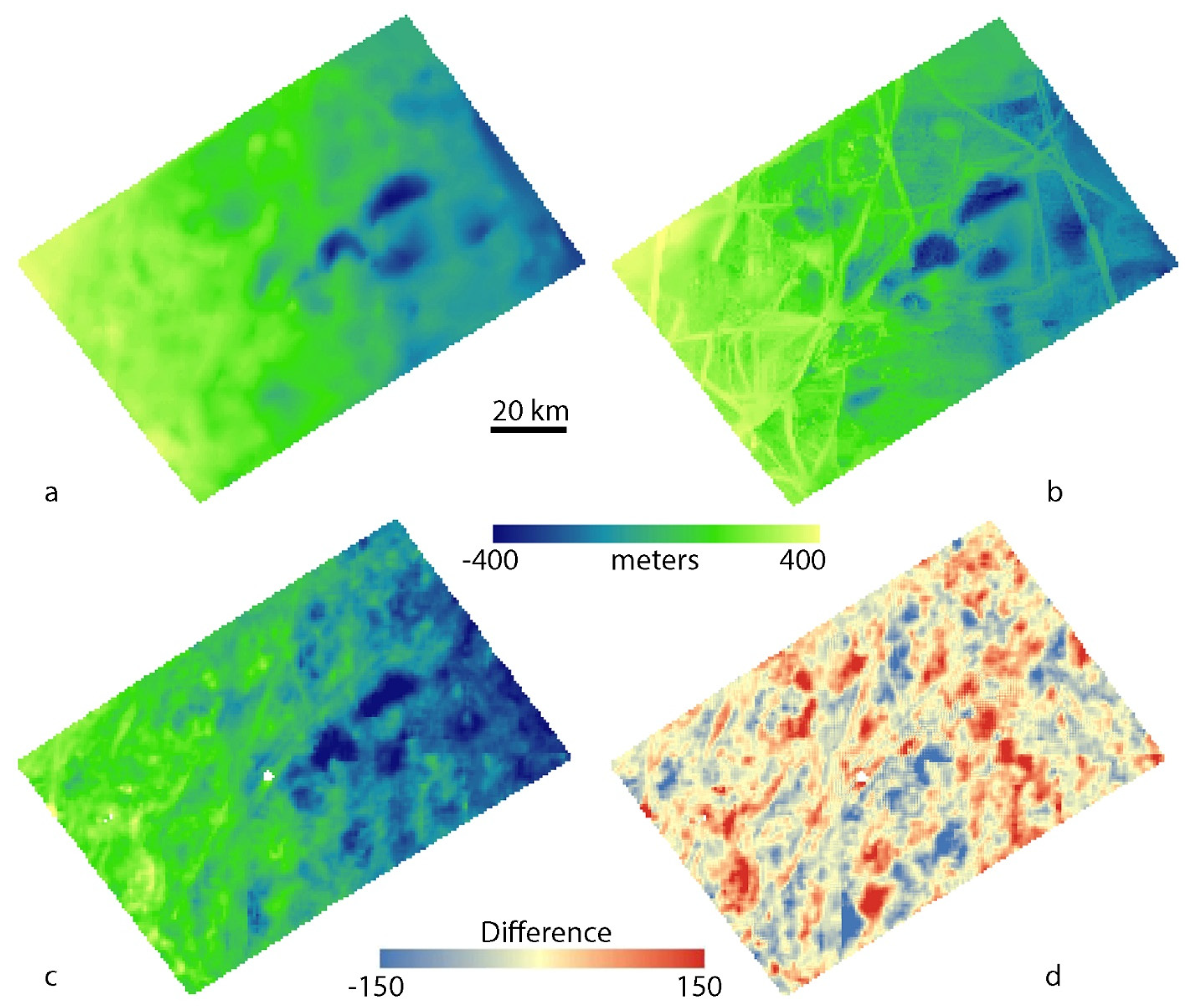
3.2. Detailed Case Study 2: Chaos and Pits near Rhadamanthys Linea
3.2.1. Visual Inspection of DTMs and Hillshades: Smallest Observable Features, Blunders and Artifacts
3.2.2. Difference Map and Statistics
3.2.3. Topographic Profiles
3.2.4. Slopes and Slope Statistics
3.3. DTMs of Pwyll Crater, Ridged Plains, and Agenor Linea: A summary
3.3.1. Pwyll Crater
3.3.2. Ridged Plains
3.3.3. Agenor Linea
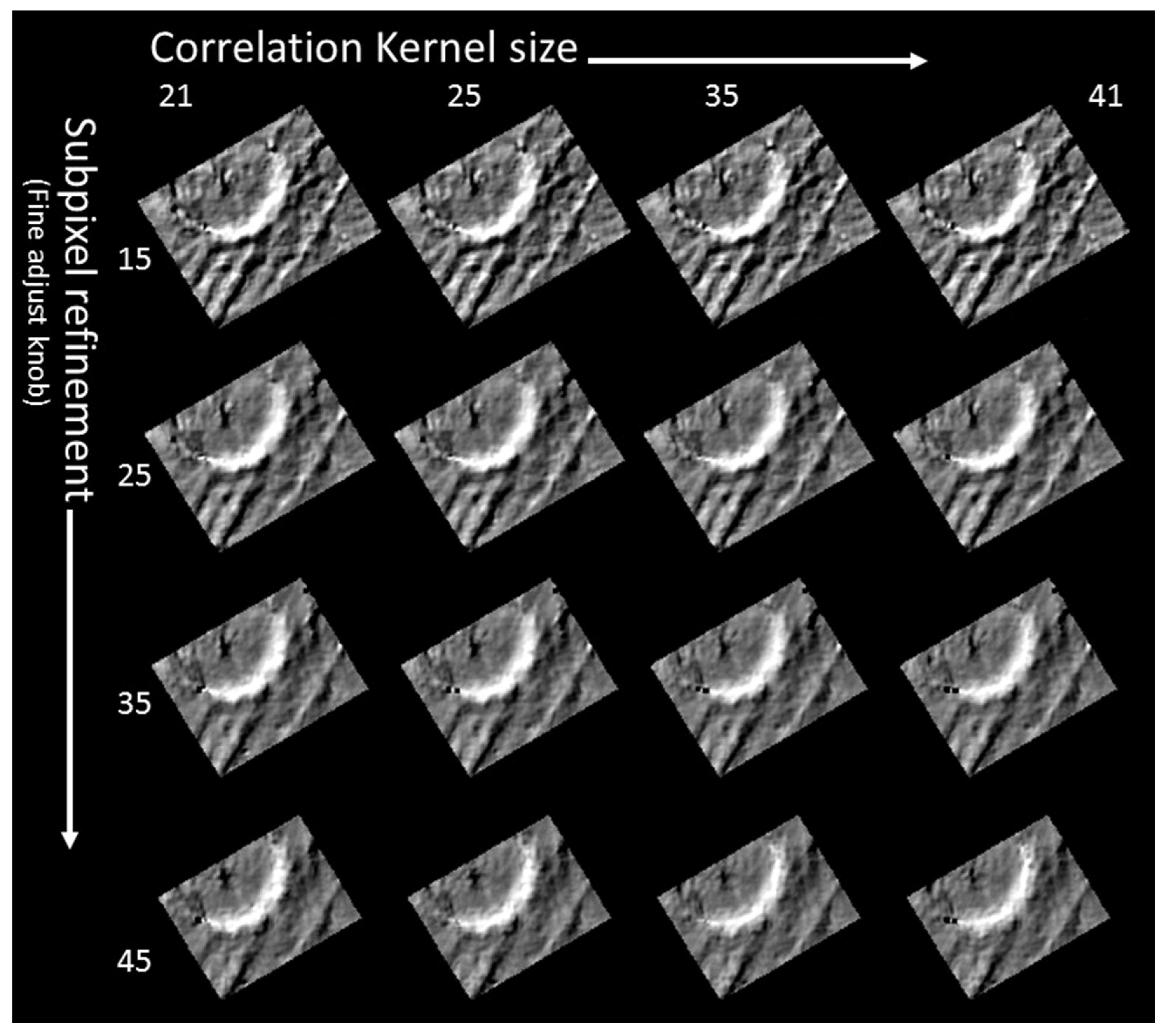
3.4. Optimization of Ames Stereo Pipeline DTM Parameters
4. Discussion
4.1. The Expected Vertical Precision as a Measure of Quality for Europa DTMs
4.2. The Horizontal Resolution of Europa DTMs
4.3. The Impact of Manual Editing
5. Conclusions
- The horizontal resolution of the DTMs (i.e., the smallest features that can be resolved) is at least an order of magnitude greater than the RMS pixel scale of the images, a finding consistent with recent work by Kirk et al. [23] on martian datasets.
- Stereo matching accuracy (ρ) is ~0.5 pixels. Matching accuracy is therefore poorer when compared to many other (mostly martian) datasets and leads to relatively large EP for Galileo-derived DTMs. However, in some cases the horizontal resolution of the Europa DTMs is better than those datasets, such that the product of resolution and error is similar across all datasets.
- Differences (i.e., uncertainty) between DTMs usually follow a quasi-normal distribution, and errors several times larger than EPderived are expected. Such differences were observed in comparisons of topographic profiles, and in two cases, the error distribution departed from normal due to large errors at both tails. The expected vertical precision should never be thought of as an upper bound on the DTM uncertainty.
- Slope information should be used cautiously, as distribution of slopes and the RMS slope as a function of baseline can vary substantially depending on the method used to generate the DTMs.
- Manual editing substantially improves the horizontal resolution of DTMs generated from Galileo images (especially when stereo quality is poor), permitting smaller-scale topographic features to be resolved.
- Users should optimize ASP parameters to generate the highest-quality DTMs possible given the limitations of the dataset. Smaller subpixel refinement kernels are generally preferable but may lead to holes in the DTM.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schubert, G.; Sohl, F.; Hussmann, H. Interior of Europa. In Europa; Pappalardo, R.T., McKinnon, W.B., Khurana, K., Eds.; The University of Arizona Press: Tucson, AZ, USA, 2009; pp. 353–368. ISBN 978-0-8165-2844-8. [Google Scholar]
- Schmidt, B.E.; Blankenship, D.D.; Patterson, G.W.; Schenk, P.M. Active formation of ‘Chaos Terrain’ over shallow subsurface water on Europa. Nature 2011, 479, 502–505. [Google Scholar] [CrossRef]
- Dombard, A.J.; Patterson, G.W.; Lederer, A.P.; Prockter, L.M. Flanking fractures and formation of double ridges on Europa. Icarus 2013, 223, 74–81. [Google Scholar] [CrossRef]
- Schenk, P.M. Thickness constraints on the icy shells of the Galilean satellites from a comparison of crater shapes. Nature 2002, 417, 419–421. [Google Scholar] [CrossRef] [PubMed]
- Turtle, E.P.; Pierazzo, E. Thickness of a Europan ice shell from impact crater simulations. Science 2001, 294, 1326–1328. [Google Scholar] [CrossRef] [PubMed]
- Nimmo, F.; Giese, B.; Pappalardo, R.T. Estimates of Europa’s ice shell thickness from elastically-supported topography. Geophys. Res. Lett. 2003, 30, 1233. [Google Scholar] [CrossRef]
- Hurford, T.A.; Beyer, R.A.; Schmidt, B.; Preblich, B.; Sarid, A.R.; Greenberg, R. Flexure of Europa’s lithosphere due to ridge loading. Icarus 2005, 177, 280–296. [Google Scholar] [CrossRef]
- Nimmo, F.; Thomas, P.C.; Pappalardo, R.T.; Moore, W.B. The global shape of Europa: Constraints on lateral shell thickness variations. Icarus 2007, 191, 183–192. [Google Scholar] [CrossRef]
- Schenk, P.M.; Matsuyama, I.; Nimmo, F. True polar wander on Europa from global-scale small-circle depressions. Nature 2008, 453, 368–371. [Google Scholar] [CrossRef] [PubMed]
- Schenk, P.M.; McKinnon, W.B. New crop circles found on Europa [but not Ganymede]! True polar wander conspiracy confirmed! Lunar Planet. Sci. Conf. 2015, 46, 1526. [Google Scholar]
- Nimmo, F.; Schenk, P.M. Normal faulting on Europa: Implications for ice shell properties. J. Struct. Geo. 2006, 28, 2194–2203. [Google Scholar] [CrossRef]
- Nimmo, F.; Pappalardo, R.T.; Giese, B. On the origins of bands topography, Europa. Icarus 2003, 166, 21–23. [Google Scholar] [CrossRef]
- Coulter, C.E.; Kattenhorn, S.A.; Schenk, P.M. Topographic profile analysis and morphologic characterization of Europa’s double ridges. Lunar Planet. Sci. Conf. 2009, 40, 1960. [Google Scholar]
- Prockter, L.M.; Patterson, G.W. Morphology and evolution of Europa’s ridges and bands. In Europa; Pappalardo, R.T., McKinnon, W.B., Khurana, K., Eds.; The University of Arizona Press: Tucson, AZ, USA, 2009; pp. 237–258. ISBN 978-0-8165-2844-8. [Google Scholar]
- Schenk, P.M.; Pappalardo, R.T. Topographic variations in chaos on Europa: Implications for diapiric formation. Geophys. Res. Lett. 2004, 31, L16703. [Google Scholar] [CrossRef]
- Prockter, L.M.; Schenk, P.M. Origins and evolution of Castalia Macula, an anomalous young depression on Europa. Icarus 2005, 177, 305–326. [Google Scholar] [CrossRef]
- Singer, K.N.; McKinnon, W.B.; Schenk, P.M. Pits, uplifts and small chaos features on Europa: Morphologic and morphometric evidence for intrusive upwelling and lower limits on ice shell thickness. Icarus 2021, 364, 114465. [Google Scholar] [CrossRef]
- Turtle, E.P.; McEwen, A.S.; Collins, G.C.; Fletcher, L.; Hansen, C.J.; Hayes, A.G.; Hurford, T.A.; Kirk, R.L.; Barr-Mlinar, A.C.; Nimmo, F.; et al. The Europa Imaging System (EIS): High-resolution imaging and topography to investigate Europa’s geology, ice shell, and potential for current activity. Lunar Planet. Sci. Conf. 2016, 47, 1626. [Google Scholar]
- Steinbrugge, G.; Schroeder, D.M.; Haynes, M.S.; Hussmann, H.; Grima, C.; Blankenship, D.D. Assessing the potential for measuring Europa’s tidal love number h2 using radar sounder and topographic imager data. Earth Planet. Sci. Lett. 2018, 482, 334–341. [Google Scholar] [CrossRef]
- Bland, M.T.; Weller, L.A.; Archinal, B.A.; Smith, E.; Wheeler, B.H. Improving the usability of Galileo and Voyager images of Jupiter’s moon, Europa. Earth Space Sci. 2021, 8, e2021EA001935. [Google Scholar] [CrossRef]
- Heipke, C.; Oberst, J.; Albertz, J.; Attwnger, M.; Dorninger, P.; Dorrer, E.; Ewe, M.; Gehrke, S.; Gwinner, K.; Hirschmuller, H.; et al. Evaluating planetary digital terrain models: The HRSC DTM test. Planet. Space Sci. 2007, 55, 2173–2191. [Google Scholar] [CrossRef]
- Beyer, R.A.; Archinal, B.; Cheng, Y.; Edmundson, K.; Howington-Kraus, E.; Kirk, R.; Li, R.; McEwen, A.; Mattson, S.; Meng, X.; et al. LROC DTM comparison Effort. Lunar Planet. Sci. Conf. 2011, 42, 2715. [Google Scholar] [CrossRef]
- Kirk, R.L.; Mayer, D.; Redding, B.; Galuszka, D.; Fergason, R.L.; Hare, T.M.; Gwinner, K. Evaluating stereo digital terrain model quality at Mars rover landing sites with HRSC, CTX, and HiRISE. Remote Sens. 2021, 13, 3511. [Google Scholar] [CrossRef]
- Kirk, R.L.; Howington-Kraus, E.; Redding, B.; Galuszka, D.; Hare, T.M.; Archina, B.A.; Soderblom, L.A.; Barrett, J.M. High-resolution topomapping of candidate MER landing sites with Mars Orbiter Camera narrow-angle images. J. Geophys. Res. 2003, 108, 8088. [Google Scholar] [CrossRef]
- Becker, K.J.; Archinal, B.A.; Hare, T.H.; Kirk, R.L.; Howington-Kraus, E.; Robinson, M.S.; Rosiek, M.R. Criteria for automated identification of stereo image pairs. Lunar Planet. Sci. Conf. 2015, 46, 2703. [Google Scholar]
- Schenk, P.M. Slope characteristics of Europa: Constraints for landers and radar sounding. Geophys. Res. Lett. 2009, 36, L15204. [Google Scholar] [CrossRef]
- Kirk, R.L.; Howington-Kraus, E.; Hare, T.M.; Jorda, L. The effects of illumination on stereo DTM quality: Simulations in support of Europa exploration. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 103–110. [Google Scholar] [CrossRef]
- Cook, A.C.; Oberst, J.; Roatsch, T.; Jaumann, R.; Acton, C. Clementine imagery: Selenographic coverage for cartographic and scientific use. Planet. Space Sci. 1996, 44, 1135–1148. [Google Scholar] [CrossRef]
- Kirk, R.L.; Howington-Kraus, E.; Hare, T.; Dorrer, E.; Cook, D.; Becker, K.; Thompson, K.; Redding, B.; Blue, J.; Galuszka, D.; et al. Digital photogrammetric analysis of the IMP Camera Images: Mapping the Mars Pathfinder landing site in three dimensions. J. Geophys. Res. 1999, 104, 8869–8887. [Google Scholar] [CrossRef][Green Version]
- Kirk, R.L.; Howington-Kraus, E.; Edmundons, K.; Redding, B.; Galuszka, D.; Hare, T.; Gwinner, K. Community tools for cartographic and photogrammetric processing of Mars Express HRSC images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 69–76. [Google Scholar] [CrossRef]
- Kirk, R.L.; Howington-Kraus, E.; Edmundons, K.; Redding, B.; Galuszka, D.; Hare, T.; Gwinner, K. Community tools for cartographic and photogrammetric processing of Mars Express HRSC images. Lunar Planet. Sci. Conf. 2018, 49, 2184. [Google Scholar]
- Kirk, R.L.; Howington-Kraus, E.; Rosiek, M.R.; Anderson, J.A.; Archinal, B.A.; Becker, K.J.; Cook, D.A.; Galuszka, D.; Geissler, P.E.; Hare, T.M.; et al. Ultrahigh resolution topographic mapping of Mars with MRO HiRISE stereo images: Meter-scale slopes of candidate Phoenix landing sites. J. Geophys. Res. 2008, 113, E00A24. [Google Scholar] [CrossRef]
- Kirk, R.L.; Shepherd, M.; Sides, S.C. A novel technique for precision geometric correction of jitter distortion for the Europa Imaging System and other rolling-shutter cameras. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 735–739. [Google Scholar] [CrossRef]
- Zhang, B. Toward a higher level of automation in softcopy photogrammetry: NGATE and LIDAR processing in SOCET SET®. In Proceedings of the GeoCue Corporation 2nd Annual Technical Exchange Conference, Nashville, TN, USA, 26–27 September 2006; p. 32. [Google Scholar]
- Zhang, B.; Miller, S. Adaptive Automatic Terrain Extraction. In Integrating Photogrammetric Techniques with Scene Analysis and Machine Vision III; McKeown, D.M., McGlone, J.C., Jamet, J.C., Eds.; 1997; Volume 3072, pp. 27–36. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/3072/1/Adaptive-automatic-terrain-extraction/10.1117/12.281065.short (accessed on 5 November 2021).
- Nefian, A.V.; Hussmann, K.; Broxton, M.; To, V.; Lundy, M.; Hancher, M.D. A bayesian formulation for sub-pixel refinement in stereo orbital imagery. IEEE Int. Conf. Image Process. (ICIP) 2009, 16, 2361–2364. [Google Scholar] [CrossRef]
- Beyer, R.A.; Alexandrov, O.; McMichael, S. The Ames Stereo Pipeline: NASA’s open source software for deriving and processing terrain data. Earth Space Sci. 2018, 5. [Google Scholar] [CrossRef]
- Phillips, C.B.; Hammond, N.P.; Robuchon, G.; Nimmo, F.; Beyer, R.; Roberts, J. Stereo imaging, crater relaxation, and thermal histories of rhea and dione. Lunar Planet. Sci. Conf. 2012, 43, 2571. [Google Scholar]
- Phillips, C.B.; El Henson, E.; Nimmo, F. Stereo topography of surface features on Europa and comparisons with formation models. In Proceedings of the AGU Fall Meeting, San Francisco CA, USA, December 2013; p. P53A-1846. [Google Scholar]
- Schenk, P.M. “Ah… not so flat as we were led to believe”: Global and regional topography characteristics of Europa. In Proceedings of the American Geophysical Union, Fall Meeting, San Francisco CA, USA, December 2010; p. P31D-02. [Google Scholar]
- Giese, B.; Oberst, J.; Roatsch, T.; Neukum, G.; Head, J.W.; Pappalardo, R.T. The Local topography of Uruk Sulcus and Galileo Regio obtained from stereo images. Icarus 1998, 135, 303–316. [Google Scholar] [CrossRef]
- Acton, C.J. Ancillary data services of NASA’s Navigation and Ancillary Information Facility. Planet. Space Sci. 1996, 44, 65–70. [Google Scholar] [CrossRef]
- Miller, S.B.; Walker, A.S. Further developments of Leica digital photogrammetric systems by Helava. ACSM/ASPRS Annu. Conv. 1993, 3, 256–263. [Google Scholar]
- Dundas, C.M. Effects of lava heating on volatile-rich slopes on Io. J. Geophys. Res. 2017, 122, 546–559. [Google Scholar] [CrossRef]
- Sides, S.C.; Beckter, T.L.; Becker, K.J.; Edmundson, K.L.; Backer, J.W.; Wilson, T.J.; Weller, L.A.; Humphrey, I.R.; Berry, K.L.; Shepard, M.R.; et al. The USGS Integrated Software for Imagers and Spectrometers (ISIS 3) instrument support, new capabilities, and releases. Lunar Planet Sci. Conf. 2017, 48, 2739. [Google Scholar]
- Broxton, M.J.; Edwards, L.J. The Ames Stereo Pipeline: Automated 3D surface reconstruction from orbital imagery. Lunar Planet. Sci. Conf. 2008, 39, 2419. [Google Scholar]
- Edwards, L.J.; Broxton, M.J. Automated digital elevation Model generation from orbital imagery. Lunar Planet. Sci. Conf. 2008, 39, 2489. [Google Scholar]
- Moratto, Z.M.; Broxton, M.J.; Beyer, R.A.; Lundy, M.; Hussmann, K. Ames Stereo Pipeline, NASA’s open source automated stereogrammetry software. Lunar Planet. Sci. Conf. 2010, 41, 2364. [Google Scholar]
- Moratto, Z.M.; McMichael, S.; Beyer, R.A.; Alexanderov, O.; Fong, T. Automated and accurate: Making DTMs from LRO-NAC using the Ames Stereo Pipeline. Lunar Planet. Sci. Conf. 2014, 45, 2892. [Google Scholar]
- McMichael, S.; Moratto, Z.M.; Beyer, R.A. LRO-NAC mass DTM pipeline. Lunar Planet. Sci. Conf. 2015, 46, 2491. [Google Scholar]
- Adoram-Kerschner, L.A.; Wheeler, B.H.; Laura, J.R.; Fergason, R.L.; Mayer, D.P. Automated Kaguya TC and MRO CTX Stereo DEM Generation. 5th Planetary Data Workshop and PSIDA (LPI Contrib. 2549). 2021. Available online: https://ui.adsabs.harvard.edu/abs/2021LPICo2549.7021A/abstract (accessed on 5 November 2021).
- Beddingfield, C.B.; Burr, D.M.; Emery, J.P. Shallow normal fault slopes on Saturnian icy satellites. J. Geophys. Res. 2015, 120. [Google Scholar] [CrossRef]
- Beddingfield, C.B.; Burr, D.M.; Emery, J.P. Fault geometries on Uranus’ satellite Miranda: Implications for internal structure and heat flow. Icarus 2015, 247, 35–53. [Google Scholar] [CrossRef]
- Fassett, C.I. Ames Stereo Pipeline-derived digital terrain models of Mercury from MESSENGER stereo imaging. Planet Space Sci. 2016, 134, 19–28. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, B. Comparison and co-registration of DEMs generated from HiRISE and CTX images. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B4, 511–517. [Google Scholar] [CrossRef]
- Della-Giustina, D.N.; Kinney-Spano, E.K.; Chojnacki, M.; Sutton, S. Comparison of digital terrain models derived using different techniques. 2nd Planet. Data Workshop 2015, 2, 7069. [Google Scholar]
- Beyer, R.A.; Alexandrov, O.; Moratto, Z.M. Aligning terrain model and laser altimeter point clouds with the Ames Stereo Pipeline. Lunar Planet. Sci. Conf. 2014, 45, 2902. [Google Scholar]
- Horn, B.K.P. Hill shading and the reflectance map. Proc. IEEE 1981, 69, 14. [Google Scholar] [CrossRef]
- Shepard, M.K.; Campbell, B.A.; Bulmer, M.H.; Farr, T.G.; Gaddis, L.R.; Plaut, J. The roughness of natural terrain: A planetary and remote sensing perspective. J. Geophys. Res. 2001, 106, 32777–32795. [Google Scholar] [CrossRef]
- Beyer, R.A.; Kirk, R.L. Meter-scale slopes of candidate MSL landing sites from point photoclinometry. Space Sci. Rev. 2012, 170, 775–791. [Google Scholar] [CrossRef]
- Steinbrugge, G.; Voigt, J.R.C.; Schroeder, D.M.; Stark, A.; Haynes, M.S.; Scanlan, K.M.; Hamilton, C.W.; Young, D.A.; Hussmann, H.; Grima, C.; et al. The surface roughness of Europa derived from Galileo stereo images. Icarus 2020, 343, 113669. [Google Scholar] [CrossRef]
- Schenk, P.M.; Turtle, E.P. Europa’s impact craters. In Europa; Pappalardo, R.T., McKinnon, W.B., Khurana, K., Eds.; The University of Arizona Press: Tucson, AZ, USA, 2009; pp. 181–198. ISBN 978-0-8165-2844-8. [Google Scholar]
- Collins, G.C.; Nimmo, F. Chaotic terrain on Europa. In Europa; Pappalardo, R.T., McKinnon, W.B., Khurana, K., Eds.; The University of Arizona Press: Tucson, AZ, USA, 2009; pp. 259–282. ISBN 978-0-8165-2844-8. [Google Scholar]
- Leonard, E.J.; Patthoff, D.A.; Senske, D.A.; Collins, G.C. The Europa global geologic map. In Proceedings of the Planetary Geologic Mappers Annual Meeting, Knoxville, TN, USA, 12–14 June 2018. LPI Contribution No. 2066, id. 7008. [Google Scholar]
- Pappalardo, R.T.; Belton, M.J.S.; Breneman, H.H.; Carr, M.H.; Chapman, C.R.; Collins, G.C.; Denk, T.; Fagents, S.; Geissler, P.E.; Giese, B.; et al. Does Europa have a subsurface ocean? Evaluation of the geologic evidence. J. Geophys. Res. 1999, 104, 24015–24056. [Google Scholar] [CrossRef]
- Greenberg, R.; Hoppa, G.V.; Tufts, B.R.; Geissler, P.; Riley, J.; Kadel, S. Chaos on Europa. Icarus 1999, 141, 263–286. [Google Scholar] [CrossRef]
- Collins, G.C.; Head, J.W.; Pappalardo, R.T.; Spaun, N.A. Evaluation of models for the formation of chaotic terrain on Europa. J. Geophys. Res. 2000, 105, 1709–1716. [Google Scholar] [CrossRef]
- Kattenhorn, S.A.; Hurford, T. Tectonics of Europa. In Europa; Pappalardo, R.T., McKinnon, W.B., Khurana, K., Eds.; The University of Arizona Press: Tucson, AZ, USA, 2009; pp. 199–236. ISBN 978-0-8165-2844-8. [Google Scholar]
- Figueredo, P.H.; Greeley, R. Resurfacing history of Europa from pole-to-pole geological mapping. Icarus 2004, 167, 287–312. [Google Scholar] [CrossRef]
- Doggett, T.; Greeley, R.; Figueredo, P.; Tanaka, K. Geologic stratigraphy and evolution of Europa’s surface. In Europa; Pappalardo, R.T., McKinnon, W.B., Khurana, K., Eds.; The University of Arizona Press: Tucson, AZ, USA, 2009; pp. 137–160. ISBN 978-0-8165-2844-8. [Google Scholar]
- Hoyer, L.; Kattenhorn, S.A.; Watkeys, M.K. Multistage evolution and variable motion history of Agenor Linea, Europa. Icarus 2014, 232, 60–80. [Google Scholar] [CrossRef]
- Shean, D.E.; Alexanderov, O.; Moratto, Z.M.; Smith, B.E.; Joughin, I.R.; Porter, C.; Morin, P. An automated, open-source pipeline for mass production of digital elevation models (DEMs) from very-high resolution commercial stereo satellite imagery. ISPRS J. Photogram. Rem. Sens. 2016, 116, 101–117. [Google Scholar] [CrossRef]
- Fergason, R.L.; Hare, T.M.; Mayer, D.P.; Galuszka, D.M.; Redding, B.L.; Smith, E.D.; Shinaman, J.R.; Cheng, Y.; Otero, R.E. Mars 2020 terrain relative navigation flight product generation: Digital terrain model and orthorectified image mosaics. Lunar Planet. Sci. Conf. 2020, 51, 2020. [Google Scholar]
- Bland, M.T.; Becker, T.L.; Edmundson, K.L.; Roatsch, T.; Archinal, B.A.; Takir, D.; Patterson, G.W.; Collins, G.C.; Schenk, P.M.; Pappalardo, R.T.; et al. A new Enceladus global control network, image mosaic, and updated pointing kernels from Cassini’s 13-year mission. Earth Space Sci. 2018, 5, 604–621. [Google Scholar] [CrossRef]














Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bland, M.T.; Kirk, R.L.; Galuszka, D.M.; Mayer, D.P.; Beyer, R.A.; Fergason, R.L. How Well Do We Know Europa’s Topography? An Evaluation of the Variability in Digital Terrain Models of Europa. Remote Sens. 2021, 13, 5097. https://doi.org/10.3390/rs13245097
Bland MT, Kirk RL, Galuszka DM, Mayer DP, Beyer RA, Fergason RL. How Well Do We Know Europa’s Topography? An Evaluation of the Variability in Digital Terrain Models of Europa. Remote Sensing. 2021; 13(24):5097. https://doi.org/10.3390/rs13245097
Chicago/Turabian StyleBland, Michael T., Randolph L. Kirk, Donna M. Galuszka, David P. Mayer, Ross A. Beyer, and Robin L. Fergason. 2021. "How Well Do We Know Europa’s Topography? An Evaluation of the Variability in Digital Terrain Models of Europa" Remote Sensing 13, no. 24: 5097. https://doi.org/10.3390/rs13245097
APA StyleBland, M. T., Kirk, R. L., Galuszka, D. M., Mayer, D. P., Beyer, R. A., & Fergason, R. L. (2021). How Well Do We Know Europa’s Topography? An Evaluation of the Variability in Digital Terrain Models of Europa. Remote Sensing, 13(24), 5097. https://doi.org/10.3390/rs13245097






