Susceptibility Assessment for Landslide Initiated along Power Transmission Lines
Abstract
:1. Introduction
2. Study Area
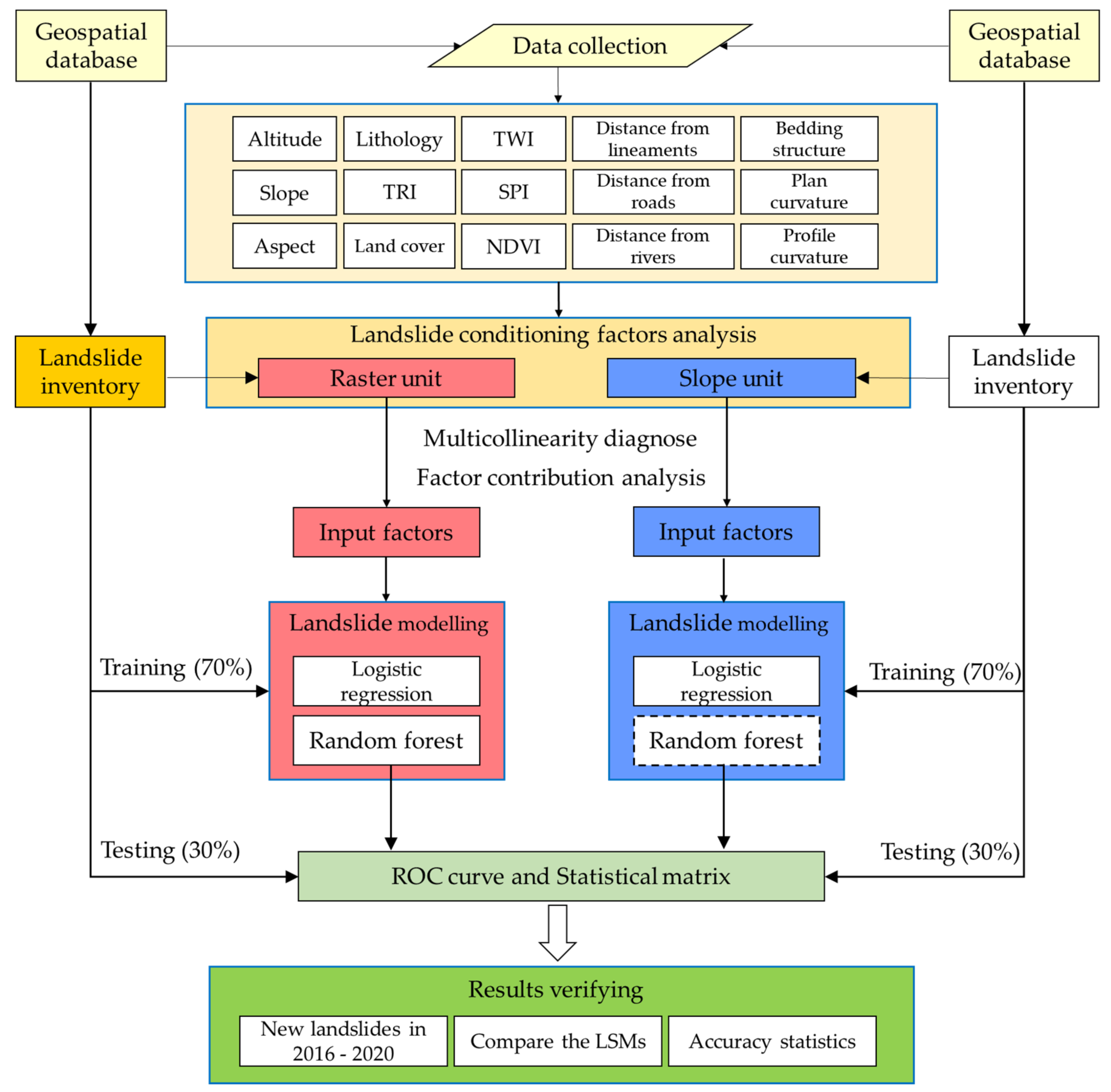
3. Methods
- (a)
- We construct a spatial database from various data sources and extract the landslide conditioning factors from the constructed database using two types of mapping units (raster and slope units).
- (b)
- We analyze the landslide conditioning factors through the optimize processes, which include multicollinearity diagnose and factor contribution analysis; then, the optimized factors are used to create the training and test datasets through resampling strategy.
- (c)
- We establish the susceptibility models using data-driven methods: logistic regression and random forest. The parameters of the involved machine learning methods are obtained by error and trial method. In addition, we assess and compare the models’ performance using some evaluation methods and an independent landslide dataset;
- (d)
- Lastly, we generate LSMs and comprehensively assess the overall performance of them. The main process is operated in ArcGIS.
3.1. Construction of a Spatial Database
3.1.1. Landslide Inventory
3.1.2. Landslide Conditioning Factors
3.1.3. Mapping Unit
3.1.4. Feature Selection Methods
3.2. Preparation of the Sample Datasets
3.3. Landslide Susceptibility Models
3.3.1. Logistic Regression
3.3.2. Random Forest
3.4. LSMs Performance and Validation
4. Results
4.1. Selection of Landslide Conditioning Factor
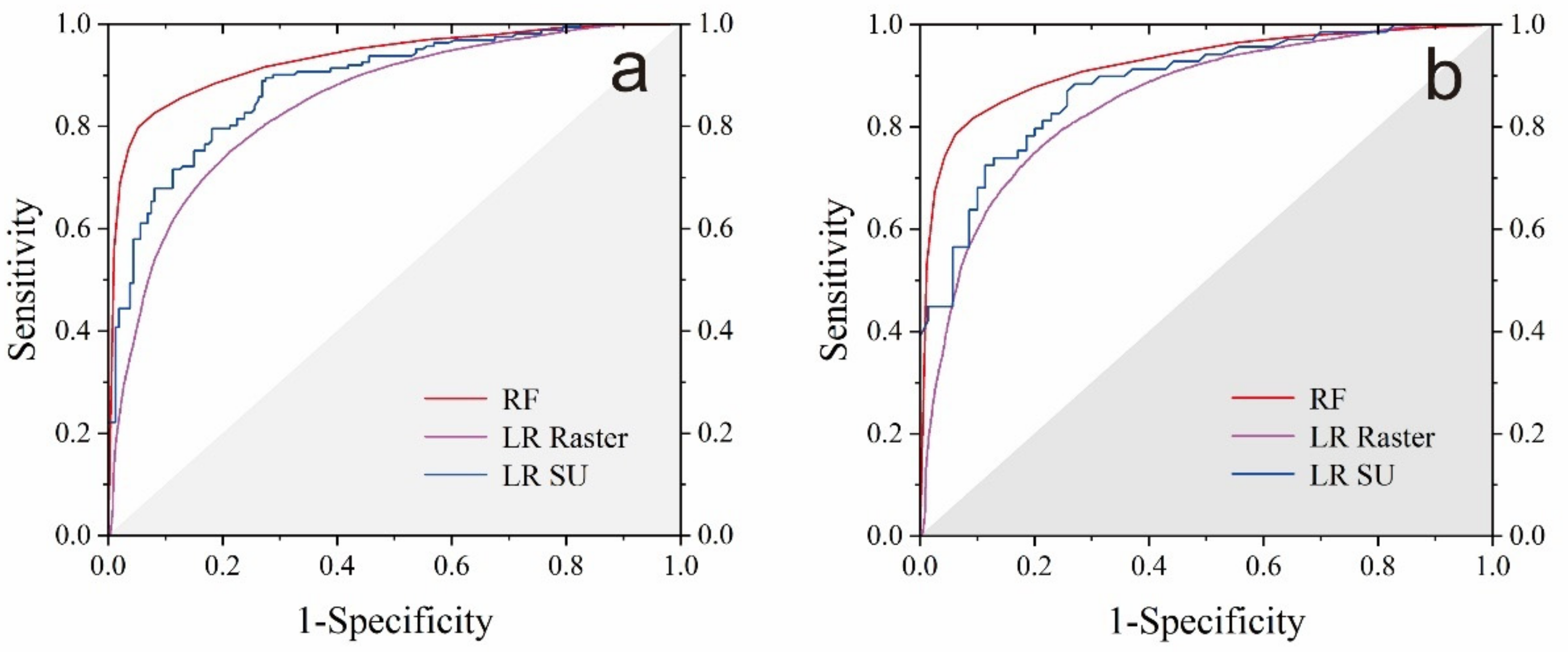
4.2. Validation and Model Comparison
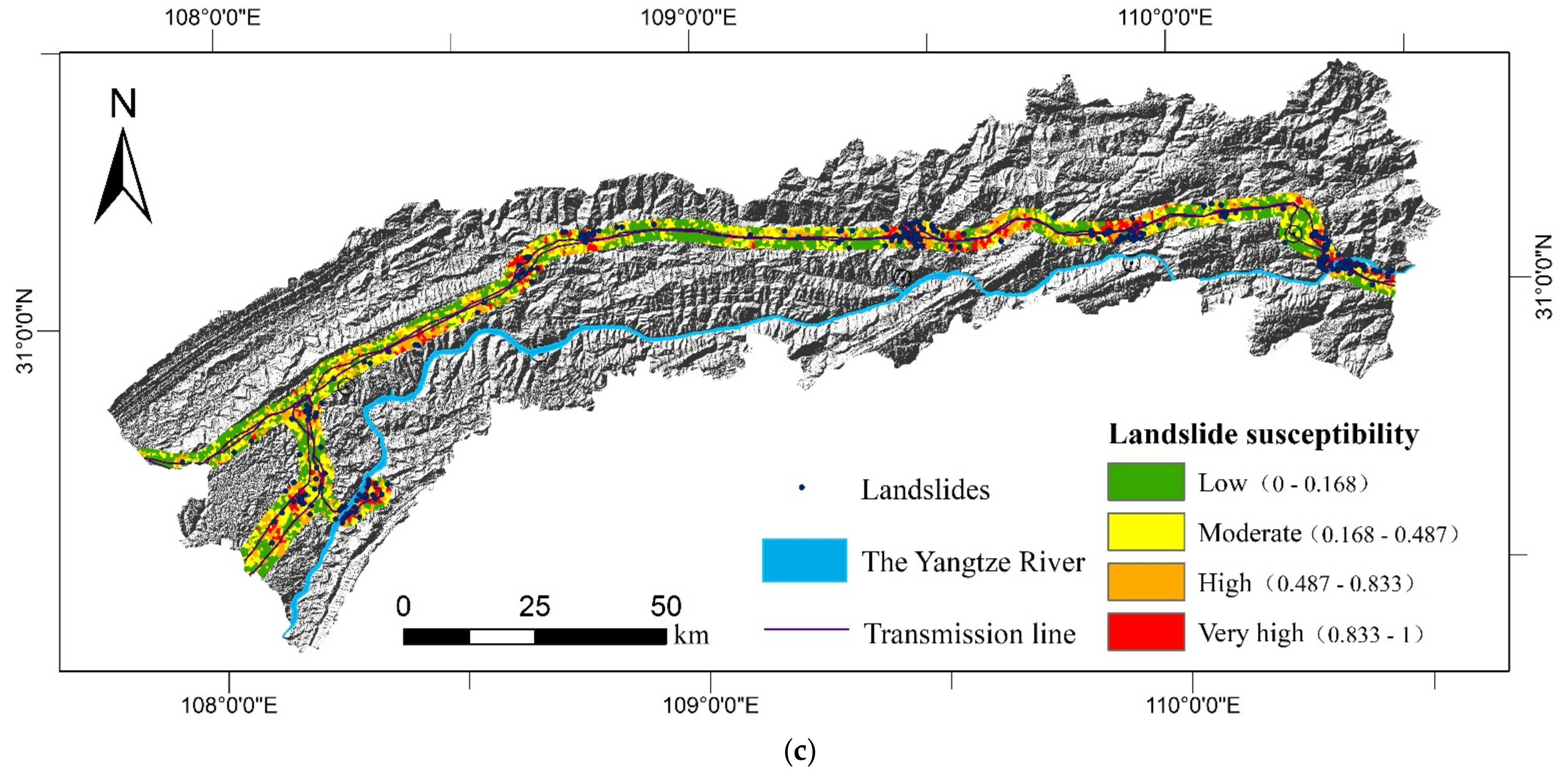
4.3. Producing LSMs and Result Evaluation
5. Discussion
5.1. Conditioning Factors
5.2. Scale Effects and Problem of Suitable Mapping Unit
5.3. Model Comparison and Performance Evaluation
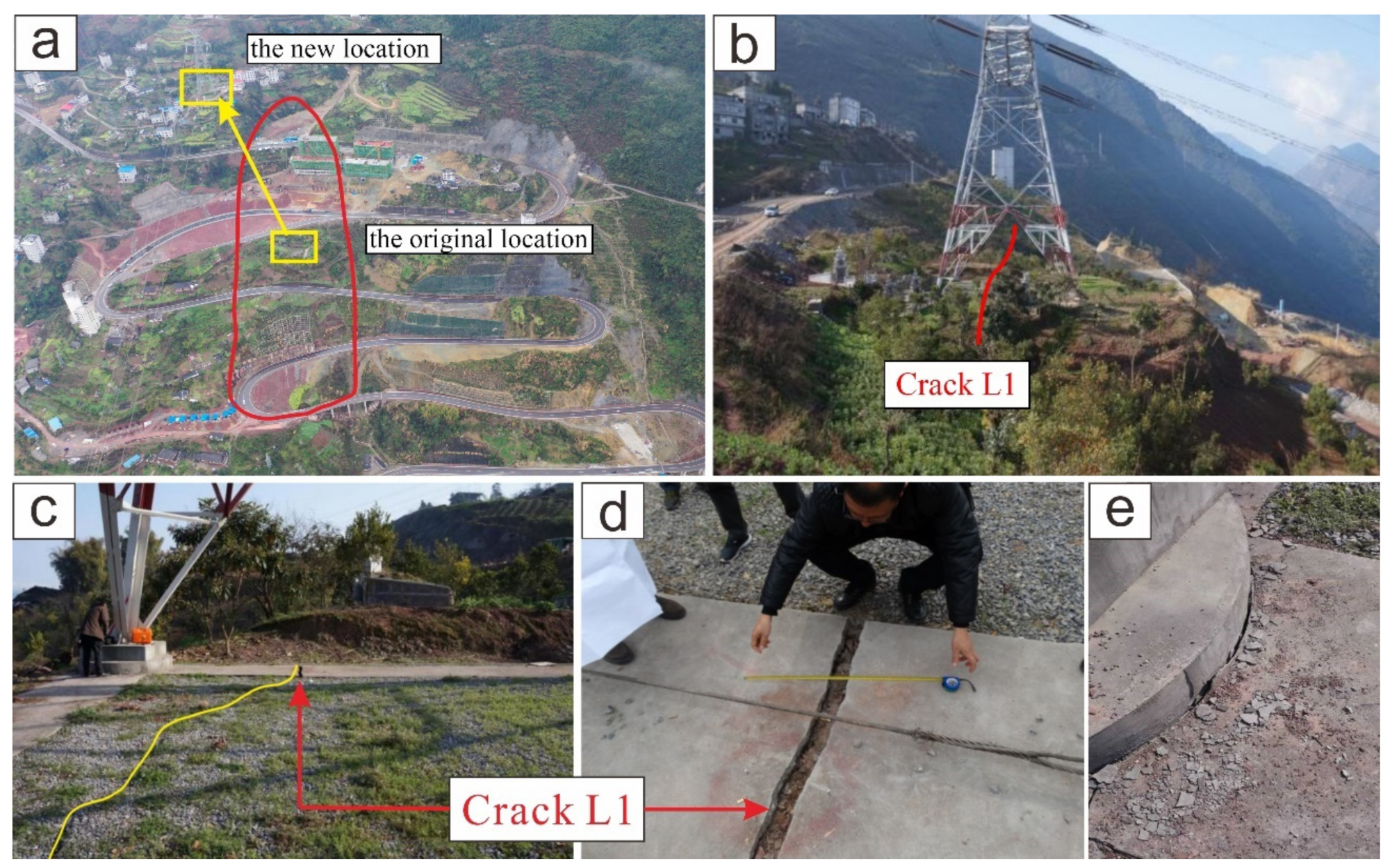
5.4. Challenge and Future Directions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arias, P.; Bellouin, N.; Coppola, E.; Jones, R.; Krinner, G.; Marotzke, J.; Naik, V.; Palmer, M.; Plattner, G.K.; Rogelj, J.; et al. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V.P., Zhai, A., Pirani, S.L., Connors, C., Péan, S., Berger, N., Caud, Y., Chen, L., Goldfarb, M.I., Gomis, M.I., et al., Eds.; MIPCC; Cambridge University Press: Cambridge, UK, 2021; In Press. [Google Scholar]
- Wu, D.; Zheng, X.; Xu, Y.; Olsen, D.; Xia, B.; Singh, C.; Xie, L. An open-source extendable model and corrective measure assessment of the 2021 Texas power outage. Adv. Appl. Energy 2021, 4, 100056. [Google Scholar] [CrossRef]
- Busby, J.W.; Baker, K.; Bazilian, M.D.; Gilbert, A.Q.; Grubert, E.; Rai, V.; Rhodes, J.D.; Shidore, S.; Smith, C.A.; Webber, M.E. Cascading risks: Understanding the 2021 winter blackout in Texas. Energy Res. Soc. Sci. 2021, 77, 102106. [Google Scholar] [CrossRef]
- Chang, J. What Happened behind the Nationwide Power Cuts? Available online: https://m.bjnews.com.cn/detail/163266456914638.html (accessed on 26 September 2021).
- State Grid Equipment Department and China Electric Power Research Institute. Investigation Report on Geological Hazards of Power Transmission Lines (Yearly Report), 2017–2021; State Grid Equipment Department and China Electric Power Research Institute: Beijing, China, 2021. [Google Scholar]
- Brabb, E.E. Innovative approaches to landslide hazard mapping. In Proceedings of the 4th International Landslide Symposium, Toronto, ON, Canada, 23–31 August 1985; pp. 307–324. [Google Scholar]
- Dai, F.; Lee, C.; Ngai, Y. Landslide risk assessment and management: An overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.-T. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef] [Green Version]
- Chalkias, C.; Polykretis, C.; Karymbalis, E.; Soldati, M.; Ghinoi, A.; Ferentinou, M. Exploring spatial non-stationarity in the relationships between landslide susceptibility and conditioning factors: A local modeling approach using geographically weighted regression. Bull. Int. Assoc. Eng. Geol. 2020, 79, 2799–2814. [Google Scholar] [CrossRef]
- Baeza, C.; Corominas, J. Assessment of shallow landslide susceptibility by means of multivariate statistical techniques. Earth Surf. Process. Landforms 2001, 26, 1251–1263. [Google Scholar] [CrossRef]
- Akgun, A. A comparison of landslide susceptibility maps produced by logistic regression, multi-criteria decision, and likelihood ratio methods: A case study at İzmir, Turkey. Landslides 2011, 9, 93–106. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Gokceoglu, C.; Aksoy, H. Landslide susceptibility mapping of the slopes in the residual soils of the Mengen region (Turkey) by deterministic stability analyses and image processing techniques. Eng. Geol. 1996, 44, 147–161. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Baum, R.L.; Godt, J.W.; Savage, W.Z. Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. Earth Surf. 2010, 118, 1999. [Google Scholar] [CrossRef]
- Goetz, J.N.; Guthrie, R.; Brenning, A. Integrating physical and empirical landslide susceptibility models using generalized additive models. Geomorphology 2011, 129, 376–386. [Google Scholar] [CrossRef]
- Tofani, V.; Bicocchi, G.; Rossi, G.; Segoni, S.; D’Ambrosio, M.; Casagli, N.; Catani, F. Soil characterization for shallow landslides modeling: A case study in the Northern Apennines (Central Italy). Landslides 2017, 14, 755–770. [Google Scholar] [CrossRef] [Green Version]
- Varnes, D. Landslide hazard zonation: A review of principles and practice. Nat. Hazards 1984, 3. Available online: https://trid.trb.org/view.aspx?id=281932 (accessed on 5 December 2021).
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar] [CrossRef]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef] [Green Version]
- Corominas, J.; Van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.-P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Int. Assoc. Eng. Geol. Environ. 2013, 73, 209–263. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Gokceoglu, C.; Sezer, E.A. A statistical assessment on international landslide literature (1945–2008). Landslides 2009, 6, 345–351. [Google Scholar] [CrossRef]
- Choi, J.; Oh, H.-J.; Lee, H.-J.; Lee, C.; Lee, S. Combining landslide susceptibility maps obtained from frequency ratio, logistic regression, and artificial neural network models using ASTER images and GIS. Eng. Geol. 2012, 124, 12–23. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Bui, D.T. Spatial prediction of landslides using a hybrid machine learning approach based on Random Subspace and Classification and Regression Trees. Geomorphology 2018, 303, 256–270. [Google Scholar] [CrossRef]
- Peethambaran, B.; Anbalagan, R.; Kanungo, D.; Goswami, A.; Shihabudheen, K. A comparative evaluation of supervised machine learning algorithms for township level landslide susceptibility zonation in parts of Indian Himalayas. Catena 2020, 195, 104751. [Google Scholar] [CrossRef]
- Xiao, T.; Yin, K.; Yao, T.; Liu, S. Spatial prediction of landslide susceptibility using GIS-based statistical and machine learning models in Wanzhou County, Three Gorges Reservoir, China. Acta Geochim. 2019, 38, 654–669. [Google Scholar] [CrossRef]
- Du, J.; Glade, T.; Woldai, T.; Chai, B.; Zeng, B. Landslide susceptibility assessment based on an incomplete landslide inventory in the Jilong Valley, Tibet, Chinese Himalayas. Eng. Geol. 2020, 270, 105572. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. An uncertainty and sensitivity analysis approach for GIS-based multicriteria landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 2014, 28, 610–638. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, L.; Kervyn, M.; Reichenbach, P.; Rossi, M.; Marchesini, I.; Alvioli, M.; Dewitte, O. Regional susceptibility assessments with heterogeneous landslide information: Slope unit- vs. pixel-based approach. Geomorphology 2020, 356, 107084. [Google Scholar] [CrossRef]
- Zêzere, J.; Pereira, S.; Melo, R.; Oliveira, S.; Garcia, R. Mapping landslide susceptibility using data-driven methods. Sci. Total Environ. 2017, 589, 250–267. [Google Scholar] [CrossRef]
- Eeckhaut, M.; Reichenbach, P.; Guzzetti, F.; Rossi, M.; Poesen, J. Combined landslide inventory and susceptibility assessment based on different mapping units: An example from the Flemish Ardennes, Belgium. Nat. Hazards Earth Syst. Sci. 2009, 9, 507–521. [Google Scholar] [CrossRef] [Green Version]
- Domènech, G.; Alvioli, M.; Corominas, J. Preparing first-time slope failures hazard maps: From pixel-based to slope unit-based. Landslides 2019, 17, 249–265. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Wang, R.; Jiang, Y.; Liu, H.; Wei, Z. GIS-based logistic regression for rainfall-induced landslide susceptibility mapping under different grid sizes in Yueqing, Southeastern China. Eng. Geol. 2019, 259, 105147. [Google Scholar] [CrossRef]
- Peng, L.; Niu, R.; Huang, B.; Wu, X.; Zhao, Y.; Ye, R. Landslide susceptibility mapping based on rough set theory and support vector machines: A case of the Three Gorges area, China. Geomorphology 2014, 204, 287–301. [Google Scholar] [CrossRef]
- Zhu, A.-X.; Wang, R.; Qiao, J.; Qin, C.-Z.; Chen, Y.; Liu, J.; Du, F.; Lin, Y.; Zhu, T. An expert knowledge-based approach to landslide susceptibility mapping using GIS and fuzzy logic. Geomorphology 2014, 214, 128–138. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from Longju in the Three Gorges Reservoir area, China. Comput. Geosci. 2018, 112, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Fu, Z.; Wang, Y.; Tang, H.; Yan, J.; Gong, W.; Yao, W.; Criss, R.E. Susceptibility of reservoir-induced landslides and strategies for increasing the slope stability in the Three Gorges Reservoir Area: Zigui Basin as an example. Eng. Geol. 2019, 261, 105279. [Google Scholar] [CrossRef]
- Xiao, T.; Segoni, S.; Chen, L.; Yin, K.; Casagli, N. A step beyond landslide susceptibility maps: A simple method to investigate and explain the different outcomes obtained by different approaches. Landslides 2020, 17, 627–640. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Shi, S.; Wen, H.; Xu, J.; Zhou, X.; Wu, J. A hybrid optimization method of factor screening predicated on GeoDetector and Random Forest for Landslide Susceptibility Mapping. Geomorphology 2021, 379, 107623. [Google Scholar] [CrossRef]
- Sun, D.; Xu, J.; Wen, H.; Wang, D. Assessment of landslide susceptibility mapping based on Bayesian hyperparameter optimization: A comparison between logistic regression and random forest. Eng. Geol. 2021, 281, 105972. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, D.; Wen, H.; Zhang, H.; Zhang, F. Comparison of Random Forest Model and Frequency Ratio Model for Landslide Susceptibility Mapping (LSM) in Yunyang County (Chongqing, China). Int. J. Environ. Res. Public Health 2020, 17, 4206. [Google Scholar] [CrossRef]
- Ferlisi, S.; Marchese, A.; Peduto, D. Quantitative analysis of the risk to road networks exposed to slow-moving landslides: A case study in the Campania region (southern Italy). Landslides 2021, 18, 303–319. [Google Scholar] [CrossRef]
- Jaiswal, P.; van Westen, C.J.; Jetten, V. Quantitative landslide hazard assessment along a transportation corridor in southern India. Eng. Geol. 2010, 116, 236–250. [Google Scholar] [CrossRef]
- Das, I.; Stein, A.; Kerle, N.; Dadhwal, V. Probabilistic landslide hazard assessment using homogeneous susceptible units (HSU) along a national highway corridor in the northern Himalayas, India. Landslides 2011, 8, 293–308. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Chen, H.; Zhao, B.; Tang, H.; Lin, Z.; Xie, Z.; Lv, L.; Zhong, P.; Zhao, B. A comparison of five methods in landslide susceptibility assessment: A case study from the 330-kV transmission line in Gansu Region, China. Environ. Earth Sci. 2018, 77, 662. [Google Scholar] [CrossRef]
- Chung, C.-J.F.; Fabbri, A.G. Validation of Spatial Prediction Models for Landslide Hazard Mapping. Nat. Hazards 2003, 30, 451–472. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- Petschko, H.; Brenning, A.; Bell, R.; Goetz, J.; Glade, T. Assessing the quality of landslide susceptibility maps—case study Lower Austria. Nat. Hazards Earth Syst. Sci. 2014, 14, 95–118. [Google Scholar] [CrossRef] [Green Version]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Corominas, J. The angle of reach as a mobility index for small and large landslides. Can. Geotech. J. 1996, 33, 260–271. [Google Scholar] [CrossRef]
- Yin, K.; Chen, L.; Ma, F.; Cheng, W. Practice and thinking of landslide risk management considering their secondary consequences in the Three-Gorges Reservoir, China. Landslides Eng. Slopes. Exp. Theory Pract. 2016, 3, 2097–2105. [Google Scholar] [CrossRef]
- Varnes, D.J. Slope movement types and processes. In Landslides, Analysis and Control, Special Report 176: Transportation Research Board; Schuster, R.L., Krizek, R.J., Eds.; National Academy of Sciences: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- Golovko, D.; Roessner, S.; Behling, R.; Wetzel, H.-U.; Kleinschmit, B. Evaluation of Remote-Sensing-Based Landslide Inventories for Hazard Assessment in Southern Kyrgyzstan. Remote Sens. 2017, 9, 943. [Google Scholar] [CrossRef] [Green Version]
- Alvioli, M.; Marchesini, I.; Reichenbach, P.; Rossi, M.; Ardizzone, F.; Fiorucci, F.; Guzzetti, F. Automatic delineation of geomorphological slope units with r.slopeunits v1.0 and their optimization for landslide susceptibility modeling. Geosci. Model. Dev. 2016, 9, 3975–3991. [Google Scholar] [CrossRef] [Green Version]
- Camilo, D.C.; Lombardo, L.; Mai, P.M.; Dou, J.; Huser, R. Handling high predictor dimensionality in slope-unit-based landslide susceptibility models through LASSO-penalized Generalized Linear Model. Environ. Model. Softw. 2017, 97, 145–156. [Google Scholar] [CrossRef] [Green Version]
- Alvioli, M.; Guzzetti, F.; Marchesini, I. Parameter-free delineation of slope units and terrain subdivision of Italy. Geomorphology 2020, 358, 107124. [Google Scholar] [CrossRef]
- Schlögel, R.; Marchesini, I.; Alvioli, M.; Reichenbach, P.; Rossi, M.; Malet, J.-P. Optimizing landslide susceptibility zonation: Effects of DEM spatial resolution and slope unit delineation on logistic regression models. Geomorphology 2018, 301, 10–20. [Google Scholar] [CrossRef]
- Chen, L.; Guo, Z.; Yin, K.; Shrestha, D.P.; Jin, S. The influence of land use and land cover change on landslide susceptibility: A case study in Zhushan Town, Xuan’en County (Hubei, China). Nat. Hazards Earth Syst. Sci. 2019, 19, 2207–2228. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. Improved Use of Continuous Attributes in C4. J. Artif. Intell. Res. 1996, 4, 77–90. [Google Scholar] [CrossRef] [Green Version]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2012, 36, 27–46. [Google Scholar] [CrossRef]
- Cox, D.R. The Regression Analysis of Binary Sequences. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1958, 20, 215–232. [Google Scholar] [CrossRef]
- Heckmann, T.; Gegg, K.; Gegg, A.; Becht, M. Sample size matters: Investigating the effect of sample size on a logistic regression susceptibility model for debris flows. Nat. Hazards Earth Syst. Sci. 2014, 14, 259–278. [Google Scholar] [CrossRef] [Green Version]
- Budimir, M.E.A.; Atkinson, P.M.; Lewis, H.G. A systematic review of landslide probability mapping using logistic regression. Landslides 2015, 12, 419–436. [Google Scholar] [CrossRef] [Green Version]
- Lombardo, L.; Mai, P.M. Presenting logistic regression-based landslide susceptibility results. Eng. Geol. 2018, 244, 14–24. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Catani, F.; Lagomarsino, D.; Segoni, S.; Tofani, V. Landslide susceptibility estimation by random forests technique: Sensitivity and scaling issues. Nat. Hazards Earth Syst. Sci. 2013, 13, 2815–2831. [Google Scholar] [CrossRef] [Green Version]
- Rossi, M.; Guzzetti, F.; Reichenbach, P.; Mondini, A.C.; Peruccacci, S. Optimal landslide susceptibility zonation based on multiple forecasts. Geomorphology 2010, 114, 129–142. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Han, Z.; Pham, B.T. Improved landslide assessment using support vector machine with bagging, boosting, and stacking ensemble machine learning framework in a mountainous watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
- Gupta, R.; Kanungo, D.; Arora, M.; Sarkar, S. Approaches for comparative evaluation of raster GIS-based landslide susceptibility zonation maps. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 330–341. [Google Scholar] [CrossRef]
- O’Brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Guzzetti, F.; Gariano, S.L.; Peruccacci, S.; Brunetti, M.T.; Marchesini, I.; Rossi, M.; Melillo, M. Geographical landslide early warning systems. Earth-Sci. Rev. 2020, 200, 102973. [Google Scholar] [CrossRef]
- Segoni, S.; Tofani, V.; Rosi, A.; Catani, F.; Casagli, N. Combination of Rainfall Thresholds and Susceptibility Maps for Dynamic Landslide Hazard Assessment at Regional Scale. Front. Earth Sci. 2018, 6, 85. [Google Scholar] [CrossRef] [Green Version]
- Pregnolato, M.; Ford, A.; Glenis, V.; Wilkinson, S.; Dawson, R. Impact of Climate Change on Disruption to Urban Transport Networks from Pluvial Flooding. J. Infrastruct. Syst. 2017, 23, 04017015. [Google Scholar] [CrossRef] [Green Version]
- Lazzari, M.; Piccarreta, M. Landslide Disasters Triggered by Extreme Rainfall Events: The Case of Montescaglioso (Basilicata, Southern Italy). Geosciences 2018, 8, 377. [Google Scholar] [CrossRef] [Green Version]
- Tsuguti, H.; Seino, N.; Kawase, H.; Imada, Y.; Nakaegawa, T.; Takayabu, I. Meteorological overview and mesoscale characteristics of the Heavy Rain Event of July 2018 in Japan. Landslides 2018, 16, 363–371. [Google Scholar] [CrossRef]


| Data Type | Data Source | Data Form | Data Scale |
|---|---|---|---|
| DEM | ASTER satellite | raster | 30 m |
| Land cover | Chongqing Municipal Bureau of Land and Resources | raster | 30 m |
| Geological map | National geological data museum | Vector | 1:200,000 |
| Satellite image | Landsat-8 OLI data | raster | 30 m |
| Administrative division | Geospatial Data Cloud platform | Vector | 1:100,000 |
| Water system | Geospatial Data Cloud platform | Vector | 1:100,000 |
| Road network | Geospatial Data Cloud platform | Vector | 1:100,000 |
| Power transmission towers | China Electric Power Research Institute | Vector (Coordinate) | / |
| Factors | Class | Classification Standard |
|---|---|---|
| Altitude (m) | 5 | 1. <400; 2. 400–600; 3. 600–800; 4. 800–1000; 5. >1000 |
| Slope (°) | 5 | 1. <10°; 2. 10°~20°; 3. 20°~30°; 4. 30°~40°; 5. 40°~90°; |
| Aspect | 9 | 1. Flat; 2. North; 3. Northeast; 4. East; 5. Southeast; 6. South; 7. Southwest; 8. West; 9. Northwest |
| Profile curvature | 6 | 1. <−2; 2. −2~−1; 3. −1~0; 4. 0~1; 5. 1~2; 6. >2; |
| Plan curvature | 6 | 1. <−2; 2. −2~−1; 3. −1~0; 4. 0~1; 5. 1~2; 6. >2; |
| Lithology | 8 | 1.J3p/J3sn/J2x; 2. J2s/J2xs; 3. J2q/J1t; 4. J1-2z/J1zl; 5. T3-J1x/T3xj/T3j; 6. T2b; 7. T1d/T1-2j; 8.Q; |
| Bedding Structure | 7 | 1.Horizontal strata slope; 2. Over-dip slope; 3. Under-dip slope; 4. Dip-oblique slope; 5. Transverse slope; 6. Anticlinal oblique slope; 7. Anticlinal slope; |
| TRI | 6 | 1. 1.0~1.1; 2. 1.1~1.3; 3. 1.3~1.5; 4. 1.50~2.0; 6. >2; |
| SPI | 7 | 1. 0~1; 2. 1~2; 3. 2~3; 4. 3~4; 5. 4~5; 6. 5~6; 7. >6; |
| TWI | 5 | 1. 1.88~4.73; 2. 4.73~5.94; 3. 5.94~7.36; 4. 7.36~9.36; 5. 9.36~20.03; |
| NDVI | 7 | 1. <0.10; 2. 0.10–0.20; 3. 0.20–0.30; 4. 0.30–0.40; 5. 0.40–0.50; 6. 0.50–0.60; 7. >0.60 |
| Distance from rivers (m) | 6 | 1. <100; 2. 100~300; 3. 300~500; 4. 500~1000; 5. 1000~2000; 6. >2000; |
| Land cover | 9 | 1.cropland; 2. Forest; 3. Grassland; 4. Shrub-land; 5. Wetland; 6. Water; 7. Tundra; 8. Impervious surface; 9. Bare land |
| Distance from roads (m) | 6 | 1. <150; 2. 150~300; 3. 300~450; 4. 450~600; 5. 600~1000; 6. >1000; |
| Distance from lineaments (m) | 6 | 1. <1000; 2. 1000~2000; 3. 2000~3000; 4. 3000~4000; 5. 4000~5000; 6. >5000; |
| Mapping Unit | Numbers | Average Size (m2) | Minimum Size (m2) | Maximum Size (m2) | Number of Landslide Units | Percentage of Landslide Units % |
|---|---|---|---|---|---|---|
| Slope Unit | 6735 | 215,764 | 5610 | 1,514,390 | 231 | 3.43 |
| Grid cell Unit | 1,426,231 | 900 | 900 | 900 | 39, 190 | 2.75 |
| Conditioning Factors | Raster Unit | Slope Unit | |||||
|---|---|---|---|---|---|---|---|
| VIF | Tolerance | IGR | VIF | Tolerance | IGR | ||
| 1 | Altitude | 1.334 | 0.750 | 0.023 | 1.254 | 0.798 | 0.025 |
| 2 | TRI | 2.732 | 0.366 | 0.019 | 3.057 | 0.327 | 0.019 |
| 3 | Land cover | 1.265 | 0.790 | 0.019 | 1.126 | 0.888 | 0.043 |
| 4 | NDVI | 1.233 | 0.818 | 0.015 | 1.164 | 0.859 | 0.018 |
| 5 | Distance from rivers | 1.052 | 0.950 | 0.014 | 1.061 | 0.942 | 0.038 |
| 6 | TWI | 1.180 | 0.847 | 0.012 | / | / | / |
| 7 | Distance from roads | 1.214 | 0.824 | 0.012 | 1.161 | 0.861 | 0.019 |
| 8 | Slope | 2.941 | 0.340 | 0.012 | 2.211 | 0.452 | 0.022 |
| 9 | Lithology | 1.172 | 0.853 | 0.011 | 1.231 | 0.812 | 0.015 |
| 10 | SPI | 1.261 | 0.793 | 0.011 | / | / | / |
| 11 | Distance from lineaments | 1.095 | 0.913 | 0.010 | 1.064 | 0.939 | 0.014 |
| 12 | Plan curvature | 1.627 | 0.615 | 0.010 | 1.025 | 0.975 | 0.014 |
| 13 | Bedding Structure | 1.120 | 0.893 | 0.010 | 1.044 | 0.958 | 0.016 |
| 14 | Profile curvature | 1.515 | 0.660 | 0.010 | 1.220 | 0.819 | 0.016 |
| 15 | Aspect | 1.059 | 0.945 | 0.009 | 1.058 | 0.945 | 0.013 |
| Model Stage | AUC | ACC | Precision | TPR | TNR | MCC | RMSE | MAE | |
|---|---|---|---|---|---|---|---|---|---|
| Training | RF (Raster) | 0.927 | 0.867 | 0.826 | 0.929 | 0.805 | 0.740 | 0.359 | 0.133 |
| LR (Raster) | 0.846 | 0.771 | 0.762 | 0.787 | 0.756 | 0.543 | 0.478 | 0.229 | |
| LR (SU) | 0.882 | 0.793 | 0.786 | 0.797 | 0.779 | 0.577 | 0.457 | 0.207 | |
| Testing | RF (Raster) | 0.915 | 0.856 | 0.817 | 0.919 | 0.793 | 0.718 | 0.374 | 0.144 |
| LR (Raster) | 0.839 | 0.766 | 0.759 | 0.781 | 0.751 | 0.532 | 0.484 | 0.234 | |
| LR (SU) | 0.879 | 0.798 | 0.809 | 0.784 | 0.813 | 0.597 | 0.465 | 0.214 | |
| Susceptibility Level | Numbers of Landslides | Units in Landslide (A) | Units in Domain (B) | Proportion of Landslide in Total Landslide (C) | Proportion of Domain in Total Domain (D) | Proportion of Landslide in Domain (A/B) | |
|---|---|---|---|---|---|---|---|
| RF (Raster) | Low | 5 | 379 | 663,979 | 0.97% | 46.56% | 0.05% |
| Moderate | 20 | 1568 | 374,940 | 4.00% | 26.29% | 0.37% | |
| High | 76 | 13,140 | 276,480 | 33.53% | 19.39% | 4.24% | |
| Very high | 164 | 24,103 | 110,832 | 61.50% | 7.75% | 19.39% | |
| LR (Raster) | Low | 16 | 1627 | 584,948 | 4.15% | 41.01% | 0.28% |
| Moderate | 32 | 5412 | 415,503 | 13.81% | 29.13% | 1.30% | |
| High | 85 | 13,054 | 283,220 | 33.31% | 19.86% | 4.61% | |
| Very high | 132 | 19,097 | 142,560 | 48.73% | 10.00% | 13.40% | |
| LR (SU) | Low | 8 | 8 | 2670 | 3.46% | 39.64% | 0.30% |
| Moderate | 43 | 38 | 2036 | 16.45% | 30.23% | 1.87% | |
| High | 86 | 82 | 1357 | 35.50% | 20.15% | 6.04% | |
| Very high | 128 | 103 | 672 | 44.59% | 9.98% | 15.32% | |
| Low | Moderate | High | Very High | |
|---|---|---|---|---|
| RF | 1 | 3 | 6 | 4 |
| LR (SU) | 1 | 3 | 4 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Yin, K.; Zhou, C.; Gui, L.; Liang, X.; Lin, W.; Zhao, B. Susceptibility Assessment for Landslide Initiated along Power Transmission Lines. Remote Sens. 2021, 13, 5068. https://doi.org/10.3390/rs13245068
Liu S, Yin K, Zhou C, Gui L, Liang X, Lin W, Zhao B. Susceptibility Assessment for Landslide Initiated along Power Transmission Lines. Remote Sensing. 2021; 13(24):5068. https://doi.org/10.3390/rs13245068
Chicago/Turabian StyleLiu, Shuhao, Kunlong Yin, Chao Zhou, Lei Gui, Xin Liang, Wei Lin, and Binbin Zhao. 2021. "Susceptibility Assessment for Landslide Initiated along Power Transmission Lines" Remote Sensing 13, no. 24: 5068. https://doi.org/10.3390/rs13245068
APA StyleLiu, S., Yin, K., Zhou, C., Gui, L., Liang, X., Lin, W., & Zhao, B. (2021). Susceptibility Assessment for Landslide Initiated along Power Transmission Lines. Remote Sensing, 13(24), 5068. https://doi.org/10.3390/rs13245068







