Abstract
Droughts are ranked among the most devastating agricultural disasters that occur naturally in the world. East Africa is the most vulnerable and drought-prone region worldwide. In this study, four drought indices were used as input variables for drought assessment from 1982 to 2015. This work applied the SMDM algorithm to the integrated approach of OLR and Hurst exponent. The Detrended Fluctuation Analysis (DFA) and Ordinary Least Square (OLR) were merged to compute the trend and persistence (Hurst exponent) of the drought indices. Result indicates that the OLR at time scale 1, 6, and 12 shows a similar distribution with positive (negative) trends scattered in the Northwest (Northeast and Southern) parts of the study area which differs with the OLR aggregated at a 3-month time scale. The percentage pixel distribution for OLR-1, OLR-3, OLR-6, and OLR-12 is 18.2 (81.8), 72.5 (27.5), 32.9 (67.1), and 36.9 (63.1) for increasing (decreasing) trends respectively. Additionally, results indicate that DFA-1 is highly persistent with few random pixels scattered around Ethiopia, South Sudan and Tanzania, with percentage pixels as 88.7, 11.3 and 0.1 representing h > 0.5, h = 0.5, and h < 0.5, respectively. DFA-6 shows high (low) pixels representing h > 0.5 (h > 1), respectively. Meanwhile, for DFA-3 and DFA-12, the distribution shows persistence and a random walk, respectively. Drought conditions may eventually persist, reverse or vary drastically in an unpredictable manner depending on the driving forces. Overall, the drought risk map at 1-, 3-, and 6-month aggregates has shown severe degradation in Southern Kenya and Tanzania while noticeable improvements are seen in western Ethiopia and South Sudan.
1. Introduction
Droughts are considered a serious natural hazard, especially in semi-arid regions where devastating and catastrophic damages are recorded [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15], and have been mainly categorized (on the basis of duration, impact and recovery rate) into meteorological (defined by a lack of precipitation over a certain period of time for a certain region), agricultural (defined by a period of declining soil moisture and reduced crop yields) and hydrological (defined by a reduced surface and subsurface water availability for a given water resource), and socio-economic drought, expressed to mean “a failure of water resource management to meet the supply and demand of water, taken as an economic good” [16,17,18,19]. The socio-economic definition of drought is a perspective that has not been applied to many studies/analyses of drought found in the literature as it is possibly seen as an outcome/impact of drought rather than a category of drought. Global estimates on the impacts of drought indicate that a total of 642 drought events were recorded globally between 1900 and 2013 resulting in the death of about 12 million people, directly affecting a population of over 2 billion, with estimated economic damage of about USD 135 billion [20,21]. Love [22], Masih et al. [21], Funk et al. [23,24,25], and Yang [26] confirm that the East African region ranks among the most vulnerable and drought-prone regions of the world with a high potential for increased risk of agricultural droughts, and a recent event recorded in 2016/2017. Hence, while the frequency and severity of drought within the region has increased in the last couple of decades, the situation is forecast to increase over the coming decades [27,28,29]. Therefore, it is considered necessary to continue investigations into better methods of understanding drought occurrence within the East Africa region as a critical step towards building resilience and adaptability among the population of the region, and indeed other semi-arid regions in other parts of Africa [30,31,32].
Although different studies have been conducted on the topic of drought related to food insecurity and poverty [21,22,24,25,26] and violence [33] within the region, Kalisa et al. [34] recently studied and analyzed drought within the East African region specifically focusing on the use of standardized precipitation index (SPI) as proposed by McKee et al. [35] and applied by Pramudya and Onishi [36]. Recently, the introduction of fractal methodology (Hurst exponent) in the study of long term memory in time series has been given significant attention [37]. OLR is a common technique that has been frequently applied to time series of environmental parameters to characterize trends over time [38]. The OLR is a simple and fast technique, but it has many limitations which include: sensitivity to data outliers and manifestation of symmetry around the high and low data values [37]. An integrated approach combining OLR and the Hurst exponent has been used by Igbawua et al. (2019), Tran et al. (2019), and Tong et al. (2018) to study persistence (sustainability) in vegetation development in a tropical [37,39] and subtropical [40] regions.
Drought suitability study takes into account a variety of climate and non-climate elements, such as natural system restrictions, compatibility with existing land uses, and existing land use policies, among others. Multi-criteria decision analysis (MCDA) is used to handle a wide range of difficulties in sustainable energy management, energy planning, transportation, manufacturing systems, water resource management, military operations, road safety, geographic information systems, budgeting and resource allocation, and a wide range of other domains where many diverse stake holders with variety of goals are brought together in participatory environments [41]. However, SMDM is considered most suitable as it can be used not only to assess the importance of options, but also to obtain insight into their spatial extent [42]. This capability can assist agriculturists in identifying drought-prone zones for future management. It is especially important when planning that tools do not give a prescriptive guidance for local planning and decision making. As a result, the technique provided here takes a comprehensive look at the use of SMDM approaches in local drought decision-making. Machine learning algorithms can also be applied to AHP multi-criteria decision-making to assess prioritization of variables [43].
The aims of this study are (1) to carry out a critical assessment of drought onset using drought indices at different time scales, (2) to determine the persistence and suitability of drought indices to understanding the largely unnoticed creeping drought which usually affects agriculture, and (3) to apply the SMDM process to produce a drought risk map of the study area. There is no single technique for characterizing drought conditions, and also there are a variety of drought indices that are available for drought studies. The variables required for use during the computation of agricultural, meteorological, and hydrological drought indices include: precipitation, temperature, potential evapotranspiration, and NDVI. These variables vary depending on the drought index and geographical location. Persistence, which employs Detrended Fluctuation Analysis (DFA), describes how the correlation between successive points in the monthly drought variables evolve as the temporal span increases. In summary, most drought episodes are not easy to detect at lower time scales; thus, fractal scaling methods are useful in this regard because they are able to assess changes in the data records both at long and short intervals of time covering the study period. An important advantage of DFA with respect to other conventional methods is that it considers the time series as whole and not as independent units.
2. Materials and Methods
2.1. Study Area
In this work, the study area selected across East Africa covers an area of about 4.32 million km2 from 11°43′52.58″S to 14°52′46.32″N and 24°7′17.6″E to 51°25′1.34″E comprising of Rwanda, Uganda, South Sudan, Tanzania, Ethiopia, Kenya, Somalia, and Burundi (Figure 1). The study area is bordered to the north, south, east, and west by North African countries, Southern Africa countries, the Indian Ocean, and Central African countries, respectively. The countries that directly border the Indian Ocean include Somalia, Tanzania, and Kenya. The region has an arid and semi-arid climate with an average annual rainfall between 800 and 1200 mm [44]. The region comprises Lake Victoria (70,000 km2) extending across the equator and some high mountains which include Mt. Kilimanjaro (5894 m), Mt. Kenya (5199 m), and Mt. Ruwenzoris (5120 m) [45]. The difficult and varying terrain affects the temperature in East Africa and the highland regions are cooler than the low land regions [46]. The influence of topography on rainfall is employed by its effect on the low-level flow and, in the highlands directs into a steady southerly current during the boreal summer [44]. Agriculture is the major source of land use in the study area and most individuals rely on it for their livelihood. Documented reports have shown that droughts tend to be more persistent, longer, and more serious in the boreal spring and summer over the study area with an abrupt decrease in the overall precipitation and water storage [47].
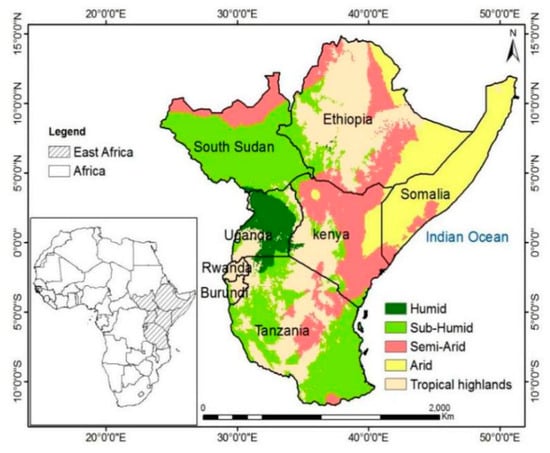
Figure 1.
Study Area.
2.2. Data
The data sets used in this study include: climatic data from the Climatic Research Unit (CRU) of University of East Anglia; and Advanced Very High-Resolution Radiometers (AVHRR) Global Inventory Modeling and Mapping Studies (GIMMS) third generation (NDVI3g). The CRU data are a collection of observation stations from meteorological stations of the world which is gridded into a global high resolution data set [48] and obtained from https://crudata.uea.ac.uk/cru/data/hrg/cru_ts_4.01/cruts.1709081022.v4.01/ retrieved on 22 April 2020. The GIMMS NDVI3g data records were obtained from https://ecocast.arc.nasa.gov/data/pub/gimms/3g.v1/ (30 August 2021) [49]. The 15-day data was composited into monthly values through a process known as Maximum Value Composite and pixels with annual values of less than 0.1 were considered non-vegetated and were subsequently expunged from study area. All the data sets were resampled to same resolution as NDVI. The summary of the data sets is shown in Table 1.

Table 1.
Data sets in this study.
2.3. Methods
2.3.1. Drought Indices
Four (4) drought indices were used in this work. The performance of each index during drought conditions over the whole study area was assessed and the four drought indices were used in this report to combine and produce a spatial drought risk map through a spatial multi-criterion decision making process. The indices include: standardized precipitation index (SPI), standardize precipitation evapotranspiration index (SPEI), temperature condition index (TCI), and vegetation condition index (VCI). SPI is ranked as the most importance drought parameter over the region according to [50]. The spatial maps of trend (slope) and persistence (DFA) from the drought indices were also computed. The criteria weighting technique according to Saaty’s [51] was done based on the statistical performance evaluation methods before the application of SMDM. SMDM was applied to merge the four drought indices into a single drought risk map for easy analysis and interpretation. Finally, a superimposed sustainability map of persistence (SMDM) and slope (SMDM) was obtained to capture drought changes at larger and shorter time scales. The flowchart of the work is show in Figure 2.
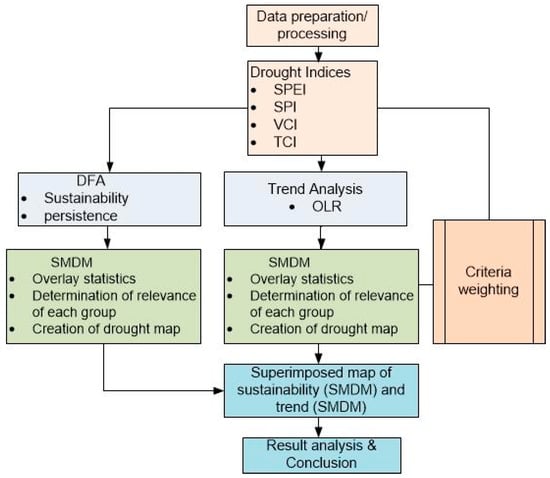
Figure 2.
Flowchart of the research work.
- (1)
- Standard Precipitation Index (SPI)
The SPI was developed by McKee et al. [35] and uses only precipitation data for its calculation. It fits a mathematical function to the time series of historical precipitation records. The algorithm for the computation of SPI fits the gamma distribution function which is given by Haroon et al. [4] and Kalisa et al. [34] as:
where α and β are the scale and shape parameters, respectively. is an ordinary gamma function of β.
The probability distribution function is given by
A composite distribution function is used in case the precipitation distribution contains zero values, and represents the probability of a zero evaluated by , in which N is the number zeros in the precipitation series with a temporal span of n.
Finally, SPI is estimated by
where .
Or
where .
The constants are given as
- (2)
- Standard Precipitation Evapotranspiration Index (SPEI)
SPEI is a drought index that is based on temperature and precipitation data which accounts for the water requirement due to evapotranspiration [52]. The difference between precipitation and potential evapotranspiration (PET) indicates a measure of water surplus or deficit for a particular time period and this is compared over time and subsequently standardized to obtain the value of SPEI. Firstly, the water budget was estimated by:
where is the precipitation data records.
After estimating the water budget using Equation (6), the value of was replaced by precipitation adopting the same algorithm earlier explained in Equations (1)–(5). The estimation of SPEI is similar to SPI. A three-parameter gamma distribution which can accommodate both positive and negative values since the value of in Equation (6) can be either positive or negative. Further details about the algorithm are given by Ogunrinde et al. [53].
- (3)
- Vegetation Condition Index (VCI)
The Vegetation Condition Index is given by [54,55,56]
where is the NDVI at any time period i. and are the long term maximum and minimum NDVI records, respectively. We used VCI-1, VCI-3, VCI-6, and VCI-12 aggregated at 1, 3, 6, and 12 months, respectively.
- (4)
- Temperature Condition Index (TCI)
The Temperature Condition Index (TCI) [54,55,56]
where is the temperature at any time period i. and are the long term maximum and minimum temperature records, respectively. We used TCI-1, TCI-3, TCI-6, and TCI-12 aggregated at 1, 3, 6, and 12 months, respectively. The ranges of values and their respective classes for the indices are shown in Table 2.

Table 2.
Drought indices and their classes.
2.3.2. Detrended Fluctuation Analysis (DFA)
In this work, the detrended fluctuation analysis (DFA) was applied to the monthly drought indices. The DFA technique, which is robust for detecting long-term memory in time series, was developed by Kantelhardt et al. [57], a modification of the method reported by Peng et al. [58]. Considering a monthly time series of drought indices then the following methods were adopted:
- Subtract the seasonal trend from the data.
- Create a profile .
- Divide the time series into equal non-overlapping segments of fixed length to determine the fluctuations in G.
- Compute the ideal polynomial fit of the profile and obtain the variance (Equation (1)) around the fit for each segment ,
- Take the mean of over all the segments () to get the value of the fluctuation function .
The relationship between and [58], according to Equation (10) indicates the presence of power law (fractal) scaling. The value of h represents the scaling Hurst exponent. If h > 0.5 the series is persistent (long range correlated), when h < 0.5 the series is non-persistent (long range anti-correlated), and for h = 0.5 the series is random.
2.3.3. Spatial Multi-Criterion Decision Making (SMDM)
Spatial multi-criteria decision-making (SMDM) is a technique that is employed in combining and converting spatial data into a decision making tool, an approach based on pairwise comparisons which was proposed by Saaty [51]. The SMDM method involves input data to be of geographical origin. The analytic hierarchy process (AHP) is the most widely accepted method and is considered by many as the most reliable multi-criteria decision making method. A recent report by Karleuša et al. [59] indicated that AHP is one of the best methods for multi-criterion decision making. The Analytical Hierarchy Process is one of the frequently used SMDM techniques applied in decision making. More details about the AHP method can be obtained from the following documented reports [60].
According to Saaty [51], the Eigen weight equation is given as:
where A is the matrix obtained from pairwise comparison, is the maximum Eigen value, and is the eigenvector [51]. The coordinates of the eigenvectors are divided by their sum (normalized) to produce the weights of the criteria.
The consistency of AHP is given by the consistency ratio (CR). CR shows the probability that the pairwise selection was done without bias. A CR of less than 10% indicates that a reasonable level of consistency was ensured.
where CI and RI are the consistency and random indices [60,61]
Prior to the application of the AHP, we applied correlation (r) analysis to study the relationship among the drought indices.
After generating the AHP criterion weights, OLR, and DFA analysis were superimposed at different time scales via SMDM to produce the final drought risk map of the study area. OLR measures the trends in the droughts indices while the DFA measures the long term memory of the data records (persistence) which describes the tendency of the records to reverse strongly or converge in a particular direction. The Hurst exponent (h) from DFA is used in fractal methodology to study persistence of data series [57,58].
The slope (trend) from an OLR is given as
where and are the dependent and independent quantities, respectively.
The proposed drought trends based on SPEI, SPI, VCI, and TCI at p < 0.05 integrated with the Hurst exponent are shown in Table 3.

Table 3.
Future drought trends based on SPEI, SPI, VCI, and TCI at p < 0.05 integrated with the Hurst exponent.
3. Results and Discussion
3.1. Precipitation Records of 34 Years over East Africa
Figure 3 shows the geographical distribution of precipitation in the study area. The northwestern and western regions and parts of the southern region received a high amount of precipitation compared to the northeastern region over the course of 34 years. Generally, the northwestern and western regions (high latitudes) received a high amount of precipitation compared to the southern region (low latitudes).
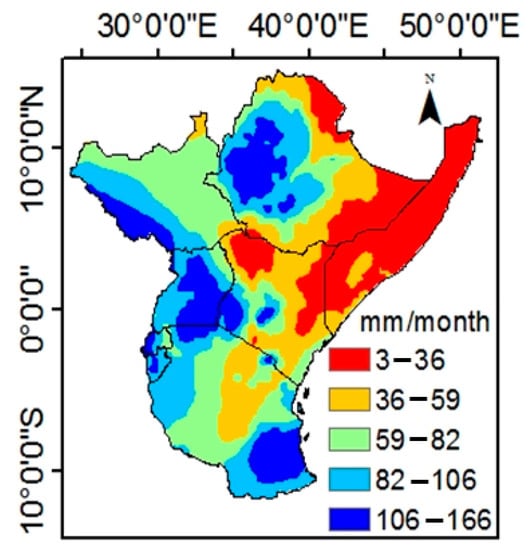
Figure 3.
Monthly mean precipitation (mm) in East Africa.
3.2. Analysis of Drought Indices
In Figure 4, the well-known historic drought episodes of 2005/06, 2009/10, and 2011/12 and the flood episode of 1997 [50,62,63,64] are well captured and represented by the SPEI and SPI compared to VCI and TCI. Meanwhile, VCI and TCI displayed more dry conditions between 2000 and 2015 compared to the other drought indices. The drought episodes of 1984/85, 2002/03, and 2010/11 were clearly outlined and discussed by Haile et al. [47]. It is on record that the 2011/12 drought was the worst recorded drought year in East Africa in recent decades, when countries such as Somalia, Kenya, and Ethiopia received low precipitation and the episode extended to 2013. In addition, the 1997/98 flood year which was caused by El Nino has been well captured by SPEI and SPI including all the other indices, as shown in Figure 4.
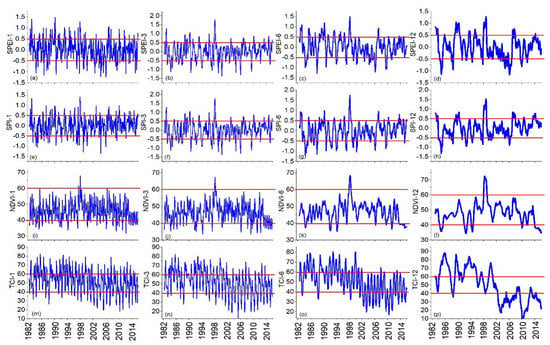
Figure 4.
Time series for SPEI, SPI, VCI and TCI from 1982 to 2015. The space in between the two red lines show normal conditions.
In Figure 5, the result shows mean spatial 1–12 month aggregated VCI and TCI grouped according to the ranges given in Table 2. The spatial representation of SPEI and SPI (though not displayed in Figure 5) indicated normal values for all the time scales. VCI-1 indicated mean drought conditions from severely dry to mildly wet while VCI-3, 6, and 12 indicated mean drought conditions from severely dry to moderately wet. In addition, TCI-1, 3, and 12 indicated drought conditions from mildly dry to mildly wet while TCI-6 ranged from normal to mildly wet conditions. Arguably, normal drought conditions dominated the study area for all the time scales followed by mildly dry. Other drought conditions, such as severely dry, moderately dry, and moderately wet conditions, were found in small percentages. Mildly dry conditions were located in parts of Ethiopia, Kenya, South Sudan, and a few scattered pixels in Uganda and Tanzania while for VCI-12, mildly dry pixels were distributed in South Sudan, northern Ethiopia, northern Kenya, and some few pixels scattered in Uganda. The rest of the pixels showed normal drought conditions.
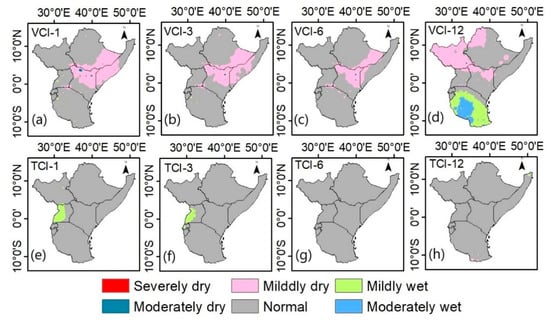
Figure 5.
Mean of (a–d) VCI-1 to VCI-12 and (e–h) TCI-1 to TCI-12.
In Table 3, the values for all drought indices do not appear to be in the same range. Prior to the analysis, all the variables were scaled and normalized within the same range to avoid the effects that might arise from gradient descent. Having data records within a similar scale can help the gradient move smoothly for all data points at the same rate. From Table 4, SPEI at all-time aggregate shows significant positive correlation with SPI while SPEI shows significant positive correlation with VCI at all-time scales except SPEI versus VCI-6 and VCI-12. Further, SPEI-1, SPEI-6, and SPEI-12 show significant correlations with TCI, except SPEI-3 versus VCI-1 to 6. Additionally, for SPI versus VCI, there exist high positive correlations at almost all the time scales, but low insignificant correlations in VCI versus TCI, except TCI-1 versus VCI-3 with a significant correlation coefficient of 0.40.

Table 4.
Correlation coefficient between different drought indices across East Africa. The asterisk * and ** shows significance at p < 0.05 and p < 0.001, respectively.
3.3. Persistence in Drought over East Africa
Figure 6 shows the DFA values of the four drought indices. DFA describes persistence in data records. Persistence is referred to as time series fluctuations of data which are expected to be succeeded by subsequent deviations in a similar manner [65]. Persistence (anti-persistence) means that any increases in data records are more likely to be succeeded by increases (decreases) over time [34,66]. The DFA approach measures the direct and indirect changes which are very hard to be explained by an ordinary least square regression model (Figure 7). Therefore, when the fractal Hurst exponent from DFA and ordinary least square regression are superimposed, more details concerning sustainability are exposed and better visualized.

Figure 6.
Spatial DFA analysis for (a–d) SPI, (e–h) SPEI, (i–l) VCI, and (m–p) TCI from 1982 to 2015.
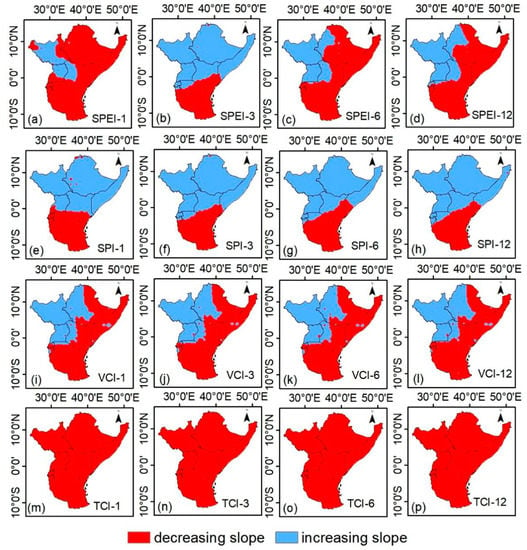
Figure 7.
Spatial regression slope analysis for (a–d) SPEI, (e–h) SPI, (i–l) VCI, and (m–p) TCI from 1982 to 2015.
In Figure 7, the spatial ordinary regression of the four drought indices has been presented at different time scales. The result shows that the spatial distribution of SPEI-3 with positive (negative) trends in the upper (lower) sections of the study area correlates with SPI-1 to 12 while the spatial distribution of SPEI-6 and 12 correlates with VCI-1 to 12. The positive trends in VCI-1 to 12 are scattered around the North West and Western regions of East Africa over South Sudan, parts of Ethiopia, Uganda, and Lake Victoria. Meanwhile, TCI-1 to 12 shows negative trends in OLR domain-wise. Table 5 shows percentage changes in pixels for DFA and OLR revealing negative (positive) trends for SPEI-1, SPEI-3, SPEI-6, and SPEI-12 including 81.8 (18.2), 27.5 (72.5), 67.1 (32.9), and 63.1 (36.9)%, respectively, and negative (positive) trends for SPI-1, SPI-3, SPI-6, and SPI-12 including 30.2 (69.8), 27.6 (72.4), 29.6 (70.4), and 28.1 (71.9)%, respectively. For VCI-1 to 12, about 59.3 (40.7), 60.0 (40.0), 60.2 (39.8), and 59.6 (40.4)% pixels indicated negative (positive) trends, respectively.

Table 5.
Percentage distribution of pixels for (a) OLR and (b) DFA for all the four indices.
3.4. Spatial Multi-Criterion Decision Making
The performance-based statistical analysis has been done in the previous section to show the indices that have more influence so that a decision matrix with linear weights will be produced to actually overlay the different indices to produce a single drought sustainability map for use by agriculturists and policy makers. In the application of AHP, the basic requirement is the determination of weights for the selected input variables [60]. Criterion weights were computed by comparing and contrasting two variables at a time using pairwise comparison matrix according to Saaty’s method [51]. We applied the model statistics comparison techniques earlier discussed in previous sections to prepare and discriminate the input variables according to their level of influence. The pairwise criterion matrix with the respective weights is given in Table 6. The consistency ratio CR was obtained as 2.1%, which is within the acceptable limit of <10%.

Table 6.
Pairwise criterion matrix with weights.
The SMDM was achieved by the weighted linear combination overlay toolbox in ArcGIS 10.5.1, with the additive weights computed using the AHP method. The pairwise criterion matrix and derived weights for the four drought indices are also shown in Table 6. A final composite map of slope, Hurst exponent, and the superimposed map of slope and Hurst exponent were produced based on the overlay capability of the software. Figure 8 shows the drought slope and Hurst exponent while the final superimposed map at different times is shown in Figure 9. Results from Figure 8a–d show the overlayed map of DFA at different time scales. For example, DFA-1 shows the overlayed map of SPEI-1, SPI-1, VCI-1, and TCI-1 (same pattern is applied to the other times scales). Results show that DFA-1 is highly persistent with few random pixels scattered around Ethiopia, South Sudan, and Tanzania with percentage pixels as 88.7, 11.3, and 0.1 representing h > 0.5, h = 0.5, and h < 0.5, respectively. DFA-6 shows high (low) pixels representing h > 0.5 (h >1). Meanwhile, for DFA-3 and DFA-12, the distribution is purely persistent and a random walk, respectively.

Figure 8.
(a–d) Composite (overlayed) map of DFA result of drought indices (e–h). Composite (overlayed) map of drought slope over East Africa at different time scales from 1982 to 2015.
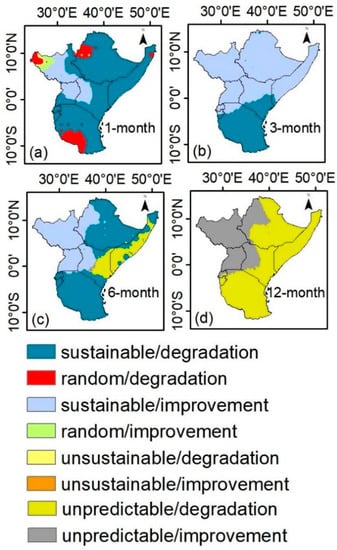
Figure 9.
Superimposed (sustainability) map over East Africa at different time scales from 1982 to 2015.
Figure 8e–h show overlayed OLR results of the four indices at different time scales. OLR-1, OLR-6, and OLR-12 show a similar distribution with positive (negative) trends scattered in the north west (Northeast and Southern) parts of the study area. OLR-3 shows positive trends scattered in the northern parts, northeast and northwest, while negative trends are distributed in the southern parts, covering Sothern Kenya and Tanzania. The percentage pixel distribution for OLR-1, OLR-3, OLR-6, and OLR-12 is 18.2 (81.8), 72.6 (27.4), 33.2 (66.8), and 36.7 (63.3) for decreasing (increasing) trends, respectively.
Figure 9 shows the superimposed map of slope (OLR) and Hurst exponent (DFA) at different time scales to reveal the final drought risk map which is an approach for mapping drought sustainability. For example, at a 1-month time scale OLR-1 and DFA-1 were superimposed to produce the final drought risk map. The results indicate that drought conditions may eventually persist, reverse, or vary drastically depending on the driving forces. At the 1-month time scale, about 73.0, 8.8, 15.7, 2.5, 0.1, and 0.0% pixels showed sustainability/degradation, random/degradation, sustainability/improvement, random/improvement, unsustainability/degradation, and unsustainability/improvement, respectively as shown in Figure 9a. Regions with severe drought but considerable improvement are located around parts of Ethiopia, Somalia, eastern Kenya, southern Uganda, Rwanda, Burundi, and some parts of Tanzania while regions with random drought distribution and considerable degradation at the 1-month time scale include eastern Ethiopia, eastern South Sudan, and southern Tanzania. At the 3-month time scale (Figure 9b), about 72.6 (27.4) % pixels showed sustainability/improvement (sustainability/degradation). Areas with sustainable/improvement are distributed in Ethiopia, Somalia, South Sudan, Uganda, Rwanda, parts of Tanzania, Burundi and Kenya while regions with sustainable and degraded portions are located in southern Burundi and Tanzania. In addition, at a 6-month time scale, about 54.2, 32.8, 12.6, and 0.4% of pixels showed sustainability/degradation, sustainable/improvement, unpredictable/degradation, and unpredictable/improvement, respectively (Figure 9c). Regions with sustainable and improved pixels are located in Northwest Ethiopia, South Sudan, Uganda, and Western Kenya while pixels with sustainable and degradation are majorly distributed in Northeast Ethiopia, parts of Kenya, Rwanda, and the entire landmass of Tanzania. Meanwhile, regions that were unpredictable but showed considerable degradation were scattered over Somalia and Eastern Kenya. More so, at the 12-month timescale (Figure 9d), about 36.70 (63.30) % of pixels were unpredictable/improved (unpredictable/degraded) over the study area.
4. Discussion
Overall, the northeastern region received a lesser amount of precipitation in the study. The amount of precipitation decreases as the distance from the lower longitudes decreases towards the Indian Ocean from longitude 14°E to 75°E (Figure 3). The region with the lowest precipitation on record is the northeast, around Somalia and parts of Ethiopia, while the highest precipitation occurs around Lake Victoria and the mountainous regions [44,67]. The hydrological climate comprises of two rainy seasons, one from March to May (MAM) and another from October to December (OND) [68]. According to Gebrechorkos et al. [8], regions located nearer to the equator are characterized by a long and short rainy season with higher amounts of precipitation during MAM and OND, while in JJAS precipitation is high around the Ethiopian highlands. Further, precipitation from January to February (JF) is low with high temperature values. The main reasons for high precipitation around the northwest and equatorial regions include local topographic factors, regional circulation, coastal influences, and remote forcing [44]. While some of the northeastern regions also experience precipitation, the magnitude and frequency are less than the areas around the equatorial and mountainous regions. The monthly evolution of precipitation makes this region more susceptible to drought. Therefore, the impacts of drought are more experienced in the northeastern parts compared to other regions.
Figure 4 shows the four drought indices (SPEI, SPI, VCI, and TCI) used in evaluating drought at four different time scales (1, 3, 6, and 12 months). While SPEI and SPI can both be used in studying droughts, the difference between the two indices is that the SPEI uses potential evapotranspiration (which serves a good purpose in revealing the net moisture balance in the soil) while the SPI, evaluated as a single numeric value, is described as the amount of standard deviations that the observed cumulative precipitation within a given time period would fluctuate from the long term average [50]. It is appropriate for monitoring short term impacts on soil moisture, snow pack, and stream flow [69] and it is generally agreed that a minimum data length of 30 yrs is needed for its computation. On the whole, a good drought index should be adapted to the climate and be induced locally to describe the drought of the region.
Figure 5 reveals that majority of the pixels show normal drought conditions in VCI and TCI (especially TCI-6 and -12). Our findings mainly show normal conditions in all drought indices when average creeping drought values are considered. Even so, there is a varying degree of correlation between the mean VCI and TCI values at the pixel scale. Despite the fact that VCI mean values correlate with TCI in some regions, there is no direct relationship between the two. In addition, Figure 4 depicts the lack of a linear relationship between meteorological, hydrological, and vegetative droughts. Furthermore, drought frequency and duration vary in a variety of ways at the pixel scale. As a result, it is not uncommon for one drought indicator to indicate drought in one place while another index indicates normal conditions at the same location and time. Because SPI is a meteorological index, it can detect drought, but the values cannot distinguish between locations that are more prone to drought than others. Equal SPEI and SPI values at two separate grid points may not always suggest a similar water deficit at these two grid sites. Furthermore, direct comparisons of occurrences with similar SPI and SPEI at different temperature conditions may be challenging. This is why the study used a combination of drought indicators, including meteorological (SPI and SPEI), temperature (TCI), and vegetation (VCI).
In general, the results on Table 3 and Table 4 show a good agreement between SPEI and SPI that may indicate the existence of drought or wet conditions as the aggregate time increases. The correlation analysis reveals that all pairs of the indices at different time scales have a more or less positive or negative correlation ranging from −0.4 to 1. We can thus apply the four drought indices concurrently in assessing drought and wet conditions over the study area. The research work adopts a spatial multicriterion decision-making model coupled with an analytical hierarchy process (AHP) to determine a drought risk map that shows the persistence or anti-persistence of drought at different time scales over the study area. This method takes into consideration the importance and effectiveness of each drought index to determine drought over the study area.
From Figure 6, drought indices that indicated persistent (h > 0.5) behavior were higher than anti-persistence indices; they include SPEI-1 to 3, SPI-1 to 6, VCI-1 to 6, and TCI-1 and TCI-6. For anti-persistence (h < 0.5), TCI-1 showed the highest percentage of pixels representing h < 0.5, while few pixels indicated a random behavior (h = 0.5) over the study area. The high persistence over the area shows that wet (dry) regions are getting wetter (dryer) while the few regions that indicated random behavior are those with transition from wet to dry conditions and vice versa. Regions with h > 1 (random walk) are those whose current condition (whether wet or dry) cannot be predicted by the previous data records. Generally, the Hurst exponent ranges from 0 to 1 and any higher value of h falls outside the predicted values. Overall, the result suggests that at low time scales (1–3 months), the records are random, persistent, or anti-persistent and any aggregation from lower to higher timesscales (6–12) may result to majorly persistent or random walk behavior of the drought time series (Figure 6).
Furthermore, the outcome of this study as presented in Table 5 and Table 6 and Figure 7, Figure 8 and Figure 9, reveal creeping drought at a one-month time interval, indicating positive changes in Kenya, Uganda, and Ethiopian Highlands while Somalia and Tanzania shows worsening conditions in drought in line with Haile et al. [70] with little disagreement from the outcomes in South Sudan at monthly time scales. Part of the area in Somalia indicated slight improvement in drought conditions while other areas remained unchanged. Over South Sudan, our work disagrees with Haile et al. [70], but agrees with Yagoub et al. [71]. Yagoub et al. used SPI to detect drought cycle patterns and their one-month SPI indicted more wet conditions than higher SPI (3 and 6) indices.
5. Conclusions
Drought is a slow-moving phenomenon that affects many different sectors of the economy and operates on a variety of time frames. This work applied the SMDM algorithm to the integrated approach of OLR and Hurst exponent drought assessment over East Africa at different time scales from 1982 to 2015. Four drought indices were used in this report to combine and produce a spatial drought risk map. The indices include SPEI, SPI, VCI, and TCI. OLR-1 represents merged trends of the drought indices at a 1-month time scale while DFA-1 represents merged Hurst exponent maps at a 1-month time scale. The OLR was employed to study trend changes while the DFA was used to study persistence in the drought indices. The DFA approach can be helpful in characterizing the direct and indirect changes which are very hard to be explained by an ordinary least square regression model.
Results from this analysis reveal both decreasing and increasing trends for SPEI, SPI, and VCI. TCI showed only decreasing trends. For DFA, all the indices displayed persistent, anti-persistent, and random behavior as captured by the Hurst exponent. OLR-1, OLR-6, and OLR-12 shows a similar distribution with positive (negative) trends scattered in the Northwest (Northeast and Southern) parts of the study area. OLR-3 shows positive trends scattered in the Northern parts, Northeast and Northwest while negative trends are distributed in the Southern parts covering Sothern Kenya and Tanzania. The percentage pixel distribution for OLR-1, OLR-3, OLR-6, and OLR-12 is 18.2 (81.8), 72.5 (27.5), 32.9 (67.1), and 36.9 (63.1) for decreasing (increasing) trends respectively. Result DFA-1 is highly persistent with few random pixels scattered around Ethiopia, South Sudan, and Tanzania with percentage pixels as 88.7, 11.3 and 0.1 representing h > 0.5, h = 0.5, and h < 0.5 respectively. DFA-6 shows high (low) pixels representing h > 0.5 (h > 1) respectively. Meanwhile, for DFA-3 and DFA-12, the distribution is purely persistent and a random walk, respectively.
The SMDM was achieved by the weighted linear combination using the AHP method and a final composite map of slope, Hurst exponent and the superimposed map of slope and Hurst exponent was produced. However, interpreting and predicting the magnitude of drought at 1-month intervals can be challenging because precipitation varies greatly across the geographical regions as well as time scales. Thus only the immediate impacts of drought such as restriction to flow and changes in hydrological cycle maybe observed short times periods, whereas the actual changes may be visible at longer time intervals. At higher time scales, dry/wet conditions become pronounced and can be easily detected and mapped. Overall, the drought risk map at 1-, 3-, and 6-month aggregates have shown severe degradation in Northwest Ethiopia, parts of South Sudan and and Tanzania while noticeable improvements are seen in Uganda, Eastern Kenya, and South Sudan.
The method applied in this work is helpful in characterizing future trends in drought. It will be valuable for future work in drought mitigation and environmental management as it can be applied in any region of the world. The results obtained from this work can help policy makers formulate appropriate drought monitoring policies in both tropical and subtropical regions.
Author Contributions
Conceptualization, W.K. and J.Z.; methodology, W.K. and T.I.; writing—original draft preparation, W.K., S.L. and F.U.; writing—review and editing, I.S.A., A.K., C.H.S., F.U., P.T. and D.N.; visualization, W.K.; supervision, J.Z.; project administration, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was jointly supported by the CAS Strategic Priority Research Program (No. XDA19030402), National Natural Science Foundation of China (No. 42071425, No. 41871253), “Taishan Scholar” Project of Shandong Province (No. TSXZ201712), Research Project of Shandong Natural Science Foundation of China (No. 2018GNC110025, No. ZR2020QE281,ZR2020QF067).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used are freely available online in public domain.
Acknowledgments
We thank editors and anonymous reviewers greatly improved the manuscript. This work was jointly supported by the CAS Strategic Priority Research Program (No. XDA19030402), National Natural Science Foundation of China (No. 42071425), Research Project of Shandong Natural Science Foundation of China (No. ZR2020QE281, No. 2018GNC110025, ZR2020QF067), “Taishan Scholar” Project of Shandong Province (No. TSXZ201712).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gil, M.; Garrido, A.; Gómez-Ramos, A. Economic analysis of drought risk: An application for irrigated agriculture in Spain. Agric. Water Manag. 2011, 98, 823–833. [Google Scholar] [CrossRef] [Green Version]
- Hijioka, Y.; Lasco, R.; Surjan, A.; Pereira, J. Climate Change 2014 Impacts, Adaptation, and Vulnerability. Part B Regional Aspects; Contribution of Working Group II to the Fifth Assessment Report of the IPCC; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Hao, C.; Zhang, J.; Yao, F. Combination of multi-sensor remote sensing data for drought monitoring over Southwest China. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 270–283. [Google Scholar] [CrossRef]
- Haroon, M.A.; Zhang, J.; Yao, F. Drought monitoring and performance evaluation of MODIS-based drought severity index (DSI) over Pakistan. Nat. Hazards 2016, 84, 1349–1366. [Google Scholar] [CrossRef]
- von Gunten, D.; Wöhling, T.; Haslauer, C.; Merchán, D.; Causapé, J.; Cirpka, O. Using an integrated hydrological model to estimate the usefulness of meteorological drought indices in a changing climate. Hydrol. Earth Syst. Sci. 2016, 20, 4159–4175. [Google Scholar] [CrossRef] [Green Version]
- Gebrechorkos, S.H.; Hülsmann, S.; Bernhofer, C. Changes in temperature and precipitation extremes in Ethiopia, Kenya, and Tanzania. Int. J. Climatol. 2018, 39, 18–30. [Google Scholar] [CrossRef] [Green Version]
- Gebrechorkos, S.H.; Hülsmann, S.; Bernhofer, C. Evaluation of multiple climate data sources for managing environmental resources in East Africa. Hydrol. Earth Syst. Sci. 2018, 22, 4547–4564. [Google Scholar] [CrossRef] [Green Version]
- Gebrechorkos, S.H.; Hülsmann, S.; Bernhofer, C. Regional climate projections for impact assessment studies in East Africa. Environ. Res. Lett. 2019, 14, 044031. [Google Scholar] [CrossRef]
- Igbawua, T.; Zhang, J.H.; Yao, F.M.; Zhang, D. Assessment of moisture budget over West Africa using MERRA-2’s aerological model and satellite data. Clim. Dyn. 2019, 52, 83–106. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Lei, T.; Peng, L. Drought evolution, severity and trends in mainland China over 1961–2013. Sci. Total Environ. 2018, 616–617, 73–89. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Liu, T.; Jiapaer, G.; Ndayisaba, F.; Jiang, L.; Kurban, A.; De Maeyer, P. Spatial and temporal characteristics of droughts in Central Asia during 1966–2015. Sci. Total Environ. 2018, 624, 1523–1538. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, S.; Zhang, H.R.; Bai, Y.; Zhang, J.H. Monitoring drought using composite drought indices based on remote sensing. Sci. Total Environ. 2020, 711, 134585. [Google Scholar] [CrossRef]
- Zhou, X.J.; Wang, P.X.; Tansey, K.; Zhang, S.Y.; Li, H.; Wang, L. Developing a fused vegetation temperature condition index for drought monitoring at field scales using Sentinel-2 and MODIS imagery. Comput. Electron. Agric. 2020, 168, 105144. [Google Scholar] [CrossRef]
- Nanzad, L.; Zhang, J.; Tuvdendorj, B.; Yang, S.; Rinzin, S.; Prodhan, F.A.; Sharma, T.P.P. Assessment of Drought Impact on Net Primary Productivity in the Terrestrial Ecosystems of Mongolia from 2003 to 2018. Remote Sens. 2021, 13, 2522. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Z.; Yao, F.; Yang, L.; Hao, C. Validating the modified perpendicular drought index in the North China region using in situ soil moisture measurement. IEEE Geosci. Remote Sens. Lett. 2015, 12, 542–546. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef] [Green Version]
- American Meteorological Society. Meteorological drought-policy statement. Bull. Am. Meteorol. Soc. 1997, 78, 847–849. [Google Scholar] [CrossRef] [Green Version]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Zink, M. Implications of Parameter Uncertainty on Soil Moisture Drought Analysis in Germany. J. Hydrometeorol. 2013, 14, 47–68. [Google Scholar] [CrossRef]
- EM-DAT. 2014 The International Disaster Database. Available online: http://www.emdat.be/glossary/9#letterd (accessed on 14 September 2020).
- Masih, I.; Maskey, S.; Mussá, F.E.F.; Trambauer, P. A review of droughts on the African continent: A geospatial and long-term perspective. Hydrol. Earth Syst. Sci. 2014, 18, 3635–3649. [Google Scholar] [CrossRef] [Green Version]
- Love, R. Economic Drivers of Conflict and Cooperation in the Horn of Africa. Chatham House Briefing Paper. December 2009. Available online: www.chathamhouse.org/publications/papers/view/109208 (accessed on 18 April 2012).
- Funk, C.; Husak, G.; Michaelsen, J.; Shukla, S.; Hoell, A.; Lyon, B.; Rowland, J. Attribution of 2012 and 2003–2012 rainfall deficits in eastern Kenya and southern Somalia. Bull. Am. Meteorol. Soc. 2013, 94, S45–S48. [Google Scholar]
- Funk, C.; Hoell, A.; Shukla, S.; Bladé, I.; Liebmann, B.; Roberts, J.B.; Robertson, F.R.; Husak, G. Predicting East African spring droughts using Pacific and Indian Ocean sea surface temperature indices. Hydrol. Earth Syst. Sci. 2014, 18, 4965–4978. [Google Scholar] [CrossRef] [Green Version]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, H.; Huntingford, C. Brief communication: Drought likelihood for East Africa. Nat. Hazards Earth Syst. Sci. 2018, 18, 491–497. [Google Scholar] [CrossRef] [Green Version]
- Mariotti, L.; Diallo, I.; Coppola, E.; Giorgi, E. Seasonal and Intraseasonal changes of African monsoon climates in 21st century CORDEX projects. Clim. Chang. 2014, 1255, 53–65. [Google Scholar] [CrossRef]
- Tierney, J.E.; Smerdon, J.E.; Anchukaitis, K.J.; Seager, R. Multidecadal variability in East African hydroclimate controlled by the Indian Ocean. Nature 2013, 493, 389–392. [Google Scholar] [CrossRef] [Green Version]
- Endris, H.S.; Lennard, C.; Hewitson, B.; Dosio, A.; Nikulin, G.; Artan, G.A. Future changes in rainfall associated with ENSO, IOD and changes in the mean state over Eastern Africa. Clim. Dyn. 2019, 52, 2029–2053. [Google Scholar] [CrossRef] [Green Version]
- Dai, A.; Lamb, P.J.; Trenberth, K.E.; Hulme, M.; Jones, P.D.; Xie, P. The recent Sahel drought is real. Int. J. Climatol. 2004, 24, 1323–1331. [Google Scholar] [CrossRef]
- Mengistu, D.; Bewket, W.; Lal, R. Recent spatiotemporal temperature and rainfall variability and trends over the Upper Blue Nile River Basin, Ethiopia. Int. J. Climatol. 2014, 34, 2278–2292. [Google Scholar] [CrossRef]
- Tefera, A.S.; Ayoade, J.O.; Bello, N.J. Analyses of the relationship between drought occurrences and their causal factors in Tigray Region, Northern Ethiopia. Tellus A Dyn. Meteorol. Oceanogr. 2020, 72, 1–18. [Google Scholar] [CrossRef]
- Linke, A.; McCabe, J.; O’Loughlin, J.; Tir, J.; Witmer, F. Drought, Local Institutional Context, and Support for Violence in Kenya. J. Confl. Resolut. 2016, 62, 1544–1578. [Google Scholar] [CrossRef]
- Kalisa, W.; Zhang, J.; Igbawua, T.; Ujoh, F.; Ebohon, O.J.; Namugize, J.N.; Yao, F. Spatio-temporal analysis of drought and return periods over the East African region using Standardized Precipitation Index from 1920 to 2016. Agric. Water Manag. 2020, 237, 106195. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January; pp. 179–184.
- Pramudya, Y.; Onishi, T. Assessment of the Standardized Precipitation Index (SPI) in Tegal City, Central Java, Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2018, 129, 012019. [Google Scholar] [CrossRef]
- Igbawua, T.; Zhang, J.; Yao, F.; Ali, S. Long range correlation in vegetation over West Africa from 1982 to 2011. IEEE Access 2019, 119151–119165. [Google Scholar] [CrossRef]
- Tran, T.V.; Tran, D.X.; Myint, S.W.; Latorre-Carmona, P.; Ho, D.D.; Tran, P.H.; Dao, H.N. Assessing spatiotemporal drought dynamics and its related environmental issues in the Mekong River Delta. Remote Sens. 2019, 11, 2742. [Google Scholar] [CrossRef] [Green Version]
- Tran, T.V.; Tran, D.X.; Nguyen, H.; Latorre-Carmona, P.L.; Myint, S.W. Charactering spatiotemporal vegetation variations using LANDSAT time-series and Hurst exponent index in the Mekong River Delta. Land Degrad. Dev. 2020, 32, 3507–3523. [Google Scholar] [CrossRef]
- Tong, S.; Zhang, J.; Bao, Y.; Lai, Q.; Lian, X.; Li, N.; Bao, Y. Analyzing vegetation dynamic trend on the Mongolian plateau based on the Hurst exponent and influencing factors from 1982–2013. J. Geogr. Sci. 2018, 28, 595–610. [Google Scholar] [CrossRef] [Green Version]
- Velasquez, M.; Hester, P.T. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Arciniegas, G.; Janssen, R.; Omtzigt, N. Map-based multicriteria analysis to support interactive land use allocation. Int. J. Geogr. Inf. Sci. 2011, 25, 1931–1947. [Google Scholar] [CrossRef]
- Lima, E.; Gorski, E.; Loures, E.F.R.; Portela Santos, E.A.; Deschamps, F. Applying Machine Learning to AHP Multcriteria Decision Making Method to Assets Prioritization in the Context of Industrial Maintenance 4.0. IFAC-PapersOnLine 2019, 52, 2152–2157. [Google Scholar] [CrossRef]
- Nicholson, S.E. Climate and Climatic Variability of Rainfall over Eastern Africa. Rev. Geophys. 2017, 55, 590–635. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, J.F. Africa, climate of. In Climatology. Encyclopedia of Earth Science; Springer: Boston, MA, USA, 1987. [Google Scholar] [CrossRef]
- Yong, W.; Zablon, S.W. Variability of Diurnal Temperature Range in East Africa During 1921–2010. J. Trop. Meteorol. 2017, 23, 345–356. [Google Scholar]
- Haile, G.G.; Tang, Q.; Sun, S.; Huang, Z.; Zhang, X.; Liu, X. Droughts in East Africa: Causes, impacts and resilience. Earth-Sci. Rev. 2019, 193, 146–161. [Google Scholar] [CrossRef]
- Harris, I.P.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
- Pinzon, J.E.; Tucker, C.J. A non-stationary 1981–2012 AVHRR NDVI3g Time series. Remote Sens. 2014, 6, 6929–6960. [Google Scholar] [CrossRef] [Green Version]
- Ntale, H.; Gan, T.Y. Drought Indices and their Application to East Africa. Int. J. Climatol. 2003, 23, 1335–1357. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw Hill: New York, NY, USA, 1980; Reprinted in RWS Publications: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Vicente-Serrano, S.; Beguería, S.; López-Moreno, J.I. A multi-scalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index—SPEI. J. Clim. Appl. Meteorol. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Ogunrinde, A.T.; Oguntunde, P.G.; Olasehinde, D.A.; Fasinmirin, J.T.; Akinwumiju, A.S. Drought Spatiotemporal Characterization using self-calibrating Palmer Drought Severity Index in the Northern Region of Nigeria. Results Eng. 2019, 8, 1–16. [Google Scholar] [CrossRef]
- Pei, Z.; Fang, S.; Wang, L.; Yang, W. Comparative Analysis of Drought Indicated by SPI and SEI at various timescales in Inner Mongolia, China. Water 2020, 12, 1925. [Google Scholar] [CrossRef]
- Bento, V.A.; Trigo, I.F.; Gouveia, C.M.; DaCamara, C.C. Contribution of Land Surface Temperature (TCI) to Vegetation Health Index: A Comparative Study Using Clear Sky and All-Weather Climate Data Records. Remote Sens. 2018, 10, 1324. [Google Scholar] [CrossRef] [Green Version]
- Jiang, R.; Liang, J.; Zhao, Y.; Wang, H.; Xie, J.; Lu, X.; Li, F. Assessment of vegetation growth and drought conditions using satellite-based indices in Jin-Jin-ji region of China. Sci. Rep. 2021, 11, 13775. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Koscielny-Bunde, E.; Rego, H.H.A.; Havlin, S.; Bunde, A. Detecting long-range correlations with detrended fluctuation analysis. Physica A 2001, 295, 441–454. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.-K.; Havlin, S.; Stanley, H.; Goldberger, A. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 82. [Google Scholar] [CrossRef] [PubMed]
- Karleuša, B.; Hajdinger, A.; Tadić, L. The Application of Multi-Criteria Analysis Methods for the Determination of Priorities in the Implementation of Irrigation Plans. Water 2019, 11, 501. [Google Scholar] [CrossRef] [Green Version]
- Ujoh, F.; Igbawua, T.; Paul, M.O. Suitability mapping for rice cultivation in Benue State, Nigeria using satellite data. Geo-Spat. Inf. Sci. 2019, 22, 332–344. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Jang, Y.; Lee, S. Application of Delphi-AHP methods to select the priorities of WEEE for recycling in a waste management decision-making tool. J. Arid Manag. 2013, 128, 941–948. [Google Scholar] [CrossRef]
- Brázdil, R.; Kiss, A.; Luterbacher, J.; Nash, D.; Řezníčková, L. Documentary data and the study of past droughts: A global state of the art. Clim. Past 2018, 14, 1915–1960. [Google Scholar] [CrossRef] [Green Version]
- Siderius, C.; Gannon, K.; Ndiyoi, M.; Opere, A.; Batisani, N.; Olago, D.; Pardoe, J.; Conway, D. Hydrological Response and Complex Impact Pathways of the 2015/2016 El Niño in Eastern and Southern Africa. Earth's Future 2018, 6, 1–22. [Google Scholar] [CrossRef]
- Karina, W.; Ursula, G.; Volker, H. Identifying Droughts Affecting Agriculture in Africa Based on Remote Sensing Time Series between 2000–2016: Rainfall Anomalies and Vegetation Condition in the Context of ENSO. Remote Sens. 2017, 9, 831. [Google Scholar]
- Dingwell, J.B.; Cusumano, J.P. Re-interpreting detrended fluctuation analyses of stride-to-stride variability in human walking. Gait Posture 2010, 32, 348–353. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koscielny-Bunde, E.; Kantelhardt, J.; Braun, P.; Bunde, A.; Havlin, S. Long-term persistence and multifractality of river runoff records: Detrended fluctuation studies. J. Hydrol. 2006, 322, 120–137. [Google Scholar] [CrossRef] [Green Version]
- Ndomeni, C.W.; Cattani, E.; Merino, A.; Levizzani, V. An observational study of the variability of East African rainfall with respect to sea surface temperature and soil moisture. Q. J. R. Meteorol. Soc. 2018, 144, 384–404. [Google Scholar] [CrossRef] [Green Version]
- Schumacher, B.; Katurji, M.; Meyer, H.; Appelhans, T.; Otte, I.; Nauss, T. Atmospheric moisture pathways of East Africa and implications for water recycling at Mount Kilimanjaro. Int. J. Climatol. 2020, 40, 4477–4496. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Carrao, H.; Barbosa, P.; Vogt, J. World Drought Frequency, Duration, and Severity for 1951–2010. Int. J. Climatol. 2013, 34, 2792–2804. [Google Scholar] [CrossRef] [Green Version]
- Haile, G.G.; Tang, Q.; Hosseini-Moghari, S.M.; Liu, X.; Gebremicael, T.G.; Leng, G.; Kebede, A.; Xu, X.; Yun, X. Projected impacts of climate change on drought patterns over East Africa. Earth's Future 2020, 8, e2020EF001502. [Google Scholar] [CrossRef]
- Yagoub, Y.; Li, Z.; Musa, O.S.; Anjum, M.N.; Wang, F.; Bo, Z. Detection of Drought cycles Pattern in two Countries (Sudan and South Sudan) by using Standardized Precipitation Index SPI. Am. J. Environ. Eng. 2017, 7, 93–105. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).