Abstract
Environmental monitoring using satellite remote sensing is challenging because of data gaps in eddy-covariance (EC)-based in situ flux tower observations. In this study, we obtain the latent heat flux (LE) from an EC station and perform gap filling using two deep learning methods (two-dimensional convolutional neural network (CNN) and long short-term memory (LSTM) neural networks) and two machine learning (ML) models (support vector machine (SVM), and random forest (RF)), and we investigate their accuracies and uncertainties. The average model performance based on ~25 input and hysteresis combinations show that the mean absolute error is in an acceptable range (34.9 to 38.5 Wm−2), which indicates a marginal difference among the performances of the four models. In fact, the model performance is ranked in the following order: SVM > CNN > RF > LSTM. We conduct a robust analysis of variance and post-hoc tests, which yielded statistically insignificant results (p-value ranging from 0.28 to 0.76). This indicates that the distribution of means is equal within groups and among pairs, thereby implying similar performances among the four models. The time-series analysis and Taylor diagram indicate that the improved two-dimensional CNN captures the temporal trend of LE the best, i.e., with a Pearson’s correlation of >0.87 and a normalized standard deviation of ~0.86, which are similar to those of in situ datasets, thereby demonstrating its superiority over other models. The factor elimination analysis reveals that the CNN performs better when specific meteorological factors are removed from the training stage. Additionally, a strong coupling between the hysteresis time factor and the accuracy of the ML models is observed.
Keywords:
eddy covariance; error analysis; deep learning; machine learning; CNN; SVM; RF; LSTM; factor elimination; hysteresis; flux tower 1. Introduction
Latent heat flux (LE) is an important hydro-meteorological variable in the investigation of climate change, hydrological cycle intensification, and plant–atmosphere interactions [1,2]. The development of reliable and long-term LE fluxes is vital for climate adaptation strategies [3] as well as disaster risk reduction plans [4], and it is one of the sustainable development goals of the United Nations initiative for global geospatial information management [5]. LE is defined as the sum of outgoing turbulent heat fluxes in the form of transpiration from plant canopies and evaporation from the soil surface [6]. In terms of global outgoing turbulent heat fluxes, LE contributes the most significantly among the components of the water cycle, as well as provides a linkage among water, energy, and the carbon cycle [7,8,9]. Accurate information pertaining to LE is a prerequisite for many agro-meteorological applications, such as water resource management, drought prediction, irrigation scheduling, and crop yield prediction [10,11]. However, owing to spatial heterogeneity in the land surface, the accurate quantification of LE is challenging [12,13].
Hitherto, the most accurate method for measuring LE is via eddy covariance (EC)-based flux tower observations [14,15,16]. To measure high-frequency flux observations from sensors, the EC method relies on three-dimensional sonic anemometers as well as infrared gas analyzers [17]. However, such high-frequency flux observations are prone to uncertainties owing to sensor malfunction and unfavorable environmental conditions [18]. Consequently, the complete time series of ground based LE observations cannot be obtained. Such unavailability in flux observations is more pronounced in forest ecosystems because of their spatial heterogeneity and complex topography [19]. Additionally, quality control procedures result in unavailable flux datasets [20]. Therefore, the gap filling of unavailable EC-based datasets must be addressed for estimating water and energy budgets. Researchers have used regression techniques based on available meteorological observations to fill the gaps in flux datasets. These methods include interpolation, nonlinear regression, mean diurnal variables, and marginal distribution sampling methods. Detailed information regarding these methods and their limitations are available in the literature [21,22,23,24].
Considering the limitations of regression-based techniques, in recent years, researchers have begun using data-driven gap-filling techniques based on machine learning (ML) algorithms [25]. For example, in regard to the latent heat of evapotranspiration, Cui, et al. [26] showed that the ML-based gap-filling method can outperform typically used gap-filling approaches such as REddyProc [27] and ONEFlux [28]. Similarly, van Wijk and Bouten [29] used an ML method that is the artificial neural network (ANN) to gap-fill carbon and water fluxes at six bio-physically different flux tower forest sites, and they demonstrated that the ANN can effectively simulate fluxes without requiring detailed meteorological parameters. Meanwhile, Schmidt, et al. [30] used a radial-based functional neural network to fill in missing gaps in water and carbon fluxes in urban regions and demonstrated a significant correlation coefficient of 0.85 as compared with independent ground-based EC observations. ML-based gap-filling methods tend to provide better performance compared with statistical and regression techniques used to gap-fill EC, as well as satellite-based datasets [31,32,33].
Owing to the current advancements in high computational technology, state-of-the-art deep-learning-based algorithms have been exploited and have demonstrated promising results in various fields, such as pattern recognition, acoustics, image understanding, and natural language processing [34,35]. On theoretical point of view, there is a key difference between ML and deep-learning methods. ML is a field of artificial intelligence that uses algorithms which parse and learn from the dataset to make informed decisions by minimizing the human interventions. The basic ML methods tend to become better at what they are assigned to do; however, they still need guidance or adjustments in case of inaccurate predictions. This limitation is addressed by a deep-learning-based method, which itself is a subfield of ML; however, it mimics the human brain-like mechanism that develops algorithms that is based on multi-layered perceptron or “artificial neural network,” which enables intelligent decision-making without human interventions. Recently, deep-learning-based models have been extended to gap-fill satellite-based datasets and EC-based flux observations [36]. For example, Nguyen and Halem [37] used two deep learning models, i.e., the feed forward neural network and long short-term memory (LSTM), to gap-fill EC-based flux observations. Additionally, Huang and Hsieh [38] used two deep learning algorithms, i.e., a deep neural network and LSTM, compared them with three ML models, and showed that the performances of all five models were consistent with gap-fill EC-based flux observations. Although only a few researchers have used deep learning algorithms for gap-filling EC-based datasets, the most recently developed deep learning algorithms have not been evaluated for gap-filling EC-based flux tower observations. Therefore, the main objectives of this study are to (1) investigate the accuracy of two deep-learning-based models (e.g., convolutional neural network (CNN) and LSTM), and two ML techniques (SVM and RF) to gap-fill EC-based LE observations in a temperate East Asian forest ecosystem, and (2) evaluate the effects of factor elimination and hysteresis on the accuracy of the four abovementioned ML models. We integrated a two-dimensional hysteresis in the CNN model, in which we considered multiple input factor hysteresis using datasets that were curated into a two-dimensional image under a moving-window framework, thereby evaluating their accuracy for the gap filling of EC-based flux tower datasets.
2. Materials and Methodology
2.1. Study Area and Datasets
This study was conducted within the extent of the Korean peninsula (33° N–44° N latitude, 124° E–132° E longitude) in Asia (Figure 1), which is the most populous continent in the world with fragile ecosystems and heterogeneous landscapes. The selected study regions are experiencing accelerated hydrological cycles owing to the recent increase in temperature as well as global warming effects. Such accelerated hydrological cycles and warming effects are more pronounced in arid regions of the continent. Additionally, we selected one forest site, Seolmacheon (SMC), which is registered in the AsiaFlux regional research network (http://asiaflux.net, last accessed date: 2 December 2021). Table 1 shows the detailed geographical characteristics of selected forest sites in East Asia, i.e., the region that is frequently afflicted with extreme floods during the monsoon season (June to August) and drought during the summer period (March to May) owing to seasonal variations.
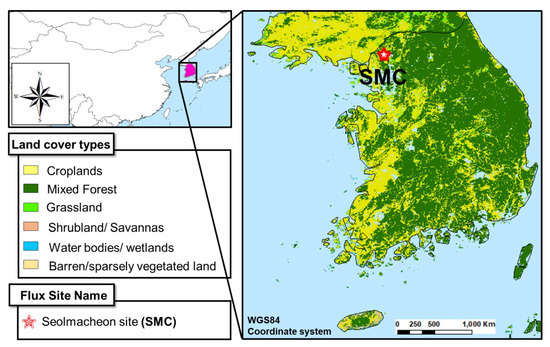
Figure 1.
Geographical location and land cover map of study area; one flux tower site in South Korea.

Table 1.
Characteristics of study area, including field and meteorological information (www.asiaflux.net/, Last accessed date: 2 December 2021).
To investigate the accuracies of the four ML-based models for gap filling LE fluxes, we selected one EC-based flux tower site. For training and assessment, we selected half-hourly datasets that are downloadable for free from a micro-meteorological regional research network from the AsiaFlux regional research network website under a fair-usage policy. To measure the turbulent heat fluxes, the flux towers were equipped with infrared gas analyzers (LI-COR, LI-7500, Lincoln, NE, USA), three-dimensional sonic anemometer (CSAT3, Campbell Sci., Inc., Logan, UT, USA), as well as hygrometers with open-path observational systems. It is noteworthy that the measurement dataset from the EC system was recorded using data loggers (CR3000, Campbell Sci., Inc., Logan, UT, USA), which were installed at the base of the flux tower.
2.2. Methodology
2.2.1. ML Models
ML models are data-driven techniques that use the correlation and internal trends in the input datasets and apply classification and regression to fill the missing gaps in the dataset. In the current study, we adopted four (CNN, SVM, RF, and LSTM) ML techniques, in which two (CNN and LSTM) were deep learning models. In the four abovementioned models, we used the grid-search technique to obtain the hyper-parameters, for which the details are mentioned in Huang and Hsieh [38].
2.2.2. CNN
We implemented a CNN using Python programming language by exploiting PyTorch, which is an open-source ML library developed by Facebook’s AI research group [40]. PyTorch-based CNN models have been implemented in natural language processing and computer vision; however, to the best of our knowledge, PyTorch-based CNNs have not been applied for gap-filling EC fluxes. We preferred PyTorch because of its ease of integration with other systems owing to its low dependencies and beginner-friendly user experience [41]. Previous researchers have used only one-dimensional CNNs similar to the RNN to gap-fill EC-based datasets owing to its capability in managing sequence datasets [38]. In this study, we updated the current one-dimensional CNN and converted it into a two-dimensional CNN. The important contribution of the current two-dimensional CNN is that it implements a two-dimensional multivariate CNN model, which we used to represent data as a two-dimensional image that can consider two sequences simultaneously (i.e., multiple input factors as the width parameter and multiple time sequences (hysteresis) as the height parameter). Because a two-dimensional CNN considers input factors as an image, we used min–max normalization [42] to scale the datasets. In fact, this approach has been corroborated by other researchers—they recommended data normalization as it accelerates the learning process [43]. The framework of a two-dimensional CNN is shown in Figure 2. We integrated an activation function (ReLU), which has been proven to effectively avoid gradient vanishing. Additionally, we implemented an improved optimizer (e.g., Adam), which enabled us to efficiently process a greater number of hyper-parameters. Moreover, to avoid overfitting, we incorporated a regularization and dropout approach [36]. More details regarding the CNN model are available in [26,44,45].
Figure 2.
Framework of two-dimensional CNN implemented in current study.
2.2.3. SVM
In the current study, an SVM was established using the E1071 package in the R programming environment; the package provides multiple functions that are suitable for both static and probabilistic algorithms. The SVM function of the E1071 package is accompanied by a robust interface that enables the efficient and reliable implementation of the SVM. The SVM was originally developed for linear datasets; however, when certain kernels (e.g., sigmoid, radial basis function, and polynomial) are used, it can integrate higher-dimensional datasets with high flexibility. To implement the SVM, we adopted the grid-search method, which is used to estimate hyper-parameters such as kernel functions. The kernel function adopted in the current study included the radial basis function; however, the eps-regression type was used to achieve the best gap-filling accuracy. More details regarding the SVM model are available in [46,47].
2.2.4. RF
To construct the RF, we used the Scikit-learn package using the Python programming language, in which we progressively increased the number of decision trees from 10 to 500. To avoid overfitting, we allowed the Scikit-learn package to automatically select the maximum depth of the tree. It is noteworthy that to achieve the best computational efficiency, we considered a maximum of four features in the current study. More details regarding the RF are available in [48].
2.2.5. LSTM
LSTM is a deep-learning-based improved recurrent neural network that yields improved results in predicting mid- to long-term events compared with other ML models [49]. In the current study, an LSTM model was implemented using the Python programming language, which exploited PyTorch [50,51]. To retain long-term memory, the LSTM model uses memory cells that consist of three different gates: forget, input, and output gates. The forget gates are critical because they define whether the data being retained is valuable. The unnecessary data are discarded, whereas the most valuable data are stored and subsequently used for forecasting in the next round. This process of discarding and retaining the most valuable information was implemented using a sigmoid function filter. The other two gates, i.e., the input and output gates, determine if the next input dataset is valuable as an output memory cell or neuron. In addition to the three gates mentioned above, a candidate gate, which defines the magnitude of the neurons, is used. The LSTM model implemented in the current study comprises three hidden layers, and each hidden layer contains 4 to 32 neurons [38]. Furthermore, it is noteworthy that both the LSTM and CNN models adopted in the current study can manage multiple variables as well as the hysteresis of each input factor at a specified time stamp. More details regarding the LSTM model are available in [49,50,51,52].
2.3. Training of ML Models
To investigate the accuracy of the four ML models for gap filling LE fluxes, we acquired a one-year (i.e., 2008) dataset with 30 min intervals in the current study; therefore, we trained four models by incorporating only key meteorological factors that directly affected LE turbulence, such as wind speed (U), relative humidity (RH), net radiation (Rn), air temperature (Ta), friction velocity (u*), and surface temperature (Ts). Researchers have considered four meteorological factors (i.e., Ta, RH, Rn, and U) for gap-filling LE fluxes [38]. However, it is noteworthy that Ts and u* directly affect LE fluxes as well [53]. Therefore, in addition to the four factors used in the previous study, we integrated two additional key meteorological factors (i.e., Ts and u*) to investigate their effect on the accuracy of gap-filling models.
Moreover, a strong hysteresis between EC-based LE and Rn has been reported in the literature [54,55]; however, its effect on the accuracy of gap filling using various ML models has rarely been investigated across temperate forest biomes. Meanwhile, key meteorological factors such as U, RH, Ta, u*, and Ts exhibit a hysteresis relationship with LE [56]. Considering this stronger hysteresis relationship, it is speculated that if we integrate all the above-mentioned hysteresis relationships into the processing pipeline, then the accuracy of gap-filling can be improved. In fact, this was partially achieved by Huang and Hsieh [38] who improved the accuracy of LE gap filling by incorporating only two factors (e.g., Rn and Ta) into its processing pipeline without considering the other four key meteorological factors, i.e., U, RH, u*, and Ts. Considering this research gap, we added six key hysteresis factors (e.g., Rn, Ta, U, RH, u*, and Ts), which significantly affected the accuracy of LE, to further investigate their effects on the accuracy of LE gap-filling.
Only a few researchers have integrated the hierarchy and existing trend of the variable under consideration to further improve the accuracy of gap-filling techniques, such as in neural network models [57,58]. Therefore, incorporating the contextual information of the variable being used for gap filling to render the four ML smarter appear promising. Hence, we added LE hysteresis in the four ML models in the current study to render them contextually aware to further investigate their effect on the accuracy of the gap-filling technique. The list of all input factors used to train the four ML models in the current study is presented in Table 2. Among all the input combinations shown in Table 2, we investigated the best input combination for the four ML models and then assessed their accuracy based on a comparison with independent ground-based flux tower observations. It is noteworthy that, among all the EC datasets used in the current study, 80% of the datasets was used for training, 10% for validation, and 10% for testing the accuracy of the four ML models. In order to test the accuracy of gap-filling results, we used only original flux tower datasets in order to maintain a fair comparison. In order to test the accuracy of our updated two-dimensional CNN model along with the other three models (LSTM, RF, and SVM) to predict the gaps, we used the available 7 months of high-quality dataset for training, and we eventually predicted latent heat fluxes for only one month (i.e., August 2008). This one month of latent heat flux was finally compared with ground-based flux tower observations. This adopted approach is explained as follows: based on four models, if input data contains large missing values, we cannot accurately train our models. If we cannot accurately train our models, then it implies that we cannot achieve accurate gap-filling results. For a model to perform accurate gap-filling, high-quality input data is required, and it is advantageous for learning if it does not contain large missing values. Moreover, after performing gap filling, to check whether our gap-filled results are accurate or if it is reasonable to use those gap-filled results, we need an indicator for evaluation, and that is called the true value or in situ ground-based value. This is the reason that the true/test value used in the current study also has no missing value, which is significantly important in order to maintain a fair comparison. It means that models with high ratings can then be expected to perform accurate gap fillings in case of real gaps when we do not have true ground-based values. This adopted approach also provides a fair comparison of our gap-filled results with reference to in situ ground-based flux tower observations. In a nutshell, the one-year flux tower dataset used in this study is of high quality and did not have significant gaps that enabled us to assess the accuracy of our gap-filling method with full confidence. Statistically, the total number of sample numbers used for training was 10,610 30-min timescale latent heat flux observations, and the total number of missing gaps that we predicted was 1104 30-min timescale latent heat flux observations.

Table 2.
List of input variables for training machine learning models.
3. Performance Metrics
To validate the accuracy of the four ML models based on a comparison with independent flux tower observations, we selected five statistical indicators: the mean absolute error (MAE), root mean square error (RMSE), coefficient of determination (R2), Pearson’s correlation (R), and normalized standard deviations (σn), which are expressed as follows:
where S denotes the modeled value, O is the ground-based observations, is the mean ground-based observed value, and is the mean modeled observations. The subscript i represents the number of samples, whereas N indicates the total number of samples used in the current study. Meanwhile,indicates the standard deviation, in which the subscript n denotes “normalized”. In addition to the four above-mentioned statistical performance metrics, we performed a time-series analysis and used a Taylor diagram to compare the four ML models comprehensively [59]. The Taylor diagram is a robust tool that has been used extensively in atmospheric research to compare the performances of multiple models using a single diagram by exploiting both σn and R in a two-dimensional space. It is noteworthy that the RMSE exaggerates the extreme uncertainties in the model predictions in contrast with the MAE, thereby resulting in significant errors [33,60].
4. Results and Discussion
4.1. Optimal Input Combination for Training ML Models
For the generation of an optimal input combination for training the two deep-learning-based models (CNN and LSTM) and two ML-based models (SVM and RF), we adopted an iterative approach as a function of MAE. To generate an optimal input combination, we used six meteorological factors (i.e., U, RH, Rn, Ta, U*, and Ts), as well as seven hysteresis factors (i.e., U, RH, Rn, Ta, U*, LE, and Ts) and iteratively conducted the experiment on various time scales, as mentioned in Table 2, in order to minimize the MAE. Based on those iterative experiments, we generated more than 25 input and hysteresis combinations, and the combination that yielded the least MAE was our optimal input combination for the four abovementioned models, and we presented this optimal input combination in Table 3. Our findings, as shown in Table 3, suggest that hysteresis contributed significantly to the establishment of an optimal input combination for the four ML-based models used in the current study. Our results further implied that integrating hysteresis factors in forest ecosystems can potentially improve the accuracy of gap filling using the four ML-based models. Our results were consistent with the findings of Cui, et al. [54] who investigated EC-based flux tower observations and discovered a similar hysteresis phenomenon between LE and environmental factors such as Rn, U, Ts, and Ta. It is noteworthy that to generate an optimal input combination, the two deep-learning-based models (e.g., CNN and LSTM) required a significant number of input factors compared with the two ML-based models (e.g., the SVM and RF), as shown in Table 3.

Table 3.
Optimal input combinations for LE turbulent heat fluxes using two deep learning models (CNN and LSTM) and two machine learning techniques (SVM and RF) in SMC forest site.
4.2. Statistical Comparison of Gap Filling Based on ML Models
A comprehensive analysis of our results is presented in this section, which comprises four main subsections. In the first subsection, we present our investigation involving more than 25 hysteresis and input combinations using four models (e.g., CNN, SVM, RF, and LSTM), as well as the estimation of the mean averaged model performances, as presented in Figure 3. The results show that the MAEs for all the four models investigated were in the acceptable range (37.50 to 40.22 Wm−2), which is corroborated with the previous study [38]. It is noteworthy that despite requiring fewer input datasets (Table 3), the SVM model outperformed all other models with an MAE value of 37.50 Wm−2, followed by the CNN, which is the second-best model for gap filling, with an MAE value of 38.91 Wm−2. Based on the mean average model performance, the ranking of the four models from the best to the worst is as follows: SVM > CNN > RF > LSTM.
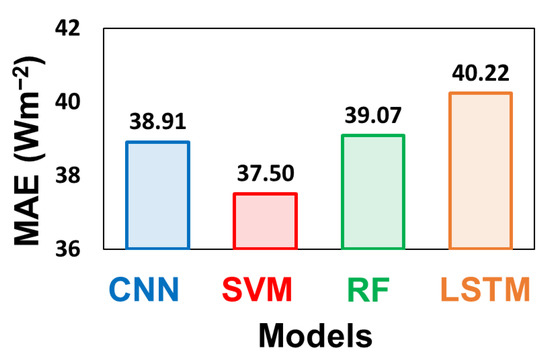
Figure 3.
Mean average model performances of two deep learning techniques (i.e., CNN, and LSTM) and two machine learning techniques (i.e., SVM and RF) in SMC forest site.
In this second subsection, we assess the accuracy of the four models (e.g., CNN, SVM, RF, and LSTM) using an optimal input combination. In terms of optimal input combinations, the statistical performance metrics of the individual models are presented in Figure 4a, which shows that all four models’ uncertainties were in an acceptable range, with MAE, RMSE, and R2 values of 36.3–39.3 Wm−2, 54.7–57.3 Wm−2, and 0.75–0.79, respectively, which is corroborated with the previous study [38]. Additionally, Figure 4a shows that the model performances of the two deep-learning-based models (CNN and LSTM) were similar. Moreover, the uncertainties of the two ML-based models (SVM and RF) were consistently similar to each other (Figure 4a). The inherent model physics of the two ML models and the two deep-learning-based models were similar, as their model uncertainties exhibited similar trends.
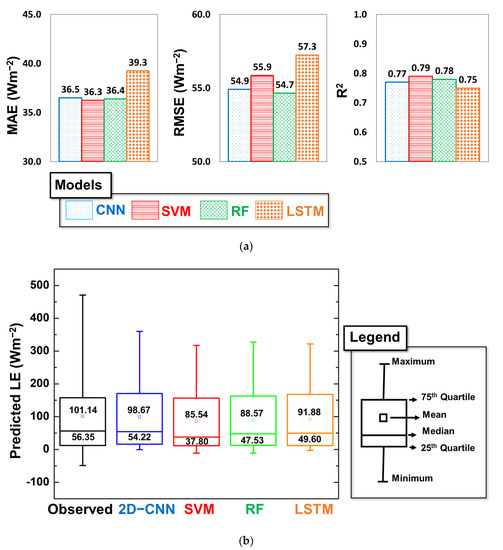
Figure 4.
(a) Performance of four models using optimal input combinations evaluated based on RMSE, MAE, and R2. (b) Boxplot analysis of predicted LE by two deep learning models (CNN, and LSTM), and two machine learning techniques (SVM, and RF) compared with observed flux tower dataset.
In terms of individual model performances, the SVM model followed by the CNN and RF performed better in gap filling the LE fluxes compared with the remaining models, whereas the accuracy of LSTM was low compared with that of the other models used in this study. Considering the individual model performances based on optimal input combinations, we discovered only a marginal difference among the accuracies of the CNN, SVM, and RF models (Figure 4a). In terms of individual model performance, the ranking of the models from best to worst was as follows: SVM > RF > CNN > LSTM. Although our results showed only a marginal difference among the performances of the four models, we further investigated their accuracies by comparing their group means using a widely used statistical tool, i.e., the analysis of variance (ANOVA) [61]. The ANOVA tests the equality of at least three group means, and statistically significant results signify that at least one group means is different. It is noteworthy that the basic assumption in the ANOVA is that the distributions within groups are normally distributed; therefore, results from the ANOVA are acceptable if the dataset adheres to its basic assumptions of normality. Therefore, prior to conducting the ANOVA, we verified the normality of our dataset using the Shapiro–Wilk normality test [62], which indicated that our dataset was not normally distributed. To test the ANOVA on datasets that are not normally distributed, a better version of the ANOVA is required. Hence, we selected the bootstrap version of the one-way ANOVA for trimmed means (i.e., 20%); the number of selected bootstrap samples was 2000, and we obtained statistically insignificant results (p-value = 0.28), which indicates that all group means were similar. Therefore, the ANOVA test implied that the performances of the four models differed marginally.
Although the ANOVA test indicated the equality of group means as well as their statistical significance, it did not identify mean pairs that were statistically significant. To test the significance of individual model pairs, we conducted robust post-hoc tests, such as the Hochberg and Bonferroni tests [63,64]. The post-hoc tests showed that our results were not significant statistically, with a p-value ranging from 0.42 to 0.76 among all pairs of models. Therefore, the post-hoc tests revealed that the means of all four models were the same, indicating their similar performances.
Since the above-mentioned analysis revealed a similar performance among four models, we further scrutinized their suitability for the gap filling of flux tower observations by visualizing the distribution of predicted LE using a Boxplot analysis, and the results are presented in Figure 4b. The results revealed that the 2D-CNN better captured the distribution of observed LE in terms of mean, median, and inter-quartile ranges. The mean and median values of predicted LE by 2D-CNN were 98.67 Wm−2 and 54.22 Wm−2, respectively, which is closer to observed flux tower observations with values of 101.14 Wm−2 and 56.35 Wm−2, respectively (Figure 4b). The observed flux tower measurements showed the largest variations in predicted LE, which was closely approximated by the 2D-CNN implemented in the current study. Specifically, the peak values of predicted LE by 2D-CNN outperformed SVM, RF, as well as LSTM estimations. On the other hand, the distribution of predicted LE by SVM, RF, and LSTM were found to be closer to each other with their mean and median values in the range of 85.54–91.88 Wm−2 and 37.80–49.60, respectively, indicating their similar performances. Overall, based on inter-comparison, our 2D-CNN model tended to slightly outperform SVM, RF, and LSTM models for the gap filling of flux tower observations.
In this third subsection, we analyze the temporal trend of ML-based predicted LE fluxes based on a comparison with ground-based flux tower observations. Hence, we conducted a time-series analysis, as presented in Figure 5. The results showed that all four models captured the temporal trend of predicted LE turbulent heat fluxes accurately, with larger values around peak sun hours and lower values during nighttime when the LE fluxes were lower, owing to the unavailability of net radiation. Our results agreed well with those published previously [65]. Additionally, Figure 5 shows that the CNN performance, in terms of capturing the temporal trend of LE fluxes, was the best compared with all the other models (R~0.87). This is attributable to the tendency of the CNN to integrate the optimum number of input factors when training the model. Additionally, we improved the CNN model in the current study and integrated into it a two-dimensional hysteresis, thereby enabling it to extract the features of each input factor and those of the multivariate hysteresis; this might have contributed to its better performance compared with those of all the other models in capturing the temporal trend of LE fluxes.
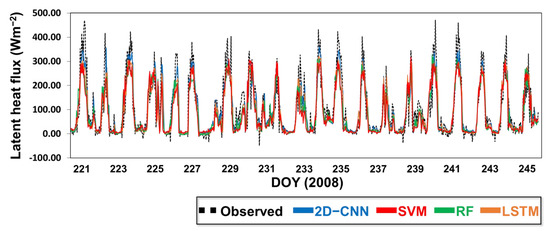
Figure 5.
Time series of predicted LE fluxes obtained from observations and two deep learning techniques (2D−CNN and LSTM) and two machine learning techniques (SVM and RF) in SMC forest site.
In this fourth subsection, we further scrutinize the performances of the four models (i.e., CNN, SVM, RF, and LSTM) used in the current study. Hence, we employed a Taylor diagram, and the results are presented in Figure 6. These results show that the and R values of the CNN (0.86 and 0.87, respectively) were the most similar to the observed ground-based values, followed by those of the SVM (0.81 and 0.87, respectively), LSTM (0.84 and 0.86, respectively), and RF (0.80 and 0.87, respectively) in current study. The main finding was that the performances of the four models differed marginally; however, with better values that were more similar to the ground-based observations, the two-dimensional CNN model adopted in the current study performed the best in gap filling LE fluxes, as shown by the Taylor diagram.
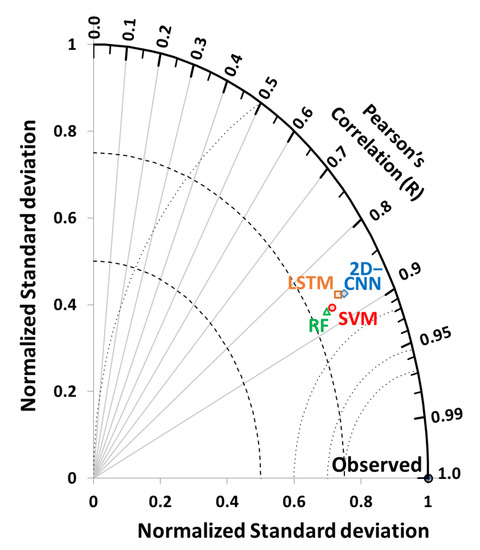
Figure 6.
Taylor diagram showing performances of two deep learning models (2D−CNN and LSTM) and two machine learning techniques (SVM and RF) in SMC forest site.
4.3. Investigation of Robustness of Models
As presented in Section 4.1, we generated an optimal input combination for training the four models based on more than 25 total combinations that were obtained using six meteorological factors (i.e., U, RH, Rn, Ta, U*, and Ts), as well as seven hysteresis factors (i.e., U, RH, Rn, Ta, U*, LE, and Ts) on various time scales. Considering the malfunctioning of EC-based sensors as well as low-cost equipment in developing countries, a significant number of meteorological datasets are unavailable, which hampers the generation of optimal input combinations. This scenario highlights the necessity to identify a robust model that affords improved accuracy even after the loss of the optimal combination or when multiple input datasets required for an optimal combination are unavailable. Therefore, in this section, we analyze the robustness of the four models when the optimal combination is lost. First, we analyze the effect of factor elimination on the accuracy of two deep learning models (CNN and LSTM) and two ML learning techniques (SVM and RF) in the SMC forest site. We iteratively removed the meteorological factors (i.e., U, U*, Ts, Ta, RH, and Rn) from the training process and examined their effects on the accuracy in gap filling LE fluxes. The results are presented in Table 4, which shows that the accuracy of the two deep learning models (CNN and LSTM) consistently improved after specific meteorological factors were removed during the training stage. For example, after removing U* from the analysis, the results, as shown in Table 4, showed that the performance of the CNN improved significantly, where the MAE and RMSE improved from 37.90 and 56.0 Wm−2 to 37.34 and 55.85 Wm−2, respectively. Our results showed that the performances of the CNN and LSTM can be improved significantly by removing inappropriate meteorological factors from the analysis and selecting only meteorological factors that significantly affect the variable being considered for gap filling. By contrast, the two ML-based models (SVM and RF) exhibited the opposite trend, in which their accuracy in gap filling deteriorated significantly after factor elimination. For example, the results presented in Table 4 show that, after removing U* from the analysis, the performance of the SVM deteriorated significantly, and the MAE and RMSE deteriorated from 36.3 and 55.9 Wm−2 to 38.32 and 58.82 Wm−2, respectively. Therefore, our results suggest that the strengths and weaknesses of ML-based models, as well as the optimal input factors, must be considered to obtain the best gap-filling accuracy. Moreover, it is important to mention the change of feature importance after removing specific factors. Therefore, based on our analysis the changes of feature importance from high to low should be indicated as follows: RN > Rh > u* > Ta > u > Ts.

Table 4.
Factor elimination analysis and accuracy of two gap-filling deep learning models (CNN and LSTM) and two machine learning techniques (SVM and RF) upon the loss of optimum combination in the forest site. MAE and RMSE expressed in units of Wm−2. Bold values represent the best performing statistics.
We further investigated the effect of factor elimination on the accuracy of gap filling by plotting the percentage improvement for all four models used in the current study. The results are presented in Figure 7. As shown in Figure 7a–e, the CNN model consistently demonstrated favorable performance after a specific factor was eliminated from the analysis, with a 0.82–2.11% improvement in the MAE. It is noteworthy that, as presented in Figure 7f, the performances of all four models deteriorated significantly after the Rn factor was removed from the analysis, for which the deterioration percentage values ranged between −5.76% and −16.87%. This result is reasonable, because Rn is highly correlated with LE [66]; therefore, if Rn is omitted from the gap-filling processing pipeline, then the performance will be degraded. Hence, our results showed that selecting highly correlated factors can significantly improve the accuracy of gap filling.
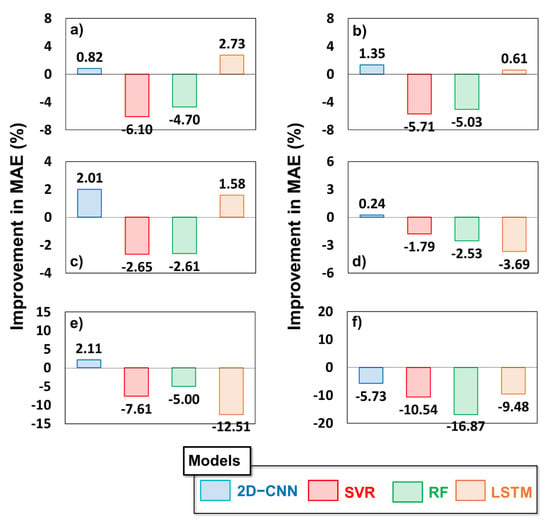
Figure 7.
Accuracy of two deep learning models (2D−CNN and LSTM) and two machine learning techniques (SVM and RF) upon the loss of optimum combination based on factor elimination. Eliminated factors include (a) wind speed, (b) friction velocity, (c) surface temperature, (d) air temperature, (e) relative humidity, and (f) net radiation. Positive values indicate improvement in model accuracy by reduction in MAE; similarly negative values indicate performance degradation. All units are in percentage.
We further examined the effect of the hysteresis time factor on the accuracy of the two deep learning and two ML-based models based on the MAE as the performance metric. The results are presented in Figure 8, which show that the MAE values increased significantly as the hysteresis time factor increased for all four models investigated. Therefore, to reduce the uncertainties and achieve the best gap-filling accuracy, our results suggest using only those hysteresis time factors that are closer to value being gap-filled.
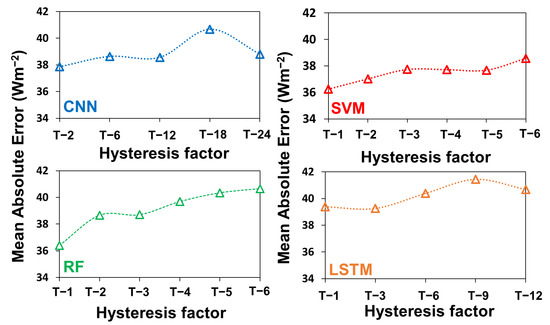
Figure 8.
Effect of hysteresis on the accuracy of two deep learning models (CNN and LSTM) and two machine learning techniques (SVM and RF) in SMC forest site. The hysteresis factor along the x-axis is a multiplier and represents 30 min of data before time t.
Here it is important to highlight the limitations as well as future prospects of this study. As explained previously in detail, LE is most directly related to surface and prevailing hydro-meteorological conditions. Due to our study site being located in a mixed forest biome, where information regarding the seasonal changes of leaf area index (LAI) might also be helpful to improve the accuracy of gap-filling when we integrate it during training stage. While the seasonal changes of LAI are more pronounced in rotational cropland and grassland ecosystems compared to a forest ecosystem, integrating this information can still be helpful to improve the accuracy of gap filling. With the monsoon climate, there are also significant seasonal differences in precipitation, which may also play a role in improving the accuracy of gap filling. However, we have not used LAI and precipitation information in the current study on purpose, and the reason is explained as follows: it is noteworthy to reiterate that, in the current study we acquired a one-year (i.e., 2008) dataset with 30-min intervals, which was downloaded from the AsiaFlux regional research network website (www.asiaflux.net/, last accessed date: 2 December 2021) for the Seolmacheon forest site in the Republic of Korea. The downloaded dataset did not have LAI information, and due to the malfunctioning of the instrument, the full year precipitation dataset was also missing. This was the reason that we could not use LAI or precipitation information in the current study. Moreover, as demonstrated in Section 4.3, one of the objectives of the current study was to use the least number of input factors to achieve the best gap-filling accuracy. Therefore, we used only available datasets and devised a methodology to achieve the best gap-filling accuracy in the current study. Therefore, in future studies, the researchers are suggested to integrate LAI and precipitation information in order to investigate its impact on the accuracy of gap-filling.
5. Conclusions
In this study, we investigated the accuracy of two deep-learning-based models (CNN and LSTM) and two ML techniques (SVM and RF) for gap filling EC-based LE observations. To train the four ML-based models, we used six meteorological factors (i.e., U, RH, Rn, Ta, U*, and Ts) and seven hysteresis factors (i.e., U, RH, Rn, Ta, U*, LE, and Ts) on various time scales and based on more than 25 input and hysteresis combinations. Subsequently, we selected an optimal input combination that yielded the best model performance. In terms of the optimal input combinations, the statistical performance metrics of the individual models showed that the uncertainties of all four models were within the acceptable range, with MAE, RMSE, and R2 values of 36.3–39.3 Wm−2, 54.7–57.3 Wm−2, and 0.75–0.79, respectively. The SVM model performed the best, followed by the RF and CNN in gap filling LE fluxes, whereas the accuracy of LSTM was low compared with all other models used in this study. Considering the above-mentioned individual model performances using optimal input combinations, our results indicated a marginal difference among the accuracies of the SVM, CNN, and RF models; in fact, this was supported by robust ANOVA and post-hoc tests. In terms of performance, the ranking of the models from best to worst was as follows: SVM > RF > CNN > LSTM. Our results further revealed that the hysteresis factor contributed significantly to establishing an optimal input combination for the four ML-based models used in the current study. It is noteworthy that the two deep-learning-based models required more input factors as compared with the two ML-based models, revealing its data-intensive approach.
Although the performances of all four models differed marginally, based on time-series analysis and Taylor diagram analysis, the two-dimensional CNN model implemented in the current study outperformed all the other models, such as the SVM, RF, and LSTM, in gap filling LE fluxes. Moreover, to extend the usability of our results to data-sparse regions, we investigated the relationship of models’ robustness upon losing their optimal input combination. Unlike the three above-mentioned models, we discovered a consistent improvement in the accuracy of the 2D-CNN after removing specific meteorological factors during training, with a 0.82–2.11% improvement in the MAE for all five factors.
As the hysteresis time factor increased, the accuracy of the four models resulted in a significant increase in the MAE. These analysis results provide useful guidelines to policy makers for selecting an appropriate hysteresis factor to achieve the best gap-filling accuracy. Furthermore, the extensive analysis conducted in the current study provides a benchmark to achieve better gap filling of EC-based flux tower observations. The two-dimensional CNN model adopted in the current study can be extended to similar application areas, such as satellite remote sensing, to generate high-quality temporally continuous observations for a wide range of climatological and agro-meteorological applications, including improved environmental monitoring, by selecting the optimum model demonstrated in the current study. Based on the guidelines provided in the current study, reliable and long-term geospatial datasets can be generated, which will benefit climate adaptation strategies, disaster risk assessment plans, and the sustainable development of geo-spatial information.
Author Contributions
Conceptualization, M.S.K.; methodology, M.S.K., S.B.J. and M.-H.J.; software, M.S.K. and S.B.J. and M.-H.J.; validation M.S.K., S.B.J. and M.-H.J.; formal analysis, M.S.K., S.B.J. and M.-H.J.; investigation, M.S.K., S.B.J. and M.-H.J.; resources, M.S.K., S.B.J. and M.-H.J.; data curation, M.S.K., S.B.J. and M.-H.J.; writing—original draft preparation, M.S.K.; writing—review and editing, M.S.K., S.B.J. and M.-H.J.; supervision, M.-H.J.; project administration and funding acquisition, M.-H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2021R1C1C1012785).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in the current study are available for free and can be downloaded from the AsiaFlux regional research network website (http://asiaflux.net, last accessed date: 2 December 2021) under a fair-usage policy.
Acknowledgments
The authors are grateful to the AsiaFlux network for providing unrestricted access to ground-based flux-tower datasets.
Conflicts of Interest
The authors declare no conflict of interest regarding the publication of this manuscript.
References
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Springer Science & Business Media: Berlin, Germany, 2013; Volume 1. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Emerson, C.W.; Anemone, R.L. Ongoing Developments in Geospatial Data, Software, and Hardware with Prospects for Anthropological Applications; Anemone, R.L., Ed.; University of New Mexico Press: Albuquerque, NM, USA, 2018; p. 21. [Google Scholar]
- Bégué, A.; Leroux, L.; Soumaré, M.; Faure, J.-F.; Diouf, A.A.; Augusseau, X.; Touré, L.; Tonneau, J.-P. Remote sensing products and services in support of agricultural public policies in Africa: Overview and challenges. Front. Sustain. Food Syst. 2020, 4, 58. [Google Scholar] [CrossRef]
- UN-GGIM. UN-GGIM (UN-Global Geospatial Information Management) Inter-Agency and Expert Group on the Sustainable Development Goal Indicators (IAEG-SDGS) Working Group Report on Geospatial Information; United Nations: New York, NY, USA, 2013. [Google Scholar]
- Anderson, M.; Kustas, W. Thermal remote sensing of drought and evapotranspiration. Eos Trans. Am. Geophys. Union 2008, 89, 233–234. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J. Evolution of evapotranspiration models using thermal and shortwave remote sensing data. Remote Sens. Environ. 2020, 237, 111594. [Google Scholar] [CrossRef]
- Cui, Y.; Song, L.; Fan, W. Generation of spatio-temporally continuous evapotranspiration and its components by coupling a two-source energy balance model and a deep neural network over the Heihe River Basin. J. Hydrol. 2021, 597, 126176. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Khan, M.S.; Jeong, J.; Choi, M. An improved remote sensing based approach for predicting actual Evapotranspiration by integrating LiDAR. Adv. Space Res. 2021, 68, 1732–1753. [Google Scholar] [CrossRef]
- Norman, J.; Kustas, W.; Prueger, J.; Diak, G. Surface flux estimation using radiometric temperature: A dual-temperature-difference method to minimize measurement errors. Water Resour. Res. 2000, 36, 2263–2274. [Google Scholar] [CrossRef]
- Shang, K.; Yao, Y.; Liang, S.; Zhang, Y.; Fisher, J.B.; Chen, J.; Liu, S.; Xu, Z.; Zhang, Y.; Jia, K. DNN-MET: A deep neural networks method to integrate satellite-derived evapotranspiration products, eddy covariance observations and ancillary information. Agric. For. Meteorol. 2021, 308, 108582. [Google Scholar] [CrossRef]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: Sap-flow, soil water budget, eddy covariance and catchment water balance. Agric. For. Meteorol. 2001, 106, 153–168. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, B.; Han, S.; Chen, H.; Wei, Z. Upscaling evapotranspiration from the instantaneous to the daily time scale: Assessing six methods including an optimized coefficient based on worldwide eddy covariance flux network. J. Hydrol. 2021, 596, 126135. [Google Scholar] [CrossRef]
- Wang, L.; Wu, B.; Elnashar, A.; Zeng, H.; Zhu, W.; Yan, N. Synthesizing a Regional Territorial Evapotranspiration Dataset for Northern China. Remote Sens. 2021, 13, 1076. [Google Scholar] [CrossRef]
- Delogu, E.; Olioso, A.; Alliès, A.; Demarty, J.; Boulet, G. Evaluation of Multiple Methods for the Production of Continuous Evapotranspiration Estimates from TIR Remote Sensing. Remote Sens. 2021, 13, 1086. [Google Scholar] [CrossRef]
- Khan, M.S.; Liaqat, U.W.; Baik, J.; Choi, M. Stand-alone uncertainty characterization of GLEAM, GLDAS and MOD16 evapotranspiration products using an extended triple collocation approach. Agric. For. Meteorol. 2018, 252, 256–268. [Google Scholar] [CrossRef]
- Khan, M.S.; Baik, J.; Choi, M. Inter-comparison of evapotranspiration datasets over heterogeneous landscapes across Australia. Adv. Space Res. 2020, 66, 533–545. [Google Scholar] [CrossRef]
- Nisa, Z.; Khan, M.S.; Govind, A.; Marchetti, M.; Lasserre, B.; Magliulo, E.; Manco, A. Evaluation of SEBS, METRIC-EEFlux, and QWaterModel Actual Evapotranspiration for a Mediterranean Cropping System in Southern Italy. Agronomy 2021, 11, 345. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H. Gap filling strategies for defensible annual sums of net ecosystem exchange. Agric. For. Meteorol. 2001, 107, 43–69. [Google Scholar] [CrossRef]
- Stauch, V.J.; Jarvis, A.J. A semi-parametric gap-filling model for eddy covariance CO2 flux time series data. Glob. Chang. Biol. 2006, 12, 1707–1716. [Google Scholar] [CrossRef]
- Hui, D.; Wan, S.; Su, B.; Katul, G.; Monson, R.; Luo, Y. Gap-filling missing data in eddy covariance measurements using multiple imputation (MI) for annual estimations. Agric. For. Meteorol. 2004, 121, 93–111. [Google Scholar] [CrossRef]
- Foltýnová, L.; Fischer, M.; McGloin, R.P. Recommendations for gap-filling eddy covariance latent heat flux measurements using marginal distribution sampling. Theor. Appl. Climatol. 2020, 139, 677–688. [Google Scholar] [CrossRef]
- Safa, B.; Arkebauer, T.J.; Zhu, Q.; Suyker, A.; Irmak, S. Net Ecosystem Exchange (NEE) simulation in maize using artificial neural networks. IFAC J. Syst. Control 2019, 7, 100036. [Google Scholar] [CrossRef]
- Cui, Y.; Ma, S.; Yao, Z.; Chen, X.; Luo, Z.; Fan, W.; Hong, Y. Developing a gap-filling algorithm using DNN for the Ts-VI triangle model to obtain temporally continuous daily actual evapotranspiration in an arid area of China. Remote Sens. 2020, 12, 1121. [Google Scholar] [CrossRef]
- Wutzler, T.; Lucas-Moffat, A.; Migliavacca, M.; Knauer, J.; Sickel, K.; Šigut, L.; Menzer, O.; Reichstein, M. Basic and extensible post-processing of eddy covariance flux data with REddyProc. Biogeosciences 2018, 15, 5015–5030. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef] [PubMed]
- van Wijk, M.T.; Bouten, W. Water and carbon fluxes above European coniferous forests modelled with artificial neural networks. Ecol. Model. 1999, 120, 181–197. [Google Scholar] [CrossRef]
- Schmidt, A.; Wrzesinsky, T.; Klemm, O. Gap Filling and Quality Assessment of CO2 and Water Vapour Fluxes above an Urban Area with Radial Basis Function Neural Networks. Bound.-Layer Meteorol. 2008, 126, 389–413. [Google Scholar] [CrossRef]
- Moffat, A.M.; Papale, D.; Reichstein, M.; Hollinger, D.Y.; Richardson, A.D.; Barr, A.G.; Beckstein, C.; Braswell, B.H.; Churkina, G.; Desai, A.R.; et al. Comprehensive comparison of gap-filling techniques for eddy covariance net carbon fluxes. Agric. For. Meteorol. 2007, 147, 209–232. [Google Scholar] [CrossRef]
- Sun, H.; Xu, Q. Evaluating Machine Learning and Geostatistical Methods for Spatial Gap-Filling of Monthly ESA CCI Soil Moisture in China. Remote Sens. 2021, 13, 2848. [Google Scholar] [CrossRef]
- Sarafanov, M.; Kazakov, E.; Nikitin, N.O.; Kalyuzhnaya, A.V. A Machine Learning Approach for Remote Sensing Data Gap-Filling with Open-Source Implementation: An Example Regarding Land Surface Temperature, Surface Albedo and NDVI. Remote Sens. 2020, 12, 3865. [Google Scholar] [CrossRef]
- Bianco, M.J.; Gerstoft, P.; Traer, J.; Ozanich, E.; Roch, M.A.; Gannot, S.; Deledalle, C.-A. Machine learning in acoustics: Theory and applications. J. Acoust. Soc. Am. 2019, 146, 3590–3628. [Google Scholar] [CrossRef]
- Yu, T.-C.; Fang, S.-Y.; Chiu, H.-S.; Hu, K.-S.; Tai, P.H.-Y.; Shen, C.C.-F.; Sheng, H. Pin accessibility prediction and optimization with deep learning-based pin pattern recognition. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 40, 2345–2356. [Google Scholar] [CrossRef]
- Peppert, F.; von Kleist, M.; Schütte, C.; Sunkara, V. On the sufficient condition for solving the gap-filling problem using deep convolutional neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.; Halem, M. Deep Learning Models for Predicting CO2 Flux Employing Multivariate Time Series; Mile TS: Anchorage, AK, USA, 2019. [Google Scholar]
- Huang, I.; Hsieh, C.-I. Gap-Filling of Surface Fluxes Using Machine Learning Algorithms in Various Ecosystems. Water 2020, 12, 3415. [Google Scholar] [CrossRef]
- Kwon, H.-J.; Lee, J.-H.; Lee, Y.-K.; Lee, J.-W.; Jung, S.-W.; Kim, J. Seasonal variations of evapotranspiration observed in a mixed forest in the Seolmacheon catchment. Korean J. Agric. For. Meteorol. 2009, 11, 39–47. [Google Scholar] [CrossRef][Green Version]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Chirodea, M.C.; Novac, O.C.; Novac, C.M.; Bizon, N.; Oproescu, M.; Gordan, C.E. Comparison of Tensorflow and PyTorch in Convolutional Neural Network-based Applications. In Proceedings of the 2021 13th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Pitesti, Romania, 1–3 July 2021; pp. 1–6. [Google Scholar]
- Banda, P.; Cemek, B.; Küçüktopcu, E. Estimation of daily reference evapotranspiration by neuro computing techniques using limited data in a semi-arid environment. Arch. Agron. Soil Sci. 2018, 64, 916–929. [Google Scholar] [CrossRef]
- Liu, Z. A method of SVM with normalization in intrusion detection. Procedia Environ. Sci. 2011, 11, 256–262. [Google Scholar] [CrossRef]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Kim, P. Convolutional neural network. In MATLAB Deep Learning; Springer: Berkeley, CA, USA, 2017; pp. 121–147. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Kim, Y.; Johnson, M.S.; Knox, S.H.; Black, T.A.; Dalmagro, H.J.; Kang, M.; Kim, J.; Baldocchi, D. Gap-filling approaches for eddy covariance methane fluxes: A comparison of three machine learning algorithms and a traditional method with principal component analysis. Glob. Chang. Biol. 2020, 26, 1499–1518. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, J.; Sun, X.; Lima, E.; Mu, Q.; Wang, X. A CFCC-LSTM model for sea surface temperature prediction. IEEE Geosci. Remote Sens. Lett. 2017, 15, 207–211. [Google Scholar] [CrossRef]
- Jeong, M.-H.; Lee, T.-Y.; Jeon, S.-B.; Youm, M. Highway Speed Prediction Using Gated Recurrent Unit Neural Networks. Appl. Sci. 2021, 11, 3059. [Google Scholar] [CrossRef]
- Jeon, S.-B.; Jeong, M.-H.; Lee, T.-Y.; Lee, J.-H.; Cho, J.-M. Bus Travel Speed Prediction Using Long Short-term Memory Neural Network. Sens. Mater 2020, 32, 4441–4447. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Alcântara, E.H.; Stech, J.L.; Lorenzzetti, J.A.; Bonnet, M.P.; Casamitjana, X.; Assireu, A.T.; de Moraes Novo, E.M.L. Remote sensing of water surface temperature and heat flux over a tropical hydroelectric reservoir. Remote Sens. Environ. 2010, 114, 2651–2665. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, Y.; Gan, G.; Wang, R. Hysteresis behavior of surface water fluxes in a hydrologic transition of an ephemeral Lake. J. Geophys. Res. Atmos. 2020, 125, e2019JD032364. [Google Scholar] [CrossRef]
- Dhungel, R.; Aiken, R.; Evett, S.R.; Colaizzi, P.D.; Marek, G.; Moorhead, J.E.; Baumhardt, R.L.; Brauer, D.; Kutikoff, S.; Lin, X. Energy Imbalance and Evapotranspiration Hysteresis Under an Advective Environment: Evidence From Lysimeter, Eddy Covariance, and Energy Balance Modeling. Geophys. Res. Lett. 2021, 48, e2020GL091203. [Google Scholar] [CrossRef]
- Zhang, Q.; Manzoni, S.; Katul, G.; Porporato, A.; Yang, D. The hysteretic evapotranspiration—Vapor pressure deficit relation. J. Geophys. Res. Biogeosciences 2014, 119, 125–140. [Google Scholar] [CrossRef]
- Lin, R.; Liu, S.; Yang, M.; Li, M.; Zhou, M.; Li, S. Hierarchical recurrent neural network for document modeling. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 899–907. [Google Scholar]
- Rodriguez, P.; Wiles, J.; Elman, J.L. A recurrent neural network that learns to count. Connect. Sci. 1999, 11, 5–40. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Miller, R.G., Jr. Beyond ANOVA: Basics of Applied Statistics; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Razali, N.M.; Wah, Y.B. Power comparisons of shapiro-wilk, kolmogorov-smirnov, lilliefors and anderson-darling tests. J. Stat. Modeling Anal. 2011, 2, 21–33. [Google Scholar]
- Yue, W.; Xu, J.; Tan, W.; Xu, L. The relationship between land surface temperature and NDVI with remote sensing: Application to Shanghai Landsat 7 ETM+ data. Int. J. Remote Sens. 2007, 28, 3205–3226. [Google Scholar] [CrossRef]
- Tarigan, S.; Stiegler, C.; Wiegand, K.; Knohl, A.; Murtilaksono, K. Relative contribution of evapotranspiration and soil compaction to the fluctuation of catchment discharge: Case study from a plantation landscape. Hydrol. Sci. J. 2020, 65, 1239–1248. [Google Scholar] [CrossRef]
- Khan, M.S.; Baik, J.; Choi, M. A physical-based two-source evapotranspiration model with Monin–Obukhov similarity theory. GIScience Remote Sens. 2021, 58, 88–119. [Google Scholar] [CrossRef]
- Wang, K.; Wang, P.; Li, Z.; Cribb, M.; Sparrow, M. A simple method to estimate actual evapotranspiration from a combination of net radiation, vegetation index, and temperature. J. Geophys. Res. Atmos. 2007, 112, D15107. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).