Abstract
We discuss results on plasma density profile modifications in the F-region ionosphere that are caused by HF heating with the frequency f0 in the range [(−150 kHz)–(+75 kHz)] around the fourth electron gyroharmonic 4fc. The experiments were conducted at the HAARP facility in June 2014. A multi-frequency Doppler sounder (MDS), which measures the phase and amplitude of reflected sounding radio waves, complemented by the observations of the stimulated electromagnetic emission (SEE) were used for the diagnostics of the plasma perturbations. We detected noticeable plasma expulsion from the reflection region of the pumping wave and from the upper hybrid region, where the expulsion from the latter was strongly suppressed for f0 ≈ 4fc. The plasma expulsion from the upper hybrid region was accompanied by the sounding wave’s anomalous absorption (AA) slower development for f0 ≈ 4fc. Furthermore, slower development and weaker expulsion were detected for the height region between the pump wave reflection and upper hybrid altitudes. The combined MDS and SEE allowed for establishing an interconnection between different manifestations of the HF-induced ionospheric turbulence and determining the altitude of the most effective pump wave energy input to ionospheric plasma by using the dependence on the offset between f0 and 4fc.
1. Introduction
A powerful O-mode electromagnetic pump wave transmitted from the ground into the bottom-site ionospheric F-region excites a wide range of plasma processes, leading to the appearance of artificial ionospheric turbulence (AIT), i.e., the generation of different HF and LF plasma modes; plasma density inhomogeneities of scales from tens of centimeters to kilometers; and causes electron heating, electron acceleration, ionization, generation of ionospheric airglow, etc. [1,2,3]. Diverse diagnostic methods and tools are used for studying the AIT, particularly, the sounding of the heated volume of the ionosphere using diagnostic waves and the registration of secondary, or stimulated, emission (SEE) in different frequency ranges.
The pump–plasma interaction is known to be the strongest near the pump wave (PW) reflection height zr0 at which fp(zr0) equals the pump frequency f0, and near the upper hybrid (UH) resonance height zUH0, where fp(zUH0) = (f02 − fc2)1/2 (here and fc = eB/2πm are the electron plasma frequency and the electron cyclotron frequency, respectively; e and m are the electron charge and mass; N is the electron density; the permittivity of free space; and B is the geomagnetic field strength). This corresponds to existing theoretical concepts and is confirmed by investigations of the HF-pumped ionospheric volume using multifrequency Doppler sounding (MDS) at the “Sura” and EISCAT heating facilities [4,5,6,7], which had revealed plasma expulsion from the resonance regions. During early MDS experiments, few low-power O-mode waves with frequencies fi, i = 1, 2, …, k, around f0 were used to probe different parts of the ionospheric plasma in or near the interaction regions. Measurements of time variations of probe wave phases allowed for measurement of the density profile modifications. In experiments, only a small number of frequencies of probing (diagnostic) waves could be used, i.e., and the distance between neighbor “probing altitudes” in the ionosphere was typically 0.5–1 km. In [8], a way of increasing the number of diagnostic wave frequencies without adding transmitter(s) and, therefore, of decreasing the height step between neighbor probing altitudes was suggested (for details see Section 2). This method was successfully used in the MDS experiments at the “Sura” facility [9].
The HF pump-induced phenomena that occur in the resonance region depend noticeably on the proximity of the PW frequency f0 to the electron cyclotron harmonics nfc (n = 2, …, 7). This concerns the SEE, the cross-section of the aspect angle scattering, the anomalous absorption (AA) of the diagnostic waves with frequencies fi close to f0, the artificial airglow, the generation of artificial ionization layers, etc. An extensive literature is devoted to studying the dependences of these phenomena on [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30].
SEE with frequencies fSEE close to the pump wave frequency f0 occurs due to the conversion of HF pump-driven electrostatic plasma modes, most notably Langmuir (L) and upper hybrid (UH) waves, into electromagnetic waves that are weaker than the reflected PW by 50–90 dB [10,31,32] and provide rich information about the AIT, thereby helping to identify nonlinear processes in the HF-pumped volume. The prominent SEE spectral features have long been used as indicators of specific nonlinear mode interactions in the altitude region between the reflection zr0 of the O-mode pump and slightly below the upper hybrid resonance zUH0. Several prominent SEE spectral features were established from numerous studies of stationary and dynamic SEE spectra that were performed at the European Incoherent Scatter (EISCAT), “Sura”, High-Frequency Active Auroral Research Program (HAARP), Arecibo and Space Plasma Exploration by Active Radar (SPEAR) heating facilities for 2.8 < f0 < 10 MHz [8,9]. SEE spectral characteristics depend on the Δfc = f0 − nfc offset of the PW frequency f0 from the multiple electron gyroresonance nfc. The most dramatic changes occur during the transition of f0 via nfc (e.g., from f0 < nfc to f0 > nfc) and allows one to estimate Δfc during the experiment [2,11,12,13,14,26].
The first attempt of a systematic study of electron density profile modifications using MDS concurrently with the SEE and AA measurements for the pump frequency f0 near the electron gyroharmonic nfc was done at the “Sura” facility in the 1990s [7]. These experiments left many questions open because of the rare net of the diagnostic wave frequencies, as well as the quite low temporal resolution in the SEE measurements.
In this paper, we report the results of the first experiments using MDS (phase) sounding of the HF-pumped ionosphere at the HAARP heating facility, located near Gakona, Alaska, USA (62.40°N, 145.15°W), that were performed in June 2014. Simultaneously, the SEE was monitored and the AA of the sounding waves was measured. The heating facility was used both for the pump wave radiation and as the pulsed Doppler HF radar. The main purpose of the experiments was to study the dependence of HF-pump-induced electron density expulsion from the resonance regions (in correlation with the AA and SEE) on the offset of the pump wave frequency from the fourth gyroharmonic, namely, Δfc = f0 − 4fc, where the experiment was performed for .
Below, Section 2.1 presents the experimental setup; Section 2.2 describes the method that was used for the phase data analysis that allowed for determination of the displacement of the sounding waves’ reflection altitudes and of the pump-induced electron density changes; the results obtained from the combined analysis of the phase sounding, AA and SEE data are presented in Section 3; and Section 4 discusses the obtained results.
2. Methods and Data
2.1. Experimental Setup
Experiments on phase–amplitude sounding of the ionosphere heated volume were performed on 4 June 2014. During the time interval 14:55–16:25 AKDT, the HAARP transmitter radiation schedule was organized as a sequence cycle at different PW frequencies f0 that varied from 5540 to 5730 kHz. The choice of the PW frequency nominals was conditioned by covering the available range around 4fc and a sufficiently large difference between f0 and fOF2, the critical frequency of the ionosphere, where fOF2 − f0 150–200 kHz. Each cycle was organized as follows: Over 4.5 min, the HAARP operated as a pulsed Doppler HF radar. The transmitters radiated vertical low-duty cycle diagnostic waves (DW): short (20 µs) pulses with an interpulse period T = 100 ms at two carrier frequencies fDW = f0 and fDW = f0 − 200 kHz with an effective radiated power (ERP) Pef~400 MW each. After 30 s, the radar mode was combined for 45 s with a quasi-continuous wave (QCW) pumping mode, i.e., high duty cycle pump wave (pulse width τ = 70 ms, the same interpulse period T = 100 ms) at a frequency f0 with the same ERP. During the QCW, the short pulses were radiated after 20 ms in the 30 ms pump-off period. After switching off the radar mode, the 30 s pause of the HAARP transmitters was used for taking ionograms and changing the PW and DW frequencies. Then, the 5 min cycle was repeated at the new f0 and fDW. The power of the 20 μs diagnostic pulses was sufficient to create a wide spectrum of DW (up to 300 kHz near each carrier frequency). The average DW power <P> = P/Q = 80 kW was far below the thresholds of the generation and maintenance of a pump-induced thermal plasma instability that is responsible for the excitation of the small-scale magnetic-field aligned plasma density inhomogeneities (striations) [17]. Furthermore, the diagnostic pulses were too short to excite ponderomotive parametric instability in the ionosphere [8,33].
Under the combined radiation mode, the QCW created a perturbation in the ionosphere, particularly at the plasma resonance (reflection altitude of the pump wave) and at the UH resonance, while the DW simultaneously provided diagnostics of the AIT. Note that the ERP used was not sufficient to generate the artificial ionization layer described in [26,28,29]. The high power of the HAARP transmitters that were used for the MDS, which involved applying a broadband radio receiver and specially developed signal processing algorithms, allowed for studying the evolution of the amplitude (Ai) and phase (φi) of the various spectral components of the reflected DW (with frequencies fi), which passed the perturbed region twice in a wide frequency range ~600 kHz, ) and, therefore, in a wide (25–35 km) altitude interval. Sometimes, when using the QCW, we could analyze spectral components of the radar pulses in a smaller range kHz (. Outside of this range, the reflected signal fell to the level of the background noise due to the AA (see below), and the signal amplitude and phase analysis gave poor results. The frequency resolution that was used for the analysis was 1 kHz; the temporal resolution was determined using the interpulse period T = 100 ms. The observational site was located under the heated region during injections at vertical. A 30 m folded-dipole BWDS receiver antenna was used in the measurements. The receiver digitized a band at 850 kHz, where the dynamic range of the instruments after spectral processing is estimated to be better than 90 dB.
Figure 1 and Figure 2 present the results that were obtained during the cycles at f0 = 5540, 5600, 5660 and 5730 kHz for the PW reflection heights 230 km; Figure 3 and Figure 4 show the results at f0 = 5600, 5630, 5660 and 5730 kHz for 220 km.
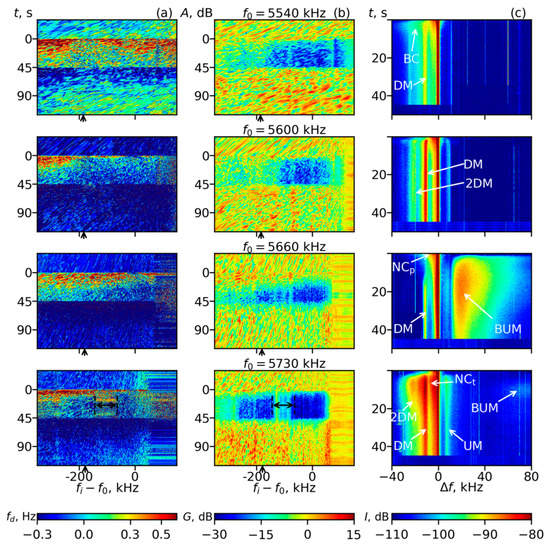
Figure 1.
Data obtained in the cycles for the PW reflection heights 230 km. The PW frequencies f0 are shown above the (b) panels. Column (a): The Doppler frequency shifts (colors) vs. time t and diagnostic wave spectral component frequency shift fi – f0. Column (b): Normalized amplitude of the diagnostic waves G (color) vs. t and frequency shift fi – f0. Column (c): The SEE spectrograms. Prominent stimulated electromagnetic emission spectral features, the ponderomotive narrow continuum (NCp), thermal narrow continuum (NCt), downshifted maximum (DM), 2nd downshifted maximum (2DM), upshifted maximum (UM), broad continuum (BC) and broad upshifted maximum (BUM) are marked. The arrows below the frequency axes correspond to the plasma frequency at the upper hybrid (UH) resonance height , in all figures. Double arrows show the contaminated frequency range for the phase data processing.
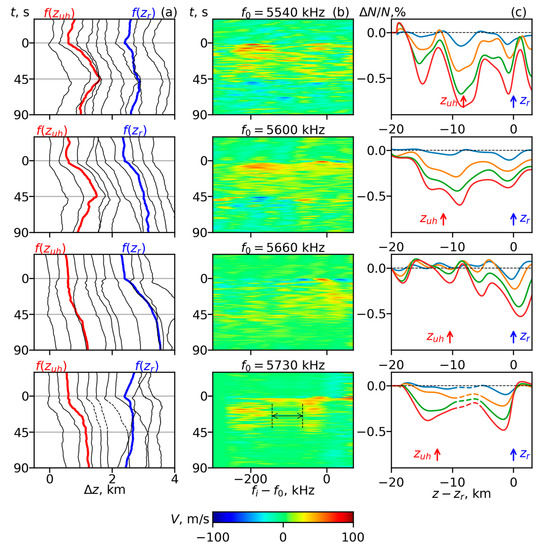
Figure 2.
Results of the phase data processing for the PW reflection heights zr0 230 km. The PW frequencies f0 are shown above the (b) panels. Column (a): Temporal variations of the reflection height shifts of different spectral components of the sounding pulses Δz (fi, t) for different cycles. The frequency step between shown spectral components Δfi = 60 kHz, starting from f0. An additional height shift of 300 m between the reflection heights of the successive shown frequencies fi at t = 0 was added for clarity. Red and blue lines correspond to the spectral components that were reflected from zUH and zr. Column (b): Velocity of the sounding waves reflection height displacement Vv = ∂Δzr (fi, t)/∂t vs. time and frequency. Column (c): Relative variations of the electron density [N(t) − N(0)]/N(0) vs. height at t = 5 s (blue), 15 s (orange), 30 s (green) and 45 s (red) in the same cycles. Double arrows show the contaminated frequency range for the data processing.
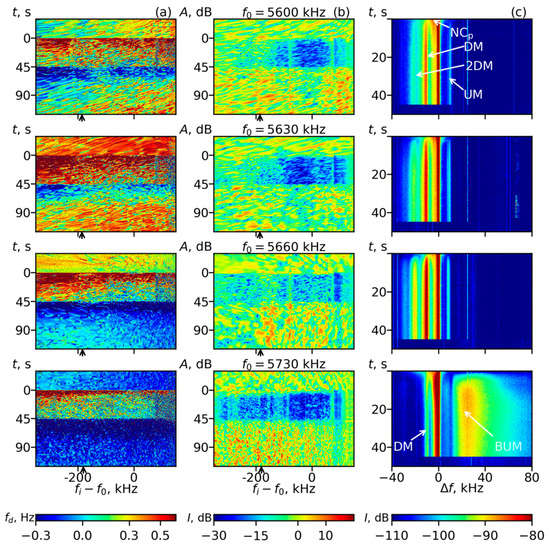
Figure 3.
Data that were obtained in the cycles for the PW reflection heights zr0 220 km. The PW frequencies f0 are shown above the (b) panels. Column (a): The Doppler frequency shifts (colors) vs. time t and diagnostic wave spectral component frequency shift fi – f0. Column (b): Normalized amplitude of the diagnostic waves G (color) vs. t and frequency shift fi – f0. Column (c): The SEE spectrograms. Prominent SEE spectral features, i.e., the NCp, DM, 2DM, UM and BUM, are marked.
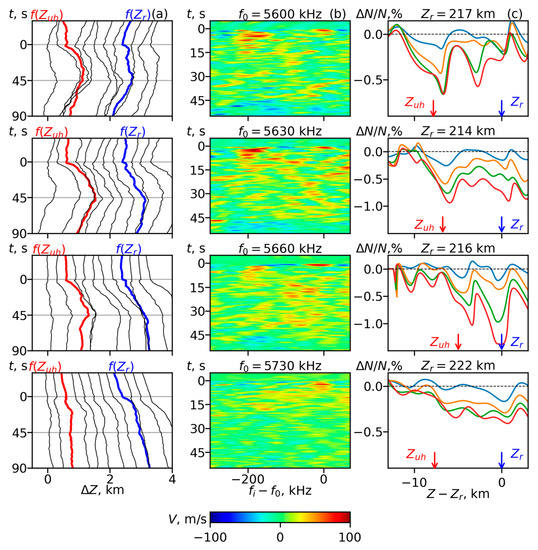
Figure 4.
Results of the phase data processing for the PW reflection heights zr0 220 km. The PW frequencies f0 are shown above the (b) panels. Column (a): Temporal variations of the reflection height shifts of different spectral components of sounding pulses Δz (fi, t) for different cycles. The frequency step between shown spectral components Δfi = 60 kHz, starting from f0. An additional height shift of 300 m between the reflection heights of the successive shown frequencies fi at t = 0 was added for clarity. Red and blue lines correspond to the spectral components that were reflected from zUH and zr. Column (b): Velocity of the sounding waves reflection height displacement Vv = ∂Δzr (fi, t)/∂t vs. time and frequency. Column (c): Relative variations of the electron density [N(t) − N(0)]/N(0) vs. height at t = 5 s (blue), 15 s (orange), 30 s (green) and 45 s (red) in the same cycles. Double arrows show the contaminated frequency range for the data processing.
Figure 1 and Figure 3 show the temporal evolution of the Doppler frequency shifts fdi(fi, t) = dφi/dt (a columns, φi is the phase incursion), normalized intensities Gi(fi, t) of the reflected DW spectral components (b columns) and SEE spectrograms (c columns). The DW intensities A2i(fi, t) were normalized using <A2i>, the intensity was averaged over 30 s before the QCW was switched on and ) characterized the AA due to the scattering of DW into plasma (UH) waves on small-scale plasma density irregularities (striations). In Figure 1b and Figure 3b, we used running averaging over 5 pulses (0.5 s). In the spectrograms, prominent SEE spectral features are marked. There are the L-related ponderomotive narrow continuum (NCp) at and the UH-related features: the thermal narrow continuum (NCt) at , the downshifted maximum (DM) with a peak at kHz and its family (the 2DM and upshifted maximum (UM) with peaks at kHz and kHz, respectively), the broad continuum (BC) at kHz and the broad upshifted maximum (BUM) at kHz. Stationary peculiarities and the temporal evolution of different SEE features are described in numerous papers; see, e.g., [2,10,11,12,14,16,17,18,26,34].
According to [11,12,14], there are quasi-periodic changes of the SEE spectral shape and emission intensity versus f0 with a period of fce, and there are five distinctive PW frequency ranges between successive gyroharmonics, i.e., nfc f0 (n + 1) fc, (n = 3 − 7), where n = 4 in our case: these ranges are the “resonance range”, f0 ≈ nfc, where the SEE is suppressed almost totally, except for the BUM, UM and NCp; the “above harmonic range”, f0 nfc, where the NCt, DM family (DM, 2DM and UM) and BUM are present in the spectrum, and the intensity of the NCt and DM family grows with f0, but the BUM intensity starts to decrease; the “strong emission range”, f0 > nfc, where the intensive DM family, NCt, BC and broad upshifted structure (BUS, which does not show up in Figure 1 and Figure 3) are present in the SEE spectrum; the “weak emission range”, f0 < (n + 1)fc, where only the DM family, NC and BC are seen in the SEE spectrum and they are much weaker than in the strong emission range; and the “below harmonic range”, f0 (n + 1)fc. Here, again, the DM family and BC (for n 5) are amplified in the SEE spectra but the BUM does not show up yet. Such SEE peculiarities can be used for rough estimations of the offsets between f0 and 4fc, i.e., Δfc = f0 − 4fc, in the range between successive gyroharmonics. More precisely, such estimations can be done for f0 ≈ 4fc and (see Equations (7) and (8) below).
For all f0, when the heating (QCW) was turned on, as a rule, an increase of all fi (positive Doppler frequency shifts fdi) was often observed. This was less pronounced for narrow ranges of the diagnostic (sounding) wave frequencies with reflection heights near the PW reflection and UH heights zr0 and zUH0, i.e., for fi~fp(zr0) and fi~fp(zUH0). Negative fdi values were observed after the heating was turned off. Such pump-induced changes of fdi occurred over the background of natural variations of the reflection heights (and fdi), where are determined by the motion of the ionosphere. The measured temporal evolution of phase incursion φi and Doppler frequency shifts fdi(t) = dφi/dt for different fi (Figure 1a and Figure 3a) provided data for the reconstruction of the electron density profile temporal evolution N(z, t) in the HF-pumped ionosphere by solving the inverse problem of the phase sounding. The method of the reconstruction is described in the next section. The obtained evolution of the electron density in the HF-pumped ionosphere in the altitude range from the region below the UH height to the region above the reflection height is shown in Figure 2 and Figure 4.
2.2. Phase Data Processing
Under a geometric optics approximation, each of the sounding waves at the angular frequency ωi = 2πfi propagating from the ground up to the reflection points zr(fi) and back to the ground, experiencing the phase incursion [35]:
where ωp(z, t) = 2πfp (z, t) is the plasma frequency and n(ω, ωp(z, t)) is the wave refractive index. The reflection altitude zr is determined by the condition n = 0 and t is the time. This can be translated into the following expression for an additional phase change Δφ(ω) = φ(ω, t0) − φ(ω, t) in the time interval [t0, t] that is associated with perturbation of the profile N(z, t) due to ionosphere HF pumping or to natural reasons:
Here, K (ω, ωp) = dn(ω, ωp)/dωp is a kernel of the integral in Equation (2); g(ω) is the angular plasma frequency at the reflection point, which is g(ω) = ω for an ordinary wave; t0 is the initial time; and Δz(ωp, t) = z(ωp, t) − z(ωp, t0) is the altitude shift, i.e., the difference between the sounding radio wave reflection altitude at the current (t) and initial (t0) times. Here, the variable of the integration is changed from the altitude z in Formula (1) to the plasma frequency ωp in Equation (2). It is taken into account that at the reflection point, n(ω, g(ω)) = 0, and at the entrance to the plasma layer, Δz = 0. The left-hand side in Equation (2), y(ω) is determined from experimental data using . On the base of the data obtained, an array ΔΦ(ω, t) = Δφ(ω, t) − Δφ(ωmin, t) was created for the phase shifts Δφ(ω, t) of the diagnostic waves. Here, ωmin is the least of the probe wave frequencies; in our experiment, we took ωmin = ω0 − 2π· (280, …, 450) kHz in different cases. The probe waves at these frequencies were reflected noticeably below (~25–35 km) zUH0, and we assumed that the phase evolutions for this and lower frequencies did not depend on the pump-induced processes in the plasma resonance regions. This was confirmed, in particular, by measurements of the AA bandwidth of the DW (Figure 1b). Moreover, the subtraction of Δφ(ωmin, t) allowed for excluding processes that are responsible for plasma density variations at lower altitudes, which are caused by the violation of the balance between ionization and recombination in the lower ionosphere. In addition, to reduce the contribution of the high-frequency phase noise in the phase spectrum ΔΦ(ω, t) at every time moment t, we applied a filtration of the experimental data using a Butterworth low-pass digital filter.
For the unmagnetized plasma, where the refractive index takes the form , from the integral in Equation (2), one can obtain the well-known Abel equation [36], which has an analytical solution. For the exact expression of the ordinary polarized wave refractive index for magnetized plasma:
where and ; Equation (2) cannot be reduced to the analytically solvable integral equation. In this case, we applied in [9,37] the regularization algorithms from [38] and solved the inverse problem numerically.
Tikhonov’s regularization method reduces solving the integral in Equation (2) to solving a system of k algebraic equations for , , for each time moment, where k is the number of sounding frequencies. However, a solution of this system suffers from a high numerical noise, which we tried to smooth by using a running average over the sounding frequencies (for details, see [9]). In this study, instead of the exact Formula (3), we used an approximate expression for that describes the ordinary wave refractive index near the reflection point for HAARP experimental conditions well:
Substituting Formula (4) into Equation (2), we obtained the generalized Abel equation [36]:
with the analytical solution:
Such an approximation gives a lower level of numerical noise compared to the Tikhonov regularization method, although with the addition of a small systematic error.
The dynamics of the reflection altitude shifts of different DW spectral components Δzr(ωi = 2πfi, t) is displayed in Figure 2a and Figure 4a. In these figures, t = 0 corresponds to the QCW switching on; the blue line corresponds to the reflection altitude of the DW at fi = f0, i.e., the PW reflection altitude (z(fi) = zr(f0)); and the red line corresponds to the reflection altitude of the DW at fi = fp(zUH0) = (f02 − fc2)1/2, i.e., reflection from the pump wave UH resonance height zUH0, respectively. The chosen frequency step between the neighboring spectral components that are displayed in Figure 2a and Figure 4a is Δf = 30 kHz. For clarity, we introduced an additional height shift of 300 m between the reflection altitude shifts of the successive DW spectral components at t = 0.
Temporal variations of the reflection heights Δz(fi, t) allowed for calculating the velocities of the vertical motion of the plasma density at a certain magnitude Ni = πfi2m/e2 as Vv = ∂Δzr (fi, t)/∂t at different fi values. The velocities of the sounding waves reflection height displacement vs. time and sounding wave frequency (pulse spectral component) Vv(fi, t) are presented in Figure 2b and Figure 4b. Positive (red) velocity values correspond to the upward motion of a certain plasma density level while negative (blue) values correspond to downward motion.
Calculating the altitude shifts Δzr(fi, t) allowed us to observe the evolution of the electron density profile N(z, t) from the reference one. The reference profile N0(z, t0) was taken from the ionogram that was registered prior to the QCW pumping session. For this, we transformed Δzr(fi, t) to Δzr(N, t) by using the univocal relation between the plasma frequency at the radio wave reflection point and electron density. Therefore,
was the dependence of the reflection height of the radio wave on the density. Then, we found the required distribution N(z, t) by calculating the inverse of Equation (7). The relative differences between the reconstructed and reference electron density profiles vs. altitude z for all f0 at the 5th, 15th, 30th and 45th seconds of pumping are presented in Figure 2c and Figure 4c.
For a better resolution, we present the initial behavior of the SEE, Vv and during the first 16 s of the QCW pumping for the cycle at f0 = 5540 kHz in Figure 5 (1, 5, 4, 8, 12, 16 s).
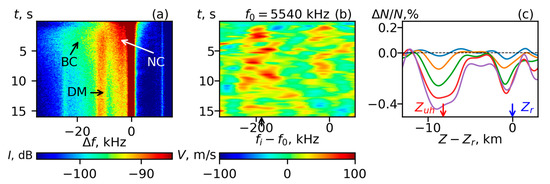
Figure 5.
Panel (a): SEE spectrograms for f0 = 5540 kHz for 0 < t < 16 s (a part of the Figure 1c, 1st row). Panel (b): Velocity of the sounding waves reflection height displacement Vv = ∂Δzr(fi, t)/∂t vs. time and frequency for f0 = 5540 kHz for 0 < t < 16 s (a part of the Figure 2b, 1st row). Panel (c): Relative variations of electron density [N(t) − N(0)]/N(0) vs. height at t = 1.5 s (blue), 4 s (orange) 8 s (green), 12 s (red) and 16 s (pink) in the same cycle.
3. Combined Analysis of the Phase Sounding, AA and SEE Data
Figure 1a and Figure 3a show that immediately after the QCW was switched on, the Doppler frequency shifts noticeably increased in comparison with the background values corresponding to the natural motion of the ionosphere. They became positive (fdi > 0) for all spectral components, except for those close to the pump frequency (fi ≈ f0), where the fdi enlargements were weaker. Such behavior of fdi was translated into increasing the reflection altitudes of the sounding waves zri with the frequencies close to the pump wave frequency f0 (Figure 2a and Figure 4a) with velocities Vv up to 100 m/s, and, in contrast, slighter decreasing zr for both fi > f0 and fi < f0 with velocities Vv up to 60 m/s (Figure 2b, Figure 4b and Figure 5b). This corresponded to an electron density decrease in the vicinity of the pump wave reflection height zr0 = zr(f0) and an increase in other heights, i.e., to the plasma expulsion from the reflection point vicinity.
The relative density depletion (hereafter reflection depletion (RD)) reaches up to ~0.1–0.2% at the fifth second of the QCW pumping (Figure 2c, Figure 4c and Figure 5c). According to Figure 2a and Figure 4a, the uplifting Δzr(fi ≈ f0) grew from 0.1 s till (3–5) s, reaching 100–300 m, and then slowed down till t = 10–15 s. Note that in the cycle at f0 = 5540 kHz, the RD depth even slightly decreased between the 10th and 15th seconds of the QCW pumping, which is clearly seen in Figure 5c.
The SEE feature NCp appeared immediately after the QCW was switched on, simultaneously with the start of the plasma expulsion from the vicinity of zr0, and then exhibited a strong overshoot effect: its spectral width and intensity noticeably dropped during the rise in zr(f0) and growth of the AA- and UH-related SEE features (Figure 1b,c and Figure 5c). Such initial behaviors of the fd(fi, t), Δzr(fi, t), Vv(fi, t), , NCp and AA were qualitatively similar for all f0 and did not depend on the offset Δfc.
A few seconds later, the phenomena related to the excitation of the UH waves and striations, resulting in the phenomena, such as the AA and the UH related SEE features, and the plasma expulsion from the UH height region (z~zUH0, the “UH depletion”, hereafter UHD) developed simultaneously. At this stage, a noticeable dependence of the observed phenomena on the offset Δfc = f0 − 4fc was obtained.
The following is an analysis for this time interval from the cycle with f0 = 5540 kHz, which is shown in the upper rows of Figure 1 and Figure 2. During this cycle, the pump frequency f0 = 5540 kHz belonged to the weak emission range between the third and fourth gyroharmonics, where the SEE spectrum contained weak BC, DM and UM (Figure 1c, row 1). In this range, the offset Δfc = f0 − 4fc could be roughly estimated from the ionograms and geomagnetic field IGRF model as Δfc ~−(130–150) kHz, where fc should be taken at z = zUH0, the upper hybrid resonance height of the pump wave. The AA, UH-related SEE and UHD started to develop during t = 1–3 s after the QCW was switched on. The expulsion from the UH height interval corresponded to the appearance of the expanding range with decreasing fdi near in Figure 1a, row 1. During 3–5 s, the UHD became deeper than the RD (Figure 2c, row 1, Figure 5c), and then the UHD developed monotonously till the QCW pumping was switched off. At t~15 s, the uplifting near the reflection point Δzr(fi ≈ f0) accelerated again and continued till the QCW stopped; for s, deepening of the UHD and RD was accompanied by a plasma density decrease in the whole altitude range (Figure 2c, row 1).
For the cycle at f0 = 5600 kHz (Figure 1 and Figure 2, second row), the results of the AA measurements (temporal development and magnitude) and the phase sounding analysis (fd(fi, t), Δzr(fi, t), Vv(fi, t) and ) were similar to those for f0 = 5540 kHz, but the SEE was quite different. According to the SEE spectrogram (Figure 1c, row 2), the PW frequency belonged to the “below harmonic” range. It showed a strong DM and resolved 2DM. With the use of the ionogram and IGRF magnetic field model, the offset could be roughly estimated as Δfc ~−(60–70) kHz. According to the ionograms, the values in the cycles at 5540 and 5600 kHz were close at . During these cycles in the DW frequency range kHz, the average anomalous absorption was smaller by ~10–15 dB (Figure 1b) in comparison with the range 150 kHz. Note that the reflection height of the DW with kHz was approximately equal to the PW UH height , where . This frequency is shown in Figure 1a,b, Figure 2b, Figure 3a,b, Figure 4b and Figure 5b by an arrow below the abscissa axis.
In the cycle at f0 = 5660 kHz (Figure 1 and Figure 2, 3rd row), the behavior of the bulk of investigated parameters differed noticeably from the cycles at f0 = 5540 and 5600 kHz, as well as from the cycle at f0 = 5730 kHz (see below). In this cycle, the RD developed similar to the cycles with other f0 values during the first 10 s of the QCW pumping but it did not slow down after t = 10 s. Smallest values of fdi appeared initially in the range surrounding fi (zr0), then this range expanded mainly to lower fi. The dependence on δN(z) looked like a shallow quasi-periodic structure that occupied a height interval that exceeded the spacing between zr0 and zUH0 with a period~3–4 km and an amplitude that grew in time and decreased along z downward from zr0 (Figure 2c). The UHD and zUH0 uplift did not resolve in this cycle. Moreover, a weak decrease of the reflection heights for frequencies surrounding was observed. Then, the AA and NCp overshoot developed slower than in other cycles, while the AA attained the same magnitudes as for f0 < 4fc till the 45 s of pumping. The difference was due to the fact that during this cycle at f0 = 5660 kHz, the PW frequency belonged to the resonant range. This was seen from the SEE spectrogram (Figure 1c). Here, the DM was not resolved till t ~10–15 s, which means that
at the PW UH height, i.e., the DM peak frequency fDM was in the double resonance. Then, the DM appeared, which was probably attributed to the amplification of the , changing of the UH height and, therefore, to a violation of Equation (8). This allowed for estimating the offset Δfc = f0 − 4fc during the cycle as 7–15 kHz; initially, Δfc ≈ ΔfDM and then changed. Detailed analyses of the SEE peculiarities (DM, UM and BUM) near the double resonance can be found in [11,14,18,26]. Note that the altitude of the double resonance obtained from Equation (8) and the IGRF model was ~240 km and exceeded the zUH0 that was obtained from the ionogram by ~10 km. However, this value fits into the error bar when determining the heights when processing the ionograms.
fDM = f0 −ΔfDM ≈ fUH0 ≈ 4fc,
The cycle at f0 = 5730 kHz (Figure 1 and Figure 2, 4th row) was the only cycle with f0 > 4fc (above harmonic range). Here, the offset Δfc = f0 − 4fc at the BUM SEE feature generation height zBUM could be estimated from the SEE spectrogram (Figure 1c, 4th row) as
where fBUM is the BUM peak frequency. According to the IGRF magnetic field model zBUM ~238 km, which exceeded, again, the zUH0 that was obtained from the ionogram by a few kilometers.
Δfc = f0 − 4fc ≈ fBUM − f0 = ΔfBUM, Δfc~+75 kHz,
From Figure 1 and Figure 2 for f0 = 5730 kHz (4th row), the following can be concluded. After the QCW pumping, switching on the plasma expulsion from the vicinity of the reflection point (RD) and the NCp development in the SEE spectrum behaved similarly to all f0. Slowing down of the RD deepening after the development of the UH-related effects was not observed. Like for f0 < 4fc, for f0 > 4fc, the UH-related effects (AA, DM, 2DM, UM SEE features and UHD) developed a few seconds later than the L-related processes near the reflection height. However, the characteristics of these processes during the cycle differed from the ones for f0 < 4fc. First, for f0 > 4fc, the AA was stronger, developed faster than for f0 < 4fc and f0 ≈ 4fc. It attained a saturation 25–30 dB at t 10–15 s, while for f0 < 4fc (f0 = 5540 kHz and 5600 kHz), 18–20 dB at t 20 s was produced, and at the double resonance case (f0 = 5660 kHz), ~18–20 dB at t 25 s was produced. The DW frequency range with a strong AA was wider at f0 > 4fc than at f0 < 4fc (Figure 1b). Due to the strong AA, in the range 5590 < fi <5650 kHz, the DW signal intensity decreased to the background noise, and measurements of the Doppler shifts/phase incursions and AA became impossible due to noise interference. This range is shown in Figure 1 and Figure 2, row 4, by double arrows and dashed parts of the lines. It shall be excluded from the analysis for t >15 s. Second, a strong NCt showed up in the SEE spectrogram atkHz with a temporal behavior that was similar to the DM, 2DM and UM; after t~1.5 s, the NCt covered NCp. The DM, 2DM and UM developed concurrently with the AA and exhibited an overshoot effect with maxima at t~6–11 s. These SEE features were more intense than in other cycles. Such SEE behavior is typical for the above harmonic range close to the strong emission range [14]. Third, the UHD started to develop at ~2 km above the nominal upper hybrid resonance height zUH0 and occupied quite a wide (>5 km) altitude interval. Later, during t~10–15 s, the interval expanded (till ~8 km) and descended below the UH height. During the whole 45 s of the QCW pumping, the UHD remained shallower than the RD (Figure 2c, 4th row).
The four cycles described above were collected during 14:55–15:15 and 16:00–16:05 AKDT. During the cycles performed during 16:05–16:25 AKDT, the ionosphere descended, the PW reflection heights zr0 were lower, i.e., zr0~215–225 km, and the nominal values of the fourth gyroharmonic were larger by 50–70 kHz. The results of these four cycles are shown in Figure 3 and Figure 4. During the first three cycles (f0 = 5600, 5630 and 5660 kHz), the PW frequencies were f0 < 4fc; in the last cycle (f0 = 5730 kHz), f0 4fc. According to the SEE spectrograms (Figure 3c), the PW frequency f0 = 5600 kHz (upper row) was in between the weak emission range and below harmonic range: the DM and UM were weak but stronger than at f0 = 5540 kHz, and the 2DM was barely resolvable. For an increase in f0 by 30 kHz in each of the next two cycles (f0 = 5630 kHz and 5660 kHz), the PW frequencies belonged to the below harmonic range) and f0 approached 4fc from below. This was confirmed by amplification of the DM, 2DM and UM in the spectrograms (Figure 3c). Using the ionograms and IGRF model, the offsets Δfc during the three cycles with f0 < 4fc could be roughly estimated as Δfc~−(110–130), −(90–100) and −(55–65) kHz. Note that the SEE spectrogram in Figure 1c at f0 = 5600 kHz was similar to the ones at f0 = 5630 kHz in Figure 3c. This shows that the offsets Δfc were close in these cycles. This happened because of a decrease in the ionosphere and an increase in the magnetic field strength at the lower heights.
For the three cycles with f0 < 4fc, the temporal behavior of fi, AA, SEE, , Vv and δN were qualitatively similar to those for larger PW reflection heights: Initially, the plasma expulsion from the PW reflection height (RD) and NCp SEE spectral feature developed. Then, for s, the UH-related phenomena (AA, DM, UM, 2DM and UHD) developed concurrently with the NCp overshoot and the RD deepening slowed down, and the UHD became deeper than the RD (at s). The AA also dropped by 10–15 dB in the DW range . Then, the uplifting near the reflection point Δzr(fi ≈ f0) accelerated again and continued till the QCW stopped, and for s, deepening of the UHD and RD was accompanied by a plasma density decrease in the whole altitude range . The difference between these cycles and the cycles shown in Figure 1 and Figure 2 lies in the fact that in the below harmonic range for the close offsets , the UHD turned out to be deeper for low altitudes of the ionosphere. In particular, at f0 = 5600 kHz (Figure 2c) at the end of pumping (t~45 s), δN was 0.6%, while at f0 = 5630 kHz and 5660 kHz (Figure 4c), δN attained 1–1.05%. At the same time, the uplifting of the UH height remained nearly the same with ~750–900 m (Figure 2a and Figure 4a). At the PW frequency that belonged to the weak emission range for different ionosphere heights (Figure 2, f0 = 5540 kHz, 16:00 AKDT and Figure 4, f0 = 5600 kHz, 15:00 AKDT), the UHD depths were close (δN~0.7–0.8%) while the UH height uplift was larger for the higher ionosphere. The plasma density reduction in the whole altitude range as well as the RD deepening at t = 15–45 s was greater for lower ionosphere heights. The greatest reflection point uplift occurred at f0 = 5630 kHz (16:15 AKDT) and f0 = 5660 kHz (16:10 AKDT) and achieved 500–600 m, while the relative depth of the RDs for these two cycles attained 0.9 and 1.3%, respectively. Note that in the cycle at f0 = 5660 kHz, the RD depth exceeded the UHD depth for t > 20–25 s (Figure 4c). Furthermore, in this cycle, the AA was the smallest with dB.
The pump frequency f0 = 5730 kHz (Figure 3 and Figure 4, 4th row, 16:20 AKDT) belonged to the lower frequency flank of the above harmonic range near the resonance range . This is seen in Figure 3c, 4th row: in the SEE spectrogram, the weak DM and UM, as well as the BUM with a peak at ΔfBUM~25 kHz, were present. Here, fc could be estimated from Equation (9) as fc ≈ 1426 kHz, which corresponded to a height of z ≈ 220 km. In this cycle, the behavior of the investigated parameters was very close to one that was obtained in the cycle at f0 = 5660 kHz (Figure 1 and Figure 2, 3rd row, 15:10 AKDT). Here, again, the dependence on δN(z) looked like a shallow quasi-periodic structure starting near zr0, expanding to a lower z and occupying a height interval that exceeded the spacing between zr0 and zUH. The difference between these two cycles was that the amplitude of the quasi-periodic structure was smaller in the cycle at a lower ionosphere, where during t~15–25 s, the small UHD could be resolved (see Figure 4a); in this cycle at f0 = 5730 kHz, the AA developed faster than at f0 = 5660 kHz but achieved close stationary values.
After the termination of the QCW, the Doppler frequency shifts fdi dropped sharply and became negative for the majority of the cycles. This led to a reduction in the pump-induced plasma density depletions around the reflection and UH heights, the depletions relaxed and disappeared during ~15–40 s after the QCW pumping turned off and the plasma motion was determined by natural causes.
4. Discussion and Conclusions
In this article, we present experimental results from the HAARP ionospheric research facility (Gakona, Alaska, USA) that were produced when studying plasma density profile modifications in the F-region caused by HF pumping with the frequency f0 in the range [(−150 kHz)–(+75 kHz)] around the fourth electron gyroharmonic 4fc. The specially elaborated pump wave radiation schedule was used for multi-frequency Doppler sounding of the HF-pumped volume of the ionosphere. Measurement of the phases and amplitudes of the reflected diagnostic signals was complemented by the observations of the SEE.
The main results of the study can be summarized as follows.
It was obtained that during all cycles, the pump wave–plasma interaction developed most quickly (in a few milliseconds) after the QCW switched on in the vicinity of the pump wave reflection height zr0. This was accompanied by the plasma expulsion from the interaction region (RD appearance), uplifting of the PW reflection point and the NCp SEE feature generation. At this time, there were no essential differences between the cycles with different f0. Both the expulsion and NCp were attributed to the excitation of L-waves due to the ponderomotive parametric instability near the PW reflection height zr0. Here, the L-waves propagated almost along the (geo)magnetic field B. The dispersion properties of the L-waves and, therefore, the NCp and RD dynamics practically did not depend on the proximity of the PW frequency f0 to 4fc. The absence of the NCp dependence on at the initial stage of pumping for n = 4, 5 was discussed by [17,19,25,26]. The RD dependence on was investigated in the presented study for the first time.
Later, during the 1–5 s after the QCW was switched on, for f0 < 4fc, the plasma expulsion from the vicinity of the upper hybrid height zUH0 (UHD development) began, along with the development of the AA; UH-related SEE features, such as DM, 2DM, UM and BC; and the suppression (overshoot) of the NCp feature and slowing down of expulsion from the vicinity of zr0. During 3–10 s, the UHDs became deeper than the RDs. The expulsion from the upper hybrid height continued until the end of the 45 s long QCW pumping. All these effects were related to the excitation of the striations and UH plasma waves under the thermal parametric instability. The slowing down of the zr0 uplifting, RD deepening (and even slight decrease of the RD depth during the cycle at f0 = 5400 kHz during t = 10–15 s) and NCp suppression indicated that the UH-related processes led to noticeable shielding of the reflection point from the pump wave energy. The sequence of the described effects was consistent with the general scenario of the phenomena developing in the HF-pumped ionosphere [2,17,33], which was clearly illustrated by [37], where the results of three successive 2 min cycles of pumping organized in a similar way at the frequency f0 = 5500 kHz obtained using the same experiment (4 June 2014, 15:40–15:46 AKDT) were presented. Similar results were also obtained at the “Sura” facility [9]. In the described experiment, during the cycles at f0 < 4fc, the RD and NCp developed similarly to the cycles at f0 = 5500 kHz till t = 5–10 s, but later ( s), the RD started to deepen again, concurrently with the UHD deepening on the background of plasma density decrease in the whole height interval . The dependence on looked like two isolated minima close to the reflection height and the UH height , respectively.
Note that for cycles at f0 < 4fc with approximately the same initial UH heights of ~225 km, the expulsion parameters , as well the AA, behaved similarly, even quantitatively, while the SEE spectra were different (Figure 1 and Figure 2, rows 1, 2). This pointed to a weak dependence of the AIT peculiarities on in the range kHz. For the smaller initial UH heights (Figure 3 and Figure 4, rows 1–3) ~207–211 km, for Δfc~−(55–100) kHz, the UHD and RD developed until noticeably larger depths. Furthermore, for f0 = 5630 kHz (Δfc~−(90–100) kHz), the RD attained approximately the same depth as the UHD, while for f0 = 5660 kHz (Δfc~−(55–65) kHz, closer to 4fc), the RD became even deeper than the UHD. The latter probably happened because in this cycle, the anomalous absorption was ~ 10 dB, which was 2–3 times less than in other cycles. Hence, the energy loss near the UH height due to the DW (and PW) energy transfer to the plasma (UH) waves on the striations was also less, and the larger portion of the PW energy was delivered to the reflection height and effectively contributed to the RD deepening.
In the single cycle with f0 > 4fc (above harmonic range near the strong emission range, Figure 1 and Figure 2, 4th rows, f0 = 5730 kHz, kHz), the developed, again, as two isolated minima, namely, RD and UHD. In this cycle, the UHD depth remained less than the RD depth during the whole OCW pumping interval; the altitude ranges that were occupied by the depletions were wider, while the AA of the DW was stronger (by ~10 dB) and occupied a larger frequency range than in the cycles with f0 < 4fc. The uplifting of the DW reflection heights zri near the PW UH height started at a t~15 s delay (Figure 2c, row 4) after the QCW was switched on. This pointed to the essential difference in the AIT excitation between the cases f0 > 4fc and f0 < 4fc. Note that the stronger AA for f0 > 4fc than for f0 < 4fc was noted in [7,21,22].
In the cycle at f0 = 5660 kHz (Figure 1 and Figure 2, rows 3), the PW frequency was close to 4fc, i.e., it got into the resonance range, where the DM was totally suppressed or very weak, but the BUM and UM were present in the SEE spectra. Taking fDM = f0 − ΔfDM ≈ 4fc(zUH) ≈ 5650 kHz and using the IGRF model for the geomagnetic field, we obtained zUH0 ≈ 239 km at the beginning of the cycle. In this cycle, the DW frequency range with a negative fdi expanded from the PW frequency f0 (Figure 1a, 3rd row), the temporal behavior of demonstrated a deepening quasi-periodic structure with a period ~3–4 km and an amplitude that grew in time and went downward from zr0 and occupied a height interval that exceeded the spacing between zr0 and zUH0. Unfortunately, the total range of the diagnostic signals that were available for the phase data processing was too narrow to estimate the lower boundary of the height interval. “Independent” zri uplifting for zri~zUH0 was not resolved in this cycle. Therefore, for f0 ≈ 4fc, the plasma expulsion from the UH region, as well as the DM generation, were quenched, and the total PW energy flux practically achieved the PW reflection point zr0. The AA, and hence the striations, developed slower than at f0 far from gyroharmonic, concurrently with the appearance of the weak DM in the SEE spectrum, but attained quite large values of ~20 dB till the end of QCW pumping in the DW frequency range −150 kHz< fi−f0 < 50 kHz (Figure 1b). In the cycle at f0 = 5730 kHz (16:20 AKDT, Figure 3 and Figure 4, row 4), the PW frequency was found in the low-frequency flank of the above harmonic range, close to the resonance range . Here, the temporal behavior of also demonstrated deepening quasi-periodic structure with a period~3–4 km, but during t~15–25 s after the PW switch on the small UHD could be resolved. Moreover, the AA developed faster than at f0 = 5660 kHz (compare Figure 1b, 3rd row and Figure 4b, 4th row).
Assuming that the height of the greatest plasma expulsion corresponds to the maximum PW energy consumption by ionospheric plasma, we can conclude that the most effective PW energy input occurred initially near the PW reflection height zr0. Later, for f0 < 4fc, the energy input became more effective near the UH height zUH0. Then, when the plasma expulsion developed throughout the whole region , the mutual influence of these two separated regions was, presumably, observed. For f0 > 4fc, these two isolated regions remained independent, although the UHD occupied a greater altitude range. The difference in the UHD behavior above and below the gyroharmonic was attributed to the different dispersion properties of plasma (UH) waves with a frequencies f > 4fc and f < 4fc and, therefore, different efficiencies of their excitation at different values [11,19,26]. Deeper and more concentrated UHDs at f0 < 4fc also provided a decrease in the average anomalous absorption in the DW range kHz, which is seen in Figure 1b and Figure 3b and noted above. This could be attributed to the focusing of the HF diagnostic radio waves that were reflected from the UH altitudes with density depletion [4].
For f0 ≈ 4fc, the PW energy was delivered mainly near and the AIT excitation near the UH height was suppressed. The slower AA (and striations) development may indicate that in the resonance range, the slowly developing striations with relatively large scales transverse to the magnetic field (say 15–30 m) experienced less suppression (if any) than the striations with smaller scales (say 2–15 m). A similar phenomenon, namely, more the important role of the larger striations in the DM generations for small offsets Δfc = f0 − 5fc, was mentioned by [20].
A reason for the observed plasma expulsion is the enhancement of the electron gas-kinetic pressure due to electron heating and the averaged high-frequency (ponderomotive) pressure. The enhancement is conditioned by the excitation of plasma (L and UH) waves by the pump wave near its reflection and UH heights. The stationary distribution of the plasma density over height z is considered in [39,40,41]. We estimated the dynamic behavior of the plasma expulsion from the altitudes of the plasma wave excitation using a one-dimensional system of transport equations. The system included an (i) electron thermal conductivity equation that took account of the electron cooling and the source related to the ohmic heating of electrons by pump-induced plasma (L and/or UH) waves, and an (ii) ambipolar diffusion equation for the electron density that took account of the thermal diffusion, electron lifetime and the term related to the ponderomotive pressure of the pump-induced plasma waves. Simple model calculations showed that the ponderomotive pressure of the excited plasma (L and UH) waves was responsible for the “independent” RD and UHD appearance and development, while the ohmic heating provided an alignment of the electron temperature along extended height interval that exceeded a distance between and , as well as the slow plasma expulsion observed in the whole interval [42]. A complete description of the electron density profile modification dynamics near PW resonances requires further theoretical efforts.
Finally, combined investigations of the HF heated volume by MDS, SEE and AA allowed for establishing the interconnection between different manifestations of the AIT and determining the position (altitude) of the most effective pump wave energy input in the HF-pumped ionosphere with respect to the offset between f0 and nfc. However, such experiments require stable ionospheric conditions (at least during 1.5–2 h) for avoiding uncontrolled changes in the pump wave reflection and upper hybrid heights, namely, and , where the pump–plasma interaction is known to be strongest, and therefore the frequency offset near , the transport (thermal conductivity and diffusion) coefficients and the presence of the PW reflection.
Author Contributions
Conceptualization, S.M.G. and E.N.S.; methodology, A.V.S., E.N.S. and S.M.G.; software, A.V.S., E.N.S. and Y.K.L.; set up and conducted the experiments, E.N.S., A.V.S., S.M.G., P.B., C.S. and M.J.M.; HAARP facility operation, M.J.M.; data curation, A.V.S.; data processing, A.V.S. and E.N.S.; theoretical modeling, Y.K.L. and S.M.G.; writing—original draft preparation, A.V.S., E.N.S. and S.M.G.; writing—review and editing, G.M.M. and S.M.G.; visualization, A.V.S.; supervision, S.M.G. All authors have read and agreed to the published version of the manuscript.
Funding
A.V.S., E.N.S., S.M.G. and Y.K.L. are supported by a Russian Science Foundation grant #20-12-00197 (Section 1, Section 3 and Section 4) and by Russian Foundation for Basic Research grants #19-02-00343 (Section 2.1) and #20-32-70198 (Section 2.2). P.B., C.S. and M.J.M. were supported by the NRL 6.1 Basic Research Program (experimental work).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Source data and code for reproducing the figures can be found in Shindin, A.V. Multifrequency Doppler Sounding data and software (HAARP 06/04/14 experiments), Zenodo. Retrieved from https://doi.org/10.5281/zenodo.4809544 and https://doi.org/10.5281/zenodo.4809544, accessed on 24 November 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gurevich, A.V. Nonlinear effects in the ionosphere. Phys.-Uspekhi 2007, 50, 1091–1121. [Google Scholar] [CrossRef]
- Grach, S.M.; Sergeev, E.N.; Mishin, E.V.; Shindin, A.V. Dynamic properties of ionospheric plasma turbulence driven by high-power high-frequency radiowaves. Phys.-Uspekhi 2016, 59, 1091–1128. [Google Scholar] [CrossRef]
- Streltsov, A.V. Effects of ionospheric heating on feedback-unstable electromagnetic waves. J. Geophys. Res. 2008, 113, A09211. [Google Scholar] [CrossRef] [Green Version]
- Vas’kov, V.V.; Golyan, S.F.; Gurevich, A.V.; Dimant, Y.S.; Zyuzin, V.A.; Kim, V.Y.; Komrakov, G.P.; Lobachevskii, L.A.; Migulin, V.V.; Mityakov, N.A.; et al. Excitation of upper hyprid resonance in the ionospheric plasma by an intense radio wave. JETP Lett. 1986, 43, 663–666. [Google Scholar]
- Berezin, I.V.; Beliansky, V.B.; Budko, V.I.; Vaskov, V.V. Diagnostics of the process of excitation of plasma-oscillations by the field of a powerful radio wave. Geomagn. Aeron. 1991, 31, 874–880. [Google Scholar]
- Lobachevsky, L.A.; Grusdev, Y.V.; Kim, V.Y.; Mikhaylova, G.A.; Panchenko, V.A.; Polimatidi, V.P.; Puchkov, V.A.; Vas’kov, V.V.; Stubbe, P.; Kopka, H. Observations of ionospheric modification by the Tromsø heating facility with the mobile diagnostic equipment of IZMIRAN. J. Atmos. Terr. Phys. 1992, 54, 75–85. [Google Scholar] [CrossRef]
- Grach, S.M.; Komrakov, G.P.; Yurishchev, M.A.; Thidé, B.; Leyser, T.B.; Carozzi, T. Multifrequency Doppler Radar Observations of Electron Gyroharmonic Effects during Electromagnetic Pumping of the Ionosphere. Phys. Rev. Lett. 1997, 78, 883–886. [Google Scholar] [CrossRef]
- Sergeev, E.N.; Grach, S.M.; Kotov, P.V.; Komrakov, G.P.; Boiko, G.N.; Tokarev, Y.V. Diagnostics of the HF-pumped ionospheric region using wide-band radio emission. Radiophys. Quantum Electron. 2007, 50, 593–610. [Google Scholar] [CrossRef]
- Shindin, A.V.; Sergeev, E.N.; Grach, S.M. Applications of broadband radio signals for diagnostics of electron density profile dynamics and spatial plasma motion in the HF-pumped ionosphere. Radio Sci. 2012, 47, RS0N04. [Google Scholar] [CrossRef]
- Leyser, T.B.; Thidé, B.; Derblom, H.; Hedberg, Å.; Lundborg, B.; Stubbe, P.; Kopka, H. Stimulated Electromagnetic Emission Near Electron Cyclotron Harmonics in the Ionosphere. Phys. Rev. Lett. 1989, 63, 1145–1147. [Google Scholar] [CrossRef]
- Leyser, T.B.; Thidé, B.; Waldenvik, M.; Goodman, S.; Frolov, V.L.; Grach, S.M.; Karashtin, A.N.; Komrakov, G.P.; Kotik, D.S. Spectral structure of stimulated electromagnetic emissions between electron cyclotron harmonics. J. Geophys. Res. 1993, 98, 17597–17606. [Google Scholar] [CrossRef]
- Leyser, T.B. Stimulated electromagnetic emissions by high frequency electromagnetic pumping of the ionospheric plasma. Space Sci. Rev. 2001, 98, 223–328. [Google Scholar] [CrossRef]
- Frolov, V.L.; Sergeev, E.N.; Ermakova, E.N.; Komrakov, G.P.; Stubbe, P. Spectral features of stimulated electromagnetic emissions, measured in the 4.3– 9.5 MHz pump wave frequency range. Geophys. Res. Lett. 2001, 28, 3103–3106. [Google Scholar] [CrossRef]
- Sergeev, E.N.; Frolov, V.L.; Grach, S.M.; Kotov, P.V. On the morphology of stimulated electromagnetic emission spectra in a wide pump wave frequency range. Adv. Space Res. 2006, 38, 2518–2526. [Google Scholar] [CrossRef]
- Grach, S.; Mityakov, N.; Rapoport, V.; Trakhtengertz, V. Thermal parametric turbulence in a plasma. Physica 2D 1981, 2, 102–106. [Google Scholar] [CrossRef]
- Carozzi, T.D.; Thidé, B.; Grach, S.M.; Leyser, T.B.; Holz, M.; Komrakov, G.P.; Frolov, V.L.; Sergeev, E.N. Stimulated electromagnetic emissions during pump frequency sweep through fourth electron cyclotron harmonic. J. Geophys. Res. 2002, 107, 1253. [Google Scholar] [CrossRef]
- Thidé, B.; Sergeev, E.N.; Grach, S.M.; Leyser, T.B.; Carozzi, T.D. Competition between Langmuir and upper-hybrid turbulence in a high-frequency-pumped ionosphere. Phys. Rev. Lett. 2005, 95, 255002. [Google Scholar] [CrossRef]
- Kotov, P.V.; Sergeev, E.N.; Grach, S.M. Spectra of Stimulated Electromagnetic Emission of the Ionosphere Sweeping of the Pump Wave Frequency Near Gyroharmonics. I. Experimental Results. Radiophys. Quantum Electron. 2008, 51, 417–430. [Google Scholar] [CrossRef]
- Bareev, D.D.; Gavrilenko, V.G.; Grach, S.M.; Sergeev, E.N. Estimation of HF artificial ionospheric turbulence characteristics using comparison of calculated plasma wave decay rates with the measured decay rates of the stimulated electromagnetic emission. Adv. Space Res. 2016, 57, 802–812. [Google Scholar] [CrossRef]
- Norin, L.; Grach, S.M.; Leyser, T.B.; Thidé, B.; Sergeev, E.N.; Berlin, M. Ionospheric plasma density irregularities measured by stimulated electromagnetic emission. J. Geophys. Res. 2008, 113, A09314. [Google Scholar] [CrossRef] [Green Version]
- Stocker, A.J.; Honary, F.; Robinson, T.R.; Jones, T.B.; Stubbe, P. Anomalous absorption during artificial modification at harmonics of the electron gyrofrequency. J. Geophys. Res. 1993, 98, 13627–13634. [Google Scholar] [CrossRef]
- Stubbe, P.; Stocker, A.J.; Honary, F.; Robinson, T.R.; Jones, T.B. Stimulated electromagnetic emission and anomalous HF wave absorption near electron gyroharmonics. J. Geophys. Res. 1994, 99, 6233. [Google Scholar] [CrossRef] [Green Version]
- Honary, F.; Robinson, T.R.; Wright, D.M.; Stocker, A.J.; Rietveld, M.T.; McCrea, I. First direct observations of the reduced striations at pump frequencies close to the electron gyroharmonics. Ann. Geophys. 1999, 17, 1235–1238. [Google Scholar] [CrossRef]
- Ponomarenko, P.V.; Leyser T., B.; Thidé, B. New electron gyroharmonic effects in HF scatter from pump-excited magnetic field-aligned ionospheric irregularities. J. Geophys. Res. 1999, 104, 10081–10087. [Google Scholar] [CrossRef]
- Sergeev, E.N.; Grach, S.M.; Komrakov, G.P.; Thide´, B.; Leyser, T.B.; Carozzi, T.D.; Holtz, M. Analyzing the process of excitation and decay of plasma turbulence near the fifth electron gyroharmonic using stimulated electromagnetic emission of the ionosphere. Radiophys. Quantum Electron. 2002, 45, 193–210. [Google Scholar] [CrossRef]
- Grach, S.M.; Sergeev, E.N.; Yashnov, V.A.; Kotov, P.V. Spectra of Stimulated Electromagnetic Emission of the Ionosphere Sweeping of the Pump Wave Frequency Near Gyroharmonics. II. Discussion of the Results. Radiophys. Quantum Electron. 2008, 51, 499–514. [Google Scholar] [CrossRef]
- Pedersen, T.; Gustavsson, B.; Mishin, E.; Kendall, E.; Mills, T.; Carlson, H.C.; Snyder, A.L. Creation of artificial ionospheric layers using high-power HF waves. Geophys. Res. Lett. 2010, 37, L02106. [Google Scholar] [CrossRef] [Green Version]
- Sergeev, E.; Grach, S.; Shindin, A.; Mishin, E.; Bernhardt, P.; Briczinski, S.; Isham, B.; Broughton, M.; LaBelle, J.; Watkins, B. Artificial ionospheric layers during pump frequency stepping near the 4th gyroharmonic at HAARP. Phys. Rev. Lett. 2013, 110, 065002. [Google Scholar] [CrossRef]
- Mishin, E.; Watkins, B.; Lehtinen, N.; Eliasson, B.; Pedersen, T.; Grach, S. Artificial ionospheric layers driven by high-frequency radiowaves: An assessment. J. Geophys. Res. Space Phys. 2016, 121, 3497–3524. [Google Scholar] [CrossRef] [Green Version]
- Sergeev, E.; Zykov, E.; Vertogradov, G.; Grach, S.; Shindin, A. Dynamic and Spectral Features of the Decameter Artificial Irregularities and the Stimulated Electromagnetic Emission over the “Sura” Heating Facility near the Fourth Electron Gyroharmonic. In Proceedings of the 2019 Russian Open Conference on Radio Wave Propagation (RWP), Kazan, Russian, 1–6 July 2019; pp. 273–276. [Google Scholar] [CrossRef]
- Thidé, B.; Kopka, H.; Stubbe, P. Observations of stimulated scattering of a strong high-frequency radio wave in the ionosphere. Phys. Rev. Lett. 1982, 49, 1561–1564. [Google Scholar] [CrossRef]
- Stubbe, P.; Kopka, H.; Thidé, B.; Derblom, H. Stimulated electromagnetic emission: A new technique to study the parametric decay instability in the ionosphere. J. Geophys. Res. 1984, 89, 7523–7536. [Google Scholar] [CrossRef]
- Frolov, V.L.; Bakhmet’eva, N.V.; Belikovich, V.V.; Vertogradov, G.G.; Vertogradov, V.G.; Komrakov, G.P.; Kotik, D.S.; Mityakov, N.A.; Polyakov, S.V.; Rapoport, V.O.; et al. Modification of the earth’s ionosphere by high-power high-frequency radio waves. Phys.-Uspekhi 2007, 50, 315–324. [Google Scholar] [CrossRef]
- Frolov, V.L.; Sergeev, E.N.; Komrakov, G.P.; Stubbe, P.; Thide, B.; Waldenvik, M.; Veszelei, E.; Leyser, T.B. The ponderomotive narrow continuum (NCp) component in stimulated electromagnetic emission spectra. J. Geophys. Res. 2004, 109, A07304. [Google Scholar] [CrossRef]
- Ginzburg, V.L. The Propagation of Electromagnetic Waves in Plasmas; Pergamon Press: London, UK, 1970; 615p. [Google Scholar]
- Sergeev, E.; Grach, S.; Shindin, A.; Milikh, G.; Mishin, E.; Bernhardt, P.; Siefreing, C.; Briczinski, S.; McCarrick, M. Exploring HF induced ionospheric turbulence by Doppler sounding and stimulated electromagnetic emissions at HAARP heating facility. Radio Sci. 2016, 51, 1118–1130. [Google Scholar] [CrossRef] [Green Version]
- Tikhonov, A.N. Numerical Methods for the Solution of Ill.-Posed Problems; Springer: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers; McGraw-Hill Book Company: New York, NY, USA; San Francisco, CA, USA; Toronto, ON, Canada; London, UK; Sydney, Australia, 1968. [Google Scholar]
- Dimant, Y.S. Thermal and Striction Perturbation of the Ionospheric Plasma Density in the Resonance Region of a High-Power Radio Wave; Tsedilina, E.E., Ed.; IZMIRAN: Moscow, Russian, 1989; pp. 19–39. (In Russian) [Google Scholar]
- Grach, S.M.; Mityakov, N.A.; Shvarts, M.M. Plasma Density Jump at the Stage of Developed of Thermal Parametric Instability. Geomagn. Aeron. 1989, 29, 453–457. [Google Scholar]
- Vas’kov, V.V.; Dimant, Y.S. Effect of the Deformation of the Normal Profile of the Ionosphere Plasma on the Anomalous Absorption of a High-Power Radiowave in the Resonance Region. Geomagn. Aeron. 1989, 29, 373–377. [Google Scholar]
- Legostaeva, Y.K.; Shindin, A.V.; Grach, S.M. On the reasons of the plasma expulsion from the regions of plasma resonances in the ionosphere. In Proceedings of the XXV Scientific Conference on Radiophysics, Nizhny Novgorod, Russia, 14–26 May 2021; pp. 162–165. (In Russian). [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).