1. Introduction
Precise positioning performance with smartphones that employ low-cost GNSS chips has attracted increasing attention in both academic and industrial communities in the past few years. After Google opened access to the GNSS raw measurements in the Android operating system in 2016, it became possible to conduct precise positioning for smartphones with raw GNSS observations. However, for Android devices, which usually adopt low-cost GNSS chipsets and antennas, their GNSS data quality is a critical issue in performing precise positioning. Studies have shown that GNSS observations from Android devices suffer from severe data quality problems and many of them are very different compared to geodetic grade receivers [
1,
2,
3]. Generally, they are subject to not only low signal strength, high measurement noise, and poor multipath suppression, but also to some unexpected errors that may be hardware-related. The C/N0 values of smart devices were around 30–40 dB-Hz, which was approximately 10 dB-Hz lower than those of geodetic receivers, and such low signal strength could lead to large observable noise [
1,
2]. It was found that the GPS pseudorange noise of the Nexus 9 tablet with a self-contained built-in antenna was 2.32 m, about two times larger than that of the Nexus 9 with an external antenna, and 10 times larger than that of geodetic receivers [
3]. The multipath error of Xiaomi Mi 8 reached several meters, which was much larger than the geodetic receivers (usually at decimeter levels) [
4], and had a significant impact on positioning precision, due to both the induced error on the measurements and the loss of lock signals [
5]. Some other errors were also noticed for different smartphones, especially the irregular gain pattern of these low-cost antennas [
6,
7], the drifts between the code and carrier-phase observables [
5], and the arbitrary initial phase offset [
8,
9]. These factors are non-negligible in performing precise positioning.
Both relative positioning and precise point positioning (PPP) techniques are utilized for precise positioning of smart terminals; the PPP approach becomes preferable when considering the fact that the smart terminals usually work under a standalone environment [
10,
11,
12,
13,
14,
15,
16]. Since the launch of Xiaomi 8 in May 2018, more Android devices are equipped with dual-frequency and even multi-frequency GNSS chipsets, making dual-frequency PPP possible. However, frequent observation interruptions are found on the second frequency for these smart devices, thus making the dual-frequency data integrity much lower than the first frequency data and degrading the classic dual-frequency PPP performances [
15,
16]. The positioning accuracy for Xiaomi Mi 8 and Huawei Mate 20 could only reach at the decimeter level in static PPP and at meter level in kinematic mode using dual-frequency measurements [
17,
18,
19]; the positioning errors showed severe variations about 4–5 m and there were only about 5–9 visible satellites per epoch [
18]. Such precision was even lower than the single-frequency PPP results reported in [
1,
2,
3].
Unlike the dual-frequency PPP, which eliminates most of the ionospheric delay by forming ionospheric-free (IF) combinations, SF-PPP has to deal with the ionospheric delay as the primary error source [
20]. The simplest method is to use external ionospheric models, such as Klobuchar [
21] and Global Ionospheric Maps (GIM) [
22]; however, the positioning accuracy is subject to the ionospheric model accuracy, which is usually at a level of several TECUs (total electron content unit) [
20]. The Group and Phase Ionospheric Correction (GRAPHIC) [
23] combination is also an applicable SF-PPP method that can eliminate ionospheric delay by code and carrier phase combination, and can obtain centimeter-to-decimeter accuracy [
24,
25]. In addition, the GRAPHIC observation model produces few redundancy observations and may lead to a rank-deficient mathematical problem [
26]; thus, code measurements must be employed, as well [
27]. A third approach is to estimate the ionospheric delay of each GNSS satellite as a process parameter during the SF-PPP process (referring to the uncombined approach hereafter). However, in such an approach, a priori constraints on the ionospheric delays become very critical, since the ionosphere parameters are heavily correlated with other parameters. Thus, external ionospheric models are necessary [
28,
29,
30]. The positioning accuracy for a Ublox-like cost-effective single-frequency receiver was 0.4–0.5 m for GPS, 0.7–0.8 m for GLONASS, and 0.3–0.4 m for the combined-system approaches when utilizing the uncombined approach [
30]. By combining multi-GNSS observations, the results can be even improved; the SF-PPP with quad-constellation GNSS reduced the convergence time by 40%, 47%, 34% in the east, north, and up directions compared to the GPS-only SF-PPP [
29].
SF-PPP performances have been evaluated for smart devices in many studies [
1,
31,
32,
33]. Using the GPS observations collected with a Nexus 9 tablet, static SF-PPP was performed and reached 0.37 m and 0.51 m at horizontal and vertical components, respectively [
31]. The PPP-wizard application developed in [
32] reached sub-meter accuracy in static mode and meter-level in dynamic mode with smartphone GNSS data. To reduce the code measurement noise of the Nexus 9 tablet, an optimized carrier-phase smoothing method was proposed and the resulting positioning accuracy of the static experiment was about 0.6 and 0.8 m in the horizontal and vertical components, respectively [
33]. The time-difference filtering approach was also adopted to suppress the systematic errors in Nexus 9 tablet data, and the results showed that the RMS error of the static positioning solution was less than 0.6 and 1.4 m in the horizontal and vertical directions, respectively [
1]. Similar SF-PPP tests were conducted using the Huawei Mate 30 module, which achieved 1 m precision in the horizontal component [
16]. The above studies focused on the algorithms of the joint use of the pseudorange, the carrier phase, and Doppler observation output from smart devices, but lacked the application of different ionospheric treatments in SF-PPP.
The focus of this study was to evaluate the performance of GRAPHIC and the uncombined SF-PPP approaches with datasets from Multi-GNSS Experiment (MGEX) stations as well as Huawei P40 smartphones. The MGEX stations, by providing geodetic-grade GNSS observations, can be treated as baselines for our SF-PPP assessment. The P40 can track dual or triple-frequency signals for different satellite systems, explicitly L1/L5 for GPS, B1I/B1C/B2a for BDS, E1/E5a for GALILEO, and L1/L5 for QZSS. However, the data continuity on the second frequency band (L5/B2a/E5a) was severely interrupted due to channel limitations, and only the measurements on the first frequency band were used for the investigation. We collected the P40 datasets both using its self-contained built-in antenna and an external geodetic antenna, thus making it possible to identify data quality problems caused by either the P40 chips or antennas. The paper is organized as follows. In
Section 2, two kinds of SF-PPP models are elaborated by formulas and instructions. Then, the effectiveness of the positioning performance of the two models is examined by geodetic receivers in
Section 3, both in terms of accuracy and convergence. In
Section 4, first, we briefly describe a quality assessment that was conducted with the dataset collected by Huawei P40, and then the SF-PPP processing is examined. Finally, the conclusions are summarized in
Section 5.
4. SF-PPP Performance Analysis of Android Mobile Phones
The MGEX stations utilize geodetic-grade GNSS receivers, which provide better data quality than the Android devices and are beneficial to SF-PPP performance. In addition, currently, most mobile Android terminals usually cannot produce reliable and continuous dual-frequency or triple-frequency observations owing to the chip and antenna limitation; the SF-PPP technique is a more feasible approach for precise positioning or location-based applications. Thus, SF-PPP with Android smartphones is the focus of this section.
The Huawei P40 smartphone is adopted for this study, which utilizes Android release version 10.0 and the latest Kirin-990 chipset. It can track dual or triple-frequency signals for different satellite systems, explicitly L1/L5 for GPS, B1I/B1C/B2a for BDS, E1/E5a for GALILEO, and L1/L5 for QZSS. However, the data continuity on the second frequency band (L5/B2a/E5a) is severely interrupted owing to channel limitations. Thus, the data from the first frequency band are our focus. To avoid environmental impacts, we collected 4 h of data on the rooftop of a tall building inside Wuhan University at a sampling rate of 1 s on 26 October 2020. Two P40 smartphones were utilized to record GNSS measurements during the same period but with different antennas; one was the P40 built-in antenna, while the other was an external geodetic antenna (Huawei helped adapt the P40 for connection with external antennas). In this way, the impacts of the built-in antenna could be compared and analyzed. In this section, the quality of the GNSS observations from the smartphone is analyzed in terms of carrier-to-noise density ratio (C/N0), pseudorange noise, and carrier phase noise. Then, the result of SF-PPP is examined.
4.1. GNSS Data Quality Analysis of Mobile Devices
The C/N0 values obtained by the receiver indicate the signal gains and losses along the transmitting chain [
40]. In general, the higher the C/N0 value, the stronger signal and the better observation quality that can be expected.
Figure 4 shows the average C/N0 values of all satellites tracked by the P40 with external antenna (P40-EXT) and internal antenna (P40-INT) at different elevation bins to demonstrate the characteristics of C/N0 values for P40. For P40-EXT, the C/N0 values showed stable increments from about 30 dB-Hz to 45 dB-Hz with respect to satellite elevations; in addition, when satellite elevation was higher than 30 degrees, the P40-EXT C/N0 values were quite stable at around 45 dB-Hz. This was identical to the elevation-dependent stochastic model in Equation (2), where the observation weight was set to an equal weight model for the elevations higher than 30 degrees. In comparison, the P40-INT C/N0 values were overall smaller than P40-EXT and their difference was close to 10 dB-Hz. Especially, the P40-INT C/N0 showed large variations between 35 dB-Hz and 40 dB-Hz for elevations higher than 30 degrees and no significant correlations could be observed. This should be because the received signal strength of P40-INT was more susceptible to the environment with a linearly polarized non-uniform gain antenna [
1,
41].
The noise level of the pseudorange and carrier phase of P40 GNSS observations were evaluated by third-order between-epoch differences [
3]. In
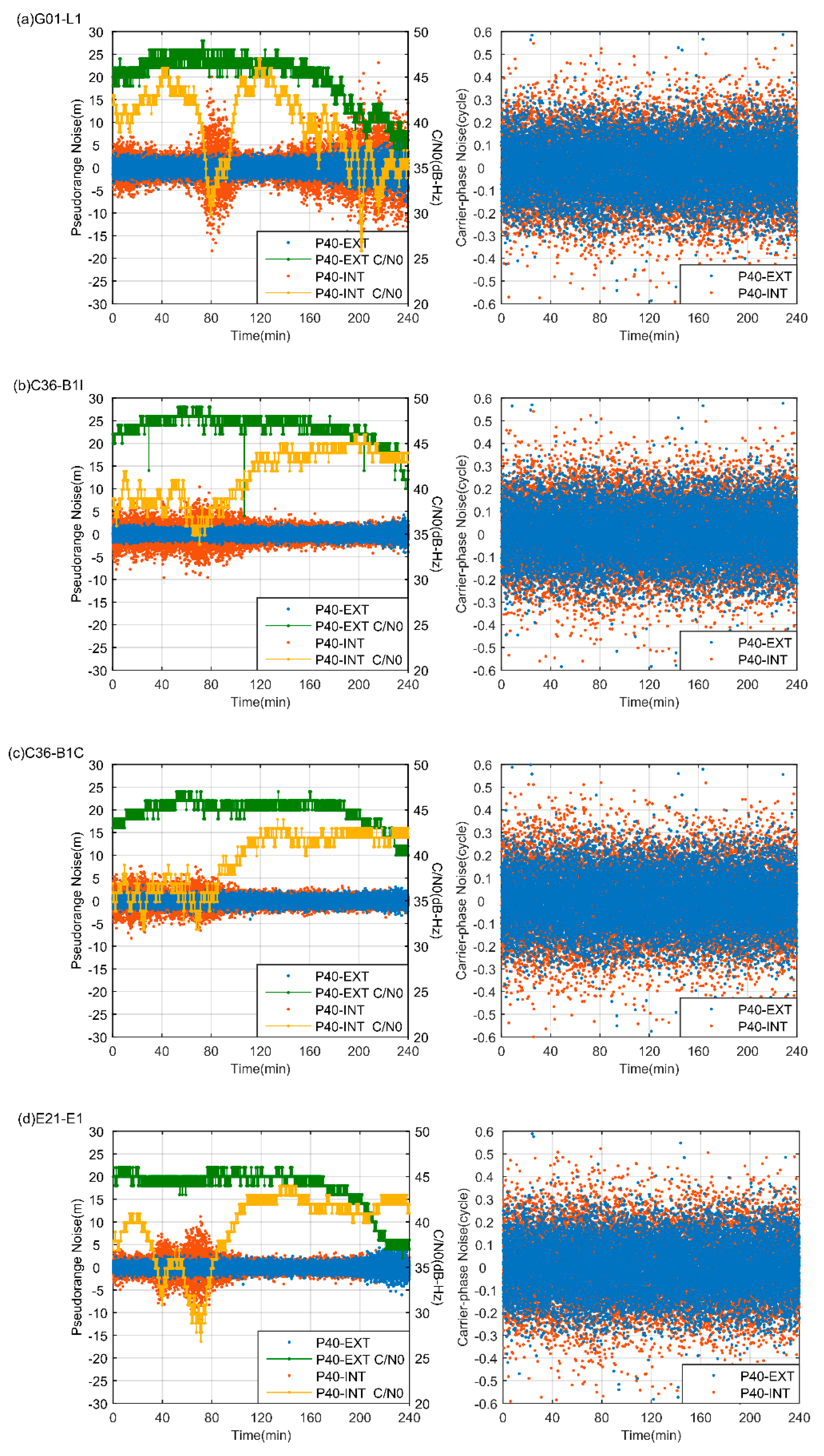
Figure 5, the noise of P40-INT and P40-EXT pseudorange and carrier-phase are depicted for different GNSS systems over 4 h; the C/N0 are also illustrated to investigate their correlations. It should be noted that the selected periods are the same for different satellites, and the B1I and B1C signals for C36 are both illustrated as an insight on BDS-3 new signal evaluation with smartphones. As seen in
Figure 5, the P40-INT data experienced large C/N0 variations from 25 dB-Hz to 40 dB-Hz. The G01 satellite from P40-INT showed the largest C/N0 variations, followed by E21. They exhibited a large C/N0 decrease over 60–80 min from approximately 40 dB-Hz to about 30 dB-Hz with a reduction as large as 12 and 10 dB-Hz, respectively. This should be attributed to signal acquisition incidents of the P40-INT devices, as such a decrease was not seen for P40-EXT. The E21 C/N0 also showed another minor decrease of 5 dB-Hz at around 40 min. However, the two BDS signals showed much smaller C/N0 fluctuations. Their C/N0 stayed at a rather lower C/N0 level (35 dB-Hz) during the first 60 min and then gradually grew to larger than 40 dB-Hz. Comparatively, the B1I C/N0 values were, overall, 2 dB-Hz larger than B1C. The P40-INT code triple-difference series showed strong correlations with respect to the C/N0 variations. The E21 and C36 code variations were within +/−3 m when their C/N0 stayed above 40 dB-Hz, while G01 were larger, at around +/−5 m. However, when C/N0 dropped below 30 dB-Hz, their variations amplified to about 10 m. The carrier-phase triple-differences mainly fluctuated around +/−0.5 cycles and barely showed any correlations with respect to C/N0. The P40-EXT C/N0 values manifested gradually variations, which were typically above 40 dB-Hz for elevations higher than 30 degrees. This was consistent with
Figure 4. As result, the P40-EXT code triple-differences stayed stably within +/−3 m, while the carrier-phase was around +/−0.5 cycles.
To further analyze the relationship between the P40 measurement noise and elevation or the C/N0 value,
Figure 6 shows the RMS values of triple-differences of pseudorange and carrier phase with different ranges of elevation and the C/N0 value for P40-EXT and P40-INT. The P40-INT dataset showed larger RMS values over all elevation bins for both the pseudorange and the carrier phase than the P40-EXT case, which should be attributed to the fact that the linearly polarized built-in antenna of P40-INT is more vulnerable to environmental interference leading to the larger observation noise. The pseudorange noise of P40-INT varied irregularly with the satellite elevation increment; however, it was more stable for P40-EXT. When the C/N0 value was lower than 25 dB-Hz, the pseudorange noise gradually reduced from 4 m to 2 m, showing good correlations, while the carrier-phase observations could not be tracked for both P40-INT and P40-EXT under such a C/N0 condition. However, when C/N0 increased to the range of 25–30 dB-Hz, the pseudorange noise from both P40-INT and P40-EXT manifested a dramatic increment to 5–6 m. To investigate such abnormal behavior, the recorded signal strength flags were checked, and it was found they were jumping between 1 and 4 constantly when C/N0 dropped below 30 dB-Hz, indicating an unstable tracking status. It was suspected that there were tracking problems owing to the P40 chips for C/N0 falling below 30 dB-Hz. Thus, in our subsequent SF-PPP processing, these measurements were discarded (the data volume for C/N0 below 30dB-Hz was only less than 5%). For C/N0 values higher than 30 dB-Hz, both the pseudorange and carrier phase noise showed a gradual decrease, and their triple-difference RMS values were at the level of 1 m and 0.1 cycles when C/N0 reached 48–50 dB-Hz, respectively. The correlations between the P40-INT pseudorange and carrier-phase noise with respect to C/N0 were much stronger than to the elevations; thus, constructing a C/N0-dependent weight model could be more appropriate in P40-INT positioning than an elevation-dependent one.
The GNSS measurement noises are derived from the above triple-difference RMS values by a normalization factor of
[
3]. The P40 observation noise of different constellations is then calculated and shown in
Table 3. The BDS B1C code noise was the smallest for both P40-EXT and P40-INT with values of 0.28 m and 0.41 m, respectively, while the GPS L1 was the largest with values of 0.56 m and 0.99 m, respectively. The BDS B1I and Galileo E1 showed very similar code noise levels at 0.40 m and 0.60 m, respectively. The noise level for different systems might be related to their C/N0 levels, as indicated in
Figure 5. The average pseudorange noise values were 0.40 m and 0.67 m for P40-EXT and P40-INT, respectively, indicating about 70% improvement using an external geodetic antenna. For the carrier phase observations, the noise level of different GNSS systems were quite close to each other and their RMS values were 0.02 cycle and 0.03 cycle for P40-EXT and P40-INT, respectively.
4.2. Positioning Performance Analysis of Android Mobile Phones
Weak signal strength and high measurement noise present a great challenge to precise GNSS positioning for the smartphones. We further investigated the SF-PPP performance by utilizing the dataset collected from P40-EXT and P40-INT.
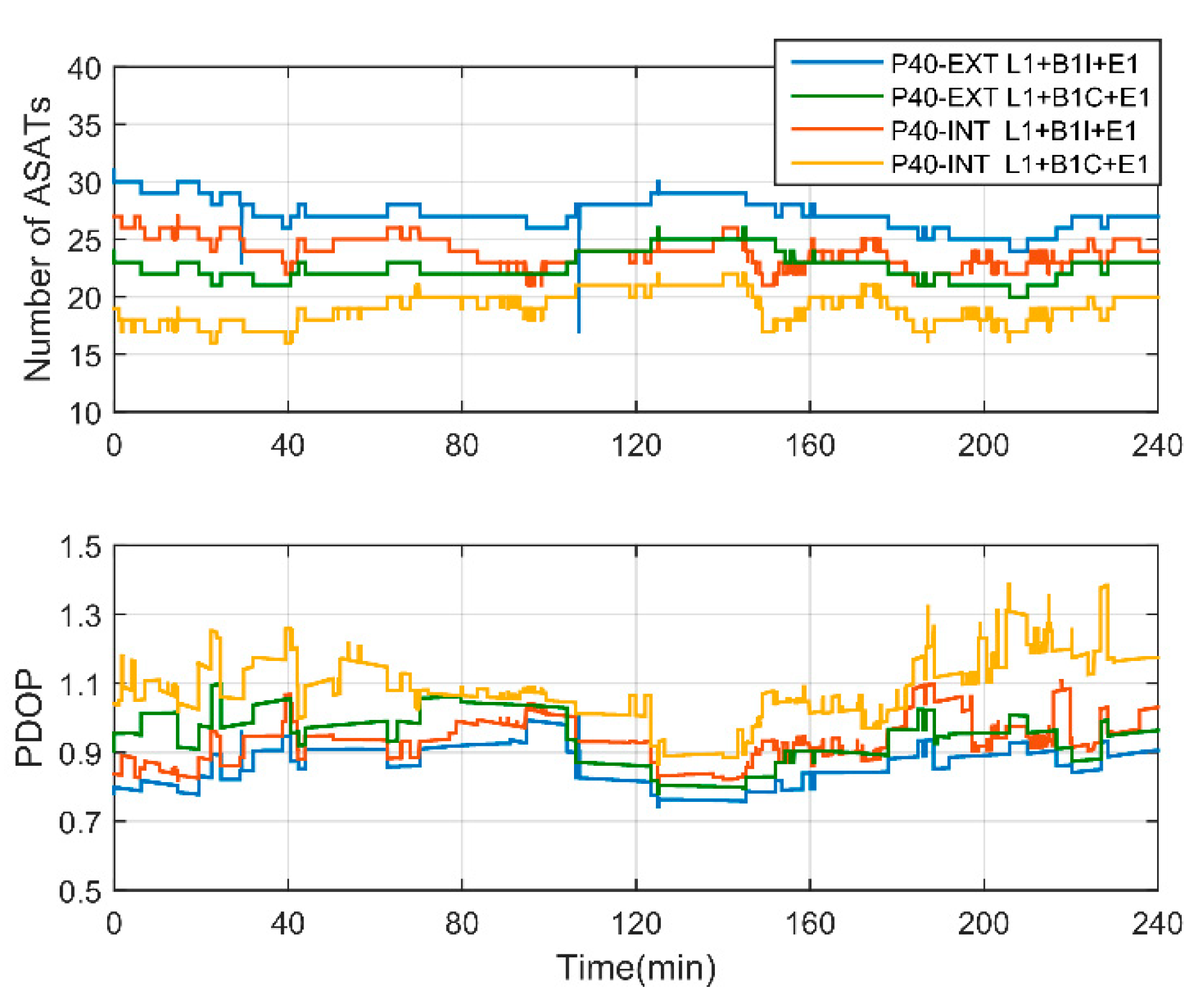
Figure 7 displays the number of available satellites (ASAT) as well as the position dilution of precision (PDOP) for different GNSS system combinations. The satellites used in SF-PPP solution are denoted as ASAT in the case of gross errors. With a geodetic-grade antenna, P40-EXT could generally track five more satellites than P40-INT. With multi-GNSS availability, the average number of ASAT of P40-EXT varied from 20 to 30 while that of P40-INT varied from 16 to 26, considering different frequency combinations. It should be noted five to six more BDS satellites could be observed at the B1I frequency than that at the B1C frequency for both P40-EXT and P40-INT. As a result, the PDOP of the GPS L1, BDS B1C, and Galileo E1 frequency combinations showed more dramatic changes than the case of using the B1I frequency, especially for P40-INT, where the PDOP even jumped from 0.9 to above 1.3. Although the B1C signal manifested a smaller code noise level than the B1I signal, it was still recommended to adopt the B1I signal to ensure more available satellites and better satellite geometry. With the GPS L1, BDS B1I, and Galileo E1 combination, the average GNSS ASAT numbers reached 27.3 and 23.9 for P40-EXT and P40-INT, respectively, while the resulting average PDOPs were 0.826 and 0.934, respectively.
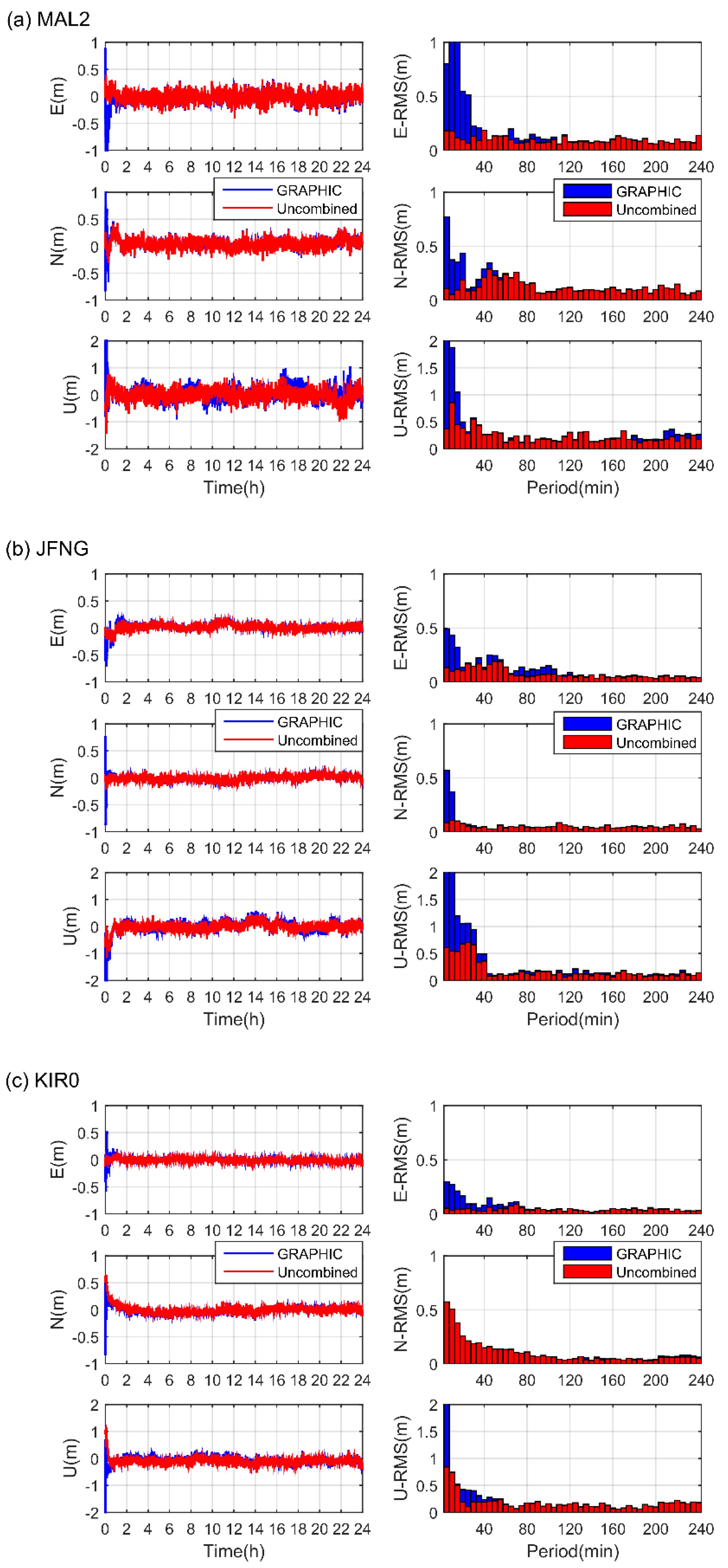
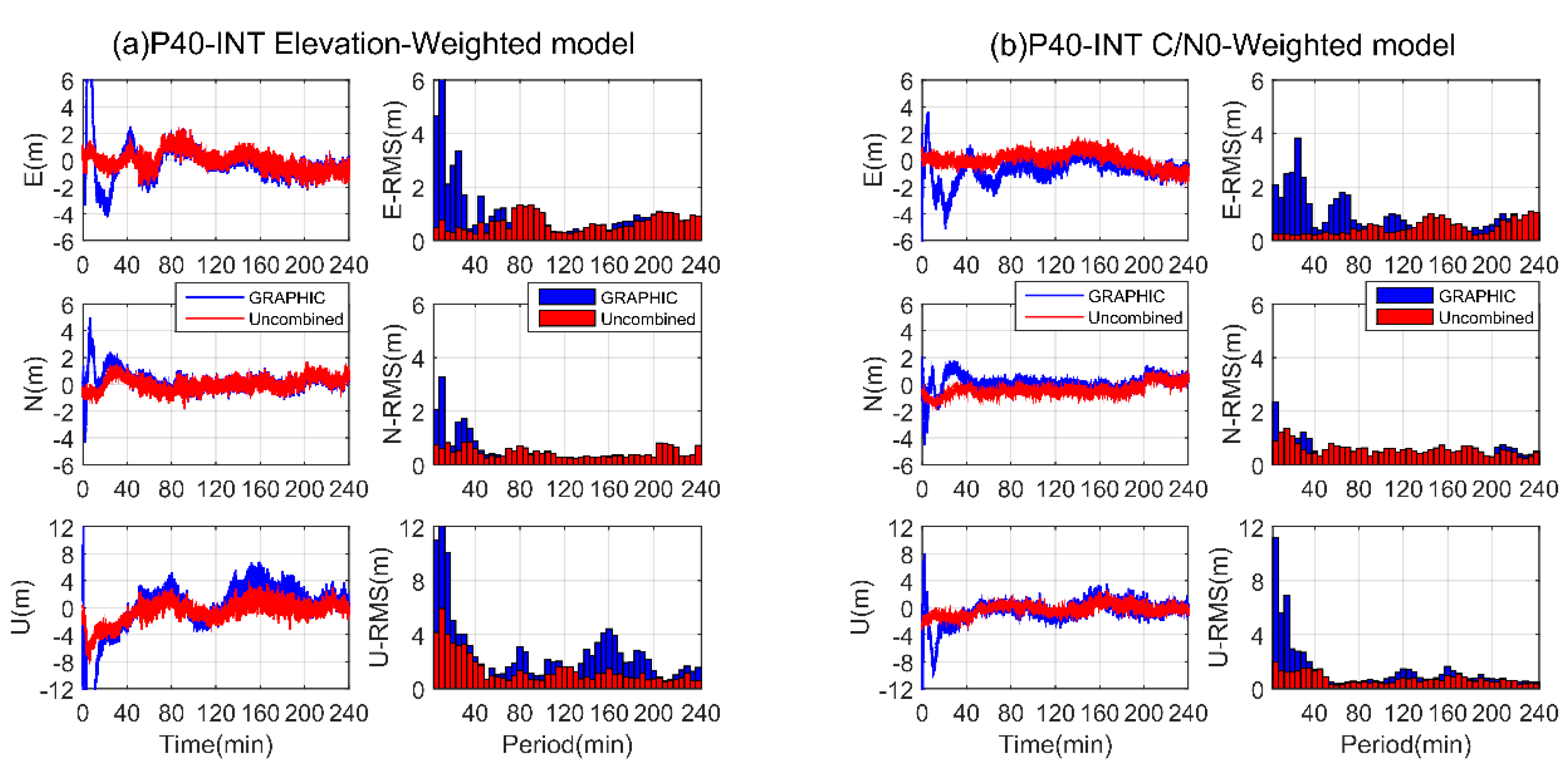
The P40-EXT positioning performance of the two SF-PPP approaches was evaluated using observations from GPS L1, BDS B1I, and Galileo E1 frequencies. The left panel of
Figure 8 shows the epoch-wise positioning errors in the east, north, and up components for the GRAPHIC and uncombined solutions of P40-EXT, while the right panel is the corresponding RMS values every 5 min. The positioning errors of the GRAPHIC and uncombined approaches were at the same order of magnitude; both could reach sub-meter level positioning accuracy after convergence. However, the uncombined model had a slightly higher accuracy in the up component. When the GRAPHIC approach was applied, the positioning errors of P40-EXT were within a few meters during the first 20 min, and it took about 40 min to stabilize. In contrast, the uncombined model could achieve accuracy within 1 m in the horizontal direction and 2 m in the vertical direction during a few minutes. The remarkable improvement in terms of convergence performance of the uncombined model should be attributed to the fact that the carrier phase observation precision is much higher than the GRAPHIC combination and that the ionospheric parameters could absorb part of observational errors.
Considering the code noise correlation with respect to C/N0, the P40-INT SF-PPP was evaluated using a C/N0-dependent weighting model in addition to the elevation-dependent model for comparison. The C/N0-dependent weighting model was represented in an exponential form related to the instantaneous C/N0 of the observations, a maximum C/N0 value for cutoff, and the corresponding pseudorange noise at maximum C/N0. Its detailed expression could be found in [
42]. Considering the P40-INT noise analysis results in
Section 4.1, the C/N0-dependent weighting model was adapted by setting the maximum C/N0 cutoff as 40 dB-Hz and the corresponding pseudorange noise 1 m. The positioning errors are shown in
Figure 9a,b. Generally, the positioning errors of P40-INT varied abruptly and needed a longer convergence time for both SF-PPP approaches and for both weight models than P40-EXT. Considering the elevation-dependent weighting model, both the GRAPHIC and uncombined approaches manifested large variations around ±2 m in the horizontal component and ±6 m in the vertical component even after convergence; very similar systematic errors could be observed for both approaches, which might be due to some systematic observation errors and remains under investigation. Comparatively, the uncombined approach showed smaller positioning errors, especially at the vertical component. With the C/N0-dependent weighting model, the P40-INT positioning results showed a significant improvement over the elevation-dependent model for both SF-PPP approaches with smaller variations. Especially, the vertical error variations were within ±4 m. However, the systematic errors were still found.
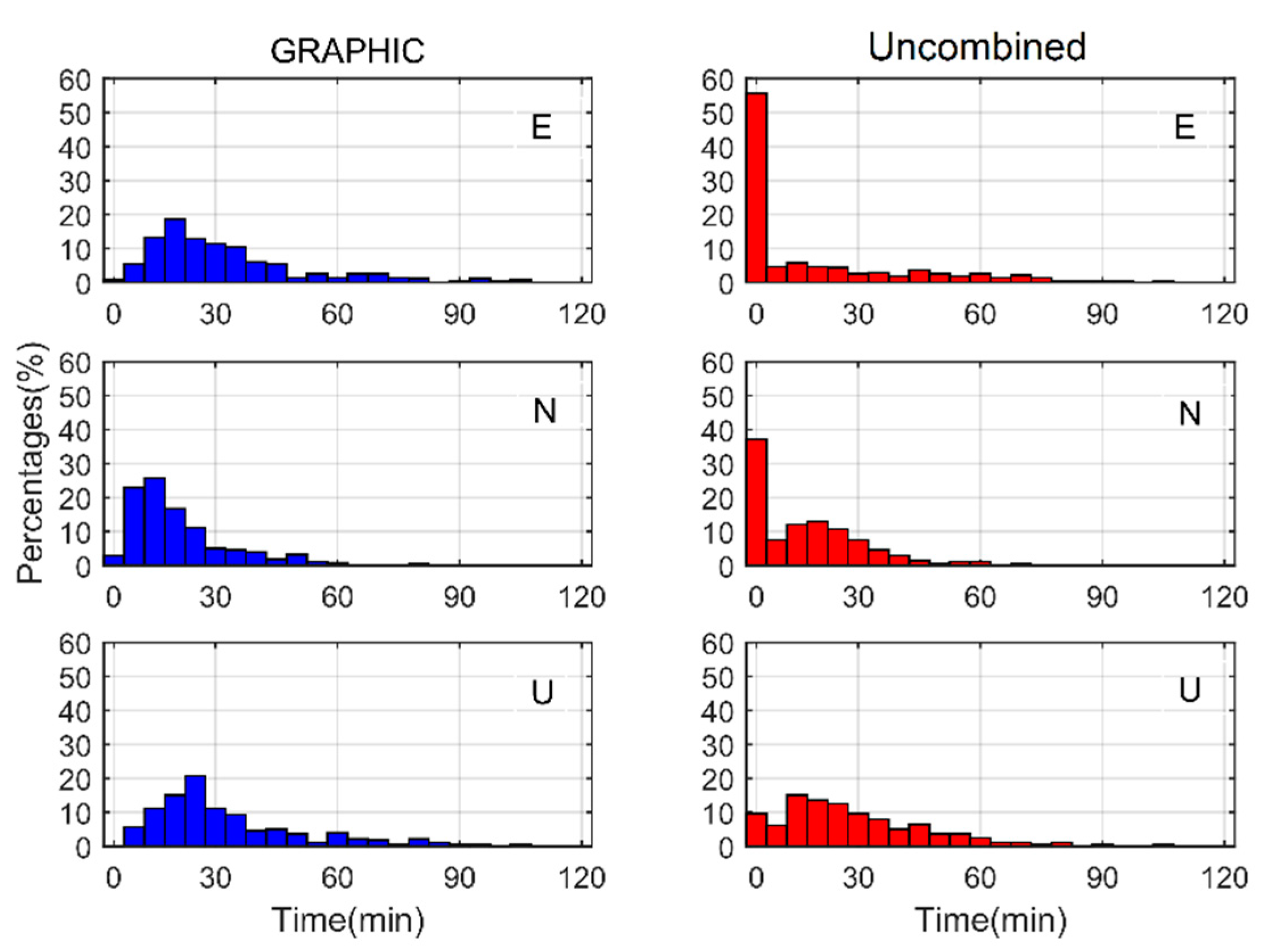
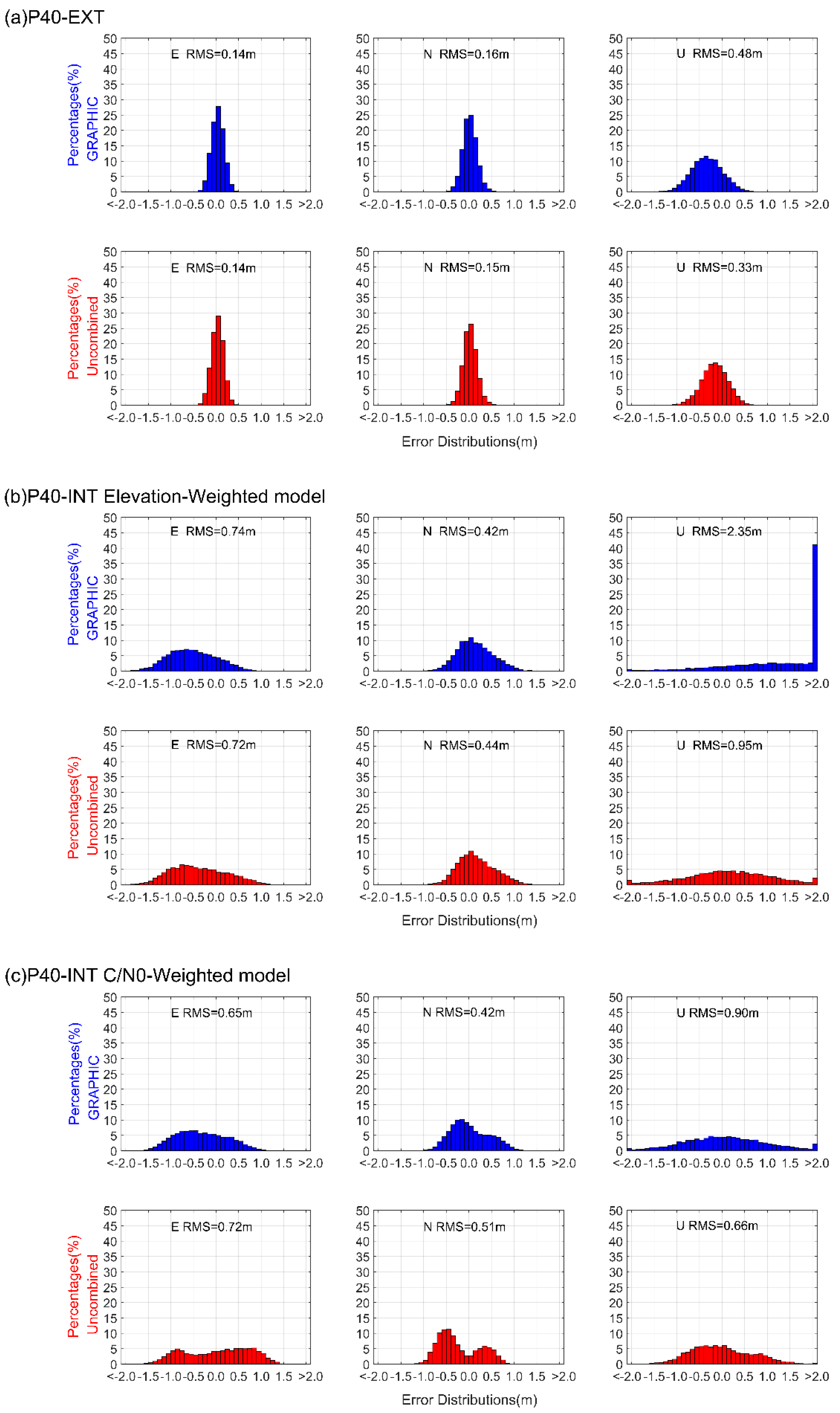
The histograms of P40-EXT and P40-INT SF-PPP positioning errors during the last 120 min are shown in
Figure 10. In
Figure 10a, it could be seen that the GRAPHIC positioning errors of the P40-EXT case achieved comparable performance with the uncombined method. Their horizontal fluctuations varied within
0.5 m and their RMS values varied around 0.15 m. However, the uncombined approach showed much smaller errors in the vertical component with an improvement of about 30%, consistent with
Figure 8.
Figure 10b,c depict the P40-INT SF-PPP errors using the elevation-dependent weighting model and the C/N0-dependent weighting model, respectively. Generally, the uncombined method overperformed the GRAPHIC method in the vertical component with dramatic improvements; for the elevation-dependent weighting model, the RMS reduction was about 1.40 m, while for C/N0-dependent model it was about 0.24 m. Their horizontal precisions were at a similar level below 1.0 m. Compared to the elevation-dependent weighting model, the C/N0-dependent model showed much better vertical precision at 0.66 m.
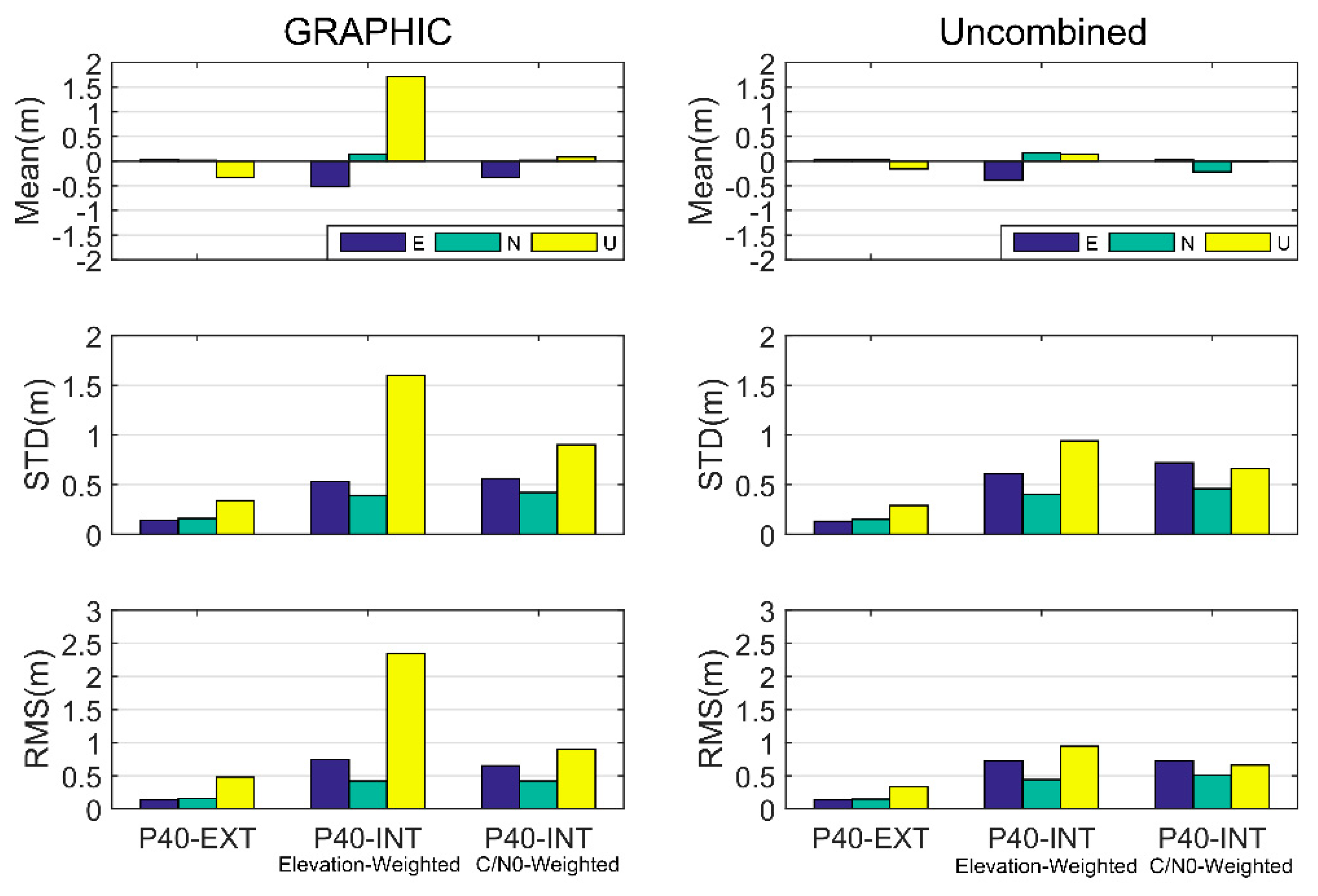
Figure 11 summarizes the SF-PPP positioning results in each coordinate component of P40-EXT (left panel bars) and P40-INT. For P40-INT, the results of both the elevation-dependent weighting method (middle panel bars) and the C/N0-dependent weighting (right panel bars) are shown. The statistical values are based on the positioning results after 120 min, when the series vary stably. In the case of P40-EXT, the GRAPHIC and uncombined models of the smartphone reached comparable accuracies of about 0.15 m in horizontal components, while the uncombined model achieved 0.33 m in the vertical component that was better than the GRAPHIC model (0.48 m), indicating an improvement of about 31%. In addition, biases at a few centimeters level in the horizontal components and several decimeters level at the vertical component could be observed for both approaches, which was different compared to the results of MGEX stations. This again indicated that there were systematic errors in the P40 measurements. For the P40-INT case, the positioning errors of the GRAPHIC model with the elevation-dependent weighting strategy were 0.74 m, 0.42 m, and 2.35 m in the east, north, and up components, respectively. However, with the C/N0-dependent weighting approach, the errors were decreased to 0.65 m, 0.42 m, and 0.90 m, respectively; an improvement as large as 62% could be observed in the vertical component. For the uncombined approach using the C/N0-dependent weighting method, the east, north, and vertical errors were 0.72 m, 0.51 m, and 0.66 m, respectively. The vertical component exhibited an improvement of about 27% compared with the GRAPHIC model, while the horizontal component showed little degradation.
The above results indicate that the uncombined approach could achieve better positioning precisions compared to the GRAPHIC model for P40 smartphones with either built-in or external antennas. For P40 GNSS data with its built-in antenna, the C/N0-dependent weighting strategy is more suitable and can improve positioning precision. Sub-meter level accuracy could be reached after about 1 h.
5. Discussion and Conclusions
In this study, the positioning performance of GRAPHIC and uncombined SF-PPP models was evaluated and compared. We firstly evaluated these two approaches using one-week datasets from 40 MGEX stations in case of any observational quality issues. The two approaches achieved very similar positioning accuracy, with 0.1 m and 0.2 m in the horizontal and vertical directions, respectively. However, the uncombined approach manifested faster convergence than GRAPHIC by 40.7%, 20.0%, and 13.8% in the east, north, and up components, respectively, owing to the adoption of high-precision carrier phase observations as well as ionospheric parameterization.
We collected smartphone-based datasets using the Huawei P40 smartphone equipped with an external geodetic-grade antenna (P40-EXT) as well as its internal antenna (P40-INT) for comparison and analysis. Firstly, the raw observations from these two smart devices were compared in terms of the C/N0 value and measurement noise. The code measurement noise with the internal antenna case were 0.27 m larger than the external, while little differences were found for carrier phase observations. In addition, the P40-INT pseudorange noise showed strong correlations with respect to the C/N0 values. The P40 observations from the GPS L1, BDS B1I, and Galileo E1 frequencies were utilized to conduct SF-PPP. The errors of uncombined SF-PPP of the external antenna case were 0.14 m, 0.15 m, and 0.33 m in the east, north, and up components, respectively, showing an improvement of about 31% in the up direction when compared with the GRAPHIC solution. The C/N0-dependent weighting model performed much better than the elevation-dependent model for the internal antenna case with an improvement of about 30–60%, especially in the vertical component. It improved the GRAPHIC positioning accuracy to 0.65 m, 0.42 m, and 0.90 m in the east, north, and up directions, respectively, and for the uncombined approach, the precision could even reach 0.72 m, 0.51 m, and 0.66 m in the east, north, and up directions, respectively.