Deep Learning Triplet Ordinal Relation Preserving Binary Code for Remote Sensing Image Retrieval Task
Abstract
:1. Introduction
- 1.
- The learning procedure of TOCEH takes into account the triplet ordinal relations, rather than the pairwise or point-wise similarity relations, which can enhance the performance of preserving the ranking orders of approximate nearest neighbor retrieval results from the high dimensional feature space to the Hamming space.
- 2.
- TOCEH establishes a triplet ordinal graph to explicitly indicate the ordinal relationship among any triplet RS images and preserves the ranking orders by minimizing the inconsistency between the probability distribution of the given triplet ordinal relation and that of the ones derived from binary codes.
- 3.
- We conduct comparative experiments on three RS image datasets: UCMD, SAT-4 and SAT-6. Extensive experimental results demonstrate that TOCEH generates highly concentrated and compact hash codes, and it outperforms some existing state-of-the-art hashing methods in large-scale RS image retrieval tasks.
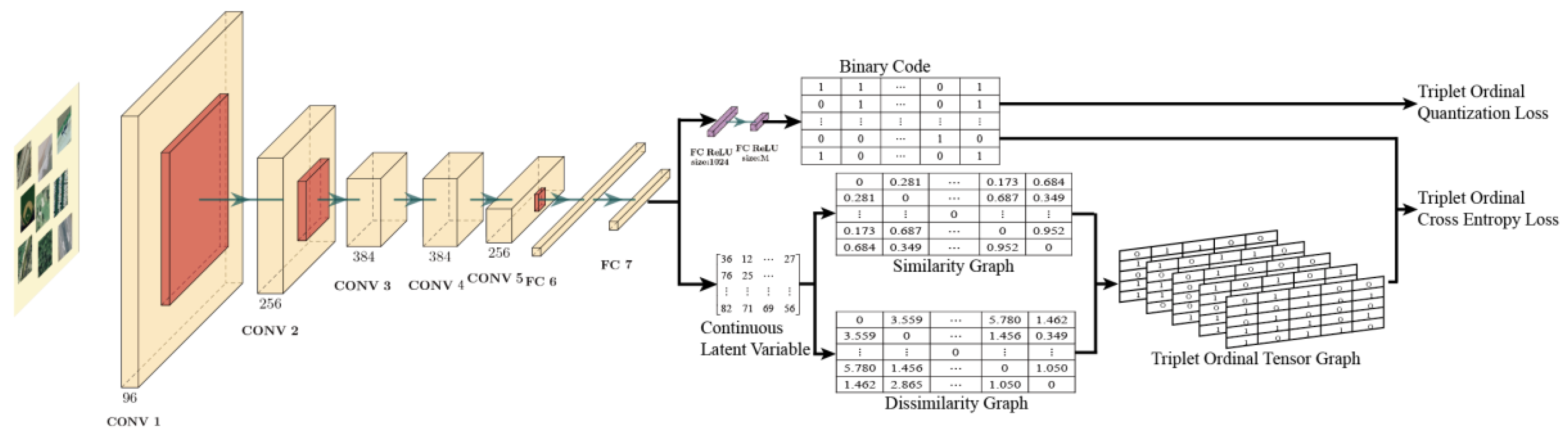
2. Triplet Ordinal Cross Entropy Hashing
2.1. Notation
2.2. Hashing Learning Problem
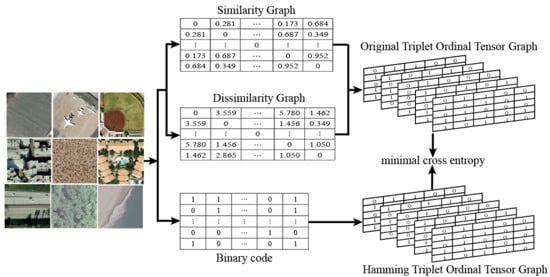
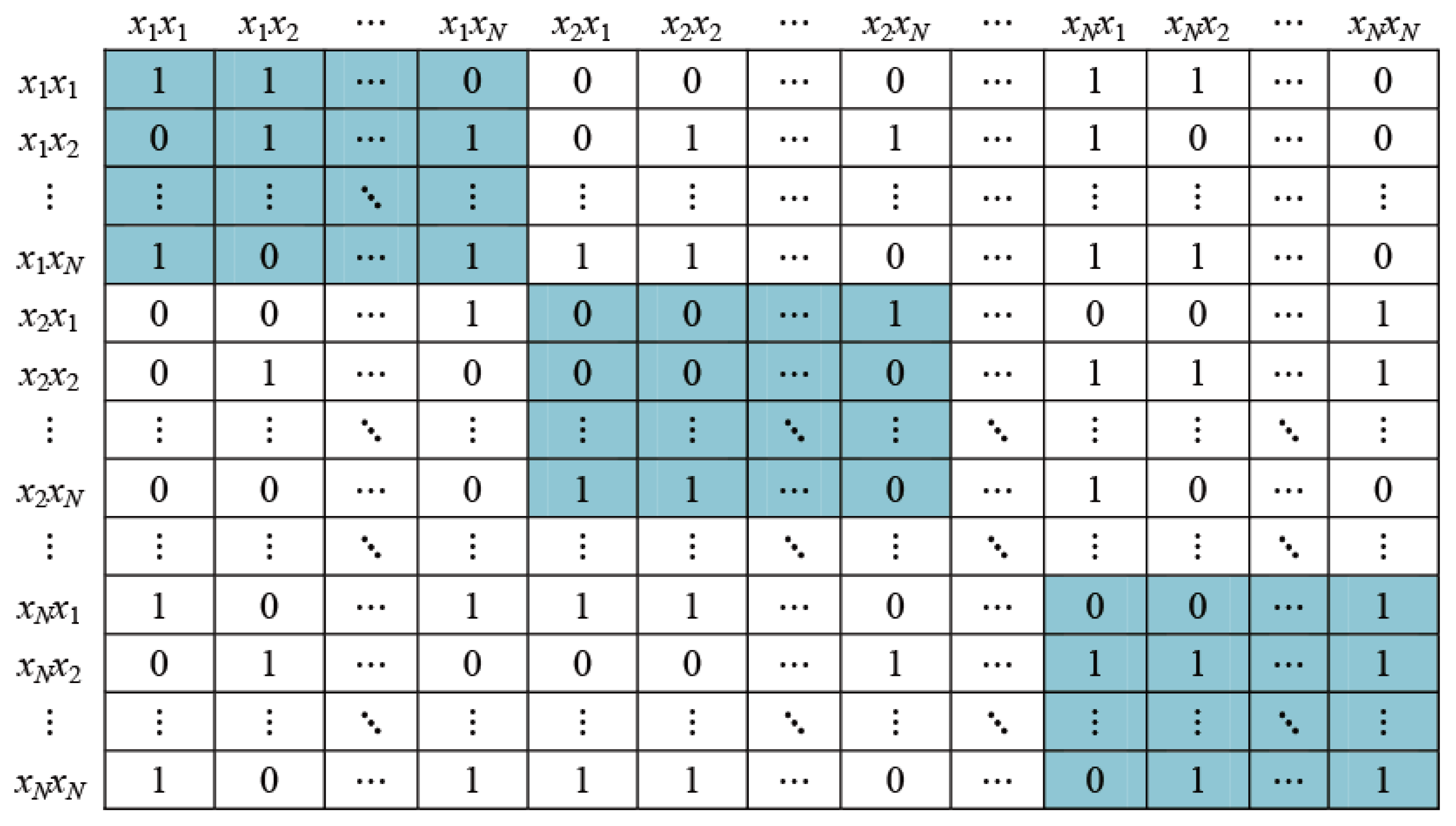
2.3. Triplet Ordinal Tensor Graph
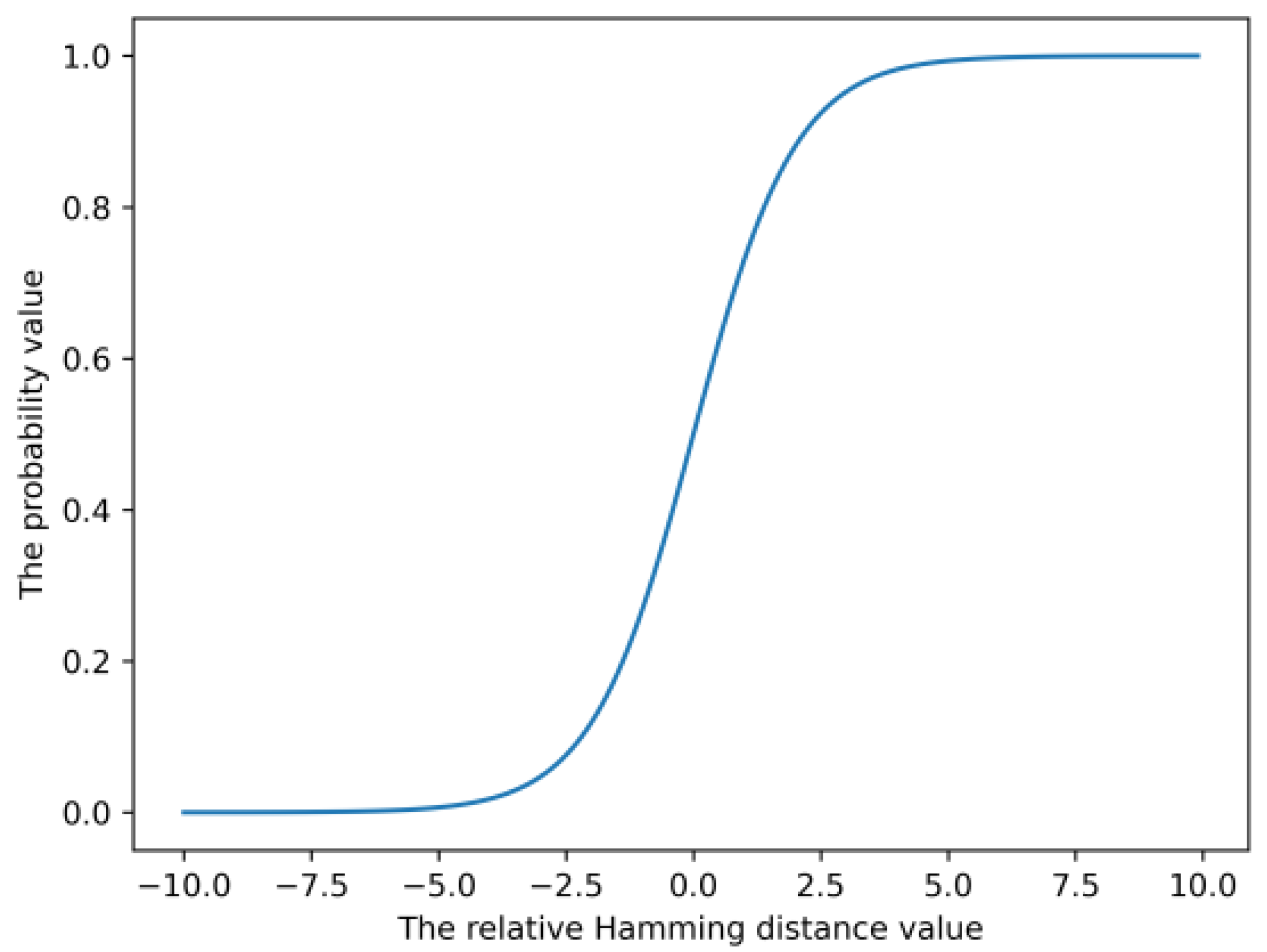
2.4. Triplet Ordinal Cross Entropy Loss
2.5. Triplet Ordinal Quantization Loss
3. Experimental Setting and Results
3.1. Datasets
- 1.
- UCMD [37] stores aerial image scenes with a human label. There are 21 land cover categories, and each category includes 100 images with the normalized size of 256 × 256 pixels. The spatial resolution of each pixel is 0.3 m. We randomly choose 420 images as query samples and the remaining 1680 images are utilized as training samples.
- 2.
- The total number of images in SAT-4 [38] is 500k and it includes four broad land cover classes: barren land, grass land, trees and other. The size of images is normalized to 28 × 28 pixels and the spatial resolution of each pixel is 1 m. We randomly select 400k images to train the network and the other 100k images to test the ANN search performance.
- 3.
- The SAT-6 [38] dataset contains 405k images covering barren land, buildings, grassland, roads, trees and water bodies. These images are normalized to 28 × 28 pixels size and the spatial resolution of each pixel is 1 m. We randomly select 81k images as query set and the other 324k images as training set.
3.2. Experimental Settings and Evaluation Matrix
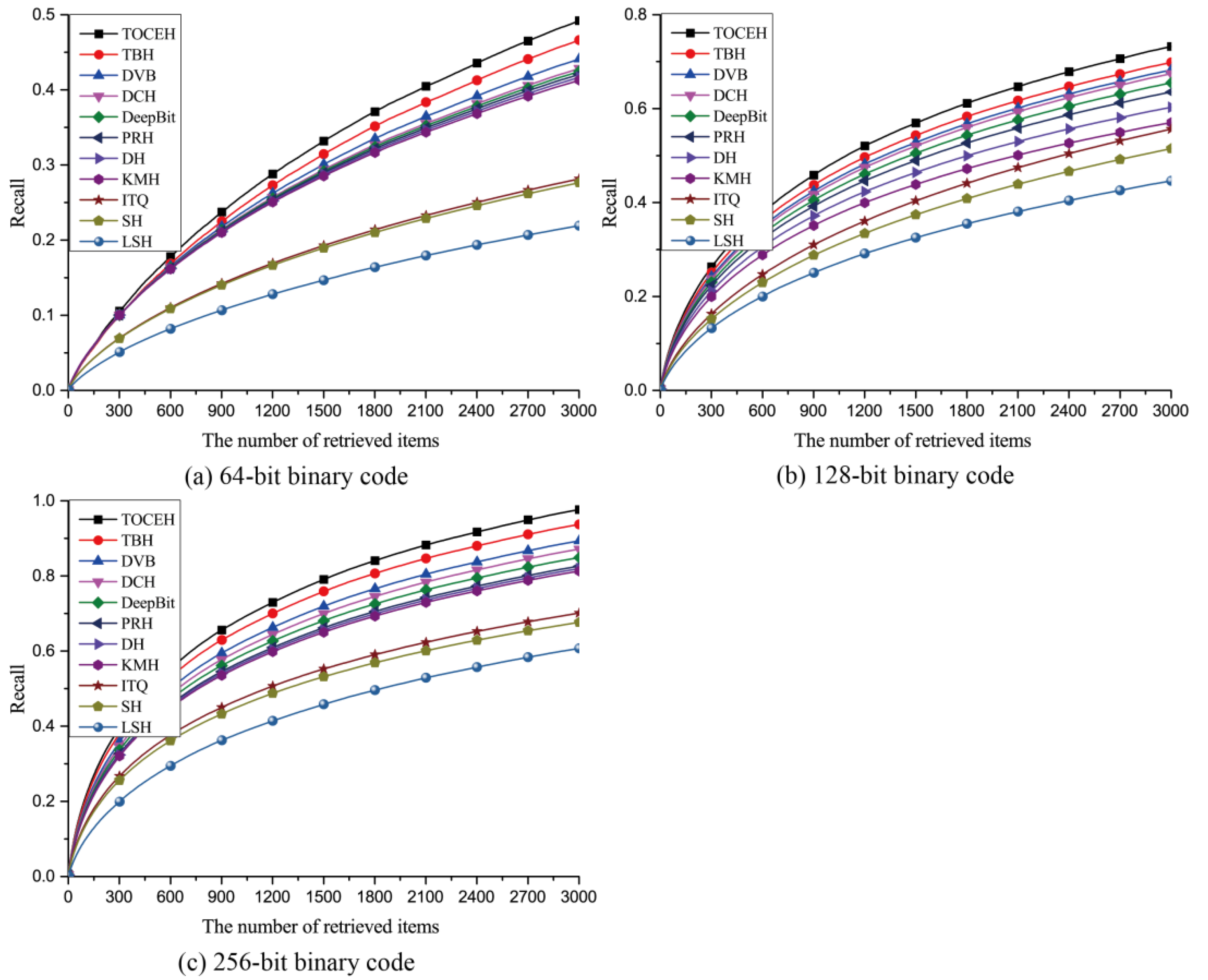
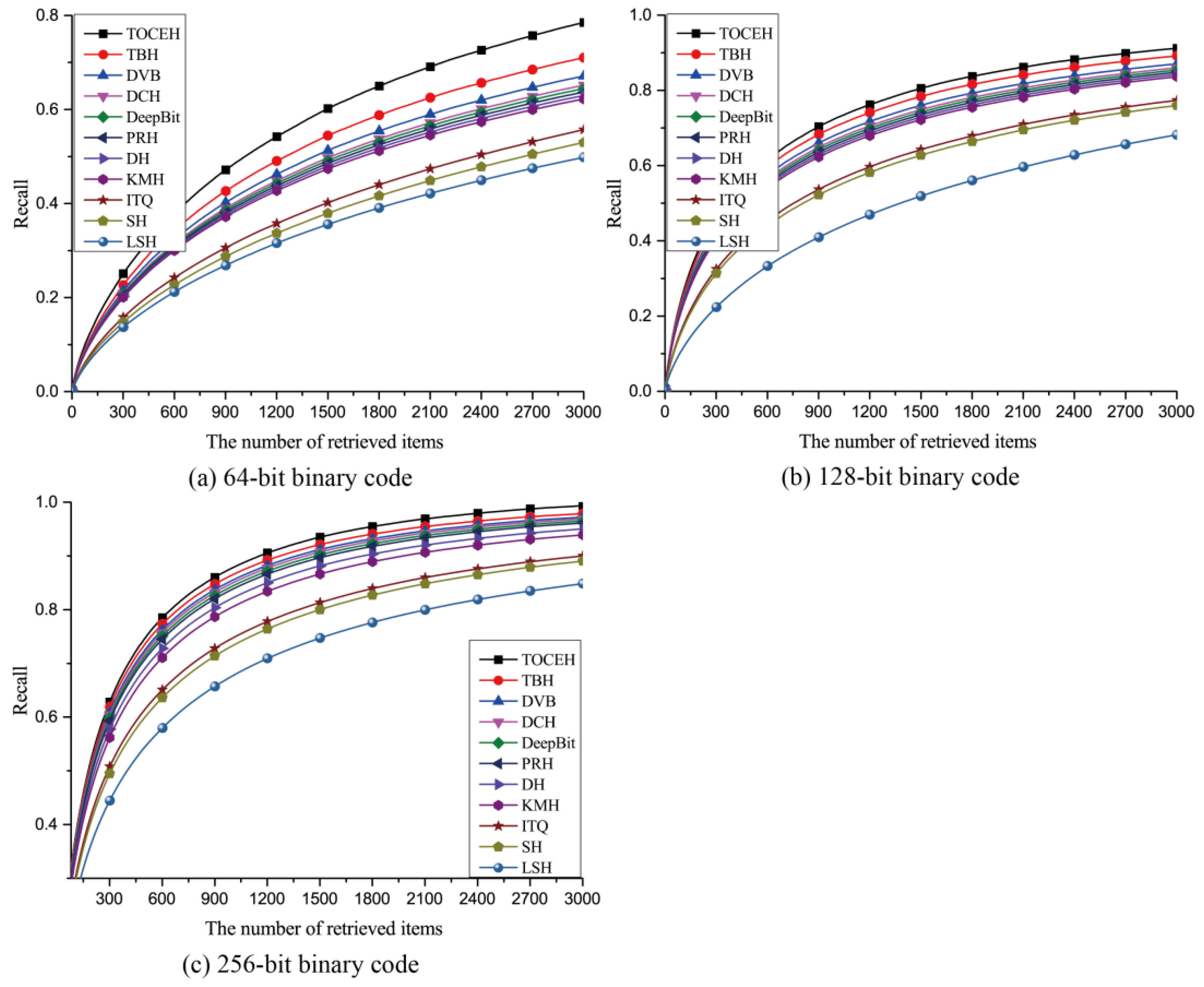
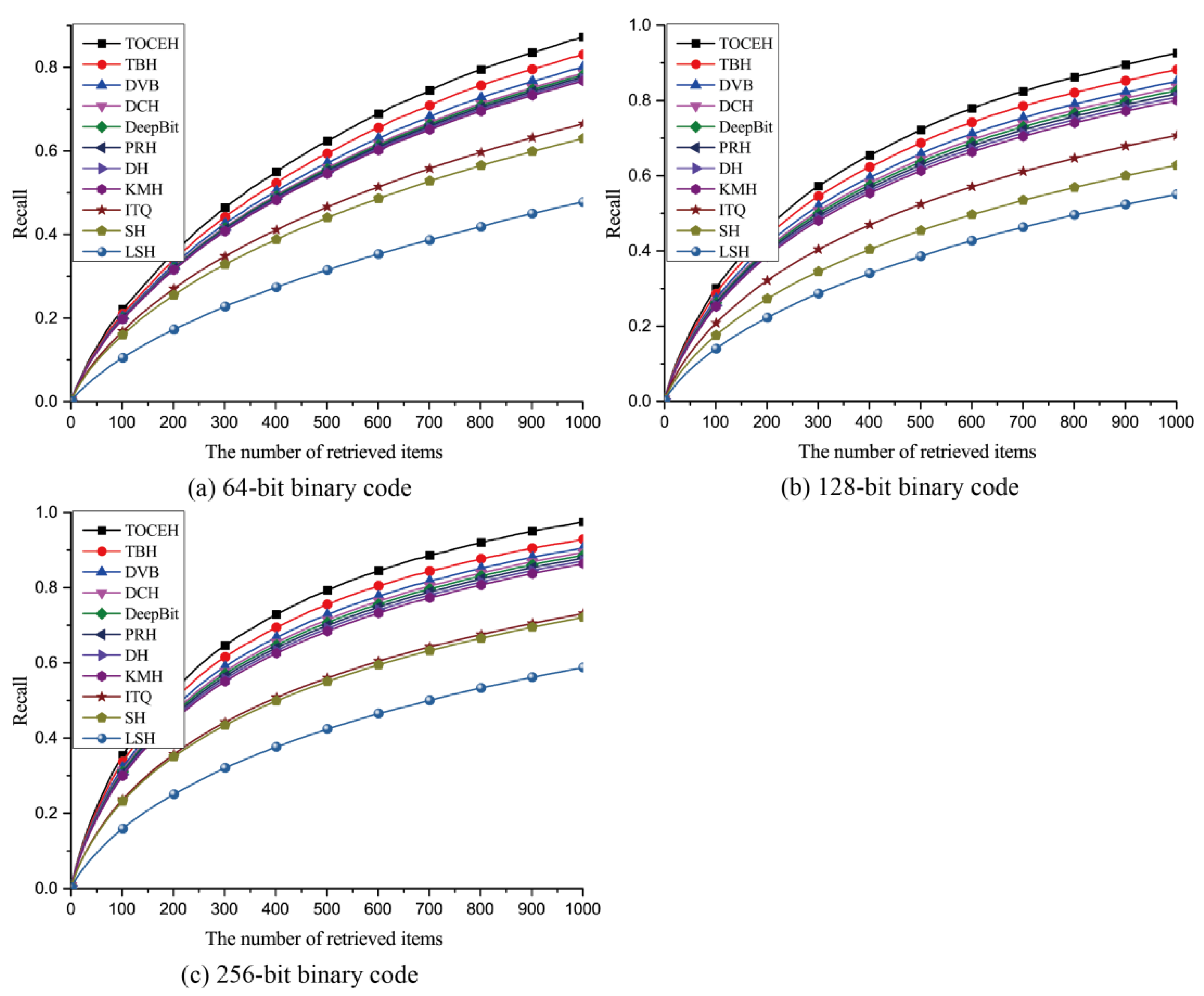
3.3. Experimental Results
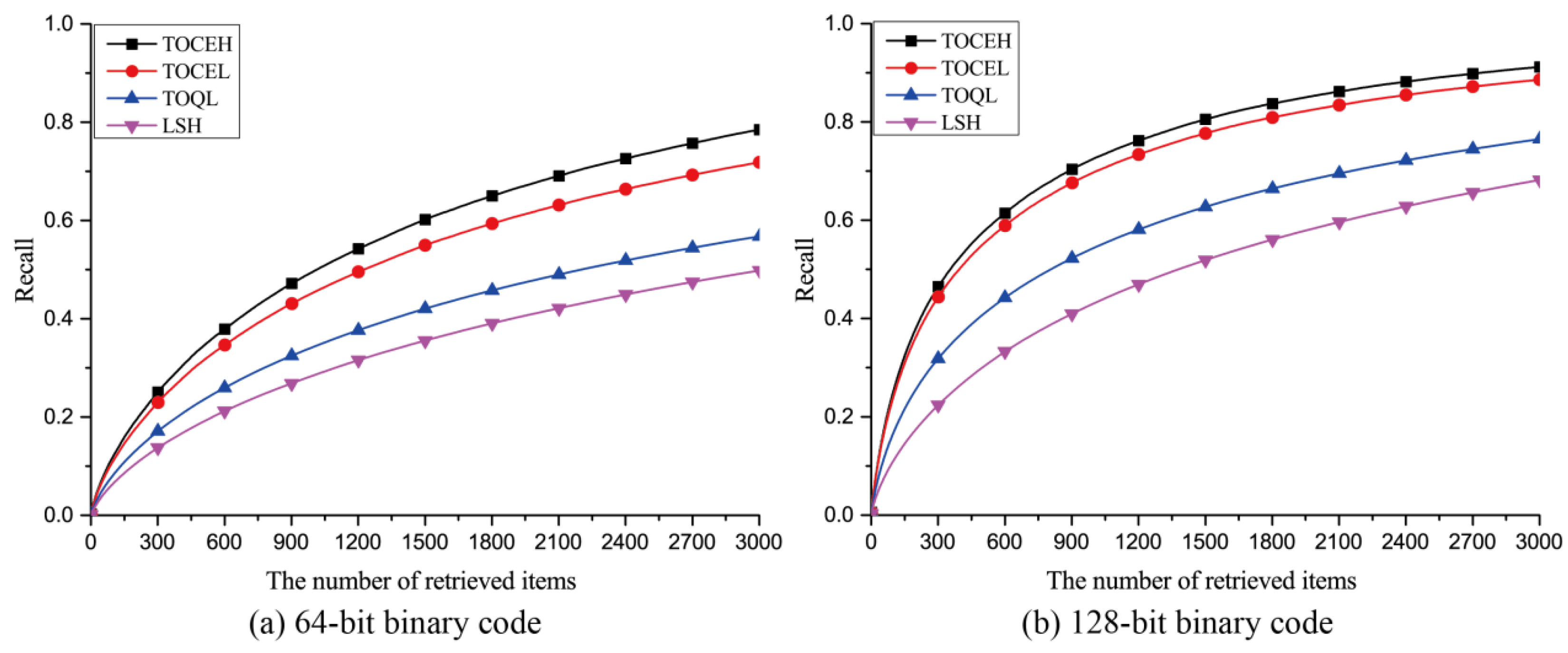
3.3.1. Qualitative Analysis
3.3.2. Quantitative Analysis
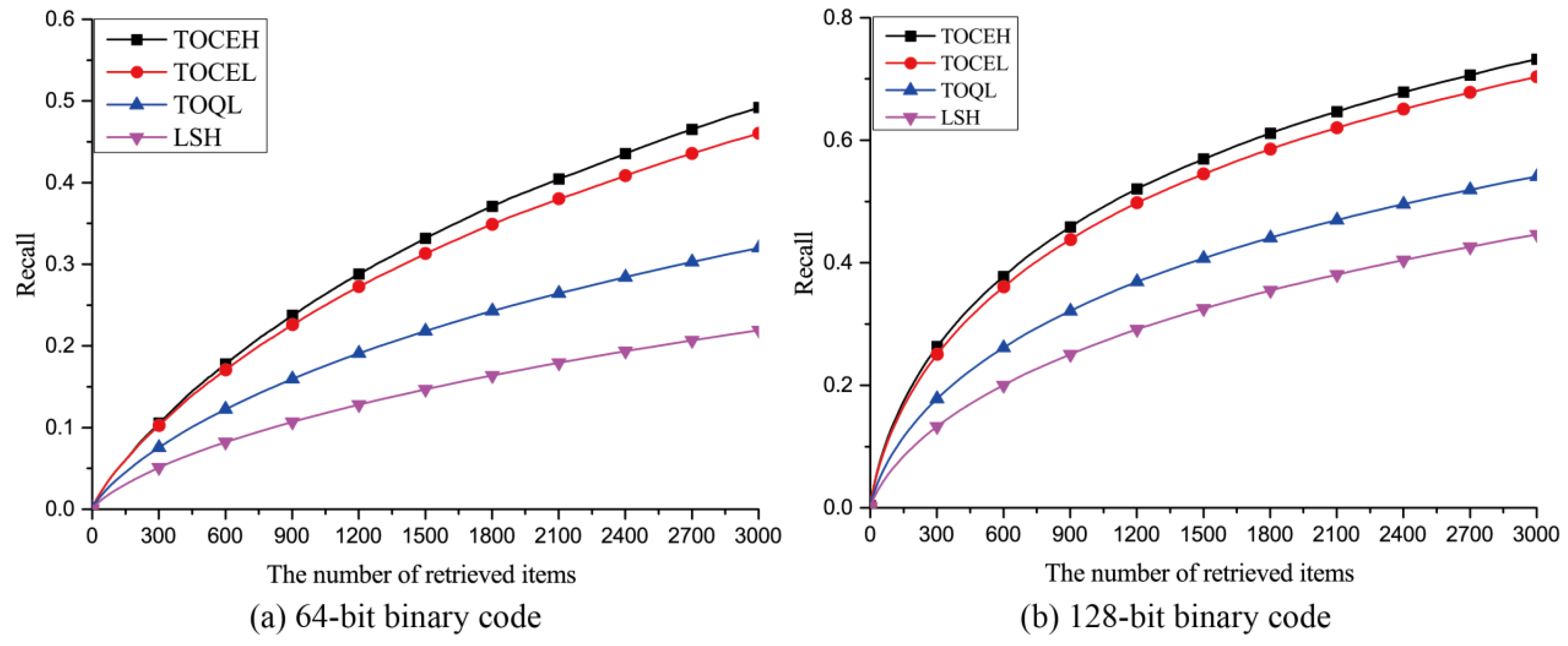
3.3.3. Ablation Experiments
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cheng, Q.; Gan, D.; Fu, P.; Huang, H.; Zhou, Y. A Novel Ensemble Architecture of Residual Attention-Based Deep Metric Learning for Remote Sensing Image Retrieval. Remote Sens. 2021, 13, 3445. [Google Scholar] [CrossRef]
- Shan, X.; Liu, P.; Wang, Y.; Zhou, Q.; Wang, Z. Deep Hashing Using Proxy Loss on Remote Sensing Image Retrieval. Remote Sens. 2021, 13, 2924. [Google Scholar] [CrossRef]
- Shan, X.; Liu, P.; Gou, G.; Zhou, Q.; Wang, Z. Deep Hash Remote Sensing Image Retrieval with Hard Probability Sampling. Remote Sens. 2020, 12, 2789. [Google Scholar] [CrossRef]
- Kong, J.; Sun, Q.; Mukherjee, M.; Lloret, J. Low-Rank Hypergraph Hashing for Large-Scale Remote Sensing Image Retrieval. Remote Sens. 2020, 12, 1164. [Google Scholar] [CrossRef] [Green Version]
- Han, L.; Li, P.; Bai, X.; Grecos, C.; Zhang, X.; Ren, P. Cohesion Intensive Deep Hashing for Remote Sensing Image Retrieval. Remote Sens. 2020, 12, 101. [Google Scholar] [CrossRef] [Green Version]
- Hou, Y.; Wang, Q. Research and Improvement of Content Based Image Retrieval Framework. Int. J. Pattern. Recogn. 2018, 32, 1850043.1–1850043.14. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Lu, G.; Ma, W.Y. A survey of content-based image retrieval with high-level semantics. Pattern. Recogn. 2007, 40, 262–282. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, T.; Song, J.; Sebe, N.; Shen, H.T. A Survey on Learning to Hash. IEEE Trans. Pattern. Anal. 2018, 40, 769–790. [Google Scholar] [CrossRef]
- Wang, J.; Liu, W.; Kumar, S.; Chang, S.F. Learning to Hash for Indexing Big Data—A Survey. Proc. IEEE 2016, 104, 34–57. [Google Scholar] [CrossRef]
- Shen, Y.; Qin, J.; Chen, J.; Yu, M.; Liu, L.; Zhu, F.; Shen, F.; Shao, L. Auto-encoding twin-bottleneck hashing. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2815–2824. [Google Scholar]
- Cao, Y.; Long, M.; Liu, B.; Wang, J. Deep cauchy hashing for hamming space retrieval. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1229–1237. [Google Scholar]
- He, K.; Wen, F.; Sun, J. K-means hashing: An affinity-preserving quantization method for learning binary compact codes. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2938–2945. [Google Scholar]
- Gong, Y.; Lazebnik, S.; Gordo, A.; Perronnin, F. Iterative Quantization: A Procrustean Approach to Learning Binary Codes for Large-Scale Image Retrieval. IEEE Trans. Pattern. Anal. 2013, 35, 2916–2929. [Google Scholar] [CrossRef] [Green Version]
- Datar, M.; Immorlica, N.; Indyk, P.; Mirrokni, V.S. Locality-sensitive hashing scheme based on p-stable distributions. In Proceedings of the 20th ACM Symposium on Computational Geometry, Brooklyn, NY, USA, 8–11 June 2004; pp. 253–262. [Google Scholar]
- Cao, Y.; Liu, B.; Long, M.; Wang, J. HashGAN: Deep learning to hash with pair conditional Wasserstein GAN. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1287–1296. [Google Scholar]
- Liu, H.; Wang, R.; Shan, S.; Chen, X. Deep supervised hashing for fast image retrieval. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2064–2072. [Google Scholar]
- Weiss, Y.; Torralba, A.; Fergus, R. Spectral hashing. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–11 December 2008; pp. 1753–1760. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Oliva, A.; Torralba, A. Modeling the shape of the scene: A holistic representation of the spatial envelope. Int. J. Comput. Vis. 2001, 42, 145–175. [Google Scholar] [CrossRef]
- Shen, F.; Xu, Y.; Liu, L.; Yang, Y.; Huang, Z.; Shen, H.T. Unsupervised Deep Hashing with Similarity-Adaptive and Discrete Optimization. IEEE Trans. Pattern. Anal. 2018, 40, 3034–3044. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Song, J.; Zhou, K.; Liu, Y. Unsupervised deep hashing with node representation for image retrieval. Pattern. Recogn. 2021, 112, 107785. [Google Scholar] [CrossRef]
- Zhang, M.; Zhe, X.; Chen, S.; Yan, H. Deep Center-Based Dual-Constrained Hashing for Discriminative Face Image Retrieval. Pattern. Recogn. 2021, 117, 107976. [Google Scholar] [CrossRef]
- Li, P.; Ren, P. Partial Randomness Hashing for Large-Scale Remote Sensing Image Retrieval. IEEE Geosci. Remote Sens. 2017, 14, 1–5. [Google Scholar] [CrossRef]
- Demir, B.; Bruzzone, L. Hashing-Based Scalable Remote Sensing Image Search and Retrieval in Large Archives. IEEE Trans. Geosci. Remote Sens. 2016, 54, 892–904. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Huang, X.; Zhu, H.; Ma, J. Large-Scale Remote Sensing Image Retrieval by Deep Hashing Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 56, 950–965. [Google Scholar] [CrossRef]
- Fan, L.; Zhao, H.; Zhao, H. Distribution Consistency Loss for Large-Scale Remote Sensing Image Retrieval. Remote Sens. 2020, 12, 175. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the NIPS, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1106–1114. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.S.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Sun, F.Z.; Zhang, L.B.; Wang, L.; Liu, P. Top Position Sensitive Ordinal Relation Preserving Bitwise Weight for Image Retrieval. Algorithms 2020, 13, 18. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Ji, R.; Wang, J.; Shen, C. Ordinal Constraint Binary Coding for Approximate Nearest Neighbor Search. IEEE Trans. Pattern Anal. 2019, 41, 941–955. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Ji, R.; Wu, Y.; Liu, W. Towards optimal binary code learning via ordinal embedding. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 1258–1265. [Google Scholar]
- Wang, J.; Liu, W.; Sun, A.X.; Jiang, Y.G. Learning hash codes with listwise supervision. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 3032–3039. [Google Scholar]
- Norouzi, M.; Fleet, D.J.; Salakhutdinov, R. Hamming distance metric learning. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1061–1069. [Google Scholar]
- Wang, Q.; Zhang, Z.; Luo, S. Ranking preserving hashing for fast similarity search. In Proceedings of the International Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; pp. 3911–3917. [Google Scholar]
- Liu, L.; Shao, L.; Shen, F.; Yu, M. Discretely coding semantic rank orders for supervised image hashing. In Proceedings of the Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5140–5149. [Google Scholar]
- Chen, S.; Shen, F.; Yang, Y.; Xu, X.; Song, J. Supervised hashing with adaptive discrete optimization for multimedia retrieval. Neurocomputing 2017, 253, 97–103. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S.D. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 3–5 November 2010; pp. 270–279. [Google Scholar]
- Basu, S.; Ganguly, S.; Mukhopadhyay, S.; DiBiano, R.; Karki, M.; Nemani, R.R. DeepSat: A learning framework for satellite imagery. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, Bellevue, WA, USA, 3–6 November 2015; pp. 1–10. [Google Scholar]
- Shen, Y.; Liu, L.; Shao, L. Unsupervised Binary Representation Learning with Deep Variational Networks. Int. J. Comput. Vis. 2019, 127, 1614–1628. [Google Scholar] [CrossRef]
- Liong, V.E.; Lu, J.; Wang, G.; Moulin, P.; Zhou, J. Deep hashing for compact binary codes learning. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1063–6919. [Google Scholar]
- Lin, K.; Lu, J.; Chen, C.S.; Zhou, J. Learning compact binary descriptors with unsupervised deep neural networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1063–6919. [Google Scholar]







| Notation | Description |
|---|---|
| B | Compact binary code matrix |
| Bi, Bj, Bk | The i-th, j-th, k-th column in B |
| H(∙) | Hashing function |
| X | Data matrix in the Euclidean space |
| xi, xj, xk | The i-th, j-th, k-th column in X |
| G | Triplet ordinal graph in the Euclidean space |
| Ĝ | Triplet ordinal relation in the Hamming space |
| gijk | The entry (i, j, k) in G |
| S | Similarity graph |
| DS | Dissimilarity graph |
| N | The number of training samples |
| L | The number of k-means centers |
| P(∙) | Probability distribution function |
| dh(∙,∙) | Hamming distance function |
| M | Binary code length |
| 1 | The binary matrix with all values of 1 |
| UCMD | SAT4 | SAT6 | |
|---|---|---|---|
| Class Number | 21 | 4 | 6 |
| Image Size | 256 × 256 | 28 × 28 | 28 × 28 |
| Dataset Size | 2100 | 500,000 | 405,000 |
| Training Set | 1470 | 400,000 | 360,000 |
| Query Set | 630 | 100,000 | 45,000 |
| Ground Truth | 100 | 1000 | 1000 |
| TOCEH | TBH | DVB | DCH | DeepBit | PRH | DH | KMH | ITQ | SH | LSH | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 64-bit | 0.3914 | 0.3415 | 0.3261 | 0.2917 | 0.2657 | 0.2462 | 0.2296 | 0.2135 | 0.1986 | 0.1724 | 0.1637 |
| 128-bit | 0.5479 | 0.4638 | 0.4259 | 0.3963 | 0.3781 | 0.3527 | 0.3467 | 0.2816 | 0.2462 | 0.2015 | 0.1842 |
| 256-bit | 0.5837 | 0.4975 | 0.4757 | 0.4319 | 0.4197 | 0.3746 | 0.3528 | 0.3168 | 0.2673 | 0.2351 | 0.2148 |
| TOCEH | TBH | DVB | DCH | DeepBit | PRH | PRH | KMH | ITQ | SH | LSH | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 64-bit | 0.7011 | 0.5768 | 0.5271 | 0.4862 | 0.4522 | 0.4361 | 0.4139 | 0.3946 | 0.3657 | 0.3482 | 0.3407 |
| 128-bit | 0.7236 | 0.6124 | 0.5537 | 0.4986 | 0.4794 | 0.4528 | 0.4385 | 0.4173 | 0.3856 | 0.3724 | 0.3615 |
| 256-bit | 0.7528 | 0.6345 | 0.6149 | 0.5128 | 0.5068 | 0.4857 | 0.4653 | 0.4361 | 0.4285 | 0.4152 | 0.3986 |
| TOCEH | TBH | DVB | DCH | DeepBit | PRH | DH | KMH | ITQ | SH | LSH | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 64-bit | 0.7124 | 0.5826 | 0.5446 | 0.4936 | 0.4725 | 0.4586 | 0.4352 | 0.4125 | 0.3764 | 0.3695 | 0.3628 |
| 128-bit | 0.7351 | 0.6268 | 0.5841 | 0.5174 | 0.4921 | 0.4795 | 0.4596 | 0.4281 | 0.3927 | 0.3864 | 0.3752 |
| 256-bit | 0.7842 | 0.6527 | 0.6261 | 0.5394 | 0.5175 | 0.4972 | 0.4628 | 0.4516 | 0.4359 | 0.4238 | 0.4175 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wu, N.; Yang, X.; Yan, B.; Liu, P. Deep Learning Triplet Ordinal Relation Preserving Binary Code for Remote Sensing Image Retrieval Task. Remote Sens. 2021, 13, 4786. https://doi.org/10.3390/rs13234786
Wang Z, Wu N, Yang X, Yan B, Liu P. Deep Learning Triplet Ordinal Relation Preserving Binary Code for Remote Sensing Image Retrieval Task. Remote Sensing. 2021; 13(23):4786. https://doi.org/10.3390/rs13234786
Chicago/Turabian StyleWang, Zhen, Nannan Wu, Xiaohan Yang, Bingqi Yan, and Pingping Liu. 2021. "Deep Learning Triplet Ordinal Relation Preserving Binary Code for Remote Sensing Image Retrieval Task" Remote Sensing 13, no. 23: 4786. https://doi.org/10.3390/rs13234786
APA StyleWang, Z., Wu, N., Yang, X., Yan, B., & Liu, P. (2021). Deep Learning Triplet Ordinal Relation Preserving Binary Code for Remote Sensing Image Retrieval Task. Remote Sensing, 13(23), 4786. https://doi.org/10.3390/rs13234786