Abstract
Image super-resolution (SR) technology aims to recover high-resolution images from low-resolution originals, and it is of great significance for the high-quality interpretation of remote sensing images. However, most present SR-reconstruction approaches suffer from network training difficulties and the challenge of increasing computational complexity with increasing numbers of network layers. This indicates that these approaches are not suitable for application scenarios with limited computing resources. Furthermore, the complex spatial distributions and rich details of remote sensing images increase the difficulty of their reconstruction. In this paper, we propose the pyramid information distillation attention network (PIDAN) to solve these issues. Specifically, we propose the pyramid information distillation attention block (PIDAB), which has been developed as a building block in the PIDAN. The key components of the PIDAB are the pyramid information distillation (PID) module and the hybrid attention mechanism (HAM) module. Firstly, the PID module uses feature distillation with parallel multi-receptive field convolutions to extract short- and long-path feature information, which allows the network to obtain more non-redundant image features. Then, the HAM module enhances the sensitivity of the network to high-frequency image information. Extensive validation experiments show that when compared with other advanced CNN-based approaches, the PIDAN achieves a better balance between image SR performance and model size.
1. Introduction
High-resolution (HR) remote sensing imagery can provide rich and detailed information about ground features and this has led to it being widely used in various tasks, including urban surveillance, forestry inspection, disaster monitoring, and military object detection [1]. However, it is difficult to guarantee the clarity of remote sensing images because it can be restricted by the imaging hardware, transmission conditions, and other factors. Considering the high cost and time-consuming research cycle of hardware sensors, the development of a practical and inexpensive algorithm for HR imaging technology in the field of remote sensing is in great demand.
Single-image super-resolution (SISR) [2] aims to obtain an HR image from its corresponding low-resolution (LR) counterpart by using the intrinsic relationships between the pixels in an image. Traditional SISR methods can be roughly divided into three main categories: Interpolation- [3,4], reconstruction- [5,6], and example learning-based methods [7,8]. However, these approaches are not suitable for image SR tasks in the remote sensing field because of their limited ability to capture detailed features and the loss of a large amount of high-frequency information (edges and contours) in the reconstruction process.
With the flourishing development of deep convolutional neural networks (DCNNs) and big-data technology, promising results have been obtained in computer vision tasks. Because of their end-to-end training strategy and powerful feature-reconstruction ability, DCNNs have been extensively applied in the domain of SR reconstruction in recent years [9,10,11,12,13,14]. Dong et al. [9] successfully introduced a CNN into the SR reconstruction task using a simple three-layer neural network, and they demonstrated that CNNs can directly learn end-to-end nonlinear mappings from LR images to their corresponding HR counterparts, achieving good results without the need for the manual features required by traditional methods. Kim et al. [10] proposed a 20-layer network for predicting residual images, and they verified that the SR model performance improves significantly when the number of structure layers is increased. Furthermore, Lim et al. [11] expanded the network to 69 layers by stacking more residual blocks, and this uses more features from each convolution layer to restore the image. Zhang et al. [12] designed a network using more than 400 layers, and this achieved obvious improvements for SISR by embedding a channel attention mechanism (CAM) [15] module into the residual block. Inspired by [9], Zeng et al. [14] employed two autoencoders to automatically extract hidden representations in LR and HR image patches. These methods have obtained promising results in SISR tasks however, there are still some limitations among CNN-based methods for the task of remote sensing SR reconstruction.
Firstly, the depth of the CNNs is important for image SR however, deeper networks are more difficult to train and require much greater computing resources. Moreover, this may result in the SR effect becoming saturated or even degraded, which illustrates that it is crucial to design a rational and efficient network that has a good balance between SR quality and model complexity.
Secondly, remote sensing images are more complex in terms of the spatial distribution of features and are richer in detailed information than natural images; moreover, the objects in remote sensing images have a relatively wide range of scales, which results in a requirement for the model to have a high restoration ability in high-frequency regions [16]. However, most existing CNN-based methods ignore the differing importance of different spatial areas, and this hinders the recovery of high-frequency information.
Thirdly, as the depth of a CNN increases, the feature information obtained in the different convolutional layers will be hierarchical in different receptive fields. Traditionally, a small-sized convolution kernel can extract low-frequency information, but this is not sufficient for the extraction of more detailed information. The work of [17] shows that applying convolutional layers with different receptive fields in the same layer can ensure the acquisition of low-frequency and high-frequency details of the source image. Therefore, the selection of suitable of receptive field and better utilization of hierarchical features should be considered when designing an SR network.
To address the urgent issues noted above, we propose a novel remote sensing SR image reconstruction network called a pyramid information distillation attention network (PIDAN), which includes a carefully designed pyramid information distillation attention block (PIDAB) that was inspired by information distillation networks (IDNs) [18]. An IDN reduces the network parameters by compressing the dimensions of its feature map, which increases the speed of processing while guaranteeing the restoration results. However, the ability of an IDN to differentially exploit different locations and channel features is still insufficient [19], which limits the further improvement of SR performance. Considering this, the PIDAB adopts a strategy of feature distillation, and its structure combines a pyramid convolution block and an attention mechanism.
A PIDAN consists of a shallow feature-extraction part, several PIDABs, and a reconstruction part. Each PIDAB is a single deep feature-extraction unit, and this contains a pyramid information distillation (PID) module, a hybrid attention mechanism (HAM) module, and a single channel compression (CC) unit. The PID can extract both deep and shallow features, and the HAM can restore high-frequency detailed information. The PID module utilizes an enhancement unit (EU) and a pyramid convolution channel split (PCCS) operation to gradually integrate the local short- and long-path features for reconstruction. The EU can be divided into two levels according to the inference order. In the first level, we use a shallow convolution network to obtain local short-path features. After the first level, the PCCS extracts the refined features by using convolution layers with different receptive fields in parallel. Then, a split operation is placed after each convolution layer, and this divides the feature channel into two parts: One for further enhancement in the second level to obtain long-path features, and another to represent reserved short-path features. In the second level of the EU, the HAM utilizes the short-path feature information by fusing a CAM and a spatial attention mechanism (SAM). Specifically, unlike the structure of a convolutional block attention module (CBAM) [20], in which the spatial feature descriptors are generated along the channel axis, our CAM and SAM are parallel branches that operate on the input features simultaneously. Finally, the CC unit is used for achieving a reduction of the channel dimensionality by taking advantage of a 1 × 1 convolution layer, as used in an IDN.
In summary, the main contributions of this work are as follows:
- (1)
- Inspired by IDNs, we constructed an effective and convenient end-to-end trainable architecture, PIDAN, which is designed for SR reconstruction of remote sensing images. Our PIDAN structure consists of a shallow feature-extraction part, stacked PIDABs, and a reconstruction part. Compared with an IDN, a PIDAN recovers more high-frequency information.
- (2)
- Specifically, we propose the PIDAB, which is composed of a PID module, a HAM module, and a single CC unit. Firstly, the PID module uses an EU and a PCCS operation to gradually integrate the local short- and long-path features for reconstruction. Secondly, the HAM utilizes the short-path feature information by fusing a CAM and SAM in parallel. Finally, the CC unit is used for achieving channel dimensionality reduction.
- (3)
- We compared our PIDAN with other advanced SISR approaches using remote sensing datasets. The extensive experimental results demonstrate that the PIDAN achieves a better balance between SR performance and model complexity than the other approaches.
The remainder of this paper is organized as follows. Section 2 introduces previous works on CNN-based SR reconstruction algorithms and attention mechanism methods. Section 3 presents a detailed description of the PIDAN, Section 4 presents a verification of its effectiveness by experimental comparisons, and Section 5 concludes our work.
2. Related Works
2.1. CNN-Based SR Methods
The basic principle of SR methods based on deep learning technology is to establish a nonlinear end-to-end mapping relationship between an input and output through a multi-layer CNN. Dong et al. [9] were the first to apply a CNN to the image SR task, producing a system named SRCNN. This uses a bicubic interpolation operation to enlarge an LR image to the target size, then it fits the nonlinear mapping using three convolution layers before finally outputting an HR image. The SRCNN system provides great improvement in the SR quality when compared with traditional algorithms, but its training speed is very low. Soon after this, Dong et al. [21] reported the Faster-SRCNN, which increases the speed of SRCNN by adding a deconvolution layer. Inspired by [9], Zeng et al. [14] developed a data-driven model named, coupled deep autoencoder (CDA), which automatically learns the intrinsic representations of LR and HR image patches by employing two autoencoders. Shi et al. [22] investigated how to directly input an LR image into the network and developed the efficient sub-pixel convolutional neural network (ESPCN), which reduces the computational effort of the network by enlarging the image through the sub-pixel convolution layer, and this improves the training speed exponentially. The network structures of the above algorithms are simple and easy to implement. However, due to the use of a large convolution kernel, even a shallow network requires the calculation of a large number of parameters. Training is therefore difficult when the network is deepened and widened, and the SR reconstruction is thus not effective.
To reduce the difficulty of model training, Kim et al. [10] deepened the network to 20 layers using a residual-learning strategy [23]; their experimental results demonstrated that the deeper the network, the better the SR effect. Then, Kim et al. [24] proposed a deeply recursive convolutional network (DRCN), which applies recursive supervision to make the deep network easier to train. Based on DRCN, Tai et al. [25] developed a deep recursive residual network (DRRN), which introduces recursive learning into the residual branch, and this deepens the network without increasing computational effort and speeds up the convergence. Lai et al. proposed the deep Laplacian super-resolution network (LapSRN) [26], which predicts the sub-band residuals in a coarse-to-fine fashion. Tong et al. [27] employed the dense connected convolutional networks, which allows the reuse of feature maps from preceding layers, and alleviates the gradient vanishing problem by facilitating the information flow in the network. Zhang et al. [28] proposed a deep residual dense network (RDN), which combines the residual skip structure with the dense connections, and this fully utilizes the hierarchical features. Lim et al. [11] built an enhanced deep SR network (EDSR), which constructs a deeper CNN by stacking more residual blocks, and this takes more features from each convolution layer to restore the image. The EDSR expanded the network to 69 layers and won the NTIRE 2017 SR challenge. Yu et al. [29] proposed a wide activation SR (WDSR) network, which shows that simply expanding features before the rectified linear unit (ReLU) activation results in obvious improvements for SISR. Based on EDSR, Zhang et al. [12] built a deep residual channel attention network (RCAN) with more than 400 layers, and this achieves promising results by embedding the channel attention [15] module into the residual block. It is noteworthy that while increasing the network’s depth may improve the SR effect, it also increases the computational complexity and memory consumption of the network, which makes it difficult to apply these methods to lightweight scenarios such as mobile terminals.
Considering this issue, many researchers have focused on finding a better balance between SR performance and model complexity when designing a CNN. Ahn et al. [30] proposed a cascading residual network (CARN), which was designed to be a high-performing SR model that implements a cascading mechanism to fuse multi-layer feature information. The IDN, which is a concise but effective SR network, was proposed by Hui et al. [18], and this uses a distillation module to gradually extract a large number of valid features. Profiting from this information distillation strategy, IDN achieves good performance at a moderate size. However, IDN treats different channel and spatial areas equally in LR feature space, and this restricts its feature representation ability.
2.2. Attention Mechanisms
For human perception, attention usually refers to the human visual system focusing on salient regions and adaptively processing visual information. Recently, many visual recognition tasks have tended to embed attention modules with networks to improve their performance. Hu et al. [15] proposed the squeeze-and-excitation network (SENet), which captures feature relationships by explicitly modeling interdependencies between channels. This ranked first in the ILSVRC 2017 classification competition. Motivated by SENet, Woo et al. [20] created the CBAM, which includes a SAM that can adaptively allocate weights in different spatial locations. Using the classical non-local means method [31], Wang et al. [32] developed a non-local (NL) block that can be plugged into a neural network. This uses a self-attention mechanism to directly model long-range dependencies instead of adopting multiple convolutions to obtain feature information with a larger receptive field. The NL block can thus provide rich semantic information for a network. Cao et al. [33] developed a global context block, which combines the simplified NL block and the squeeze-and-excitation (SE) block of SENet to reduce the computational effort while making full use of global contextual information.
Recently, several works have focused on introducing attention mechanisms to the SISR task. Inspired by SENet [15], Zhang et al. [12] produced the RCAN, which enhances the representation ability by using the channel attention mechanism to differentially treat the feature channels in each layer so that the reconstructed image contains more texture information. Zhang et al. [34] built a very deep residual non-local attention network, which includes residual local and non-local attention blocks as the basic building modules. This improves the local and non-local information learning ability using the hierarchical features. Anwar et al. [35] proposed a densely residual Laplacian network, which replaces the CAM with a proposed Laplacian module to learn features at multiple sub-band frequencies. Guo et al. [36] proposed a novel image SR approach named the multi-view aware attention network. This applies locally and globally aware attention to unequally deal with LR images. Dai et al. [37] proposed a deep second-order attention network, in which a second-order channel attention mechanism captures feature inter-dependencies by using second-order feature statistics. Hui et al. [38] proposed a contrast-aware channel attention mechanism, and this is particularly suited to low-level vision tasks such as image SR and image enhancement. Zhao et al. [39] proposed a pixel attention mechanism, which generates three-dimensional attention maps instead of a one-dimensional vector or a two-dimensional map, and this achieves better SR results with fewer additional parameters. Wang et al. [40] built a spatial pyramid pooling attention module via integrating the channel-wise and multi-scale spatial information, which is beneficial for capturing spatial context cues and then establishing the accurate mapping from low-dimension space to high-dimension space.
Considering that the previous promising results have benefited from the introduction of an attention mechanism, we propose PIDAN, which also includes an attention mechanism, to focus on extracting high-frequency details from images.
3. Methodology
In this section, we will describe PIDAN in detail. An overall graphical depiction of PIDAN is shown in Figure 1. Firstly, we will give an overview of the proposed network architecture. After this, we will present each module of the PIDAB in detail. Finally, we will give the loss function used in the training process. Here, we denote an initial LR input image and an SR output image as ILR and ISR, respectively.
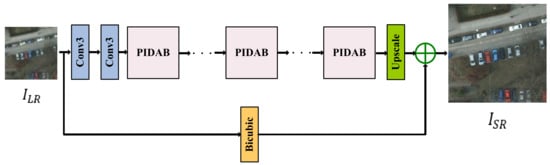
Figure 1.
Overview of the PIDAN network structure.
3.1. Network Architecture
As shown in Figure 1, the PIDAN approach consists of a shallow feature-extraction part, a deep feature-extraction part (stacked PIDABs), and a reconstruction part. As with the operation of an IDN, the shallow features are extracted from the LR input via two convolutional layers:
where denotes two convolutional layers with a kernel size of 3 × 3 to extract C initial feature maps. The resulting contributes to the next deep feature-extraction part using the PIDABs. Moreover, the proposed PIDAB can be regarded as a basic component for residual feature extraction. The operation of the n-th PIDAB can be defined as:
where denotes the function of the n-th PIDAB, and and are the inputs and outputs of the n-th PIDAB, respectively.
After obtaining the deep features of the LR images, an up-sampling operation aims to project these features into the HR space. Previous approaches, such as EDSR [11], RCAN [12], and the information multi-distillation network (IMDN) [38] have shown that a sub-pixel [22] convolution operation can reserve more parameters and achieve a better SR effect than other up-sampling approaches. Considering this, we used a transition layer with a 3 × 3 kernel and a sub-pixel convolution layer as our reconstruction part. This operator can be expressed as:
where denotes a convolutional layer with a convolution kernel size of 3 × 3, denotes a sub-pixel convolution, is the output of the last PIDAB, and is the upscaled feature maps.
Finally, using the idea of global residual learning [23], the output of the PIDAN is estimated by combining the up-sampled image with the interpolated image using an element-wise summation. This can be formulated as:
where denotes the bicubic interpolation operation.
3.2. PIDAB
In this section, we will present a description of the overall structure using a PIDAB. Figure 2 compares the PIDAB with the original IDB in an IDN. As noted, the PIDAB was developed using a PID module, a HAM module, and a CC unit. The PID module can extract both deep and shallow features, and the HAM module can restore high-frequency detailed information.
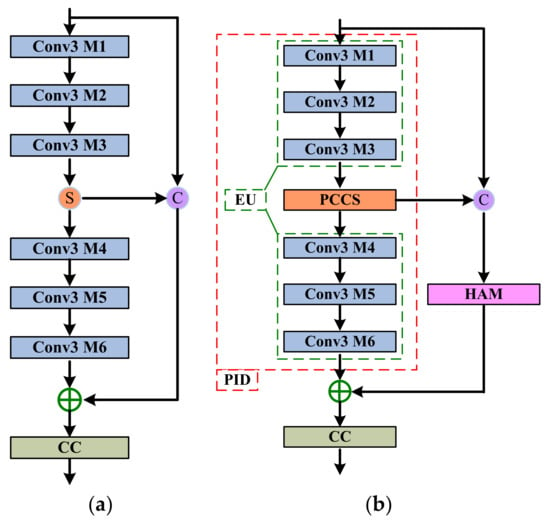
Figure 2.
Illustrations of (a) original IDB structure of an IDN and (b) the PIDAB structure in a PIDAN.
3.2.1. PID Module
As shown in Figure 2b, the PID module consists of two parts: An EU and a PCCS component. The EU can be roughly divided into two modules, the upper shallow convolution network and the lower shallow convolution network. Each module has three cascaded convolutional layers with a convolution kernel size of 3 × 3; each of these is followed by a leaky rectified linear unit (LReLU) activation function, which is omitted here. We label the feature map dimensions of the i-th layer as , and the relationship among the upper three convolutions can be formulated as:
where m denotes the difference between the first layer and second layer or between the first layer and third layer. Simultaneously, the relationship among the lower three convolution layers can be described as:
where . Supposing the input of this module is , we have:
where denotes the output of the (n − 1)-th PIDAB (which is also the input of the n-th PIDAB), denotes the upper shallow convolution network in the enhancement unit, and denotes the output of the upper shallow convolution network in the n-th PIDAB.
As shown in Figure 2a, in the original IDN, the output of the upper cascaded convolutional layers is split into two parts: One for further enhancement in the lower shallow convolution network to obtain the long-path features, and another to represent reserved short-path features via concatenation with the input of the current block. In PIDAN, to obtain more non-redundant and extensive feature information, a feature-purification component with parallel structures was designed.
The convolutional layers in the CNN can extract local features from a source image by automatically learning convolutional kernel weights during the training process. Therefore, choosing an appropriate size of convolution kernel is crucial for feature extraction. Traditionally, a small-sized convolution kernel can extract low-frequency information, but this is not sufficient for the extraction of more detailed information. Considering this, the PCCS component is proposed to extract the features of multiple receptive fields. In the pyramid structure, the size of the convolution kernel of each parallel branch is different, which allows the network to perceive a wider range of hierarchical features. As presented in Figure 3, the PCCS component is built from three parallel feature-purification branches and two feature-fusion operations.
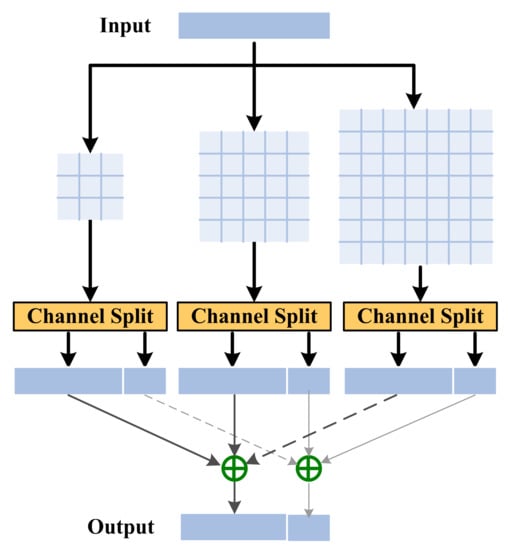
Figure 3.
Structure of PCCS component.
For a PCCS component, assuming that the given input feature map is , the pyramid convolution layer operation is applied to the extraction of refined features with different kernel sizes. The split operation is performed after each feature-refinement branch, and this can split the channel into two parts. The process can be formulated as:
where: denotes the j-th convolution layer (including an LReLU activation unit) with a convolution kernel size of k × k; denotes a channel-splitting operation similar to that used in an IDN; and denotes the j-th distilled features; denotes the j-th coarse features that will be further processed by the lower shallow convolution network in the n-th PIDAB, specifically, the number of channels of is defined as , therefore the number of channels of is set to .
All the distilled features and remaining features are then respectively added together:
Then, as shown in Figure 2b, will be concatenated with the input of the current PIDAB to obtain the retained short-path features:
where denotes the concatenation operator, and denotes partially retained local short-path information. We take as the input of the lower shallow convolution network, which obtains the long-path feature information:
where and denote the output and cascaded convolution layer operations of the lower shallow convolution network, respectively. As shown in Figure 2a, in the initial IDB structure of an IDN, the reserved local short-path information and the long-path information are summed before the CC unit. In PIDAN, to fully utilize the local short-path feature information, we embed an attention mechanism module to enable the network to focus on more useful high-frequency feature information and improve the SR effect. Therefore, before the CC unit, the fusion of short-path and long-path feature information can be formulated as:
where HAM(·) denotes the hybrid attention mechanism operation, which will be illustrated in detail in the next subsection.
3.2.2. HAM Module
In an IDN, the information distillation module is used to gradually extract a large number of valid features, and the intention of the channel-split operation is to combine short- and long-path hierarchical information. However, an IDN treats different channels and spatial areas equally in LR feature space, which restricts the feature representation ability of the network. Moreover, if sufficient features are not extracted in the short path, information learned later will also become inadequate. Considering that an attention mechanism can make a network pay more attention to high-frequency information, which is beneficial for the SR reconstruction task, we further utilize the extracted short-path features by fusing a CAM and SAM to construct a HAM, which makes the split operation yield better performance. Specifically, unlike the structure of a CBAM [20], in which the spatial feature descriptors are generated along the channel axis, our SAM and CAM are parallel branches that operate on the input features simultaneously. In this way, our HAM makes maximum use of the attention mechanism through self-optimization and mutual optimization of the channel and spatial attention during the gradient back-propagation process. The formula of the HAM is:
where: F denotes the input of the HAM; and CAM(·), SAM(·), and HAM(·) respectively denote the CAM, SAM, and HAM functions. Here ⮾ denotes element-wise multiplication between the CAM and SAM functions. Like an RCAN, short-skip connections are added to enable the network to directly learn more complex high-frequency information while improving the ease of model training. The structure of the HAM is presented in Figure 4.
HAMF(F) = CAM(F) ⮾ SAMF(F) + F,
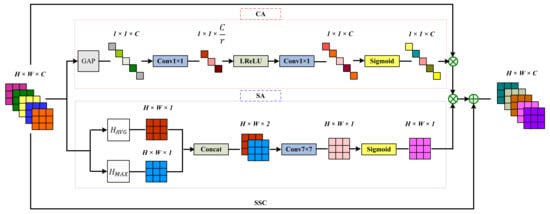
Figure 4.
Overview of the HAM.
Channel Attention Mechanism
The high performance of CNNs for feature extraction has been demonstrated however, the standard convolution kernel treats different channels equally and is restricted by its convolutional calculation being translation invariant. This makes it difficult for the network to use contextual information to effectively learn features. A previous report has shown that the attention mechanism can help capture channel correlations between features [15]. In PIDAN, by following RCAN [12], we consider channel-wise information by using the global pooling average operation, which can transform the information in the global space into channel descriptors.
Suppose the input features have channels with size (as shown in Figure 4). The global average pooling operation is adopted to obtain the channel descriptor (one-dimensional feature vector) of each feature map:
After the pooling operation, we use a similar perceptron network as that used in a CBAM [20] to fully learn the nonlinear interactions between different channels. Specifically, we replace ReLU with LReLU activation. The calculation process of the CAM can be described:
where: and denote the weight matrices of two convolution layers with a kernel size of 1 × 1, in which the channel dimensions of the features are defined as C/r and C, respectively; SIGMOID[·] and LReLU(·) denote the sigmoid and LReLU functions, respectively; and ⮾ denotes element-wise multiplication.
Spatial Attention Mechanism
Generally, the LR images have rich low-frequency information and valuable high-frequency information components. The difference between low-frequency information and high-frequency information is that the former is generally flat, while the latter is usually filled with edges, textures, and details in certain areas. Compared to low-frequency information, high-frequency information is usually more difficult to restore in the image SR task. Moreover, remote sensing images are more complex in their spatial distribution and richer in detailed information than natural images, which means that the designed SR network needs to show adequate perception of the high-frequency information regions. However, existing CNN-based algorithms usually ignore the variability of different spatial locations, and this tends to weaken the weight of high-frequency information. Considering this, in PIDAN, the SAM is designed to emphasize the attention to high-frequency areas, thus improving the accuracy of the SR algorithm.
As shown in Figure 4, we produce two efficient two-dimensional spatial feature descriptors by performing average-pooling and max-pooling operations:
These two spatial feature descriptors are then concatenated and convolved by a standard convolution layer, producing the spatial attention map. The calculation process of the SAM can be described as:
where: Concat(·) denotes the feature-map concatenation operation; (·) denotes the weight matrix of a convolution layer with a kernel size of 7 × 7, which reduces the channel dimensions of the spatial feature maps to one; Sigmoid[·] denotes the sigmoid function; and ⮾ denotes element-wise multiplication.
3.2.3. CC Unit
We realize the channel dimensionality reduction by taking advantage of a 1 × 1 convolution layer. Thus, the compression unit can be expressed as:
where: Pn denotes the result of the fusion of short- and long-path feature information in the n-th PIDAB; Fb,n denotes the output of the n-th PIDAB; and ⮾ denotes the weight matrix of a convolution layer with a kernel size of 1 × 1, which compresses the number of channels of features to be consistent with the input of the n-th PIDAB.
Table 1 presents the network structure parameter settings of a PIDAB. It should be noted that: C is defined as 64 in line with an IDN; in the PID module, we set m as 16, and we define s as 4; and in the HAM module, the reduction ratio r is set as 16, consistent with an RCAN.

Table 1.
PIDAB block parameter settings.
3.3. Loss Function
In our approach, the gradient is updated by minimizing the difference between the reconstruction result and the real image. The loss function is one of the key factors affecting the performance of the network, and there are two commonly used loss functions in CNN-based SR algorithms, namely the L1 norm [11,18] and L2 norm [27]. Compared to the L2 norm, the L1 norm loss function tends to perceive more high-frequency detailed information and results in higher-quality test metrics. In line with the IDN approach [18], the minimum loss function was formulated as:
where: N denotes the number of input images; HPIDAN(·) denotes the PIDAN network reconstruction process; Yi denotes the reconstructed image; Θ = {Wi,bi}, which denote the weight and bias parameters that the network needs to learn; Xi denotes the corresponding HR image; and ‖·‖1 denotes the L1 norm.
4. Experiments and Results
In this section, firstly, we demonstrate the experimental settings, including datasets, evaluation metrics, and training implementation details. Then, we report the experimental results and correlation analysis.
4.1. Settings
4.1.1. Dataset Settings
Following the previous work [41], we used the recently popular Aerial Image Dataset (AID) [42] for training. We augmented our training dataset using horizontal flipping, vertical flipping, and 90° rotation strategies. During the tests, to evaluate the trained SR model, we used two available remote sensing image datasets, namely, the NWPU VHR-10 [43] dataset and the Cars Overhead With Context (COWC) [44] dataset. In our experiments, the AID, NWPU VHR-10, and COWC datasets consisted of 10,000, 650, and 3000 images, respectively. Specifically, for the fast validation of the convergence speed of SR models, we constructed a new data set called FastTest10, which consists of 10 randomly selected samples from the NWPU VHR-10 dataset. The LR images were obtained by downsampling the corresponding HR label samples through bicubic interpolation with ×2, ×3, and ×4 scale factors. Some examples from each of these remote sensing datasets are shown in Figure 5.

Figure 5.
Examples of images in the three remote sensing datasets. In order, the top–bottom lines show samples from the AID, NWPU VHR-10, and COWC datasets.
4.1.2. Evaluation Metrics
We adopted the average peak signal-to-noise ratio (PSNR) [45] and structural similarity (SSIM) [46] as the SR reconstruction evaluation metrics. The PSNR measures the quality of an image by calculating the difference in pixel values between the reconstructed image and original HR image. The PSNR indicator mainly judges the similarity of the images from the perspective of the signal, and it is not completely consistent with human visual perception. Therefore, the SSIM was adopted because it models image distortion as a combination of three factors—luminance, contrast, and structure—so as to estimate the degree of similarity between two images from the perspective of overall image composition. Larger PSNR and SSIM values indicate a better SR image reconstruction result that is closer to the original image. Following the previous work in this field [9], SR is only performed on the luminance (Y) channel of the transformed YCbCr space.
4.1.3. Implementation Details
All experiments adopted the deep-learning framework PyTorch, and four Nvidia GTX-2080Ti GPUs were used to train all CNN models. The SR network was optimized with Adam [47] by setting β1 = 0.9, β2 = 0.999, and ϵ = 10−8. We set the initial learning rate to 10−4, and this was decreased by a factor of 10 after every 500 epochs. The training for PIDAN was iterated for 1500 epochs in total. The batch size was set to 16. Patches with a size of 48 × 48 were randomly cropped from LR images as the input of the model, and the corresponding input HR label images were divided into 96 × 96, 144 × 144, and 192 × 192 sizes according to upscaling factors of ×2, ×3, and ×4, respectively.
4.2. Results and Analysis
4.2.1. Comparison with Other Approaches
We compared our PIDAN with the bicubic interpolation, SRCNN [9], very deep super resolution (VDSR) [10], LapSRN [26], DRCN [24], pixel attention network (PAN) [39], DRRN [25], WDSR [29], CARN [30], residual feature distillation network (RFDN) [48], IDN [18], and IMDN [38] approaches. Specifically, for a fair comparison, the number of PIDABs was set to four in line with the IDN approach. Table 2 shows quantitative comparisons using the NWPU VHR-10 and COWC datasets. The best performances are indicated in bold, and the second-best performances are indicated with an underline. Our PIDAN performed better than all other approaches in most datasets with upscaling factors of ×2, ×3, and ×4.

Table 2.
Quantitative evaluation of PIDAN and other advanced SISR approaches. Bold indicates the optimal performance, and an underline indicates the second-best performance.
We take the NWPU VHR-10 dataset as an example. Compared with other SISR approaches, the PIDAN produces superior PSNR and SSIM values. Under the SR upscaling factor of ×2, the PSNR of the PIDAN is 0.01679 dB higher than that obtained with the second-best DRRN method and 0.03318 dB higher than that of the basic IDN; the SSIM of the PIDAN is 0.0002 higher than that obtained with the second-best DRRN method and 0.0005 higher than that of the IDN. Under the SR upscaling factor of ×3, the PSNR of the PIDAN is 0.00797 dB higher than that of the second-best WDSR method and 0.04455 dB than that of the IDN; the SSIM of the PIDAN is 0.0002 higher than that of the second-best WDSR method and 0.0009 higher than that of the IDN. Under the SR upscaling factor of ×4, the PSNR of the PIDAN is 0.00301 dB higher than that of the second-best WDSR method and 0.04669 dB than that of the IDN; the SSIM of the PIDAN is 0.0002 higher than that of the WDSR method and 0.0006 higher than that of the IDN.
We take the NWPU VHR-10 dataset as an example. Compared with other SISR approaches, the PIDAN produces superior PSNR and SSIM values. Under the SR upscaling factor of ×2, the PSNR of the PIDAN is 0.01679 dB higher than that obtained with the second-best DRRN method and 0.03318 dB higher than that of the basic IDN; the SSIM of the PIDAN is 0.0002 higher than that obtained with the second-best DRRN method and 0.0005 higher than that of the IDN. Under the SR upscaling factor of ×3, the PSNR of the PIDAN is 0.00797 dB higher than that of the second-best WDSR method and 0.04455 dB than that of the IDN; the SSIM of the PIDAN is 0.0002 higher than that of the second-best WDSR method and 0.0009 higher than that of the IDN. Under the SR upscaling factor of ×4, the PSNR of the PIDAN is 0.00301 dB higher than that of the second-best WDSR method and 0.04669 dB than that of the IDN; the SSIM of the PIDAN is 0.0002 higher than that of the WDSR method and 0.0006 higher than that of the IDN.
Next, we consider the COWC dataset as an example. Under the SR upscaling factor of ×2, the PSNR of the PIDAN is 0.07053 dB higher than that obtained with the second-best IMDN method and 0.09525 dB higher than that of the basic IDN; the SSIM of the PIDAN is 0.0006 higher than that obtained with the second-best DRRN method and 0.0008 higher than that of the IDN. Under the SR upscaling factor of ×3, the PSNR of the PIDAN is 0.05481 dB higher than that of the second-best WDSR method and 0.11112 dB higher than that of the IDN; the SSIM of the PIDAN is 0.0008 higher than that of the second-best WDSR method and 0.0017 higher than that of the IDN. Under the SR upscaling factor of ×4, the PSNR and SSIM of the PIDAN are both second-best, and the PSNR of the PIDAN is 0.00242 dB lower than that of the optimal WDSR method and 0.07886 dB higher than that of the IDN; the SSIM of the PIDAN is 0.0002 lower than that of the optimal WDSR method and 0.0017 higher than that of the IDN.
Figure 6 shows a comparison of the PSNR values between the PIDAN and DRRN, WDSR, CARN, RFDN, IDN, and IMDN networks using the FastTest10 dataset in the epoch range of 0 to 100. Compared to the other methods, the PIDAN converges faster and achieves better accuracy.
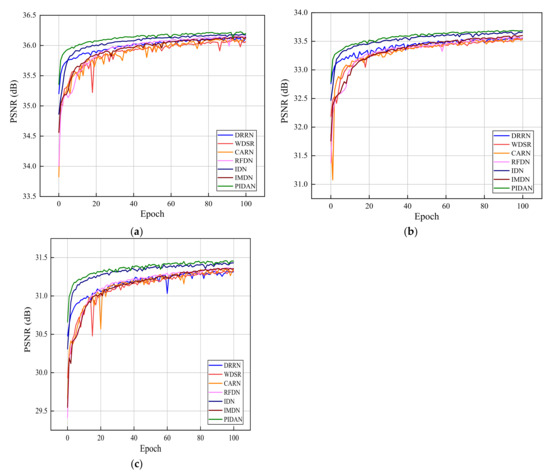
Figure 6.
Performance curves for PIDAN and other methods using the FastTest10 dataset with scale factors of (a) ×2, (b) ×3, and (c) ×4.
4.2.2. Model Size Analyses
We compared the model sizes of our PIDAN with other DCNN-based approaches. The results of an upscaling factor of ×2 SR on the COWC test set are shown in Figure 7. The x axis denotes the SR model size, with M indicating the number of parameters in millions, and the y axis denoting the average PSNR score. It can be concluded that our proposed PIDAN achieves an optimal PSNR score with a model parameter that is less than one-third of that of DRRN. This finding demonstrates that our PIDAN is relatively lightweight while ensuring a promising SR reconstruction performance.
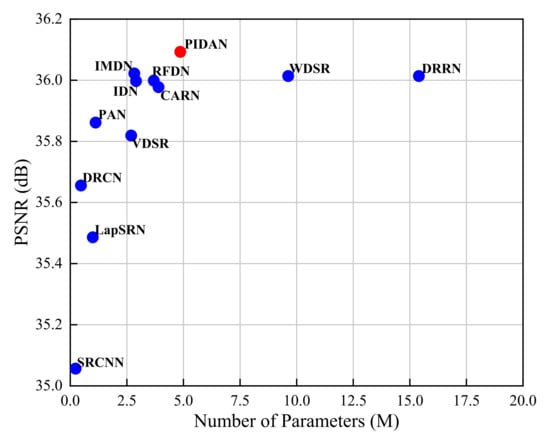
Figure 7.
Comparison of model parameters and mean PSNR values of different DCNN-based methods.
4.2.3. Visual Effect Comparison
In addition to the comparison of the objective indicators, we also conducted evaluations in terms of the visual results. Figure 8 presents a visual comparison between the PIDAN and other advanced approaches using image samples from the COWC test sets with three upscaling factors, ×2, ×3, and ×4. Specifically, in each case, we enlarged a small rectangle area for a clearer presentation and comparison. As can be seen, the images reconstructed by the bicubic interpolation algorithm are the most blurred. Figure 8a shows that the PIDAN obtains more promising results with fewer jaggies and ringing artifacts, and meanwhile reconstructs clearer image contours than the compared advanced approaches. In Figure 8b, the reconstructed vehicle result obtained using PIDAN restores sharper edge details and maintains the maximum structural integrity with less distortion. Figure 8c shows that the PIDAN can reconstruct the parallel lines more completely and precisely than the other approaches. The PIDAN also obtains the highest quantitative analysis values when compared with the other advanced SISR approaches. These visual results indicate that our model recovers feature information with rich high-frequency details, producing better SR results.


Figure 8.
Visual comparison of SR results using samples from the COWC dataset with (a) upscaling factor ×2, (b) upscaling factor ×3, and (c) upscaling factor ×4.
4.2.4. Analysis of PIDAB
The PIDAB is the most critical aspect of the PIDAN. To demonstrate the necessity of the PCCS operation and the HAM in the PIDAB, we carried out a set of ablation experiments on the NWPU VHR-10 and COWC datasets. As shown in Table 3, when we removed PCCS and HAM, the PSNR scores on the two datasets were 34.55616 and 35.99601 dB, respectively. When we added the PCCS component, the PSNR scores were 34.58637 and 36.03984 dB; when we added the HAM module, the PSNR scores were 34.57436 and 36.03683 dB, respectively. With the addition of both PCCS and HAM, the PSNR scores for images from the NWPU VHR-10 and COWC datasets were 34.59635 and 36.09257 dB, respectively. We can conclude from Table 3 that the network structure with both PCCS and HAM yields optimal SR reconstruction results.

Table 3.
Results of ablation study of PCCS and HAM. Bold indicates optimal performance.
The PCCS uses three convolution layers with different kernel sizes in parallel to obtain more non-redundant and extensive feature information from an image. Table 3 indicates that the PCCS component leads to performance gains (e.g., 0.03021 dB on NWPU VHR-10 and 0.04383 dB on COWC). This is mainly due to the PCCS, which makes the network flexible in processing feature information at different scales. Furthermore, we explored the influence of different convolution kernel settings in the PCCS components on the SR performance. Table 4 shows the experimental results of different convolution kernel settings with an upscaling factor of ×2. Broadly, the models with multiple convolutional kernels achieve better results than those with only a single convolutional kernel, and our PCCS obtains the best results owing to its three parallel progressive feature-purification branches.

Table 4.
Results of comparison experiments using different convolution kernel settings in the PID component. Bold indicates optimal performance.
HAM generates more balanced attention information by adopting a structure that has both channel and spatial attention mechanisms in parallel. Table 3 indicates that the PCCS component leads to performance gains (e.g., 0.01820 dB on NWPU VHR-10 and 0.04082 dB on COWC). To further verify the effectiveness of the proposed HAM, we compared HAM with the SE block [15] and CBAM [20]. The SE block comprises a gating mechanism that obtains a completely new feature map by multiplying the obtained feature map with the response of each channel. Compared to the SE block, CBAM includes both channel and spatial attention mechanisms, which requires the network to be able to understand which parts of the feature map should have higher responses at the spatial level. Our HAM also includes channel and spatial attention mechanisms however, CBAM connects them serially while HAM accesses these two parts in parallel and combines them with the input feature map in a residual structure. As can be seen from Table 5, the addition of attention modules can improve the performance to different degrees. The effects of the dual attention modules are better than that of the SE block, which only adopts a CAM. Moreover, compared with CBAM, our HAM component leads to performance gains (e.g., 0.01000 dB on NWPU VHR-10 and 0.00662 dB on COWC). This finding illustrates that connecting a SAM and CAM in parallel is more effective for feature discrimination. These comparisons show that HAM in our PIDAB is advanced and effective.

Table 5.
Results of comparison experiments using different attention modules. Bold indicates optimal performance.
4.2.5. Effect of Number of PIDABs
In this subsection, we report the results of adjusting the depth of the network by simply increasing the number of PIDAB. Specifically, numbers of PIDABs ranging from 4 to 20 were used. Figure 9 shows the performance with different numbers of PIDABs using the FastTest10 dataset in the epoch range 0 to 100. When simply increasing the value of N to 20, the improvement increases, and a gain of approximately 0.08 dB is achieved when compared to the basic network (N = 4) with a scaling factor of ×2, which demonstrates that the PIDAN can achieve a higher average PSNR with a larger number of PIDABs.
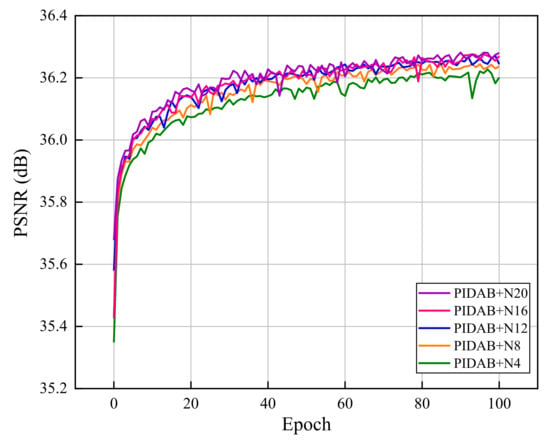
Figure 9.
Performance curve for PIDAN with different numbers of PIDABs using the FastTest10 dataset with a scale factor of ×2.
5. Conclusions
To achieve SR reconstruction of remote sensing images more efficiently, based on the IDN, we proposed a convenient but very effective approach named pyramid information distillation attention network (PIDAN). The main contribution of our work is the pyramid information distillation attention block (PIDAB), which is constructed as the building block of the deep feature-extraction part of the proposed PIDAN. To obtain more extensive and non-redundant image features, the PIDAB includes a pyramid information distillation module, which introduces a pyramid convolution channel split to allow the network to perceive a wider range of hierarchical features and reduce output feature maps, decreasing the model parameters. In addition, we proposed a hybrid attention mechanism module to further improve the restoration ability for high-frequency information. The results of extensive experiments demonstrated that the PIDAN outperforms other comparable deep CNN-based approaches and could maintain a good trade-off between the factors that affect practical application, including objective evaluation, visual quality, and model size. In future, we will further explore this approach in other computer vision tasks in remote sensing scenarios, such as object detection and recognition.
Author Contributions
Conceptualization, B.H. (Bo Huang); Investigation, B.H. (Bo Huang), and Y.L.; Formal analysis, B.H. (Bo Huang), Z.G., and B.H. (Boyong He); Validation, Z.G., B.H. (Boyong He), and X.L.; Writing—original draft, B.H. (Bo Huang); Supervision, L.W.; Writing—review & editing B.H. (Bo Huang) and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (no. 51276151).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments and helpful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Som-ard, J.; Atzberger, C.; Izquierdo-Verdiguier, E.; Vuolo, F.; Immitzer, M. Remote sensing applications in sugarcane cultivation: A review. Remote Sens. 2021, 13, 4040. [Google Scholar] [CrossRef]
- Glasner, D.; Bagon, S.; Irani, M. Super-resolution from a single image. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 349–356. [Google Scholar]
- Chang, H.; Yeung, D.; Xiong, Y. Super-resolution through neighbor embedding. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; pp. 275–282. [Google Scholar]
- Zhang, L.; Wu, X. An edge-guided image interpolation algorithm via directional filtering and data fusion. IEEE Trans. Image Process. 2006, 15, 2226–2238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, K.; Gao, X.; Tao, D.; Li, X. Single image super-resolution with non-local means and steering kernel regression. IEEE Trans. Image Process. 2012, 21, 4544–4556. [Google Scholar] [CrossRef] [PubMed]
- Protter, M.; Elad, M.; Takeda, H.; Milanfar, P. Generalizing the nonlocal-means to super-resolution reconstruction. IEEE Trans. Image Process. 2009, 18, 36–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freeman, W.; Jones, T.; Pasztor, E. Example-based super-resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef] [Green Version]
- Mu, G.; Gao, X.; Zhang, K.; Li, X.; Tao, D. Single image super resolution with high resolution dictionary. In Proceedings of the 2011 18th IEEE Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 1141–1144. [Google Scholar]
- Dong, C.; Loy, C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.; Lee, J.; Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NY, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photorealistic single image super-resolution using a generative adversarial network. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Zeng, K.; Yu, J.; Wang, R.; Li, C.; Tao, D. Coupled deep autoencoder for single image super-resolution. IEEE Trans. Cybern. 2017, 47, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Zhang, D.; Shao, J.; Li, X.; Shen, H.T. Remote sensing image super-resolution via mixed high-order attention network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5183–5196. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Hui, Z.; Wang, X.; Gao, X. Fast and accurate single image super-resolution via information distillation network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 723–731. [Google Scholar]
- Dun, Y.; Da, Z.; Yang, S.; Qian, X. Image super-resolution based on residually dense distilled attention network. Neurocomputing 2021, 443, 47–57. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y. CBAM: Convolutional Block Attention Module; Springer: Cham, Switzerland, 2018; p. 112211. [Google Scholar]
- Dong, C.; Loy, C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 391–407. [Google Scholar]
- Shi, W.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kim, J.; Lee, J.; Lee, K. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1637–1645. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X. Image super-resolution via deep recursive residual network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3147–3155. [Google Scholar]
- Lai, W.; Huang, J.; Ahuja, J.; Yang, M. Deep Laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 624–632. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image super-resolution using dense skip connections. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4809–4817. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar]
- Yu, J.; Fan, Y.; Yang, J.; Xu, N.; Wang, Z.; Wang, X.; Huang, T. Wide activation for efficient and accurate image super-resolution. arXiv 2018, arXiv:1808.08718. [Google Scholar]
- Ahn, N.; Kang, B.; Sohn, K.A. Fast, accurate, and lightweight super-resolution with cascading residual network. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 252–268. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 60–65. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Cao, Y.; Xu, J.; Lin, S.; Wei, F.; Hu, H. GCNet: Non-local networks meet squeeze-excitation networks and beyond. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshop, Seoul, Korea, 27–28 October 2019; pp. 1971–1980. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Zhong, B.; Fu, Y. Residual non-local attention networks for image restoration. arXiv 2019, arXiv:1903.10082. [Google Scholar]
- Anwar, S.; Barnes, N. Densely residual Laplacian super-resolution. arXiv 2019, arXiv:1906.12021. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Ma, S.; Guo, S. MAANet: Multi-view aware attention networks for image super-resolution. arXiv 2019, arXiv:1904.06252. [Google Scholar]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.-T.; Zhang, L. Second-order attention network for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11065–11074. [Google Scholar]
- Hui, Z.; Gao, X.; Yang, Y.; Wang, X. Lightweight image super-resolution with information multi-distillation network. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; Volume 10, pp. 2024–2032. [Google Scholar]
- Zhao, H.; Kong, X.; He, J.; Qiao, Y.; Dong, C. Efficient image super-resolution using pixel attention. arXiv 2020, arXiv:2010.01073. [Google Scholar]
- Wang, H.; Wu, C.; Chi, J.; Yu, X.; Hu, Q.; Wu, H. Image super-resolution using multi-granularity perception and pyramid attention networks. Neurocomputing 2021, 443, 247–261. [Google Scholar] [CrossRef]
- Huang, B.; He, B.; Wu, L.; Guo, Z. Deep residual dual-attention network for super-resolution reconstruction of remote sensing images. Remote Sens. 2021, 13, 2784. [Google Scholar] [CrossRef]
- Xia, G.-S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L. AID: A benchmark data det for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef] [Green Version]
- Cheng, G.; Zhou, P.; Han, J. Learning rotation-invariant convolutional neural networks for object detection in VHR optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7405–7415. [Google Scholar] [CrossRef]
- Mundhenk, T.N.; Konjevod, G.; Sakla, W.A.; Boakye, K. A large contextual dataset for classification, detection and counting of cars with deep learning. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 785–800. [Google Scholar]
- Horé, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the International Conference on Computer Vision, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Liu, J.; Tang, J.; Wu, G. Residual feature distillation network for lightweight image super-resolution. arXiv 2020, arXiv:2009.11551. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).