Abstract
Due to their great potential for a variety of applications, digital building models are well established in all phases of building projects. Older stock buildings however frequently lack digital representations, and creating these manually is a tedious and time-consuming endeavor. For this reason, the automated reconstruction of building models from indoor mapping data has arisen as an active field of research. In this context, many approaches rely on simplifying suppositions about the structure of buildings to be reconstructed such as, e.g., the well-known Manhattan World assumption. This however not only presupposes that a given building structure itself is compliant with this assumption, but also that the respective indoor mapping dataset is aligned with the coordinate axes. Indoor mapping systems, on the other hand, typically initialize the coordinate system arbitrarily by the sensor pose at the beginning of the mapping process. Thus, indoor mapping data need to be transformed from the local coordinate system, resulting from the mapping process, to a local coordinate system where the coordinate axes are aligned with the Manhattan World structure of the building. This necessary preprocessing step for many indoor reconstruction approaches is also frequently known as pose normalization. In this paper, we present a novel pose-normalization method for indoor mapping point clouds and triangle meshes that is robust against large portions of the indoor mapping geometries deviating from an ideal Manhattan World structure. In the case of building structures that contain multiple Manhattan World systems, the dominant Manhattan World structure supported by the largest fraction of geometries was determined and used for alignment. In a first step, a vertical alignment orienting a chosen axis to be orthogonal to horizontal floor and ceiling surfaces was conducted. Subsequently, a rotation around the resulting vertical axis was determined that aligned the dataset horizontally with the axes of the local coordinate system. The performance of the proposed method was evaluated quantitatively on several publicly available indoor mapping datasets of different complexity. The achieved results clearly revealed that our method is able to consistently produce correct poses for the considered datasets for different input rotations with high accuracy. The implementation of our method along with the code for reproducing the evaluation is made available to the public.
1. Introduction
The importance of digital models of building environments has been steadily increasing in recent years [1,2]. Currently, many building projects are planned digitally in 3D using Building Information Modeling (BIM) techniques [3]. Thus, a valid digital three-dimensional model arises along with the construction of the respective building, which can be profitably used during all the stages of its life cycle, i.e., usage and maintenance, e.g., in the context of facility management, changes and modifications of the building, and eventually, dismantling [4,5,6,7]. However, in the case of older, already existing buildings, three-dimensional digital models often do not exist and two-dimensional plans are often faulty or outdated. Manually reconstructing digital models (as-is BIM models) for such buildings is a tedious and time-consuming process [8,9].
However, there currently exists a broad range of sensor systems that can be deployed in the task of accurately mapping indoor environments [10,11,12,13]. Terrestrial Laser Scanners (TLSs), for instance, can provide a high geometric accuracy of acquisition depending on the respective conditions, e.g., in terms of surface characteristics and scanning geometry [14,15]. In order to achieve a complete capture of an environment, however, multiple scans have to be conducted from different positions. Especially in the case of mapping the interior of building structures, this can be quite cumbersome as the device needs to be set up at numerous positions, while the resulting scans subsequently need to be aligned in a common coordinate system.
Mobile mapping systems, however, alleviate these restrictions by continuously tracking their own position and orientation with respect to an initial pose. Indoor mapping geometries acquired over time can thus be projected successively into a common coordinate system while the operator can achieve a complete scene capture by walking through the scene. Mobile mapping systems encompass, e.g., trolley-based (such as NavVis (https://www.navvis.com/m6, accessed on 22 November 2021)) or backpack-mounted sensors [16,17,18,19], or even UAV-based systems [20], as well as hand-carried (e.g., Leica BLK2GO (https://blk2go.com, accessed on 22 November 2021)) or head-worn devices (e.g., Microsoft HoloLens (https://www.microsoft.com/de-de/hololens, accessed on 22 November 2021)). In particular, the Microsoft HoloLens designed as an Augmented Reality (AR) system offers the additional advantage of directly visualizing the already captured geometries within the view of the operator, facilitating the complete coverage of an indoor environment.
While conventional TLS or mobile laser scanning systems provide indoor mapping data in the form of point clouds, some consumer-grade systems such as, e.g., the mentioned Microsoft HoloLens or the Matterport system (https://matterport.com/, accessed on 22 November 2021), sometimes provide indoor mapping data in the form of preprocessed, condensed triangle meshes. Such triangle meshes being a derived product from the primary point-based measurements were found to still provide sufficient accuracy for a wide range of applications [21,22], while being significantly more compact in terms of data size and, thus, more efficient in terms of the required processing time.
This broad range of available indoor mapping systems can provide an ample database for the digital, three-dimensional reconstruction of built indoor environments. Instead of having to take individual distance measurements in the respective building or having to bridge the mental gap between conventional, two-dimensional floor plans and the three-dimensional modeling environment, indoor mapping data representing existent buildings can be loaded directly into the modeling environment. However, the manual digital reconstruction on the basis of indoor mapping data can still be a time-consuming endeavor. Hence, automating this process has become the focus of a currently quite active field of research [23,24,25].
While recent approaches in the field of automated indoor reconstruction are becoming more flexible regarding the building structure represented by the indoor mapping data [26,27,28,29,30,31], restricting assumptions about the building structure are still oftentimes applied. A frequently applied simplification in this context is the Manhattan World assumption, which was for instance relied on in the indoor reconstruction approaches presented in [32,33,34,35].
The Manhattan World assumption, as first proposed by Coughlan and Yuille [36,37], presupposes all surfaces to be perpendicular to one of the three coordinate axes. Applied to the context of building structures, this assumption thus prohibits curved room surfaces, as well as surfaces being oriented diagonally with respect to the main building structure, i.e., diagonal walls or slanted ceilings. The Manhattan World assumption was later extended to the Atlanta World assumption by Schindler and Dellaert [38], which weakens the Manhattan World assumption by permitting vertical surfaces to have arbitrary angles around a common vertical coordinate axis, while horizontal surfaces are still expected to be perpendicular to the vertical axis. Thus, an Atlanta World structure can be regarded as a composition of multiple Manhattan World structures varying by a rotation around a common (vertical) coordinate axis. Besides in the context of indoor reconstruction, the Manhattan World assumption, as well as the weaker Atlanta World assumption have been used in a range of other application fields such as point cloud segmentation [39,40,41], the extraction of road structures from low-resolution airborne imagery [42], or for stabilization and drift reduction in the context of Visual Odomentry (VO) [41,43,44] and Simultaneous Localization and Mapping (SLAM) [45,46,47,48].
The fact that a given indoor reconstruction approach relies on the Manhattan World assumption does not only imply that the building structure to be reconstructed itself must be compliant with the Manhattan World assumption. Rather, this also implies that the geometric representation of the respective building in the indoor mapping data must be correctly aligned with the coordinate axes in accordance with the definition of the Manhattan World assumption, i.e., that the surfaces pertaining to the three main directions (or six when considering oriented directions) are aligned with the three axes of the respective local coordinate system in which the data are given.
In the context of indoor mapping, however, the pose of the captured building structure with respect to the coordinate axes does not necessarily fulfill this requirement. Frequently, the local coordinate system is determined by the initial pose of the indoor mapping system at the beginning of the mapping process. Thus, the orientation of the indoor mapping data can deviate from the Manhattan World assumption by a rotation around the vertical coordinate axis even if the mapped building structure itself is totally compliant with the Manhattan World assumption. Moreover, the orientation of the vertical axis itself can also deviate from its optimal orientation according to the Manhattan World assumption, i.e., being perpendicular to horizontal ceiling and floor surfaces. This is generally not the case when a leveled mounting of the respective indoor mapping sensor is used, e.g., in the case of tripod-mounted systems such as TLS or trolley-based systems. In the case of hand-held or head-worn indoor mapping systems where a perfectly leveled orientation at the start of the indoor mapping process cannot be guaranteed, an eventual misalignment of the indoor mapping data with respect to the vertical coordinate axis needs to be taken into account.
Aligning the Manhattan World structure of an indoor mapping dataset with the local coordinate axes—horizontally and, depending on the used indoor mapping system, also vertically—is thus a necessary preprocessing step for automated indoor reconstruction approaches that rely on the Manhattan World assumption. Moreover, such an alignment process—also known as pose normalization [49]—can still be a reasonable choice, even if the respective indoor reconstruction method does not presuppose a Manhattan World-compliant building structure. This is for instance the case when a respective indoor reconstruction approach makes use of a voxel grid or octree representation of the input data [50,51,52,53]. Even if a voxel-based indoor reconstruction approach is able to handle building structures deviating from the Manhattan World assumption, having room surfaces aligned with the coordinate axes and thus with the voxel grid will result in a cleaner and visually more appealing reconstruction in the voxel space. Furthermore, spatially discretizing data that are not aligned with the coordinate axes can lead to aliasing effects, which can impede a successful reconstruction process [49,54,55]. Besides, pose normalization often—but not necessarily always, depending on the respective building structure—results in a minimal axis-aligned bounding box circumscribing the indoor mapping data and thus to the reduced memory size of the voxel grid structure.
Lastly, pose normalization of indoor mapping data can also be of benefit in the context of the coregistration of multiple datasets representing the same indoor environment that are to be aligned with each other [56,57,58]. The respective datasets to be aligned can be acquired by different sensor systems or at different times, e.g., in the context of change detection [59,60,61]. While pose normalization with respect to a Manhattan World structure does not entirely solve this problem as the ambiguity of rotations of multiples of 90 around the vertical axis remains, it nonetheless can be reasonable to apply pose normalization when coregistering indoor mapping datasets as it reduces the problem to finding the correct one of only four possible states per dataset.
The same arguments speaking in favor of pose normalization—even if an indoor reconstruction approach does not necessarily depend on it—also hold true for the case of building structures that are only partly compliant with the Manhattan World assumption. Thus, a pose normalization approach should be robust against a substantial amount of the given indoor mapping geometries deviating from the Manhattan World structure of the building. Particularly in the case of building environments that contain multiple Manhattan World structures with different orientations with respect to rotations around a common vertical axis (i.e., Atlanta World), the dominant Manhattan World structure (e.g., in terms of the largest fraction of supporting geometries) should be used for alignment with the coordinate axes. In situations where multiple Manhattan World structures have about the same support, it might be reasonable to detect them all and create multiple solutions for a valid pose normalization.
In a more general context, a range of pose normalization approaches has been presented, which aim at aligning arbitrary three-dimensional objects with the coordinate axes. In this case, the concerned objects do not necessarily represent building structures [62,63,64,65,66,67,68,69]. These approaches are mainly motivated by the need to design rotation-invariant shape descriptors in the context of shape retrieval, i.e., finding all similar three-dimensional objects to a given query shape from a large database of 3D objects [70,71].
In this context, variations of the Principal Component Analysis (PCA) algorithm [72] are often used [62,63,64,67]. Furthermore, symmetries in the geometry of the respective object are often exploited as well [64,65,67]. Other approaches rely on the geometric property of rectilinearity [66,68] or aim to minimize the size of a surface-oriented bounding box circumscribing the target object [69].
More specifically concerning building structures, a recent pose normalization approach makes use of point density histograms, discretizing and aggregating the points of an indoor mapping point cloud along the direction of one of the horizontal coordinate axes [49,54]. The optimal horizontal alignment of the point cloud is determined by maximizing the size and distinctness of peaks in this histogram varying with the rotation around the vertical axis.
Other approaches, including the one proposed in this paper, do not discretize the data with respect to their position, but with respect to their orientation [73,74,75,76]. This is conducted on the Extended Gaussian Image (EGI) [77], which consists of the normal vectors of the individual indoor mapping geometries projected on the unit sphere. Besides its application in the context of pose normalization, the EGI is also frequently applied to the segmentation of point clouds [39,41,78,79,80] or plane detection [81], in particular with regard to building structures.
In a straightforward approach, for instance, the points in the EGI are subjected to a k-means clustering [82,83] to determine three clusters corresponding to the main directions of the Manhattan World structure, while disregarding the absolute orientation of the normal vectors (i.e., projecting them all in the same hemisphere) [74,75]. This, however, is not robust to deviations of the indoor mapping point cloud from an ideal Manhattan World structure. In contrast, using DBSCAN [84] for clustering on the EGI has been proposed [76], which is more robust, as it does not fix the number of clusters to exactly three. This allows for the presence of surfaces deviating from an ideal Manhattan World system. The proposed approach however only aims at detecting dominant planes to remove them from the point cloud and does not assemble the detected orientation clusters into Manhattan World structures. In another approach, dominant horizontal directions are detected by projecting the normal vectors to the horizontal plane and binning the resulting angles to a horizontal reference coordinate axis in a similar manner to the approach presented in this paper [73].
All of the approaches mentioned above only concern themselves with determining an orientation around the vertical axis to achieve an alignment of the Manhattan World structure of an indoor mapping dataset with the axes of a reference coordinate system. To the best of our knowledge, no approach to pose normalization of indoor mapping point clouds or triangle meshes has yet been proposed that aims at determining an optimal alignment with respect to the orientation of the vertical axis as well. Furthermore, the presented approaches do not address the topic of robustness to deviations of the respective building structure from an ideal Manhattan World scenario or the presence of multiple Manhattan World structures in the same building.
In this work, we present a novel pose-normalization method for indoor mapping point clouds and triangle meshes that is robust to the represented building structures being only partly compliant with the Manhattan World assumption. In case there are multiple major Manhattan World structures present in the data, the dominant one is detected and used for alignment. Besides the horizontal alignment of the Manhattan World structure with the coordinate system axes, vertical alignment is also supported for cases where the deployed indoor mapping system is not leveled and the resulting dataset is thus misaligned with respect to the vertical coordinate axis. In this context, we presumed that the indoor mapping dataset is coarsely leveled to within ±30° of the optimal vertical direction, which can usually be expected to be the case for hand-held or head-worn mobile indoor mapping systems. We furthermore presupposed the individual indoor mapping geometries to have normal vectors, which however do not need to be consistently oriented and can thus be easily determined as a preprocessing step for point clouds, while triangle meshes already have normal vectors inherent in the geometries of the individual triangles. Our implementation of the proposed pose normalization approach along with the code for the presented quantitative evaluation on publicly available indoor mapping datasets is made available to the public at https://github.com/huepat/im-posenorm (accessed on 22 November 2021).
The presented approach for pose normalization is described in Section 2 along with a method to resolve the ambiguity of a rotation of multiples of 90 around the vertical axis and the procedure applied for the quantitative evaluation. The results of this evaluation procedure applied to several publicly available indoor mapping point clouds and triangle meshes are subsequently presented in Section 3 and discussed in detail in Section 4. Finally, in Section 5, we provide concluding remarks and an outlook for future research.
2. Materials and Methods
In this section, we present a novel method for automatic pose normalization of indoor mapping point clouds or triangle meshes that represent building structures that are at least partially compliant with the Manhattan World assumption. The presented method aims at rotating the given indoor mapping geometries to a pose with respect to the surrounding coordinate system for which the largest possible fraction of normal vectors is aligned with the three Cartesian coordinate axes. This comprises an optional leveling step to orient horizontal surfaces such as floors and ceilings to be orthogonal to a chosen vertical axis if this is not already achieved by the data-acquisition process (e.g., by using leveled tripod or trolley-mounted acquisition systems). Subsequently, a second step determines the optimal rotation angle around this vertical axis in order to align the largest possible fraction of the building surfaces with the horizontal pair of orthogonal coordinate axes. The workflow of the proposed method is visually summarized in Figure 1.
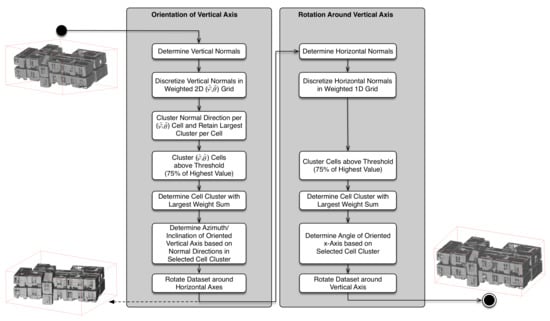
Figure 1.
Overview of our pose-normalization method as described in Section 2. The depicted triangle mesh is the dataset “Office” from [31].
The presented method is applicable to all kinds of indoor mapping point clouds and triangle meshes. However, we assumed the individual geometric primitives comprising the input data to have normal vectors. While these are intrinsically given for the individual triangles comprising a triangle mesh, the individual points of indoor mapping point clouds do not generally have normal vectors. These can however be easily determined by means of established methods such as in [85,86,87,88], which we assumed in this work as a necessary preprocessing step. Note that these normal vectors need not be oriented, i.e., pointing consistently towards the inside or outside of the building. Determining such oriented normals for indoor mapping point clouds is a more complex task compared to just determining unoriented normals based on local neighborhoods [89]. However, as normal vectors contribute to the same Manhattan World structure regardless of their orientation, only their direction is of importance. Furthermore, we assumed the input data to be at least coarsely leveled, i.e., we assumed the represented building structures to be coarsely aligned with the vertical axis within the range of ±30.
In the following, denotes the i-th normal vector of N given input geometries (i.e., points or triangles), while, in the scope of this paper, denotes the dot product of two 3D vectors. Furthermore, the vector determining the initial vertical axis of the coordinate system in which the indoor mapping data are represented is denoted by , while the initial horizontal axes are denoted by and . The orientation of these initial axes in the input data is however only vertical/horizontal within ±30 w.r.t. the represented building geometry. Aligning these axes of the local coordinate system with the building geometry in such a way that is optimally vertical w.r.t. the building is the aim of the presented method.
Different indoor mapping systems use different definitions of the respective local coordinate system, i.e., the axis need not necessarily equal (with denoting the transpose operation in the scope of this paper). Thus, the vectors of the and axes are to be chosen by the user as an input parameter to the presented method. The chosen vectors are checked for orthogonality, and is determined as:
In the following, Section 2.1 first presents the proposed method for determining an optimal rotation around the vertical axis in order to horizontally align the indoor mapping data with the coordinate system in case the dataset is already vertically aligned in relation to the vertical axis. A suitable method for ensuring this vertical alignment that can be applied as a preprocessing step to datasets that are only coarsely aligned with the vertical direction (±30) is subsequently presented in Section 2.2. As the proposed method for determining the rotation around the vertical axis is ambiguous with regard to multiples of 90, Section 2.3 presents an approach to solve this ambiguity. Lastly, Section 2.4 presents the evaluation methodology applied in this study, and Section 2.5 gives an overview of the datasets used for the evaluation.
2.1. Rotation around the Vertical Axis
In this section, we preliminarily assumed that the given indoor mapping data (comprised of triangles or points) is already leveled with regard to a chosen vertical axis (that does not necessarily need to equal ). Thus, only one rotation angle around this vertical axis is to be determined in order to align the two horizontal axes of the coordinate system with the horizontal directions of the dominant Manhattan World structure underlying the respective building represented by the input data.
In case the given input data are not entirely compliant with the Manhattan World assumption, a best-possible solution in terms of the alignment of all normal vectors with the horizontal coordinate axes is to be found. Even indoor mapping data that represent building structures entirely compliant with the Manhattan World assumption can have a significant amount of normal vector directions deviating from the directions of the respective Manhattan World system. These deviating normal vector directions can be caused by the actual unevenness of walls, by noise inherent in the data acquisition and normal determination, as well as by clutter such as furniture objects being present in the indoor mapping data, in addition to the building structure itself.
Besides being robust against these restrictions, the presented method is also applicable to building structures that are only partially Manhattan World conforming. Building structures with multiple Manhattan World systems such as the one depicted in Figure 2 are aligned according to the respective Manhattan World system supported by the largest fraction of normal vector directions.
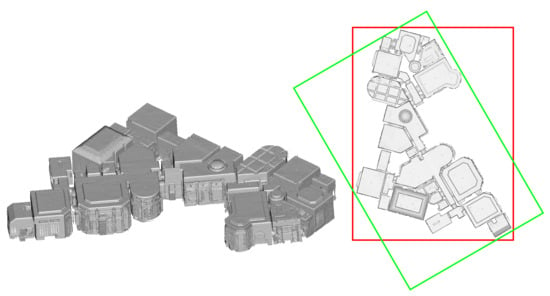
Figure 2.
Exemplary triangle mesh of a building with multiple Manhattan World systems (dataset “mJXqzFtmKg4” from Matterport3D [90]). The green bounding box on the top-down-view on the right-hand side illustrates the alignment along the dominant Manhattan World structure, considered as the ground truth pose, while the red bounding box illustrates the pose rotated by 30 around the vertical axis, as exemplarily used in Section 2.1.
Thus, the task at hand is to determine an angle of rotation around the vertical axis that leads to the largest positive fraction of normal vectors being aligned with the horizontal axes and . To this aim, we first filtered the normal vectors that can be considered coarsely horizontal with respect to the vertical axis . For this, we considered all normal vectors that are within the range of ±45 of a horizontal orientation; thus:
where denotes the smallest angle between two 3D vectors. For the indoor mapping mesh depicted in Figure 2, the corresponding horizontal normal vectors are depicted in the form of an extended Gaussian image in Figure 3. In this example, the triangle mesh of Figure 2 is rotated by 30 around the vertical axis relative to the ground truth pose aligned with the dominant Manhattan World structure.
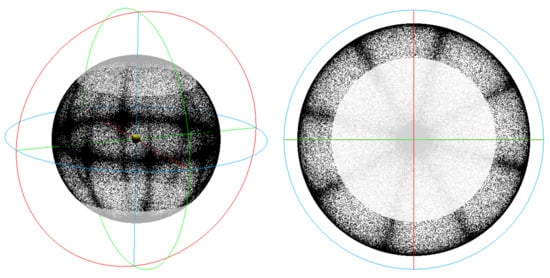
Figure 3.
The normal vectors of the triangle mesh shown in Figure 2 visualized as an extended Gaussian image (thinned out by a factor of 25 for the sake of visibility). The normal vectors that are horizontal within the range of ±45 are visualized in black, while the others are visualized in gray. The coordinate axes are visualized in red for , green for , and blue for the vertical axis .
These horizontal normal vectors can subsequently be projected to the horizontal plane formed by the horizontal axes and by:
where their respective angles to the reference direction of around as the axis of rotation:
can be determined.
The problem at hand can be formulated as determining the rotation angle around the vertical axis that minimizes the sum of angular distances of each horizontal normal vector to the respectively nearest horizontal coordinate axis, i.e.,
Here, the angular distances of each angle to the nearest horizontal axis are weighted by factor . This factor can be constantly set to 1 for the points of an indoor mapping point cloud. In the case of triangle meshes, however, it allows weighing the individual triangles by their respective area, as larger triangles imply a larger quantity of points in a corresponding point cloud representation.
Equation (5) is not analytically solvable. It can however be solved numerically by derivative-free minimization methods such as, e.g., Brent minimization [91]. This, however, does not scale well with the size of the input data, as all the angles derived from the horizontal normal vectors need to be iterated in each step of the respective numeric method. Particularly in the case of indoor mapping point clouds, the amount of geometric primitives and thus of angles to be processed can reach a tremendous size.
Consequently, in this work, we propose an approach that discretizes the input data into a one-dimensional grid of fixed resolution by means of which the angle of rotation for aligning the input data with the horizontal coordinate system can be determined noniteratively in one step. In this context, a resolution of 1 proved to be suitable for a coarse initial determination of the rotation angle for horizontal alignment, which can subsequently be refined. For each angle , the respective grid cell is determined, which is incremented by the respective weight , which again is constantly 1 for points of point clouds, but in the case of triangle meshes, weights the respective angle by the area of the corresponding triangle.
Figure 4 visualizes such a one-dimensional grid representation of the horizontal angles over the full circle of 360 for the mesh presented in Figure 2. The peaks in the summarized weights per grid cell correspond to the eight horizontal main directions of the two Manhattan World systems present in the dataset depicted in Figure 2.
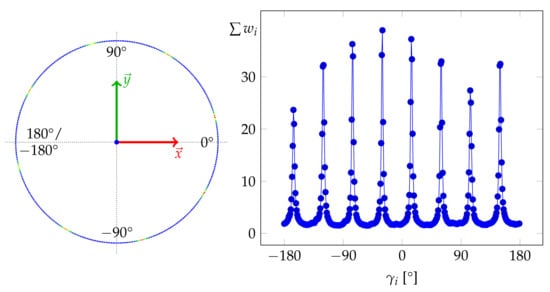
Figure 4.
Visualization of a one-dimensional 360 grid corresponding to Figure 2. The grid cells contain the summarized weights of the contained angles with value colorization ranging from blue for low values over green and yellow to red for large values.
To decide about the dominance of the two Manhattan World systems involved and to determine the corresponding rotation angle for an alignment of the input data with it, the weights of the involved grid cells need to be summarized over all peaks pertaining to the same Manhattan World system. To this end, the peaks belonging to the same Manhattan World system and thus having an angular difference of a multiple of 90 between each other need to be identified and associated. Thus, we map the angles to by:
and:
The discretized grid representation of the angles thus needs only a quarter of the size in comparison to discretizing the angles with the same resolution. Furthermore, the resulting grid as visualized in Figure 5 enables the coarse initial determination of the rotation angle . To this end, the weight sums per grid cell are thresholded with a threshold value of 0.75-times the maximal weight sum of the whole grid and subsequently clustered. While clustering, the fact that clusters can extend over the discontinuity between 0 and 90 needs to be taken into account.
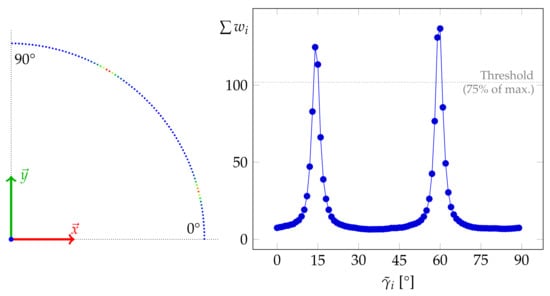
Figure 5.
Visualization of a one-dimensional 90 grid corresponding to Figure 2. The grid cells contain the summarized weights of the contained angles with value colorization ranging from blue for low values over green and yellow to red for large values.
Finally, the grid cell cluster with the largest weight summarized over the contained cells is selected, and is determined as the weighted average of the angle values corresponding to the cluster cells (with 1 resolution) weighted by their respective weight sum values. Figure 6a shows the horizontal triangle mesh faces of Figure 2 corresponding to the largest peak at 60 in Figure 5 that determines the dominant Manhattan World system of that dataset. The faces corresponding to the second peak at 15 in Figure 5 are visualized in Figure 6b.

Figure 6.
The horizontal faces of the triangle mesh presented in Figure 2 corresponding to the horizontal normal vectors . The faces corresponding to the two peaks shown in Figure 5 are depicted in red. (a) Faces corresponding to the largest peak at 60 in Figure 5 determining the dominating Manhattan World structure. (b) Faces corresponding to the minor peak at 15 in Figure 5.
The resulting value for can subsequently be further refined by determining the weighted median over all within a certain angular distance of the initial value for while applying the weights . A threshold of 5 was found to be suitable for this task.
Finally, the indoor mapping data can be rotated by the thusly refined angle around the vertical axis to achieve the alignment of the building geometry with the horizontal coordinate axes. In the case of a triangle mesh, it is sufficient to rotate the vertices of the triangles, as the respective normal vectors of the rotated triangles can be calculated on the basis of the triangle geometry. In the case of point clouds, however, the respective normal vectors of the points need to be explicitly updated along with the coordinates of the points.
2.2. Orientation of the Vertical Axis
In the preceding Section 2.1, the rotation around the vertical axis was determined under the assumption that the vertical axis is perfectly leveled with respect to the building structure, i.e., that it is orthogonal to horizontal floor and ceiling surfaces. In the case of tripod-mounted indoor mapping systems such as terrestrial laser scanners, this assumption is justified as these devices are typically leveled before usage. However, in the case of mobile indoor mapping systems such as hand-held or head-worn devices, this is generally not the case. In these cases, the coordinate system of the indoor mapping data is often defined by the initial pose of the mobile mapping device when starting the data acquisition process. In consideration of the typical usage postures of such mobile systems, it can be assumed that the respective vertical axis of the coordinate system is still roughly pointing upwards within the range of ±30. If this is not the case, a coarse leveling within this range can easily be conducted manually.
To justify the assumption made in the previous section, this section presents an approach for automatically leveling indoor mapping point clouds or triangle meshes where a chosen vertical axis corresponds coarsely within ±30 with the actual upwards direction of the building structure standing orthogonally on horizontal floor surfaces. As in the preceding section, the input data for conducting this alignment of the input mapping data with the coordinate system are again the N normal vectors of the individual geometric primitives comprising the indoor mapping data (i.e., points or triangles).
Analogous to Equation (5), we can formulate the task of vertically aligning the indoor mapping geometries with the coordinate system axis as:
where are the normal vectors that are vertically oriented within the range:
and again is a weighting factor, being constant for points of a point cloud, but corresponding to the respective triangle area for the faces of a triangle mesh. Furthermore, denotes a rotation matrix determined by two rotation angles and around the two horizontal coordinate axes and , respectively. Note that in Equation (9), we use an angular range of for filtering vertical normal vector directions, which is larger than the assumed range of the coarse initial leveling of the input data within . This wider angular range was applied because the horizontal building surfaces that are initially leveled within can have a certain amount of variation in the directions of the respective normal vectors in noisy indoor mapping data, as acquired for instance with the Microsoft HoloLens.
The aim of Equation (8) is to find the optimal vertical axis as a vector:
in the initially given coordinate system that has a minimal sum of angles to the vertical normals . This optimal vertical axis , as well as the initial vertical axis are exemplarily depicted in Figure 7 for a building with slanted ceilings only coarsely aligned with the actual vertical direction.
Figure 7.
Exemplary triangle mesh of a building with a partially slanted ceiling (dataset “Attic” from [31]). The green line visualizes the reference orientation of the vertical axis considered as the ground truth, while the red line visualizes the vertical axis rotated by around the horizontal axis and by 15 around the horizontal axis, as exemplarily used in Section 2.2.
As already was the case with Equation (5) in Section 2.1, Equation (8) is not analytically solvable. Solving Equation (8) numerically is even more inefficient than in the case of Equation (5), as here, a two-dimensional minimization is concerned. Thus, as in the case of determining the rotation angle around the vertical axis in Section 2.1, we again sought to formulate the problem at hand as the task of searching a maximum peak within a discrete grid representation of the relevant input elements.
The relevant input elements in this case are the three-dimensional vertical normal vectors . However, the problem at hand is actually two-dimensional, as a rotation around the two horizontal axes and by the rotation angles and is sufficient for aligning the vertical axis with the optimal vertical direction .
In an alternative formulation, this can also be considered as the task of finding the position of the optimal vertical direction on the surface of a unit sphere, i.e., within the extended Gaussian image. The orientation of a normal vector with respect to the coordinate system can be expressed via the polar angles’ azimuth:
and inclination:
indicating the position of a respective normal vector on the unit sphere. The definition of the azimuth and inclination with respect to the coordinate system is further illustrated in Figure 8.
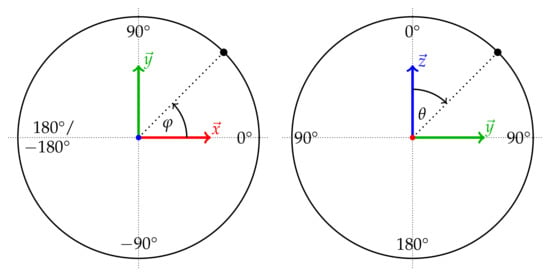
Figure 8.
Azimuth and inclination .
This representation allowed us to construct a two-dimensional azimuth/inclination grid analogous to the approach presented in Section 2.1, whose cells are weighted by the summarized weights of the contained normal vectors . Such a grid of a resolution of 1 extending over the whole unit sphere is depicted in Figure 9, corresponding to the exemplary case presented in Figure 7.
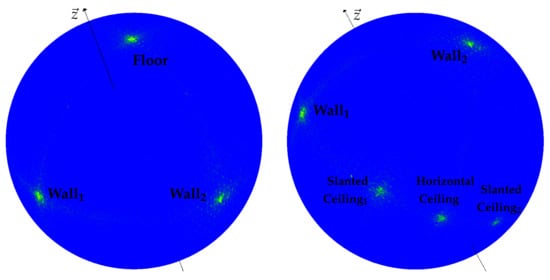
Figure 9.
Azimuth/inclination grid of a 1 resolution over the whole surface of the unit sphere corresponding to Figure 7. The grid cells contain the summarized weights of the contained normal vectors at polar angles with value colorization ranging from blue for low values over green and yellow to red for large values.
As before in Section 2.1, we wanted to transform this grid over the full range of the sphere surface to a smaller grid where the weights of cells pertaining to opposing normal vectors become accumulated. This is achieved by:
and:
while restricting the extension of the grid in the dimension of the inclination to the range of and, thus, only considering the vertical normal vectors . A schematic visualization of this transformation is depicted in Figure 10a, while Figure 11 shows the resulting two-dimensional azimuth/inclination grid corresponding to the dataset presented in Figure 7.
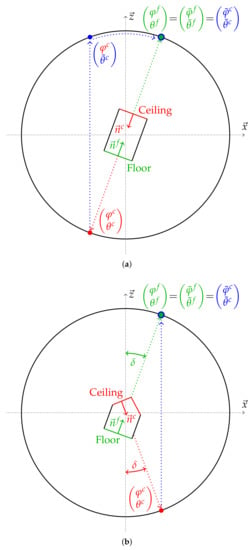
Figure 10.
Transformation of positions on the whole unit sphere to positions on one-eighth of the unit sphere by Equations (13) and (14). (a) Generally, points corresponding to opposing normal vectors are transformed to the same point. (b) In case the vertical axis is the angle bisector between the directions of two normal vectors (same angle to the axis), these are transformed to the same point even if they are not opposed. This needs to be dealt with by means of a cluster analysis per grid cell.
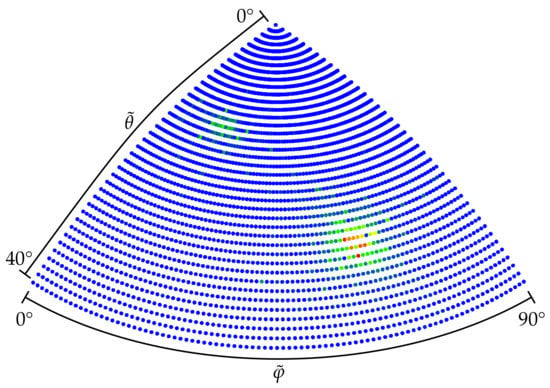
Figure 11.
Transformed azimuth/inclination grid of a 1 resolution corresponding to Figure 7. The grid cells contain the summarized weights of the contained vertical normal vectors at polar angles with value colorization ranging from blue for low values over green and yellow to red for large values. The larger peak corresponds to the floor and the horizontal part of the ceiling, while the minor peak corresponds to one of the slanted ceiling surfaces.
Subsequently, peaks with cell grid weights above a threshold of 75% of the highest weight value are again clustered as in the case of the one-dimensional grid of Section 2.1. While doing so, however, not only the azimuth discontinuity between 0 and 90 needs to be considered, but also the pole point at a 0 inclination, where all azimuth values merge into one and the same grid cell.
While in the case of the one-dimensional grid of Section 2.1, the grid cell indices could be directly mapped to the angles by multiplication with the grid resolution, here, it is not possible to infer the direction of the optimal vertical axis from grid cell indices as the transformed azimuth values are ambiguous by multiples of 90. This ambiguousness also exists in Section 2.1. However, it did not affect the correctness of the resulting horizontal alignment, as the case here.
Thus, to be able to deduce correct directions from peaks in the two-dimensional grid, the respective normal vectors need to be hashed per grid cell. Therefore, the correct direction of the vertical axis can be initialized by a weighted average of all the hashed normal directions weighted by their respective value of the cluster with the largest summarized weight. In doing so, normal vectors pointing downwards need to be corrected by inverting the direction to point upwards when calculating the weighted average vector. As in Section 2.1, the initial result is further refined by a weighted median of all normal vectors within ±5 of the coarsely determined resulting vertical axis.
Besides the need to deduce the correct direction from the detected maximum peak grid cells, there is a second reason to hash normal directions per grid cell. As illustrated in Figure 10b, two normal vectors that are oriented by the same angle around the vertical axis in a way that the axis is the angle bisector between both normals become projected to the same grid cell by Equations (13) and (14). On the one hand, this can distort the weight sums of the individual grid cells that are used for peak detection. On the other hand, the presence of normal vectors with deviating orientations beyond the ambiguity of ±180 between opposing surfaces can severely distort the initial determination of the vertical direction from the largest peak in the grid.
For this reason, a cluster analysis was conducted among the hashed normal vectors per grid cell. In doing so, all the normal vectors in a grid cell are assigned to clusters. A normal vector can be assigned to an existing cluster if its direction coincides within ±2 with the average direction of the cluster (with the consideration of an ambiguity of ±180). Else, the respective normal vector initializes a new cluster. Finally, for each grid cell, only the largest cluster of normals is retained, while the others are discarded. The grid cell weights and the hashed normal vectors are adapted accordingly.
2.3. Unambiguousness of the Rotation around the Vertical Axis
The alignment of indoor mapping point clouds or triangle meshes along the coordinate axes as described in the preceding Section 2.1 and Section 2.2 is ambiguous with respect to a rotation around the vertical axis by multiples of 90. This is per se not a problem, as the aim of the presented approach is to align the indoor mapping data with respect to their Manhattan World structure, which inherently implies this ambiguity of four possible rotations around the vertical axis, i.e., all four possible result poses are equally valid in hindsight for the stated aim.
However, in some situations, it can be desirable to derive an unambiguous pose of the indoor mapping data. For instance, this can be the case when multiple indoor mapping results of the same building environment are to be aligned by the proposed method. These multiple datasets of the same building can, e.g., be obtained by different indoor mapping systems or be acquired at different times in the context of change detection.
For this reason, we present a simple method for resolving the ambiguity in the rotation around the vertical axis by reproducibly choosing one of the four possible horizontal orientations. The proposed method presents a straightforward solution that does not require any semantic interpretation of the indoor mapping data or any elaborate analysis. It can however fail in cases of building layouts that are highly symmetric with respect to the four inherent Manhattan World directions. We furthermore presupposed that two datasets to be aligned unambiguously by this method cover approximately the same section of an indoor environment. If this is not the case, an approach that incorporates semantic knowledge of the represented indoor environment would be more promising. In this context, constellations of detected openings such as doors or windows could, for instance, be used.
Currently, however, we propose to resolve the unambiguousness between the four possible horizontal orientations by first aligning one of the two possible horizontal Manhattan World directions with the chosen reference axis that corresponds to a larger extent of the bounding box of the respective dataset in this horizontal direction, i.e., the longer horizontal edges of the bounding box should be parallel with the axis. This is quite straightforward, but can fail in cases where the bounding box is nearly quadratic.
The ambiguity is now reduced to a rotation of 180. To resolve this, we propose to consider the weighted count of indoor mapping geometries in both proximal 10% sections of the bounding box in the direction and to choose the rotation for which the proximal 10% section of the bounding box pointing towards the positive axis has the higher weight sum. In this context, the indoor mapping geometries are again weighted by a constant in the case of points of point clouds and by the triangle area in the case of triangle mesh faces. This approach will fail when the amount of mapped indoor structures in both proximal sections of the bounding box along the axis are about equal.
2.4. Evaluation Method
Quantitatively evaluating the proposed method is fortunately quite straightforward, as ground truth data can be easily obtained. If an indoor mapping dataset is not already correctly aligned with the coordinate system axes in the sense of the aim of this study, it can be aligned manually without great effort. A thusly aligned dataset can then be rotated to an arbitrary pose within the defined range applicable for the presented method. For this, a ground truth rotation matrix is created, determined by the rotation angles around the horizontal axes and , respectively, and an arbitrary rotation around the vertical axis . To create , the rotation by around the vertical axis is applied first and then successively the rotations by and around the respective horizontal axis.
Finally, the method presented in Section 2.1 and Section 2.2 is applied to the rotated dataset, which should return the rotated dataset back to its aligned state. The resulting rotation matrix is constituted by:
where first is determined by aligning the rotated dataset vertically with the vertical axis as described in Section 2.2, and subsequently, the rotation around the vertical axis is determined as described in Section 2.1.
As an evaluation metric, the angular difference between the vector of the ground truth axis and the resulting vector:
is determined by:
as well as the analogous angular difference for the horizontal axis . In case of horizontal deviation , the ambiguity of valid rotations around the vertical axis by multiples of 90 needs to be considered. To this aim, we iteratively applied:
until .
The proposed evaluation metrics and can be determined for multiple randomly chosen rotations within the mentioned ranges of for the horizontal axes and for the vertical axis in sufficient quantity to allow for a statistical analysis.
2.5. Used Materials
For evaluation purposes, a range of different publicly available datasets of varying complexity were considered. Firstly, the four triangle meshes of the dataset presented in [31] were used to this aim. These triangle meshes are depicted in Figure 12 along with 3D bounding boxes indicating their respective ground truth pose. They were acquired by means of the augmented reality headset Microsoft HoloLens, providing coarse triangle meshes of its indoor environment. In studies evaluating this device for the use case of indoor mapping, its triangle meshes were found to be accurate in the range of a few centimeters in comparison to ground truth data acquired by a terrestrial laser scanner [92,93,94].
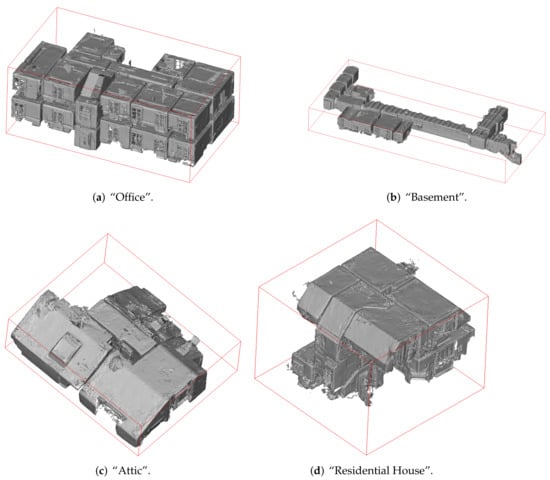
Figure 12.
The Microsoft HoloLens triangle meshes published in [31] and used for evaluation in this paper. The red box indicates the aligned ground truth pose.
The poses in relation to the local coordinate system of these datasets as they are published were determined by the pose-normalization procedure presented here. Thus, for evaluation purposes, we manually aligned the datasets with the axes of the local coordinate system and used these manually derived poses as the ground truth within the scope of the evaluation presented here.
All four represented indoor environments show a clearly defined Manhattan World structure. While the dataset “Office” has mostly horizontal ceiling surfaces with the exception of the stairwell, the datasets “Attic” and “Residential House” datasets have slanted ceiling surfaces. The dataset “Basement”, on the other hand, shows a range of different barrel-shaped ceilings.
Furthermore, the six indoor mapping point clouds of the ISPRS Indoor Modeling Benchmark dataset presented in [95,96] were used for evaluation purposes. These point clouds as visualized in Figure 13 were acquired by means of different indoor mapping systems with a broad variety of sensor characteristics regarding accuracy and noise. Furthermore, the represented indoor environments are characterized by varying amounts of clutter.
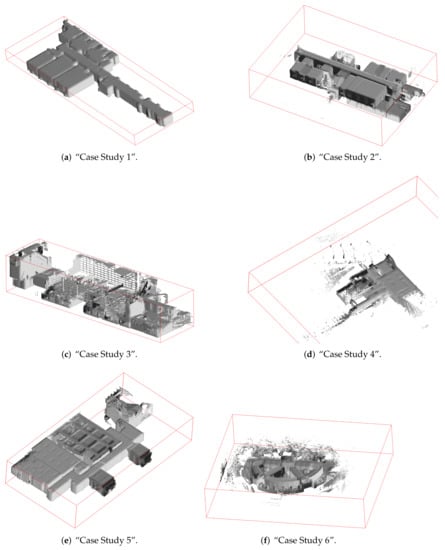
Figure 13.
The point clouds of the ISPRS Indoor Modeling Benchmark dataset [95,96] used for evaluation. The red box indicates the aligned ground truth pose.
While the other five datasets mostly adhere to the Manhattan World assumption, the dataset “Case Study 6” has a high amount of horizontally curved wall surfaces and rooms oriented diagonally with respect to the dominant Manhattan World structure defined by three rooms. Furthermore, the point cloud includes a part of the surrounding outdoor terrain with uneven topography and vegetation. As the dataset “Case Study 6” is quite challenging with respect to the aim of this work, it is depicted in more detail in Figure 14.
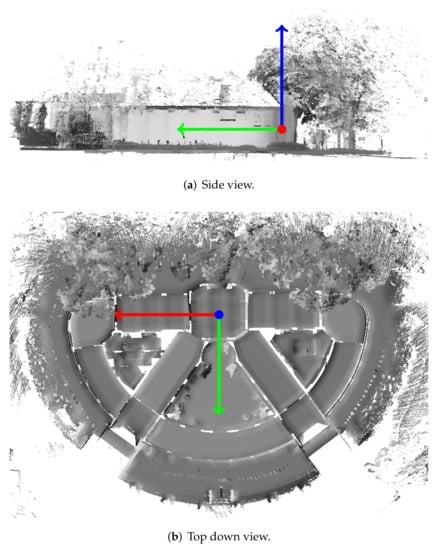
Figure 14.
Detailed visualization of the dataset “Case Study 6” from the ISPRS Indoor Modeling Benchmark dataset [96], also depicted in Figure 13f. The depicted axes represent the pose w.r.t. the local coordinate system as resulting from the proposed approach. The vertical axis is visualized in blue, while the two horizontal axes aligned with the dominant Manhattan World structure of the building are depicted in red and green, respectively. Note that, despite the large amount of uneven terrain, vegetation, and building structure deviating from the Manhattan World assumption, the building is aligned w.r.t. the three rooms with the Manhattan World structure.
The point clouds of the ISPRS benchmark dataset as they are published are already aligned with the coordinate axes, in accordance with the aim of this work. Thus, the poses of the point clouds could directly be used as ground truth poses without any manual adjustment. Contrary to triangle meshes, however, point clouds do not intrinsically provide a normal vector per point. Instead, the normal vector can be calculated for each point from a subset of respectively neighboring points. This is also the case with the point clouds of the ISPRS Indoor Modeling Benchmark. We thus computed normal vectors for the points after subsampling the point clouds with a resolution of 2 cm using CloudCompare 2.10-alpha [97] (subsampling method “Space” with 2 cm as the minimal space between points for subsampling and surface approximation “Plane” with default parameters for normal estimation).
Lastly, we also considered some triangle meshes from the Matterport3D dataset [90]. Matterport3D includes 90 triangle meshes of various kinds of indoor environments acquired with the trolley-mounted Matterport indoor mapping system consisting of multiple RGBD cameras. Among the represented indoor environments are some for which the proposed alignment approach is not applicable, as they are not subject to any clearly identifiable Manhattan World structure. Many others do have a clearly identifiable Manhattan World structure, but are to a large extent comparable to general building layouts already covered by the HoloLens triangle meshes or ISPRS point clouds used in the scope of this evaluation.
We thus selected 14 triangle meshes from the Matterport3D dataset that we deemed particularly interesting and challenging in the context of pose normalization. This, for instance, comprises triangle meshes representing indoor environments that contain more than one underlying Manhattan World system, such as the one already presented in Figure 2. In these cases, the presented alignment method is supposed to align the triangle mesh with the most dominant of the Manhattan World structures at hand being supported by the largest fraction of geometries. The 14 selected triangle meshes from the Matterport3D dataset are depicted in Figure 15.

Figure 15.
The triangle meshes of the Matterport3D dataset [90] used for evaluation. The red box indicates the aligned ground truth pose.
As with the ISPRS benchmark point clouds, we again treated the poses of the triangle meshes as they are published as ground truth alignments without any manual adjustments. To what extent this decision is justified will be discussed in Section 4.
3. Results
In order to quantitatively evaluate the approach presented in Section 2.1 and Section 2.2, the evaluation procedure proposed in Section 2.4 was applied to the indoor mapping datasets introduced in Section 2.5.
The different datasets used in the scope of this evaluation are listed in Table 1 along with the respective number of points or triangles and the respective evaluation results. To conduct the evaluation, the evaluation procedure was applied to the individual datasets. In doing so, each dataset was rotated 50 times, while each time, the respective rotation consisted of a randomly determined rotation angle around the vertical axis and two random rotations around the respective horizontal coordinate axes.

Table 1.
Evaluation results for the datasets presented in Figure 12, Figure 13 and Figure 15. The presented values represent 50 randomly chosen orientations per dataset within the range of for rotations around the vertical axis and for rotations around the horizontal axes. The reported numbers of points for the point clouds of the ISPRS Indoor Modeling Benchmark refer to point clouds downsampled to a resolution of 2 cm as used in this evaluation. The values marked in red are discussed in more detail in Section 4.
For each of the 50 random input rotations, the alignment procedure described in Section 2.1 and Section 2.2 was applied and the resulting vertical and horizontal angular deviations and as defined in Section 2.4 were determined. Table 1 lists the mean values and standard deviations for these evaluation metrics aggregated over all 50 samples per dataset. Furthermore, the mean values and standard deviations for the processing time are given as well. The stated values refer to a system with a i7-8550U CPU with 24 GB RAM and do not include data import and export. The implementation, which will be released upon acceptance for publication, is CPU parallelized.
4. Discussion
Taking a closer look at the evaluation results presented in Table 1, the overall quite low values for the horizontal and vertical angular deviations and with equally low standard deviations indicate that the proposed alignment method works quite well for a large range of different indoor mapping point clouds and triangle meshes with randomly varying input rotations within the defined bounds. The consistently larger and values for the triangle meshes acquired with the Microsoft HoloLens may be attributable to them being less accurate and more affected by noise. Triangles pertaining to an actually smooth planar room surface show a considerable variation in the normal vector direction. However, the reported and values for these datasets are still mostly below 1.
Some datasets however showed significantly higher averaged values for or , sometimes with the corresponding standard deviation being significantly raised as well. These outliers are marked red in Table 1 and will be discussed in more detail in the following paragraphs. To analyze these cases, we take a closer look at the distribution of the individual 50 deviations constituting the respective mean value and standard deviation.
In the case of the HoloLens triangle mesh “Attic”, for instance, the histogram of values depicted in Figure 16 indicate that the heightened mean and standard deviation values for the angular deviation in the vertical alignment were not caused by a large variability in the resulting vertical alignment. The vertical orientations resulting from the evaluated alignment method rather fluctuated between two clearly defined states, one being the correct vertical orientation according to the ground truth pose at around 0 angular deviation of the vertical axis supported by 45 of the 50 measurements. The other state is a vertical orientation with an angular deviation of about 30 occurring in the remaining five measurements. As visualized by the red box in Figure 17, this corresponds to an alignment where the vertical axis is oriented orthogonally to one of the slanted ceiling surfaces.
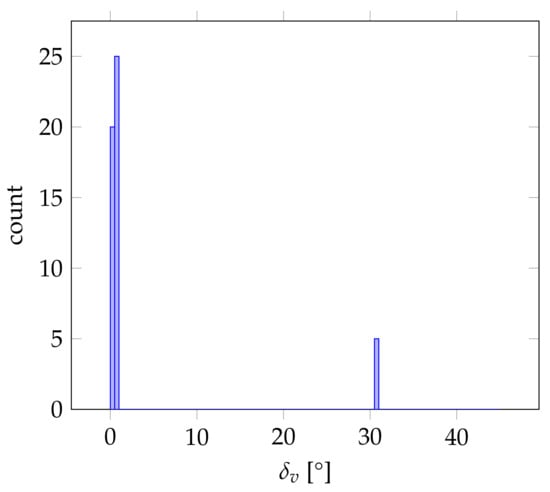
This is the only case where the vertical alignment did not work satisfyingly in all 50 samples for all the datasets used in the evaluation. We suspect that the misalignments occurring sporadically on this dataset can be ascribed to the noisy surfaces of the HoloLens triangle meshes. The triangles comprising the large horizontal floor surface for instance differ significantly in the direction of their normal vectors. Thus, only a fraction of the triangles comprising the floor actually corresponds to the proper vertical direction with respect to the applied resolution of 1. Depending on the input rotation, a peak caused by a slanted ceiling surface with a not insignificant area in comparison to horizontal surfaces such as in the case of the dataset at hand representing only the attic story may thus induce a larger peak and consequently a misalignment. In cases such as this, applying an angular resolution of more than 1 may be more appropriate to prevent such misalignments.
Besides the discussed outlier in the vertical alignment, some outliers in the horizontal alignment do exist. The Matterport3D datasets “mJXqzFtmKg4” and “PuKPg4mmafe” for instance show heightened average values along with high standard deviations. The histograms showing the distribution of all 50 values are again depicted in Figure 18 and Figure 19, respectively. As in the case before, it is apparent that the alignment results fluctuated between two states depending on the input rotation for both cases, while each time, one peak at 0 corresponds to the correct horizontal alignment according to the respective ground truth pose. As can be seen in Figure 20 and Figure 21, the respective second peak corresponds in both cases to a valid second Manhattan World structure present in the respective indoor environment.
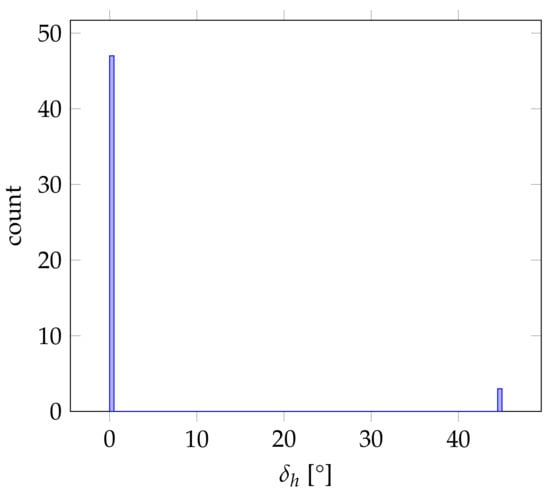
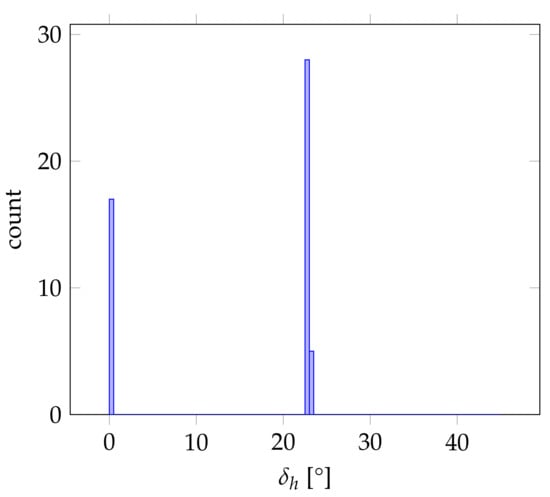
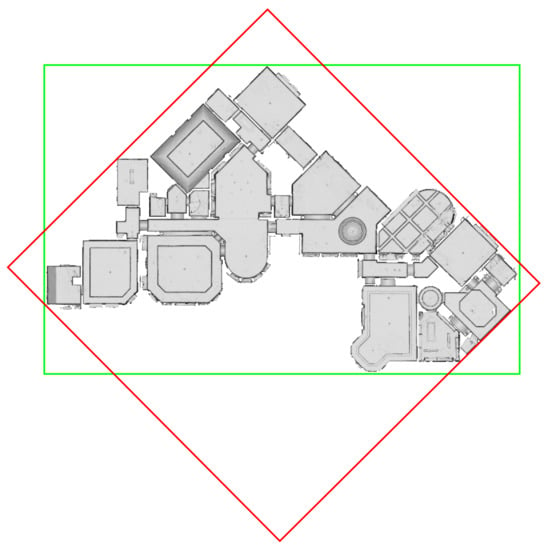
Figure 20.
Resulting horizontal alignments of the triangle mesh “mJXqzFtmKg4” from Figure 15f for the two peaks in the histogram of values depicted in Figure 18. The green bounding box corresponds to the peak at (i.e., the ground truth pose), while the red bounding box corresponds to the minor peak at .
In the case of the dataset “mJXqzFtmKg4”, this seems immediately plausible, as both Manhattan World structures present in the indoor environment are supported by a comparable amount of geometries, as was already demonstrated in Figure 5 and Figure 6. Thus, different input rotations may result in slightly different discretizations within the grid of 1 resolution, sometimes favoring one and sometimes the other Manhattan World structure as having the largest peak of summarized geometry weights.
In the case of the dataset “PuKPg4mmafe”, however, the two Manhattan World structures present in the indoor environment apparently do not seem to be supported by an approximately equal fraction of geometries. Instead, the upper right section in Figure 21 constituting the one Manhattan World structure seems to be far smaller than the section on the lower left constituting the other Manhattan World structure. In this case, the ground truth pose of the triangle mesh as published in [90] is aligned with the apparently smaller Manhattan World structure. It is thus not surprising that in the evaluation, a majority of measurements resulted in high deviations, as the evaluated alignment method favors the larger Manhattan World structure. However, it is surprising that a significant fraction of 17 of the 50 randomly chosen input rotations resulted in a horizontal alignment along the apparently significantly smaller Manhattan World structure.
This situation may be explainable by taking a closer look at the walls constituting the respective Manhattan World structures. As can be seen in Figure 22, the smaller Manhattan World section on the right-hand side consists of wall surfaces that are generally smooth and completely covered with geometries. In case of the larger section on the left, however, the wall surfaces comprise large window openings that are not represented by geometries, as the Matterport system used for the acquisition of this dataset cannot capture transparent glass surfaces. Furthermore, large parts of the actually represented wall surfaces are covered with curtains or other structures, resulting in inhomogeneous normal vector directions. In consideration of this, it seems plausible that the actual support for both Manhattan World structures present in the building could be approximately equal and the applied alignment method could thus be prone to fluctuate between both Manhattan World systems with varying input rotations.

Figure 22.
Detailed view of the triangle mesh “PuKPg4mmafe” from the Matterport3D dataset also depicted in Figure 15h and Figure 21. Note that in the case of the larger part of the building structure determining the Manhattan World system visualized by the red bounding box in Figure 21, large parts of the wall surfaces are missing as wall openings or constituted by curtains or other structures with inhomogeneous normal direction. The smaller part of the building structure on the right-hand side, which determines the Manhattan World system visualized by the green bounding box in Figure 21, however, has largely closed, smooth wall surfaces.
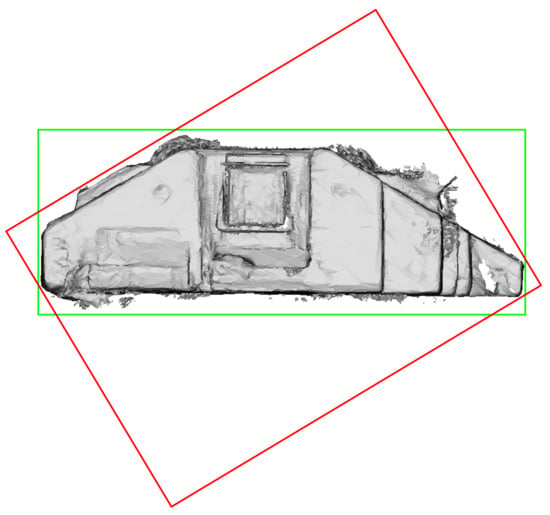
Besides these two cases discussed so far, there are two further datasets with high average horizontal angular alignment deviations in the evaluation results reported in Table 1. These are the triangle meshes “ULsKaCPVFJR” and “ur6pFq6Qu1A”, which are also part of the Matterport3D dataset. Unlike the cases discussed before, these however only show heightened mean values for , while the respective standard deviations are low in a range comparable to the other Matterport3D triangle meshes where the evaluated alignment method proved to be consistently successful.
This suggests that the proposed method consistently results in the same horizontal orientation for all 50 input rotations for both datasets. The respective resulting alignment however deviates from the assumed ground truth pose in the rotation around the vertical axis. This is further illustrated by Figure 23 and Figure 24, where it is easily discernible that the depicted buildings again respectively contain two Manhattan World structures and that the evaluated alignment method consistently chooses the respective other Manhattan World structure that does not coincide with the ground truth pose.
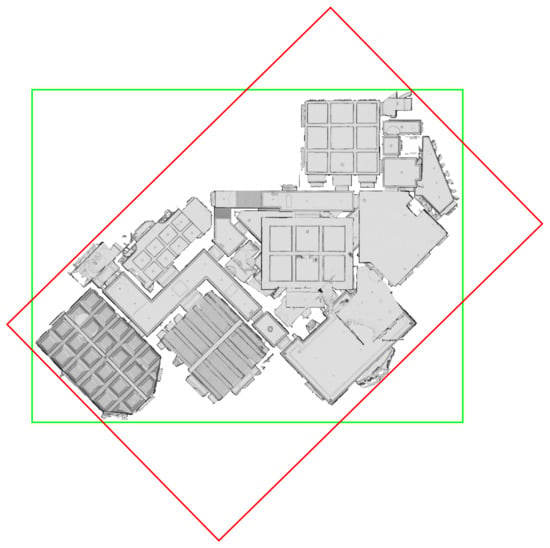
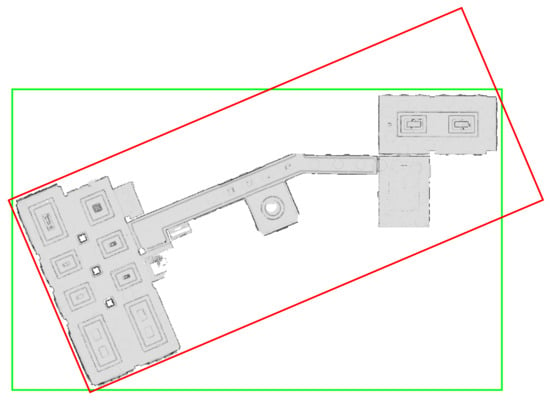
Figure 23.
The green bounding box represents the horizontal alignment of the triangle mesh “ULsKaCPVFJR” from Figure 15i as it is published in [90] and used as the ground truth pose for the evaluation results presented in Table 1. The red bounding box, on the other hand, represents the horizontal alignment resulting from our presented approach.
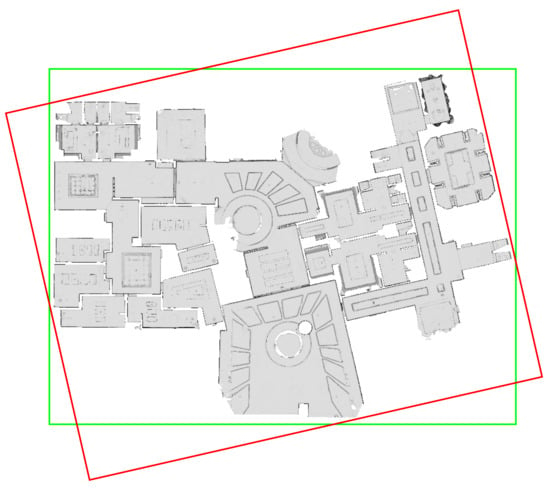
Figure 24.
The green bounding box represents the horizontal alignment of the triangle mesh “ur6pFq6Qu1A” from Figure 15j as it is published in [90] and used as the ground truth pose for the evaluation results presented in Table 1. The red bounding box, on the other hand, represents the horizontal alignment resulting from our presented approach.
Arguably, it is disputable which of the two Manhattan World structures respectively present in the datasets is the “correct” one, as again, in these two examples, both seem to encompass more or less the same fraction of the represented building environment, and it is not readily discernible which is the dominant one. Nevertheless, our proposed method proved to find a reasonable alignment with high accuracy in almost all cases with the only exception being the vertical alignment of the HoloLens triangle mesh “Attic”. In all other cases where the resulting pose deviates from the ground truth pose, the resulting alignment is still reasonable in the sense that it corresponds to another Manhattan World structure inherent in the respective dataset that is readily identifiable by a human observer, even if it may differ from the given ground truth pose corresponding to another alternative Manhattan World structure.
Besides aligning an indoor mapping dataset with the dominant Manhattan World structure supported by the largest fraction of geometries, the proposed method can easily be augmented to identify all major Manhattan World structures along with the respective sets of associated geometries. Among other possible fields of application that will be briefly discussed in the following Section 5, this allows for providing multiple possible alternatives for alignment to the user to choose from in cases where multiple major Manhattan World structures are present in the dataset at hand and it is not readily apparent which among these to use for alignment.
5. Conclusions
In this work, we presented a novel method for the automated pose normalization of indoor mapping data such as point clouds and triangle meshes. The aim of the proposed method was to align an indoor mapping point cloud or triangle mesh along the coordinate axes of the local coordinate system in a way that a chosen vertical axis points upwards with respect to the represented building structure, i.e., the chosen vertical axis is expected to be orthogonal to horizontal floor and ceiling surfaces. Furthermore, a rotation around this vertical axis is to be determined in a way that aligns the two horizontal coordinate axes with the main direction of the dominant Manhattan World structure of the respective building geometry. In case multiple Manhattan World systems are present in the data, the dominant structure supported by the largest fraction of geometries should determine the horizontal alignment. A CPU-parallelized implementation of the proposed method along with the code for the automated evaluation procedure are be made available to the public https://github.com/huepat/im-posenorm (accessed on 22 November 2021).
The proposed method was quantitatively evaluated on a range of different indoor mapping point clouds and triangle meshes that are publicly available (4 datasets captured with the Microsoft HoloLens [31], 6 datasets of the ISPRS Indoor Modeling Benchmark [95,96], and 14 of the Matterport 3D datasets [90]). The presented results showed that the approach is overall able to consistently produce correct poses for the considered datasets for different input rotations with high accuracy. Furthermore, cases where high deviations with respect to the given ground truth pose occurred were presented and discussed.
Concerning potential for future research, it has already been mentioned that the proposed method offers the possibility to not only identify the dominant Manhattan World structure along with the associated geometries in an indoor mapping dataset, but also to detect multiple Manhattan World structures that are sufficiently supported by geometries. Besides enabling presenting multiple reasonable alternatives for alignment to choose from, this could potentially also be used in the context of automated indoor reconstruction. In particular, knowing the major Manhattan World structures and their associated geometries could be beneficial for abstracting and idealizing indoor surfaces, i.e., reconstructing suitable surfaces as planes that perfectly conform to the Manhattan World assumption. In addition, automatically detecting the involved Manhattan World structures in a building may also be of interest in the context of automatically analyzing the architectural structure of buildings [98,99].
Furthermore, the presented methodology could possibly also be used in the context of Simultaneous Localization and Mapping (SLAM) in indoor environments and indoor mapping in general. Here, identifying Manhattan World structures during the mapping process (or in postprocessing if the individual indoor mapping geometries have associated timestamps to reconstruct the sequence of acquisition) could potentially be used to correct or reduce drift effects by applying the assumption that building structures that apparently seem to deviate only slightly from an ideal Manhattan World system are to be corrected according to the Manhattan World assumption [41,43,44,45,46,48].
Author Contributions
P.H., M.W., S.W. and S.H. jointly contributed to the concept of this paper and the discussion of the derived results. Writing, implementation, data processing, and visualization were performed by the first author (P.H.). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The code of this study is made available at https://github.com/huepat/im-posenorm (accessed on 22 November 2021). The datasets used for evaluation are publicly available via the reference provided in Table 1.
Acknowledgments
We acknowledge support by Deutsche Forschungsgemeinschaft and Open Access Publishing Fund of Karlsruhe Institute of Technology. We acknowledge the ISPRS WG IV/5 for the provision of the data used in the scope of the ISPRS Benchmark on Indoor Modelling.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Volk, R.; Stengel, J.; Schultmann, F. Building Information Modeling (BIM) for Existing Buildings—Literature Review and Future Needs. Autom. Constr. 2014, 38, 109–127. [Google Scholar] [CrossRef] [Green Version]
- Jung, W.; Lee, G. The Status of BIM Adoption on Six Continents. Int. J. Civil, Struct. Constr. Arch. Eng. 2015, 9, 406–410. [Google Scholar]
- Borrmann, A.; König, M.; Koch, C.; Beetz, J. (Eds.) Building Information Modeling: Why? What? How? In Building Information Modeling; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–24. [Google Scholar]
- Arayici, Y.; Onyenobi, T.; Egbu, C. Building Information Modeling (BIM) for Facilities Management (FM): The Mediacity Case Study Approach. Int. J. 3-D Inf. Model. 2012, 1, 55–73. [Google Scholar]
- Becker, R.; Falk, V.; Hoenen, S.; Loges, S.; Stumm, S.; Blankenbach, J.; Brell-Cokcan, S.; Hildebrandt, L.; Vallée, D. BIM—Towards the Entire Lifecycle. Int. J. Sustain. Dev. Plan. 2018, 13, 84–95. [Google Scholar] [CrossRef]
- Mirarchi, C.; Pavan, A.; De Marco, F.; Wang, X.; Song, Y. Supporting Facility Management Processes through End-Users’ Integration and Coordinated BIM-GIS Technologies. ISPRS Int. J. Geo-Inf. 2018, 7, 191. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Pishdad-Bozorgi, P. BIM-Enabled Facilities Operation and Maintenance: A Review. Adv. Eng. Inform. 2019, 39, 227–247. [Google Scholar] [CrossRef]
- Pătrăucean, V.; Armeni, I.; Nahangi, M.; Yeung, J.; Brilakis, I.; Haas, C. State of Research in Automatic As-Built Modeling. Adv. Eng. Inform. 2015, 29, 162–171. [Google Scholar] [CrossRef] [Green Version]
- Becker, R.; Lublasser, E.; Martens, J.; Wollenberg, R.; Zhang, H.; Brell-Cokcan, S.; Blankenbach, J. Enabling BIM for Property Management of Existing Buildings Based on Automated As-Is Capturing. In Proceedings of the 36th International Symposium on Automation and Robotics in Construction (ISARC 2019), Banff, AB, Canada, 21–24 May 2019; pp. 201–208. [Google Scholar]
- Lehtola, V.V.; Kaartinen, H.; Nüchter, A.; Kaijaluoto, R.; Kukko, A.; Litkey, P.; Honkavaara, E.; Rosnell, T.; Vaaja, M.T.; Virtanen, J.P.; et al. Comparison of the Selected State-of-the-Art 3D Indoor Scanning and Point Cloud Generation Methods. Remote Sens. 2017, 9, 796. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Tang, J.; Jiang, C.; Zhu, L.; Lehtomäki, M.; Kaartinen, H.; Kaijaluoto, R.; Wang, Y.; Hyyppä, J.; Hyyppä, H.; et al. The Accuracy Comparison of Three Simultaneous Localization and Mapping (SLAM)-Based Indoor Mapping Technologies. Sensors 2018, 18, 3228. [Google Scholar] [CrossRef] [Green Version]
- Nocerino, E.; Menna, F.; Remondino, F.; Toschi, I.; Rodríguez-Gonzálvez, P. Investigation of Indoor and Outdoor Performance of Two Portable Mobile Mapping Systems. Proc. SPIE 2017, 10332, 125–139. [Google Scholar]
- Masiero, A.; Fissore, F.; Guarnieri, A.; Pirotti, F.; Visintini, D.; Vettore, A. Performance Evaluation of Two Indoor Mapping Systems: Low-Cost UWB-Aided Photogrammetry and Backpack Laser Scanning. Appl. Sci. 2018, 8, 416. [Google Scholar] [CrossRef] [Green Version]
- Soudarissanane, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Scanning geometry: Influencing factor on the quality of terrestrial laser scanning points. ISPRS J. Photogramm. Remote Sens. 2011, 66, 389–399. [Google Scholar] [CrossRef]
- Weinmann, M. Reconstruction and Analysis of 3D Scenes—From Irregularly Distributed 3D Points to Object Classes; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Nüchter, A.; Borrmann, D.; Koch, P.; Kühn, M.; May, S. A Man-Portable, IMU-Free Mobile Mapping System. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W5, 17–23. [Google Scholar] [CrossRef] [Green Version]
- Blaser, S.; Cavegn, S.; Nebiker, S. Development of a Portable High Performance Mobile Mapping System Using the Robot Operating System. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, IV-1, 13–20. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Hou, S.; Wen, C.; Gong, Z.; Li, Q.; Sun, X.; Li, J. Semantic Line Framework-Based Indoor Building Modeling Using Backpacked Laser Scanning Point Cloud. ISPRS J. Photogramm. Remote Sens. 2018, 143, 150–166. [Google Scholar] [CrossRef]
- Karam, S.; Vosselman, G.; Peter, M.; Hosseinyalamdary, S.; Lehtola, V. Design, Calibration, and Evaluation of a Backpack Indoor Mobile Mapping System. Remote Sens. 2019, 11, 905. [Google Scholar] [CrossRef] [Green Version]
- Hillemann, M.; Weinmann, M.; Mueller, M.S.; Jutzi, B. Automatic Extrinsic Self-Calibration of Mobile Mapping Systems Based on Geometric 3D Features. Remote Sens. 2019, 11, 1955. [Google Scholar] [CrossRef] [Green Version]
- Bassier, M.; Vergauwen, M.; Poux, F. Point Cloud vs. Mesh Features for Building Interior Classification. Remote Sens. 2020, 12, 2224. [Google Scholar] [CrossRef]
- Weinmann, M.; Jäger, M.A.; Wursthorn, S.; Jutzi, B.; Weinmann, M.; Hübner, P. 3D Indoor Mapping with the Microsoft HoloLens: Qualitative and Quantitative Evaluation by Means of Geometric Features. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, V-1-2020, 165–172. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, S. A Review of 3D Reconstruction Techniques in Civil Engineering and their Applications. Adv. Eng. Inform. 2018, 37, 163–174. [Google Scholar] [CrossRef]
- Kang, Z.; Yang, J.; Yang, Z.; Cheng, S. A Review of Techniques for 3D Reconstruction of Indoor Environments. ISPRS Int. J. Geo-Inf. 2020, 9, 330. [Google Scholar] [CrossRef]
- Pintore, G.; Mura, C.; Ganovelli, F.; Fuentes-Perez, L.; Pajarola, R.; Gobbetti, E. State-of-the-Art in Automatic 3D Reconstruction of Structured Indoor Environments. In Proceedings of the Eurographics 2020, Norrkoping, Sweden, 25–29 May 2020; Volume 39, pp. 667–699. [Google Scholar]
- Ochmann, S.; Vock, R.; Klein, R. Automatic Reconstruction of Fully Volumetric 3D Building Models from Point Clouds. ISPRS J. Photogramm. Remote Sens. 2019, 151, 251–262. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Zhou, G.; Su, F.; Zuo, X.; Tang, L.; Liang, Y.; Zhu, H.; Li, L. Automatic Indoor Reconstruction from Point Clouds in Multi-Room Environments with Curved Walls. Sensors 2019, 19, 3798. [Google Scholar] [CrossRef] [Green Version]
- Nikoohemat, S.; Diakité, A.A.; Zlatanova, S.; Vosselman, G. Indoor 3D Reconstruction from Point Clouds for Optimal Routing in Complex Buildings to Support Disaster Management. Autom. Constr. 2020, 113, 103109. [Google Scholar] [CrossRef]
- Tran, H.; Khoshelham, K. Procedural Reconstruction of 3D Indoor Models from Lidar Data Using Reversible Jump Markov Chain Monte Carlo. Remote Sens. 2020, 12, 838. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Shi, W.; Ahmed, W. Structural Elements Detection and Reconstruction (SEDR): A Hybrid Approach for Modeling Complex Indoor Structures. ISPRS Int. J. Geo-Inf. 2020, 9, 760. [Google Scholar] [CrossRef]
- Hübner, P.; Weinmann, M.; Wursthorn, S.; Hinz, S. Automatic Voxel-based 3D Indoor Reconstruction and Room Partitioning from Triangle Meshes. ISPRS J. Photogramm. Remote Sens. 2021, 181, 254–278. [Google Scholar] [CrossRef]
- Furukawa, Y.; Curless, B.; Seitz, S.M.; Szeliski, R. Reconstructing Building Interiors from Images. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; pp. 80–87. [Google Scholar]
- Gankhuyag, U.; Han, J.H. Automatic 2D Floorplan CAD Generation from 3D Point Clouds. Appl. Sci. 2020, 10, 2817. [Google Scholar] [CrossRef] [Green Version]
- Otero, R.; Frías, E.; Lagüela, S.; Arias, P. Automatic gbXML Modeling from LiDAR Data for Energy Studies. Remote Sens. 2020, 12, 2679. [Google Scholar] [CrossRef]
- Shi, P.; Ye, Q.; Zeng, L. A Novel Indoor Structure Extraction Based on Dense Point Cloud. ISPRS Int. J. Geo-Inf. 2020, 9, 660. [Google Scholar] [CrossRef]
- Coughlan, J.; Yuille, A. Manhattan World: Compass Direction from a Single Image by Bayesian Inference. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 941–947. [Google Scholar]
- Coughlan, J.M.; Yuille, A.L. Manhattan World: Orientation and Outlier Detection by Bayesian Inference. Neural Comput. 2003, 15, 1063–1088. [Google Scholar] [CrossRef]
- Schindler, G.; Dellaert, F. Atlanta World: An Expectation Maximization Framework for Simultaneous Low-Level Edge Grouping and Camera Calibration in Complex Man-Made Environments. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Washington, DC, USA, 27 June–2 July 2004; pp. 1–7. [Google Scholar]
- Straub, J.; Rosman, G.; Freifeld, O.; Leonard, J.J.; Fisher III, J.W. A Mixture of Manhattan Frames: Beyond the Manhattan World. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 24–27 June 2014; pp. 3770–3777. [Google Scholar]
- Kim, P.; Coltin, B.; Kim, H. Visual Odometry with Drift-Free Rotation Estimation Using Indoor Scene Regularities. In Proceedings of the British Machine Vision Conference (BMVC), London, UK, 4–7 September 2017; pp. 62.1–62.12. [Google Scholar]
- Straub, J.; Freifeld, O.; Rosman, G.; Leonard, J.J.; Fisher, J.W., III. The Manhattan Frame Model—Manhattan World Inference in the Space of Surface Normals. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 235–249. [Google Scholar] [CrossRef] [Green Version]
- Faber, A.; Förstner, W. Detection of Dominant Orthogonal Road Structures in Small Scale Imagery. Int. Arch. Photogramm. Remote Sens. 2000, XXXIII, 274–281. [Google Scholar]
- Saurer, O.; Fraundorfer, F.; Pollefeys, M. Homography Based Visual Odometry with Known Vertical Direction and Weak Manhattan World Assumption. In Proceedings of the IROS Workshop on Visual Control of Mobile Robots (ViCoMoR), Algarve, Portugal, 11 October 2012; pp. 1–6. [Google Scholar]
- Straub, J.; Bhandari, N.; Leonard, J.J.; Fisher, J.W., III. Real-Time Manhattan World Rotation Estimation in 3D. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1913–1920. [Google Scholar]
- Peasley, B.; Birchfield, S.; Cunningham, A.; Dellaert, F. Accurate On-Line 3D Occupancy Grids using Manhattan World Constraints. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 5283–5290. [Google Scholar]
- Yazdanpour, M.; Fan, G.; Sheng, W. Online Reconstruction of Indoor Scenes With Local Manhattan Frame Growing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019; pp. 964–970. [Google Scholar]
- Li, Y.; Brasch, N.; Wang, Y.; Navab, N.; Tombari, F. Structure-SLAM: Low-Drift Monocular SLAM in Indoor Environments. IEEE Robot. Autom. Lett. 2020, 5, 6583–6590. [Google Scholar] [CrossRef]
- Liu, J.; Meng, Z. Visual SLAM with Drift-Free Rotation Estimation in Manhattan World. IEEE Robot. Autom. Lett. 2020, 5, 6512–6519. [Google Scholar] [CrossRef]
- Martens, J.; Blankenbach, J. An Evaluation of Pose-Normalization Algorithms for Point Clouds Introducing a Novel Histogram-Based Approach. Adv. Eng. Inform. 2020, 46, 101132. [Google Scholar] [CrossRef]
- Fichtner, F.W.; Diakité, A.A.; Zlatanova, S.; Voûte, R. Semantic Enrichment of Octree Structured Point Clouds for Multi-Story 3D Pathfinding. Trans. GIS 2017, 22, 233–248. [Google Scholar] [CrossRef]
- Gorte, B.; Zlatanova, S.; Fadli, F. Navigation in Indoor Voxel Models. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, IV-2/W5, 279–283. [Google Scholar] [CrossRef] [Green Version]
- Coudron, I.; Puttemans, S.; Goedemé, T.; Vandewalle, P. Semantic Extraction of Permanent Structures for the Reconstruction of Building Interiors from Point Clouds. Sensors 2020, 20, 6916. [Google Scholar] [CrossRef]
- Hübner, P.; Weinmann, M.; Wursthorn, S. Voxel-Based Indoor Reconstruction from HoloLens Triangle Meshes. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, V-4-2020, 79–86. [Google Scholar] [CrossRef]
- Martens, J.; Blankenbach, J. An Automated Approach for Point Cloud Alignment Based on Density Histograms. In Proceedings of the 26th International Workshop on Intelligent Computing in Engineering, Leuven, Belgium, 30 June–3 July 2019; pp. 1–11. [Google Scholar]
- Xu, Y.; Tong, X.; Stilla, U. Voxel-Based Representation of 3D Point Clouds: Methods, Applications, and its Potential Use in the Construction Industry. Autom. Constr. 2021, 126, 103675. [Google Scholar] [CrossRef]
- Wijmans, E.; Furukawa, Y. Exploiting 2D Floorplan for Building-Scale Panorama RGBD Alignment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 308–316. [Google Scholar]
- Chen, S.; Nan, L.; Xia, R.; Zhao, J.; Wonka, P. PLADE: A Plane-Based Descriptor for Point Cloud Registration with Small Overlap. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2530–2540. [Google Scholar] [CrossRef]
- Huang, R.; Xu, Y.; Hoegner, L.; Stilla, U. Efficient Estimation of 3D Shifts Between Point Clouds Using Low-Frequency Components of Phase Correlation. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, V-2-2020, 227–234. [Google Scholar] [CrossRef]
- Bassier, M.; Vincke, S.; Mattheuwsen, L.; de Lima Hernandez, R.; Derdaele, J.; Vergauwen, M. Percentage of Completion of In-Situ Cast Concrete Walls using Point Cloud Data and BIM. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-5/W2, 21–28. [Google Scholar] [CrossRef] [Green Version]
- Koeva, M.; Nikoohemat, S.; Oude Elberink, S.; Morales, J.; Lemmen, C.; Zevenbergen, J. Towards 3D Indoor Cadastre Based on Change Detection from Point Clouds. Remote Sens. 2019, 6, 206. [Google Scholar] [CrossRef] [Green Version]
- Maalek, R.; Lichti, D.D.; Ruwanpura, J.Y. Automatic Recognition of Common Structural Elements from Point Clouds for Automated Progress Monitoring and Dimensional Quality Control in Reinforced Concrete Construction. Remote Sens. 2019, 11, 1102. [Google Scholar] [CrossRef] [Green Version]
- Kazhdan, M. An Approximate and Efficient Method for Optimal Rotation Alignment of 3D Models. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 7, 1221–1229. [Google Scholar] [CrossRef]
- Papadakis, P.; Pratikakis, I.; Perantonis, S.; Theoharis, T. Efficient 3D Shape Matching and Retrieval Using a Concrete Radialized Spherical Projection Representation. Pattern Recognit. 2007, 40, 2437–2452. [Google Scholar] [CrossRef] [Green Version]
- Chaouch, M.; Verroust-Blondet, A. A Novel Method for Alignment of 3D Models. In Proceedings of the IEEE International Conference on Shape Modeling and Applications, Stony Brook, NY, USA, 4–6 June 2008; pp. 187–195. [Google Scholar]
- Fu, H.; Cohen-Or, D.; Dror, G.; Sheffer, A. Upright Orientation of Man-Made Objects. In Proceedings of the ACM SIGGRAPH, Los Angeles, CA, USA, 11–15 August 2008; p. 42. [Google Scholar]
- Lian, Z.; Rosin, P.L.; Sun, X. A Rectilinearity Measurement for 3D Meshes. In Proceedings of the 1st ACM International Conference on Multimedia Information Retrieval (MIR ’08), Vancouver, BC, Canada, 30–31 October 2008; pp. 395–402. [Google Scholar]
- Chaouch, M.; Verroust-Blondet, A. Alignment of 3D Models. Graph. Model. 2009, 71, 63–76. [Google Scholar] [CrossRef] [Green Version]
- Lian, Z.; Rosin, P.L.; Sun, X. Rectilinearity of 3D Meshes. Int. J. Comput. Vis. 2010, 89, 130–151. [Google Scholar] [CrossRef]
- Sfikas, K.; Theoharis, T.; Pratikakis, I. ROSy+: 3D Object Pose Normalization based on PCA and Reflective Object Symmetry with Application in 3D Object Retrieval. Int. J. Comput. Vis. 2011, 91, 262–279. [Google Scholar] [CrossRef]
- Zhang, D.; Lu, G. Content-Based Shape Retrieval Using Different Shape Descriptors: A Comparative Study. In Proceedings of the IEEE International Conference on Multimedia and Expo, Tokyo, Japan, 22–25 August 2001; pp. 317–320. [Google Scholar]
- Tangelder, J.W.H.; Veltkamp, R.C. A Survey of Content Based 3D Shape Retrieval Methods. Multimed. Tools Appl. 2007, 39, 441–471. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal Component Analysis: A Review and Recent Developments. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Okorn, B.; Xiong, X.; Akinci, B.; Huber, D. Toward Automated Modeling of Floor Plans. In Proceedings of the International Symposium 3D Data Processing, Visualization and Transmission 3DPVT, Paris, France, 17–20 May 2010; pp. 1–8. [Google Scholar]
- Khoshelham, K.; Díaz-Vilariño, L. 3D Modeling of Interior Spaces: Learning the Language of Indoor Architecture. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-5, 321–326. [Google Scholar] [CrossRef] [Green Version]
- Díaz-Vilariño, L.; Khoshelham, K.; Martínez-Sánchez, J.; Arias, P. 3D Modeling of Building Indoor Spaces and Closed Doors from Imagery and Point Clouds. Sensors 2015, 15, 3491–3512. [Google Scholar] [CrossRef] [Green Version]
- Czerniawski, T.; Nahangi, M.; Walbridge, S.; Haas, C. Automated Removal of Planar Clutter from 3D Point Clouds for Improving Industrial Object Recognition. In Proceedings of the 33rd International Symposium in Automation and Robotics in Construction ISARC, Auburn, AL, USA, 18–21 July 2016; pp. 357–365. [Google Scholar]
- Horn, B.K.P. Extended Gaussian Images. Proc. IEEE 1984, 72, 1671–1686. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Hao, W.; Ning, X.; Zhao, M.; Zhang, J.; Shi, Z. Automatic Segmentation of Urban Point Clouds Based on the Gaussian Map. Photogramm. Rec. 2013, 28, 342–361. [Google Scholar] [CrossRef]
- Shui, W.; Liu, J.; Ren, P.; Maddock, S.; Zhou, M. Automatic Planar Shape Segmentation from Indoor Point Clouds. In Proceedings of the ACM SIGGRAPH Conference on Virtual-Reality Continuum and Its Applications in Industry, Zhuhai, China, 3–4 December 2016; Volume 1, pp. 363–372. [Google Scholar]
- Zhao, B.; Hua, X.; Yu, K.; Xuan, W.; Chen, X.; Tao, W. Indoor Point Cloud Segmentation Using Iterative Gaussian Mapping and Improved Model Fitting. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7890–7907. [Google Scholar] [CrossRef]
- Limberger, F.A.; Oliveira, M.M. Real-Time Detection of Planar Regions in Unorganized Point Clouds. Pattern Recognit. 2015, 48, 2043–2053. [Google Scholar] [CrossRef] [Green Version]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1967; Volume 5.1, pp. 281–297. [Google Scholar]
- Lloyd, S. Least Squares Quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD’96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Mitra, N.J.; Nguyen, A. Estimating Surface Normals in Noisy Point Cloud Data. In Proceedings of the Nineteenth Annual Symposium on Computational Geometry (SCG ’03), San Diego, CA, USA, 8–10 June 2003; pp. 322–328. [Google Scholar]
- Boulch, A.; Marlet, R. Fast and Robust Normal Estimation for Point Clouds with Sharp Features. In Proceedings of the Eurographics Symposium on Geometry Processing, Tallinn, Estonia, 16–18 July 2012; Volume 31, pp. 1765–1774. [Google Scholar]
- Yu, Z.; Wang, T.; Guo, T.; Li, H.; Dong, J. Robust Point Cloud Normal Estimation via Neighborhood Reconstruction. Adv. Mech. Eng. 2019, 11, 1–19. [Google Scholar] [CrossRef]
- Sanchez, J.; Denis, F.; Coeurjolly, D.; Dupont, F.; Trassoudaine, L.; Checchin, P. Robust Normal Vector Estimation in 3D Point Clouds through Iterative Principal Component Analysis. ISPRS J. Photogramm. Remote Sens. 2020, 163, 18–35. [Google Scholar] [CrossRef] [Green Version]
- Ochmann, S.; Klein, R. Automatic Normal Orientation in Point Clouds of Building Interiors. In Proceedings of the Computer Graphics International Conference, Calgary, AB, Canada, 17–20 June 2019; pp. 556–563. [Google Scholar]
- Chang, A.; Dai, A.; Funkhouser, T.; Halber, M.; Nießner, M.; Savva, M.; Song, S.; Zeng, A.; Zhang, Y. Matterport3D: Learning from RGB-D Data in Indoor Environments. In Proceedings of the International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 667–676. [Google Scholar]
- Brent, R.P. An Algorithm with Guaranteed Convergence for Finding a Zero of a Function. In Algorithms for Minimization without Derivatives; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1973; Chapter 4. [Google Scholar]
- Khoshelham, K.; Tran, H.; Acharya, D. Indoor Mapping Eyewear: Geometric Evaluation of Spatial Mapping Capability of HoloLens. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 805–810. [Google Scholar] [CrossRef] [Green Version]
- Hübner, P.; Landgraf, S.; Weinmann, M.; Wursthorn, S. Evaluation of the Microsoft HoloLens for the Mapping of Indoor Building Environments. In Proceedings of the Dreiländertagung der DGPF, der OVG und der SGPF, Wien, Austria, 20–22 February 2019; Volume 28, pp. 44–53. [Google Scholar]
- Hübner, P.; Clintworth, K.; Liu, Q.; Weinmann, M.; Wursthorn, S. Evaluation of HoloLens Tracking and Depth Sensing for Indoor Mapping Applications. Sensors 2020, 20, 1021. [Google Scholar] [CrossRef] [Green Version]
- Khoshelham, K.; Díaz Vilariño, L.; Peter, M.; Kang, Z.; Acharya, D. The ISPRS Benchmark on Indoor Modeling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W7, 367–372. [Google Scholar] [CrossRef] [Green Version]
- Khoshelham, K.; Tran, H.; Acharya, D.; Díaz Vilariño, L.; Kang, Z.; Dalyot, S. The ISPRS Benchmark on Indoor Modeling—Preliminary Results. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 207–211. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D. CloudCompare: 3D Point Cloud and Mesh Processing Software. Available online: http://www.cloudcompare.org (accessed on 12 April 2021).
- Ahmed, S.; Liwicki, M.; Weber, M.; Dengel, A. Improved Automatic Analysis of Architectural Floor Plans. In Proceedings of the International Conference on Document Analysis and Recognition, Beijing, China, 18–21 September 2011; pp. 864–869. [Google Scholar]
- Roth, K.; Hageny, E.; Gillmann, C. Shape Analysis and Visualization in Building Floor Plans. In Proceedings of the Leipzig Symposium on Visualization in Applications (LEVIA’20), Leipzig, Germany, 15–16 October 2020; pp. 1–9. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).