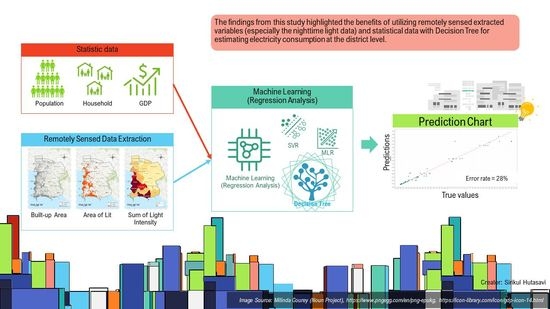
Estimating District-Level Electricity Consumption Using Remotely Sensed Data in Eastern Economic Corridor, Thailand
Abstract
:1. Introduction
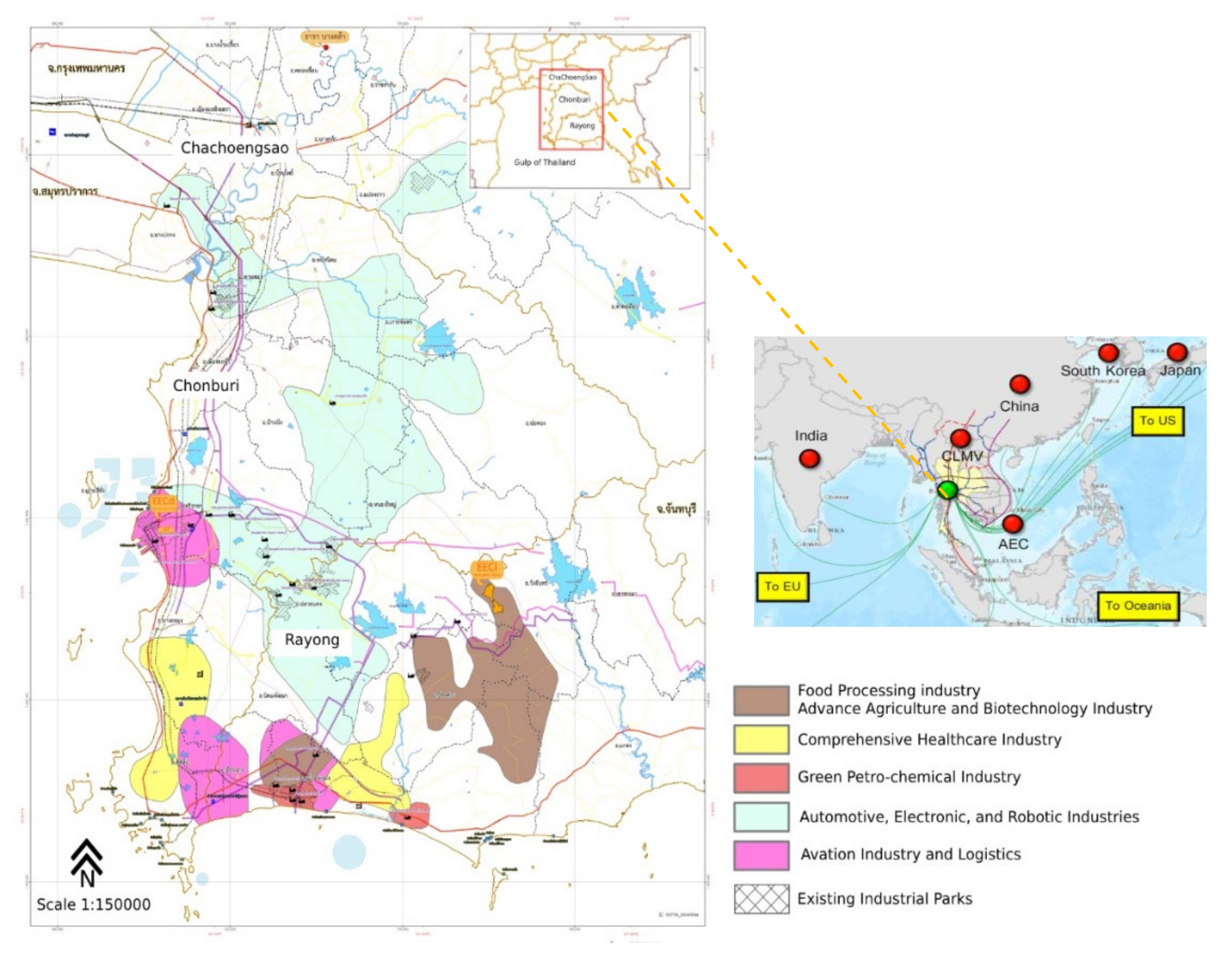
2. Materials and Methods
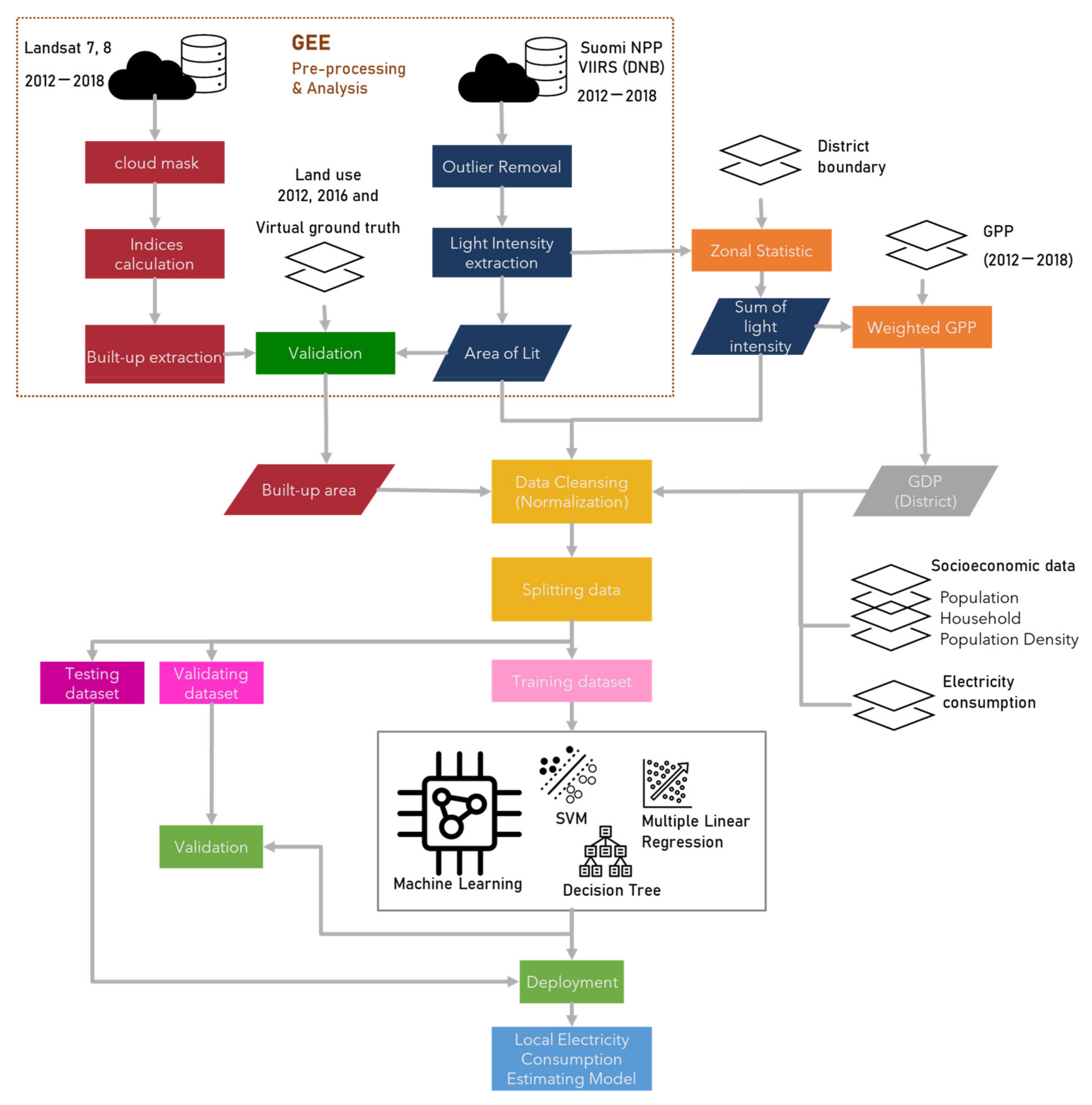
2.1. Study Flowchart
2.2. Data
2.2.1. Socioeconomic Data
2.2.2. Remotely Sensed Data
2.3. Data Preparation for Machine Learning Models
2.4. ML Model Setting
2.4.1. Multiple Regression (MR)
2.4.2. Decision Tree (DT)
2.4.3. Support Vector Regression (SVR)
2.5. Model Evaluation and Validation
3. Results
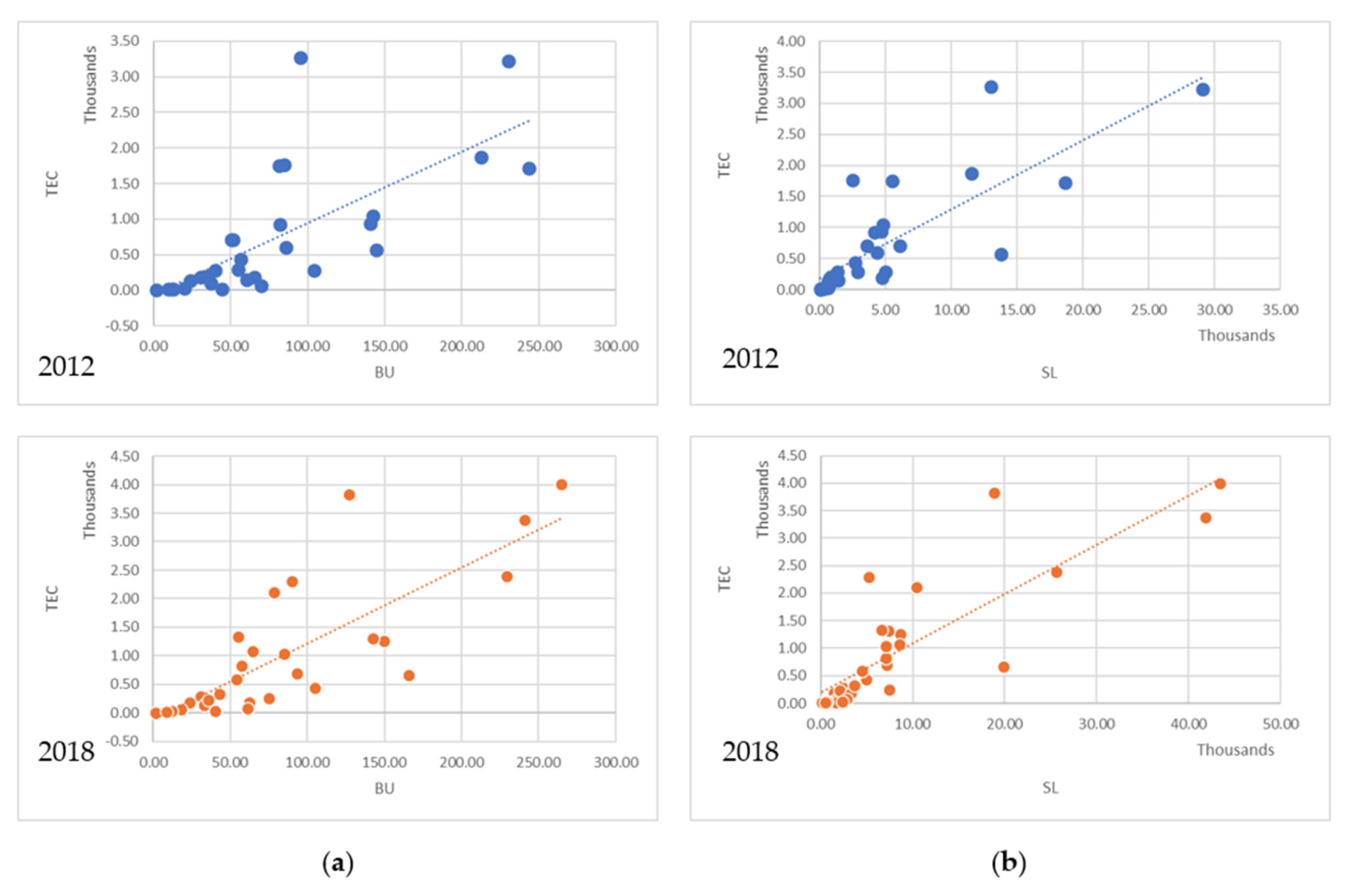
3.1. Variable Correlation
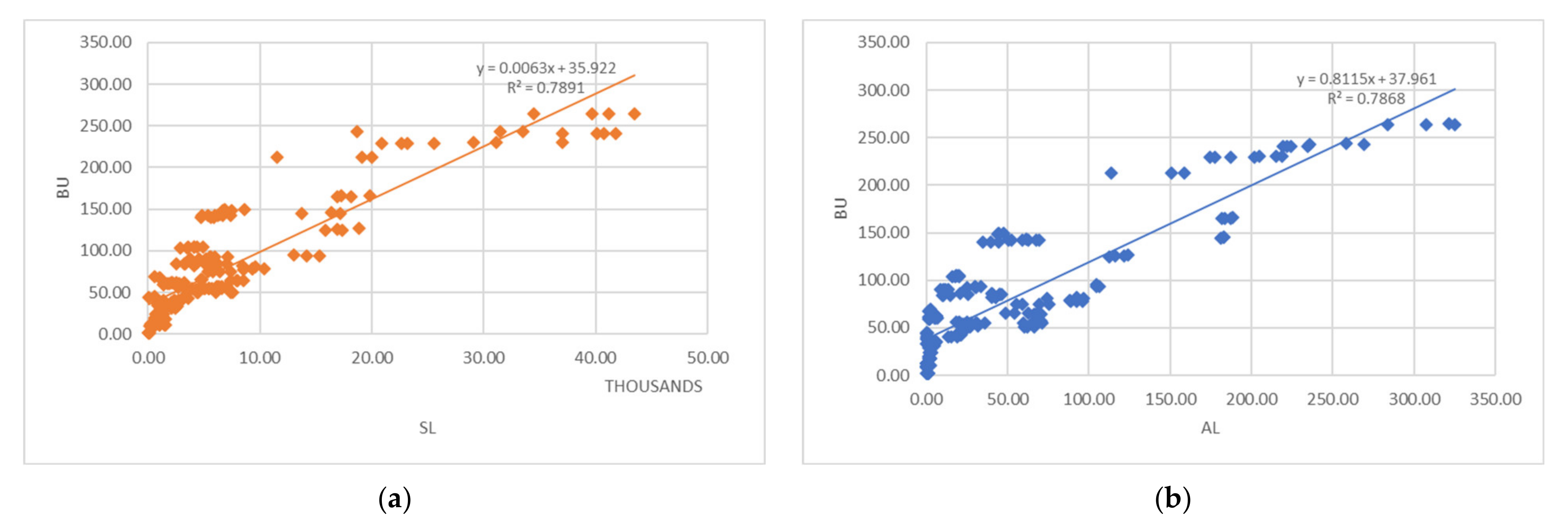
3.2. Variables Selection
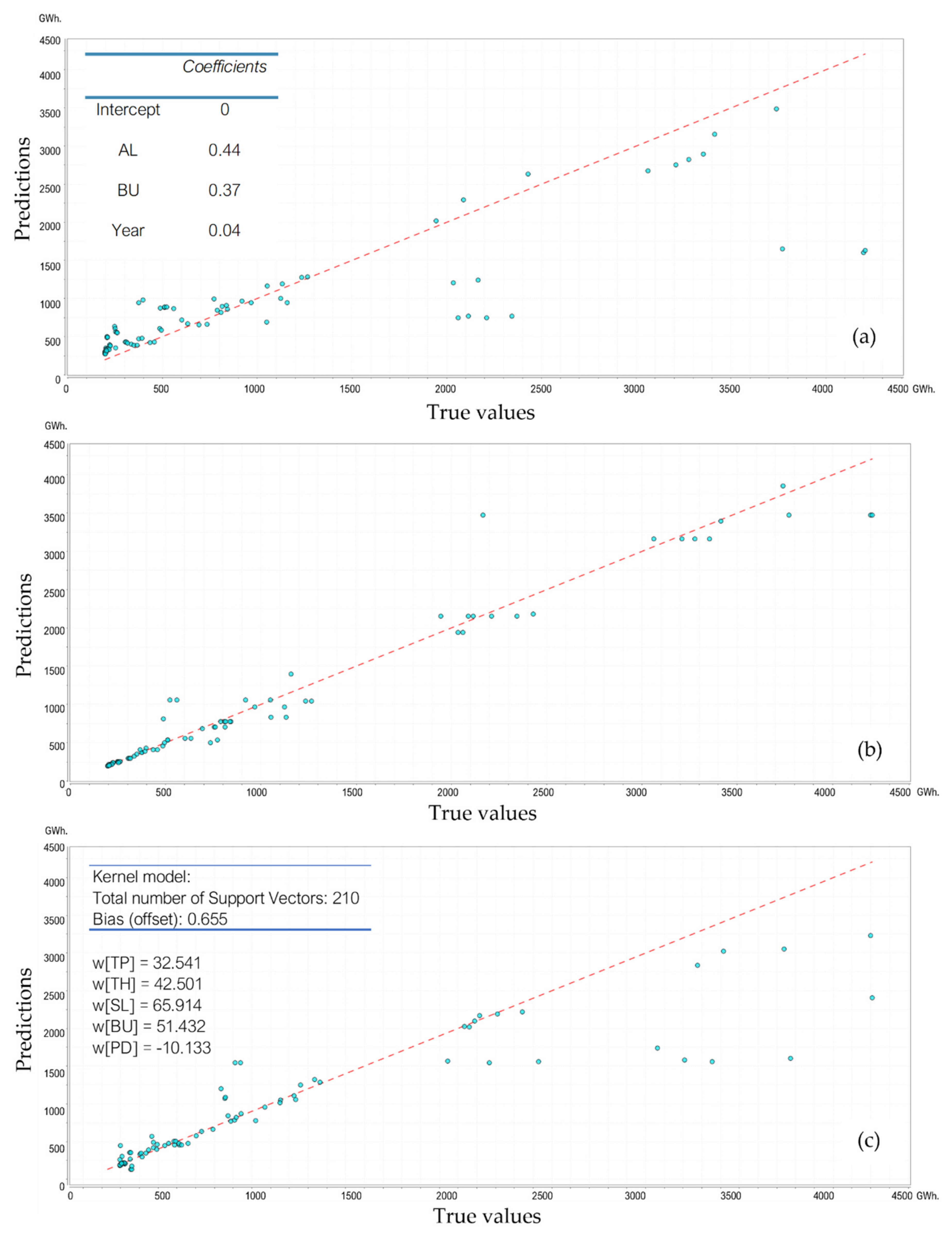
3.3. Estimation Models and Validation
4. Discussion
4.1. High Correlation of Geographic Variables to Electricity Consumption
4.2. Remotely Sensed Data—High Performance and Ease of Extraction
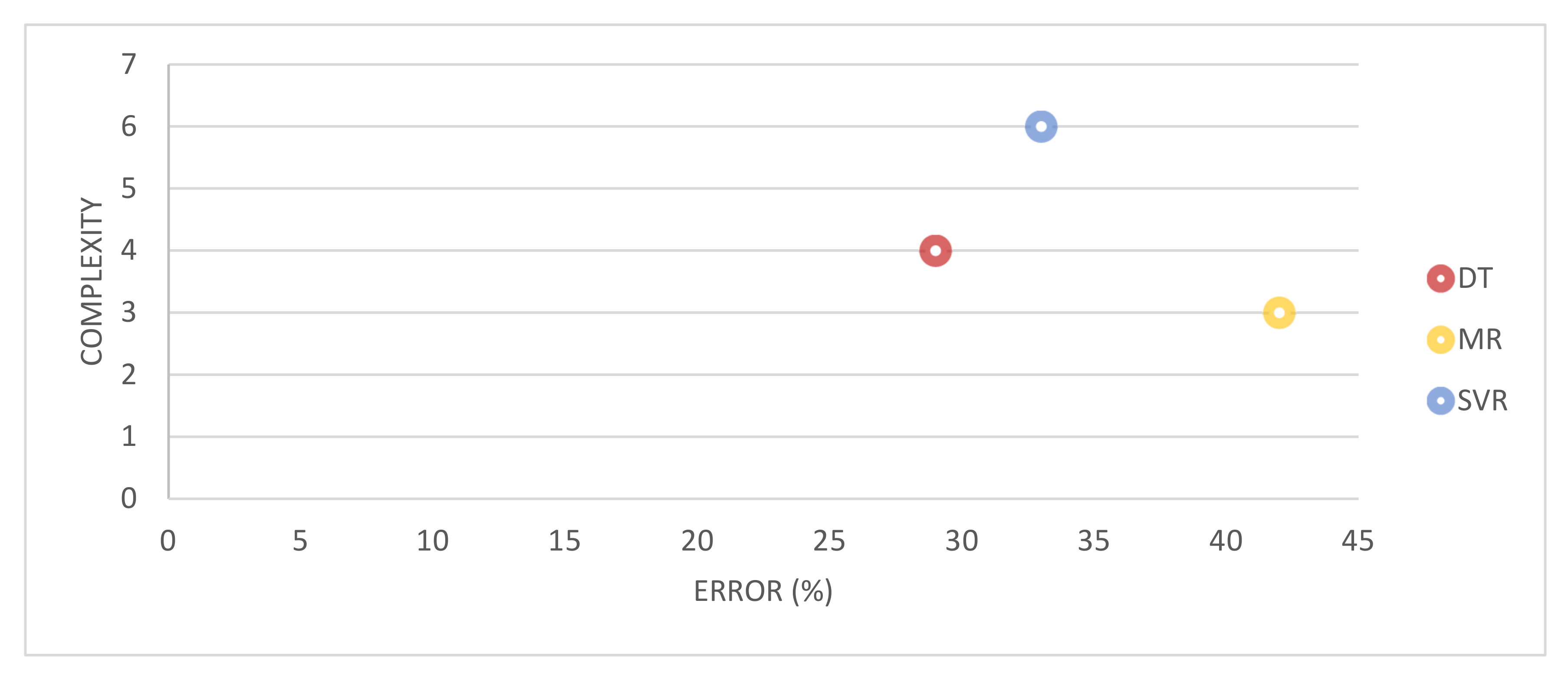
4.3. Model Complexity and Accuracy, Key Caveats, and Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| TH > −0.148 |
| | BU > 2.255 |
| | | BU > 2.619: 2.732 {count = 4} |
| | | BU ≤ 2.619 |
| | | | PD > 0.317 |
| | | | | BU > 2.419 |
| | | | | | PD > 0.417: 2.385 {count = 2} |
| | | | | | PD ≤ 0.417: 2.301 {count = 3} |
| | | | | BU ≤ 2.419: 2.072 {count = 3} |
| | | | PD ≤ 0.317: 1.505 {count = 2} |
| | BU ≤ 2.255 |
| | | PD > −0.441 |
| | | | BU > 1.644 |
| | | | | TH > 1.683: 1.340 {count = 4} |
| | | | | TH ≤ 1.683: 1.029 {count = 3} |
| | | | BU ≤ 1.644 |
| | | | | TH > 0.011 |
| | | | | | Area > −0.591 |
| | | | | | | PD > −0.374 |
| | | | | | | | PD > 0.524 |
| | | | | | | | | BU > 0.510: 0.320 {count = 6} |
| | | | | | | | | BU ≤ 0.510: 0.076 {count = 7} |
| | | | | | | | PD ≤ 0.524: 0.857 {count = 2} |
| | | | | | | PD ≤ −0.374 |
| | | | | | | | TH > 0.034: −0.160 {count = 2} |
| | | | | | | | TH ≤ 0.034: −0.190 {count = 2} |
| | | | | | Area ≤ −0.591: −0.217 {count = 9} |
| | | | | TH ≤ 0.011 |
| | | | | | PD > −0.008 |
| | | | | | | BU > −0.133 |
| | | | | | | | TH > −0.084 |
| | | | | | | | | BU > 0.113: 1.192 {count = 3} |
| | | | | | | | | BU ≤ 0.113: 1.038 {count = 5} |
| | | | | | | | TH ≤ −0.084 |
| | | | | | | | | PD > 0.282: 0.904 {count = 2} |
| | | | | | | | | PD ≤ 0.282: 0.836 {count = 2} |
| | | | | | | BU ≤ −0.133: 0.108 {count = 3} |
| | | | | | PD ≤ −0.008 |
| | | | | | | BU > 0.644 |
| | | | | | | | TH > −0.058: 0.256 {count = 2} |
| | | | | | | | TH ≤ −0.058: 0.150 {count = 2} |
| | | | | | | BU ≤ 0.644: −0.218 {count = 5} |
| | | PD ≤ −0.441 |
| | | | TH > 0.176 |
| | | | | PD > −0.534: 3.203 {count = 2} |
| | | | | PD ≤ −0.534 |
| | | | | | TH > 0.436: 2.740 {count = 2} |
| | | | | | TH ≤ 0.436: 2.473 {count = 2} |
| | | | TH ≤ 0.176: 1.705 {count = 2} |
| TH ≤ −0.148 |
| | TH > −0.306 |
| | | PD > −0.369 |
| | | | PD > −0.302 |
| | | | | PD > 0.117: −0.089 {count = 3} |
| | | | | PD ≤ 0.117: 0.046 {count = 2} |
| | | | PD ≤ −0.302: −0.459 {count = 2} |
| | | PD ≤ −0.369 |
| | | | PD > −0.388: 0.402 {count = 2} |
| | | | PD ≤ −0.388 |
| | | | | PD > −0.397: 0.168 {count = 2} |
| | | | | PD ≤ −0.397: 0.057 {count = 3} |
| | TH ≤ −0.306 |
| | | BU > −0.877 |
| | | | Area > 0.778 |
| | | | | BU > −0.632 |
| | | | | | Area > 2.736 |
| | | | | | | TH > −0.534: −0.784 {count = 3} |
| | | | | | | TH ≤ −0.534: −0.791 {count = 4} |
| | | | | | Area ≤ 2.736 |
| | | | | | | TH > −0.425: −0.741 {count = 3} |
| | | | | | | TH ≤ −0.425 |
| | | | | | | | PD > −0.690: −0.749 {count = 2} |
| | | | | | | | PD ≤ −0.690: −0.752 {count = 2} |
| | | | | BU ≤ −0.632 |
| | | | | | TH > −0.566: −0.691 {count = 4} |
| | | | | | TH ≤ −0.566: −0.708 {count = 3} |
| | | | Area ≤ 0.778 |
| | | | | TH > −0.391 |
| | | | | | BU > −0.302 |
| | | | | | | TH > −0.323: −0.488 {count = 2} |
| | | | | | | TH ≤ −0.323: −0.564 {count = 3} |
| | | | | | BU ≤ −0.302 |
| | | | | | | TH > −0.363 |
| | | | | | | | TH > −0.331: −0.261 {count = 2} |
| | | | | | | | TH ≤ −0.331: −0.189 {count = 2} |
| | | | | | | TH ≤ −0.363: −0.281 {count = 2} |
| | | | | TH ≤ −0.391 |
| | | | | | BU > −0.629 |
| | | | | | | BU > −0.325 |
| | | | | | | | PD > −0.190 |
| | | | | | | | | TH > −0.533: −0.587 {count = 2} |
| | | | | | | | | TH ≤ −0.533: −0.610 {count = 2} |
| | | | | | | | PD ≤ −0.190 |
| | | | | | | | | BU > −0.280: −0.637 {count = 5} |
| | | | | | | | | BU ≤ −0.280: −0.658 {count = 3} |
| | | | | | | BU ≤ −0.325 |
| | | | | | | | Area > −0.759 |
| | | | | | | | | BU > −0.382: −0.387 {count = 5} |
| | | | | | | | | BU ≤ −0.382: −0.311 {count = 3} |
| | | | | | | | Area ≤ −0.759 |
| | | | | | | | | BU > −0.575: −0.506 {count = 4} |
| | | | | | | | | BU ≤ −0.575: −0.541 {count = 3} |
| | | | | | BU ≤ −0.629 |
| | | | | | | TH > −0.696 |
| | | | | | | | PD > −0.641 |
| | | | | | | | | TH > −0.483: −0.604 {count = 2} |
| | | | | | | | | TH ≤ −0.483: −0.625 {count = 5} |
| | | | | | | | PD ≤ −0.641 |
| | | | | | | | | PD > −0.751: −0.571 {count = 4} |
| | | | | | | | | PD ≤ −0.751: −0.611 {count = 3} |
| | | | | | | TH ≤ −0.696 |
| | | | | | | | TH > −0.703: −0.650 {count = 3} |
| | | | | | | | TH ≤ −0.703: −0.673 {count = 4} |
| | | BU ≤ −0.877 |
| | | | BU > −0.972 |
| | | | | TH > −0.650: −0.755 {count = 3} |
| | | | | TH ≤ −0.650: −0.776 {count = 4} |
| | | | BU ≤ −0.972 |
| | | | | BU > −1.019 |
| | | | | | TH > −0.772 |
| | | | | | | TH > −0.768: −0.779 {count = 3} |
| | | | | | | TH ≤ −0.768: −0.785 {count = 2} |
| | | | | | TH ≤ −0.772: −0.792 {count = 2} |
| | | | | BU ≤ −1.019 |
| | | | | | TH > −0.796 |
| | | | | | | BU > −1.065 |
| | | | | | | | TH > −0.640: −0.796 {count = 3} |
| | | | | | | | TH ≤ −0.640 |
| | | | | | | | | Area > −0.527: −0.797 {count = 4} |
| | | | | | | | | Area ≤ −0.527: −0.797 {count = 3} |
| | | | | | | BU ≤ −1.065 |
| | | | | | | | BU > −1.069: −0.794 {count = 2} |
| | | | | | | | BU ≤ −1.069: −0.796 {count = 2} |
| | | | | | TH ≤ −0.796 |
| | | | | | | TH > −0.815: −0.802 {count = 3} |
| | | | | | | TH ≤ −0.815 |
| | | | | | | | PD > 2.167: −0.803 {count = 2} |
| | | | | | | | PD ≤ 2.167: −0.803 {count = 2} |
References
- Jasiński, T. Modeling electricity consumption using nighttime light images and artificial neural networks. Energy 2019, 179, 831–842. [Google Scholar] [CrossRef]
- Pfaff, A.S.P. What Drives Deforestation in the Brazilian Amazon? Evidence from Satellite and Socioeconomic Data. J. Environ. Econ. Manag. 1999, 37, 26–43. [Google Scholar] [CrossRef]
- Lambert, J.G.; Hall, C.A.S.; Balogh, S.; Gupta, A.; Arnold, M. Energy, EROI and quality of life. Energy Policy 2014, 64, 153–167. [Google Scholar] [CrossRef] [Green Version]
- Arto, I.; Capellán-Pérez, I.; Lago, R.; Bueno, G.; Bermejo, R. The energy requirements of a developed world. Energy Sustain. Dev. 2016, 33, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Martínez, D.M.; Ebenhack, B.W. Understanding the role of energy consumption in human development through the use of saturation phenomena. Energy Policy 2008, 36, 1430–1435. [Google Scholar] [CrossRef]
- Mei, J.; Goude, Y.; Hebrail, G.; Kong, N. Spatial estimation of electricity consumption using socio-demographic information. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 753–757. [Google Scholar] [CrossRef]
- Schneider, S.; Hollmuller, P.; le Strat, P.; Khoury, J.; Patel, M.; Lachal, B. Spatial–Temporal analysis of the heat and electricity demand of the Swiss building stock. Front. Built Environ. 2017, 3, 1–17. [Google Scholar] [CrossRef]
- Bogomolov, A.; Lepri, B.; Larcher, R.; Antonelli, F.; Pianesi, F.; Pentland, A. Energy consumption prediction using people dynamics derived from cellular network data. EPJ Data Sci. 2016, 5, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Townsend, A.C.; Bruce, D.A. The use of night-time lights satellite imagery as a measure of regional electricity consumption and population distribution. Int. J. Remote Sens. 2010, 31, 4459–4480. [Google Scholar] [CrossRef]
- Min, B.; Gaba, K.M.; Sarr, O.F.; Agalassou, A. Detection of rural electrification in Africa using DMSP-OLS night lights imagery. Int. J. Remote Sens. 2013, 34, 8118–8141. [Google Scholar] [CrossRef]
- Falchetta, G.; Pachauri, S.; Parkinson, S.; Byers, E. A high-resolution gridded dataset to assess electrification in sub-Saharan Africa. Sci. Data 2019, 6, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Xu, D.; Ali, S.H.; Ma, R.; Cheng, J. Can nighttime light data be used to estimate electric power consumption? New evidence from causal-effect inference. Energies 2019, 12, 3154. [Google Scholar] [CrossRef] [Green Version]
- Cipriano, C.L.S.; Silva, M.G.; Corrˆ, W.A.; Silva, I.A. Electric Energy Consumption Forecast Based on Spatial Information. In Proceedings of the GEOProcessing 2020: The 12th International Conference on Advanced Geographic Information Systems, Valencia, Spain, 21–25 November 2020; pp. 29–35, ISBN 978-1-61208-762-7. [Google Scholar]
- Hindman, M. Building Better Models: Prediction, Replication, and Machine Learning in the Social Sciences. Ann. Am. Acad. Pol. Soc. Sci. 2015, 659, 48–62. [Google Scholar] [CrossRef]
- Tso, G.K.F.; Yau, K.K.W. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Kaytez, F.; Taplamacioglu, M.C.; Cam, E.; Hardalac, F. Forecasting electricity consumption: A comparison of regression analysis, neural networks and least squares support vector machines. Int. J. Electr. Power Energy Syst. 2014, 67, 431–438. [Google Scholar] [CrossRef]
- Xiao, H.; Ma, Z.; Mi, Z.; Kelsey, J.; Zheng, J.; Yin, W.; Yan, M. Spatio-temporal simulation of energy consumption in provinces based on satellite nighttime light data. Appl. Energy 2018, 231, 1070–1078. [Google Scholar] [CrossRef]
- Smpokos, G.; Elshatshat, M.A.; Lioumpas, A.; Iliopoulos, I. On the energy consumption forecasting of data centers based on weather conditions: Remote sensing and machine learning approach. In Proceedings of the 11th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Khan, Z.A.; Hussain, T.; Ullah, A.; Rho, S.; Lee, M.; Baik, S.W. Towards efficient electricity forecasting in residential and commercial buildings: A novel hybrid CNN with a LSTM-AE based framework. Sensors 2020, 20, 1399. [Google Scholar] [CrossRef] [Green Version]
- Yue, Y.; Tian, L.; Yue, Q.; Wang, Z. Spatiotemporal variations in energy consumption and their influencing factors in China based on the integration of the DMSP-OLS and NPP-VIIRS nighttime light datasets. Remote Sens. 2020, 12, 1151. [Google Scholar] [CrossRef] [Green Version]
- Lu, W.C. Electricity consumption and economic growth: Evidence from 17 Taiwanese industries. Sustainability 2017, 9, 50. [Google Scholar] [CrossRef]
- Eastern Economic Corridor (EEC) Office. แผนภาพรวมเพื่อการพัฒนาเขตพัฒนาพิเศษภาคตะวันออก (พ.ศ.2560–2565). 2018. Available online: http://shorturl.at/wzANR (accessed on 16 April 2019).
- Phamornchantaramast, S.; Karnchanasutham, S.; Nualchawee, K.; Pleerux, N. Application of Geo Information Technology to Forecast Electricity Demand: A Case Study of Chon Buri Province. J. King Mongkut’s Univ. Technol. North Bangkok 2015, 26, 113–120. [Google Scholar] [CrossRef]
- Social Statistics Division. สรุปผลที่สำคัญประชากรแฝงในประเทศไทย พ.ศ. ๒๕๖๒. 2020. Available online: http://shorturl.at/cAF18 (accessed on 16 April 2019).
- Eastern Economic Corridor (EEC) Office. Eastern Economic Corridor (EEC). 2018. Available online: https://www.eeco.or.th/en (accessed on 7 November 2018).
- Liu, X.; Hu, G.; Chen, Y.; Li, X.; Xu, X.; Li, S.; Pei, F.; Wang, S. High-Resolution multi-temporal mapping of global urban land using Landsat images based on the Google Earth Engine Platform. Remote Sens. Environ. 2018, 209, 227–239. [Google Scholar] [CrossRef]
- Pu, D.C.; Sun, J.Y.; Ding, Q.; Zheng, Q.; Li, T.T.; Niu, X.F. Mapping urban areas using dense time series of landsat images and google earth engine. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.–ISPRS Arch. 2020, 42, 403–409. [Google Scholar] [CrossRef] [Green Version]
- Hutasavi, S.; Chen, D. Socioeconomic status from space: Example of estimating sub-district household income based on remotely sensed and geospatial data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.–ISPRS Arch. 2020, 43, 109–116. [Google Scholar] [CrossRef]
- Hutasavi, S.; Chen, D. Multi-temporal Mapping of Built-Up Areas Using Day and Nighttime Satellite Images Based on The Google Earth Engine Platform. Int. J. Civ. Archit. Eng. 2021, 15, 345–353. [Google Scholar]
- Otsu, N. A Tlreshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man. Cybern. 1979, C, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Nischal, K.N.; Radhakrishnan, R.; Mehta, S.; Chandani, S. Correlating Night-Time Satellite Images with Poverty and Other Census Data of India and Estimating Future Trends. In Proceedings of the Second ACM IKDD Conference on Data Sciences (CoDS ‘15), Bangalore, India, 18–21 March 2015; pp. 75–79. [Google Scholar] [CrossRef]
- Bouhennache, R.; Bouden, T.; Taleb-Ahmed, A.; Cheddad, A. A new spectral index for the extraction of built-up land features from Landsat 8 satellite imagery. Geocarto Int. 2019, 34, 1531–1551. [Google Scholar] [CrossRef]
- Campagna, M.; Craglia, M. The socioeconomic impact of the spatial data infrastructure of Lombardy. Environ. Plan. B Plan. Des. 2012, 6, 1069–1083. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Zhizhin, M.; Ghosh, T.; Hsu, F.C.; Taneja, J. Annual time series of global viirs night-time lights derived from monthly averages: 2012 to 2019. Remote Sens. 2021, 13, 922. [Google Scholar] [CrossRef]
- Angra, S.; Ahuja, S. Implementation of data mining algorithms on data using rapid miner. In Proceedings of the 2017 International Conference on Big Data Analytics and Computational Intelligence (ICBDAC), Chirala, India, 23–25 March 2017; pp. 387–391. [Google Scholar] [CrossRef]
- Hobohm, U.; Scharf, M.; Schneider, R.; Sander, C. Selection of representative protein data sets. Protein Sci. 1992, 1, 409–417. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borovicka, T.; Jirin, M.; Kordik, P.; Jiri, M. Selecting Representative Data Sets. Adv. Data Min. Knowl. Discov. Appl. 2012, 12, 43–70. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Liu, H. Challenges of Feature Selection for Big Data Analytics. IEEE Intell. Syst. 2017, 32, 9–15. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Haghighat, F.; Fung, B.C.M.; Yoshino, H. A decision tree method for building energy demand modeling. Energy Build. 2010, 42, 1637–1646. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. Programs for machine learning Part I. Inf. Control 1962, 5, 347–367. [Google Scholar] [CrossRef] [Green Version]
- Torgo, L. Inductive learning to tree-based regression models. AI Commun. 2000, 13, 137–138. Available online: http://www.ncc.up.pt/~ltorgo/PhD/ (accessed on 1 August 2021).
- Ghosh, T.; Anderson, S.J.; Elvidge, C.D.; Sutton, P.C. Using Nighttime Satellite Imagery as a Proxy Measure of Human Well-Being. Sustainability 2013, 5, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Domingos, P. A few useful things to know about machine learning. Commun. ACM 2012, 55, 78–87. [Google Scholar] [CrossRef] [Green Version]
- Automatic Feature Engineering–RapidMiner Documentation. Available online: https://docs.rapidminer.com/latest/studio/operators/modeling/optimization/automatic_feature_engineering.html (accessed on 1 August 2021).
- Buranasingh, N. หลอด LED: นวัตกรรมเพื่อการอนุรักษ์และประหยัดพลังงาน. 2015. Available online: http://shorturl.at/kFIT3 (accessed on 1 August 2021).
| Mean | STD. Error | SD. | Min | Max | |
|---|---|---|---|---|---|
| Total Electricity Consumption 1 (TEC) | 847.98 | 78.60 | 1054.48 | 6.73 | 4293.21 |
| Population (TP) | 75,633.17 | 5003.59 | 67,130.15 | 4580.00 | 294,682.00 |
| Household (TH) | 38,892.08 | 3224.76 | 43,264.70 | 1903.00 | 199,851.00 |
| Sum of Light 2 (SL) | 6682.55 | 674.82 | 9053.65 | 49.40 | 41,146.70 |
| Area of Lit 3 (AL) | 50.75 | 5.32 | 71.34 | - | 324.81 |
| Built up Area 3 (BU) | 79.51 | 4.92 | 66.05 | 1.74 | 264.27 |
| Population Density (PD) | 216.80 | 15.97 | 214.25 | 32.00 | 1130.00 |
| Area 3 | 445.46 | 21.79 | 292.34 | 7.07 | 1422.90 |
| Year | 2014.50 | 0.13 | 1.71 | 2012 | 2017 |
| Gross Domestic Product 4 (GDP) | 592,073.89 | 57,014.05 | 764,923.78 | 3265.83 | 4.08 × 106 |
| Year | TP | TH | SL | AL | BU | PD | Area | GDP | TEC | |
|---|---|---|---|---|---|---|---|---|---|---|
| Year | 1 | |||||||||
| TP | 0.10 | 1 | ||||||||
| TH | 0.14 | 0.95 | 1 | |||||||
| SL | 0.12 | 0.75 | 0.83 | 1 | ||||||
| AL | 0.04 | 0.79 | 0.87 | 0.96 | 1 | |||||
| BU | 0.03 | 0.84 | 0.84 | 0.89 | 0.89 | 1 | ||||
| PD | 0.00 | 0.65 | 0.64 | 0.34 | 0.46 | 0.38 | 1 | |||
| Area | 0.00 | 0.17 | 0.09 | 0.13 | 0.04 | 0.22 | −0.32 | 1 | ||
| GDP | 0.07 | 0.68 | 0.75 | 0.97 | 0.90 | 0.83 | 0.27 | 0.14 | 1 | |
| TEC | 0.08 | 0.56 | 0.63 | 0.83 | 0.78 | 0.77 | 0.15 | 0.12 | 0.83 | 1 |
| Variables | Year | TP | TH | SL | AL | BU | GDP | PD | Area | |
|---|---|---|---|---|---|---|---|---|---|---|
| Models | ||||||||||
| Multiple Regression (MR) | 0.12 | 0.86 | 0.49 | |||||||
| Decision Tree (DT) | 0.51 | 0.20 | 0.004 | 0.09 | ||||||
| Support Vector Regression (SVR) | 0.03 | 0.04 | 0.08 | 0.06 | 0.05 | 0.06 | ||||
| Multiple Regression (MR) | Decision Tree (DT) | Support Vector Regression (SVM) | |
|---|---|---|---|
| MAE | 0.33 | 0.12 | 0.20 |
| RMSE | 0.51 | 0.24 | 0.39 |
| R2 | 0.81 | 0.95 | 0.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hutasavi, S.; Chen, D. Estimating District-Level Electricity Consumption Using Remotely Sensed Data in Eastern Economic Corridor, Thailand. Remote Sens. 2021, 13, 4654. https://doi.org/10.3390/rs13224654
Hutasavi S, Chen D. Estimating District-Level Electricity Consumption Using Remotely Sensed Data in Eastern Economic Corridor, Thailand. Remote Sensing. 2021; 13(22):4654. https://doi.org/10.3390/rs13224654
Chicago/Turabian StyleHutasavi, Sirikul, and Dongmei Chen. 2021. "Estimating District-Level Electricity Consumption Using Remotely Sensed Data in Eastern Economic Corridor, Thailand" Remote Sensing 13, no. 22: 4654. https://doi.org/10.3390/rs13224654
APA StyleHutasavi, S., & Chen, D. (2021). Estimating District-Level Electricity Consumption Using Remotely Sensed Data in Eastern Economic Corridor, Thailand. Remote Sensing, 13(22), 4654. https://doi.org/10.3390/rs13224654