A Google Earth Engine Application to Retrieve Long-Term Surface Temperature for Small Lakes. Case: San Pedro Lagoons, Chile
Abstract
:1. Introduction
2. Study Area
3. Data and Methodology
3.1. Data
3.1.1. In Situ
3.1.2. Satellite
3.2. Satellite Data Processing
3.2.1. Method 1 (M1)
3.2.2. Method 2 (M2)
3.2.3. Method 3 (M3)
3.2.4. Methods 4 and 5 (M4 y M5)
3.2.5. Method 6 (M6)
3.3. Work Strategy
3.3.1. LSWT Series
3.3.2. Calibration Process
3.3.3. LSWT Field Data Set and Climatology
4. Results and Discussion
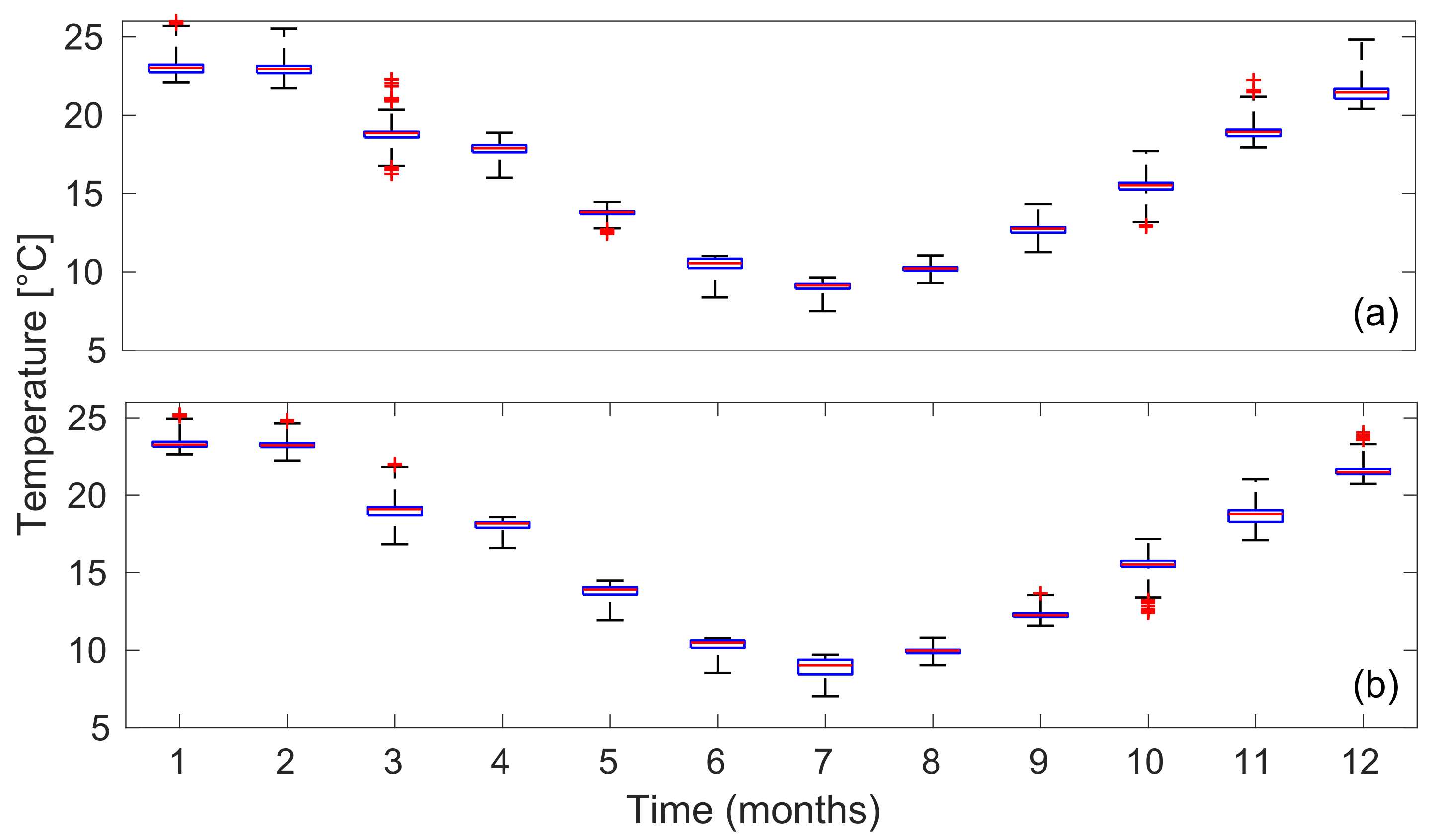
4.1. LSWT Series
4.2. Calibration Process
4.3. LSWT Field Data Set and Climatology
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Piccolroaz, S.; Toffolon, M.; Majone, B. A simple lumped model to convert air temperature into surface water temperature in lakes. HESS 2013, 17, 3323. [Google Scholar]
- Beutel, M.W.; Horne, A.J.; Roth, J.C.; Barratt, N.J. Limnological effects of anthropogenic desiccation of a large, saline lake, Walker Lake, Nevada. Hydrobiologia 2001, 466, 91–105. [Google Scholar] [CrossRef]
- Parra, O.; Valdovinos, C.; Urrutia, R.; Cisternas, M.; Habit, E.; Mardones, M. Caracterización y tendencias tróficas de cinco lagos costeros de Chile central. Limnetica 2003, 22, 51–83. [Google Scholar]
- Parra, O.; Baeza, C.; Almanza, V.; Urrutia, R.; Figueroa, R.; Fernández, X.; de Orúe, P.; González, P.; Beltrán, J.; Becerra, J.; et al. Una aproximación interdisciplinaria al estudio de floraciones de algas nocivas en Lagos Urbanos En Chile. In Desarrollo Sustentable; Barra, R., Rojas, J., Eds.; University of Concepción: Concepción, Chile, 2016; pp. 133–146. [Google Scholar]
- Prats, J.; Reynaud, N.; Rebière, D.; Peroux, T.; Tormos, T.; Danis, P. A. LakeSST: Lake Skin Surface Temperature in French inland water bodies for 1999–2016 from Landsat archives. ESSD 2018, 10, 727–743. [Google Scholar] [CrossRef] [Green Version]
- Randrianiaina, J.; Rakotonirina, I.; Ratiarimanana, R.; Lahatra, F. Temperature Retrieval of Lake Itasy Using Remote Sensing. Resour. Environ. 2018, 8, 241–244. [Google Scholar]
- Elachi, C.; Van Zyl, J.J. Introduction. In Introduction to the Physics and Techniques of Remote Sensing; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 1–18. [Google Scholar]
- Lieberherr, G.; Wunderle, S. Lake surface water temperature derived from 35 years of AVHRR sensor data for European lakes. Remote Sens. 2018, 10, 990. [Google Scholar] [CrossRef] [Green Version]
- Pareeth, S.; Salmaso, N.; Adrian, R.; Neteler, M. Homogenised daily lake surface water temperature data generated from multiple satellite sensors: A long-term case study of a large sub-Alpine lake. Sci. Rep. 2016, 6, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Copernicus Global Land Service. Available online: https://land.copernicus.eu/global/products/lswt (accessed on 1 June 2021).
- Edinburgh Data Share. Available online: https://datashare.ed.ac.uk/handle/10283/88 (accessed on 1 June 2021).
- Lake Water Temperatures. Available online: https://www.beachtemp.us/beach/870958/ (accessed on 1 June 2021).
- Guo, L.; Zheng, H.; Wu, Y.; Fan, L.; Wen, M.; Li, J.; Zhang, F.; Zhu, L.; Zhang, B. An integrated dataset of daily lake surface water temperature over Tibetan Plateau. Earth Syst. Sci. Data Discuss. Under review. 2021. [Google Scholar]
- Kumar, L.; Mutanga, O. Google Earth Engine applications since inception: Usage, trends, and potential. Remote Sens. 2018, 10, 1509. [Google Scholar]
- Amani, M.; Ghorbanian, A.; Ahmadi, S.A.; Kakooei, M.; Moghimi, A.; Mirmazloumi, S.M.; Moghaddam, S.H.A.; Mahdavi, S.; Ghahremanloo, M.; Parsian, S.; et al. Google Earth Engine Cloud Computing Platform for Remote Sensing Big Data Applications: A Comprehensive Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5326–5350. [Google Scholar]
- Traganos, D.; Poursanidis, D.; Aggarwal, B.; Chrysoulakis, N.; Reinartz, P. Estimating satellite-derived bathymetry (SDB) with the google earth engine and sentinel-2. Remote Sens. 2018, 10, 859. [Google Scholar]
- Sazib, N.; Mladenova, I.; Bolten, J. Leveraging the google earth engine for drought assessment using global soil moisture data. Remote Sens. 2018, 10, 1265. [Google Scholar]
- Solheim, A.L.; Globevnik, L.; Austnes, K.; Kristensen, P.; Moe, S.J.; Persson, J.; Phillips, G.; Poikane, S.; van de Bund, W.; Birk, S. A new broad typology for rivers and lakes in Europe: Development and application for large-scale environmental assessments. Sci. Total Environ. 2019, 697, 134043. [Google Scholar] [CrossRef]
- Ogilvie, A.; Belaud, G.; Massuel, S.; Mulligan, M.; Le Goulven, P.; Calvez, R. Surface water monitoring in small water bodies: Potential and limits of multi-sensor Landsat time series. HESS 2018, 22, 4349. [Google Scholar]
- Tavares, M.H.; Cunha, A.H.F.; Motta-Marques, D.; Ruhoff, A.L.; Cavalcanti, J.R.; Fragoso, C.R.; Bravo, J.M.; Munar, A.M.; Fan, F.M.; Rodrigues, L.H.R. Comparison of methods to estimate lake-surface-water temperature using landsat 7 ETM+ and MODIS imagery: Case study of a large shallow subtropical lake in Southern Brazil. Water 2019, 11, 168. [Google Scholar] [CrossRef] [Green Version]
- U.S. Geological Survey. Available online: https://www.usgs.gov/ (accessed on 1 August 2020).
- Google Earth Engine Code. Available online: https://code.earthengine.google.com/ (accessed on 15 August 2020).
- Earth Engine Data Catalog. Available online: https://developers.google.com/earth-engine/datasets/catalog/LANDSAT_LO08_C01_T1_RT (accessed on 15 August 2020).
- Earth Engine Data Catalog. Available online: https://developers.google.com/earth-engine/datasets/catalog/LANDSAT_LC08_C01_T1_TOAEarthEngineDataCatalog. (accessed on 15 August 2020).
- Earth Engine Data Catalog. Available online: https://developers.google.com/earth-engine/datasets/catalog/LANDSAT_LC08_C01_T1_SR (accessed on 15 August 2020).
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An Atmospheric Correction Parameter Calculator for a Single Thermal Band Earth-Sensing Instrument. Int. Geosci. Remote Sens. Symp. 2003, 5, 3014–3016. [Google Scholar]
- Barsi, J.A.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. Validation of a web-based atmospheric correction tool for single thermal band instruments. Earth Obs. Syst. X 2005, 5882, 58820E-1–58820E-7. [Google Scholar]
- Ermida, S.L.; Soares, P.; Mantas, V.; Göttsche, F.-M.; Trigo, I.F. Google Earth Engine open-source code for Land Surface Temperature estimation from the Landsat series. Remote Sens. 2020, 12, 1471. [Google Scholar] [CrossRef]
- Bayat, F.; Hasanlou, M. Feasibility study of Landsat-8 imagery for retrieving sea surface temperature (case study Persian Gulf). ISPRS Arch. 2003, 41, 1107–1110. [Google Scholar]
- Rajeshwari, A.; Mani, N.D. Estimation of land surface temperature of Dindigul district using Landsat 8 data. IJRET 2014, 3, 122–126. [Google Scholar]
- Allan, M.; Hamilton, D.P.; Trolle, D.; Muraoka, K.; McBride, C. Spatial heterogeneity in geothermally-influenced lakes derived from atmospherically corrected Landsat thermal imagery and three-dimensional hydrodynamic modelling. Int. J. Appl. Earth Observ. Geoinf. 2016, 50, 106–116. [Google Scholar] [CrossRef]
- Gianello, D.; Ávila-Hernández, E.; Aguer, I.; Crettaz-Minaglia, M.C. Water quality assessment of a temperate urban lagoon using physico-chemical and biological indicators. SN Appl. Sci. 2019, 1, 470. [Google Scholar] [CrossRef] [Green Version]
- Odunuga, S.; Udofia, S.; Osho, O.E.; Adegun, O. Environmental Degradation in the Ikorodu Sub-Urban Lagos-Lagoon Coastal Environment, Nigeria. Open Environ. Sci. 2018, 10, 16–33. [Google Scholar] [CrossRef] [Green Version]
- Sarricolea, P.; Herrera-Ossandon, M.; Meseguer-Ruiz, Ó. Climatic regionalisation of continental Chile. J. Maps 2017, 13, 66–73. [Google Scholar] [CrossRef]
- Bertrán, C.; Arenas, J.; Parra, O. Macrofauna del curso inferior y estuario del río Biobío (Chile): Cambios asociados a variabilidad estacional del caudal hídrico. Rev. Chil. Hist. Nat. 2001, 74, 331–340. [Google Scholar] [CrossRef]
- Peña Cortés, F.A. Geomorfología de la ribera norte del río Bío-Bío en su curso inferior: Limitaciones y potencialidades del área. RGNG 1995, 22, 27–33. [Google Scholar]
- Municipalidad de San Pedro de la Paz. Guía de Patrimonio Ambiental de San Pedro de la Paz; Dirección de Medio Ambiente: San Pedro de la Paz, Chile, 2019. [Google Scholar]
- Rojas, O.; Zamorano, M.; Vega, C.; Pacheco, F.; Figueroa, R. Percepción científica de los Servicios Ecosistémicos en el humedal Los Batros San Pedro de la Paz. In Urbanización en el Humedal Los Batros; Rojas, C., de la Fuente, H., Matínez, M., Rueda, I., Eds.; University of Concepción: Concepción, Chile, 2017; pp. 46–51. [Google Scholar]
- Parra, O.; Basualto, S.; Urrutia, R.; Valdovinos, C. Estudio comparativo de la diversidad fitoplanctónica de cinco lagos de diferentes niveles de eutroficación del área litoral de la región del Biobio (Chile). Gayana Bot. 1999, 56, 93–108. [Google Scholar]
- Dirección General de Aguas. Available online: https://dga.mop.gob.cl/servicioshidrometeorologicos/Paginas/default.aspx (accessed on 1 August 2020).
- Infraestructura de Datos Espaciales (IDE) del Ministerio del Medio Ambiente. Available online: https://ide.mma.gob.cl/ (accessed on 15 August 2020).
- Git Hub. Available online: https://github.com/mpedreros/LSWT_methods.git (accessed on 1 December 2020).
- Atmospheric Correction Parameter Calculator. Available online: https://atmcorr.gsfc.nasa.gov/ (accessed on 30 August 2020).
- Earth Engine Data Catalog. Available online: https://developers.google.com/earth-engine/datasets/catalog/NASA_ASTER_GED_AG100_003?hl=en (accessed on 15 August 2020).
- Earth Engine Data Catalog. Available online: https://developers.google.com/earth-engine/datasets/catalog/LANDSAT_LE07_C01_T1_RT?hl=en (accessed on 15 August 2020).
- Sayler, K. Product Guide Landsat 4-7 Collection 1 (C1) Surface Reflectance (LEDAPS); Zanter, K., Ed.; USGS: Reston, VA, USA, 2020. [Google Scholar]
- Sayler, K. Product Guide Landsat 8 Collection 1 (C1) Land Surface Reflectance Code (LaSRC); Zanter, K., Ed.; USGS: Sioux Falls, SD, USA, 2020. [Google Scholar]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Martins, J.; Trigo, I.; Bento, V.; da Camara, C. A Physically Constrained Calibration Database for Land Surface Temperature Using Infrared Retrieval Algorithms. Remote Sens. 2016, 8, 808. [Google Scholar] [CrossRef] [Green Version]
- Ji, L.; Senay, G.B.; Verdin, J.P. Evaluation of the global land data assimilation system (GLDAS) air temperature data products. JHM 2015, 16, 2463–2480. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- McClain, E.P.; Pichel, W.G.; Walton, C.C. Comparative performance of AVHRR-based multichannel sea surface temperatures. J. Geophys. Res. Oceans. 1985, 90, 11587–11601. [Google Scholar] [CrossRef]
- Eom, J.; Park, W.; Syifa, M.; Lee, C.; Yoon, S. Monitoring Variation in Sea Surface Temperature in the Nakdong River Estuary, Korea, Using Multiple Satellite Images. J. Coast. Res. 2019, 90, 183–189. [Google Scholar]
- O’Sullivan, P.; Reynolds, C.S. The Lakes Handbook: Limnology and Limnetic Ecology, 2nd ed.; Blackwell Publishing Company: Malden, MA, USA, 2008; Volume 1, pp. 107–114. [Google Scholar]
- Rooney, G.G.; Lipzig, N.V.; Thiery, W. Estimating the effect of rainfall on the surface temperature of a tropical lake. Hydrol. Earth Syst. Sci. 2018, 22, 6357–6369. [Google Scholar]
- Piccolroaz, S.; Healey, N.C.; Lenters, J.D.; Schladow, S.G.; Hook, S.J.; Sahoo, G.B.; Toffolon, M. On the predictability of lake surface temperature using air temperature in a changing climate: A case study for Lake Tahoe (USA). Limnol. Oceanogr. 2018, 63, 243–261. [Google Scholar] [CrossRef] [Green Version]
- Piccolroaz, S. Prediction of lake surface temperature using the air2water model: Guidelines, challenges, and future perspectives. Adv. Oceanogr. Limnol. 2016, 7, 36–50. [Google Scholar] [CrossRef] [Green Version]
- Ptak, M.; Sojka, M.; Nowak, B. Characteristics of daily water temperature fluctuations in lake kierskie (West Poland). Quaest. Geogr. 2019, 38, 41–49. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Yu, Z.; Luo, Y. Analysis on driving factors of lake surface water temperature for major lakes in Yunnan-Guizhou Plateau. Water Res. 2020, 184, 116018. [Google Scholar]
- Peña, M.A. Relationships between remotely sensed surface parameters associated with the urban heat sink formation in Santiago, Chile. Int. J. Remote Sens. 2008, 29, 4385–4404. [Google Scholar]
- Hala, E.; Nepravishta, F.; Panariti, A. The wind flow effects and high-rise buildings in urban spatial morphology. In Cities in Transitions, Proceedings of the 1st International Forum on Architecture and Urbanism, Tirana, Albania, 14–16 December 2017; La scuola di Pitagora Editrice: Napoli, Italy, 2019. [Google Scholar]
- Mittal, H.; Sharma, A.; Gairola, A. A review on the study of urban wind at the pedestrian level around buildings. J. Build. Eng. 2018, 18, 154–163. [Google Scholar] [CrossRef]
- Bharat, A.; Ahmed, A. S. Effects of high rise building complex on the wind flow patterns on surrounding urban pockets. Int. J. Eng. Res. Dev. 2012, 4, 21–26. [Google Scholar]
- Stetler, J.T.; Girdner, S.; Mack, J.; Winslow, L.A.; Leach, T.H.; Rose, K.C. Atmospheric stilling and warming air temperatures drive long-term changes in lake stratification in a large oligotrophic lake. Limnol. Oceanogr. 2021, 66, 954–964. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Abarca-del-Río, R.; Bergé-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake Volume Monitoring from Space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar]
- Crétaux, J.F.; Arsen, A.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
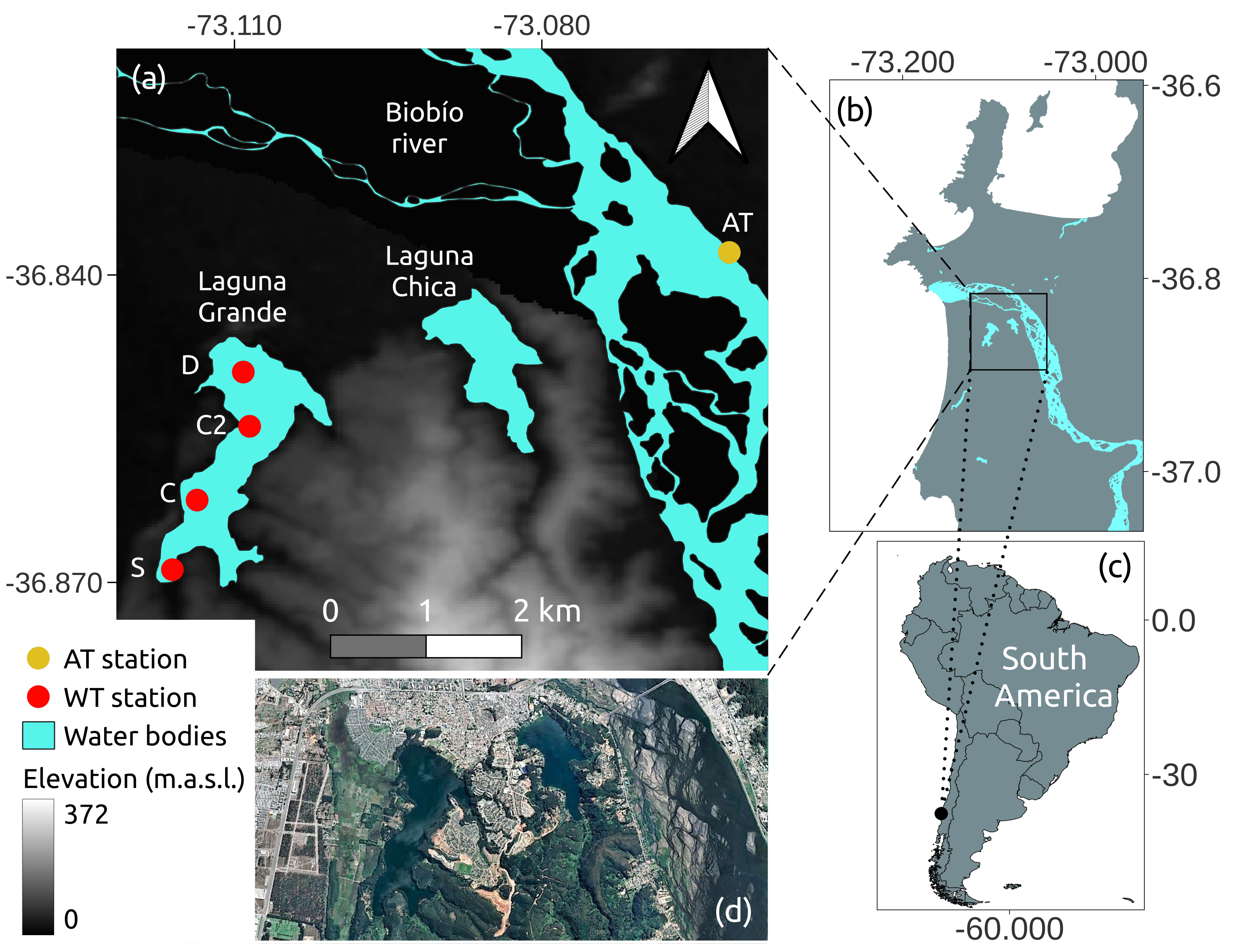
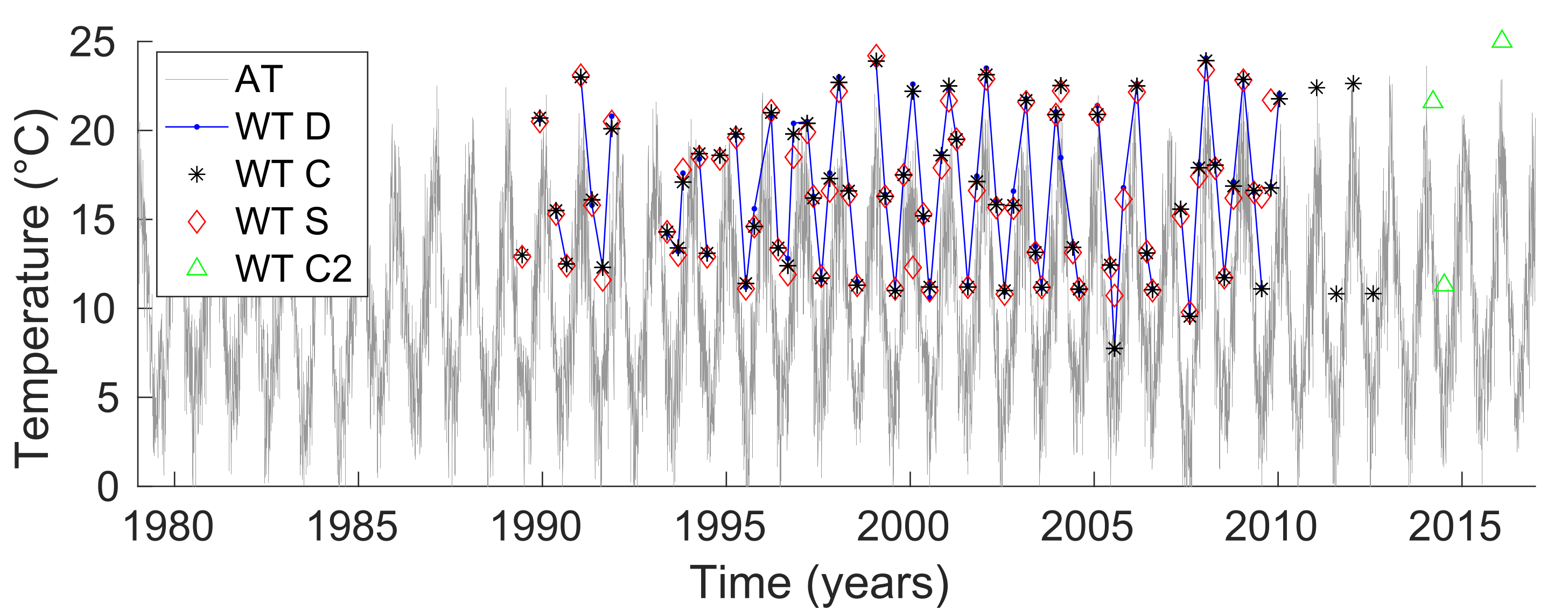

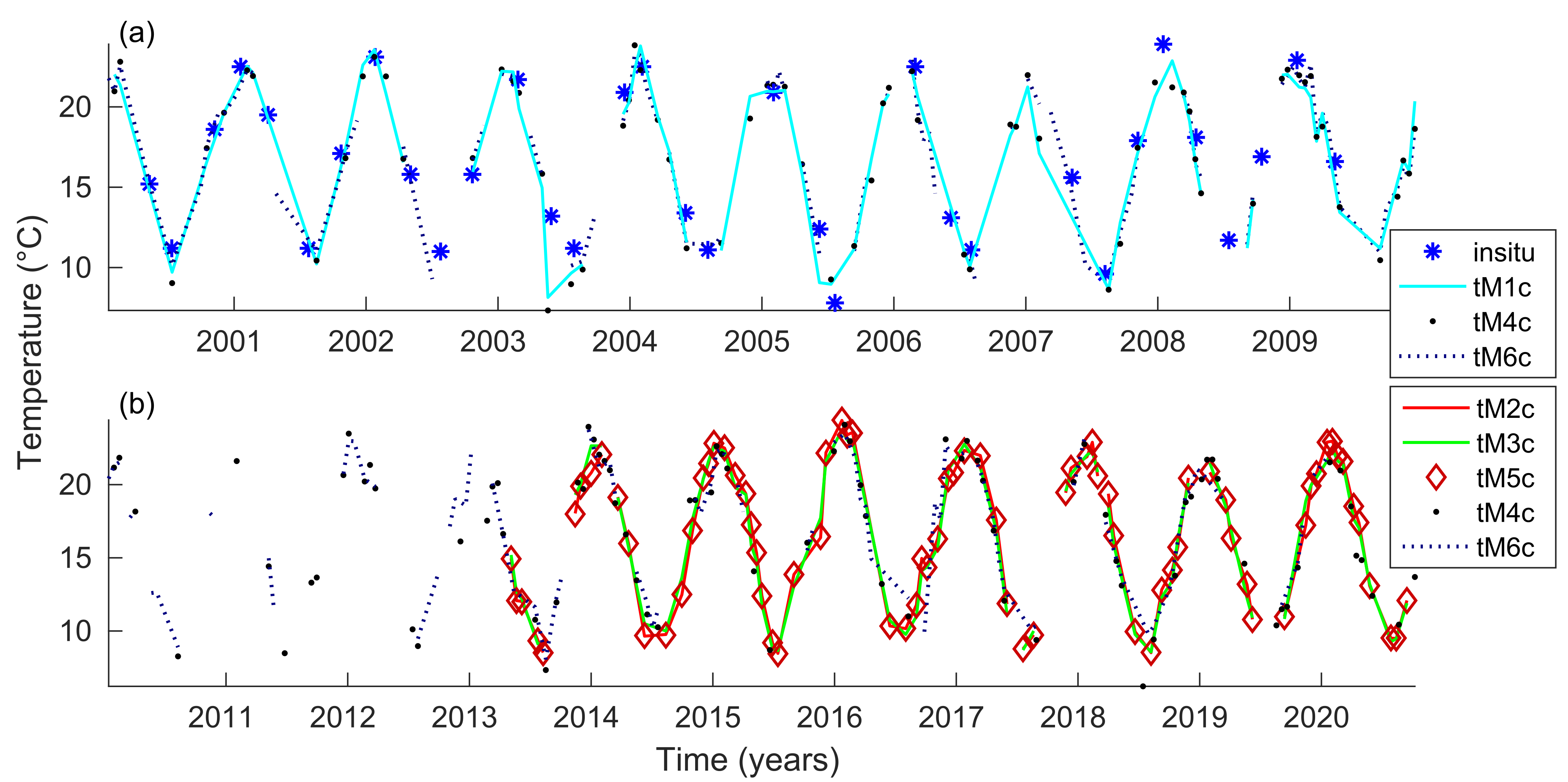
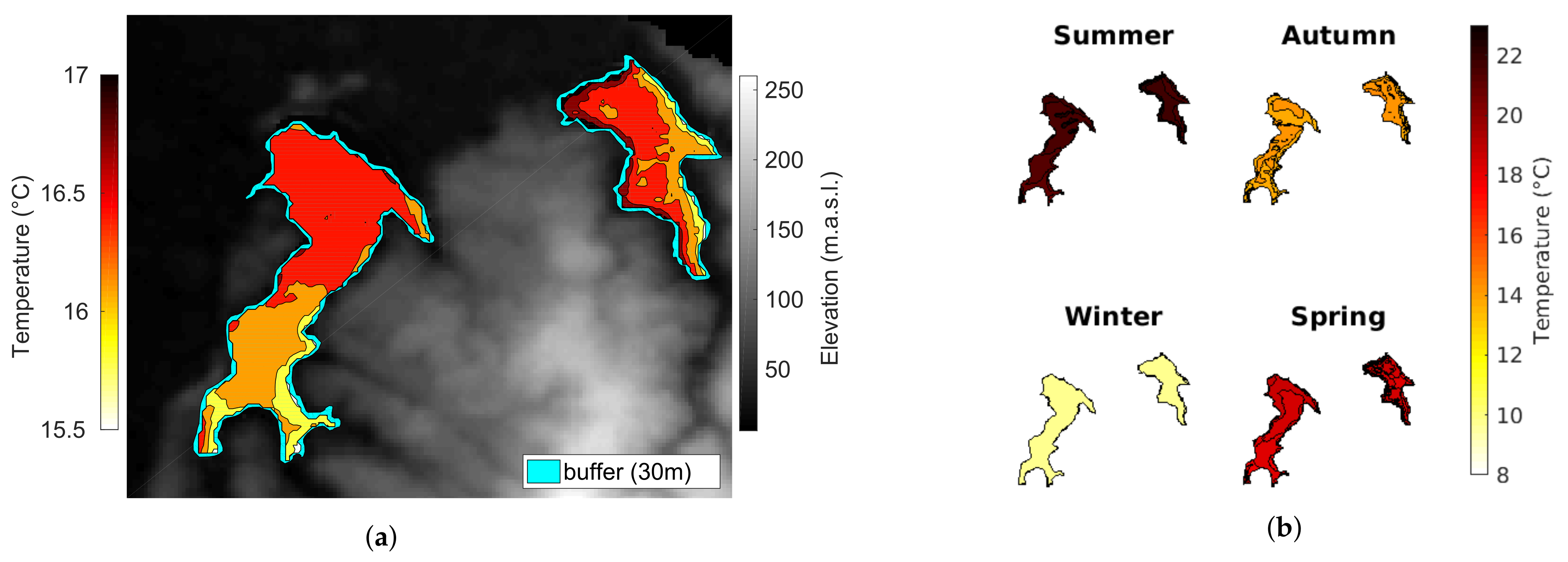
| PARAMETER | L. CHICA | L. GRANDE |
|---|---|---|
| Lake area (km) | 0.82 | 1.55 |
| Mean depth (m) | 10.3 | 8.1 |
| Maximum depth (m) | 17 | 13.5 |
| Maximum length (km) | 1.9 | 2.7 |
| Height (m.a.s.l.) | 5 | 4 |
| Station | Coordinates (Decimal Degrees) | Period |
|---|---|---|
| D | −36.8495, −73.1091 | |
| C | −36.8620, −73.1136 | 1988–2013 |
| S | −36.8688, −73.1161 | |
| C2 | −36.8582, −73.1105 | 2014–2016 |
| AT | −36.8378, −73.0617 | 1979–2016 |
| Image Collection | Available Period (DD/MM/YYYY) | Used Period (DD/MM/YYYY) | Possible Images | Tier 1 Images | Images Filtered by Clouds | Min and Max of Images per Year |
|---|---|---|---|---|---|---|
| L7 Tier 1 L7 Surface Reflectance Tier 1 | 15/4/1999 –present | 1/1/2000–31/12/2009 1/1/2000–7/10/2020 | 205 401 | 128 298 | 76 168 | 4 and 12 |
| L8 Tier 1 L8 Surface Reflectance Tier 1 | 11/2/2013 –present | 11/2/2013–13/9/2020 | 173 | 146 | 85 | 10 and 13 |
| Method | Input | Reference |
|---|---|---|
| M1 | Atmospheric parameters Water emissivity L7 Tier 1 (Table 3) | [43] Equation (6) or [44] [45] |
| M2 | L8 Tier 1 (Table 3) | [23] |
| M3 | L8 Tier 1 (Table 3) | [23] |
| M4 | L7 Surface Reflectance Tier 1 (Table 3) | [46] |
| M5 | L8 Surface Reflectance Tier 1 (Table 3) | [47] |
| M6 | Atmospheric parámeters Collection L7 Tier 1 (Table 3) | GEE code provided by [28] [45] |
| Data Set | Mean Images per Month (Month) | Min. Images per Month (Month) | Max. Images per Month (Month) |
|---|---|---|---|
| i | 7 | 2 (June) | 13 (February) |
| ii | 14 | 6 (June) | 26 (February) |
| iii | 7 | 4 (October) | 9 (April, December) |
| Time Serie | Period | Bf Cal | Af Cal | (°C) | |
|---|---|---|---|---|---|
| (°C) | |||||
| in situ | 2000–2009 | 16.18 | 4.34 | ||
| tM1 | 16.54 | 16.18 | 3.96 | ||
| tM2 | 2013–2020 | 15.22 | 3.90 | ||
| tM3 | 8.67 | 16.00 | 4.00 | ||
| tM5 | 14.43 | 3.89 | |||
| tM4 | 2000–2020 | 15.22 | 16.06 | 3.90 | |
| tM6 | 16.98 | 16.36 | 4.29 | ||
| Time Serie | Comparisson Period | R | Before Calibration | After Calibration | |||
|---|---|---|---|---|---|---|---|
| RMSE | Bias | d | Bias | d | |||
| in situ–tM1 | 2000–2009 | 0.74 | 2.08 | −0.36 | 0.92 | 0.92 | |
| in situ–tM4 | 0.71 | 2.35 | 1.25 | 0.88 | 0 | 0.91 | |
| in situ–tM6 | 0.67 | 2.53 | −0.30 | 0.90 | 0.91 | ||
| tM4c–tM2 | 2013–2020 | 0.87 | 1.75 | 0.77 | 0.95 | 0.96 | |
| tM4c–tM3 | 0.89 | 7.46 | 7.33 | 0.61 | 0 | 0.97 | |
| tM4c–tM5 | 0.87 | 2.21 | 1.57 | 0.93 | 0.96 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedreros-Guarda, M.; Abarca-del-Río, R.; Escalona, K.; García, I.; Parra, Ó. A Google Earth Engine Application to Retrieve Long-Term Surface Temperature for Small Lakes. Case: San Pedro Lagoons, Chile. Remote Sens. 2021, 13, 4544. https://doi.org/10.3390/rs13224544
Pedreros-Guarda M, Abarca-del-Río R, Escalona K, García I, Parra Ó. A Google Earth Engine Application to Retrieve Long-Term Surface Temperature for Small Lakes. Case: San Pedro Lagoons, Chile. Remote Sensing. 2021; 13(22):4544. https://doi.org/10.3390/rs13224544
Chicago/Turabian StylePedreros-Guarda, María, Rodrigo Abarca-del-Río, Karen Escalona, Ignacio García, and Óscar Parra. 2021. "A Google Earth Engine Application to Retrieve Long-Term Surface Temperature for Small Lakes. Case: San Pedro Lagoons, Chile" Remote Sensing 13, no. 22: 4544. https://doi.org/10.3390/rs13224544
APA StylePedreros-Guarda, M., Abarca-del-Río, R., Escalona, K., García, I., & Parra, Ó. (2021). A Google Earth Engine Application to Retrieve Long-Term Surface Temperature for Small Lakes. Case: San Pedro Lagoons, Chile. Remote Sensing, 13(22), 4544. https://doi.org/10.3390/rs13224544






