Abstract
Water vapor is one of the most important greenhouse gases in the world. There are many techniques that can measure water vapor directly or remotely. In this work, we first study the Global Positioning System (GPS)- and the Global Navigation Satellite System (GLONASS)-derived Zenith Wet Delay (ZWD) time series based on 11 years of the second reprocessing campaign of International Global Navigation Satellite Systems (GNSS) Service (IGS) using 320 globally distributed stations. The amount of measurement, the local environment, and the antenna radome are shown to be the main factors that affect the GNSS ZWDs and the corresponding a posteriori formal errors. Furthermore, antenna radome is able to effectively reduce the systematic bias of ZWDs and a posteriori formal errors between the GPS- and GLONASS-based solutions. With the development of the GLONASS, the ZWD differences between the GPS- and the GLONASS-based solutions have gradually decreased to sub-mm-level after GLONASS was fully operated. As the GPS-based Precipitable Water Vapor (PWV) is usually used as the reference to evaluate the other PWV products, the PWV consistency among several common techniques is evaluated, including GNSSs, spaceborne sensors, and numerical products from the European Center for Medium-Range Weather Forecasts (ECMWF). As an example of the results from a detailed comparison analysis, the long-term global analysis shows that the PWV obtained from the GNSS and the ECMWF have great intra-agreements. Based on the global distribution of the magnitude of the PWV and the PWV drift, most of the techniques showed superior agreement and proved their ability to do climate research. With a detailed study performed for the ZWDs and PWV on a long-term global scale, this contribution provides a useful supplement for future research on the GNSS ZWD and PWV.
1. Introduction
Water vapor is the most abundant greenhouse gas in the atmosphere. It can amplify the climatic effects caused by other greenhouse gases such as carbon dioxide and methane [1,2]. The heat-trapping effect of water vapor in the atmosphere estimated by the Atmospheric Infrared Sounder (AIRS) confirms that water vapor plays the dominant role in climate change [3]. Therefore, water vapor measurement has an important guiding role in human life and production [4].
Electronic transducers, moistened thermometers, or hygroscopic materials measure the water vapor directly. Water vapor can also be measured by microwave radiometer and other techniques. However, a microwave radiometer is expensive and can be affected by weather conditions and calibrations. Based on the long-term records from the late 1940s and data in a global network, radiosondes have become one of the most important techniques for measuring water vapor [5]. However, due to the disturbance of different biases, sparse sites, the drift of the balloon, and continuous changes in instrumentation, the homogeneously global products of water vapor are difficult to be achieved using radiosonde [6]. Atmosphere-oriented space missions provide an alternative approach for water vapor monitoring. Terra and Aqua are twin satellites designed to collect information about the Earth’s water cycle, including water vapor in the atmosphere [7]. They were launched by the National Aeronautics and Space Administration (NASA) in 1999 and 2002, respectively, equipped with a Moderate Resolution Imaging Spectroradiometer (MODIS) payload each. AIRS is another sensor on the Aqua platform used to perform water vapor monitoring. Spaceborne sensors are capable of detecting water vapor both on land and ocean under a clear-sky environment with an unchangeable temporal resolution, which is determined by the period of the satellite orbit [8]. Apart from radiosonde and spaceborne sensors, numerical weather datasets can also be used to analyze water vapor. The European Center for Medium-Range Weather Forecasts (ECMWF), as an example, is the source of the world’s largest numerical weather dataset, providing data from 1957 to the present. The (ERA5) [9] and the ECMWF Reprocessing-Interim (ERA-Interim) [10] are the two most widely used ECMWF weather datasets.
In addition to the abovementioned approaches, atmospheric water vapor can be retrieved with high precision from space-geodetic techniques such as Very Long Baseline Interferometry (VLBI), and Global Navigation Satellite Systems (GNSSs) [11,12]. The water vapor retrieved from these two approaches fifth ECMWF Reprocessing aches has a high temporal resolution of one or two hours, and is robust against severe weather conditions. Compared to the sparsely distributed VLBI stations, GNSS has a denser global network. The International GNSS Service (IGS), for example, has been providing high-precision and high-resolution Zenith Total Delays (ZTD) products since 1992 [13]. The ZTD can further be divided into the Zenith Hydrostatic Delay (ZHD), a hydrostatic term caused by the dry gases in the atmosphere, and the Zenith Wet Delay (ZWD), a wet term caused mainly by the refractivity due to water vapor [14]. The ZHD is quite stable and can thus normally be well modeled without parameter estimation, while the ZWD is difficult to be perfectly modeled and usually requires estimation [15]. The IGS daily final products of the ZTDs estimated with the Precise Point Positioning (PPP) [16] have, for example, the dry part modeled with the Niell model [17] and the Global Mapping Function (GMF) [18] to estimate the ZWDs [19]. With a conversion factor calculated with the mean temperature with respect to the water vapor content, ZWD can then be converted to the Precipitable Water Vapor (PWV).
Douša et al. [20] demonstrated that the GNSS products revealed the capability to provide more detailed atmosphere structures than the numerical weather models. Studies were performed for long-term GNSS-based ZWDs. Klos et al. [21] conducted an in-depth study of the ZWD residuals using homogenously reprocessed Global Positioning System (GPS) observations of 120 global stations from 1995 to 2017. Wu et al. [22] studied the variation characteristics of GNSS PWV from the Crustal Movement Observation Network of China (CMONOC) from 2011 to 2019. Studies have also compared the ZWD or PWV produced using GPS and other techniques [23,24,25,26,27,28,29] such as radiosonde, numerical weather models, and satellite sensor products [8,30,31,32,33] such as AIRS and MODIS. Most of these works are focused on local regions with a limited period from a few months to 2~3 years. The GPS PWV is usually used as the reference in these works. The performance of GNSS-based PWV and the intraconsistency between different products, however, are seldom mentioned. One example is the intraconsistency between the ZWDs or PWVs obtained with the GPS- and the Global Navigation Satellite System (GLONASS)-based solutions, especially on a long-term global scale.
Following the full constellation development of the GPS in 1994, three more GNSSs appeared, namely the Russian GLONASS, the Galileo of the European Union (EU), and the Beidou Satellite Navigation System (BDS) of China. The consistency among the ZWDs estimated with different GNSSs awaits further investigation. In the study of Algonquin Park station from 1997 to 2004, Steigenberger et al. [34] showed that the different Phase Center Offset (PCO) and Variation (PCV) models of antennas resulted in a systematic bias between the IGS ZTDs and their homogeneously reprocessed GPS ZTDs. The IGS products are a combination of near real-time analyses of several analysis centers (ACs). They are therefore affected by differences in the modeling and processing strategies of different ACs, and by changes in the definition of the geodetic datum. In contrast, the homogeneous reprocessed GPS ZTDs were estimated using consistent models and processing strategies, so that degradations from that side can be avoided. It shows the necessity of evaluating the GNSS PWVs using consistent models and reference frames. By late 2013, IGS performed their second reprocessing (repro2) using GPS and GLONASS observations from 1994 to 2013 in a fully consistent way using the latest models and methodology by then [35]. By late 2019, IGS performed the third reprocessing [36], which has not yet released the final products.
This work mainly focuses on the systematic bias between the ZWDs obtained with GPS- and the GLONASS-based solutions using the products of the IGS repro2. Since the PWVs retrieved from the GPS-based ZWDs are usually used as the reference to evaluate other PWVs products, this work also focuses on the PWVs consistency among different common techniques. Firstly, the covered regions, the studied period, the multi-technique water vapor products, and the algorithm to retrieve the GNSS-based PWVs are introduced. Next, the systematic bias between the GPS- and GLONASS-based ZWDs is studied. It is followed by the assessment of the intraconsistency among the PWVs obtained with the GPS and the GLONASS, the MODIS Aqua and the MODIS Terra, the ERA5 and the ERA-Interim products; and the assessment of the interconsistency between PWVs obtained with the ERA5 products and the GPS, the MODIS Aqua, and the AIRS.
2. Data and Methods
In this section, the covered region, period, and PWV products from several techniques are introduced. The algorithm to retrieve the GNSS-based PWVs is also explained in detail.
2.1. Multi-Technique and GNSS Data
The multi-technique water vapor measurements are collected from the following sources:
- The spaceborne sensors, i.e., the MODIS infrared PWV products of the Aqua and Terra platform, and the AIRS level-2 products from the Aqua platform;
- The numerical weather model Integrated Water Vapor (IWV) products from the ERA5 and the ERA-Interim—IWV can be converted to PWV by dividing by the density of liquid water;
- The GNSS-based ZWDs.
The PWV products retrieved with spaceborne sensors and the numerical weather model IWV products are globally gridded. Horizontal resolutions of the ERA5, ERA-Interim, MODIS, and AIRS products are 0.25° 0.25°, 0.75° 0.75°, 5 km 5 km, and 1° 1°, respectively. Temporal resolutions of ERA5, ERA-Interim products, and those from the three spaceborne sensors are 1, 6, and 12 h, respectively.
In this study, the PWV derived from the gridded spaceborne sensors and the IWV products are interpolated to the positions of 320 globally distributed IGS stations, for which the ZWDs were estimated within the IGS repro2 with three types of solutions, namely the GPS, the GLONASS, and the combined GPS/GLONASS (“Combined” for short) solutions. All of the stations could receive GPS signals, and 154 of them could receive both GPS and GLONASS signals, as shown in Figure 1.
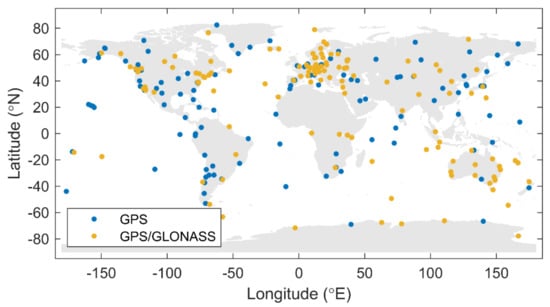
Figure 1.
Global Navigation Satellite Systems (GNSS) network of 320 stations.
Figure 2a shows the number of stations (weekly averaged) used in the three abovementioned solution types. For the GPS-based and the Combined solutions, there were approximately 220~250 stations used per day. For the GLONASS solutions, the station number has gradually increased from 30 in 2003 to nearly 120 in 2012. The number of GPS satellites is around 30 in general, while the GLONASS satellites reached 19 in 2009 and was around 24 after 2011, as shown in Figure 2b (weekly averaged).
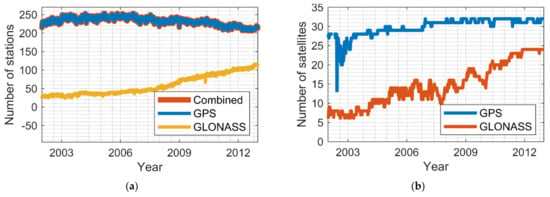
Figure 2.
(a) Number of stations used in each solution. (b) Weekly averaged number of available satellites.
2.2. GNSS PWV Retrieval Algorithm
The PWV can be converted from the GNSS-based ZWD using a conversion factor. To minimize the impact caused by model differences, in this work, we used GNSS-based ZWDs that were homogeneously reprocessed as global double-difference solutions using signals from the GPS, the GLONASS, and these two systems combined, i.e., the IGS repro2 products. The homogeneous reprocessing using consistent models avoided systematic bias caused by model changes. Note that double-difference ambiguities were only fixed for GPS. Instead of relative corrections, absolute corrections for antenna phase center offset (PCO) and phase center variation (PCV) were used for receiver and satellites [37,38] to avoid systematic errors [39].
In the global parameter estimation of this work, the 6-hourly ECMWF-based hydrostatic delays mapped with the dry Vienna Mapping Function (VMF1) [19] are used as the a priori tropospheric delay. The 2-hourly piecewise linear ZWDs are estimated, mapped with the wet VMF1 mapping function. The 24-hourly troposphere gradients [40] are estimated for each station. The solid Earth tides [41,42], the pole tides [43], the ocean loading [44], and atmospheric pressure tidal [45] are modeled according to the International Earth Rotation and Reference Systems Service (IERS) Conversions 2003 [46]. The station coordinates are shown to have millimeter-level accuracy, which implies a high accuracy of the estimated ZWDs based on their high correlations [47]. More details of model and strategy were described by Steigenberger et al. [48] and Fritsche et al. [35].
The ZWDs obtained based on GNSS estimation are multiplied with the conversion factor to get the IWV. The IWV can then be easily transformed to PWV, as expressed below [49]:
with
where , are the refractivity constants, is the gas constant for water vapor, is the weighted mean temperature of the atmosphere in Kelvin, and is the density of liquid water.
From (1), it can be seen that in addition to a few constant values, the conversion factor mainly depends on the weighted mean temperature of the troposphere with respect to its water vapor content. The method of calculating weighted mean temperature is expressed below [50]:
where is the partial water pressure in hPa, is the temperature in Kelvin, is inverse compressibility of wet air, and is the surface/antenna height. Details about the method to calculate and are described by Schüler [51].
3. Case Study of the GNSS-Based ZWDs
In this section, the comparison between GNSS-based ZWDs is studied first. It is followed by the analyses concerning the different types of solutions based on the reprocessed ZWDs.
3.1. The Time Series
In this part, we study the long-term behaviors of the ZWDs and their corresponding a posteriori formal errors (“formal errors” for short) of the three solution types mentioned before for 320 stations from 2002 to 2012. From Figure 1, it can be seen that during this period the number of GPS satellites is almost 32 after 2007. The number of stations that can receive GPS signals is quite stable, approximately equaling 220. The number of GLONASS satellites is gradually growing. After 2009, the growth rate of the stations tracking GLONASS signals has increased. Since the model-related error sources are controlled by the homogeneous reprocessing [35], the number of measurements and hardware replacements are the remaining two main error sources in the ZWDs, which will be discussed later.
Figure 3a,b shows the formal errors of the GPS- and GLONASS-based ZWDs, respectively. One hundred fifty-four dual-system stations are sorted by latitude from north to south. The black horizontal line is the dividing line between the northern and southern hemispheres. After 2009, the GPS formal errors are about 0.3 mm, which are about 0.4 mm smaller than before. The GLONASS formal errors have also been reduced from approximately 2 to 1.5 mm. These improvements are mainly related to the increase in the number of measurements.
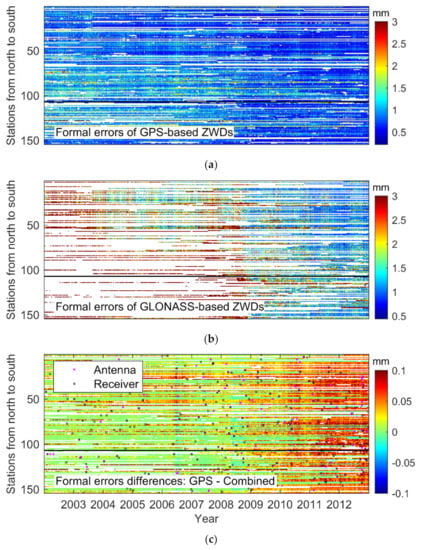
Figure 3.
Time series of 154 global stations that can receive dual-system signals. (a) The Global Positioning System (GPS)-based formal errors for the Zenith Wet Delay (ZWD). (b) The Global Navigation Satellite System (GLONASS)-based formal errors for the ZWDs. (c) The formal error differences between the GPS-based and the Combined-based ZWDs. (Stations are sorted by latitude from north to south. The black horizontal line is the dividing line between the northern and southern hemispheres. Black and pink squares are the receiver and antenna replacement marks, respectively).
Figure 3c shows the formal error differences between the GPS-based and the dual-system ZWDs since their magnitudes are very close and difficult to distinguish. The black square denotes the receiver replacement mark, the pink square represents the antenna replacement mark. As receivers and antennas are replaced or updated, increasingly more GLONASS measurements can be received and incorporated into the Combined solution, the formal error differences have thus increased, and become more or less stable after GLONASS is fully operational in 2011.
Figure 4 shows the ZWD differences between the GPS-based and the Combined solutions, together with those between the GPS-based and the GLONASS-based solutions. From 2002 to 2012, the magnitude of ZWD differences in the former case is generally smaller than 1.5 mm. For the latter case, one could observe an increase with a factor of 10. After 2009, the differences between the GPS-based and the Combined solutions have increased, and the differences between GPS- and GLONASS-based solutions have decreased. It shows that the increase in the GLONASS measurements has improved the model strength, thereby achieving more accurate ZWDs and playing a more important role in the joint solution.
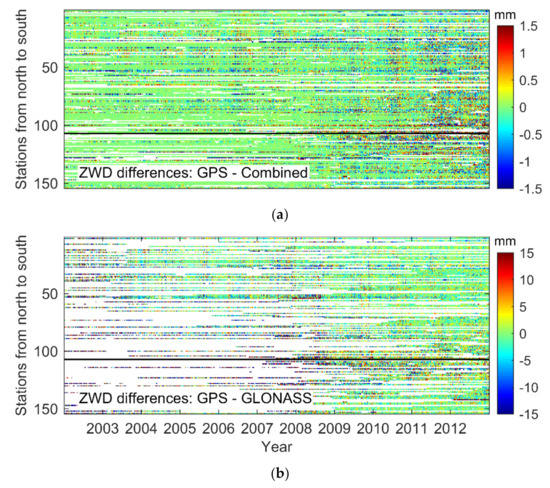
Figure 4.
Time series of 154 global stations that can receive dual-system signals. (a) The ZWD differences between the GPS-based and the Combined solutions, and (b) between the GPS- and the GLONASS-based solutions.
The weighted mean of the ZWD differences (thin and thick solid lines are the raw values and the one-order polynomial fitting curves, respectively) and their corresponding standard deviations (STDs) (shadows) are shown in Figure 5. The thick solid lines are the one-order polynomial fitting curve of the weighted mean of the ZWD differences. The formal errors are used as the weight. The one-order polynomial is performed as follows:
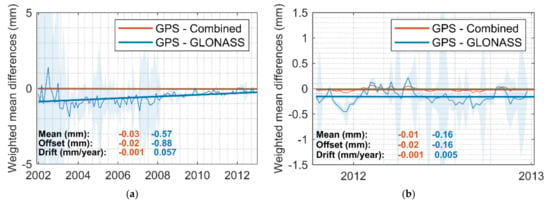
Figure 5.
Time series of the weighted mean of the ZWD differences (thin and thick solid lines are the raw values and the one-order polynomial fitting curves, respectively) of 154 global stations between the GPS-based and the Combined solutions, the GLONASS-based solutions, and their corresponding standard deviation (shadows). (a) January 2002–December 2012, 1 value per month. (b) October 2011–December 2012, one value per week.
Figure 5a shows the monthly weighted mean ZWD differences from January 2002 to December 2012. Figure 5b shows the weekly weighted mean ZWD differences from October 2011 to December 2012, when both measurements of GPS and GLONASS are stable, respectively. It can be seen that the magnitude of the ZWD differences between the GPS-based and the Combined solutions are much smaller than the differences between the GPS- and the GLONASS-based solutions. After October 2011, the mean value, offset, and drift of the differences between GPS and Combined are at the same level as before. For GPS and GLONASS, the change is much more significant. From Figure 5, we can see that as the GLONASS satellite number increases, the ZWD differences between the GPS- and the GLONASS-based solutions are steadily decreasing. After October 2011, when there are sufficient GLONASS satellites and ground-based tracking stations, the ZWD differences between the GPS- and the GLONASS-based solutions become rather stable. The mean value varies from −0.57 to −0.16 mm. The offset changes from −0.88 to −0.16 mm, and the drift dropped from 0.057 to 0.005 mm/year. The mean value and offset reflect the systematic bias between different GNSSs, and the drift reflects the changes in the systematic bias. A small drift means a stable systematic bias, which should correspond to the actual situation. The results reflect the progress of GLONASS construction. Still, GPS plays a dominant role in a joint solution.
From the time series of the GNSS-based ZWDs, their formal errors, and the number of stations and satellites, it can be seen that the amount of measurement is crucial to reduce the systematic bias between different GNSS-based ZWDs and to reduce the formal errors of the GNSS-based ZWDs.
3.2. The Global Distribution
To better study the global distribution of the ZWDs, the period from October 2011 to October 2012 is selected to avoid the impact of the amount of measurement. In addition, to avoid potential influences of the hardware, 86 stations that have upgraded their hardware equipment and did not change during the test period are used.
Figure 6 shows the global distribution of the ZWDs, their formal errors, the ZWD differences, and the formal error differences between the GPS- and the GLONASS-based solutions. The size of the circles represents the magnitude of the values. Different colors represent different antenna brands. For comparison purpose, all values are normalized in each subplot.
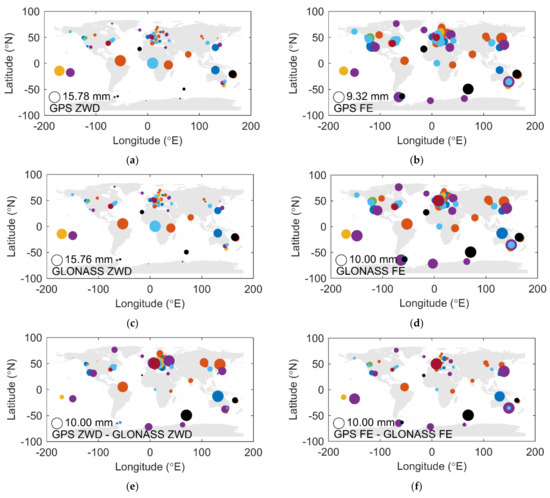
Figure 6.
Global distribution of the GNSS-based ZWDs (a,c); formal errors (FE) (b,d); ZWD differences (e); and the FE differences (f). Values are normalized to make them comparable. Different colors indicate different antenna brands.
From Figure 6a,c it can be seen that the magnitude of the ZWDs is closely related to the latitude. However, there are no significant latitude-related patterns in the other subplots. In general, the distribution of the ZWD differences and the formal error differences shown in Figure 6e,f appears consistent. The distribution of formal errors in Figure 6f shows a similar but more stable pattern compared to the ZWD differences in Figure 6e.
Since the selected stations completed the hardware upgrade after GLONASS was fully operational, in this case, the amount of measurement is not a major issue affecting the ZWDs and the formal errors. Possible reasons for the irregular distribution with latitude of the magnitude of differences could be the local environment and the ocean current.
3.3. The Hardware Equipment—Antenna Radome
The correct orientation of the antenna has great influence on the vertical parameters such as the ZWD [37]. The antenna radome serves as an important protection to the antennas. Its impact on the ZWD determination is therefore studied in this section.
Figure 7 shows the formal errors of the station REUN (Le Tampon, France) and the station BRMU (Town of St. George’s, UK). Before 2011, the receiver or an antenna change leads to noticeable improvements in the formal errors. After 2011, the hardware equipment no longer causes such large jumps as before. The fundamental reason is still the amount of measurement. During the development of the GNSS constellations, new equipment often means capability to track more signals.
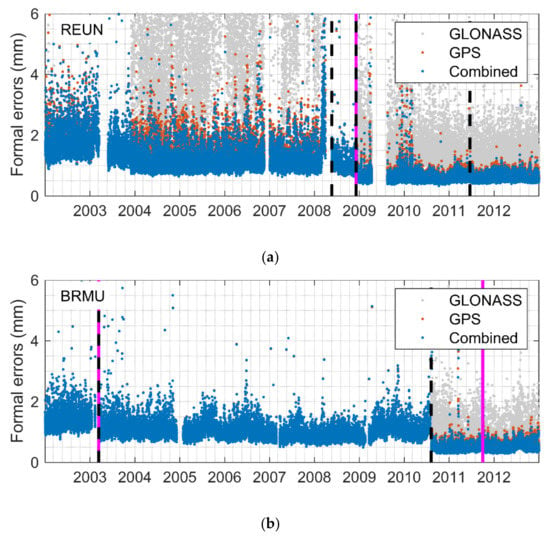
Figure 7.
Formal error series of station REUN (a) and station BRMU (b). The black dashed line and the pink line represents the receiver and antenna change mark, respectively.
In order to evaluate the performance of the antenna radome, the local environment and the amount of measurement should be considered. Co-located stations are selected, and eligible test periods are selected without hardware equipment changes.
The selected six pairs of co-located stations are only characterized by the antenna radome, with different types of antenna brands or series. The locations of the six pairs of co-located stations are shown in Figure 8, and the details of these stations are listed in Table 1.
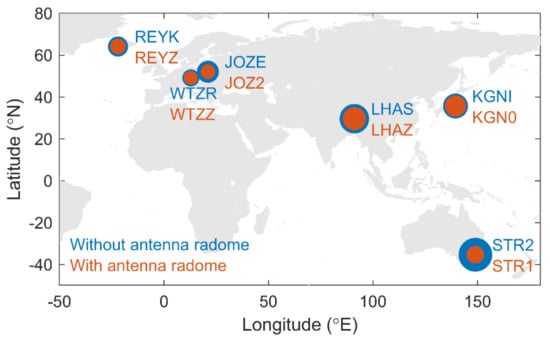
Figure 8.
Normalized formal errors of six pairs of co-located stations.

Table 1.
Information of the co-located Global Positioning System (GPS) stations have both radome and non-radome antenna.
During the selected period, all these stations have only GPS measurements. Therefore, the GPS-based formal errors are compared for each pair of co-located stations (see the last column of Table 1). Outliers are removed according to the three-sigma rule. The size of the circles in Figure 8 represents the mean value of the formal errors. From both Figure 8 and Table 1, it can be seen that for each pair, the formal errors of the stations with an antenna radome (red circles) are always smaller and more stable than those without an antenna radome (blue circles). This implies better accuracy of the GPS-based ZWDs that could be achieved by the antenna radome.
Next, eight pairs of co-located stations are selected to see if the antenna radome could reduce the formal error differences between the two co-located stations. Each pair has the same antenna type. In the eligible period of each pair, only GPS measurements are considered.
The locations and the details of these eight pairs of co-located stations are shown in Figure 9 and Table 2, respectively. There are four pairs having the antenna radomes (red circles in Figure 9) and the others are not (blue circles in Figure 9). The absolute formal error differences are listed in the last column of Table 2, and the size of the circles in Figure 9 represents the mean value of the absolute formal error differences. It can be seen that the four pairs with antenna radomes have smaller formal error differences than those without radomes.
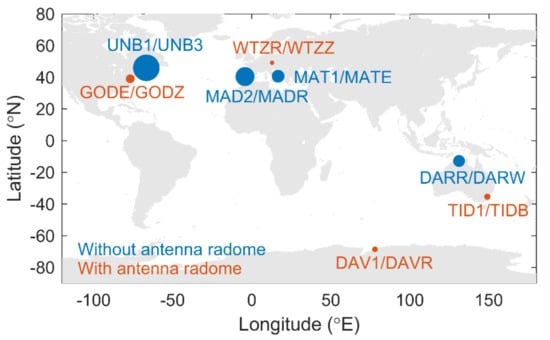
Figure 9.
Normalized formal error differences for eight pairs of co-located stations.

Table 2.
Information of the co-located GPS stations having the same antenna type.
Figure 10 shows the time series of the eight pairs of formal error differences. It shows that although there is a slight height difference between the station WTZR and station WTZZ, which could lead to very slight environmental differences, their formal errors are still very close. This proves that, in this case, such a small height difference is not an issue that may affect the performance of the formal errors. This analysis shows that the antenna radome can reduce the systematic bias between the formal errors.
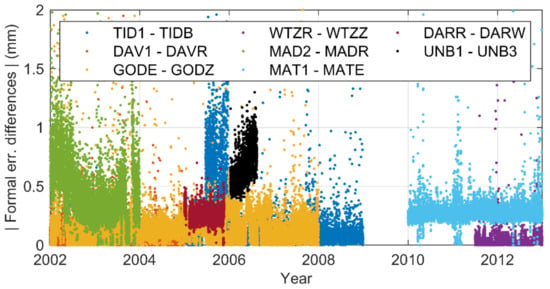
Figure 10.
Time series of formal error differences for eight pairs of co-located stations.
Finally, larger samples containing 86 stations are analyzed considering the antenna radome issue. There is no change in the hardware equipment during the test period for these stations. Among them, 36 stations have antenna radomes. The histogram of the differences is shown in Figure 11. After removing outliers according to the three-sigma rule, the statistical results are listed in Table 3. It can be seen that for both formal error differences and the ZWD differences, those with antenna radomes show better performance.
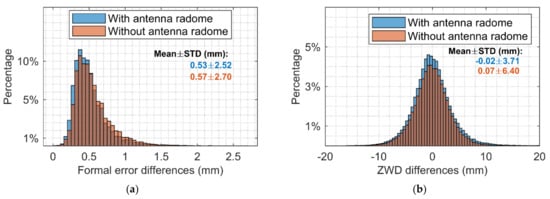
Figure 11.
Formal error differences (a) and ZWD differences (b) between the GPS- and the GLONASS-based solutions.

Table 3.
Statistical results of the formal error differences and the ZWD differences between the GPS- and the GLONASS-based solutions.
In conclusion, the ZWDs and the formal errors are analyzed from the time series perspective, the global distribution perspective, and the antenna radome perspective. The statistical results show that the amount of measurement is the main reason for the systematic bias between the GPS- and the GLONASS-based ZWDs and their formal errors. In addition, the local environment is another important issue that affects the differences between the GPS- and the GLONASS-based ZWDs and their formal errors. Lastly, the antenna radome is proved to be able to effectively reduce the formal errors of the ZWDs, as well as the formal error differences and the ZWD differences of co-located stations.
4. Evaluation of Consistency among Different Techniques
In the previous part, the systematic bias is studied for the GNSS-based ZWD. Since the PWV retrieved from the GPS-based ZWD is usually used as the reference to evaluate the PWV products from other techniques and there is seldom a need to study the accuracy of GNSS-based PWV. In this part, we focus on the consistency of PWV among different techniques, including PWV retrieved from GNSS-based ZWD. Since the Aqua satellite contained in this section was launched in May 2002, the study period here is 10 years from January 2003 to December 2012.
4.1. Intraconsistency Evaluation
Here we first focus on the intraconsistency evaluation of each technique since we have ERA5 and ERA-Interim from ECMWF, GPS, and GLONASS from GNSS, MODIS Aqua, and MODIS Terra from the MODIS platform. Linear interpolation is used to extract data at the position of 320 stations from the gridded dataset for 10 years. Monthly averaged values are used for the comparison.
From Figure 12(left) one can see the global distribution of correlation coefficients of three groups, which are ERA5/ERA-Interim (a), GPS/GLONASS (b), and MODIS Aqua/MODIS Terra (c). The histogram of the PWV differences of each group is shown on the right. In general, the ECMWF group has fewer outliers than the other two groups. The outliers in the GNSS group are mostly near the ocean, which makes sense because the variation of water vapor in those regions is larger than in others. For the MODIS group, there is a significant systematic bias between MODIS Aqua and MODIS Terra, which can be seen in the right bottom of Figure 12.
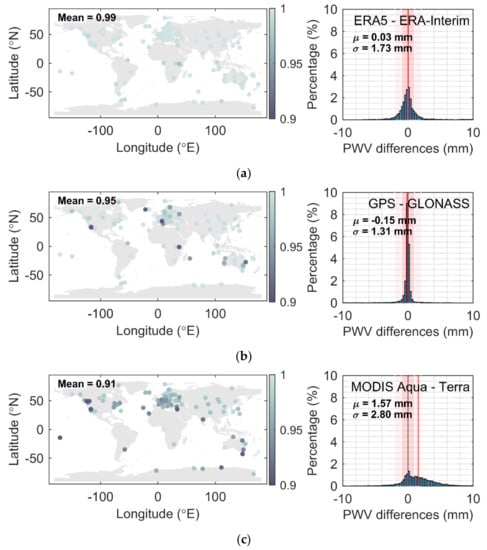
Figure 12.
Global correlation coefficients (left) and histogram of the Precipitable Water Vapor (PWV) differences (right) of group (a) The fifth European Center for Medium-Range Weather Forecasts (ECMWF) Reprocessing (ERA5)/ECMWF Reprocessing-Interim (ERA-Interim), (b) GPS/GLONASS, and (c) Moderate Resolution Imaging Spectroradiometer (MODIS) Aqua/MODIS Terra.
The statistical results are listed in Table 4. The global averaged correlation coefficients of each group in Figure 12 from top to bottom are 0.99, 0.95, and 0.91. Except for MODIS Terra, the averaged PWV of the other techniques are very close. The mean differences of each group are 0.03, −0.15, and 1.57 mm. Their corresponding STDs are 1.73, 1.31, and 2.80 mm. The magnitude of mean differences of the MODIS group, which can be also interpreted as the intrasystematic bias, is approximately 10 times larger than the other two groups, and the STD of the MODIS group is twice larger than the others. It clearly shows the large systematic bias between MODIS Aqua and MODIS Terra. The percentage of differences smaller than 1 and 2 mm of the ECMWF and GNSS group are significantly more than that in the MODIS group.

Table 4.
Statistical results of intracomparison.
Figure 13 shows the PWV differences time series of each group. It can be seen that as time increases, differences between GPS and GLONASS become closer due to the replenishment of the GLONASS constellation and construction of more ground-based GNSS stations. The systematic bias in the ECMWF group is always extremely small, but in the last 5 years the bias in GNSS seems to be smaller than that in ECMWF. That may be due to the ECMWF reanalysis strategies. For MODIS, besides the offset, there are annual and semiannual periodic terms in their differences, which is the main reason why they have a smaller correlation coefficient than the other two groups.
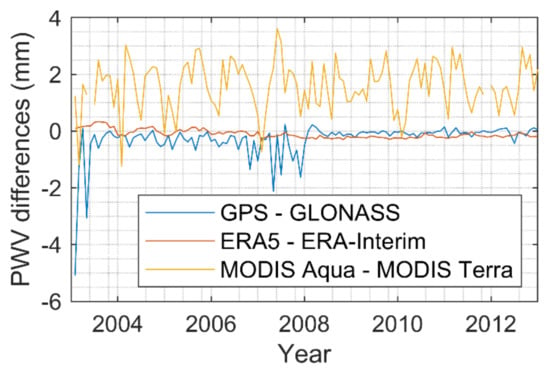
Figure 13.
Time series of the PWV intradifferences of each technique.
4.2. Interconsistency Evaluation
Interconsistency is evaluated in this section. We choose ERA5 out of two ECMWF datasets as the reference since ECMWF has a good intra-agreement. Sensor AIRS is added in this part. AIRS is a spaceborne sensor that focuses on water vapor, which is also a payload on the Aqua platform. AIRS creates 3D maps of air and surface temperature, water vapor, and cloud properties. It provides more accurate information on the vertical profiles and is one of the most advanced atmospheric sounding systems in space. It is necessary to evaluate two sensors on the same platform to see if there are any platform-dependent issues. Meanwhile, we select GPS and MODIS Aqua due to less valid data of GLONASS and the large systematic bias in MODIS Terra on the global averaged PWV.
The left side in Figure 14 shows the global distribution of correlation coefficients that are between GPS, MODIS Aqua, AIRS, and the reference ERA5, from top to bottom. The right side of Figure 14 shows the histograms of PWV differences between the reference ERA5 and other techniques. It can be seen that GPS and AIRS show better consistency with ERA5 than MODIS Aqua. However, a systematic bias exists between AIRS and ERA5 (see Figure 14, right bottom panel).
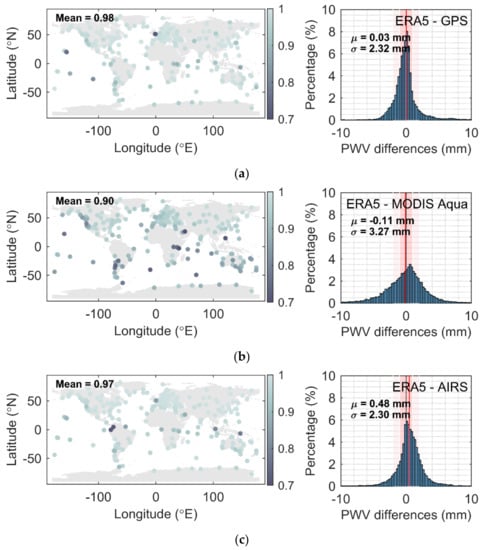
Figure 14.
Global distribution of the correlation coefficients (left) and the histograms of the PWV differences (right) of group (a) ERA5/GPS, (b) ERA5/MODIS Aqua, and (c) ERA5/Atmospheric Infrared Sounder (AIRS).
The statistical results are listed in Table 5. The global averaged PWV of ERA5 is different from the value in Table 5, as GLONASS is not involved here and more valid overlap data are available. The global averaged PWV of GPS is the closest to ERA5. AIRS has a less accurate global averaged PWV compared to other techniques, but it has a high correlation with ERA5 and a small STD of PWV differences between AIRS and ERA5. From the last three lines in Table 5, it can be seen that GPS is more consistent with ERA5 than others at different PWV difference intervals.

Table 5.
Statistical results of intercomparison between GPS, MODIS Aqua, Atmospheric Infrared Sounder (AIRS), and reference ERA5.
Figure 15 shows the time series of PWV differences between GPS, MODIS Aqua, AIRS, and the reference ERA5. It shows that GPS approaches ERA5 with increasing time. The systematic bias between AIRS and ERA5 is quite stable without very large variation. For MODIS Aqua, significant annual and semiannual periodic terms can be observed in their differences with ERA5, which seems to be sensor-dependent, as AIRS does not have similar periodic effects.
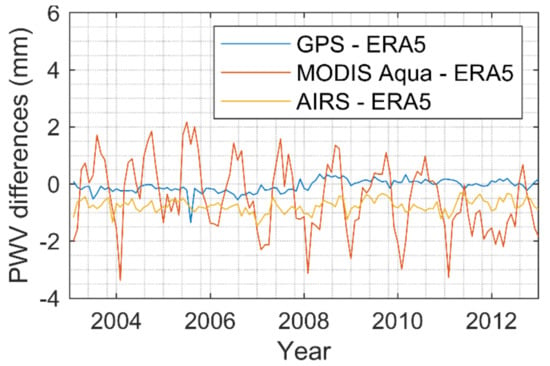
Figure 15.
Time series of the PWV interdifferences between ERA5 and other techniques.
4.3. The Global Distribution of PWV and the PWV Drift
Representatives of each technology are selected for analysis. They are ERA5, GPS, AIRS, and MODIS Aqua. Figure 16 shows the global distribution of the PWV values retrieved from ERA5, GPS, AIRS, and MODIS Aqua. These values are the mean PWV from 2003 to 2012. The range of PWV is from 0 mm to around 60 mm. It can be seen that the PWV in each subplot shows a latitude-related pattern, although the PWV from MODIS shows less consistency compared to others, as shown in the previous subsections. On a global scale, it is not an issue to study the magnitude of PWV.
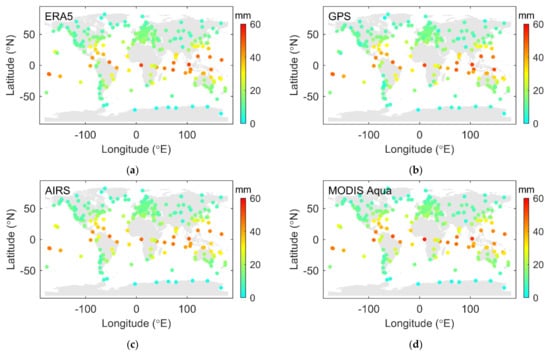
Figure 16.
Global distribution of PWV from ERA5 (a), GPS (b), AIRS (c), and MODIS Aqua (d).
Figure 17 shows the global distribution of the PWV drift from ERA5, GPS, AIRS, and MODIS Aqua. The drifts are calculated from 2003 to 2012. The range of PWV drift is from around −0.3 mm/year to around 0.3 mm/year. It can be seen that the drift in the ERA5, GPS, and the AIRS subplot shows consistent patterns. The individual outliers in the GPS subplot are caused by measurement gaps. The drift in the MODIS Aqua subplot, however, seems to be smaller than others, in general. Furthermore, some of the positive drifts in the other three subplots are shown to be negative in the MODIS Aqua subplot. The drift of PWV is an important index for climate research. As such, calibrations are suggested for the PWVs from MODIS before their use for potential climate research.
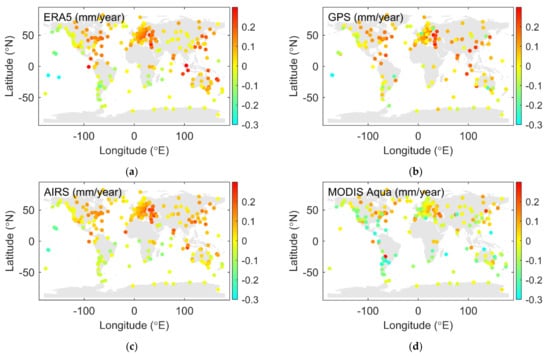
Figure 17.
The global distribution of PWV drift for the period from 2003 to 2012 from ERA5 (a), GPS (b), AIRS (c), and MODIS Aqua (d).
In conclusion, the global reanalysis from a large number of different technical sources should be the reason for the good consistency between the numerical datasets within ECMWF. The reason that GNSS-based results show a good intraconsistency should be the high-precision model of IERS 2003. The reason for the good consistency between AIRS and ERA5 could be related to the 2378 spectral channels of AIRS, which lead to a spectral resolution that is better than other infrared sounders, such as MODIS. It is difficult to see if there is any platform-dependent issue for the MODIS Aqua and AIRS due to the large magnitude values of MODIS Aqua.
For the global distribution of the PWV and the PWV drift, the 2 mm bias in MODIS Aqua is not an issue to evaluate the global PWV. However, its drift bias will affect the climate research.
5. Summary
In this work, we analyzed 11 years of reprocessed ZWD time series for 320 globally distributed GNSS stations using the IGS repro2 product with three types of solutions, i.e., GPS, GLONASS, and GPS/GLONASS combined.
A comparison of the GNSS-based ZWD was performed in this work first. During the period from 2002 to 2012, the weighted mean ZWD differences between the GPS- and the GLONASS-based solutions steadily decreased. As the number of GLONASS satellites increased, GLONASS played an increasingly more important role in the Combined solution, although GPS still led a dominant role. After October 2011, when GLONASS was almost fully operational, the ZWD differences between GPS and GLONASS were quite stable with a very slight drift. It means that the amount of measurement is the key to the systematic bias between different GNSSs. The global distribution of the ZWD differences and the formal error differences shows that there local environmental issues for each station. According to the analysis of several co-located station samples, the antenna radome can effectively improve the formal errors of ZWDs, and reduce the systematic bias between their formal errors. The global samples showed that antenna radome can effectively reduce the formal error differences and the ZWD differences between the GPS- and the GLONASS-based solutions.
Since the GPS-based PWV retrieve from the GPS-based ZWD, it is usually used as the benchmark for evaluating the PWV products from other techniques; the performance of GPS-based or GNSS-based PWV is rarely studied. Thus, the intraconsistency and interconsistency of PWV from different techniques, including GNSS-based PWV, were evaluated next. The intraconsistency of PWV in each technique group, such as GPS/GLONASS, ERA5/ERA-Interim, and MODIS Aqua/MODIS Terra, was also assessed. We chose the one with better behaviors in each group and evaluated their interconsistencies with ERA5, which was used as the reference. The results showed that the intraconsistency of ECMWF and GNSS group performed better than the MODIS group. GPS and AIRS both showed better interconsistency with ERA5 compared to MODIS Aqua. However, a systematic bias was observed between AIRS and ERA5, and there was a significant annual periodic term in MODIS Terra and MODIS Aqua as well. The mean global PWV of GPS is the one closest to ERA5. This work first shows that GNSS PWV has good intraconsistency and interconsistency with ERA5.
In general, spaceborne sensors can provide a dataset covering more than 95% of Earth’s surface, which is a necessity for a short-term weather forecast or early warning on a global scale. However, the temporal resolution of spaceborne sensors is determined by their orbit and cannot be changed. Numerical weather datasets can provide high temporal resolution gridded data. However, it has an availability delay of several months. The greatest advantage of the GNSS-based water vapor is its good intraconsistency and interconsistency with the numerical dataset. In addition, it has a high temporal resolution, which is determined by the sampling of the GNSS observation data. Furthermore, GNSS can provide a permanent service regardless of weather conditions, unlike spaceborne sensors, which can only work under good weather conditions. Although GNSS stations are sparsely distributed on the ground, they can provide region-specific monitoring, and they can be used as a reference for calibration due to their advantages of good consistency. In general, different techniques should work together and complement each other. As denser ground networks can be expected in the future and different GNSSs are experiencing rapid development, GNSS is capable of performing a more important role in climate monitoring and weather forecasting. As such, this work will provide a useful supplement for future research.
Author Contributions
H.S. performed the main data analysis and wrote the original draft; T.Y. performed part of the experiments with constructive discussion, and contributed to language editing; K.W. performed part of the experiments and contributed to language editing; B.S. contributed to constructive comments; X.Y. contributed to constructive comments. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Youth Innovation Project of the National Time Service Center (NTSC); the Natural Science Foundation of Shaanxi Province, grant number 2021JQ-322; the National Nature Science Foundation of China, grant number 12073034 and 12003041; and the West Light Foundation of the Chinese Academy of Sciences, grant number XAB2018YDYL01, XAB2019A06.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The GNSS data used in this work were provided by the MPG ETH Zurich. The numerical products are available on the ECMWF website (https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 21 March 2021)). The spaceborne sensor products are available at NASA GESDISC (https://disc.gsfc.nasa.gov/data-access (accessed on 31 October 2019)).
Acknowledgments
The authors would like to thank the Group of Mathematical and Physical Geodesy (MPG), ETH Zurich, for providing the GNSS ZWD data. The support from Markus Rothacher is much appreciated. The authors would also like to thank C3S (2017) and the NASA Goddard Earth Sciences Data Information and Services Center (GESDISC) for providing water vapor products used in this article, and appreciate the support from the International GNSS Monitoring and Assessment system (iGMAS), the iGMAS analysis center at NTSC, the National Space Science Data Center, and the National Science and Technology Infrastructure of China.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haeld, I.M.; Soden, B.J. Water vapor feedback and global warming. Annu. Rev. Energy Environ. 2000, 25, 441–475. [Google Scholar] [CrossRef] [Green Version]
- Minschwaner, K.; Dessler, A.E. Water vapor feedback in the tropical upper troposphere: Model results and observations. J. Clim. 2004, 17, 1272–1282. [Google Scholar] [CrossRef]
- Dessler, A.; Zhang, Z.; Yang, P. Water-vapor climate feedback inferred from climate uctuations, 2003–2008. Geophys. Res. Lett. 2008, 35, L20704. [Google Scholar] [CrossRef] [Green Version]
- Gradinarsky, L.; Johansson, J.; Bouma, H.; Scherneck, H.G.; Elgered, G. Climate monitoring using GPS. Phys. Chem. Earth Parts ABC 2002, 27, 335–340. [Google Scholar] [CrossRef]
- Elliott, W.P.; Gaffen, D.J. On the utility of radiosonde humidity archives for climate studies. Bull. Am. Meteorol. Soc. 1991, 72, 1507–1520. [Google Scholar] [CrossRef]
- Ross, R.J.; Elliott, W.P. Radiosonde-based northern hemisphere tropospheric water vapor trends. J. Clim. 2001, 14, 1602–1612. [Google Scholar] [CrossRef]
- Parkinson, C.L. Aqua: An earth-observing satellite mission to examine water and other climate variables. IEEE Trans. Geosci. Remote Sens. 2003, 41, 173–183. [Google Scholar] [CrossRef]
- Chang, L.; Gao, G.; Li, Y.; Zhang, Y.; Zhang, C.; Zhang, Y.; Feng, G. Variations in water vapor from AIRS and MODIS in response to Arctic sea ice change in December 2002–November 2016. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7395–7405. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (C3S). ERA5: Fifth Generation of ECMWF Atmospheric Reanalysis of the Global Climate. Copernicus Climate Change Service Climate Data Store (CDS). 2017. Available online: https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 21 March 2021).
- ECMWF—European Centre for Medium-Range Weather Forecasts. The ERA-Interim Reanalysis Dataset, Copernicus Climate Change Service (C3S). European Centre for Medium-Range Weather Forecast. 2011. Available online: https://www.ECMWF.int/en/forecasts/datasets/archive-datasets/reanalysis-datasets/era-interim (accessed on 3 October 2019).
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Resch, G. Water vapor radiometry in geodetic applications. In Geodetic Refraction; Springer: Cham, Switzerland, 1984; pp. 53–84. [Google Scholar]
- Beutler, G.; Rothacher, M.; Schaer, S.; Springer, T.; Kouba, J.; Neilan, R. The international GPS service (IGS): An interdisciplinary service in support of earth sciences. Adv. Space Res. 1999, 23, 631–653. [Google Scholar] [CrossRef]
- Davis, J.; Herring, T.; Shapiro, I.; Rogers, A.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Emardson, T.R.; Elgered, G.; Johansson, J.M. Three months of continuous monitoring of atmospheric water vapor with a network of global positioning system receivers. J. Geophys. Res. Atmos. 1998, 103, 1807–1820. [Google Scholar] [CrossRef]
- Zumberge, J.; Hein, M.; Jefferson, D.; Watkins, M.; Webb, F. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. Solid Earth 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global mapping function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef] [Green Version]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-range Weather Forecasts operational analysis data. J. Geophys. Res. Solid Earth 2006, 111, B02406. [Google Scholar] [CrossRef]
- Douša, J.; Dick, G.; Kačmařík, M.; Brožková, R.; Zus, F.; Brenot, H.; Stoycheva, A.; Möller, G.; Kaplon, J. Benchmark campaign and case study episode in central europe for development and assessment of advanced GNSS tropospheric models and products. Atmos. Meas. Tech. 2016, 9, 2989–3008. [Google Scholar] [CrossRef] [Green Version]
- Klos, A.; Hunegnaw, A.; Teferle, F.N.; Abraha, K.E.; Ahmed, F.; Bogusz, J. Statistical significance of trends in zenith wet delay from re-processed GPS solutions. GPS Solut. 2018, 22, 51. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Jin, S.; Li, Z.; Cao, Y.; Ping, F.; Tang, X. High-precision GNSS PWV and its variation characteristics in China based on individual station meteorological data. Remote Sens. 2021, 13, 1296. [Google Scholar] [CrossRef]
- Wilgan, K.; Rohm, W.; Bosy, J. Multi-observation meteorological and GNSS data comparison with numerical weather prediction model. Atmos. Res. 2015, 156, 29–42. [Google Scholar] [CrossRef]
- Ning, T.; Wickert, J.; Deng, Z.; Heise, S.; Dick, G.; Vey, S.; Schöne, T. Homogenized time series of the atmospheric water vapor content obtained from the GNSS reprocessed data. J. Clim. 2016, 29, 2443–2456. [Google Scholar] [CrossRef]
- Gurbuz, G.; Jin, S. Long-time variations of precipitable water vapour estimated from GPS, MODIS and radiosonde observations in Turkey. Int. J. Climatol. 2017, 37, 5170–5180. [Google Scholar] [CrossRef]
- Shoji, Y.; Sato, K.; Yabuki, M.; Tsuda, T. Comparison of shipborne GNSS-derived precipitable water vapor with radiosonde in the western North Pacific and in the seas adjacent to Japan. EPS Earth Planets Space 2017, 69, 153. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, C.; Chen, B.; Dai, W. Consistency evaluation of precipitable water vapor derived from ERA5, ERA-Interim, GNSS, and radiosondes over China. Radio Sci. 2019, 54, 561–571. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Zhang, S. GNSS-derived PWV and comparison with radiosonde and ECMWF ERA-Interim data over mainland China. J. Atmos. Sol. Terr. Phys. 2019, 182, 85–92. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, Z. Evaluating the accuracy of Jason-3 water vapor product using PWV data from global radiosonde and GNSS stations. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4008–4017. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, K.; Pan, Z.; Qin, J.; Chen, D.; Lin, C.; Chen, Y.; Tang, W.; Han, M.; Lu, N.; et al. Evaluation of precipitable water vapor from four satellite products and four reanalysis datasets against GPS measurements on the southern Tibetan plateau. J. Clim. 2017, 30, 5699–5713. [Google Scholar] [CrossRef]
- Alraddawi, D.; Sarkissian, A.; Keckhut, P.; Bock, O.; Noël, S.; Bekki, S.; Irbah, A.; Meftah, M.; Claud, C. Comparison of total water vapour content in the Arctic derived from GNSS, AIRS, MODIS and SCIAMACHY. Atmos. Meas. Tech. 2018, 11, 2949–2965. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Xu, T.; Nie, W.; Jiang, C.; Yang, Y.; Fang, Z.; Li, M.; Zhang, Z. Evaluation of precipitable water vapor from five reanalysis products with ground-based GNSS observations. Remote Sens. 2020, 12, 1817. [Google Scholar] [CrossRef]
- Khaniani, A.S.; Nikraftar, Z.; Zakeri, S. Evaluation of MODIS Near-IR water vapor product over Iran using ground-based GPS measurements. Atmos. Res. 2020, 231, 104657. [Google Scholar] [CrossRef]
- Steigenberger, P.; Tesmer, V.; Krügel, M.; Thaller, D.; Schmid, R.; Vey, S.; Rothacher, M. Comparisons of homogeneously reprocessed GPS and VLBI long timeseries of troposphere zenith delays and gradients. J. Geod. 2007, 81, 503–514. [Google Scholar] [CrossRef]
- Fritsche, M.; Sośnica, K.; Rodríguez-Solano, C.J.; Steigenberger, P.; Wang, K.; Dietrich, R.; Dach, R.; Hugentobler, U.; Rothacher, M. Homogeneous reprocessing of GPS, GLONASS and SLR observations. J. Geod. 2014, 88, 625–642. [Google Scholar] [CrossRef]
- Rebischung, P.; Villiger, A.; Herring, T.; Moore, M. Preliminary results from the third IGS reprocessing campaign. In AGU Fall Meeting Abstracts; American Geophysical Union: San Francisco, CA, USA, 2019; Volume 2019, p. G11A-03. [Google Scholar]
- Schmid, R.; Steigenberger, P.; Gendt, G.; Ge, M.; Rothacher, M. Generation of a consistent absolute phase-center correction model for GPS receiver and satellite antennas. J. Geod. 2007, 81, 781–798. [Google Scholar] [CrossRef] [Green Version]
- Dach, R.; Schmid, R.; Schmitz, M.; Thaller, D.; Schaer, S.; Lutz, S.; Steigenberger, P.; Wübbena, G.; Beutler, G. Improved antenna phase center models for GLONASS. GPS Solut. 2011, 15, 49–65. [Google Scholar] [CrossRef]
- Schmid, R.; Mader, G.; Herring, T. From relative to absolute antenna phase center corrections. In Proceedings of the IGS Workshop and Symposium, Bern, Switzerland, 1–4 March 2004; Meindl, M., Ed.; Astronomical Institute, University of Bern: Bern, Switzerland, 2005; pp. 209–219. [Google Scholar]
- Chen, G.; Herring, T. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophys. Res. Solid Earth 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Scherneck, H.G. A parametrized solid earth tide model and ocean tide loading effects for global geodetic baseline measurements. Geophys. J. Int. 1991, 106, 677–694. [Google Scholar] [CrossRef] [Green Version]
- Mathews, P.; Buffett, B.; Shapiro, I. Love numbers for a rotating spheroidal earth new definitions and numerical values. Geophys. Res. Lett. 1995, 22, 579–582. [Google Scholar] [CrossRef]
- Wahr, J.M. Deformation induced by polar motion. J. Geophys. Res. Solid Earth 1985, 90, 9363–9368. [Google Scholar] [CrossRef]
- Farrell, W. Deformation of the earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Rabbel, W.; Zschau, J. Static deformations and gravity changes at the earth’s surface due to atmospheric loading. J. Geophys. 1985, 56, 81–89. [Google Scholar]
- McCarthy, D.D.; Petit, G.; International Earth Rotation and Reference Systems Service (IERS). IERS Conventions (2003); Technical Report No. 32; International Earth Rotation and Reference Systems Service: Frankfurt am Main, Germany, 2004. [Google Scholar]
- Rothacher, M. Estimation of station heights with GPS. In Vertical Reference Systems; Drewes, H., Dodson., A.H., Fortes, L.P.S., Sánchez, L., Sandoval, P., Eds.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Steigenberger, P.; Rothacher, M.; Dietrich, R.; Fritsche, M.; Rülke, A.; Vey, S. Reprocessing of a global GPS network. J. Geophys. Res. Solid Earth 2006, 111, B05402. [Google Scholar] [CrossRef] [Green Version]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Mendes, V.; Prates, G.; Santos, L.; Langley, R. An evaluation of the accuracy of models for the determination of the weighted mean temperature of the atmosphere. In Proceedings of the 2000 National Technical Meeting of the Institute of Navigation, Anaheim, CA, USA, 26–28 January 2000; pp. 433–438. [Google Scholar]
- Schüler, T. On ground-Based GPS Tropospheric Delay Estimation. Ph.D. Thesis, Universtät der Bundeswehr München, Neubiberg, Germany, February 2001. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).