Accuracy of Copernicus Altimeter Water Level Data in Italian Rivers Accounting for Narrow River Sections
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
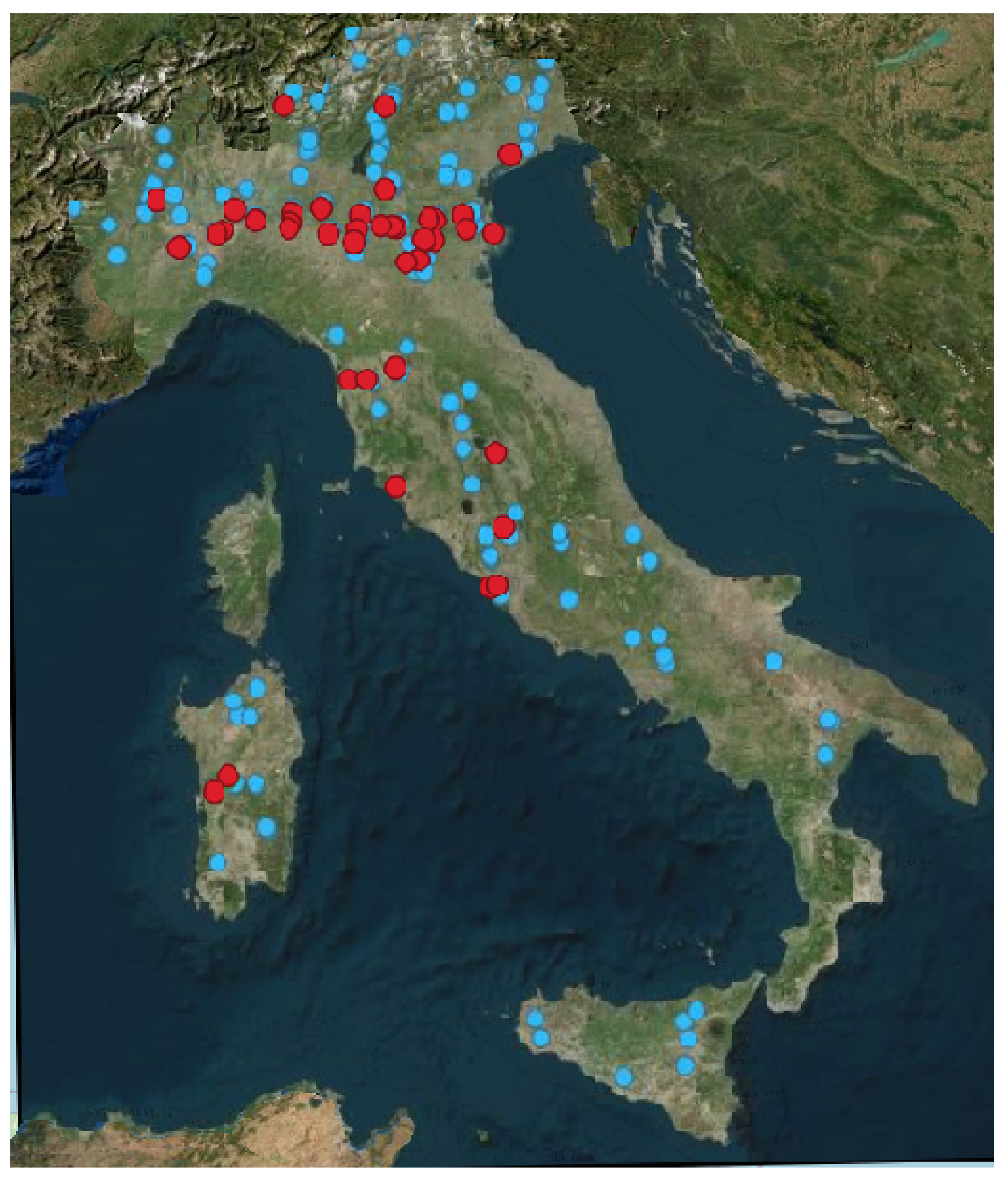
2.2. Methodology
- Stations (virtual and in situ) that are geographically close to each other (according to the distance criterion) but that are not on the same river branch are not selected;
- Stations (virtual and in situ) that are on the same river branch but present in the middle an interference (among the ones mentioned above), are not selected.
- If there are two in situ stations close to one satellite station, we compare the satellite station with both of them, the same for the opposite situation.
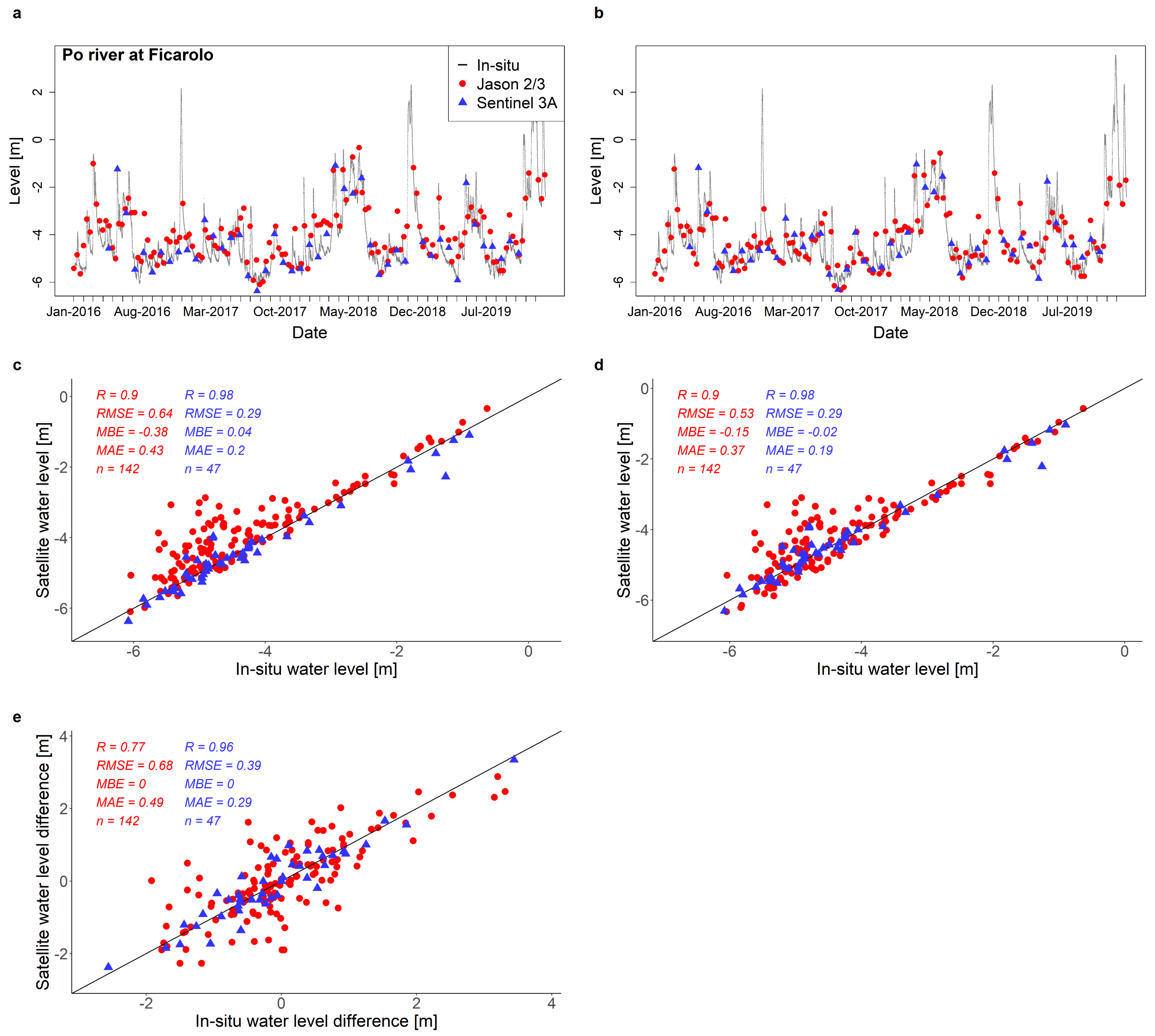
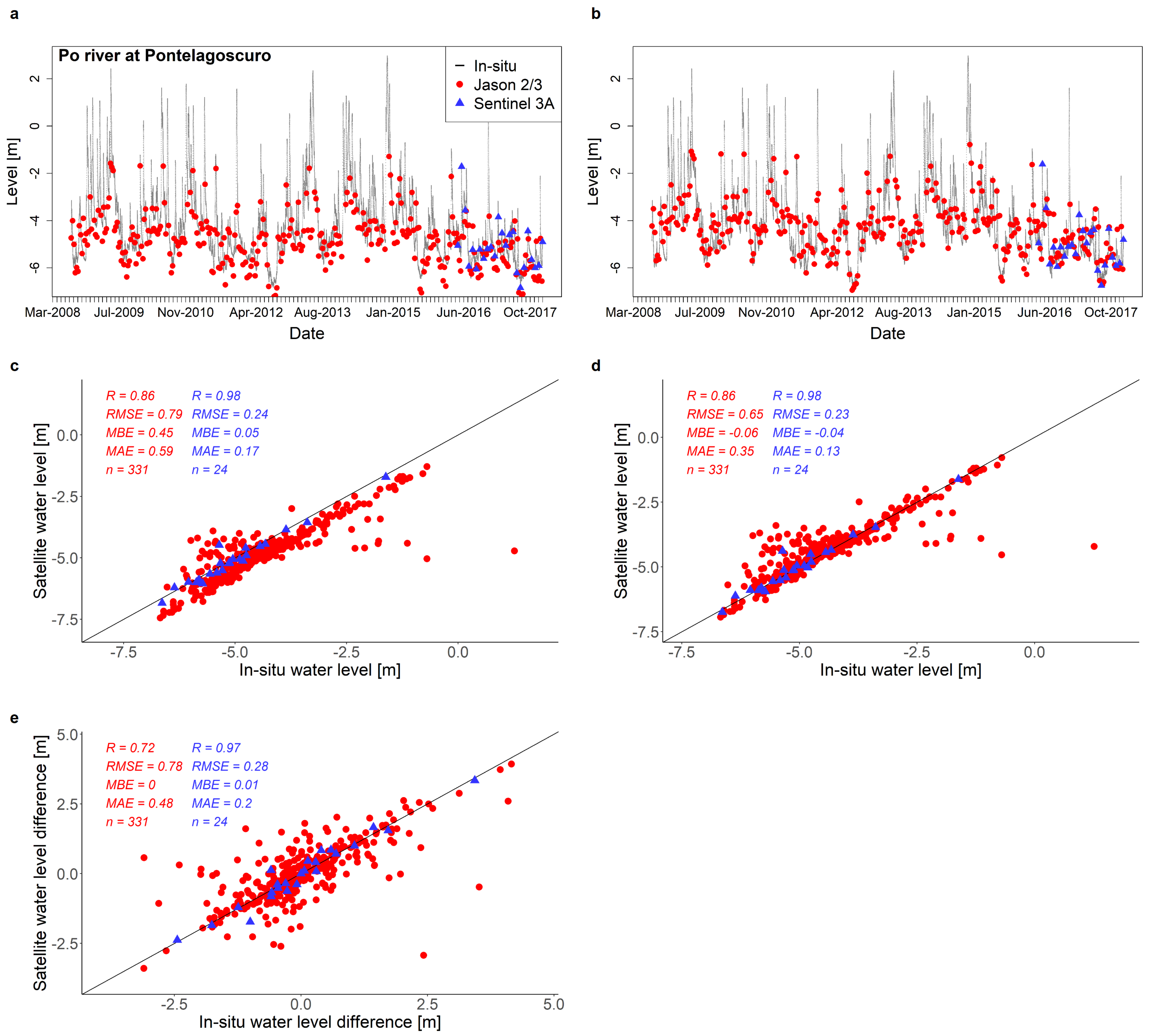
3. Results and Discussion
4. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1

Appendix A.2
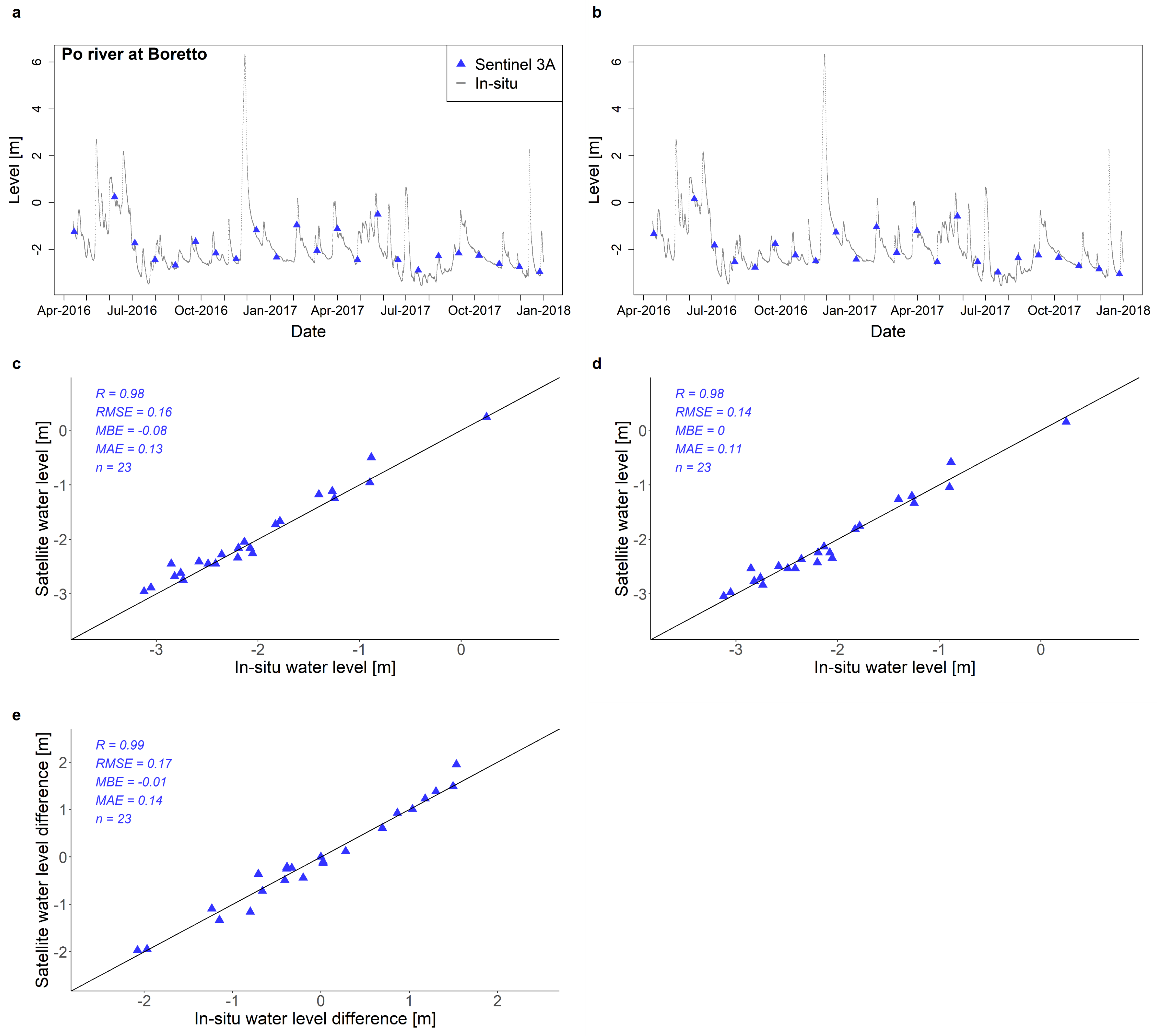
Appendix A.3
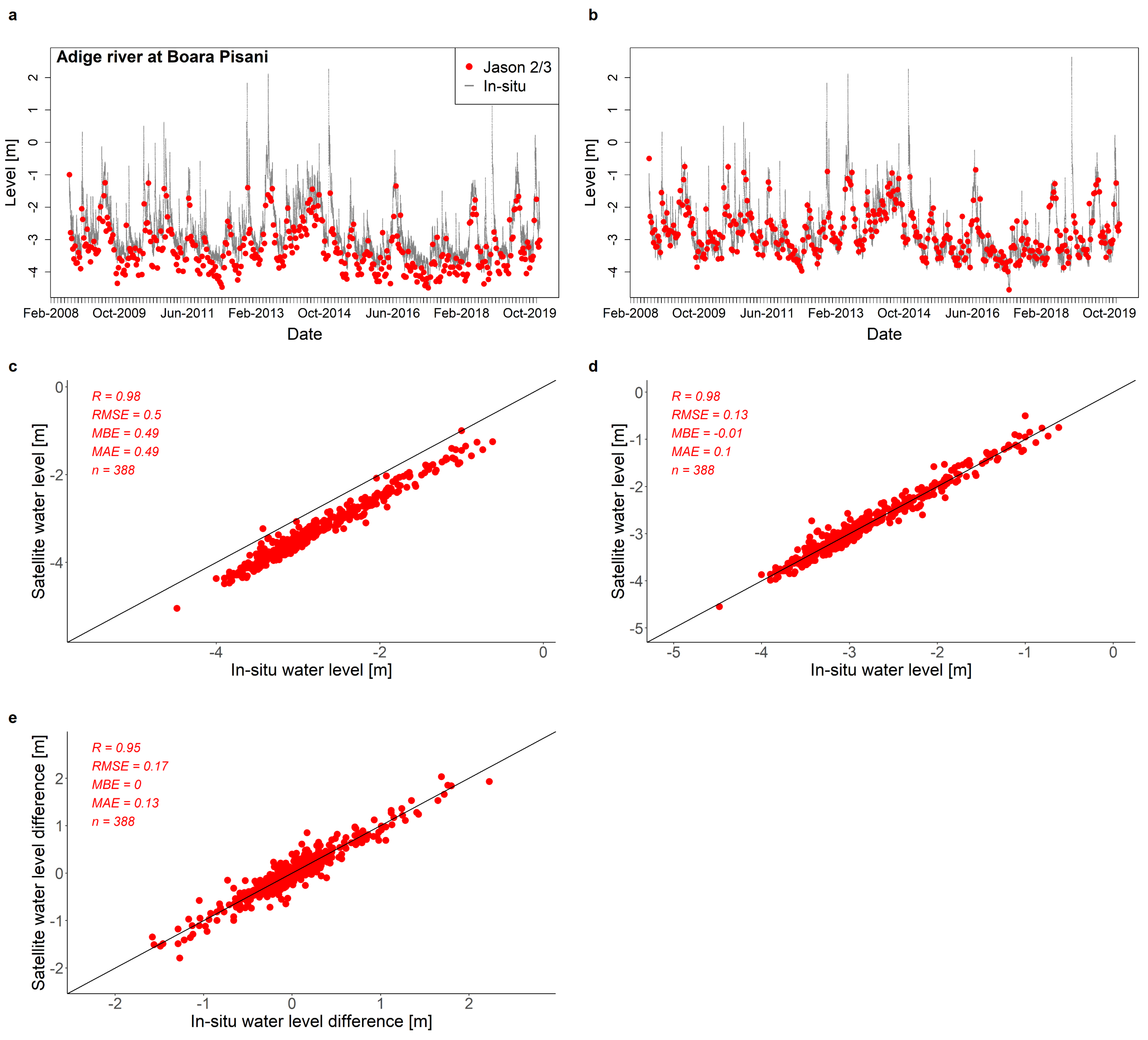
Appendix A.4
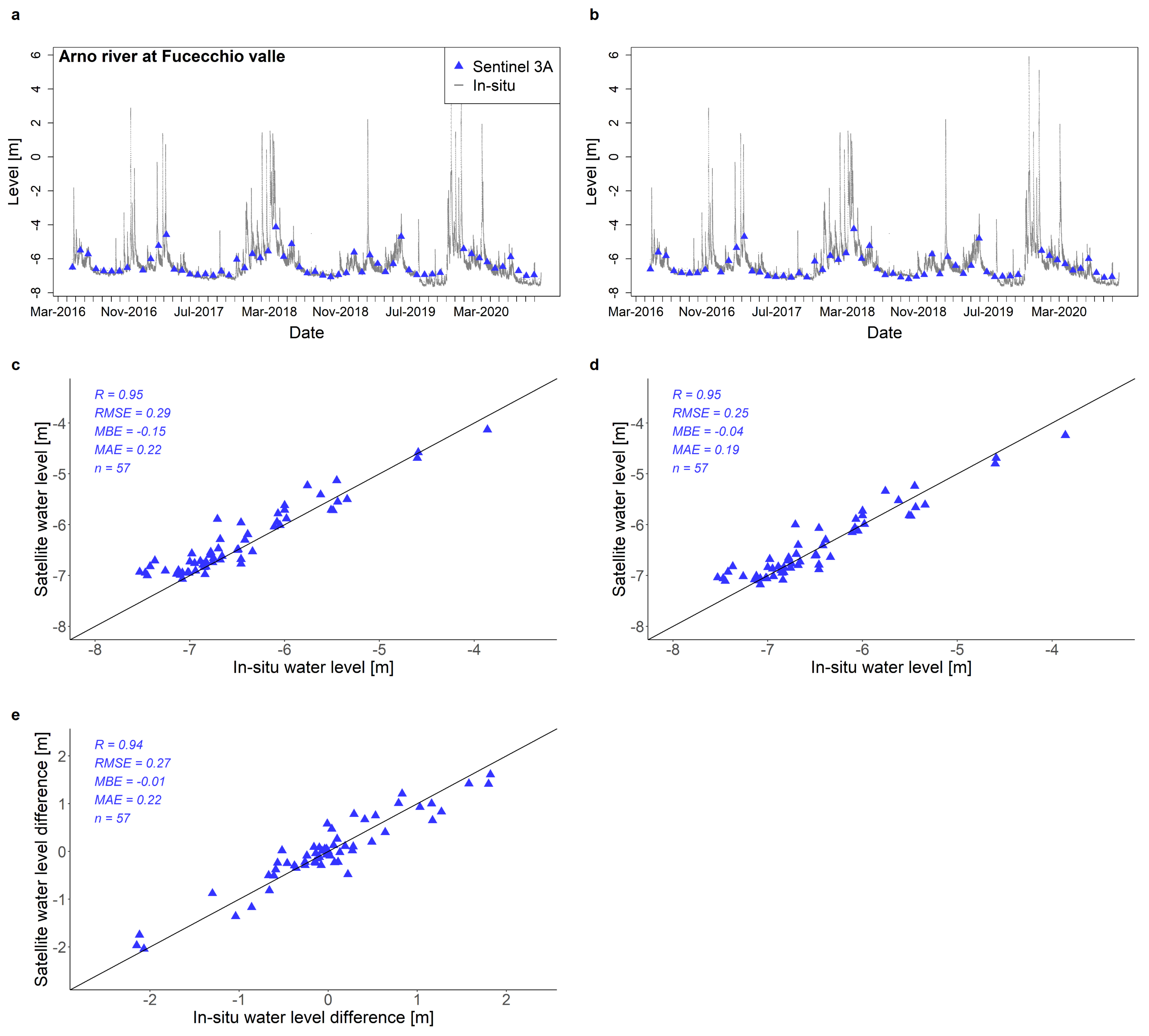
References
- Ponziani, F.; Pandolfo, C.; Stelluti, M.; Berni, N.; Brocca, L.; Moramarco, T. Assessment of rainfall thresholds and soil moisture modeling for operational hydrogeological risk prevention in the Umbria region (central Italy). Landslides 2012, 9, 229–237. [Google Scholar] [CrossRef]
- Mondino, E.; Scolobig, A.; Borga, M.; Albrecht, F.; Mård, J.; Weyrich, P.; Di Baldassarre, G. Exploring changes in hydrogeological risk awareness and preparedness over time: A case study in northeastern Italy. Hydrol. Sci. J. 2020, 65, 1049–1059. [Google Scholar] [CrossRef] [Green Version]
- Trigila, A.; Iadanza, C.; Bussettini, M.; Lastoria, B. Dissesto idrogeologico in Italia: Pericolosità e indicatori di rischio—ISPRA Edizione 2018; Report 287/2018; ISPRA: Rome, Italy, 2018.
- EU Water Directors. Best Practices on Flood Prevention, Protection and Mitigation. Meetings in Budapest on 30 November and 1 December 2002, and in Bonn on 5/6 February 2003. 2003. Available online: https://ec.europa.eu/environment/water/flood_risk (accessed on 19 July 2021).
- Dixon, H.; Hannaford, J.; Fry, M.J. The effective management of national hydrometric data: Experiences from the United Kingdom. Hydrol. Sci. J. 2013, 58, 1383–1399. [Google Scholar] [CrossRef] [Green Version]
- ISPRA—Idro: V Riunione: Il Monitoraggio delle Portate: Stato e Criticità. Available online: http://www.isprambiente.gov.it (accessed on 27 September 2021).
- WMO Hydrological Observing System (WHOS). Available online: https://community.wmo.int/activity-areas/wmo-hydrological-observing-system-whos (accessed on 27 September 2021).
- Engman, E.T. Applications of microwave remote sensing of soil moisture for water resources and agriculture. Remote Sens. Environ. 1991, 35, 213–226. [Google Scholar] [CrossRef]
- Gould, W. Remote sensing of vegetation, plant species, and regional biodiversity hotspots. Ecol. Appl. 2000, 10, 1861–1870. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M. Landslide susceptibility mapping using GIS-based statistical models and Remote sensing data in tropical environment. Sci. Rep. 2015, 5, 9899. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stisen, S.; Sandholt, I. Evaluation of remote-sensing-based rainfall products through predictive capability in hydrological runoff modelling. Hydrol. Process. 2010, 24, 879–891. [Google Scholar] [CrossRef]
- Paciolla, N.; Corbari, C.; Al Bitar, A.; Kerr, Y.; Mancini, M. Irrigation and Precipitation Hydrological Consistency with SMOS, SMAP, ESA-CCI, Copernicus SSM1km, and AMSR-2 Remotely Sensed Soil Moisture Products. Remote Sens. 2020, 12, 3737. [Google Scholar] [CrossRef]
- Arslan, A.; Akyürek, Z. Remote Sensing of Snow and Its Applications; MDPI: Basel, Switzerland, 2021. [Google Scholar] [CrossRef]
- Bongio, M.; Arslan, A.N.; Tanis, C.M.; De Michele, C. Snow depth time series retrieval by time-lapse photography: Finnish and Italian case studies. Cryosphere 2021, 15, 369–387. [Google Scholar] [CrossRef]
- Munyaneza, O.; Wali, U.G.; Uhlenbrook, S.; Maskey, S.; Mlotha, M.J. Water level monitoring using radar remote sensing data: Application to Lake Kivu, central Africa. Phys. Chem. Earth 2009, 34, 722–728. [Google Scholar] [CrossRef]
- Brando, V.E.; Dekker, A.G. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1378–1387. [Google Scholar] [CrossRef]
- Taburet, N.; Vayre, M.; Calmettes, B.; Zawadzki, L.; Paris, A.; Calmant, S.; Crétaux, J.F. Copernicus Global Land Operations “Cryosphere and Water”: Quality Assessment Report—Lake and River Water Level, pp. 1–60. 2020. Available online: https://land.copernicus.eu/global (accessed on 20 August 2021).
- Calmant, S.; Seyler, F. Continental surface waters from satellite altimetry. C. R. Geosci. 2006, 338, 1113–1122. [Google Scholar] [CrossRef]
- Jiang, L.; Nielsen, K.; Andersen, O.B.; Bauer-Gottwein, P. CryoSat-2 radar altimetry for monitoring freshwater resources of China. Remote Sens. Environ. 2017, 200, 125–139. [Google Scholar] [CrossRef] [Green Version]
- Song, C.; Huang, B.; Ke, L. Modeling and analysis of lake water storage changes on the Tibetan Plateau using multi-mission satellite data. Remote Sens. Environ. 2013, 135, 25–35. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry databases and satellite imagery data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- Kropáček, J.; Braun, A.; Kang, S.; Feng, C.; Ye, Q.; Hochschild, V. Analysis of lake level changes in Nam Co in central Tibet utilizing synergistic satellite altimetry and optical imagery. Int. J. Appl. Earth Observ. Geoinf. 2012, 17, 3–11. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Famiglietti, J.S.; Prigent, C.; Rossow, W.B.; Seyler, F. Interannual variations of river water storage from a multiple satellite approach: A case study for the Rio Negro River basin. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Sichangi, A.W.; Wang, L.; Yang, K.; Chen, D.; Wang, Z.; Li, X.; Zhou, J.; Liu, W.; Kuria, D. Estimating continental river basin discharges using multiple remote sensing data sets. Remote Sens. Environ. 2016, 179, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Michailovsky, C.I.; McEnnis, S.; Berry, P.A.M.; Smith, R.; Bauer-Gottwein, P. River monitoring from satellite radar altimetry in the Zambezi River basin. Hydrol. Earth Syst. Sci. 2012, 16, 2181–2192. [Google Scholar] [CrossRef] [Green Version]
- Leon, J.; Calmant, S.; Seyler, F.; Bonnet, M.P.; Cauhopé, M.; Frappart, F.; Filizola, N.; Fraizy, P. Rating curves and estimation of average water depth at the upper Negro River based on satellite altimeter data and modeled discharges. J. Hydrol. 2006, 328, 481–496. [Google Scholar] [CrossRef] [Green Version]
- Tarpanelli, A.; Barbetta, S.; Brocca, L.; Moramarco, T. River Discharge Estimation by Using Altimetry Data and Simplified Flood Routing Modeling. Remote Sens. 2013, 5, 4145–4162. [Google Scholar] [CrossRef] [Green Version]
- Crétaux, J.F.; Birkett, C. Lake studies from satellite radar altimetry. C. R. Geosci. 2006, 338, 1098–1112. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Lettenmaier, D. Tracking freshwater from space. Science 2003, 301, 1098–1112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coe, M.T.; Birkett, C.M. Calculation of river discharge and prediction of lake height from satellite radar altimetry: Example for the Lake Chad basin. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45, 1–24. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI—An innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef] [Green Version]
- Frappart, F.; Calmant, S.; Cauhopé, M.; Seyler, F.; Cazenave, A. Preliminary results of ENVISAT RA-2-derived water levels validation over the Amazon basin. Remote Sens. Environ. 2006, 100, 252–264. [Google Scholar] [CrossRef] [Green Version]
- Cretaux, J.; Bergé-Nguyen, M.; Calmant, S.; Jamangulova, N.; Satylkanov, R.; Lyard, F.; Perosanz, F.; Verron, J.; Samine Montazem, A.; Guilcher, G.; et al. Absolute Calibration or Validation of the Altimeters on the Sentinel-3A and the Jason-3 over Lake Issykkul (Kyrgyzstan). Remote Sens. 2018, 10, 1679. [Google Scholar] [CrossRef] [Green Version]
- Birkinshaw, S.J.; O’Donnell, G.M.; Moore, P.; Kilsby, C.G.; Fowler, H.J.; Berry, P.A.M. Using satellite altimetry data to augment flow estimation techniques on the Mekong River. Hydrol. Process. 2010, 24, 3811–3825. [Google Scholar] [CrossRef]
- Bogning, S.; Frappart, F.; Blarel, F.; Niño, F.; Mahé, G.; Bricquet, J.P.; Seyler, F.; Onguéné, R.; Etamé, J.; Paiz, M.C.; et al. Monitoring Water Levels and Discharges Using Radar Altimetry in an Ungauged River Basin: The Case of the Ogooué. Remote Sens. 2018, 10, 350. [Google Scholar] [CrossRef] [Green Version]
- De Oliveira Campos, I.; Mercier, F.; Maheu, C.; Cochonneau, G.; Kosuth, P.; Blitzkow, D.; Cazenave, A. Temporal variations of river basin waters from Topex/Poseidon satellite altimetry. Application to the Amazon basin. C. R. Acad. Sci.–Ser. IIA–Earth Planet. Sci. 2001, 333, 633–643. [Google Scholar] [CrossRef]
- Birkett, C.M.; Mertes, L.A.; Dunne, T.; Costa, M.H.; Jasinski, M.J. Surface water dynamics in the Amazon Basin: Application of satellite radar altimetry. J. Geophys. Res. Atmos. 2002, 107, LBA-26. [Google Scholar] [CrossRef]
- Santos da Silva, J.; Calmant, S.; Seyler, F.; Rotunno Filho, O.C.; Cochonneau, G.; Mansur, W.J. Water levels in the Amazon basin derived from the ERS 2 and ENVISAT radar altimetry missions. Remote Sens. Environ. 2010, 114, 2160–2181. [Google Scholar] [CrossRef]
- Le Roy, Y.; Deschaux-Beaume, M.; Mavrocordatos, C.; Aguirre, M.; Hélière, F. SRAL SAR radar altimeter for Sentinel-3 mission. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Barcelona, Spain, 23–28 July 2007; pp. 219–222. [Google Scholar] [CrossRef]
- Liibusk, A.; Kall, T.; Rikka, S.; Uiboupin, R.; Suursaar, Ü.; Tseng, K.H. Validation of Copernicus Sea Level Altimetry Products in the Baltic Sea and Estonian Lakes. Remote Sens. 2020, 12, 4062. [Google Scholar] [CrossRef]
- Gao, Q.; Makhoul, E.; Escorihuela, M.J.; Zribi, M.; Quintana Seguí, P.; García, P.; Roca, M. Analysis of Retrackers’ Performances and Water Level Retrieval over the Ebro River Basin Using Sentinel-3. Remote Sens. 2019, 11, 718. [Google Scholar] [CrossRef] [Green Version]
- Frappart, F.; Blarel, F.; Fayad, I.; Bergé-Nguyen, M.; Cretaux, J.; Shu, S.; Schregenberger, J.; Baghdadi, N. Evaluation of the Performances of Radar and Lidar Altimetry Missions for Water Level Retrievals in Mountainous Environment: The Case of the Swiss Lakes. Remote Sens. 2021, 13, 2196. [Google Scholar] [CrossRef]
- Huang, Q.; Li, X.; Han, P.; Long, D.; Zhao, F.; Hou, A. Validation and application of water levels derived from Sentinel-3A for the Brahmaputra River. Sci. China Technol. Sci 2019, 62, 1760–1772. [Google Scholar] [CrossRef]
- Kittel, C.; Jiang, L.; Tøttrup, C.; Bauer-Gottwein, P. Sentinel-3 radar altimetry for river monitoring—A catchment-scale evaluation of satellite water surface elevation from Sentinel-3A and Sentinel-3B. Hydrol. Earth Syst. Sci. 2021, 25, 333–357. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Camici, S.; Nielsen, K.; Brocca, L.; Moramarco, T.; Benveniste, J. Potentials and limitations of Sentinel-3 for river discharge assessment. Adv. Space Res. 2021, 68, 593–606. [Google Scholar] [CrossRef]
- Jiang, L.; Nielsen, K.; Dinardo, S.; Andersen, O.B.; Bauer-Gottwein, P. Evaluation of Sentinel-3 SRAL SAR altimetry over Chinese rivers. Remote Sens. Environ. 2020, 237, 111546. [Google Scholar] [CrossRef]
- Zakharova, E.; Nielsen, K.; Kamenev, G.; Kouraev, A. River discharge estimation from radar altimetry: Assessment of satellite performance, river scales and methods. J. Hydrol. 2020, 583, 124561. [Google Scholar] [CrossRef]
- Fernández, J.; Fernández, C.; Féménias, P.; Peter, H. The Copernicus Sentinel-3 Mission. In Proceedings of the ILRS Workshop 2016, Potsdam, Germany, 9–14 October 2016; pp. 1–6. [Google Scholar]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Taburet, N.; Zawadzki, L.; Calmant, S.; Crétaux, J.F.; Mercier, F.; Vayre, M. Copernicus Global Land Operations “Cryosphere and Water”: Product User Manual—Lake and River Water Level; pp. 1–41. 2020. Available online: https://land.copernicus.eu/global (accessed on 20 August 2021).
- Bauer-Marschallinger, B. Copernicus Global Land Operations “Vegetation and Energy”; p. 51. 2018. Available online: https://land.copernicus.eu/global (accessed on 20 August 2021).
- Aviso Pass Locator. Available online: https://www.aviso.altimetry.fr/es/data/tools/pass-locator.html (accessed on 19 July 2021).
- Biancamaria, S.; Schaedele, T.; Blumstein, D.; Frappart, F.; Boy, F.; Desjonquères, J.D.; Pottier, C.; Blarel, F.; Niño, F. Validation of Jason-3 tracking modes over French rivers. Remote Sens. Environ. 2018, 209, 77–89. [Google Scholar] [CrossRef] [Green Version]
- Tourian, M.J.; Tarpanelli, A.; Elmi, O.; Qin, T.; Brocca, L.; Moramarco, T.; Sneeuw, N. Spatiotemporal densification of river water level time series by multimission satellite altimetry. Water Resour. Res. 2016, 52, 1140–1159. [Google Scholar] [CrossRef] [Green Version]
- Biancamaria, S.; Frappart, F.; Leleu, A.S.; Marieu, V.; Blumstein, D.; Desjonquères, J.D.; Boy, F.; Sottolichio, A.; Valle-Levinson, A. Satellite radar altimetry water elevations performance over a 200 m wide river: Evaluation over the Garonne River. Adv. Space Res. 2017, 59, 128–146. [Google Scholar] [CrossRef] [Green Version]
- Taburet, N.; Zawadzki, L.; Vayre, M.; Blumstein, D.; Le Gac, S.; Boy, F.; Raynal, M.; Labroue, S.; Crétaux, J.F.; Femenias, P. S3MPC: Improvement on Inland Water Tracking and Water Level Monitoring from the OLTC Onboard Sentinel-3 Altimeters. Remote Sens. 2020, 12, 3055. [Google Scholar] [CrossRef]
- Egido, A.; Smith, W. Fully Focused SAR Altimetry: Theory and Applications. IEEE Trans. Geosci. Remote Sens. 2017, 55, 392–406. [Google Scholar] [CrossRef]
- Altimeter Open Loop Tracking Command for Hydrology. Available online: https://www.altimetry-hydro.eu/ (accessed on 19 July 2021).
- Blumstein, D.; Biancamaria, S.; Guérin, A.; Maisongrande, P. A potential constellation of small altimetry satellites dedicated to continental surface waters (SMASH mission). AGU Fall Meeting Abstracts; H43N-2257. 2019. Available online: https://ui.adsabs.harvard.edu/abs/2019AGUFM.H43N2257B/abstract (accessed on 20 August 2021).
- Morrow, R.; Blurmstein, D.; Dibarboure, G. Fine-scale Altimetry and the Future SWOT Mission. In New Frontiers in Operational Oceanography; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2018. [Google Scholar] [CrossRef] [Green Version]

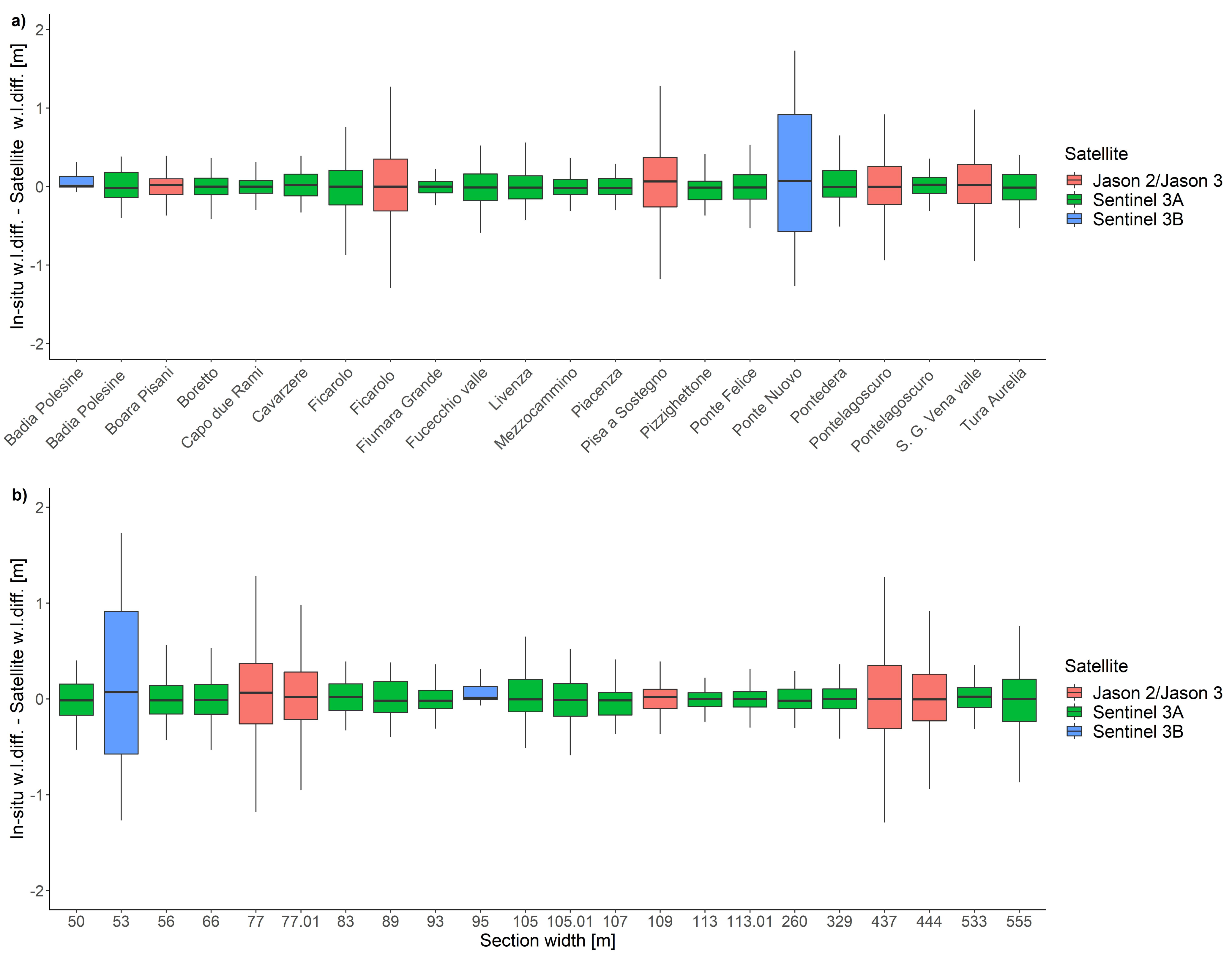
| In-Situ Stat. | River | Region | Lat. [N] | Long. [E] | Sect. Width [m] | Satellite | Virtual Stat. ID | Pair Dist. [km] | Num. Data |
|---|---|---|---|---|---|---|---|---|---|
| Boretto | Po | Emilia Romagna | 44.91 | 10.56 | 329 | Sentinel 3A | 8634 | 4.33 | 23 |
| Piacenza | Po | Emilia Romagna | 45.06 | 9.70 | 260 | Sentinel 3A | 8633 | 2.06 | 23 |
| Pontelagoscuro | Po | Emilia Romagna | 44.89 | 11.61 | 444 | Jason 2/3 | 8631 | 4.67 | 331 |
| Pontelagoscuro | Po | Emilia Romagna | 44.89 | 11.61 | 533 | Sentinel 3A | 8636 | 6.32 | 24 |
| Ponte Felice | Tevere | Lazio | 42.35 | 12.46 | 66 | Sentinel 3A | 9906 | 2.99 | 45 |
| Fiumara Grande | Tevere | Lazio | 41.75 | 12.26 | 113 | Sentinel 3A | 9907 | 4.96 | 43 |
| Mezzocammino | Tevere | Lazio | 41.81 | 12.42 | 93 | Sentinel 3A | 9905 | 5.49 | 45 |
| Capo due rami | Tevere | Lazio | 41.78 | 12.28 | 113.01 * | Sentinel 3A | 9907 | 0.56 | 43 |
| La Salute | Livenza | Veneto | 45.66 | 12.80 | 56 | Sentinel 3A | 12,810 | 2.98 | 36 |
| Boara Pisani | Adige | Veneto | 45.10 | 11.78 | 109 | Jason 2/3 | 9726 | 4.70 | 388 |
| Cavarzere | Adige | Veneto | 45.14 | 12.08 | 83 | Sentinel 3A | 9730 | 0.05 | 44 |
| Badia Polesine | Adige | Veneto | 45.10 | 11.48 | 95 | Sentinel 3B | 9731 | 11.37 | 15 |
| Badia Polesine | Adige | Veneto | 45.10 | 11.48 | 89 | Sentinel 3A | 9728 | 10.69 | 42 |
| Ficarolo | Po | Veneto | 44.94 | 11.43 | 555 | Sentinel 3A | 8636 | 9.92 | 47 |
| Ficarolo | Po | Veneto | 44.94 | 11.43 | 437 | Jason 2/3 | 8631 | 11.39 | 142 |
| Pisa a Sostegno | Arno | Toscana | 43.71 | 10.39 | 77 | Jason 2/3 | 12,738 | 9.86 | 388 |
| S.G. alla Vena valle | Arno | Toscana | 43.68 | 10.59 | 77.01 * | Jason 2/3 | 12,738 | 6.06 | 389 |
| Pontedera | Arno | Toscana | 43.67 | 10.63 | 105 | Sentinel 3A | 12,740 | 9.89 | 57 |
| Fucecchio valle | Arno | Toscana | 43.72 | 10.81 | 105.01* | Sentinel 3A | 12,740 | 5.93 | 57 |
| Ponte Tura Aurelia | Ombrone | Toscana | 42.76 | 11.14 | 50 | Sentinel 3A | 9882 | 5.80 | 54 |
| Ponte Nuovo | Tevere | Umbria | 43.01 | 12.43 | 53 | Sentinel 3B | 9908 | 2.54 | 19 |
| Pizzighettone | Adda | Lombardia | 45.19 | 9.78 | 107 | Sentinel 3A | 8627 | 0.62 | 24 |
| Water Level Difference | Water Level | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| In-Situ Stat. | Satellite | R [-] | RMSE [m] | MBE [m] | MAE [m] | R [-] | RMSE [m] | MBE [m] | MAE [m] |
| Boretto | Sentinel 3A | 0.99 | 0.17 | −0.01 | 0.14 | 0.98 | 0.16 | −0.08 | 0.13 |
| Piacenza | Sentinel 3A | 0.93 | 0.35 | −0.01 | 0.20 | 0.93 | 0.24 | 0.01 | 0.14 |
| Pontelagoscuro | Jason 2/3 | 0.72 | 0.78 | 0 | 0.48 | 0.86 | 0.79 | 0.45 | 0.59 |
| Pontelagoscuro | Sentinel 3A | 0.97 | 0.28 | 0.01 | 0.20 | 0.98 | 0.24 | 0.05 | 0.17 |
| Ponte Felice | Sentinel 3A | 0.80 | 0.31 | −0.01 | 0.23 | 0.88 | 0.40 | −0.33 | 0.35 |
| Fiumara Grande | Sentinel 3A | 0.59 | 0.17 | −0.02 | 0.11 | 0.61 | 0.25 | −0.19 | 0.20 |
| Mezzocammino | Sentinel 3A | 0.84 | 0.16 | −0.01 | 0.13 | 0.79 | 0.35 | −0.32 | 0.33 |
| Capo due rami | Sentinel 3A | 0.63 | 0.16 | −0.02 | 0.11 | 0.68 | 0.26 | −0.22 | 0.22 |
| La Salute | Sentinel 3A | 0.70 | 0.25 | 0 | 0.19 | 0.76 | 0.21 | 0.03 | 0.14 |
| Boara Pisani | Jason 2/3 | 0.95 | 0.17 | 0 | 0.13 | 0.98 | 0.50 | 0.49 | 0.49 |
| Cavarzere | Sentinel 3A | 0.39 | 0.61 | 0 | 0.34 | 0.65 | 0.45 | 0.09 | 0.22 |
| Badia Polesine | Sentinel 3B | 0.28 | 1.25 | −0.01 | 0.73 | 0.49 | 0.92 | 0.41 | 0.45 |
| Badia Polesine | Sentinel 3A | 0.96 | 0.22 | 0 | 0.19 | 0.98 | 0.23 | 0.14 | 0.18 |
| Ficarolo | Sentinel 3A | 0.96 | 0.39 | 0 | 0.29 | 0.98 | 0.29 | 0.04 | 0.20 |
| Ficarolo | Jason 2/3 | 0.77 | 0.68 | 0 | 0.49 | 0.90 | 0.64 | −0.38 | 0.43 |
| Pisa a Sostegno | Jason 2/3 | 0.60 | 0.60 | 0 | 0.45 | 0.63 | 0.93 | −0.44 | 0.73 |
| S.G. alla Vena valle | Jason 2/3 | 0.79 | 0.47 | 0 | 0.35 | 0.90 | 0.68 | −0.33 | 0.52 |
| Pontedera | Sentinel 3A | 0.84 | 0.42 | −0.03 | 0.25 | 0.85 | 1.91 | −1.88 | 1.88 |
| Fucecchio valle | Sentinel 3A | 0.94 | 0.27 | −0.01 | 0.22 | 0.95 | 0.29 | −0.15 | 0.22 |
| Ponte Tura Aurelia | Sentinel 3A | 0.89 | 0.43 | 0 | 0.27 | 0.90 | 0.32 | −0.07 | 0.23 |
| Ponte Nuovo | Sentinel 3B | 0.77 | 0.97 | 0.15 | 0.82 | 0.65 | 0.90 | 0.62 | 0.70 |
| Pizzighettone | Sentinel 3A | 0.49 | 1.45 | 0 | 0.63 | 0.56 | 1.03 | −0.32 | 0.36 |
| Water Level | |||||
|---|---|---|---|---|---|
| In-Situ Stat. | Satellite | R [-] | RMSE [m] | MBE [m] | MAE [m] |
| Boretto | Sentinel 3A | 0.98 | 0.14 | 0 | 0.11 |
| Piacenza | Sentinel 3A | 0.93 | 0.24 | 0.03 | 0.14 |
| Pontelagoscuro | Jason 2/3 | 0.86 | 0.65 | −0.06 | 0.35 |
| Pontelagoscuro | Sentinel 3A | 0.98 | 0.23 | −0.04 | 0.13 |
| Ponte Felice | Sentinel 3A | 0.88 | 0.23 | −0.03 | 0.18 |
| Fiumara Grande | Sentinel 3A | 0.61 | 0.15 | −0.01 | 0.10 |
| Mezzocammino | Sentinel 3A | 0.79 | 0.14 | 0.01 | 0.10 |
| Capo due rami | Sentinel 3A | 0.68 | 0.14 | −0.02 | 0.09 |
| La Salute | Sentinel 3A | 0.76 | 0.21 | 0.04 | 0.14 |
| Boara Pisani | Jason 2/3 | 0.98 | 0.13 | −0.01 | 0.10 |
| Cavarzere | Sentinel 3A | 0.65 | 0.45 | 0.07 | 0.22 |
| Badia Polesine | Sentinel 3B | 0.49 | 0.88 | 0.29 | 0.44 |
| Badia Polesine | Sentinel 3A | 0.98 | 0.18 | 0.04 | 0.14 |
| Ficarolo | Sentinel 3A | 0.98 | 0.29 | −0.02 | 0.18 |
| Ficarolo | Jason 2/3 | 0.90 | 0.53 | −0.15 | 0.37 |
| Pisa a Sostegno | Jason 2/3 | 0.63 | 0.84 | −0.16 | 0.70 |
| S.G. alla Vena valle | Jason 2/3 | 0.90 | 0.61 | −0.10 | 0.49 |
| Pontedera | Sentinel 3A | 0.85 | 0.37 | −0.05 | 0.23 |
| Fucecchio valle | Sentinel 3A | 0.95 | 0.25 | −0.04 | 0.19 |
| Ponte Tura Aurelia | Sentinel 3A | 0.90 | 0.32 | −0.03 | 0.23 |
| Ponte Nuovo | Sentinel 3B | 0.65 | 0.65 | 0.06 | 0.57 |
| Pizzighettone | Sentinel 3A | 0.56 | 1.02 | −0.29 | 0.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deidda, C.; De Michele, C.; Arslan, A.N.; Pecora, S.; Taburet, N. Accuracy of Copernicus Altimeter Water Level Data in Italian Rivers Accounting for Narrow River Sections. Remote Sens. 2021, 13, 4456. https://doi.org/10.3390/rs13214456
Deidda C, De Michele C, Arslan AN, Pecora S, Taburet N. Accuracy of Copernicus Altimeter Water Level Data in Italian Rivers Accounting for Narrow River Sections. Remote Sensing. 2021; 13(21):4456. https://doi.org/10.3390/rs13214456
Chicago/Turabian StyleDeidda, Cristina, Carlo De Michele, Ali Nadir Arslan, Silvano Pecora, and Nicolas Taburet. 2021. "Accuracy of Copernicus Altimeter Water Level Data in Italian Rivers Accounting for Narrow River Sections" Remote Sensing 13, no. 21: 4456. https://doi.org/10.3390/rs13214456
APA StyleDeidda, C., De Michele, C., Arslan, A. N., Pecora, S., & Taburet, N. (2021). Accuracy of Copernicus Altimeter Water Level Data in Italian Rivers Accounting for Narrow River Sections. Remote Sensing, 13(21), 4456. https://doi.org/10.3390/rs13214456









