Spatial Correlation Length Scales of Sea-Ice Concentration Errors for High-Concentration Pack Ice
Abstract
:1. Introduction
2. Materials
3. Methods
4. Results
5. Discussion
5.1. Methodological Aspects
5.2. Interpretation of the Results
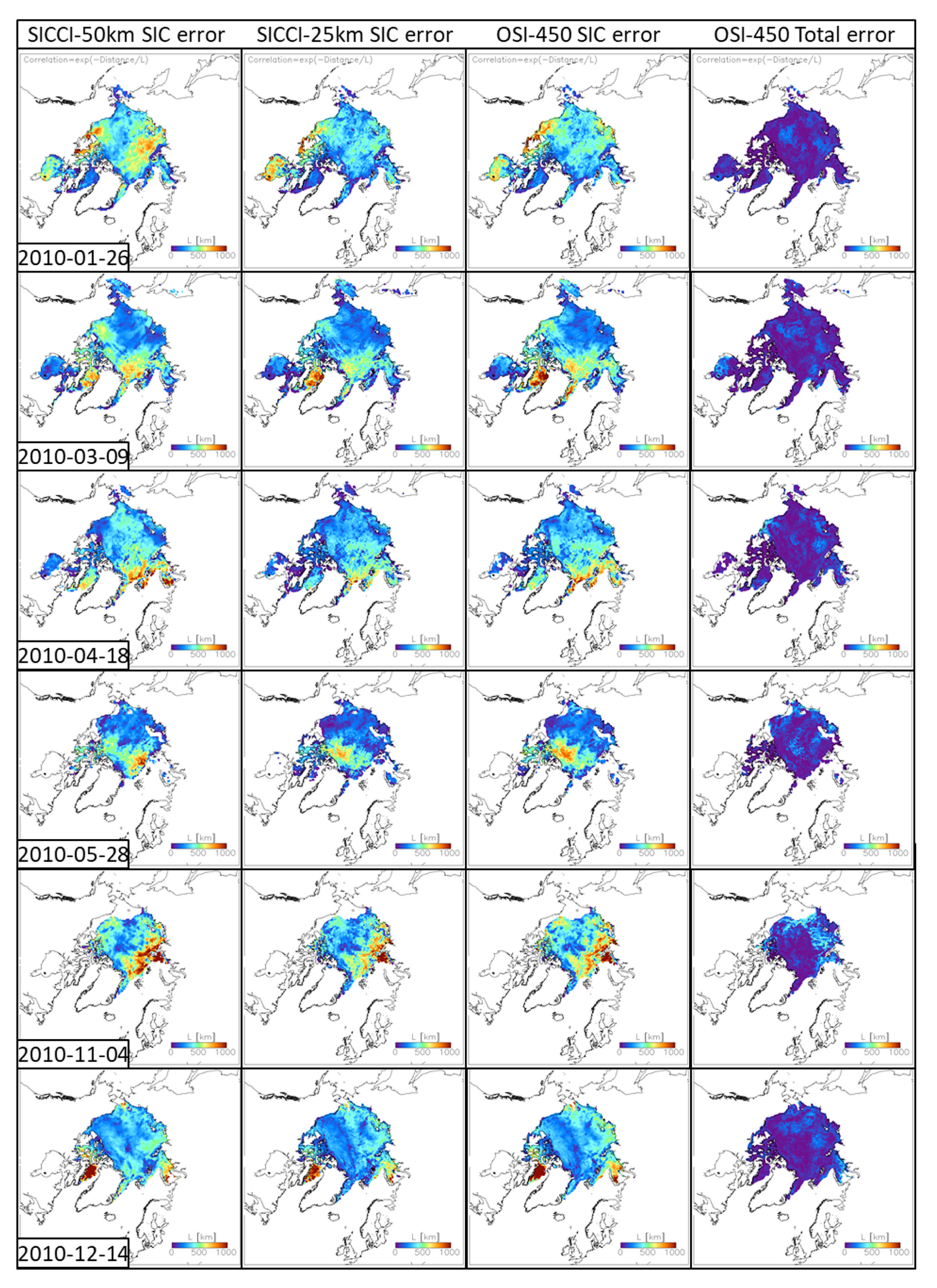
- The ice type (new ice, first-year ice, multi-year ice) because changes in surface emissivity by weather influence or the seasonal cycle are a function of the ice type. The rather sharp gradient in the SIC error correlation length scale across the central Arctic Ocean I find for all three products (Figure 6, 2010-05-28, left three columns) appears to point in this direction.
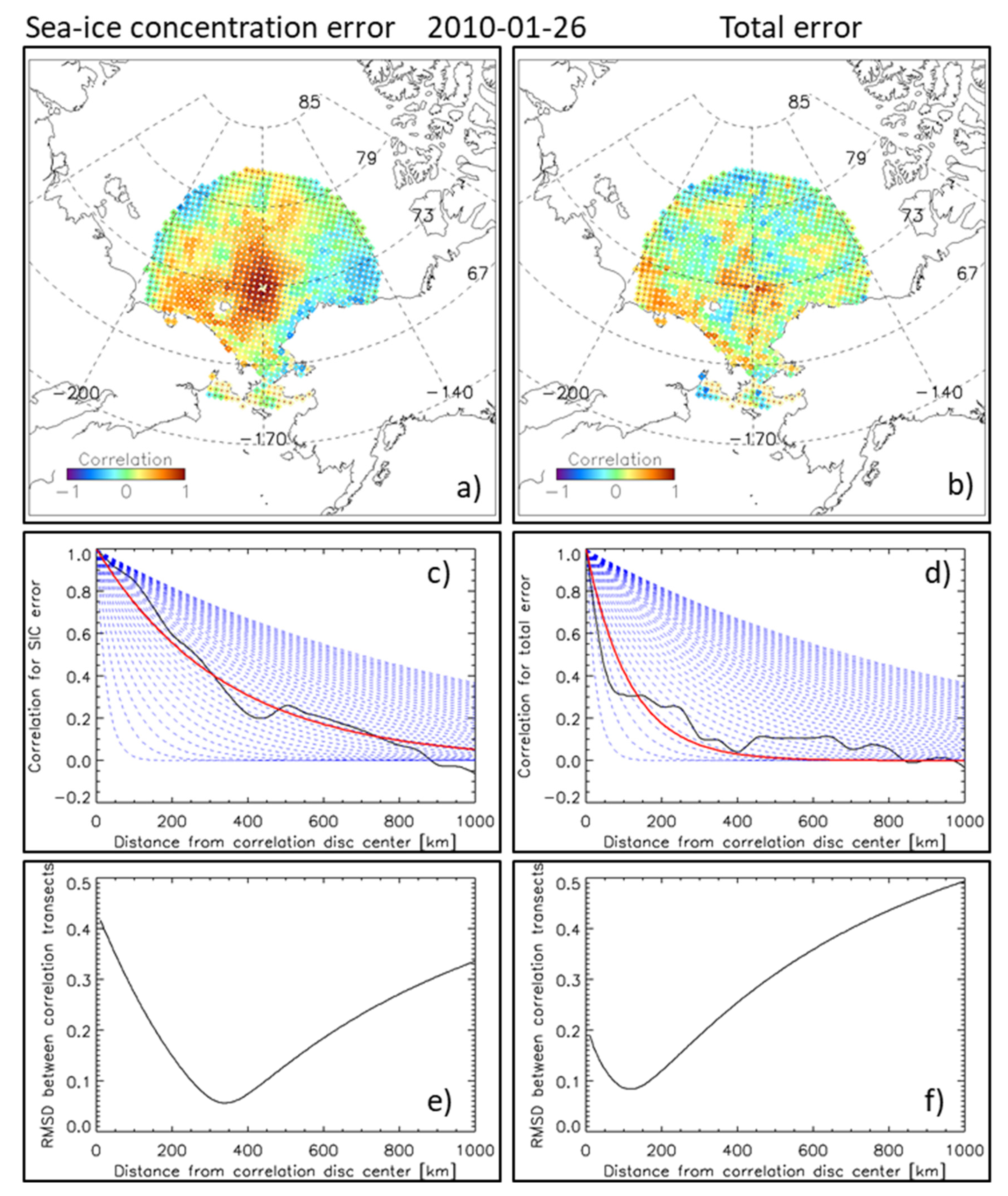
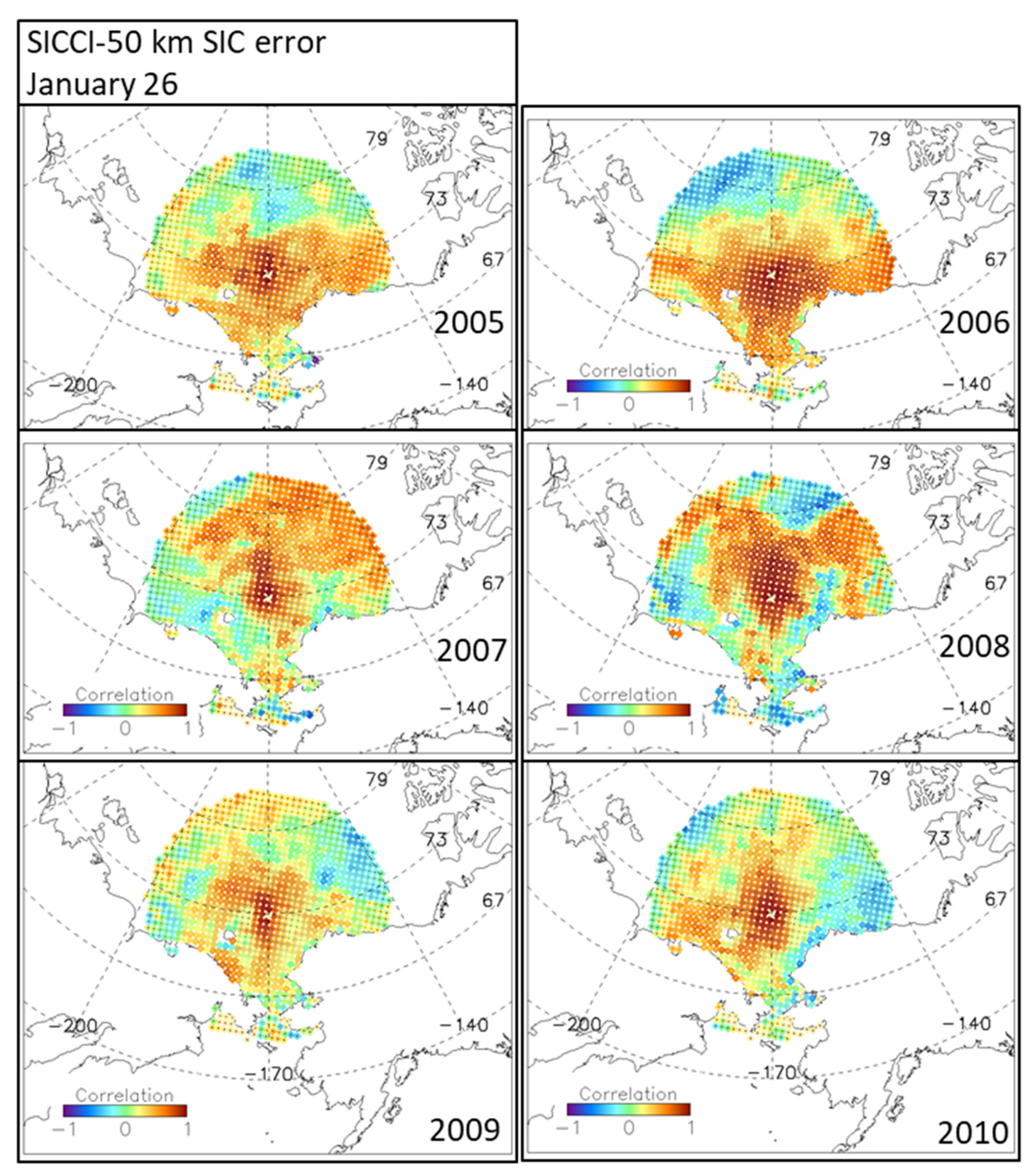
- The age of the seasonal sea ice because the surface emissivity changes most during the first days/weeks of its formation in response to changes in sea-ice surface properties such as salinity and temperature. The comparably well-defined area with (high) positive correlations near the correlation disc’s center paired with negative correlations north of Alaska and towards the West (Figure 3a) appears to point towards the importance of this parameter.
- The surface temperature and/or snow accumulation history (melt/freeze cycles, snowfall events) because sea-ice surface emissivity is, to a large extent, determined by the properties of the overlying snow (snow metamorphism) and interactions at the snow–ice interface (flooding, formation of meteoric ice). The importance of this information is evident in Figure 4a by a quite substantial variation in the SIC error time-series correlation across the correlation disc and in Figure 7 (left three columns) by the large spatial variability of the SIC error correlation length scale over basically the entire high-concentration sea-ice cover.
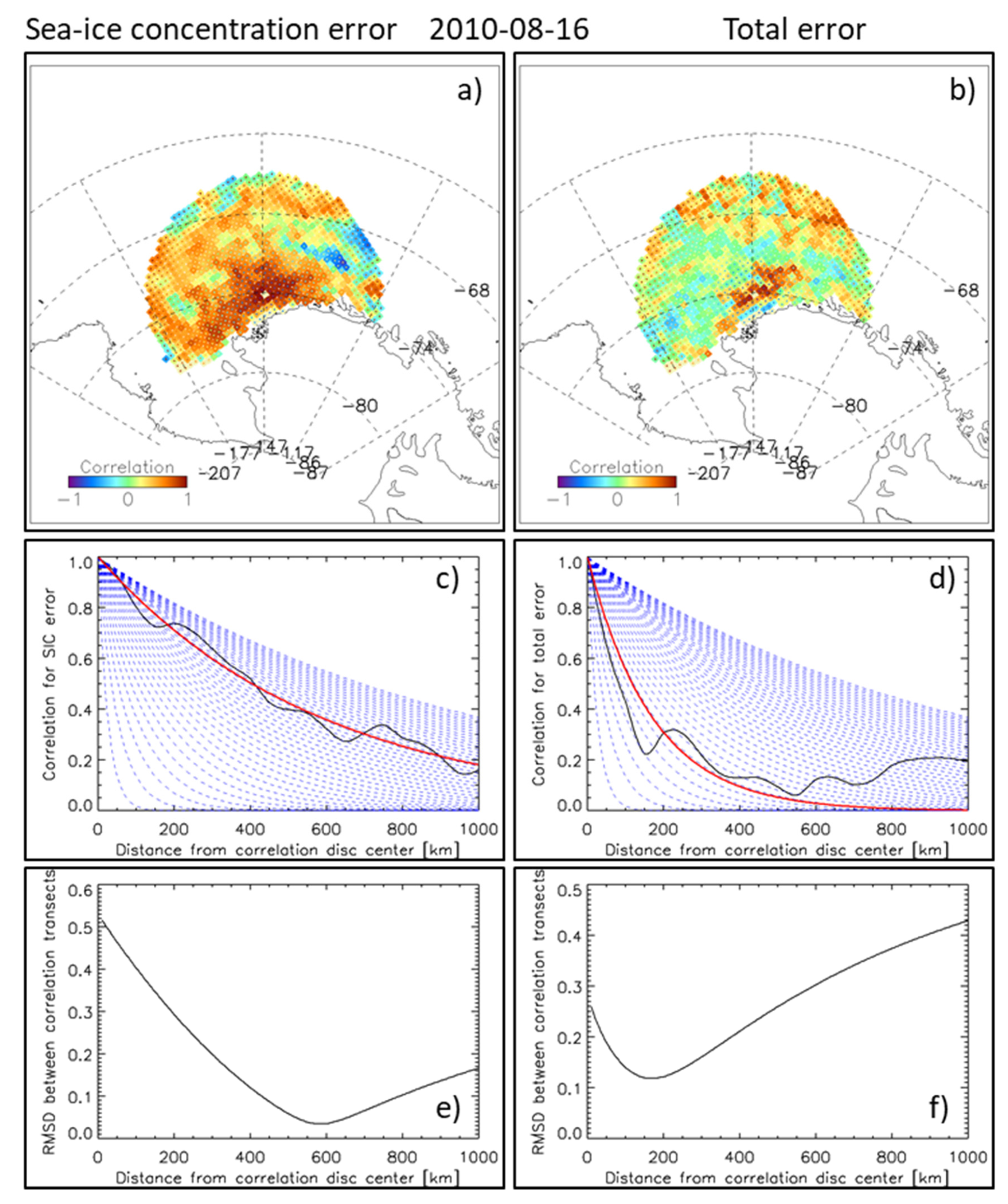
- Finally, the lead frequency because reduction in the SIC below 100% by sub-grid-scale openings and thin ice areas influences the SIC error time series and its spatial correlation in regions with high sea-ice dynamics and is suggested to result in comparably large SIC error correlation length scales as evidenced in Figure 6, 2010-01-26 and 2010-03-09 in the Beaufort Sea.
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meier, W.N.; Hovelsrud, G.K.; van Oort, B.E.H.; Key, J.R.; Kovacs, K.M.; Michel, C.; Haas, C.; Granskog, M.A.; Gerland, S.; Perovich, D.K.; et al. Arctic sea ice in transformation: A review of recent observed changes and impacts on biology and human activity. Rev. Geophys. 2014, 51, 185–217. [Google Scholar] [CrossRef]
- Parkinson, C.L.; DiGirolamo, N.E. New visualizations highlight new information on the contrasting Arctic and Antarctic sea-ice trends since the late 1970s. Remote Sens. Environ. 2016, 183, 198–204. [Google Scholar] [CrossRef] [Green Version]
- Stroeve, J.C.; Notz, D. Changing state of Arctic sea ice across all seasons. Environ. Res. Lett. 2018, 13, 103001. [Google Scholar] [CrossRef]
- Comiso, J.C.; Meier, W.N.; Gersten, R.A. Variability and trends in the Arctic Sea ice cover: Results from different techniques. J. Geophys. Res. Oceans 2017, 122, 6883–6900. [Google Scholar] [CrossRef]
- Comiso, J.C.; Gersten, R.A.; Stock, L.V.; Turner, J.; Perez, G.J.; Cho, K. Positive trends in the Antarctic sea ice cover and associated changes in surface temperature. J. Clim. 2017, 30, 2251–2267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parkinson, C.L. A 40-y record reveals gradual Antarctic sea ice increases followed by decreases at rates far exceeding the rates seen in the Arctic. Proc. Natl. Acad. Sci. USA 2019, 116, 14414–14423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meier, W.N.; Peng, G.; Scott, D.J.; Savoie, M.H. Verification of a new NOAA/NSIDC passive microwave sea-ice concentration climate record. Polar Res. 2014, 33, 21004. [Google Scholar] [CrossRef] [Green Version]
- Ivanova, N.; Pedersen, L.T.; Tonboe, R.T.; Kern, S.; Heygster, G.; Lavergne, T.; Sørensen, A.M.; Saldo, R.; Dybkjær, G.; Brucker, L.; et al. Inter-comparison and evaluation of sea ice algorithms: Towards further identification of challenges and optimal approach using passive microwave observations. Cryosphere 2015, 9, 1797–1817. [Google Scholar] [CrossRef] [Green Version]
- Lavergne, T.; Macdonald Sørensen, A.; Kern, S.; Tonboe, R.; Notz, D.; Aaboe, S.; Bell, L.; Dybkjær, G.; Eastwood, S.; Gabarro, C.; et al. Version 2 of the EUMETSAT OSI SAF and ESA-CCI sea-ice concentration climate data records. Cryosphere 2019, 13, 49–78. [Google Scholar] [CrossRef] [Green Version]
- Kern, S.; Lavergne, T.; Notz, D.; Pedersen, L.T.; Tonboe, R.T.; Saldo, R.; Sørensen, A.M. Satellite passive microwave sea-ice concentration data set intercomparison: Closed ice and ship-based observations. Cryosphere 2019, 13, 3261–3307. [Google Scholar] [CrossRef] [Green Version]
- Kern, S.; Lavergne, T.; Notz, D.; Pedersen, L.T.; Tonboe, R.T. Satellite passive microwave sea-ice concentration data set intercomparison for Arctic summer conditions. Cryosphere 2020, 14, 2469–2493. [Google Scholar] [CrossRef]
- Peng, G.; Meier, W.N.; Scott, D.; Savoie, M. A long-term and reproducible passive microwave sea ice concentration data record for climate studies and monitoring. Earth Syst. Sci. Data 2013, 5, 311–318. [Google Scholar] [CrossRef] [Green Version]
- Tonboe, R.T.; Eastwood, S.; Lavergne, T.; Sørensen, A.M.; Rathmann, N.; Dybkjær, G.; Pedersen, L.T.; Høyer, J.L.; Kern, S. The EUMETSAT sea ice concentration climate data record. Cryosphere 2016, 10, 2275–2290. [Google Scholar] [CrossRef] [Green Version]
- Burgard, C.; Notz, D.; Pedersen, L.T.; Tonboe, R.T. The Arctic Ocean observation operator for 6.9 GHz (ARC3O)—Part 2: Development and evaluation. Cryosphere 2020, 14, 2387–2407. [Google Scholar] [CrossRef]
- Tietsche, S.; Alonso-Balmaseda, M.; Rosnay, P.; Zuo, H.; Tian-Kunze, X.; Kaleschke, L. Thin Arctic sea ice in L-band observations and an ocean reanalysis. Cryosphere 2018, 12, 2051–2072. [Google Scholar] [CrossRef] [Green Version]
- Koldunov, N.V.; Köhl, A.; Serra, N.; Stammer, D. Sea ice assimilation into a coupled ocean-sea ice model using its adjoint. Cryosphere 2017, 11, 2265–2281. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Losch, M.; Losa, S.N.; Jung, T.; Nerger, L.; Lavergne, T. The challenge and benefit of using sea ice concentration satellite data products with uncertainty estimates in summer sea ice data assimilation. Cryosphere 2016, 10, 761–774. [Google Scholar] [CrossRef] [Green Version]
- Merchant, C.J.; Paul, F.; Popp, T.; Ablain, M.; Bontemps, S.; Defourny, P.; Hollmann, R.; Lavergne, T.; Laeng, A.; de Leeuw, G.; et al. Uncertainty information in climate data records from Earth observation. Earth Syst. Sci. Data 2017, 9, 511–527. [Google Scholar] [CrossRef] [Green Version]
- Merchant, C.J.; Embury, O.; Bulgin, C.E.; Block, T.; Corlett, G.K.; Fiedler, E.; Good, S.A.; Mittaz, J.; Rayner, N.A.; Berry, D.; et al. Satellite-based time-series of sea-surface temperature since 1981 for climate applications. Sci. Data 2019, 6, 223. [Google Scholar] [CrossRef] [Green Version]
- Ponsoni, L.; Massonnet, F.; Fichefet, T.; Chevallier, M.; Docquier, D. On the timescales and length scales of the Arctic sea ice thickness anomalies: A study based on 14 reanalyes. Cryosphere 2019, 13, 521–543. [Google Scholar] [CrossRef] [Green Version]
- Comiso, J.C. Characteristics of arctic winter sea ice from satellite multispectral microwave observations. J. Geophys. Res. 1986, 91, 975–994. [Google Scholar] [CrossRef]
- Comiso, J.C.; Nishio, F. Trends in the sea ice cover using enhanced and compatible AMSR-E, SSM/I, and SMMR data. J. Geophys. Res. 2008, 113, C02S07. [Google Scholar] [CrossRef]
- Comiso, J.C.; Cavalieri, D.J.; Parkinson, C.L.; Gloersen, P. Passive microwave algorithms for sea ice concentration: A comparison of two techniques. Remote Sens. Environ. 1997, 60, 357–384. [Google Scholar] [CrossRef]
- Comiso, J.C.; Cavalieri, D.J.; Markus, T. Sea ice concentration, ice temperature, and snow depth, using AMSR-E data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 243–252. [Google Scholar] [CrossRef]
- Smith, D.M.; Barrett, E.C. Satellite Mapping and Monitoring of Sea Ice; Report. CB/RAE/9/2/4/2034/113/ARE, RSU; University of Bristol: Bristol, UK, 1994. [Google Scholar]
- Smith, D.M. Extraction of winter total sea ice concentration in the Greenland and Barents Seas from SSM/I data. Int. J. Remote Sens. 1996, 17, 2625–2646. [Google Scholar] [CrossRef]
- Brodzik, M.J.; Billingsley, B.; Haran, T.; Raup, B.; Savoie, M.H. EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets. ISPRS Int. Geo-Inf. 2012, 1, 32–45. [Google Scholar] [CrossRef] [Green Version]
- Brodzik, M.J.; Billingsley, B.; Haran, T.; Raup, B.; Savoie, M.H. Correction: Brodzik, M.J. et al. EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets. ISPRS Int. Geo-Inf. 2012, 1, 32–45, Erratum in 2014, 3, 1154–1156. [Google Scholar] [CrossRef] [Green Version]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Bellprat, O.; Massonnet, F.; Siegert, S.; Prodhomme, C.; Macias-Gomez, D.; Guemas, V.; Doblas-Reyes, F. Uncertainty propagation in observational references to climate model scales. Remote Sens. Environ. 2017, 203, 101–108. [Google Scholar] [CrossRef] [Green Version]
- Blanchard-Wrigglesworth, E.; Bitz, C.M. Characteristics of Arctic sea-ice thickness variability in GCMs. J. Clim. 2014, 27, 8244–8258. [Google Scholar] [CrossRef] [Green Version]
- Voss, S.; Heygster, G.; Ezraty, R. Improving sea ice type discrimination by the simultaneous use of SSM/I and scatterometer data. Polar Res. 2003, 22, 35–42. [Google Scholar] [CrossRef] [Green Version]
- Krumpen, T.; von Albedyll, L.; Goessling, H.F.; Hendricks, S.; Juhls, B.; Spreen, G.; Willmes, S.; Belter, H.J.; Dehtloff, K.; Haas, C.; et al. MOSAiC drift expedition from October 2019 to July 2020: Sea ice conditions from space and comparison with previous years. Cryosphere 2021, 15, 3897–3920. [Google Scholar] [CrossRef]
- Willmes, S.; Heinemann, G. Pan-Arctic lead detection from MODIS thermal infrared imagery. Ann. Glaciol. 2015, 56, 29–37. [Google Scholar] [CrossRef] [Green Version]
- Reiser, F.; Willmes, S.; Heinemann, G. A new algorithm for daily sea ice lead identification in the Arctic and Antarctic winter from thermal-infrared satellite imagery. Remote Sens. 2020, 12, 1957–1972. [Google Scholar] [CrossRef]
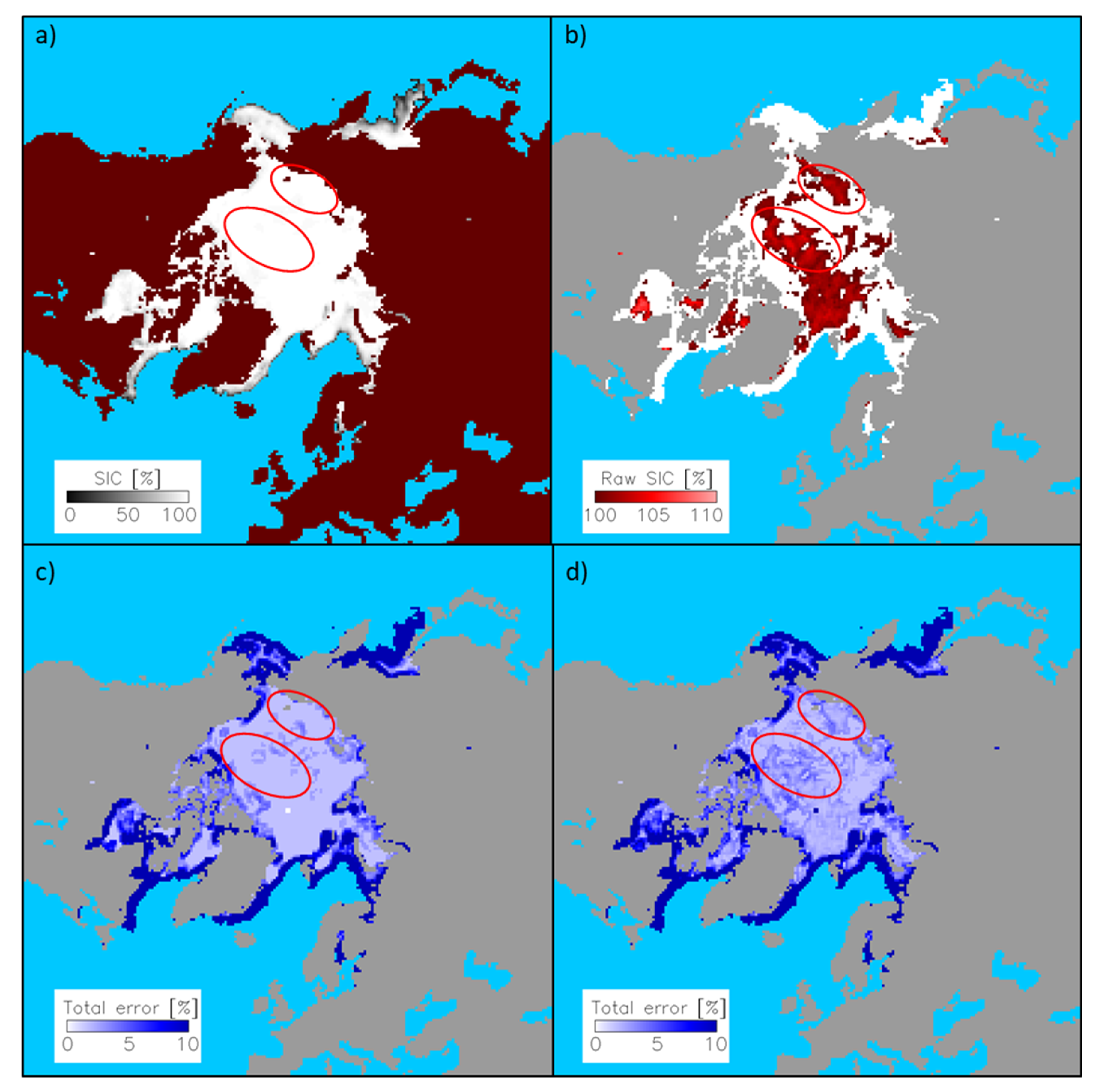
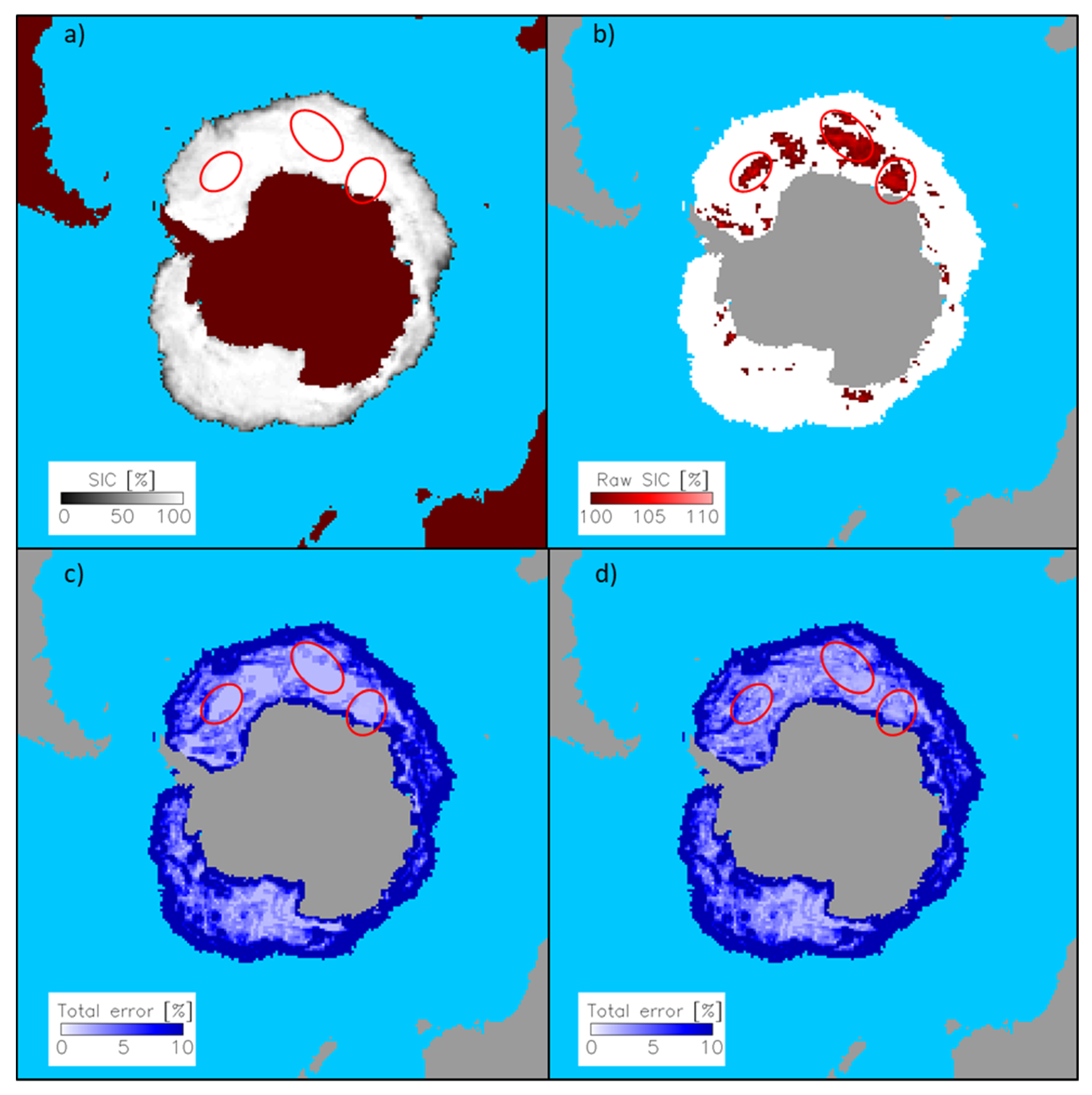





| Product | Input Data and Frequencies | Grid Resolution and Type | Footprint Sizes (for SSMIS and AMSR-E Channels Only) | Reference |
|---|---|---|---|---|
| OSI-450 | SMMR, SSM/I, SSMIS 19.35 and 37.0 GHz | 25 km × 25 km EASE2.0 | 70 km × 45 km (19 GHz) and 38 km × 30 km (37 GHz) | [9,13] |
| SICCI-25km | AMSR-E, AMSR2 18.7 and 36.5 GHz | 25 km × 25 km EASE2.0 | 27 km × 16 km (18.7 GHz) and 14 km × 9 km (36.5 GHz) | [9] |
| SICCI-50km | AMSR-E, AMSR2 6.9 and 36.5 GHz | 50 km × 50 km EASE2.0 | 75 km × 43 km (6.9 GHz and 14 km × 9 km (36.5 GHz) | [9] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kern, S. Spatial Correlation Length Scales of Sea-Ice Concentration Errors for High-Concentration Pack Ice. Remote Sens. 2021, 13, 4421. https://doi.org/10.3390/rs13214421
Kern S. Spatial Correlation Length Scales of Sea-Ice Concentration Errors for High-Concentration Pack Ice. Remote Sensing. 2021; 13(21):4421. https://doi.org/10.3390/rs13214421
Chicago/Turabian StyleKern, Stefan. 2021. "Spatial Correlation Length Scales of Sea-Ice Concentration Errors for High-Concentration Pack Ice" Remote Sensing 13, no. 21: 4421. https://doi.org/10.3390/rs13214421
APA StyleKern, S. (2021). Spatial Correlation Length Scales of Sea-Ice Concentration Errors for High-Concentration Pack Ice. Remote Sensing, 13(21), 4421. https://doi.org/10.3390/rs13214421






