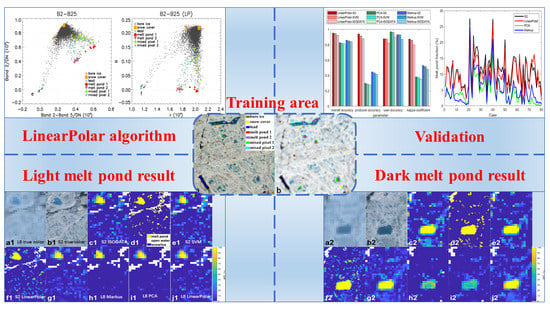
Melt Pond Retrieval Based on the LinearPolar Algorithm Using Landsat Data
Abstract
:1. Introduction
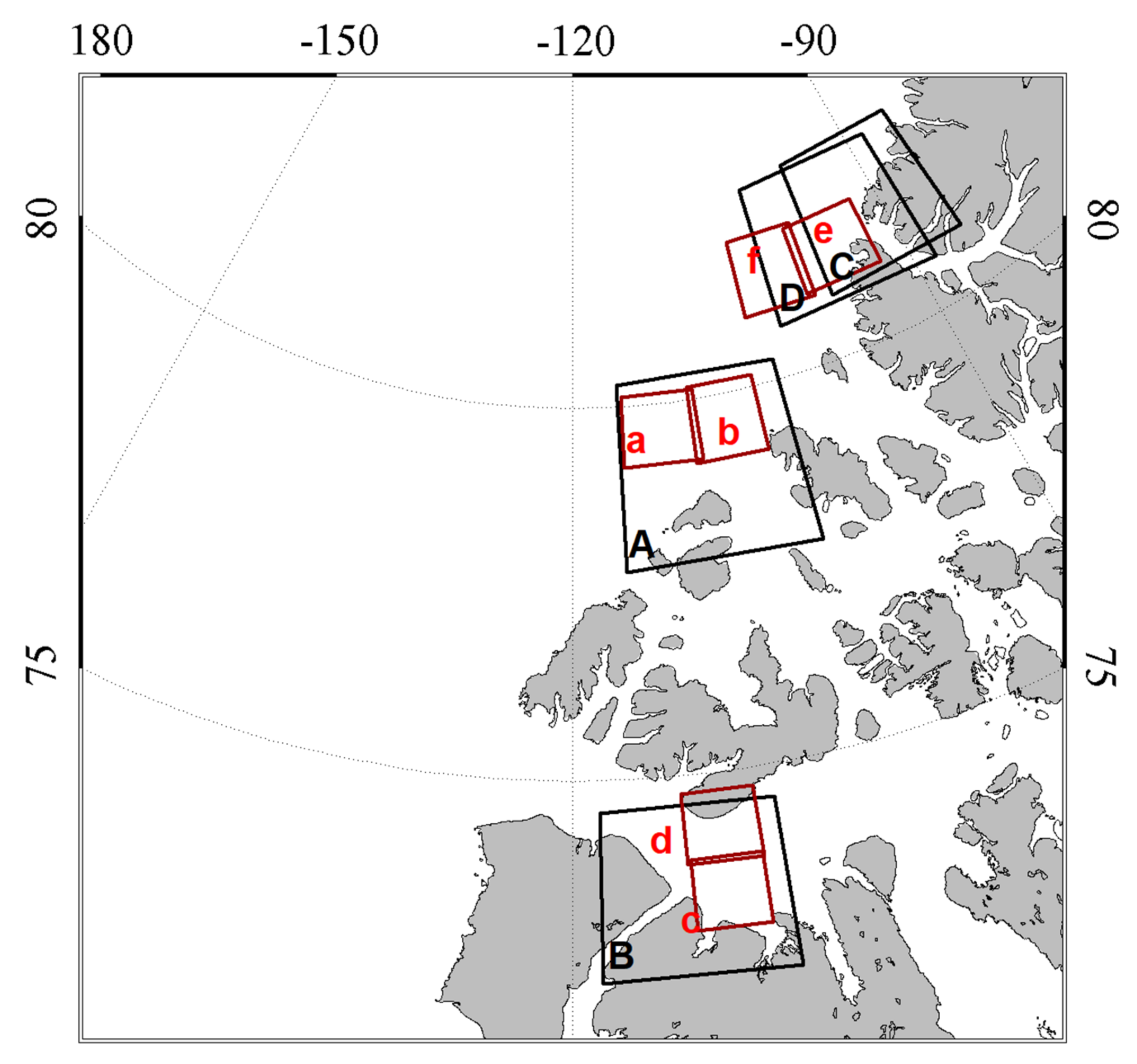
2. Data
2.1. L8 Data
2.2. Sentinel-2A Data
2.3. Data Process
3. Methods
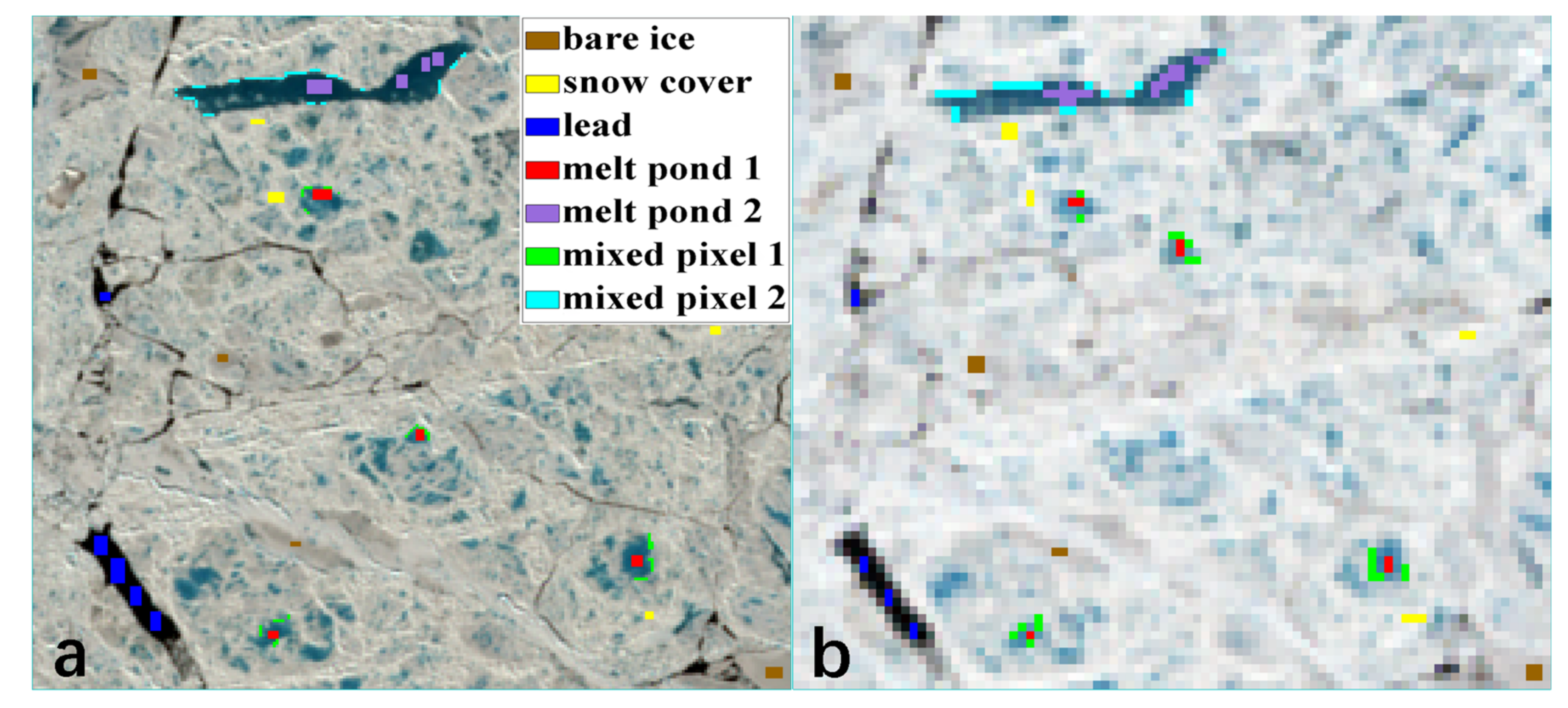
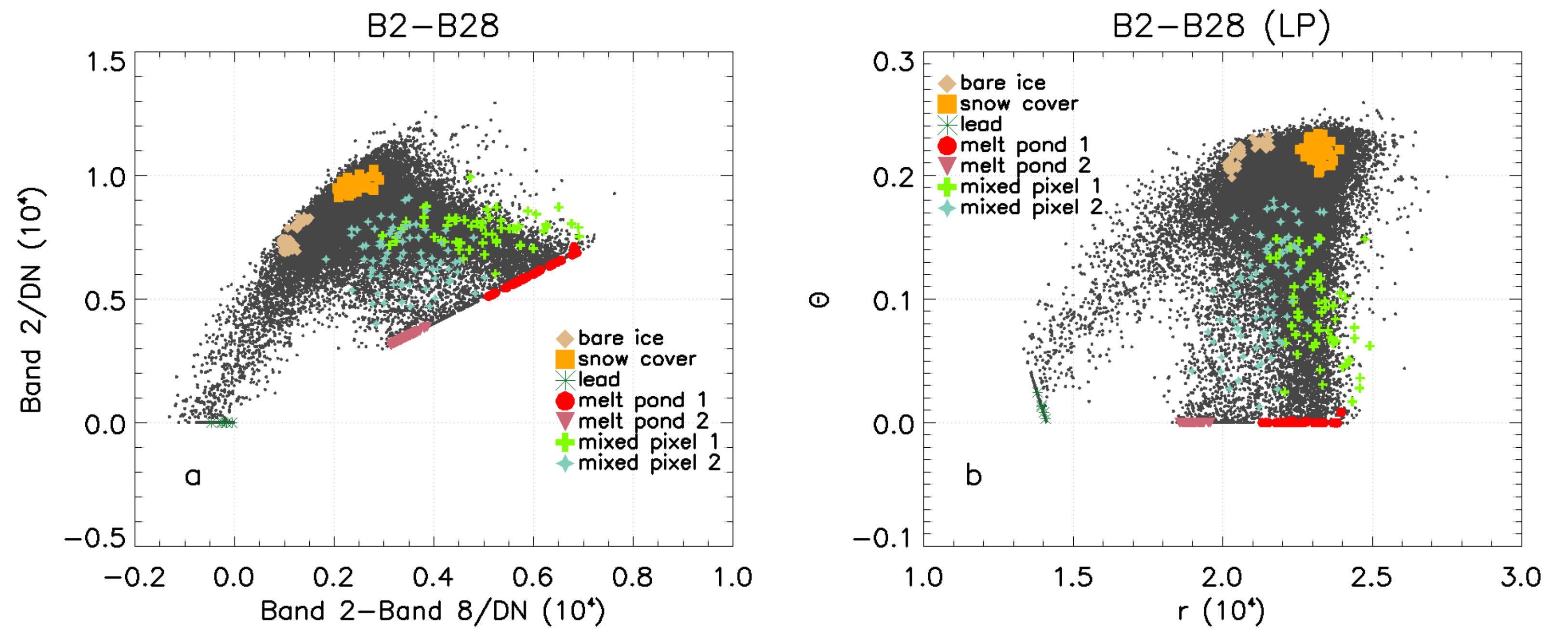
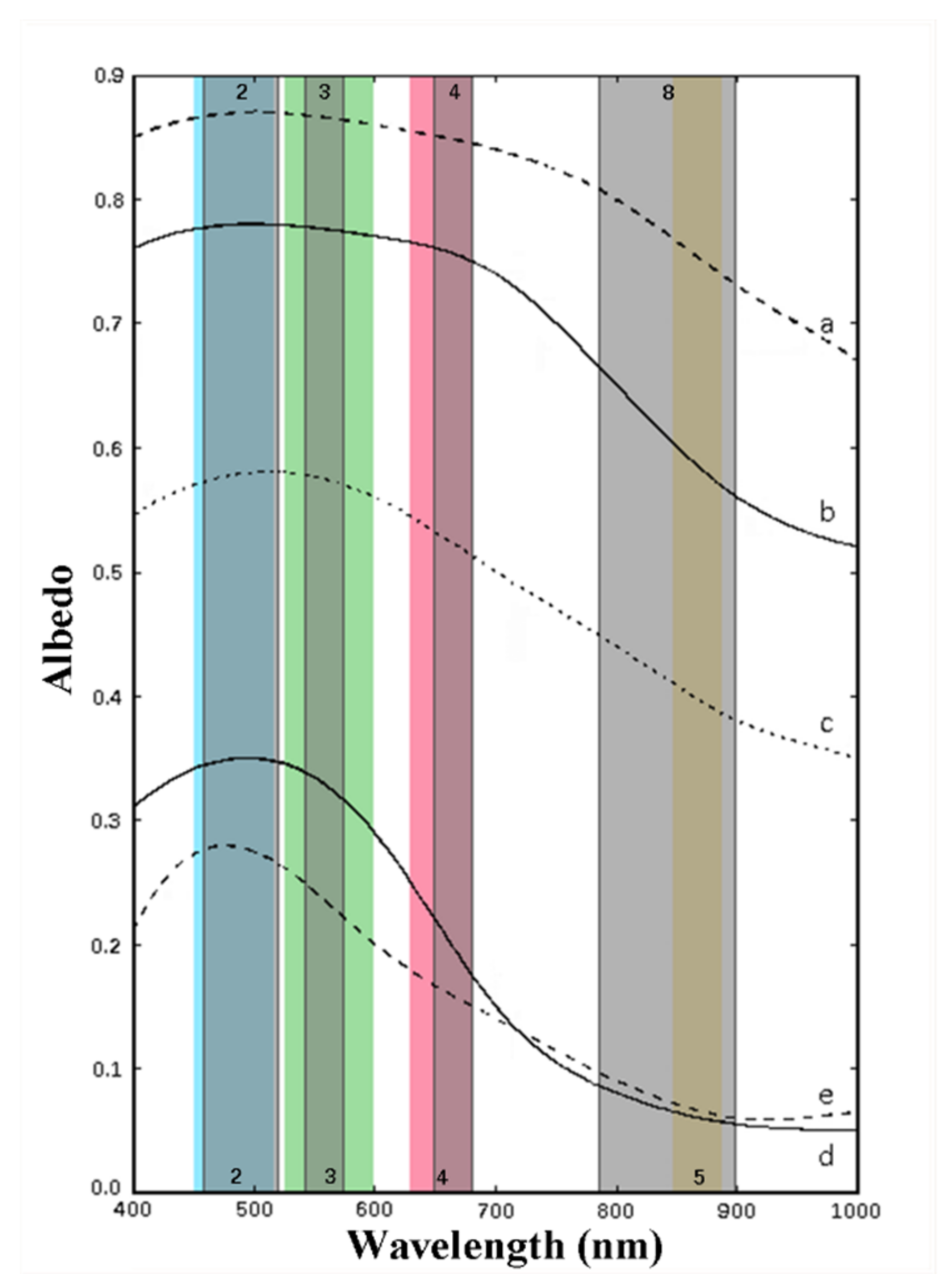
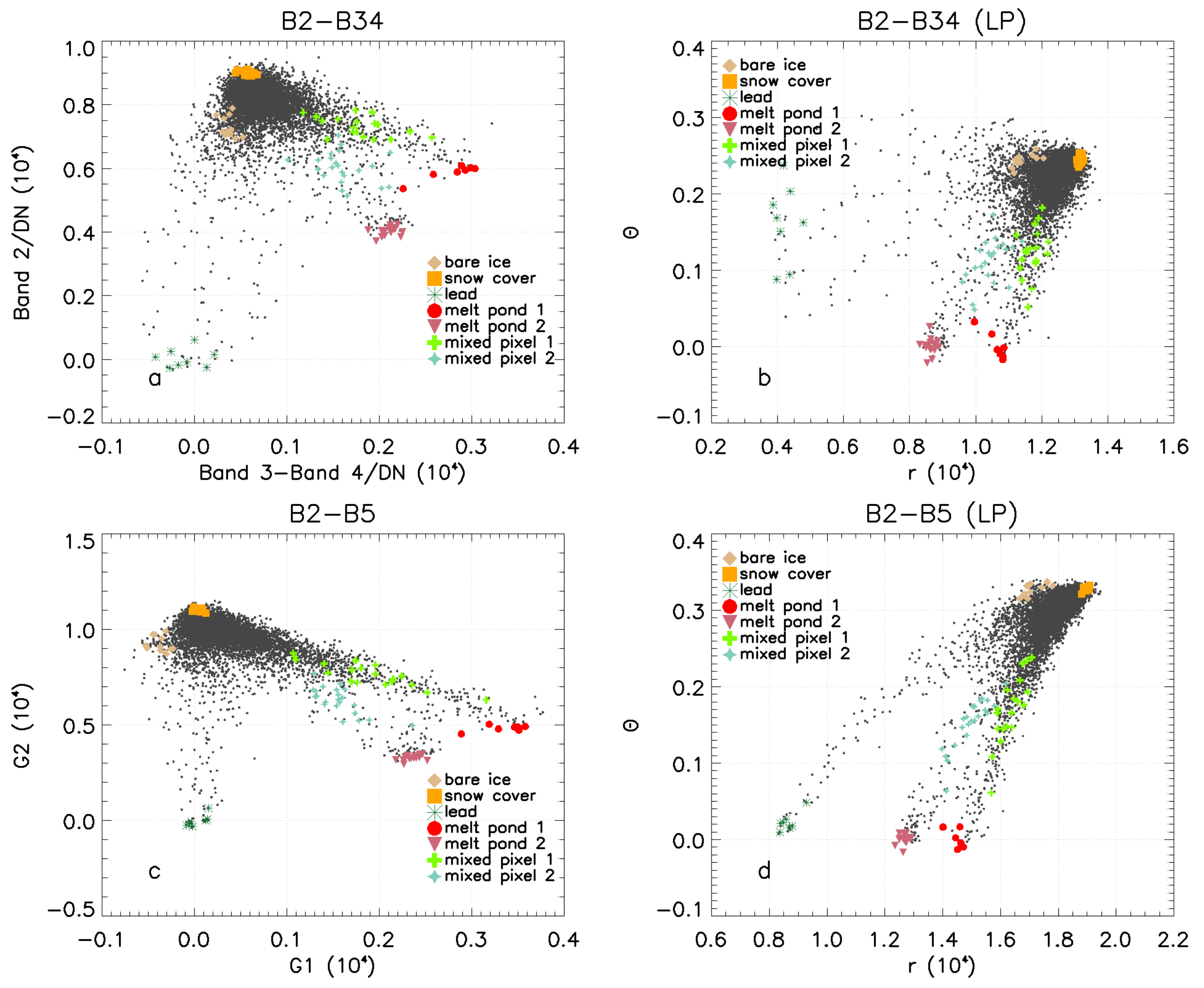
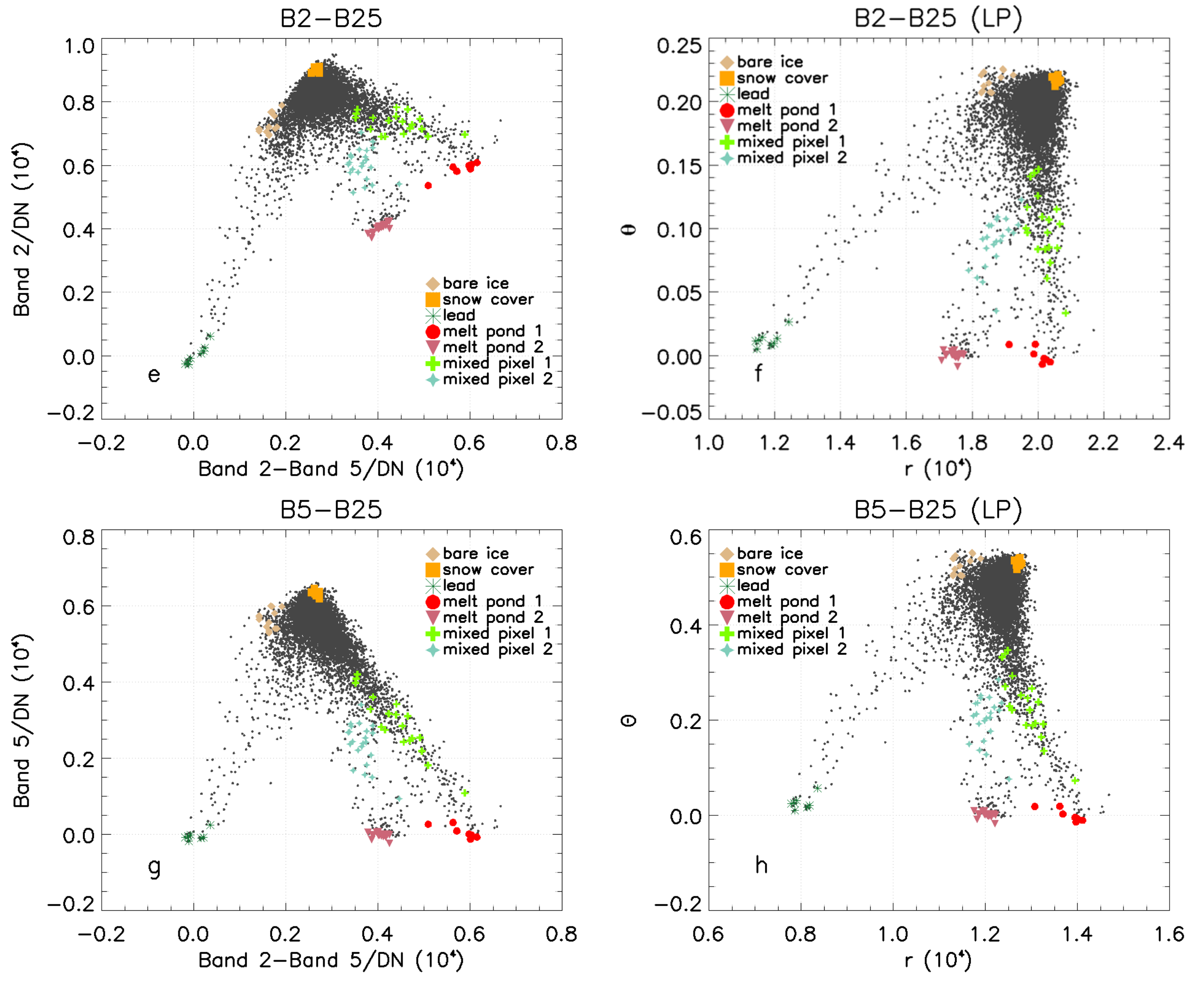
3.1. Band Combination Experiments
3.2. Retrieval Algorithm
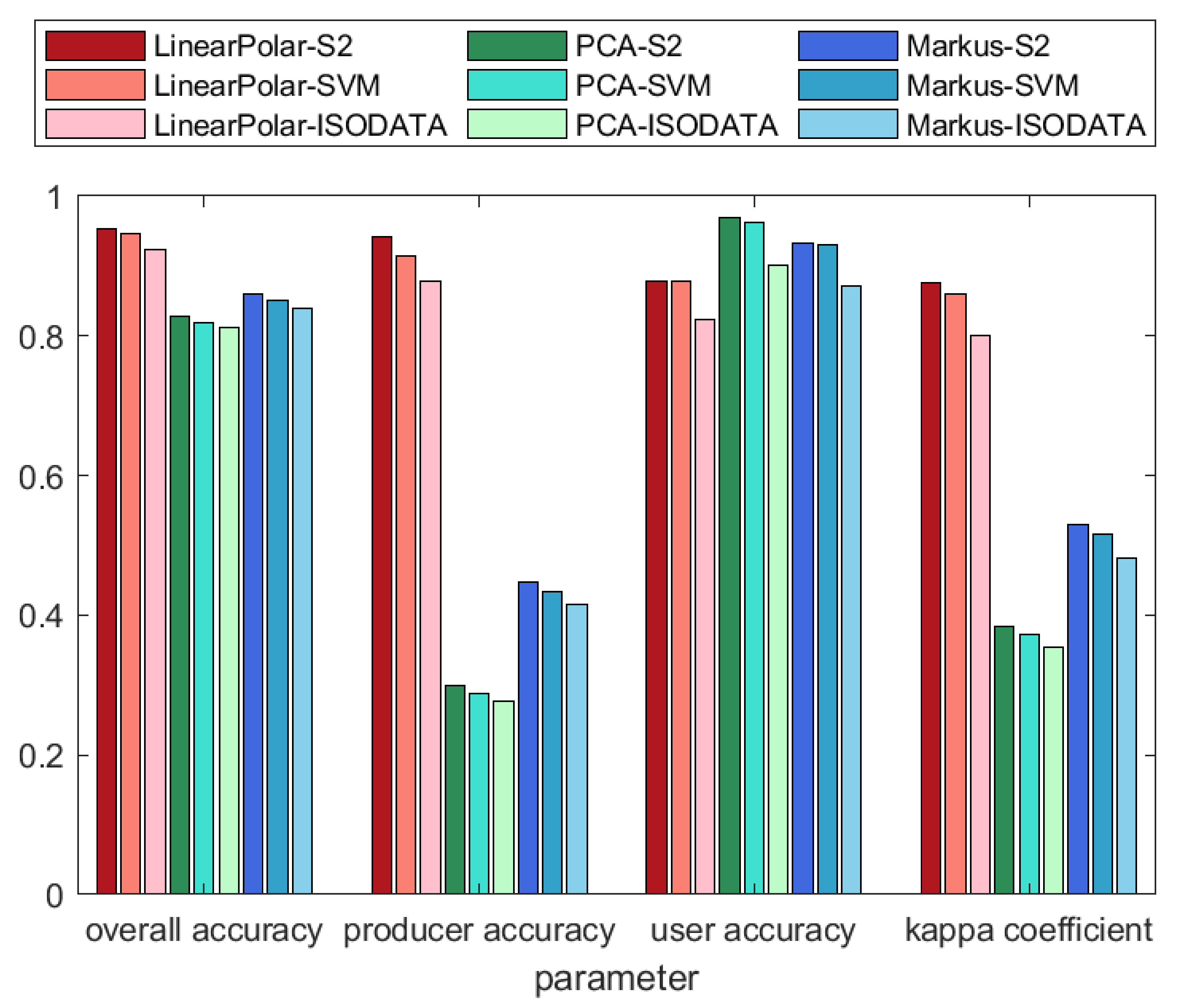
3.3. Verification and Comparison Methods
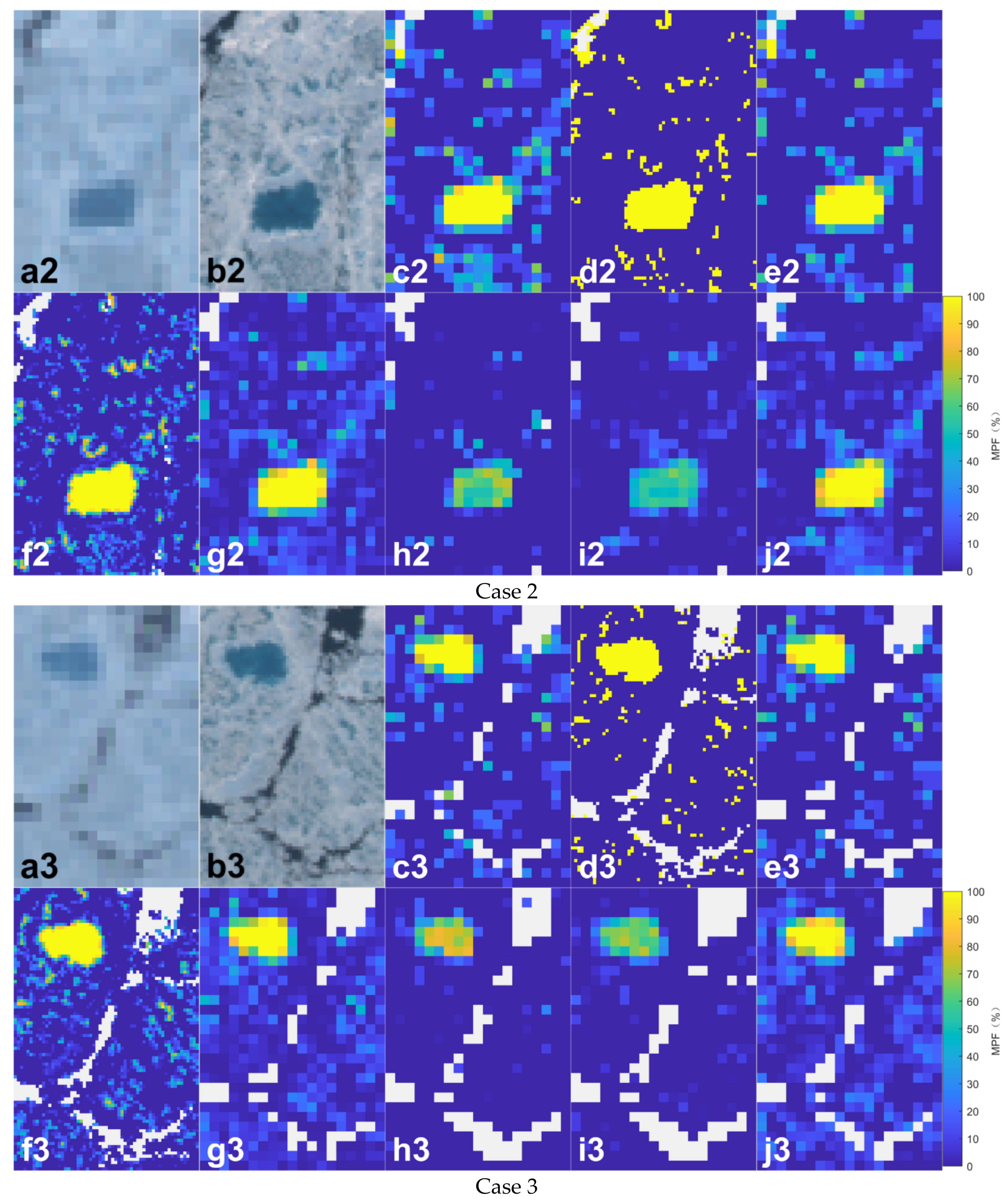
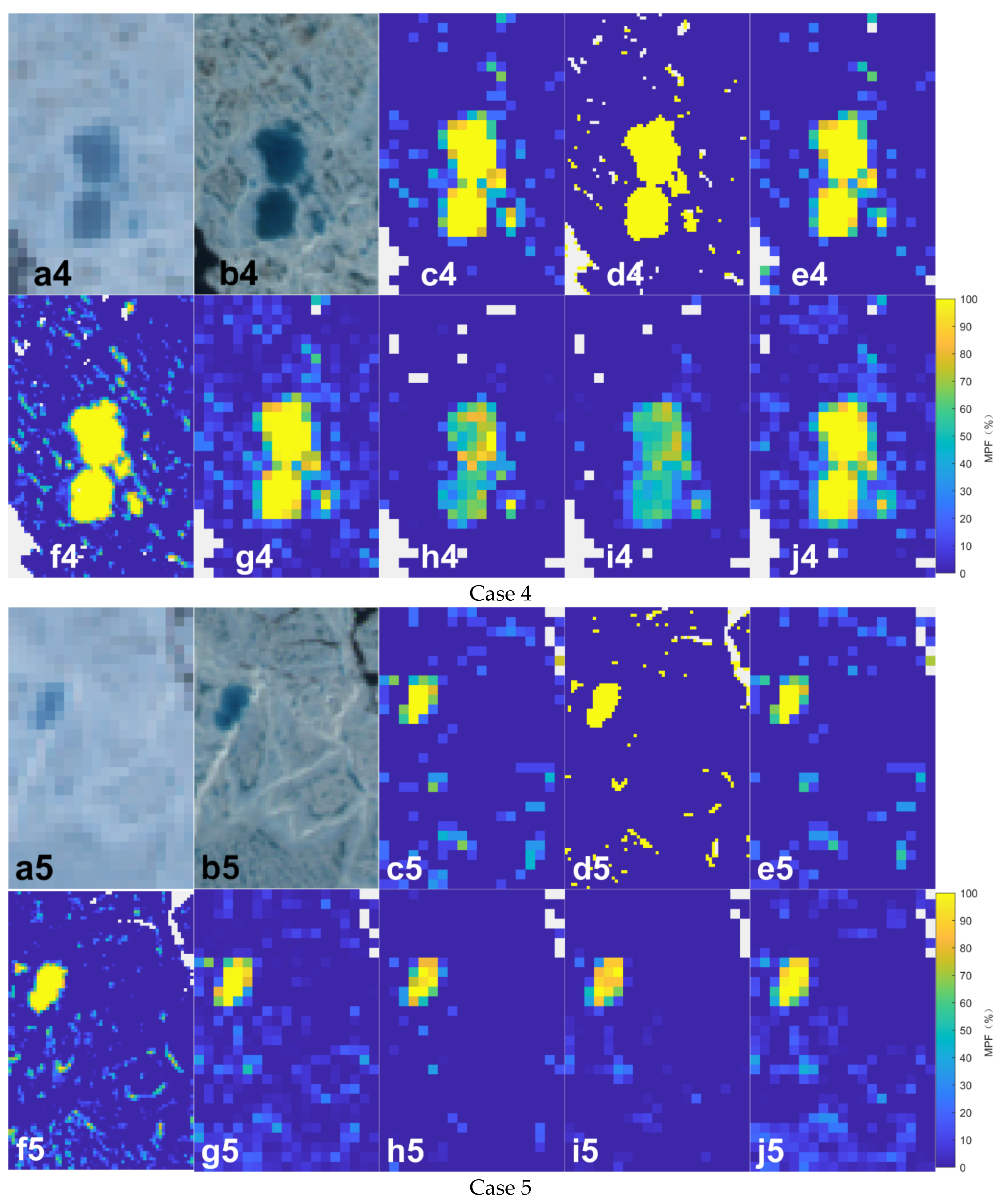
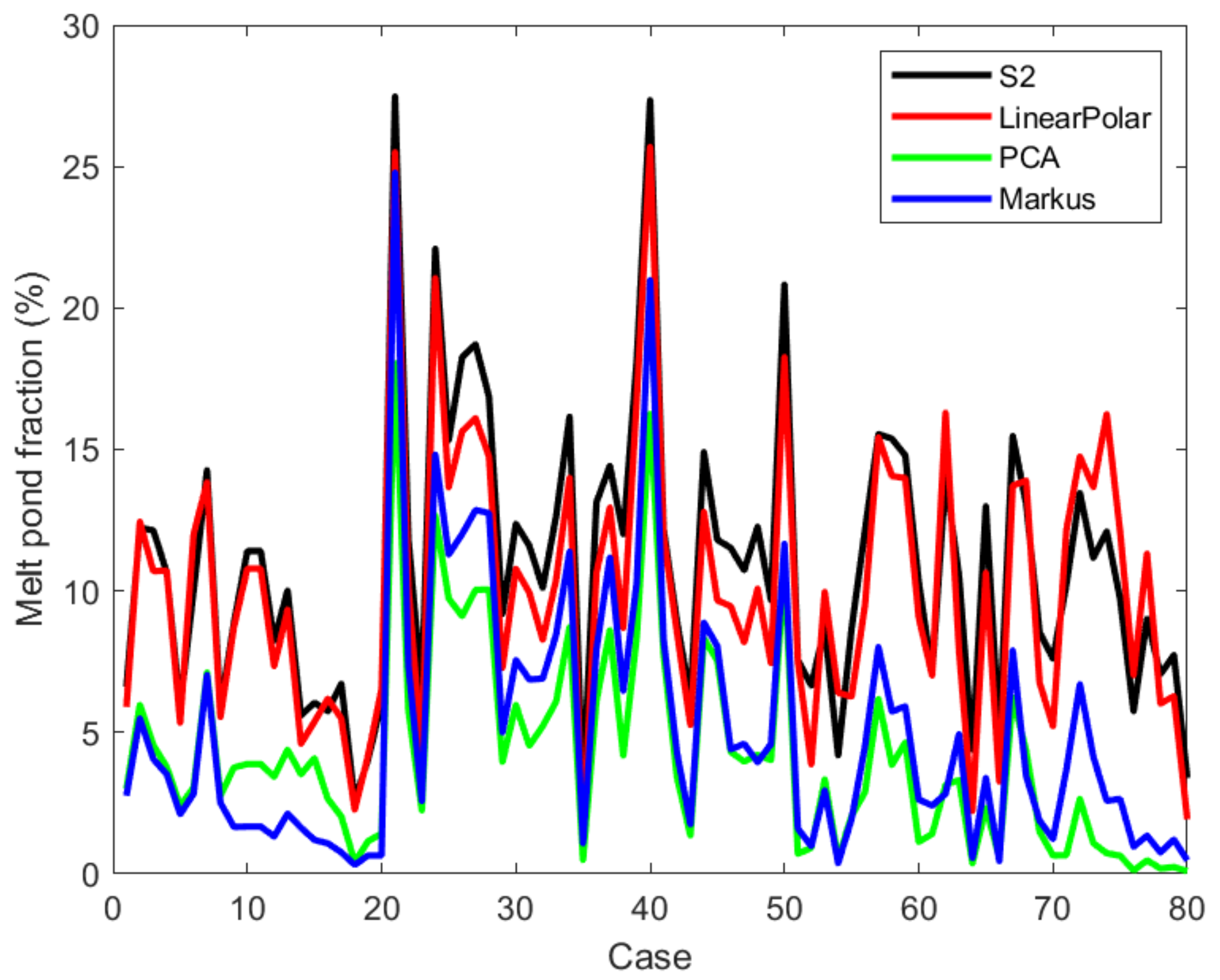
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Case | MPF (%) | RMSE (%) | |||||
|---|---|---|---|---|---|---|---|
| L8_Markus | L8_PCA | L8_LP | S2_LP | Mk | PCA | LP | |
| 1 | 2.76 | 3 | 5.9 | 6.62 | 8.02 | 6.86 | 5.35 |
| 2 | 5.49 | 5.97 | 12.45 | 12.23 | 13.26 | 13.16 | 8.94 |
| 3 | 4.06 | 4.55 | 10.7 | 12.14 | 15.01 | 14.01 | 8.63 |
| 4 | 3.52 | 3.78 | 10.72 | 10.66 | 11.77 | 11.63 | 5.89 |
| 5 | 2.11 | 2.41 | 5.34 | 5.89 | 11.01 | 10.79 | 8.98 |
| 6 | 2.83 | 3.05 | 11.99 | 10 | 12.64 | 11.8 | 7.09 |
| 7 | 7.03 | 7.12 | 13.84 | 14.27 | 15.71 | 15.35 | 7.35 |
| 8 | 2.51 | 2.76 | 5.54 | 5.86 | 7.9 | 7.14 | 5.26 |
| 9 | 1.66 | 3.76 | 8.72 | 8.86 | 12.75 | 9.55 | 7.94 |
| 10 | 1.67 | 3.88 | 10.79 | 11.41 | 14.15 | 11.27 | 8.74 |
| 11 | 1.67 | 3.88 | 10.79 | 11.41 | 14.15 | 11.27 | 8.74 |
| 12 | 1.32 | 3.43 | 7.34 | 8.25 | 12.24 | 11.08 | 10.35 |
| 13 | 2.13 | 4.39 | 9.34 | 10.01 | 13.64 | 11.3 | 8.47 |
| 14 | 1.63 | 3.52 | 4.6 | 5.6 | 8.92 | 7.57 | 6.66 |
| 15 | 1.2 | 4.09 | 5.38 | 6.05 | 10 | 8.73 | 8.02 |
| 16 | 1.08 | 2.65 | 6.19 | 5.75 | 8.9 | 7.27 | 6.15 |
| 17 | 0.76 | 2.03 | 5.49 | 6.72 | 10.19 | 8.68 | 6.88 |
| 18 | 0.32 | 0.41 | 2.27 | 2.57 | 5.43 | 4.11 | 5.1 |
| 19 | 0.65 | 1.16 | 4.2 | 4.05 | 7.08 | 5.86 | 5.85 |
| 20 | 0.65 | 1.42 | 6.54 | 6.05 | 9.42 | 8.02 | 6.4 |
| 21 | 24.79 | 18.05 | 25.51 | 27.48 | 15.97 | 15.65 | 11.79 |
| 22 | 7.35 | 5.78 | 10.13 | 11.81 | 10.71 | 10.21 | 7.32 |
| 23 | 2.57 | 2.24 | 4.27 | 6.52 | 8.44 | 8.24 | 6.37 |
| 24 | 14.82 | 12.66 | 21.06 | 22.1 | 21.4 | 20.27 | 18.06 |
| 25 | 11.29 | 9.73 | 13.66 | 15.33 | 12.02 | 9.8 | 7.82 |
| 26 | 12.01 | 9.11 | 15.64 | 18.26 | 15.1 | 16.2 | 11.56 |
| 27 | 12.86 | 10.04 | 16.11 | 18.72 | 19.58 | 18.2 | 15.98 |
| 28 | 12.75 | 10.05 | 14.74 | 16.85 | 14.91 | 13.96 | 11.32 |
| 29 | 5 | 3.96 | 7.28 | 9.19 | 13.02 | 12.4 | 11.53 |
| 30 | 7.56 | 5.97 | 10.78 | 12.37 | 11.98 | 11.12 | 8.38 |
| 31 | 6.87 | 4.53 | 9.94 | 11.6 | 13.11 | 13.02 | 8.55 |
| 32 | 6.9 | 5.22 | 8.28 | 10.11 | 13.48 | 12.52 | 10.93 |
| 33 | 8.46 | 6.09 | 10.41 | 12.65 | 14.75 | 13.02 | 11.24 |
| 34 | 11.39 | 8.72 | 14 | 16.16 | 17.43 | 14.95 | 12.96 |
| 35 | 1.08 | 0.49 | 1.24 | 2.98 | 6.41 | 5.59 | 4.81 |
| 36 | 7.93 | 6.11 | 10.63 | 13.13 | 16.33 | 15.13 | 13.21 |
| 37 | 11.18 | 8.61 | 12.95 | 14.42 | 13.64 | 12.34 | 9.89 |
| 38 | 6.47 | 4.18 | 8.69 | 12.01 | 13.24 | 12.48 | 8.34 |
| 39 | 10.3 | 8.37 | 16.75 | 18.14 | 17.06 | 15.76 | 9.16 |
| 40 | 20.99 | 16.26 | 25.7 | 27.35 | 15.38 | 16.15 | 7.99 |
| 41 | 8.29 | 7.75 | 11.96 | 12.19 | 13.83 | 11.57 | 9.9 |
| 42 | 4.28 | 3.41 | 8.53 | 8.91 | 9.63 | 9.92 | 4.79 |
| 43 | 1.75 | 1.36 | 5.26 | 6.19 | 8.76 | 8.25 | 4.29 |
| 44 | 8.88 | 8.32 | 12.8 | 14.91 | 10.71 | 10.68 | 7.62 |
| 45 | 8.05 | 7.54 | 9.67 | 11.81 | 12.33 | 10.75 | 9.51 |
| 46 | 4.4 | 4.31 | 9.46 | 11.52 | 11.24 | 10.49 | 5.45 |
| 47 | 4.6 | 3.97 | 8.19 | 10.73 | 10.5 | 10.03 | 5.55 |
| 48 | 3.95 | 4.21 | 10.08 | 12.27 | 13.52 | 12.81 | 9.21 |
| 49 | 4.59 | 4.02 | 7.45 | 9.67 | 10.48 | 10.11 | 7.49 |
| 50 | 11.67 | 10.86 | 18.27 | 20.83 | 17.49 | 17.69 | 12.1 |
| 51 | 1.6 | 0.71 | 7.52 | 7.56 | 10.71 | 11.09 | 6.01 |
| 52 | 0.98 | 0.92 | 3.87 | 6.66 | 10.62 | 10.7 | 9.64 |
| 53 | 2.95 | 3.34 | 9.97 | 8.71 | 10.42 | 9.44 | 6.79 |
| 54 | 0.38 | 0.53 | 6.4 | 4.19 | 6.99 | 7.08 | 6.19 |
| 55 | 1.94 | 2.05 | 6.27 | 8.67 | 11.31 | 9.91 | 6.24 |
| 56 | 4.52 | 2.89 | 9.51 | 12.15 | 13.75 | 13.8 | 9.23 |
| 57 | 8.02 | 6.18 | 15.43 | 15.54 | 14.46 | 14.48 | 12.09 |
| 58 | 5.74 | 3.85 | 14.06 | 15.38 | 16.33 | 16.35 | 10.36 |
| 59 | 5.92 | 4.64 | 13.99 | 14.79 | 14.84 | 14.78 | 9.88 |
| 60 | 2.63 | 1.13 | 9.07 | 10.32 | 12.23 | 13.32 | 9.36 |
| 61 | 2.41 | 1.41 | 7.01 | 7.09 | 10.08 | 9.54 | 9.27 |
| 62 | 2.83 | 3.15 | 16.3 | 14.02 | 15.51 | 14.83 | 11.5 |
| 63 | 4.94 | 3.31 | 7.91 | 10.54 | 10.99 | 12.02 | 9.05 |
| 64 | 0.56 | 0.37 | 2.22 | 4.39 | 7.52 | 7.48 | 5.18 |
| 65 | 3.39 | 2.33 | 10.65 | 13 | 14.27 | 14.04 | 9.91 |
| 66 | 0.45 | 0.58 | 3.26 | 4.92 | 7.78 | 7.49 | 5.12 |
| 67 | 7.9 | 6.23 | 13.72 | 15.48 | 13.9 | 13.96 | 7.92 |
| 68 | 3.46 | 4.35 | 13.9 | 13.08 | 15.38 | 14.29 | 10.47 |
| 69 | 1.88 | 1.49 | 6.76 | 8.54 | 11.33 | 10.94 | 6.52 |
| 70 | 1.23 | 0.65 | 5.22 | 7.61 | 10 | 9.67 | 5.3 |
| 71 | 3.69 | 0.66 | 12.17 | 10.24 | 13.67 | 14.22 | 10.83 |
| 72 | 6.7 | 2.65 | 14.75 | 13.46 | 13.81 | 15.31 | 9.92 |
| 73 | 4.15 | 1.09 | 13.67 | 11.17 | 14.06 | 14.87 | 9.8 |
| 74 | 2.58 | 0.73 | 16.25 | 12.1 | 14.46 | 15.09 | 10.75 |
| 75 | 2.65 | 0.64 | 12.08 | 9.72 | 12.27 | 13.29 | 8.06 |
| 76 | 0.96 | 0.12 | 7.02 | 5.75 | 8.9 | 9.39 | 6.96 |
| 77 | 1.35 | 0.48 | 11.32 | 9.01 | 12.09 | 12.73 | 10.23 |
| 78 | 0.76 | 0.19 | 6.02 | 7.06 | 10.65 | 11.33 | 6.84 |
| 79 | 1.21 | 0.24 | 6.28 | 7.73 | 10.78 | 11.62 | 9.03 |
| 80 | 0.48 | 0.1 | 1.93 | 3.39 | 6.52 | 7.04 | 5.14 |
| Mean | 4.95 | 4.20 | 10.03 | 10.91 | 12.25 | 11.69 | 8.54 |
Appendix B
| Case | S2_LP | L8_LP | S2_Isodata | ME (%) | MAE (%) | RMSE (%) | STD (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S2 | L8 | S2 | L8 | S2 | L8 | S2 | L8 | ||||
| 1 | 6.62 | 5.9 | 7.47 | 0.9 3 | −1.31 | 4.68 | 4.38 | 9.11 | 8.85 | 9.07 | 8.76 |
| 2 | 12.23 | 12.45 | 13.48 | 1.23 | −0.84 | 4.91 | 6.18 | 8.85 | 11.75 | 8.77 | 11.72 |
| 3 | 12.14 | 10.7 | 11.12 | −1.12 | 0.07 | 5.03 | 5.73 | 8.92 | 10.46 | 8.85 | 10.46 |
| 4 | 10.66 | 10.72 | 8.85 | −1.89 | 1.71 | 4.38 | 5.46 | 6.45 | 8.76 | 6.16 | 8.59 |
| 5 | 5.89 | 5.34 | 5.96 | 0.22 | −0.77 | 2.18 | 4.13 | 4.75 | 10.3 | 4.74 | 10.27 |
| 6 | 10 | 11.99 | 12.89 | 3.4 | −0.78 | 5.43 | 6.71 | 9.16 | 10.3 | 8.5 | 10.27 |
| 7 | 14.27 | 13.84 | 11.57 | −2.97 | 2.31 | 3.97 | 4.63 | 6.97 | 9.58 | 6.31 | 9.3 |
| 8 | 5.86 | 5.54 | 4.95 | −0.95 | 0.63 | 3.92 | 4.01 | 8.06 | 8.79 | 8 | 8.76 |
| 9 | 8.86 | 8.72 | 9 | 0.59 | −0.28 | 5.47 | 6.91 | 9.52 | 12.14 | 9.5 | 12.14 |
| 10 | 11.41 | 10.79 | 8.09 | −2.64 | 2.78 | 6.33 | 8.4 | 9.02 | 12.53 | 8.62 | 12.22 |
| 11 | 11.41 | 10.79 | 8.09 | −2.64 | 2.78 | 6.33 | 8.4 | 9.02 | 12.53 | 8.62 | 12.22 |
| 12 | 8.25 | 7.34 | 8.91 | 0.83 | −1.57 | 5 | 7.77 | 7.89 | 12.77 | 7.85 | 12.67 |
| 13 | 10.01 | 9.34 | 8.17 | −1.7 | 1.17 | 6.24 | 8 | 10.36 | 13.04 | 10.22 | 12.99 |
| 14 | 5.6 | 4.6 | 5.62 | −0.26 | −0.8 | 3.43 | 3.93 | 7.05 | 8.82 | 7.05 | 8.78 |
| 15 | 6.05 | 5.38 | 8.74 | 2.28 | −3.36 | 5.28 | 7.23 | 9.5 | 13.89 | 9.22 | 13.47 |
| 16 | 5.75 | 6.19 | 6.46 | 0.39 | −0.34 | 4.45 | 5.87 | 7.39 | 10.04 | 7.38 | 10.04 |
| 17 | 6.72 | 5.49 | 8.07 | 1.52 | −2.37 | 5.97 | 6.3 | 10.61 | 11.91 | 10.5 | 11.67 |
| 18 | 2.57 | 2.27 | 5.02 | 2.92 | −2.44 | 5.27 | 4.73 | 11.12 | 10.05 | 10.73 | 9.76 |
| 19 | 4.05 | 4.2 | 4.75 | 0.92 | −0.26 | 4.82 | 4.43 | 9.34 | 8.63 | 9.29 | 8.62 |
| 20 | 6.05 | 6.54 | 6.36 | 0.2 | 1.45 | 5.79 | 5.43 | 10.15 | 9.27 | 10.15 | 9.15 |
| 21 | 27.48 | 25.51 | 24.17 | −3.31 | 1.34 | 7.14 | 10.17 | 9.62 | 14.96 | 9.03 | 14.9 |
| 22 | 11.81 | 10.13 | 10.7 | −1.13 | −0.54 | 5.5 | 6.17 | 8.62 | 11.37 | 8.54 | 11.35 |
| 23 | 6.52 | 4.27 | 6.93 | 0.39 | −2.64 | 3.93 | 4.31 | 6.98 | 10.03 | 6.97 | 9.68 |
| 24 | 22.1 | 21.06 | 22.28 | 0.17 | −1.22 | 7.38 | 15.6 | 11.22 | 23.44 | 11.22 | 23.4 |
| 25 | 15.33 | 13.66 | 15.8 | 0.46 | −2.13 | 5.06 | 5.86 | 7.9 | 10.89 | 7.89 | 10.68 |
| 26 | 18.26 | 15.64 | 17.06 | −1.2 | −1.41 | 4.7 | 7.9 | 7.47 | 14.32 | 7.37 | 14.25 |
| 27 | 18.72 | 16.11 | 18 | −0.72 | −1.89 | 6.06 | 11.05 | 9.29 | 19.5 | 9.26 | 19.41 |
| 28 | 16.85 | 14.74 | 16.69 | −0.16 | −1.94 | 4.2 | 6.98 | 7.1 | 13.81 | 7.1 | 13.68 |
| 29 | 9.19 | 7.28 | 9.61 | 0.47 | −2.34 | 4.68 | 7.84 | 7.91 | 15.54 | 7.9 | 15.36 |
| 30 | 12.37 | 10.78 | 12.6 | 0.35 | −1.94 | 5.42 | 7.12 | 8.88 | 12.29 | 8.87 | 12.12 |
| 31 | 11.6 | 9.94 | 9.63 | −1.97 | 0.31 | 5.94 | 6.26 | 9.87 | 12.73 | 9.67 | 12.73 |
| 32 | 10.11 | 8.28 | 9.94 | −0.17 | −1.66 | 4.73 | 7.85 | 8.66 | 15.66 | 8.66 | 15.57 |
| 33 | 12.65 | 10.41 | 14.74 | 2.1 | −4.33 | 5.69 | 9 | 9.82 | 16.62 | 9.59 | 16.05 |
| 34 | 16.16 | 14 | 17.52 | 1.35 | −3.52 | 5.93 | 10.42 | 9.12 | 17.47 | 9.02 | 17.12 |
| 35 | 2.98 | 1.24 | 2.47 | −0.49 | −1.24 | 2.18 | 2.17 | 4.6 | 6.66 | 4.57 | 6.54 |
| 36 | 13.13 | 10.63 | 12.69 | −0.45 | −2.06 | 4.97 | 8.88 | 8.02 | 16.83 | 8.01 | 16.7 |
| 37 | 14.42 | 12.95 | 15.85 | 1.44 | −2.9 | 4.33 | 7.84 | 7.41 | 14.32 | 7.27 | 14.02 |
| 38 | 12.01 | 8.69 | 12.92 | 0.81 | −4.12 | 5.31 | 6.95 | 8.47 | 12.64 | 8.43 | 11.94 |
| 39 | 18.14 | 16.75 | 17.5 | −0.63 | −0.75 | 6.42 | 8.45 | 9.72 | 14 | 9.7 | 13.98 |
| 40 | 27.35 | 25.7 | 27.61 | 0.25 | −1.91 | 7.61 | 8.99 | 11.71 | 14.74 | 11.71 | 14.62 |
| 41 | 12.19 | 11.96 | 11.12 | −0.97 | 0.78 | 4.26 | 5.85 | 6.89 | 11.88 | 6.82 | 11.86 |
| 42 | 8.91 | 8.53 | 7.35 | −1.56 | 1.17 | 4.54 | 4.73 | 7.01 | 8.09 | 6.83 | 8 |
| 43 | 6.19 | 5.26 | 5.8 | −0.4 | −0.54 | 4.61 | 4.96 | 7.82 | 9.65 | 7.81 | 9.64 |
| 44 | 14.91 | 12.8 | 13.39 | −1.51 | −0.58 | 7.08 | 6.27 | 10.76 | 11.08 | 10.66 | 11.06 |
| 45 | 11.81 | 9.67 | 11.8 | −0.01 | −2.12 | 4.6 | 5.7 | 7.78 | 11.95 | 7.78 | 11.76 |
| 46 | 11.52 | 9.46 | 13.37 | 1.85 | −3.91 | 6.16 | 6.24 | 9.5 | 10.97 | 9.32 | 10.25 |
| 47 | 10.73 | 8.19 | 12.69 | 1.95 | −4.32 | 6.18 | 6.46 | 10.57 | 12.09 | 10.38 | 11.29 |
| 48 | 12.27 | 10.08 | 11.96 | −0.3 | −1.88 | 6.63 | 8.89 | 10.25 | 15.33 | 10.24 | 15.21 |
| 49 | 9.67 | 7.45 | 8 | −1.67 | −0.55 | 4.31 | 5.33 | 6.43 | 9.89 | 6.21 | 9.88 |
| 50 | 20.83 | 18.27 | 18.23 | −2.57 | 0.04 | 5.25 | 7.38 | 7.51 | 14.25 | 7.05 | 14.25 |
| 51 | 7.56 | 7.52 | 7.07 | −0.56 | 0.45 | 5.1 | 6.51 | 8.27 | 10.9 | 8.25 | 10.89 |
| 52 | 6.66 | 3.87 | 6.56 | −0.16 | −2.58 | 5.27 | 6.58 | 8.81 | 13.79 | 8.81 | 13.54 |
| 53 | 8.71 | 9.97 | 7.48 | −1.23 | 2.48 | 6.17 | 8.48 | 9.83 | 12.77 | 9.75 | 12.52 |
| 54 | 4.19 | 6.4 | 3.85 | −0.4 | 2.64 | 3.76 | 5.54 | 7.97 | 10.15 | 7.96 | 9.8 |
| 55 | 8.67 | 6.27 | 7.04 | −1.64 | −0.76 | 6.88 | 6.85 | 10.4 | 12.17 | 10.27 | 12.14 |
| 56 | 12.15 | 9.51 | 14.33 | 2.28 | −4.66 | 7.13 | 9.32 | 11.3 | 15.07 | 11.07 | 14.34 |
| 57 | 15.54 | 15.43 | 17.44 | 1.91 | −2.02 | 6.95 | 11.75 | 11.09 | 18.35 | 10.93 | 18.24 |
| 58 | 15.38 | 14.06 | 17.56 | 2.02 | −3.3 | 8.85 | 11.64 | 13.23 | 17.97 | 13.08 | 17.66 |
| 59 | 14.79 | 13.99 | 14.3 | −0.73 | −0.01 | 8.31 | 9.43 | 12.04 | 14.54 | 12.01 | 14.54 |
| 60 | 10.32 | 9.07 | 11.7 | 1.34 | −2.05 | 8.08 | 10.4 | 12.71 | 16.4 | 12.64 | 16.27 |
| 61 | 7.09 | 7.01 | 10.22 | 3.18 | −3.44 | 5.97 | 8.8 | 11 | 15.24 | 10.53 | 14.84 |
| 62 | 14.02 | 16.3 | 13.93 | −0.21 | 2.61 | 10.34 | 12.78 | 14.97 | 18.41 | 14.97 | 18.22 |
| 63 | 10.54 | 7.91 | 9.11 | −1.41 | −1.09 | 4.94 | 6.13 | 9 | 12.15 | 8.89 | 12.1 |
| 64 | 4.39 | 2.22 | 5.44 | 1.1 | −2.92 | 4.01 | 3.96 | 8.16 | 9.83 | 8.09 | 9.39 |
| 65 | 13 | 10.65 | 12.74 | −0.22 | −2.13 | 9.86 | 11.54 | 14.53 | 18.99 | 14.53 | 18.88 |
| 66 | 4.92 | 3.26 | 2.76 | −2.2 | 0.5 | 4.35 | 3.68 | 7.38 | 8.01 | 7.04 | 7.99 |
| 67 | 15.48 | 13.72 | 11.43 | −4.08 | 2.29 | 5.99 | 6.42 | 8.77 | 11.19 | 7.77 | 10.96 |
| 68 | 13.08 | 13.9 | 12.87 | −0.22 | 1.03 | 6.65 | 8.84 | 10.33 | 14.12 | 10.33 | 14.08 |
| 69 | 8.54 | 6.76 | 7.39 | −1.17 | −0.63 | 5.77 | 6.22 | 9.23 | 11.36 | 9.15 | 11.34 |
| 70 | 7.61 | 5.22 | 6.94 | −0.69 | −1.73 | 6.11 | 5.85 | 9.4 | 10.77 | 9.37 | 10.63 |
| 71 | 10.24 | 12.17 | 9.2 | −1.13 | 3.22 | 7.52 | 10.49 | 11.76 | 15.65 | 11.71 | 15.31 |
| 72 | 13.46 | 14.75 | 14.11 | 0.65 | 0.64 | 7.5 | 10.76 | 11.45 | 15.7 | 11.44 | 15.69 |
| 73 | 11.17 | 13.67 | 10.54 | 0.33 | 2.09 | 6.4 | 9.59 | 9.89 | 13.98 | 9.89 | 13.82 |
| 74 | 12.1 | 16.25 | 11.96 | −0.26 | 4.66 | 8.79 | 13.29 | 12.82 | 17.42 | 12.82 | 16.79 |
| 75 | 9.72 | 12.08 | 9.5 | −0.39 | 3.14 | 7.65 | 9.22 | 12.13 | 13.34 | 12.13 | 12.96 |
| 76 | 5.75 | 7.02 | 7.15 | 1.34 | −0.13 | 6.61 | 7.98 | 11.03 | 12.72 | 10.95 | 12.72 |
| 77 | 9.01 | 11.32 | 8.24 | −0.8 | 3.08 | 6.95 | 10.23 | 11.2 | 15.78 | 11.18 | 15.48 |
| 78 | 7.06 | 6.02 | 6.92 | −0.26 | −0.87 | 6.19 | 6.87 | 10.99 | 12.88 | 10.99 | 12.85 |
| 79 | 7.73 | 6.28 | 7.24 | −0.5 | −0.84 | 6.19 | 8.11 | 10.99 | 15.06 | 10.98 | 15.04 |
| 80 | 3.39 | 1.93 | 3 | −0.39 | −1.07 | 2.77 | 3.06 | 6.03 | 8.37 | 6.01 | 8.3 |
| Mean | 10.91 | 10.03 | 10.75 | 9.34 | −0.66 | −0.14 | 7.38 | 5.71 | 12.88 | 9.21 | 12.71 |
References
- Perovich, D.K.; Polashenski, C. Albedo evolution of seasonal Arctic sea ice. Geophys. Res. Lett. 2012, 39, L08501. [Google Scholar] [CrossRef]
- Perovich, D.K.; Light, B.; Eicken, H.; Jones, K.F.; Runciman, K.; Nghiem, S.V. Increasing solar heating of the arctic ocean and adjacent seas, 1979–2005: Attribution and role in the ice-albedo feedback. Geophys. Res. Lett. 2007, 34, L19505. [Google Scholar] [CrossRef] [Green Version]
- Scharien, R.K.; Segal, R.; Nasonova, S. Winter Sentinel-1 backscatter as a predictor of spring Arctic sea ice melt pond fraction. Geophys. Res. Lett. 2017, 44, 12262–12270. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Song, M.; Horton, R.M.; Hu, Y. Revisiting the potential of melt ponds fraction as a predictor for the seasonal Arctic sea ice extent minimum. Environ. Res. Lett. 2015, 10, 054017. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Cheng, X.; Liu, J.; Hui, F.; Wang, Z. Investigation of spatiotemporal variability of melt pond fraction and its relationship with sea ice extent during 2000–2017 using a new data. Cryosphere Discuss 2019, preprint. [Google Scholar]
- Tschudi, M.A.; Maslanik, J.A.; Perovich, D.K. Derivation of melt pond coverage on Arctic sea ice using MODIS observations. Remote Sens. Environ. 2008, 112, 26052614. [Google Scholar] [CrossRef]
- Rösel, A.; Kaleschke, L.; Birnbaum, G. Melt ponds on arctic sea ice determined from MODIS satellite data using an artificial neural network. Cryosphere 2012, 6, 431–446. [Google Scholar] [CrossRef] [Green Version]
- Zege, E.; Malinka, A.; Katsev, I.; Prikhach, A.; Heygster, G.; Istomina, L.; Birnbaum, G.; Schwarz, P. Algorithm to retrieve the melt pond fraction and the spectral albedo of Arctic summer ice from satellite optical data. Remote Sens. Environ. 2015, 163, 153–164. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Cheng, X.; Liu, J.; Hui, F.; Wang, Z.; Chen, S. Retrieval of Melt Pond Fraction over Arctic Sea Ice during 2000–2019 Using an Ensemble-Based Deep Neural Network. Remote Sens. 2020, 12, 2746. [Google Scholar] [CrossRef]
- Markus, T.; Cavalieri, D.J.; Tschudi, M.A.; Ivanoff, A. Comparison of aerial video and Landsat 7 data over ponded sea ice. Remote Sens. Environ. 2003, 86, 458–469. [Google Scholar] [CrossRef]
- Rösel, A.; Kaleschke, L. Comparison of different retrieval techniques for melt ponds on Arctic sea ice from Landsat and MODIS satellite data. Ann. Glaciol. 2011, 52, 185–191. [Google Scholar] [CrossRef] [Green Version]
- Tschudi, M.A.; Curry, J.A.; Maslanik, J.A. Airborne observations of summertime surface features and their effect on surface albedo during FIRE/SHEBA. J. Geophys. Res. 2001, 106, 15335–15344. [Google Scholar] [CrossRef]
- Perovich, D.K.; Tucker, W.B.; Ligett, K.A. Aerial observations of the evolution of ice surface conditions during summer. J. Geophys. Res. 2002, 107, 8048. [Google Scholar] [CrossRef]
- Polashenski, C.; Perovich, D.K.; Courville, Z. The mechanisms of sea ice melt pond formation and evolution. J. Geophys. Res. 2012, 117, C01001. [Google Scholar] [CrossRef]
- Wang, M.; Su, J.; Landy, J.; Lepparanta, M.; Guan, L. A new algorithm for melt pond fraction estimation from high-resolution optical satellite imagery. J. Geophys. Res. Oceans 2020, 125, e2019JC015716. [Google Scholar] [CrossRef]
- Aksenov, Y.; Popova, E.; Yool, A.; Nurser, A.; Williams, T.; Bertino, L.; Bergh, J. On the future navigability of arctic sea routes: High-resolution projections of the arctic ocean and sea ice. Mar. Policy 2016, 75, 300–317. [Google Scholar] [CrossRef] [Green Version]
- Howell, S.; Tivy, A.; Yackel, J.; Mccourt, S. Multi-year sea-ice conditions in the western Canadian Arctic Archipelago region of the northwest passage: 1968–2006. Atmosphere 2008, 46, 229–242. [Google Scholar] [CrossRef]
- Bindschadler, R.; Vornberger, P.; Fleming, A.; Fox, A.; Mullins, J.; Binnie, D.; Paulsen, S.J.; Granneman, B.; Gorodetzky, D. The Landsat image mosaic of Antarctica. Remote Sens. Environ. 2008, 112, 4214–4226. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMEs operational services. Remote Sens. Environ. 2012, 10, 25–36. [Google Scholar] [CrossRef]
- Grenfell, T.C.; Maykut, G.A. The optical properties of ice and snow in the Arctic basin. J. Glaciol. Geocryol. 1977, 18, 445–463. [Google Scholar] [CrossRef] [Green Version]
- Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 1115. [Google Scholar] [CrossRef]
- Bruzzone, L.; Persello, C. Approaches Based on Support Vector Machine to Classification of Remote Sensing Data. In Handbook of Pattern Recognition and Computer Vision; World Scientific: Singapore, 2009; pp. 329–352. [Google Scholar]
- Ball, G.H.; Hall, D.J. Isodata, A Novel Method of Data Analysis and Pattern Classification; Technol. Rep. 5RI; Stanford Research Inst: Menlo Park, CA, USA, 1965; Volume 5533. [Google Scholar]
- Buckley, E.M.; Farrell, S.L.; Duncan, K.; Connor, L.N.; Kuhn, J.M.; Dominguez, R.A. Classfication of sea ice summer melt features in high-resolution IceBridgr imagery. J. Geophys. Res. Oceans 2020, 125, e2019JC01573. [Google Scholar] [CrossRef]

| Band Combination | MPF (%) | ME (%) | MAE (%) | RMSE (%) | STD (%) |
|---|---|---|---|---|---|
| B2–B5 | 11.22 | −2.32 | 10.38 | 16.39 | 16.02 |
| B2–B25 | 12.75 | −0.71 | 10.35 | 16.22 | 16.05 |
| B2–B34 | 9.95 | −3.51 | 10.63 | 16.88 | 16.22 |
| B5–B25 | 12.59 | −0.87 | 10.63 | 16.61 | 16.13 |
| Band Combination | Producer’s Accuracy (%) | User’s Accuracy (%) | Overall Accuracy (%) | Kappa Coefficient |
|---|---|---|---|---|
| B2–B5 | 80.93 | 94.58 | 94.20 | 0.8384 |
| B2–B25 | 90.77 | 91.92 | 95.79 | 0.8842 |
| B2–B34 | 81.76 | 92.20 | 93.91 | 0.8265 |
| B5–B25 | 91.88 | 90.21 | 95.58 | 0.8797 |
| Band Combination | B2–B5 | B2–B25 | B2–B34 | B5–B25 | ||||
|---|---|---|---|---|---|---|---|---|
| Threshold | −3% | +3% | −3% | +3% | −3% | +3% | −3% | +3% |
| STD (%) | 1.23 | 1.17 | 1.20 | 1.14 | 1.22 | 1.19 | 1.22 | 1.18 |
| Threshold | −5% | +5% | −5% | +5% | −5% | +5% | −5% | +5% |
| STD (%) | 2.01 | 1.58 | 1.97 | 1.80 | 1.99 | 1.88 | 2.01 | 1.87 |
| Band Combination | B2–B5 | B2–B25 | B2–B34 | B5–B25 | ||||
|---|---|---|---|---|---|---|---|---|
| Axis | Ice/ snow | Melt pond | Ice/ snow | Melt pond | Ice/ snow | Melt pond | Ice/ snow | Melt pond |
| STD (%) | 0.65 | 0.79 | 0.55 | 0.42 | 0.67 | 1.24 | 1.44 | 0.87 |
| Case | MPF (%) | |||||
|---|---|---|---|---|---|---|
| L8_Markus | L8_PCA | L8_LinearPolar | S2_LinearPolar | SVM | ISODATA | |
| 1 | 2.8 | 3.0 | 5.9 | 6.6 | 7.4 | 7.5 |
| 2 | 4.1 | 4.6 | 10.7 | 12.1 | 13.6 | 11.1 |
| 3 | 3.5 | 3.8 | 10.7 | 10.7 | 8.8 | 8.9 |
| 4 | 7.0 | 7.1 | 13.8 | 14.3 | 12.4 | 11.6 |
| 5 | 2.5 | 2.8 | 5.5 | 5.9 | 5.6 | 5.0 |
| mean | 3.98 | 4.26 | 9.32 | 9.92 | 9.56 | 8.82 |
| Data | True Class (S2) | Algorithm (L8) | Producer’s Accuracy (%) | User’s Accuracy (%) | Overall Accuracy (%) | Kappa Coefficient |
|---|---|---|---|---|---|---|
| 1 | LinearPolar | LinearPolar | 97.55 | 84.60 | 93.40 | 0.86 |
| PCA | 54.49 | 99.63 | 85.07 | 0.62 | ||
| Markus | 65.10 | 96.08 | 87.73 | 0.70 | ||
| SVM | LinearPolar | 97.63 | 80.35 | 91.87 | 0.82 | |
| PCA | 56.99 | 98.88 | 86.47 | 0.64 | ||
| Markus | 68.17 | 95.48 | 89.13 | 0.72 | ||
| ISODATA | LinearPolar | 98.97 | 67.79 | 87.60 | 0.72 | |
| PCA | 66.41 | 95.90 | 90.60 | 0.73 | ||
| Markus | 75.71 | 88.25 | 91.13 | 0.76 | ||
| 2 | LinearPolar | LinearPolar | 98.54 | 90.92 | 91.80 | 0.80 |
| PCA | 13.55 | 100.00 | 40.53 | 0.09 | ||
| Markus | 35.09 | 96.00 | 54.13 | 0.23 | ||
| SVM | LinearPolar | 96.97 | 92.00 | 91.80 | 0.80 | |
| PCA | 13.18 | 100.00 | 38.67 | 0.09 | ||
| Markus | 34.22 | 96.27 | 52.67 | 0.22 | ||
| ISODATA | LinearPolar | 94.11 | 93.44 | 90.73 | 0.76 | |
| PCA | 12.59 | 100.00 | 35.53 | 0.08 | ||
| Markus | 32.79 | 96.53 | 49.60 | 0.19 | ||
| 3 | LinearPolar | LinearPolar | 88.10 | 81.42 | 91.93 | 0.79 |
| PCA | 25.27 | 88.46 | 94.80 | 0.36 | ||
| Markus | 36.26 | 76.74 | 95.47 | 0.48 | ||
| SVM | LinearPolar | 85.17 | 81.42 | 91.07 | 0.77 | |
| PCA | 17.42 | 88.46 | 92.27 | 0.28 | ||
| Markus | 25.76 | 79.07 | 92.87 | 0.36 | ||
| ISODATA | LinearPolar | 85.20 | 74.57 | 89.53 | 0.73 | |
| PCA | 15.17 | 84.62 | 91.33 | 0.25 | ||
| Markus | 22.76 | 76.74 | 91.87 | 0.32 | ||
| 4 | LinearPolar | LinearPolar | 93.69 | 95.08 | 91.87 | 0.80 |
| PCA | 10.79 | 100.00 | 85.20 | 0.17 | ||
| Markus | 18.26 | 91.67 | 86.60 | 0.27 | ||
| SVM | LinearPolar | 93.59 | 94.81 | 91.60 | 0.79 | |
| PCA | 10.16 | 96.15 | 84.87 | 0.16 | ||
| Markus | 17.48 | 89.58 | 86.13 | 0.25 | ||
| ISODATA | LinearPolar | 92.84 | 93.88 | 90.40 | 0.76 | |
| PCA | 9.23 | 92.31 | 84.07 | 0.16 | ||
| Markus | 16.15 | 87.50 | 85.07 | 0.23 | ||
| 5 | LinearPolar | LinearPolar | 86.30 | 84.56 | 97.13 | 0.84 |
| PCA | 43.84 | 100.00 | 93.93 | 0.56 | ||
| Markus | 50.68 | 93.67 | 94.87 | 0.63 | ||
| SVM | LinearPolar | 81.70 | 83.89 | 96.53 | 0.81 | |
| PCA | 41.83 | 100.00 | 93.47 | 0.54 | ||
| Markus | 48.37 | 93.67 | 94.40 | 0.61 | ||
| ISODATA | LinearPolar | 86.30 | 84.56 | 97.13 | 0.84 | |
| PCA | 41.30 | 59.38 | 91.73 | 0.43 | ||
| Markus | 45.65 | 53.16 | 91.93 | 0.45 | ||
| 6 | LinearPolar | LinearPolar | 89.44 | 86.75 | 97.33 | 0.86 |
| PCA | 79.50 | 88.89 | 96.60 | 0.82 | ||
| Markus | 82.61 | 85.26 | 96.53 | 0.82 | ||
| SVM | LinearPolar | 84.62 | 86.14 | 96.67 | 0.83 | |
| PCA | 74.56 | 87.50 | 95.80 | 0.78 | ||
| Markus | 78.11 | 84.62 | 95.87 | 0.79 | ||
| ISODATA | LinearPolar | 77.09 | 83.13 | 95.33 | 0.78 | |
| PCA | 67.60 | 84.03 | 94.47 | 0.72 | ||
| Markus | 70.95 | 81.41 | 94.53 | 0.73 |
| (%) | L8_LinearPolar | L8_PCA | L8_Markus | ||||||
|---|---|---|---|---|---|---|---|---|---|
| All | With OMPs | Without OMPs | All | With OMPs | Without OMPs | All | With OMPs | Without OMPs | |
| RMSE | 8.5 | 9.1 | 7.9 | 11.7 | 12.6 | 10.7 | 12.3 | 13.2 | 11.2 |
| ME | −0.9 | −1.4 | −0.3 | −6.7 | −6.9 | −6.5 | −5.9 | −5.6 | −6.3 |
| MAE | 5.4 | 5.6 | 5.2 | 7.4 | 7.8 | 6.9 | 7.6 | 8.0 | 7.1 |
| RE | 8.1 | 10.8 | 3.2 | 61.5 | 52.5 | 77.9 | 54.6 | 42.8 | 76.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Su, J.; Wang, M. Melt Pond Retrieval Based on the LinearPolar Algorithm Using Landsat Data. Remote Sens. 2021, 13, 4674. https://doi.org/10.3390/rs13224674
Qin Y, Su J, Wang M. Melt Pond Retrieval Based on the LinearPolar Algorithm Using Landsat Data. Remote Sensing. 2021; 13(22):4674. https://doi.org/10.3390/rs13224674
Chicago/Turabian StyleQin, Yuqing, Jie Su, and Mingfeng Wang. 2021. "Melt Pond Retrieval Based on the LinearPolar Algorithm Using Landsat Data" Remote Sensing 13, no. 22: 4674. https://doi.org/10.3390/rs13224674
APA StyleQin, Y., Su, J., & Wang, M. (2021). Melt Pond Retrieval Based on the LinearPolar Algorithm Using Landsat Data. Remote Sensing, 13(22), 4674. https://doi.org/10.3390/rs13224674