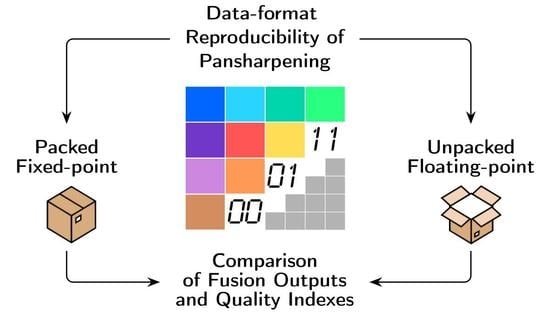
Reproducibility of Pansharpening Methods and Quality Indexes versus Data Formats
Abstract
:1. Scenario and Motivations
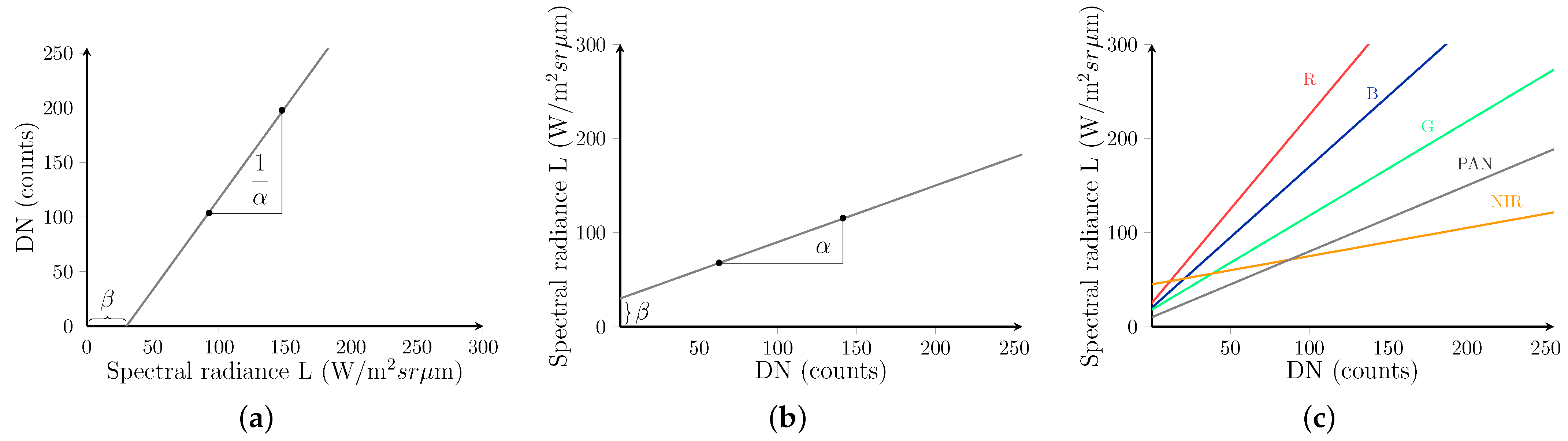
2. Data Formats and Products
3. Basics of CS and MRA Pansharpening
3.1. Notation
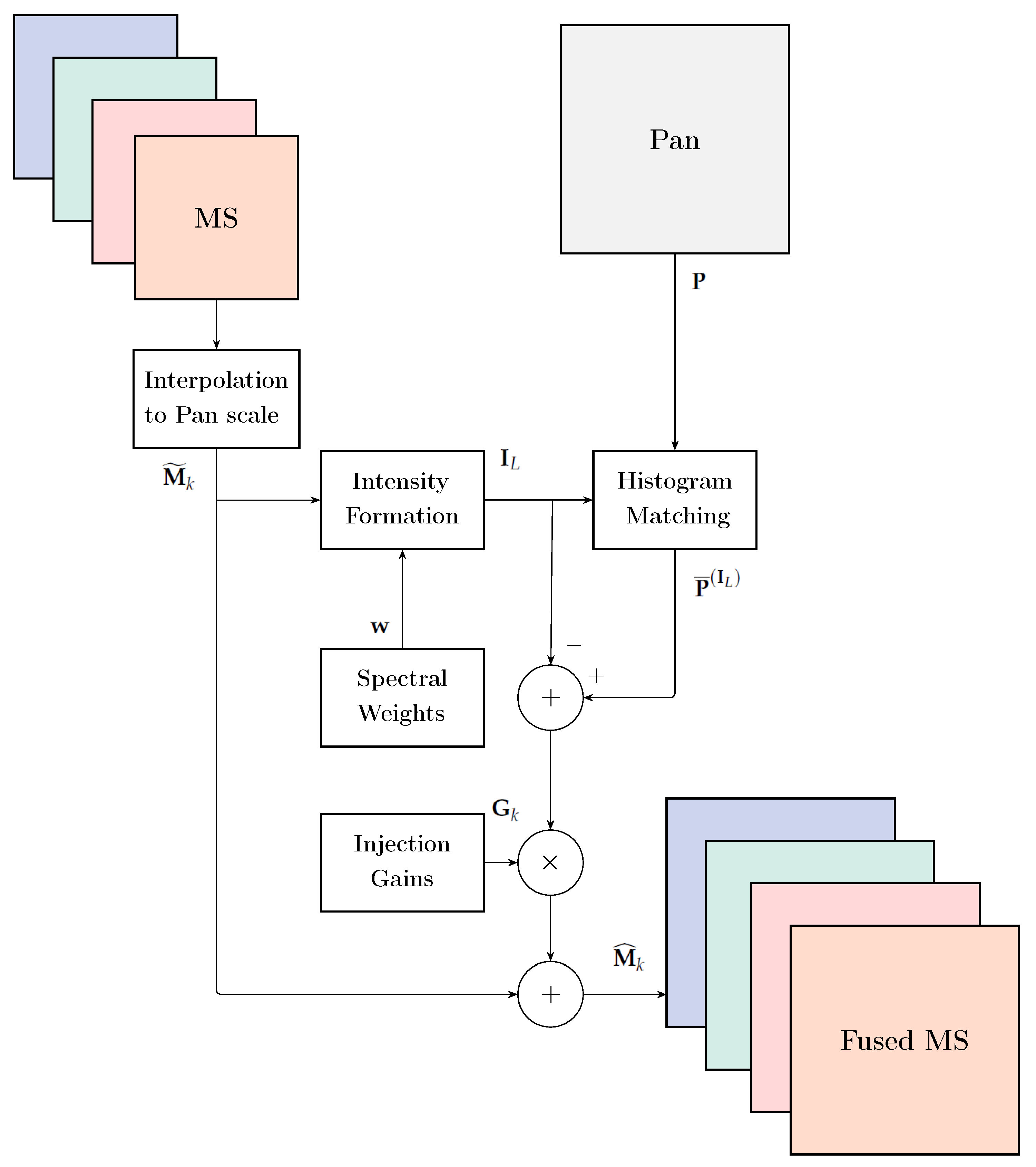
3.2. CS
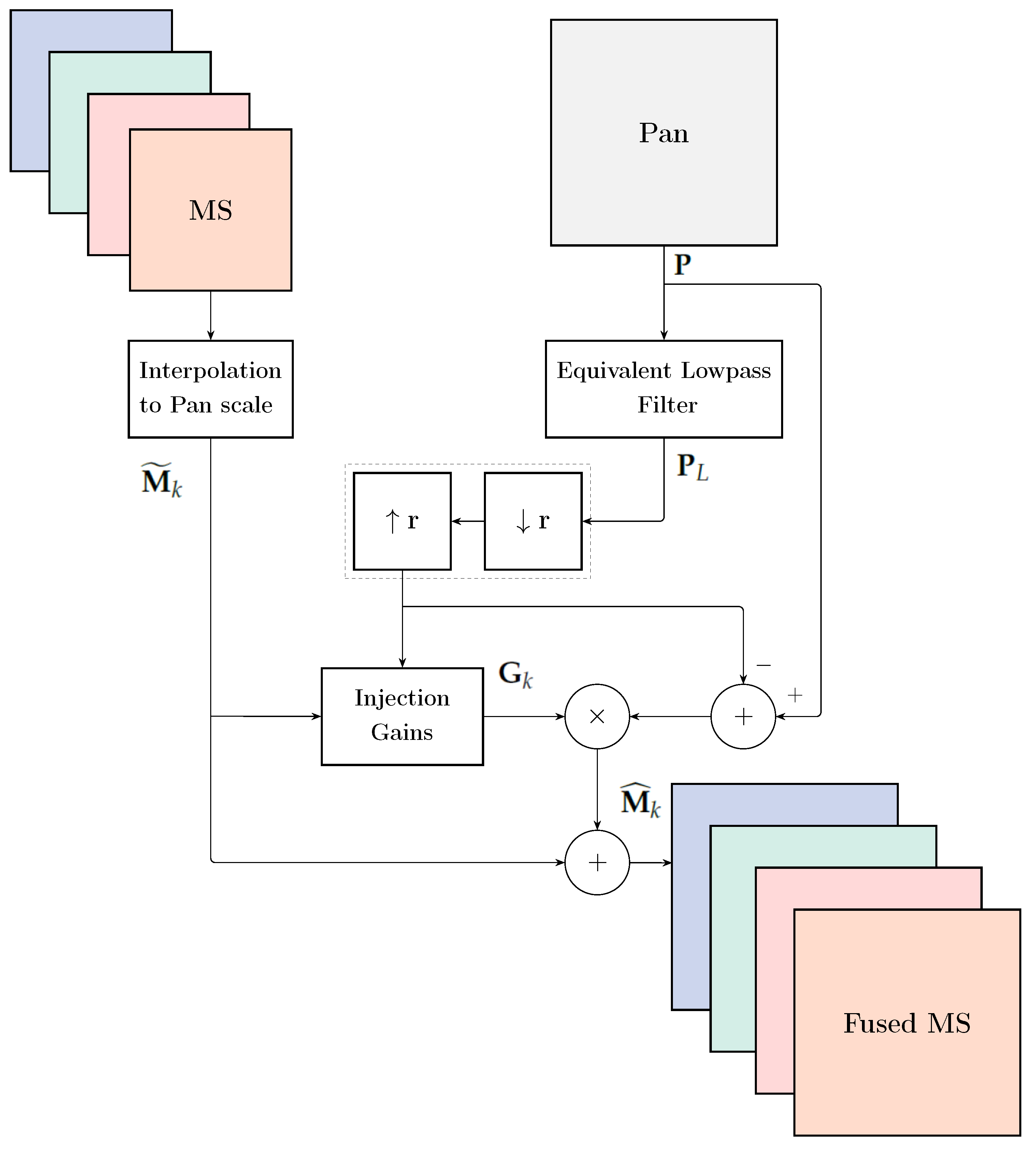
3.3. MRA
4. Reproducibility of Results of Pansharpening Methods with the Data Format
4.1. CS
4.2. MRA
5. Reproducibility of Quality Indexes Varying with Data Formats
5.1. SAM
5.2. ERGAS
5.3. Multivariate UIQI
6. Experimental Results and Discussion
6.1. Data Sets
6.1.1. Collazzone Dataset
6.1.2. Sydney Dataset
6.2. Spectral Imbalance Factor
6.3. Analysis of the LS Intensity Component
6.4. Simulations
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Remote Sensing Image Fusion; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Restaino, R.; Scarpa, G.; Ulfarsson, M.; Alparone, L.; Chanussot, J. A new benchmark based on recent advances in multispectral pansharpening: Revisiting pansharpening with classical and emerging pansharpening methods. IEEE Geosci. Remote Sens. Mag. 2021, 9, 53–81. [Google Scholar] [CrossRef]
- Arienzo, A.; Alparone, L.; Aiazzi, B.; Garzelli, A. Automatic fine alignment of multispectral and panchromatic images. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Waikoloa, HI, USA, 26 September–2 October 2020; pp. 228–231. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Argenti, F.; Baronti, S. Wavelet and pyramid techniques for multisensor data fusion: A performance comparison varying with scale ratios. In Proceedings of the SPIE Image Signal Processing Remote Sensing V, Florence, Italy, 20–24 September 1999; Serpico, S.B., Ed.; Volume 3871, pp. 251–262. [Google Scholar]
- Garzelli, A.; Nencini, F.; Alparone, L.; Baronti, S. Multiresolution fusion of multispectral and panchromatic images through the curvelet transform. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seoul, Korea, 24–29 July 2005; pp. 2838–2841. [Google Scholar]
- Baronti, S.; Aiazzi, B.; Selva, M.; Garzelli, A.; Alparone, L. A theoretical analysis of the effects of aliasing and misregistration on pansharpened imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 446–453. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R.; Garzelli, A.; Santurri, L. Sensitivity of pansharpening methods to temporal and instrumental changes between multispectral and panchromatic data sets. IEEE Trans. Geosci. Remote Sens. 2017, 55, 308–319. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Vivone, G. Intersensor statistical matching for pansharpening: Theoretical issues and practical solutions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4682–4695. [Google Scholar] [CrossRef]
- Vivone, G.; Marano, S.; Chanussot, J. Pansharpening: Context-based generalized Laplacian pyramids by robust regression. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6152–6167. [Google Scholar] [CrossRef]
- Li, H.; Jing, L. Improvement of a pansharpening method taking into account haze. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 5039–5055. [Google Scholar] [CrossRef]
- Lolli, S.; Alparone, L.; Garzelli, A.; Vivone, G. Haze correction for contrast-based multispectral pansharpening. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2255–2259. [Google Scholar] [CrossRef]
- Garzelli, A.; Aiazzi, B.; Alparone, L.; Lolli, S.; Vivone, G. Multispectral pansharpening with radiative transfer-based detail-injection modeling for preserving changes in vegetation cover. Remote Sens. 2018, 10, 1308. [Google Scholar] [CrossRef] [Green Version]
- Vivone, G.; Alparone, L.; Garzelli, A.; Lolli, S. Fast reproducible pansharpening based on instrument and acquisition modeling: AWLP revisited. Remote Sens. 2019, 11, 2315. [Google Scholar] [CrossRef] [Green Version]
- Addesso, P.; Longo, M.; Restaino, R.; Vivone, G. Sequential Bayesian methods for resolution enhancement of TIR image sequences. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 233–243. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Arienzo, A.; Garzelli, A.; Zoppetti, C. Monitoring of changes in vegetation status through integration of time series of hyper-sharpened Sentinel-2 red-edge bands and information-theoretic textural features of Sentinel-1 SAR backscatter. In Image and Signal Processing for Remote Sensing XXV; Bruzzone, L., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 11155, p. 111550Z. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S. Information-theoretic heterogeneity measurement for SAR imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 619–624. [Google Scholar] [CrossRef]
- Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing, 2nd ed.; Academic Press: Orlando, FL, USA, 1997. [Google Scholar]
- Vivone, G. Robust band-dependent spatial-detail approaches for panchromatic sharpening. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6421–6433. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R. Assessment of pyramid-based multisensor image data fusion. In SPIE Image Signal Processing Remote Sensing IV; Serpico, S.B., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 1998; Volume 3500, pp. 237–248. [Google Scholar]
- Du, Q.; Younan, N.H.; King, R.L.; Shah, V.P. On the performance evaluation of pan-sharpening techniques. IEEE Geosci. Remote Sens. Lett. 2007, 4, 518–522. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R.; Garzelli, A.; Santurri, L. Full scale assessment of pansharpening methods and data products. In SPIE Image Signal Processing Remote Sensing XX; Bruzzone, L., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 9244, p. 924402. [Google Scholar]
- Carlà, R.; Santurri, L.; Aiazzi, B.; Baronti, S. Full-scale assessment of pansharpening through polynomial fitting of multiscale measurements. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6344–6355. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Vivone, G. Spatial consistency for full-scale assessment of pansharpening. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 5132–5134. [Google Scholar]
- Vivone, G.; Restaino, R.; Chanussot, J. A Bayesian procedure for full resolution quality assessment of pansharpened products. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4820–4834. [Google Scholar] [CrossRef]
- Agudelo-Medina, O.; Benitez-Restrepo, H.; Vivone, G.; Bovik, A. Perceptual quality assessment of pan-sharpened images. Remote Sens. 2019, 11, 877. [Google Scholar] [CrossRef] [Green Version]
- Arienzo, A.; Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Reproducibility of spectral and radiometric normalized similarity indices for multiband images. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 839–842. [Google Scholar]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O.; Benediktsson, J.A. Quantitative quality evaluation of pansharpened imagery: Consistency versus synthesis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1247–1259. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Barducci, A.; Baronti, S.; Pippi, I. Estimating noise and information of multispectral imagery. Opt. Eng. 2002, 41, 656–668. [Google Scholar]
- Alparone, L.; Selva, M.; Capobianco, L.; Moretti, S.; Chiarantini, L.; Butera, F. Quality assessment of data products from a new generation airborne imaging spectrometer. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 12–17 July 2009; Volume IV, pp. IV422–IV425. [Google Scholar]
- Pacifici, F.; Longbotham, N.; Emery, W.J. The importance of physical quantities for the analysis of multitemporal and multiangular optical very high spatial resolution images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6241–6256. [Google Scholar] [CrossRef]
- Lolli, S.; Di Girolamo, P. Principal component analysis approach to evaluate instrument performances in developing a cost-effective reliable instrument network for atmospheric measurements. J. Atmos. Ocean. Technol. 2015, 32, 1642–1649. [Google Scholar] [CrossRef]
- Bilal, M.; Nazeer, M.; Nichol, J.; Bleiweiss, M.; Qiu, Z.; Jakel, E.; Campbell, J.; Atique, L.; Huang, X.; Lolli, S. A simplified and robust surface reflectance estimation method (SREM) for use over diverse land surfaces using multi-sensor data. Remote Sens. 2019, 11, 1344. [Google Scholar] [CrossRef] [Green Version]
- Shah, V.P.; Younan, N.H.; King, R.L. An efficient pan-sharpening method via a combined adaptive-PCA approach and contourlets. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1323–1335. [Google Scholar] [CrossRef]
- Licciardi, G.; Vivone, G.; Dalla Mura, M.; Restaino, R.; Chanussot, J. Multi-resolution analysis techniques and nonlinear PCA for hybrid pansharpening applications. Multidim. Syst. Signal Process. 2016, 27, 807–830. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Arienzo, A.; Garzelli, A.; Lolli, S. Fast multispectral pansharpening based on a hyper-ellipsoidal color space. In Image and Signal Processing for Remote Sensing XXV; Bruzzone, L., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 11155, p. 1115507. [Google Scholar]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images-II. Channel ratio and “Chromaticity” Transform techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening, 2000. U.S. Patent # 6,011,875, 4 January 2000. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. Advantages of Laplacian pyramids over “à trous” wavelet transforms for pansharpening of multispectral images. In SPIE Image Signal Processing Remote Sensing XVIII; Bruzzone, L., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; Volume 8537, p. 853704. [Google Scholar]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison of pansharpening algorithms. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 191–194. [Google Scholar]
- Yuhas, R.H.; Goetz, A.F.H.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the Spectral Angle Mapper (SAM) algorithm. In Proceedings of the Summaries 3rd Annu. JPL Airborne Geosci. Workshop, Pasadena, CA, USA, 1–5 June 1992; pp. 147–149. [Google Scholar]
- Wald, L. Data Fusion: Definitions and Architectures—Fusion of Images of Different Spatial Resolutions; Les Presses de l’École des Mines: Paris, France, 2002. [Google Scholar]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F. Hypercomplex quality assessment of multi-/hyper-spectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 662–665. [Google Scholar] [CrossRef]
- Restaino, R.; Vivone, G.; Addesso, P.; Chanussot, J. Hyperspectral sharpening approaches using satellite multiplatform data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 578–596. [Google Scholar] [CrossRef]
- Vivone, G.; Chanussot, J. Fusion of short-wave infrared and visible near-infrared WorldView-3 data. Inform. Fusion 2020, 61, 71–83. [Google Scholar] [CrossRef]
- Ma, J.; Yu, W.; Chen, C.; Liang, P.; Guo, X.; Jiang, J. Pan-GAN: An unsupervised pan-sharpening method for remote sensing image fusion. Inform. Fusion 2020, 62, 110–120. [Google Scholar] [CrossRef]



| GE-1 | Pan | B | G | R | NIR | SIF% |
|---|---|---|---|---|---|---|
| 0.0178 | 0.0250 | 0.0172 | 0.0277 | 0.0096 | 65.34% | |
| 0 | 0 | 0 | 0 | 0 | - |
| WV-2 | Pan | C | B | G | Y | R | RE | NIR1 | NIR2 | SIF% |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1331 | 0.1965 | 0.2322 | 0.1542 | 0.1364 | 0.1923 | 0.1155 | 0.1238 | 0.0908 | 60.89% | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - |
| GE-1 | B | G | R | NIR | CD | ||
|---|---|---|---|---|---|---|---|
| 0.0637 | 0.4398 | 0.4609 | 0.1557 | −17.5223 | 1.1200 | 0.9858 | |
| −0.1010 | 0.5408 | 0.4474 | 0.1474 | - | 1.0346 | 0.9856 | |
| 0.0453 | 0.4554 | 0.2956 | 0.2888 | −0.3117 | 1.0850 | 0.9858 | |
| −0.0718 | 0.5600 | 0.2869 | 0.2734 | - | 1.0486 | 0.9856 |
| WV-2 | C | B | G | Y | R | RE | NIR1 | NIR2 | CD | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.3643 | −0.0269 | 0.1127 | 0.2368 | 0.2636 | 0.1353 | 0.0225 | 0.1477 | −37.5550 | 1.2560 | 0.9857 | |
| 0.1170 | 0.1245 | 0.0987 | 0.2934 | 0.2245 | 0.1251 | 0.0233 | 0.1506 | - | 1.1571 | 0.9855 | |
| 0.2468 | −0.0154 | 0.0973 | 0.2311 | 0.1825 | 0.1560 | 0.0242 | 0.2166 | −4.9996 | 1.1390 | 0.9857 | |
| 0.0792 | 0.0714 | 0.0852 | 0.2864 | 0.1555 | 0.1442 | 0.0251 | 0.2208 | - | 1.0678 | 0.9855 |
| DN | Qavg ●↓ | Q4 ●↓ | SAM ●↓ | ERGAS ●↓ | |
|---|---|---|---|---|---|
| DN|SR | |||||
| REF | 1 | 1 | 0 | 0 | |
| EXP ■→ | 0.7814 | 0.7814 | 0.7779 | 0.7779 | 2.3534 | 2.3534 | 3.1821 | 3.1821 | |
| GS ■→ | 0.8456 | 0.8544 | 0.8182 | 0.8291 | 2.5814 | 2.8921 | 2.8376 | 2.8127 | |
| GSA ■→ | 0.8595 | 0.8595 | 0.8673 | 0.8673 | 2.9923 | 2.9923 | 2.8786 | 2.8786 | |
| GIHS ■→ | 0.8378 | 0.8694 | 0.8175 | 0.8654 | 2.8407 | 2.3580 | 2.9159 | 2.4197 | |
| PCA ■→ | 0.8490 | 0.8140 | 0.8332 | 0.8241 | 2.6032 | 3.6255 | 3.0049 | 3.3031 | |
| BT ■→ | 0.8670 | 0.8677 | 0.8599 | 0.8625 | 2.3534 | 2.3534 | 2.4315 | 2.4556 | |
| MTF-GLP ■→ | 0.8625 | 0.8625 | 0.8625 | 0.8625 | 2.5338 | 2.5338 | 2.9208 | 2.9208 | |
| BDSD ■→ | 0.8994 | 0.8994 | 0.9027 | 0.9027 | 2.5043 | 2.5043 | 2.1717 | 2.1717 | |
| ATWT ■→ | 0.8723 | 0.8723 | 0.8688 | 0.8688 | 2.4686 | 2.4686 | 2.6631 | 2.6631 | |
| SR | Qavg ●↓ | Q4 ●↓ | SAM ●↓ | ERGAS ●↓ | |
| DN|SR | |||||
| EXP ■→ | 0.7814 | 0.7814 | 0.7048 | 0.7048 | 2.9896 | 2.9896 | 3.1821 | 3.1821 | |
| GS ■→ | 0.8456 | 0.8544 | 0.7377 | 0.7472 | 3.2935 | 3.6044 | 2.8376 | 2.8127 | |
| GSA ■→ | 0.8595 | 0.8595 | 0.8021 | 0.8021 | 3.6930 | 3.6930 | 2.8786 | 2.8786 | |
| GIHS ■→ | 0.8378 | 0.8694 | 0.7534 | 0.7998 | 3.6549 | 2.9516 | 2.9159 | 2.4197 | |
| PCA ■→ | 0.8490 | 0.8140 | 0.7652 | 0.7635 | 3.4756 | 4.5339 | 3.0049 | 3.3031 | |
| BT ■→ | 0.8670 | 0.8677 | 0.7862 | 0.7979 | 2.9896 | 2.9896 | 2.4315 | 2.4556 | |
| MTF-GLP ■→ | 0.8625 | 0.8625 | 0.8001 | 0.8001 | 3.2838 | 3.2838 | 2.9208 | 2.9208 | |
| BDSD ■→ | 0.8994 | 0.8994 | 0.8352 | 0.8352 | 3.0302 | 3.0302 | 2.1717 | 2.1717 | |
| ATWT ■→ | 0.8723 | 0.8723 | 0.8033 | 0.8033 | 3.1489 | 3.1489 | 2.6631 | 2.6631 | |
| REF | 1 | 1 | 0 | 0 | |
| DN | Qavg ●↓ | Q8 ●↓ | SAM ●↓ | ERGAS ●↓ | |
|---|---|---|---|---|---|
| DN|SR | |||||
| REF | 1 | 1 | 0 | 0 | |
| EXP ■→ | 0.7077 | 0.7077 | 0.7000 | 0.7000 | 5.0636 | 5.0636 | 6.4271 | 6.4271 | |
| GS ■→ | 0.8158 | 0.8288 | 0.7487 | 0.7861 | 7.2114 | 6.3689 | 4.8309 | 4.1664 | |
| GSA ■→ | 0.8460 | 0.8460 | 0.8495 | 0.8495 | 4.5789 | 4.5789 | 3.3967 | 3.3967 | |
| GIHS ■→ | 0.7750 | 0.8247 | 0.6760 | 0.7888 | 6.0590 | 4.9979 | 4.7732 | 3.5853 | |
| PCA ■→ | 0.7912 | 0.8271 | 0.7138 | 0.7460 | 7.4372 | 6.1357 | 7.9097 | 5.9057 | |
| BT ■→ | 0.8030 | 0.8167 | 0.6940 | 0.7554 | 5.0636 | 5.0636 | 4.2299 | 3.4069 | |
| MTF-GLP ■→ | 0.8302 | 0.8302 | 0.8247 | 0.8247 | 5.0954 | 5.0954 | 4.0518 | 4.0518 | |
| BDSD ■→ | 0.8439 | 0.8439 | 0.8430 | 0.8430 | 5.0104 | 5.0104 | 3.8416 | 3.8416 | |
| ATWT ■→ | 0.8366 | 0.8366 | 0.8310 | 0.8310 | 4.9530 | 4.9530 | 3.8678 | 3.8678 | |
| SR | Qavg ●↓ | Q8 ●↓ | SAM ●↓ | ERGAS ●↓ | |
| DN|SR | |||||
| EXP ■→ | 0.7077 | 0.7077 | 0.6906 | 0.6906 | 4.8254 | 4.8254 | 6.4271 | 6.4271 | |
| GS ■→ | 0.8158 | 0.8288 | 0.7465 | 0.7835 | 6.0258 | 5.3841 | 4.8309 | 4.1664 | |
| GSA ■→ | 0.8460 | 0.8460 | 0.8377 | 0.8377 | 4.0870 | 4.0870 | 3.3967 | 3.3967 | |
| GIHS ■→ | 0.7750 | 0.8247 | 0.6735 | 0.7807 | 5.9163 | 4.6071 | 4.7732 | 3.5853 | |
| PCA ■→ | 0.7912 | 0.8271 | 0.7100 | 0.7427 | 6.8330 | 5.4468 | 7.9097 | 5.9057 | |
| BT ■→ | 0.8030 | 0.8167 | 0.6924 | 0.7503 | 4.8254 | 4.8254 | 4.2299 | 3.4069 | |
| MTF-GLP ■→ | 0.8302 | 0.8302 | 0.8133 | 0.8133 | 4.3498 | 4.3498 | 4.0518 | 4.0518 | |
| BDSD ■→ | 0.8439 | 0.8439 | 0.8371 | 0.8371 | 4.5094 | 4.5094 | 3.8416 | 3.8416 | |
| ATWT ■→ | 0.8366 | 0.8366 | 0.8199 | 0.8199 | 4.2917 | 4.2917 | 3.8678 | 3.8678 | |
| REF | 1 | 1 | 0 | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arienzo, A.; Aiazzi, B.; Alparone, L.; Garzelli, A. Reproducibility of Pansharpening Methods and Quality Indexes versus Data Formats. Remote Sens. 2021, 13, 4399. https://doi.org/10.3390/rs13214399
Arienzo A, Aiazzi B, Alparone L, Garzelli A. Reproducibility of Pansharpening Methods and Quality Indexes versus Data Formats. Remote Sensing. 2021; 13(21):4399. https://doi.org/10.3390/rs13214399
Chicago/Turabian StyleArienzo, Alberto, Bruno Aiazzi, Luciano Alparone, and Andrea Garzelli. 2021. "Reproducibility of Pansharpening Methods and Quality Indexes versus Data Formats" Remote Sensing 13, no. 21: 4399. https://doi.org/10.3390/rs13214399
APA StyleArienzo, A., Aiazzi, B., Alparone, L., & Garzelli, A. (2021). Reproducibility of Pansharpening Methods and Quality Indexes versus Data Formats. Remote Sensing, 13(21), 4399. https://doi.org/10.3390/rs13214399