Accurate Refraction Correction—Assisted Bathymetric Inversion Using ICESat-2 and Multispectral Data
Abstract
:1. Introduction
2. Materials and Methods
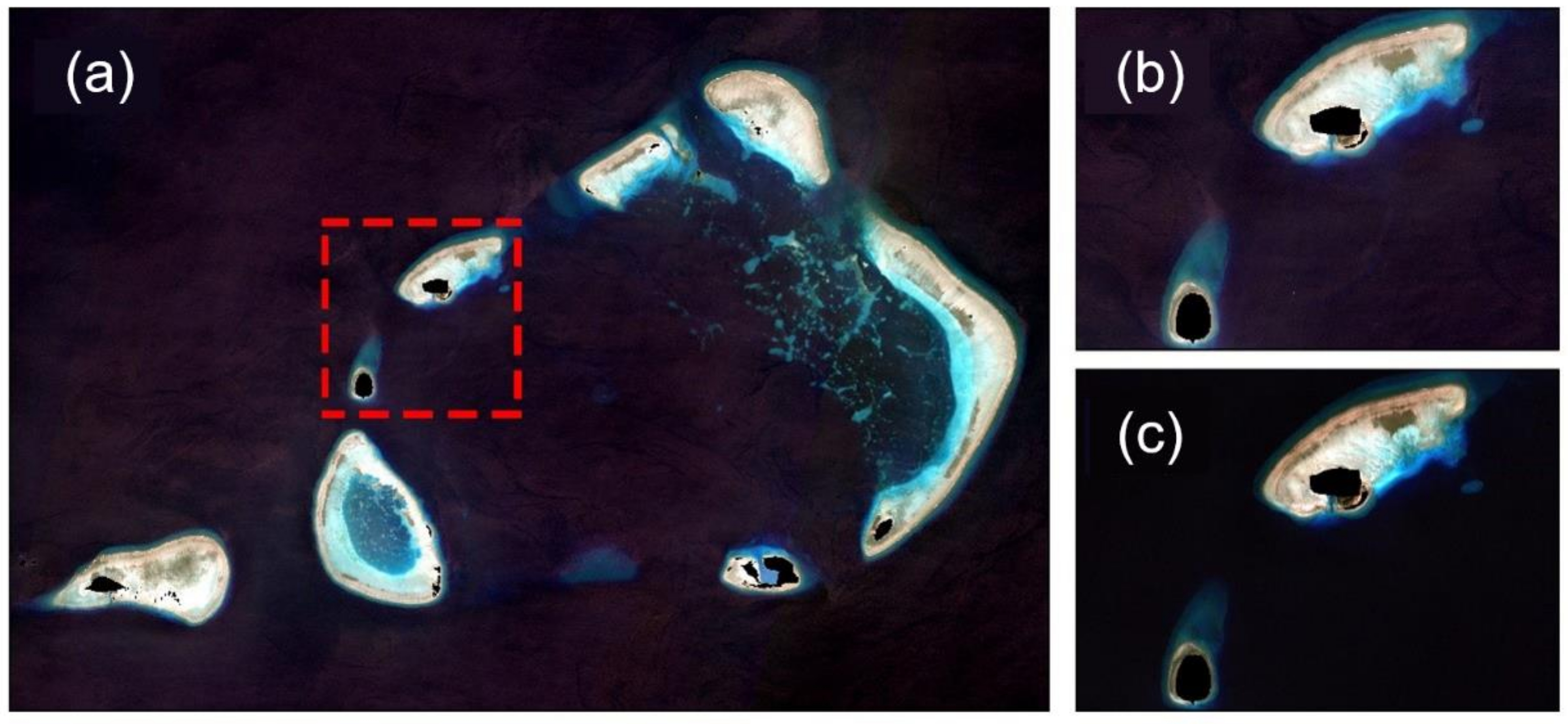
2.1. ICESat-2 Data Processing
2.2. Sentinel-2 Data Processing
3. Results
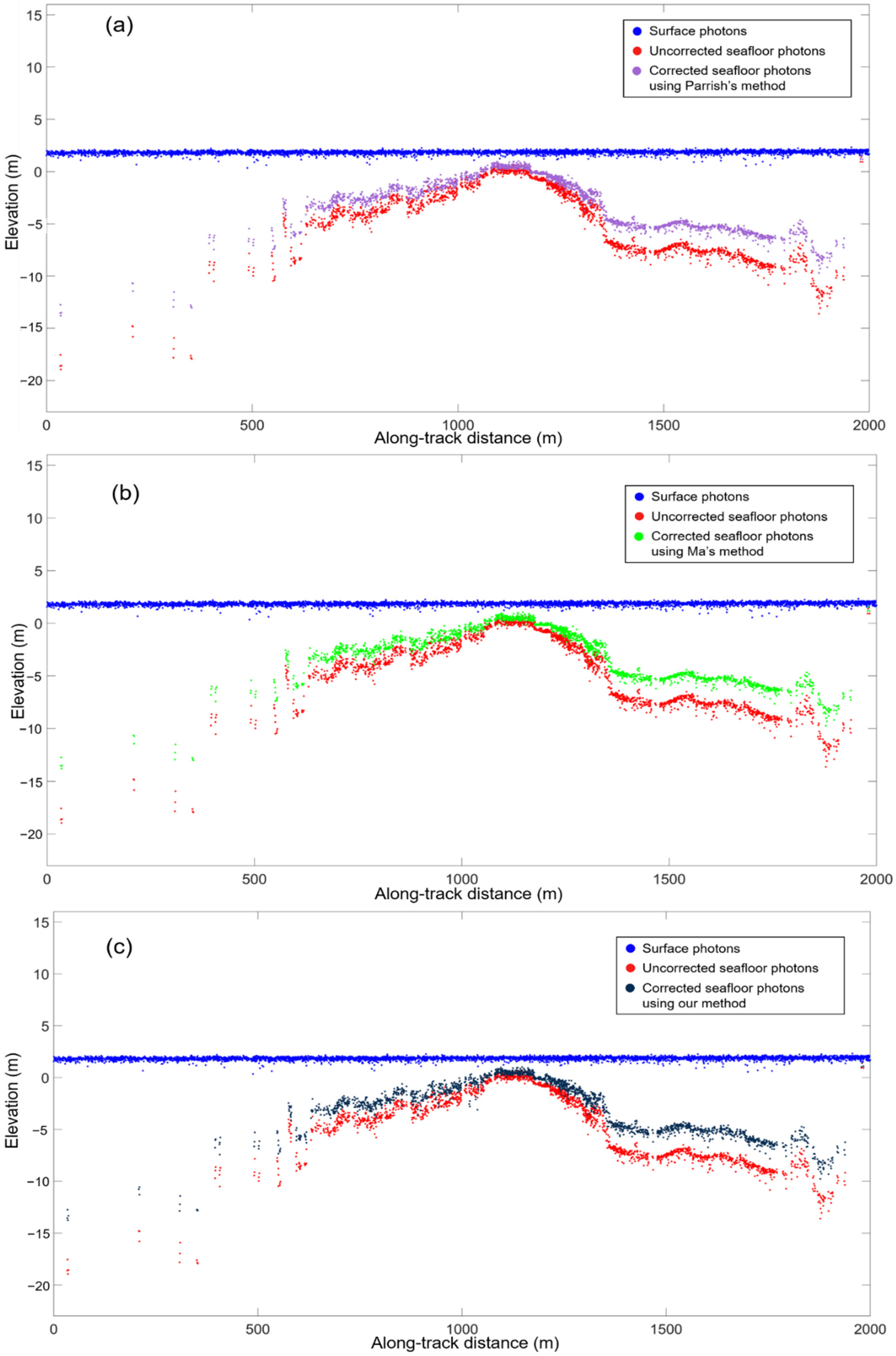
3.1. Correction Results of ICESat-2
3.2. Processing Results of Sentinel-2
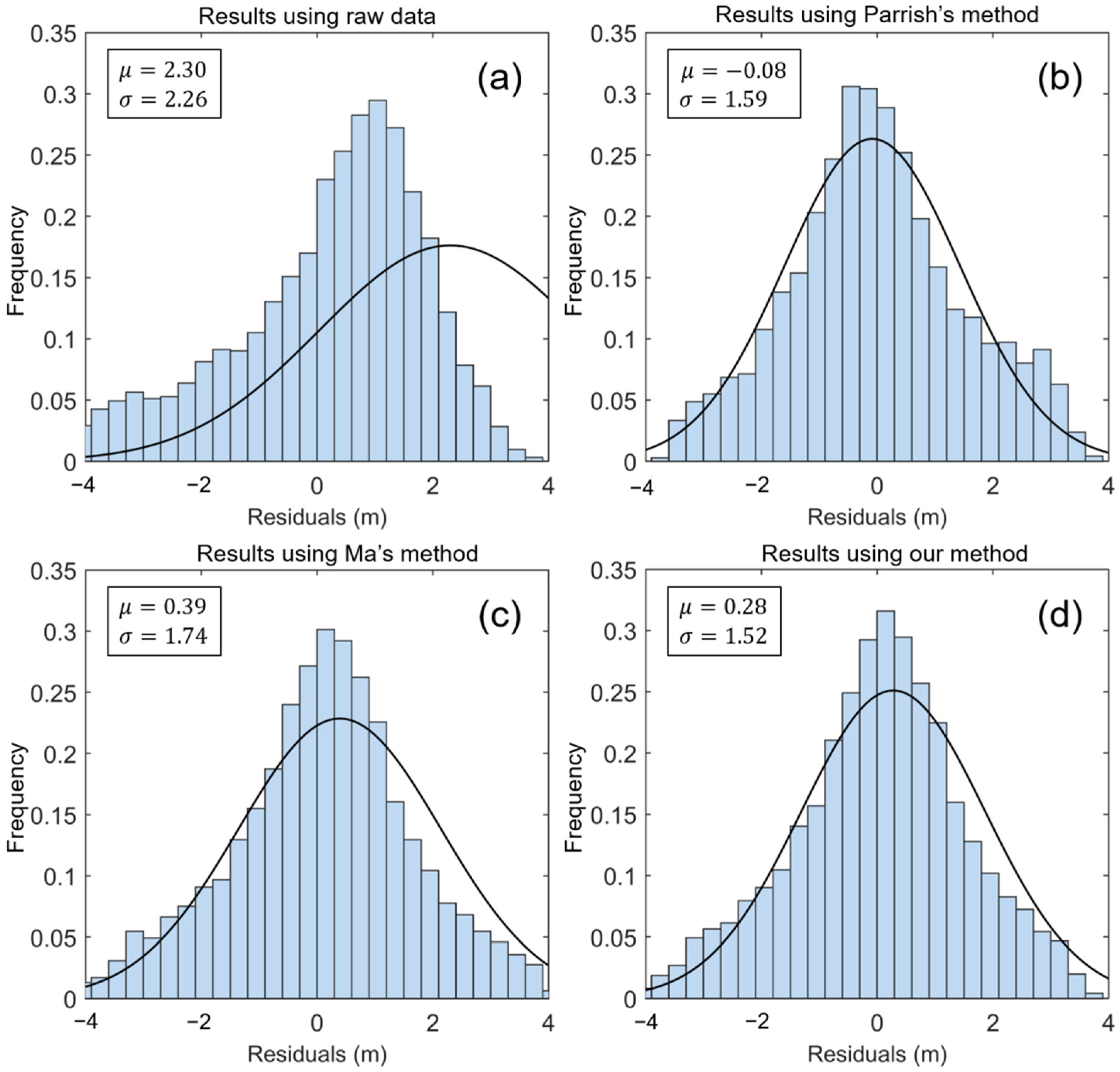
3.3. Results of the SDB Method
4. Discussions
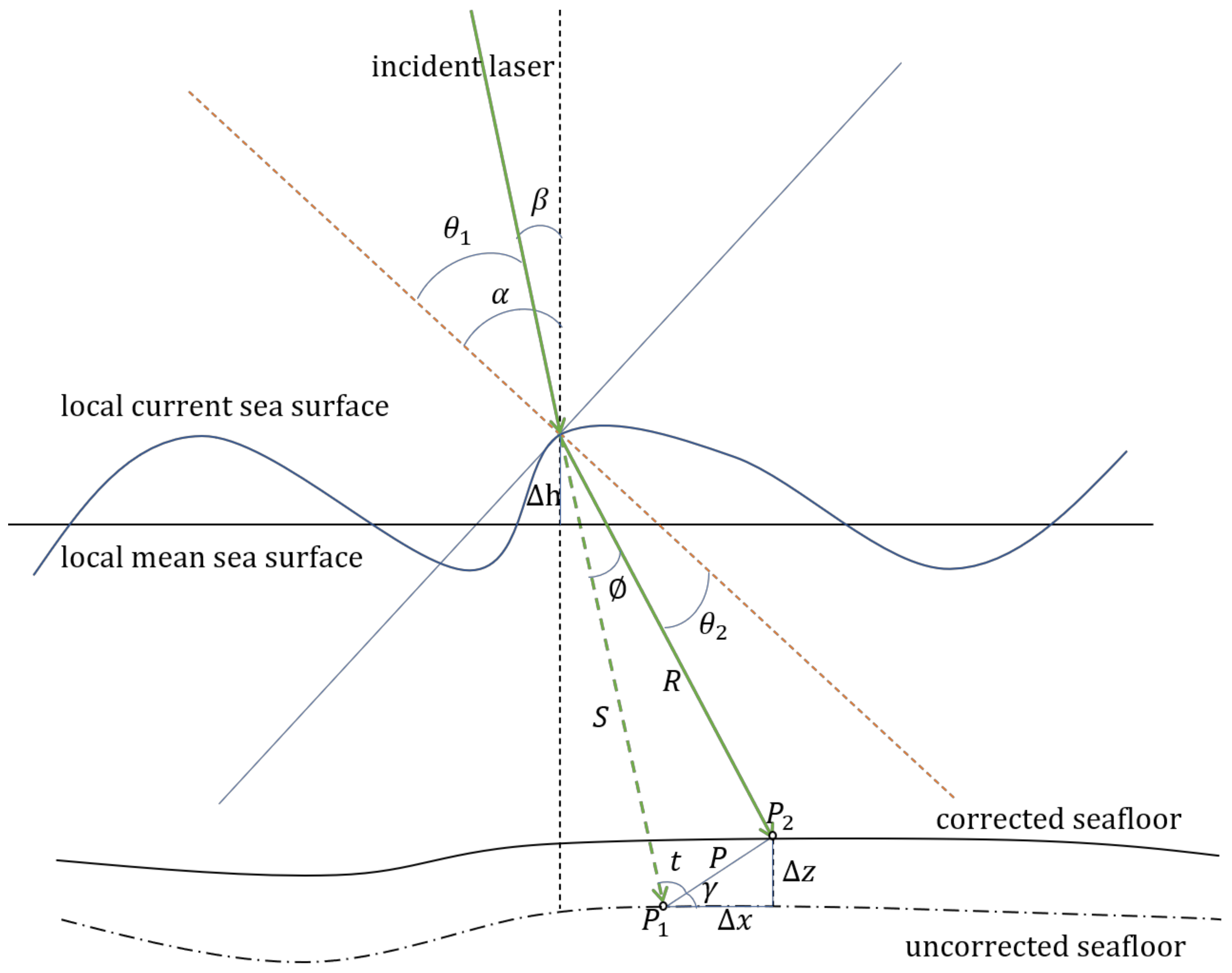
4.1. Error Analyses of Underwater Photon Position
4.2. Potential Contributions and Limitations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mancini, S.; Olsen, R.C.; Abileah, R.; Lee, K.R. Automating nearshore bathymetry extraction from wave motion in satellite optical imagery. SPIE Proc. 2012, 8390, 83900P. [Google Scholar]
- Moore, L.J. Shoreline mapping techniques. J. Coast. Res. 2000, 16, 111–124. [Google Scholar]
- Amiri-Simkooei, A.; Snellen, M.; Simons, D.G. Riverbed sediment classification using multi-beam echo-sounder backscatter data. J. Acoust. Soc. Am. 2009, 126, 1724. [Google Scholar] [CrossRef]
- Kogut, T.; Bakuła, K. Improvement of Full Waveform Airborne Laser Bathymetry Data Processing based on Waves of Neighborhood Points. Remote Sens. 2019, 11, 1255. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Yang, F.; Zhang, H.; Su, D.; Li, Q. Morphological characterization of coral reefs by combining lidar and MBES data: A case study from Yuanzhi Island, South China Sea. J. Geophys. Res. Oceans 2017, 122, 4779–4790. [Google Scholar] [CrossRef]
- Armon, M.; Dente, E.; Shmilovitz, Y.; Mushkin, A.; Cohen, T.J.; Morin, E.; Enzel, Y. Determining Bathymetry of Shallow and Ephemeral Desert Lakes Using Satellite Imagery and Altimetry. Geophys. Res. Lett. 2020, 47, e2020GL087367. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Zimmerman, R.C.; Leathers, R.A.; Downes, T.V.; Davis, C.O. Ocean color remote sensing of seagrass and bathymetry in the Bahamas Banks by high-resolution airborne imagery. Limnol. Oceanogr. 2003, 48, 444–455. [Google Scholar] [CrossRef]
- Sagawa, T.; Yamashita, Y.; Okumura, T.; Yamanokuchi, T. Satellite Derived Bathymetry Using Machine Learning and Multi-Temporal Satellite Images. Remote Sens. 2019, 11, 1155. [Google Scholar] [CrossRef] [Green Version]
- Duplančić Leder, T.; Leder, N.; Peroš, J. Satellite Derived Bathymetry Survey Method—Example of Hramina Bay. Trans. Marit. Sci. 2019, 8, 99–108. [Google Scholar] [CrossRef] [Green Version]
- Thomas, N.; Pertiwi, A.P.; Traganos, D.; Lagomasino, D.; Poursanidis, D.; Moreno, S.; Fatoyinbo, L. Space-Borne Cloud-Native Satellite-Derived Bathymetry (SDB) Models Using ICESat-2 And Sentinel-2. Geophys. Res. Lett. 2021, 48, e2020G–e92170G. [Google Scholar] [CrossRef]
- Vinayaraj, P. Development of Algorithms for Near-shore Satellite Derived Bathymetry Using Multispectral Remote Sensing Images. Ph.D. Thesis, Osaka City University, Osaka, Japan, 2019. Available online: http://dlisv03.media.osaka-cu.ac.jp/contents (accessed on 21 July 2021).
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Poursanidis, D.; Traganos, D.; Chrysoulakis, N.; Reinartz, P. Cubesats Allow High Spatiotemporal Estimates of Satellite-Derived Bathymetry. Remote Sens. 2019, 11, 1299. [Google Scholar] [CrossRef] [Green Version]
- Hsu, H.J.; Huang, C.Y.; Jasinski, M.; Li, Y.; Gao, H.; Yamanokuchi, T.; Wang, C.G.; Chang, T.M.; Ren, H.; Kuo, C.Y.; et al. A semi-empirical scheme for bathymetric mapping in shallow water by ICESat-2 and Sentinel-2: A case study in the South China Sea. ISPRS J. Photogramm. 2021, 178, 1–19. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The Ice, Cloud, and Land Elevation Satellite-2 mission: A global geolocated photon product derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Cao, B.; Gao, L.; Hu, H.; Jiang, Z. Development and application of lidar mapping satellite. Hongwai Yu Jiguang Gongcheng/Infrared Laser Eng. 2020, 49, 20201044-1. [Google Scholar]
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS Bathymetry and Analysis of ATLAS’s Bathymetric Mapping Performance. Remote Sens. 2019, 11, 1634. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Xu, N.; Ma, Y.; Yang, B.; Zhang, Z.; Wang, X.H.; Li, S. A maximum bathymetric depth model to simulate satellite photon-counting lidar performance. Isprs J. Photogramm. 2021, 174, 182–197. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Ma, Y.; Xu, N.; Zhang, W.; Li, S. Signal Photon Extraction Method for Weak Beam Data of ICESat-2 Using Information Provided by Strong Beam Data in Mountainous Areas. Remote Sens. 2021, 13, 863. [Google Scholar]
- Cao, B.; Fang, Y.; Gao, L.; Hu, H.; Jiang, Z.; Sun, B.; Lou, L. An active-passive fusion strategy and accuracy evaluation for shallow water bathymetry based on ICESat-2 ATLAS laser point cloud and satellite remote sensing imagery. Int. J. Remote Sens. 2021, 42, 2783–2806. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhou, T.; Nelson, R.; Neuenschwander, A.; Sheridan, R.; Narine, L.; Walsh, K.M. Photon counting LiDAR: An adaptive ground and canopy height retrieval algorithm for ICESat-2 data. Remote Sens. Environ. 2018, 208, 154–170. [Google Scholar] [CrossRef]
- Chen, Y.; Le, Y.; Zhang, D.; Wang, Y.; Qiu, Z.; Wang, L. A photon-counting LiDAR bathymetric method based on adaptive variable ellipse filtering. Remote Sens. Environ. 2021, 256, 112326. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Zhang, W.; Wang, X.H.; Yang, F.; Su, D. Monitoring Annual Changes of Lake Water Levels and Volumes over 1984–2018 Using Landsat Imagery and ICESat-2 Data. Remote Sens. 2020, 12, 4004. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Satellite-derived bathymetry using the ICESat-2 lidar and Sentinel-2 imagery datasets. Remote Sens. Environ. 2020, 250, 112047. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Sun, J.; Wang, X.H.; Yang, F.; Li, S. Estimating water levels and volumes of lakes dated back to the 1980s using Landsat imagery and photon-counting lidar datasets. Remote Sens. Environ. 2019, 232, 111287. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, Z.; Le, Y.; Qiu, Z.; Chen, G.; Wang, L. Refraction correction and coordinate displacement compensation in nearshore bathymetry using ICESat-2 lidar data and remote-sensing images. Opt. Express 2021, 29, 2411. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd 1996, 96, 226–231. [Google Scholar]
- Forfinski-Sarkozi, N.; Parrish, C. Analysis of MABEL Bathymetry in Keweenaw Bay and Implications for ICESat-2 ATLAS. Remote Sens. 2016, 8, 772. [Google Scholar] [CrossRef] [Green Version]
- Neuenschwander, A.; Magruder, L. The Potential Impact of Vertical Sampling Uncertainty on ICESat-2/ATLAS Terrain and Canopy Height Retrievals for Multiple Ecosystems. Remote Sens. 2016, 8, 1039. [Google Scholar] [CrossRef] [Green Version]
- Vernimmen, R.; Hooijer, A.; Pronk, M. New ICESat-2 Satellite LiDAR Data Allow First Global Lowland DTM Suitable for Accurate Coastal Flood Risk Assessment. Remote Sens. 2020, 12, 2827. [Google Scholar] [CrossRef]
- Thomas, T.C.; Luthcke, S.B.; Pennington, T.A.; Nicholas, J.B.; Rowlands, D.D. ICESat-2 Precision Orbit Determination. Earth Space Sci. 2021, 8, e2020EA001496. [Google Scholar] [CrossRef]
- Padman, L.; Erofeeva, S. Tide model driver (TMD) manual. Earth Space Res. 2005. Available online: https://svn.oss.deltares.nl/repos/openearthtools/trunk/matlab/applications/DelftDashBoard/utils/tmd/Documentation/README_TMD_vs1.2.pdf (accessed on 21 July 2021).
- Hedley, J.D.; Harborne, A.R.; Mumby, P.J. Technical note: Simple and robust removal of sun glint for mapping shallow-water benthos. Int. J. Remote Sens. 2007, 26, 2107–2112. [Google Scholar] [CrossRef]
- Yuan, C.; Gong, P.; Bai, Y. Performance assessment of ICESat-2 laser altimeter data for water-level measurement over lakes and reservoirs in China. Remote Sens. 2020, 12, 770. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Gao, H.; Zhao, G.; Tseng, K. A high-resolution bathymetry dataset for global reservoirs using multi-source satellite imagery and altimetry. Remote Sens. Environ. 2020, 244, 111831. [Google Scholar] [CrossRef]
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geogr. Earth Environ. 2009, 33, 103–116. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Jasinski, M.F.; Zhang, S.; Stoll, J.D. Deriving high-resolution reservoir bathymetry from ICESat-2 prototype photon-counting lidar and landsat imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7883–7893. [Google Scholar] [CrossRef]

| Data | Acquisition Time | Tide Height (cm) |
|---|---|---|
| Sentinel-2 | 24 February 2019 03:11:16 | 0.04 |
| ICESat-2 | 22 October 2018 15:38:35 | 12.52 |
| ICESat-2 | 22 February 2019 21:51:59 | −42.79 |
| ICESat-2 | 21 April 2019 06:58:16 | 6.52 |
| ICESat-2 | 19 April 2020 13:37:23 | 17.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Qi, J.; Li, J.; Tang, Q.; Xu, W.; Zhou, X.; Meng, W. Accurate Refraction Correction—Assisted Bathymetric Inversion Using ICESat-2 and Multispectral Data. Remote Sens. 2021, 13, 4355. https://doi.org/10.3390/rs13214355
Liu C, Qi J, Li J, Tang Q, Xu W, Zhou X, Meng W. Accurate Refraction Correction—Assisted Bathymetric Inversion Using ICESat-2 and Multispectral Data. Remote Sensing. 2021; 13(21):4355. https://doi.org/10.3390/rs13214355
Chicago/Turabian StyleLiu, Changda, Jiawei Qi, Jie Li, Qiuhua Tang, Wenxue Xu, Xinghua Zhou, and Wenjun Meng. 2021. "Accurate Refraction Correction—Assisted Bathymetric Inversion Using ICESat-2 and Multispectral Data" Remote Sensing 13, no. 21: 4355. https://doi.org/10.3390/rs13214355
APA StyleLiu, C., Qi, J., Li, J., Tang, Q., Xu, W., Zhou, X., & Meng, W. (2021). Accurate Refraction Correction—Assisted Bathymetric Inversion Using ICESat-2 and Multispectral Data. Remote Sensing, 13(21), 4355. https://doi.org/10.3390/rs13214355






