Satellite Image Classification Using a Hierarchical Ensemble Learning and Correlation Coefficient-Based Gravitational Search Algorithm
Abstract
1. Introduction
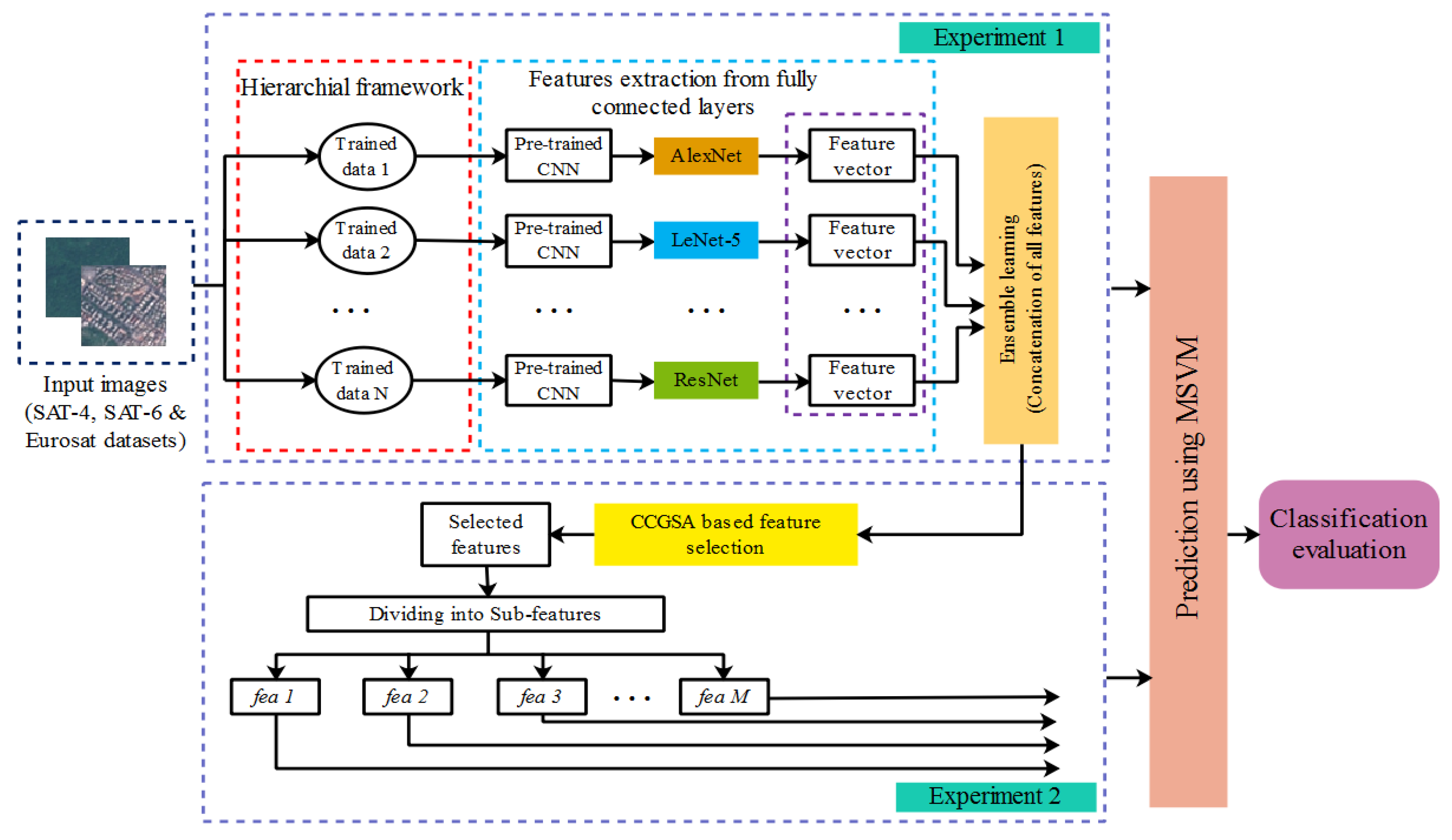
- The refined and semantic features are extracted from the fully connected layers of AlexNet, LeNet-5 and ResNet. Further, these extracted features are concatenated together to obtain multiple ensembles of features.
- From the extracted features, the optimal set of features is selected using the CCGSA technique. Hence, the combination of multiple ensemble features from the HFEL and optimal features selected from the CCGSA is used to increase the classification accuracy of satellite images.
- Three different datasets, i.e., SAT-4, SAT-6 and Eurosat datasets, are considered to analyze the performance of the HFEL–CCGSA method.
Solution
2. HFEL–CCGSA Method
2.1. Image Acquisition
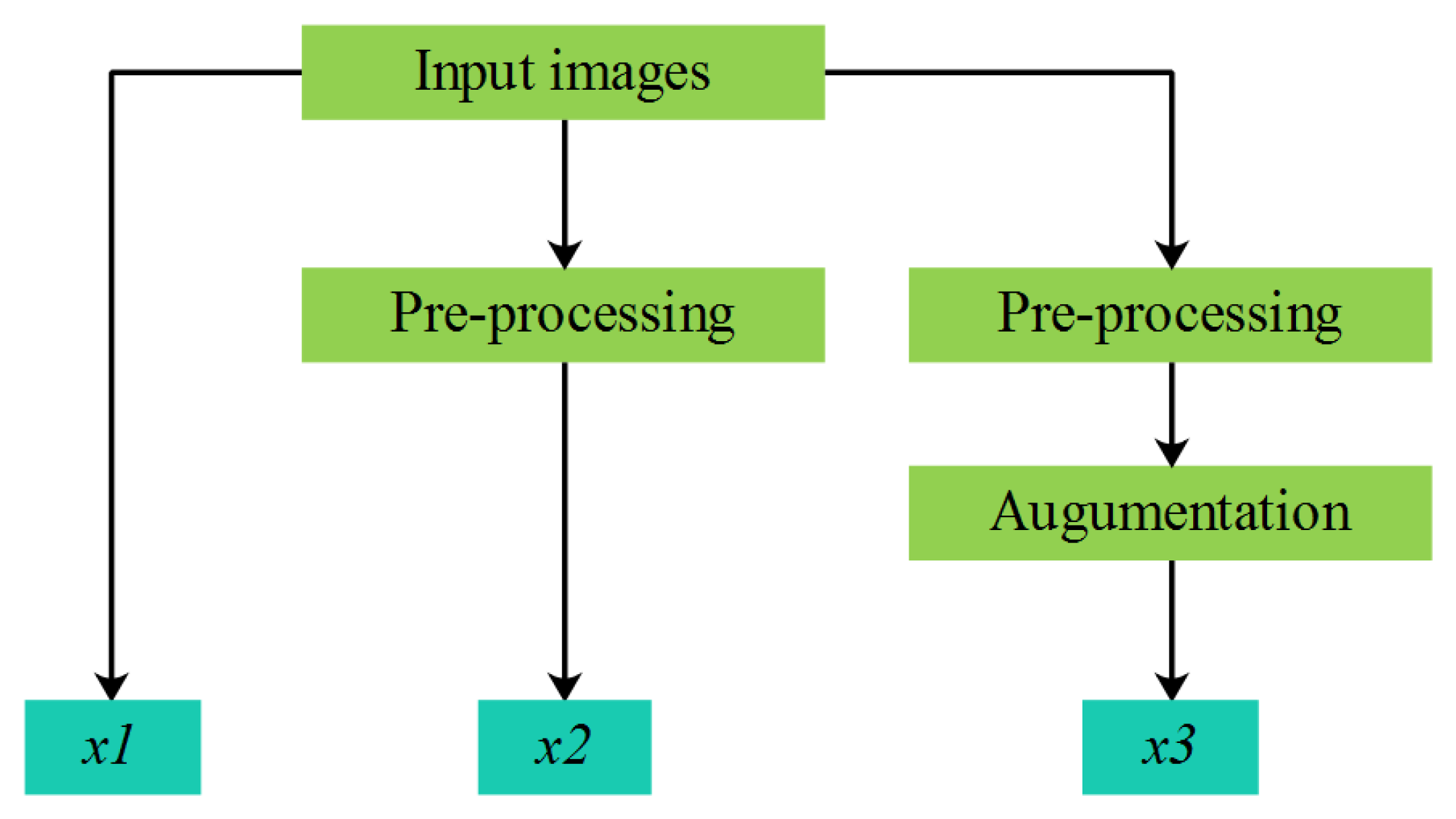
2.2. Hierarchical Framework
2.2.1. Image Pre-Processing
2.2.2. Data Augmentation
2.3. Feature Extraction from the CNN
2.3.1. AlexNet
2.3.2. LeNet-5
2.3.3. ResNet
2.4. Feature Selection Using CCGSA
2.5. Classification Using MSVM
3. Results and Discussion
- (i)
- Accuracy
- (ii)
- Precision
- (iii)
- Recall
3.1. Quantitative Analysis on SAT-4 Dataset
3.2. Quantitative Analysis on SAT-6 Dataset
3.3. Quantitative Analysis on Eurosat Dataset
3.4. Comparative Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Banerjee, B.; Bovolo, F.; Bhattacharya, A.; Bruzzone, L.; Chaudhuri, S.; Mohan, B.K. A new self-training-based unsupervised satellite image classification technique using cluster ensemble strategy. IEEE Geosci. Remote Sens. Lett. 2015, 12, 741–745. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y.; Yang, X.; Gao, S.; Li, F.; Kong, A.; Zu, D.; Sun, L. Improved remote sensing image classification based on multi-scale feature fusion. Remote Sens. 2020, 12, 213. [Google Scholar] [CrossRef]
- Pan, Z.; Xu, J.; Guo, Y.; Hu, Y.; Wang, G. Deep learning segmentation and classification for urban village using a worldview satellite image based on U-Net. Remote Sens. 2020, 12, 1574. [Google Scholar] [CrossRef]
- Xia, M.; Tian, N.; Zhang, Y.; Xu, Y.; Zhang, X. Dilated multi-scale cascade forest for satellite image classification. Int. J. Remote Sens. 2020, 41, 7779–7800. [Google Scholar] [CrossRef]
- Bekaddour, A.; Bessaid, A.; Bendimerad, F.T. Multi spectral satellite image ensembles classification combining k-means, LVQ and SVM classification techniques. J. Indian Soc. Remote Sens. 2015, 43, 671–686. [Google Scholar] [CrossRef]
- Pelletier, C.; Valero, S.; Inglada, J.; Champion, N.; Marais Sicre, C.; Dedieu, G. Effect of training class label noise on classification performances for land cover mapping with satellite image time series. Remote Sens. 2017, 9, 173. [Google Scholar] [CrossRef]
- Bhatt, M.S.; Patalia, T.P. Content-based high-resolution satellite image classification. Int. J. Inf. Technol. 2019, 11, 127–140. [Google Scholar] [CrossRef]
- Senthilnath, J.; Kulkarni, S.; Benediktsson, J.A.; Yang, X.S. A novel approach for multispectral satellite image classification based on the ba1t algorithm. IEEE Geosci. Remote Sens. Lett. 2016, 13, 599–603. [Google Scholar] [CrossRef]
- do Nascimento Bendini, H.; Fonseca, L.M.G.; Schwieder, M.; Körting, T.S.; Rufin, P.; Sanches, I.D.A.; Leitao, P.J.; Hostert, P. Detailed agricultural land classification in the Brazilian cerrado based on phenological information from dense satellite image time series. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101872. [Google Scholar] [CrossRef]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal convolutional neural network for the classification of satellite image time series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef]
- Ngo, L.T.; Mai, D.S.; Pedrycz, W. Semi-supervising Interval Type-2 Fuzzy C-Means clustering with spatial information for multi-spectral satellite image classification and change detection. Comput. Geosci. 2015, 83, 1–16. [Google Scholar] [CrossRef]
- Liu, Q.; Hang, R.; Song, H.; Li, Z. Learning multiscale deep features for high-resolution satellite image scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 117–126. [Google Scholar] [CrossRef]
- Yu, H.; Yang, W.; Xia, G.S.; Liu, G. A color-texture-structure descriptor for high-resolution satellite image classification. Remote Sens. 2016, 8, 259. [Google Scholar] [CrossRef]
- Yang, W.; Yin, X.; Xia, G.S. Learning high-level features for satellite image classification with limited labeled samples. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4472–4482. [Google Scholar] [CrossRef]
- Zhang, G.; Lu, S.; Zhang, W. CAD-Net: A context-aware detection network for objects in remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10015–10024. [Google Scholar] [CrossRef]
- Unnikrishnan, A.; Sowmya, V.; Soman, K.P. Deep learning architectures for land cover classification using red and near-infrared satellite images. Multimed. Tools Appl. 2019, 78, 18379–18394. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, F.; Xu, Y.; Huang, H. Multi-spectral RGB-NIR image classification using double-channel CNN. IEEE Access 2019, 7, 20607–20613. [Google Scholar] [CrossRef]
- Yang, N.; Tang, H.; Yue, J.; Yang, X.; Xu, Z. Accelerating the Training Process of Convolutional Neural Networks for Image Classification by Dropping Training Samples Out. IEEE Access 2020, 8, 142393–142403. [Google Scholar] [CrossRef]
- Weng, L.; Qian, M.; Xia, M.; Xu, Y.; Li, C. Land Use/Land Cover Recognition in Arid Zone Using A Multi-dimensional Multi-grained Residual Forest. Comput. Geosci. 2020, 144, 104557. [Google Scholar] [CrossRef]
- Zhong, Y.; Fei, F.; Liu, Y.; Zhao, B.; Jiao, H.; Zhang, L. SatCNN: Satellite image dataset classification using agile convolutional neural networks. Remote Sens. Lett. 2017, 8, 136–145. [Google Scholar] [CrossRef]
- Yamashkin, S.A.; Yamashkin, A.A.; Zanozin, V.V.; Radovanovic, M.M.; Barmin, A.N. Improving the Efficiency of Deep Learning Methods in Remote Sensing Data Analysis: Geosystem Approach. IEEE Access 2020, 8, 179516–179529. [Google Scholar] [CrossRef]
- Syrris, V.; Pesek, O.; Soille, P. SatImNet: Structured and Harmonised Training Data for Enhanced Satellite Imagery Classification. Remote Sens. 2020, 12, 3358. [Google Scholar] [CrossRef]
- Hu, J.; Tuo, H.; Wang, C.; Zhong, H.; Pan, H.; Jing, Z. Unsupervised satellite image classification based on partial transfer learning. Aerosp. Syst. 2019, 3, 21–28. [Google Scholar] [CrossRef]
- Basu, S.; Ganguly, S.; Mukhopadhyay, S.; DiBiano, R.; Karki, M.; Nemani, R. DeepSat-A Learning framework for Satellite Imagery. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2015; ACM SIGSPATIAL: New York, NY, USA, 2015; pp. 1–10. [Google Scholar]
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. Eurosat: A novel dataset and deep learning benchmark for land use and land cover classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2217–2226. [Google Scholar] [CrossRef]
- Abdullah-Al-Wadud, M.; Kabir, M.H.; Dewan, M.A.A.; Chae, O. A dynamic histogram equalization for image contrast enhancement. IEEE Trans. Consum. Electron. 2007, 53, 593–600. [Google Scholar] [CrossRef]
- Han, X.; Zhong, Y.; Cao, L.; Zhang, L. Pre-trained alexnet architecture with pyramid pooling and supervision for high spatial resolution remote sensing image scene classification. Remote Sens. 2017, 9, 848. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Wei, G.; Li, G.; Zhao, J.; He, A. Development of a LeNet-5 gas identification CNN structure for electronic noses. Sensors 2019, 19, 217. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Sun, J.; Wang, J.; Yue, X.G. Visual object tracking based on residual network and cascaded correlation filters. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 8427–8440. [Google Scholar] [CrossRef]
- Taradeh, M.; Mafarja, M.; Heidari, A.; Faris, H.; Aljarah, I.; Mirjalili, S.; Fujita, H. An Evolutionary Gravitational Search-based Feature Selection. Inf. Sci. 2019, 497, 219–239. [Google Scholar] [CrossRef]
- Mafarja, M.; Aljarah, I.; Heidari, A.A.; Faris, H.; Fournier-Viger, P.; Li, X.; Mirjalili, S. Binary dragonfly optimization for feature selection using time-varying transfer functions. Knowl.-Based Syst. 2018, 161, 185–204. [Google Scholar] [CrossRef]
- Akhtar, S.; Hussain, F.; Raja, F.; Ehatisham-ul-Haq, M.; Baloch, N.; Ishmanov, F.; Zikria, Y. Improving Mispronunciation Detection of Arabic Words for Non-Native Learners Using Deep Convolutional Neural Network Features. Electronics 2020, 9, 963. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Gangsar, P.; Tiwari, R. Taxonomy of induction-motor mechanical-fault based on time-domain vibration signals by multiclass SVM classifiers. Intell. Ind. Syst. 2016, 2, 269–281. [Google Scholar] [CrossRef][Green Version]



| Experiments | Performance | Classes | ||||
|---|---|---|---|---|---|---|
| Grassland | Tree | Barren Land | Others | Overall | ||
| without CCGSA | Precision (%) | 98.87 | 97.12 | 98.15 | 97.12 | 97.81 |
| Recall (%) | 100 | 98.84 | 97.68 | 98.49 | 98.75 | |
| Accuracy (%) | 98.40 | 97.68 | 98.09 | 98.76 | 98.23 | |
| HFEL–CCGSA (Experiment 1 + Experiment 2) | Precision (%) | 99.98 | 99.94 | 99.96 | 99.97 | 99.96 |
| Recall (%) | 99.79 | 99.96 | 99.97 | 99.93 | 99.91 | |
| Accuracy (%) | 100 | 99.98 | 100 | 99.98 | 99.99 | |
| CNN | Performance | Classes | ||||
|---|---|---|---|---|---|---|
| Grassland | Tree | Barren Land | Others | Overall | ||
| EL with AlexNet | Precision (%) | 99.45 | 98.97 | 97.18 | 99.17 | 98.69 |
| Recall (%) | 99.08 | 97.17 | 99.38 | 98.45 | 98.52 | |
| Accuracy (%) | 99.97 | 98.99 | 99.76 | 99.19 | 99.47 | |
| EL with LeNet-5 | Precision (%) | 98.47 | 99.08 | 98.07 | 99.03 | 98.66 |
| Recall (%) | 97.08 | 97.67 | 98.79 | 98.97 | 98.12 | |
| Accuracy (%) | 98.76 | 99.08 | 98.68 | 97.04 | 98.39 | |
| EL with ResNet | Precision (%) | 99.01 | 97.56 | 98.07 | 97.43 | 98.01 |
| Recall (%) | 98.43 | 98.89 | 98.69 | 99.18 | 98.79 | |
| Accuracy (%) | 97.78 | 97.04 | 99.02 | 97.99 | 97.95 | |
| HFEL–CCGSA (AlexNet + LeNet-5 + ResNet) | Precision (%) | 99.98 | 99.94 | 99.96 | 99.97 | 99.96 |
| Recall (%) | 99.79 | 99.96 | 99.97 | 99.93 | 99.91 | |
| Accuracy (%) | 100 | 99.98 | 100 | 99.98 | 99.99 | |
| Feature Selection Methods | Performance | Classes | ||||
|---|---|---|---|---|---|---|
| Grassland | Tree | Barren Land | Others | Overall | ||
| Particle Swarm Optimization (PSO) | Precision (%) | 98.49 | 97.06 | 97.37 | 98.16 | 97.77 |
| Recall (%) | 99.08 | 99.28 | 98.78 | 97.33 | 98.61 | |
| Accuracy (%) | 98.19 | 98.15 | 99.14 | 98.02 | 98.37 | |
| Binary Dragonfly Algorithm (BDA) | Precision (%) | 99.07 | 99.12 | 98.06 | 98.79 | 98.76 |
| Recall (%) | 98.46 | 99.88 | 97.67 | 99.02 | 98.75 | |
| Accuracy (%) | 98.97 | 97.76 | 98.44 | 97.55 | 98.18 | |
| HFEL–CCGSA (CCGSA) | Precision (%) | 99.98 | 99.94 | 99.96 | 99.97 | 99.96 |
| Recall (%) | 99.79 | 99.96 | 99.97 | 99.93 | 99.91 | |
| Accuracy (%) | 100 | 99.98 | 100 | 99.98 | 99.99 | |
| Experiments | Performance | Classes | ||||||
|---|---|---|---|---|---|---|---|---|
| Grassland | Trees | Barren Land | Roads | Buildings | Water Bodies | Overall | ||
| without CCGSA | Precision (%) | 98.46 | 99.78 | 99.67 | 98.42 | 98.06 | 98.46 | 98.8 |
| Recall (%) | 99.08 | 97.67 | 97.99 | 99.05 | 99.45 | 98.05 | 98.54 | |
| Accuracy (%) | 97.37 | 98.06 | 99.07 | 97.09 | 98.67 | 99.05 | 98.21 | |
| HFEL–CCGSA (Experiment 1 + Experiment 2) | Precision (%) | 99.88 | 99.95 | 99.96 | 99.93 | 99.98 | 99.94 | 99.94 |
| Recall (%) | 99.97 | 99.98 | 100 | 99.99 | 99.97 | 99.89 | 99.96 | |
| Accuracy (%) | 99.99 | 99.98 | 99.99 | 100 | 99.98 | 100 | 99.99 | |
| CNN | Performance | Classes | ||||||
|---|---|---|---|---|---|---|---|---|
| Grassland | Trees | Barren Land | Roads | Buildings | Water Bodies | Overall | ||
| EL with AlexNet | Precision (%) | 98.45 | 99.94 | 98.16 | 97.08 | 99.47 | 98.47 | 98.59 |
| Recall (%) | 99.98 | 99.76 | 99.47 | 98.02 | 98.89 | 98.73 | 99.14 | |
| Accuracy (%) | 99.12 | 98.74 | 99.08 | 98.57 | 99.37 | 99.43 | 99.05 | |
| EL with LeNet-5 | Precision (%) | 98.06 | 99.52 | 97.69 | 98.77 | 98.84 | 98.64 | 98.58 |
| Recall (%) | 98.15 | 97.17 | 98.87 | 99.34 | 98.58 | 97.35 | 98.24 | |
| Accuracy (%) | 99.01 | 98.05 | 98.64 | 99.33 | 99.22 | 99.03 | 98.88 | |
| EL with ResNet | Precision (%) | 97.24 | 98.99 | 97.08 | 98.42 | 99.33 | 98.11 | 98.19 |
| Recall (%) | 99.05 | 99.15 | 98.49 | 99.67 | 98.42 | 99.08 | 98.97 | |
| Accuracy (%) | 98.46 | 98.66 | 97.88 | 98.94 | 98.64 | 99.57 | 98.69 | |
| HFEL–CCGSA (AlexNet + LeNet-5 + ResNet) | Precision (%) | 99.88 | 99.95 | 99.96 | 99.93 | 99.98 | 99.94 | 99.94 |
| Recall (%) | 99.97 | 99.98 | 100 | 99.99 | 99.97 | 99.89 | 99.96 | |
| Accuracy (%) | 99.99 | 99.98 | 99.99 | 100 | 99.98 | 100 | 99.99 | |
| Feature Selection Methods | Performance | Classes | ||||||
|---|---|---|---|---|---|---|---|---|
| Grassland | Trees | Barren Land | Roads | Buildings | Water Bodies | Overall | ||
| PSO | Precision (%) | 98.89 | 98.77 | 97.08 | 98.46 | 99.52 | 99.08 | 98.63 |
| Recall (%) | 99.33 | 97.45 | 98.69 | 99.67 | 98.68 | 98.88 | 98.78 | |
| Accuracy (%) | 98.45 | 98.42 | 99.07 | 97.37 | 99.47 | 99.77 | 98.75 | |
| BDA | Precision (%) | 99.08 | 98.47 | 98.55 | 97.66 | 99.06 | 98.94 | 98.62 |
| Recall (%) | 98.62 | 98.66 | 99.11 | 98.88 | 98.79 | 98.63 | 98.78 | |
| Accuracy (%) | 98.33 | 99.08 | 99.03 | 98.67 | 98.79 | 98.99 | 98.81 | |
| HFEL–CCGSA (CCGSA) | Precision (%) | 99.88 | 99.95 | 99.96 | 99.93 | 99.98 | 99.94 | 99.94 |
| Recall (%) | 99.97 | 99.98 | 100 | 99.99 | 99.97 | 99.89 | 99.96 | |
| Accuracy (%) | 99.99 | 99.98 | 99.99 | 100 | 99.98 | 100 | 99.99 | |
| Experiments | Performance | Overall |
|---|---|---|
| without CCGSA | Precision (%) | 98.15 |
| Recall (%) | 99.67 | |
| Accuracy (%) | 98.56 | |
| HFEL–CCGSA | Precision (%) | 98.93 |
| Recall (%) | 99.15 | |
| Accuracy (%) | 99.49 |
| CNN | Performance | Overall |
|---|---|---|
| EL with AlexNet | Precision (%) | 98.42 |
| Recall (%) | 99.11 | |
| Accuracy (%) | 98.99 | |
| EL with LeNet-5 | Precision (%) | 98.22 |
| Recall (%) | 97.54 | |
| Accuracy (%) | 98.42 | |
| EL with ResNet | Precision (%) | 97.38 |
| Recall (%) | 96.44 | |
| Accuracy (%) | 97.45 | |
| HFEL–CCGSA (AlexNet + LeNet-5 + ResNet) | Precision (%) | 98.93 |
| Recall (%) | 99.15 | |
| Accuracy (%) | 99.49 |
| Feature Selection Methods | Performance | Overall |
|---|---|---|
| PSO | Precision (%) | 98.04 |
| Recall (%) | 98.74 | |
| Accuracy (%) | 96.48 | |
| BDA | Precision (%) | 97.11 |
| Recall (%) | 98.57 | |
| Accuracy (%) | 97.57 | |
| HFEL–CCGSA (CCGSA) | Precision (%) | 98.93 |
| Recall (%) | 99.15 | |
| Accuracy (%) | 99.49 |
| Dataset | Method | Classification Accuracy (%) |
|---|---|---|
| SAT-4 dataset | 2-Band AlexNet [16] | 99.66 |
| Hyperparameter-Tuned AlexNet [16] | 98.45 | |
| 2-Band ConvNet [16] | 99.03 | |
| Hyperparameter-Tuned ConvNet [16] | 98.45 | |
| 2-Band VGG [16] | 99.03 | |
| Hyperparameter-Tuned VGG [16] | 98.59 | |
| DCCNN [17] | 98.00 | |
| MGSS [19] | 99.97 | |
| HFEL–CCGSA | 99.99 | |
| SAT-6 dataset | 2-Band AlexNet [16] | 99.08 |
| Hyperparameter-Tuned AlexNet [16] | 97.43 | |
| 2-Band ConvNet [16] | 99.10 | |
| Hyperparameter-Tuned ConvNet [16] | 97.48 | |
| 2-Band VGG [16] | 99.15 | |
| Hyperparameter-Tuned VGG [16] | 97.95 | |
| DCCNN [17] | 97.00 | |
| MGSS [19] | 99.95 | |
| HFEL–CCGSA | 99.99 | |
| Eurosat dataset | GeoSystemNet [21] | 95.30 |
| HFEL–CCGSA | 99.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiagarajan, K.; Manapakkam Anandan, M.; Stateczny, A.; Bidare Divakarachari, P.; Kivudujogappa Lingappa, H. Satellite Image Classification Using a Hierarchical Ensemble Learning and Correlation Coefficient-Based Gravitational Search Algorithm. Remote Sens. 2021, 13, 4351. https://doi.org/10.3390/rs13214351
Thiagarajan K, Manapakkam Anandan M, Stateczny A, Bidare Divakarachari P, Kivudujogappa Lingappa H. Satellite Image Classification Using a Hierarchical Ensemble Learning and Correlation Coefficient-Based Gravitational Search Algorithm. Remote Sensing. 2021; 13(21):4351. https://doi.org/10.3390/rs13214351
Chicago/Turabian StyleThiagarajan, Kowsalya, Mukunthan Manapakkam Anandan, Andrzej Stateczny, Parameshachari Bidare Divakarachari, and Hemalatha Kivudujogappa Lingappa. 2021. "Satellite Image Classification Using a Hierarchical Ensemble Learning and Correlation Coefficient-Based Gravitational Search Algorithm" Remote Sensing 13, no. 21: 4351. https://doi.org/10.3390/rs13214351
APA StyleThiagarajan, K., Manapakkam Anandan, M., Stateczny, A., Bidare Divakarachari, P., & Kivudujogappa Lingappa, H. (2021). Satellite Image Classification Using a Hierarchical Ensemble Learning and Correlation Coefficient-Based Gravitational Search Algorithm. Remote Sensing, 13(21), 4351. https://doi.org/10.3390/rs13214351








