1. Introduction
Coastal bathymetry is key to supporting different maritime and coastal applications, such as the safety of ship navigation and assessment of coastal risks. Underwater acoustic techniques are undoubtedly the most popular way to obtain high-precision depth data [
1,
2,
3]. However, the risk due to sea states and the time consumption often increase the difficulty of in situ operation. Remote sensing provides potential ways to obtain coastal bathymetric information more efficiently. Both optical video and radar images have been proven to be feasible for determining coastal bathymetry [
4,
5,
6,
7,
8,
9,
10]. Video image sequences, whose temporal and spatial resolutions are better than those of radar image sequences, are helpful in determining the water depth in shallower sea areas. However, the range of bathymetry determination using X-band radar images can be much larger, up to several kilometers. Nautical X-band radar is normally used to detect coastlines and obstacles on the sea surface on board a ship. Studies have proven its feasibility for presenting the patterns of ocean waves since the late 1970s [
11,
12], and X-band radar is currently one of the most popular tools for ocean remote sensing.
The wave dispersion relation of the linear theory for surface gravity waves, which describes the wavenumber–frequency features of gravity waves at different water depth conditions, is the most common way to estimate bathymetry from remotely sensed images. Because the wavenumber–frequency structure can be obtained from the spatial–temporal wave patterns in sea surface image sequences [
4], different algorithms have been proposed to extract wavenumber–frequency information accurately and efficiently.
Regardless of whether wave pattern image analysis is implemented in the spatial-temporal domains or in the spectral domains [
5,
13,
14], the window size of the image is always the result of a tradeoff between the accuracy of the estimates and the homogeneity constraints on the sea parameters [
15]. Because the fast Fourier transform algorithm reduces the number of computations, an increasing number of studies have focused on depth determination from the spectral domain. The wavenumber obtained from the image spectrum is a popular and reliable method. However, the precise wavenumber result comes from the high-resolution image spectrum, which necessitates a spectral transform from the large window size of the image. When large wave pattern images are analyzed, the inhomogeneity within coastal images is often unfavorable for obtaining bathymetry maps with high spatial resolution.
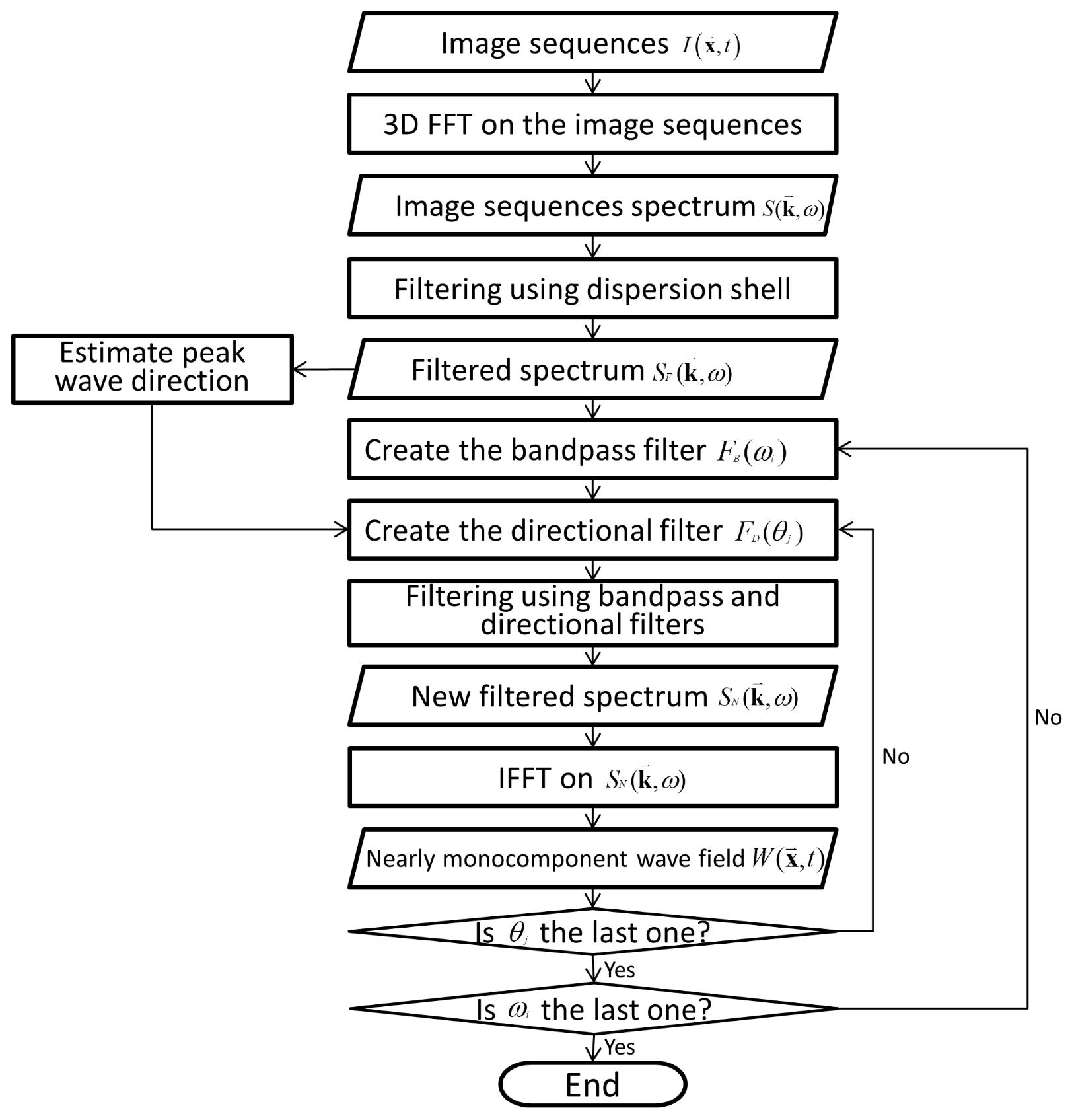
In addition to image analysis with a specific window size, another category of bathymetry retrieval methods estimates the wavenumber from the local phase gradient (PG) within a monofrequency image and then calculates the wavenumber–frequency pair [
16,
17]. The PG over the Fourier transform technique allows higher spatial resolution and computational efficiency [
18]. A depth result can be determined from one wavenumber–frequency pair using the dispersion relation. However, errors of local phase estimation under the joint influences of the imaging mechanism, observation noise, and multiple wave frequencies are unavoidable [
19]. As a result, error in depth determination using a single wavenumber–frequency pair that is estimated from sea surface images is inevitable. Although the water depth value can be determined by fitting the dispersion relationship curve using all frequency-dependent wavenumbers, the derived wavenumbers for each frequency bin using the PG method are still uncertain. If a sequence of records is processed, we can average the bathymetry maps to reduce noise or implement a Kalman filter to objectively update the bathymetry estimates [
18,
20]. However, both the average and Kalman filter methods rely on sufficient records with clear wave pattern images. In the case of limited image records, we need to implement another way to improve the accuracy of depth determination. Under the PG method, this study aims to estimate the plural local wavenumbers at each of the frequency bins to determine the bathymetry using marine radar images. To obtain abundant local wavenumbers at each location, spectral bandpass filtering and directional filtering are carried out on individual pixels in isolation. In subsequent sections, we will demonstrate the entire image processing procedure and confirm its practicability using coastal radar images.
3. Results and Discussion
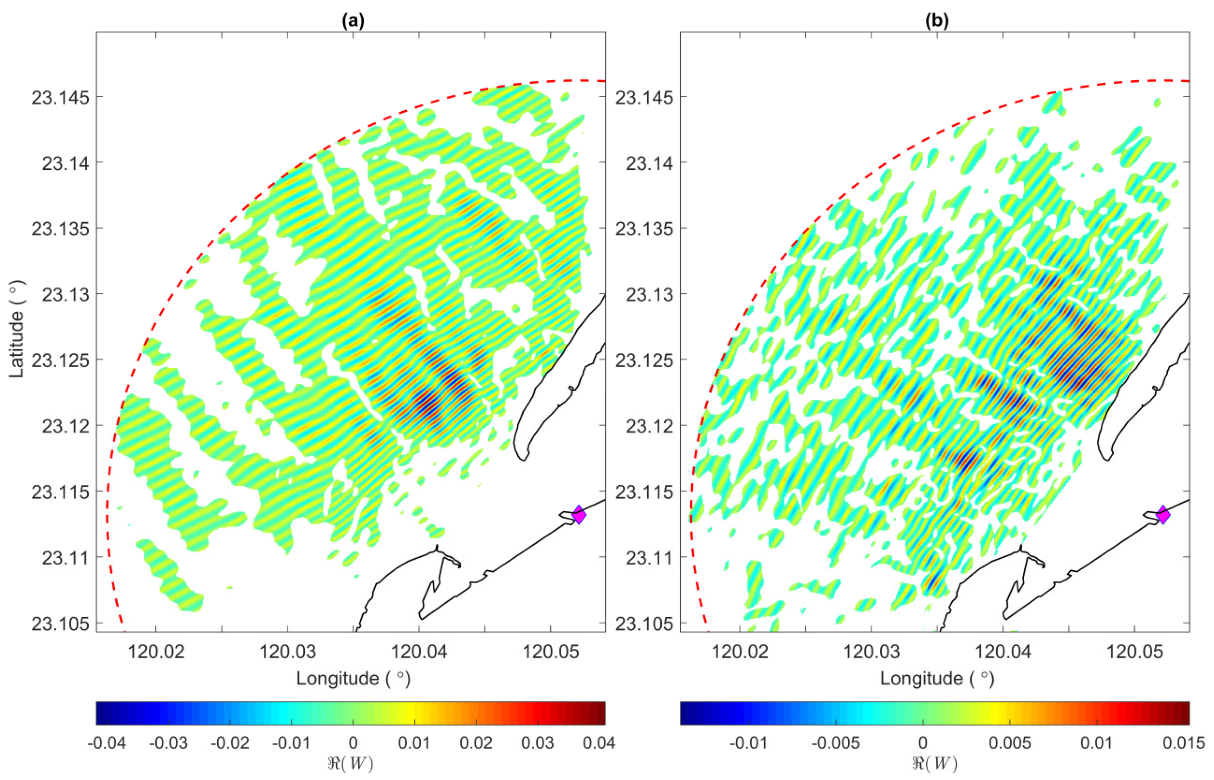
Figure 3 shows the nearly monocomponent images of ocean waves after bandpass and directional filtering. For the image process of our study, there are 23 angular frequency bins (
) within the range of
(rad/s) to
(rad/s).
Figure 3 shows the results of bandpass filtering using
, which is near the in situ peak wave angular frequency. The dominant wave direction
, which is estimated from radar images, is 313°.
Figure 3a,b shows the results using the directional bands of
and
, respectively. The wave patterns show different directions between these two figures.
Because we remove the results of when the normalized magnitude is less than 0.2, some parts of the wave field are excluded due to weak wave signals. Even though we implemented 31 directional filters to produce 31 nearly monocomponent wave fields, we could not obtain all 31 wavenumbers at a specified angular frequency at locations where the wave signal was weak. Because sufficient wavenumbers are necessary to fit the dispersion relation curve with local depth, we skip the fitting process when the total number of wavenumber–frequency pairs is less than 300.
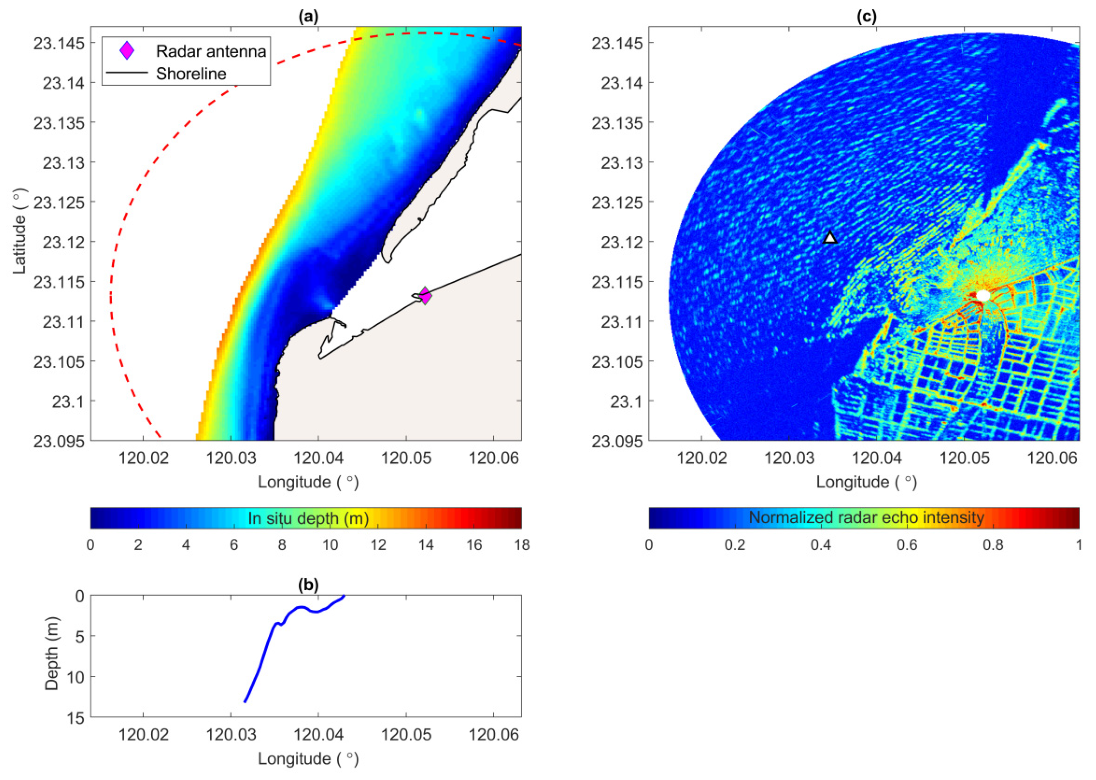
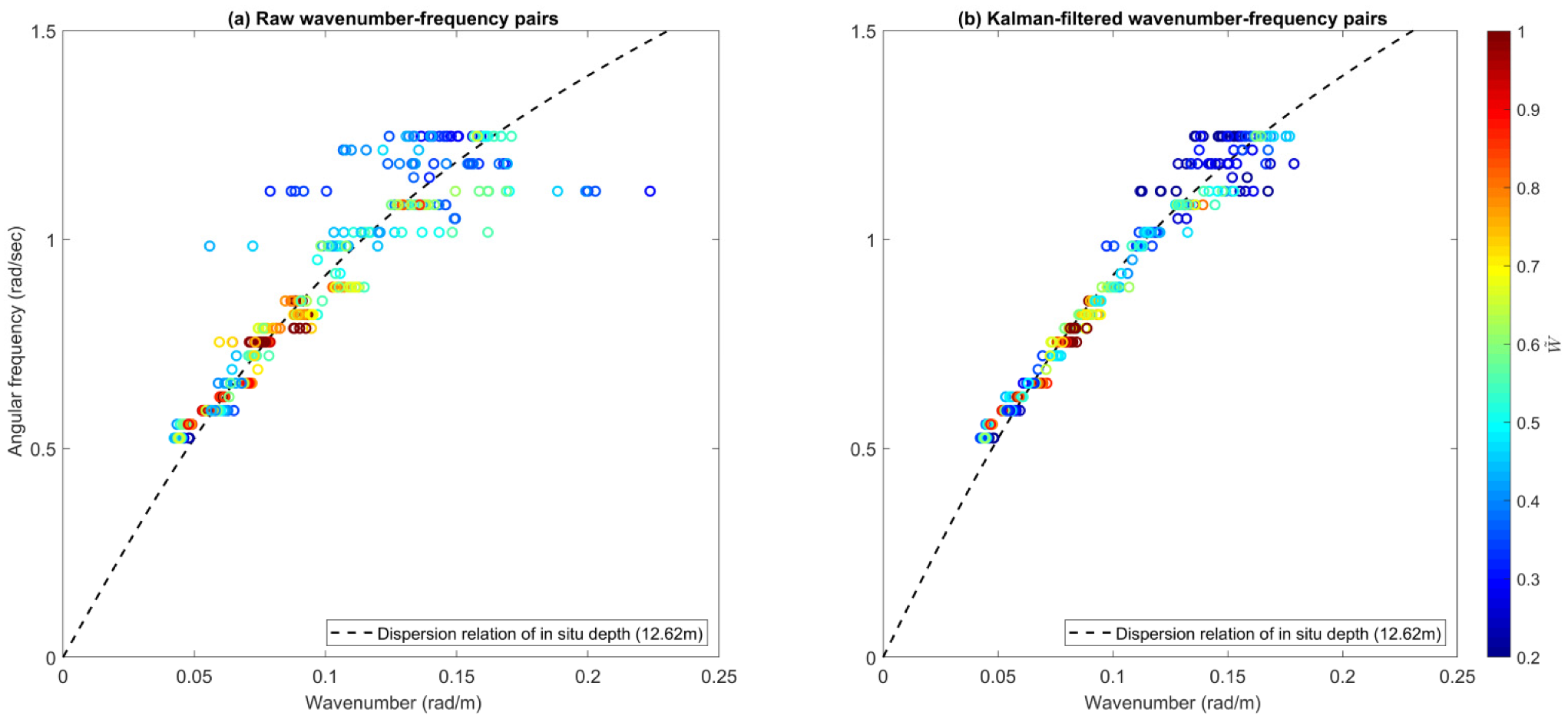
Figure 4 shows the abundant wavenumber–frequency pairs estimated at the fixed location of a triangle marker in the radar image of
Figure 2c.
Figure 4a shows the raw wavenumbers estimated directly from different nearly monocomponent wave fields. The dispersion relation curve using the survey depth of this specified location is also presented in the figure. Although parts of the raw wavenumber–frequency pairs are consistent with the dispersion relation curve, the raw wavenumbers show high variance in higher-frequency bins. This poor reliability from raw wavenumber–frequency pairs is obvious and therefore needs to be improved.
Figure 4b shows the wavenumber–frequency pairs that are corrected using Kalman filtering. The Kalman-filtered wavenumber–frequency pairs show much smaller variance and are more consistent with the dispersion relation curve.
Figure 4 also shows that the deviated wavenumbers from high-frequency bins are mostly estimated from weak
. Note that our study applies the magnitudes of wave signals
as the weights for the least-squares fit of the dispersion relation curve.
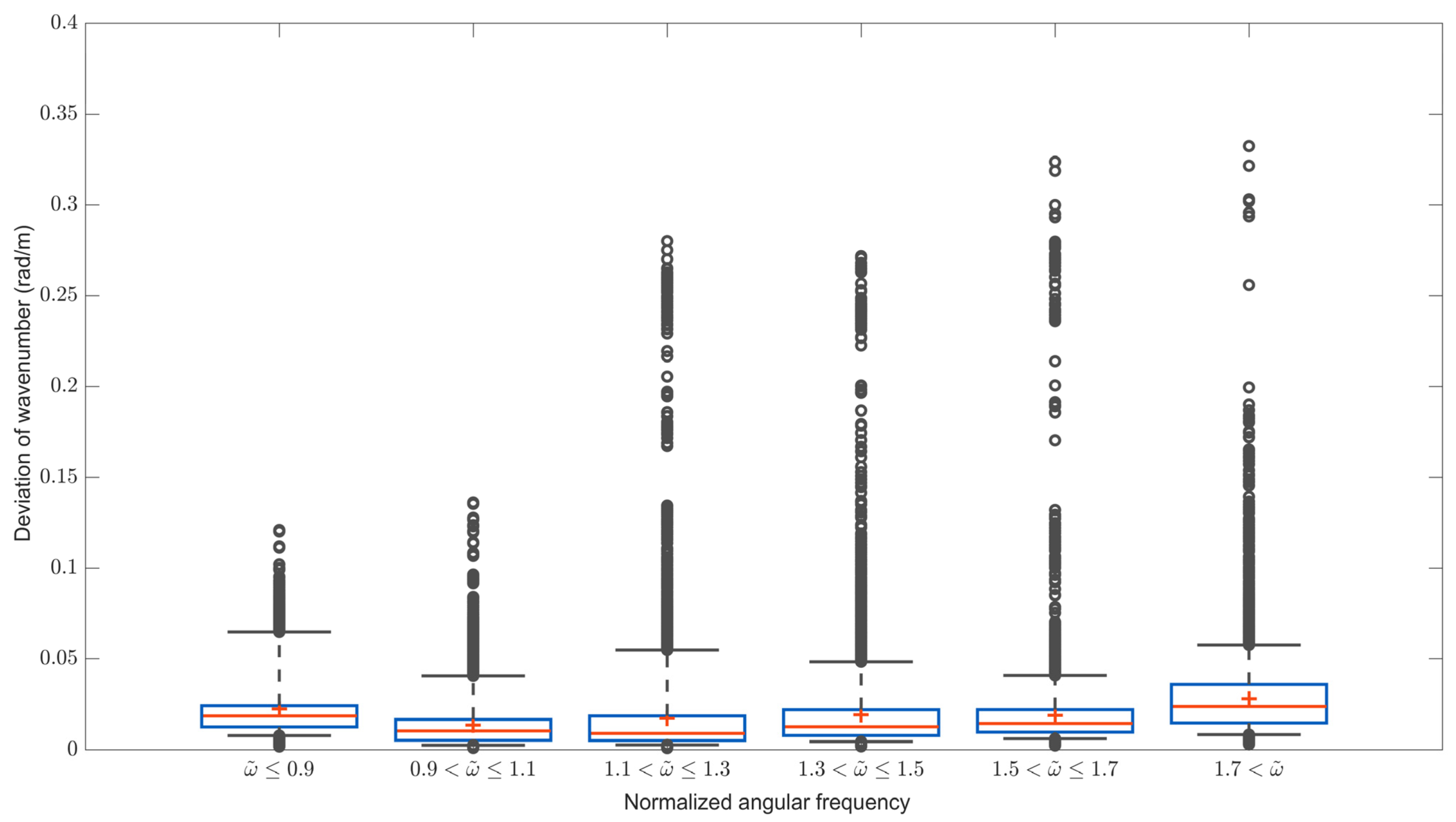
Figure 4 shows only one case at a specified location. We further discuss the features of the wavenumbers extracted from all locations within the wave field. As shown in
Figure 5, the different upper whiskers show unclear connections with the frequencies. The normalized frequency
in
Figure 5 is defined as:
where
is the peak angular frequency of the ocean waves, which can be obtained from the filtered image spectrum.
Figure 5 shows that all of the upper whiskers are smaller than 0.08 (rad/m). However, we observe that the distributions of the upper outliers are related to the wave frequency. From the cases of higher frequency bins, more inaccurate wavenumber estimations are revealed. This should be a reason that higher wave frequency bins are sensitive to the sea surface current
. We will discuss this issue in a subsequent section.
As we mentioned above, the inaccurate wavenumbers are also due to the local phase gradient from the wave field with weak wave signals.
Figure 6 shows the relationship between wavenumber deviations and
, which represents the magnitude of wave signals for the analysis of the local phase gradient. The accuracy of wavenumber estimations is obviously poor, and the value of
is too low. In general, the higher the value of
is, the more reliable the results of wavenumber estimations.
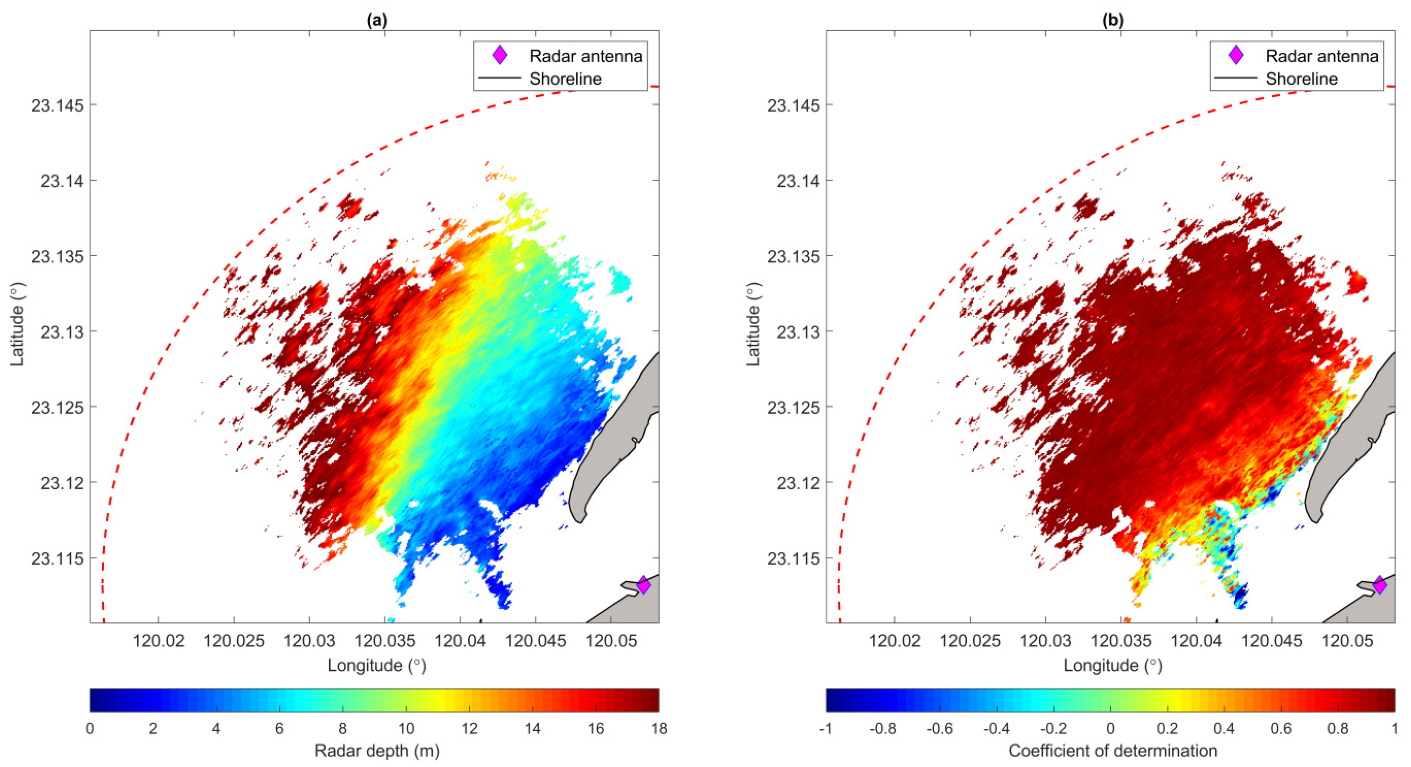
After determining the best weighted least-squares fits of the dispersion relation curve from the estimated wavenumbers of different spatial locations
, we obtain the bathymetry result, which is shown in
Figure 7a. The resolution of the estimated depth is set to 0.01 m. The relationship between the estimated wavenumbers and the fitted dispersion curve is also key to quantifying the accuracy of the depth determination. For each of the fitting results from different locations, we can estimate the coefficient of determination
from the estimated wavenumbers and modeled wavenumbers of the fitted dispersion relation curve:
where
is the modeled wavenumber of the fitted dispersion relation curve and
is the average value of
.
In general,
is defined as the square of the correlation between the modeled wavenumber and the estimated wavenumbers
. However,
can produce a negative value when the model poorly fits
[
24].
Figure 7b shows the results of
in the spatial domain. Compared to the bathymetry map in
Figure 7a, we observe that poor results of
occur mostly in shallow-water locations. The defect of the linear dispersion relation in the determination of shallow water depth is obvious. Because our depth estimations are based on the fits of the dispersion relation curve using estimated wavenumbers, the accuracy of depth estimation should be related to
.
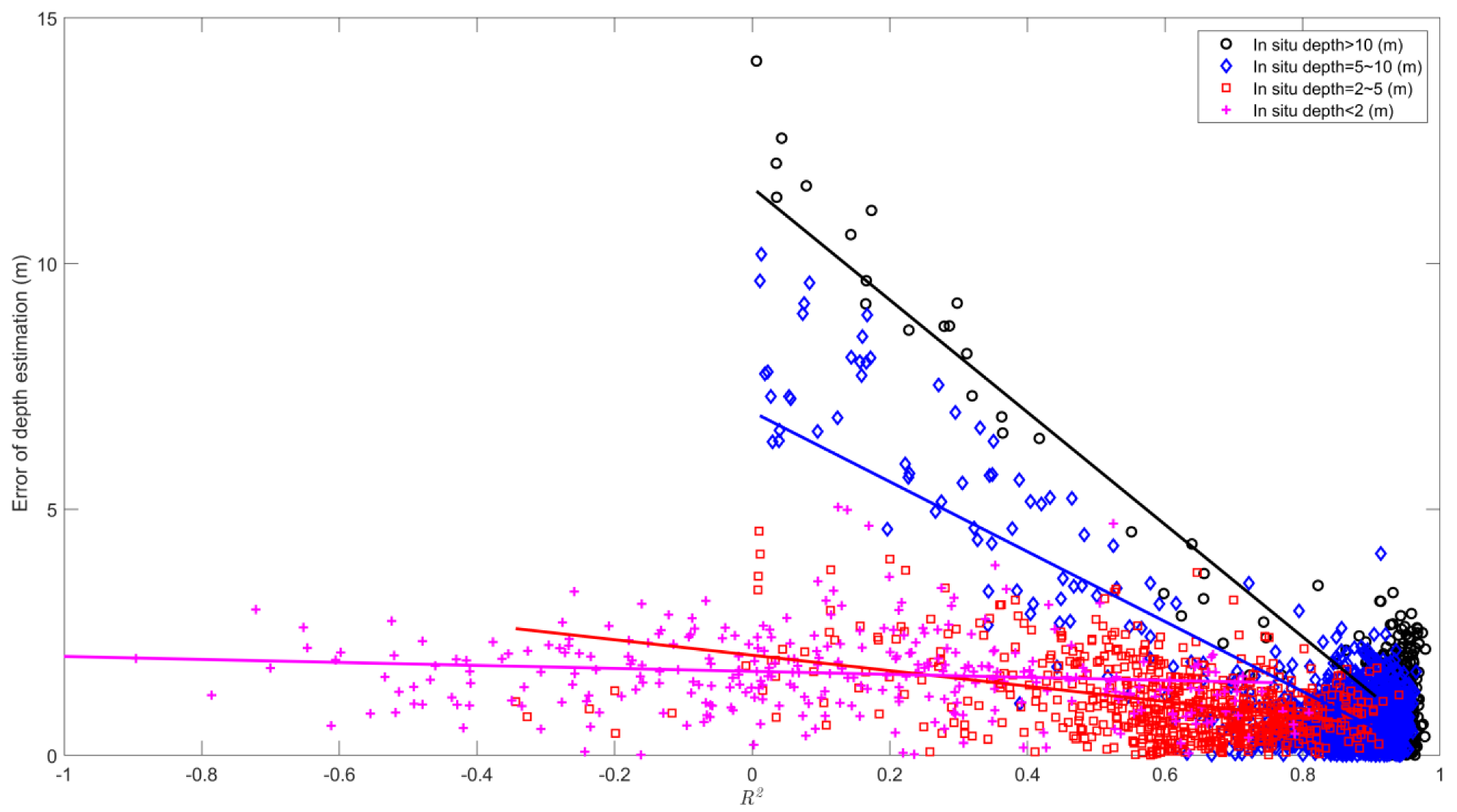
As shown in
Figure 8, all the cases with negative values of the coefficient of determination are from locations where the in situ depths are less than 2 m. Wave nonlinearity, which is unavoidable in shallow-water areas, makes the wavenumber–frequency pairs deviate clearly from the linear wave dispersion relation curve and makes the depth estimation unreliable. Compared to the errors of depth estimation from shallow-water areas, the relationships between
and depth errors from deeper-water areas show clearer trends. To determine these trends, the linear regression lines of different categories are also presented in
Figure 8. The relations between
and the errors of depth estimations from deeper-water areas of radar images are obvious. The lower the values of
are, the higher the errors of depth estimation from deeper-water areas. We can confirm the quality of depth estimations according to the value of
.
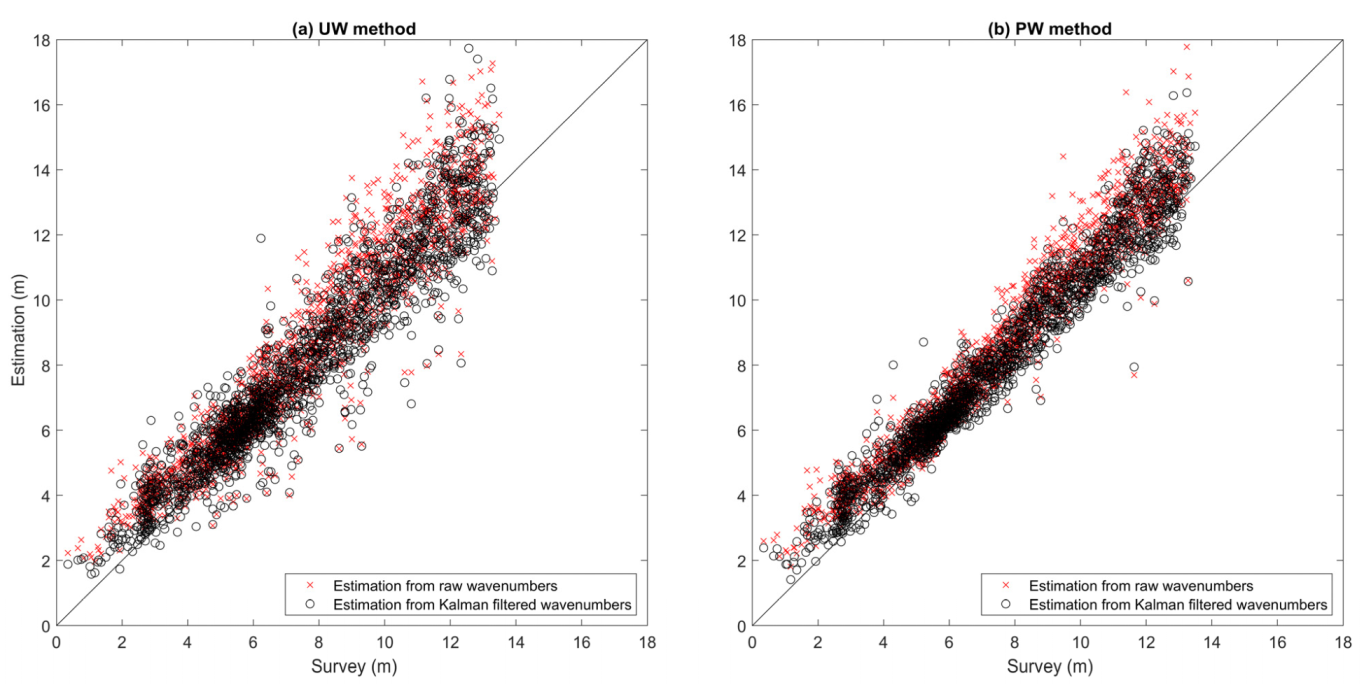
Figure 9 shows the comparisons of the depth estimations between the radar-estimated depth and survey depth. For some safety-related applications, e.g., ship navigation, depth information with poor accuracy can be worse than insufficient depth information. In consideration of the quality of depth estimations, we remove the estimated depth results whose
values are less than 0.6.
Although the depth results from
Figure 9a,b are all obtained by the least-squares fit, the depth estimations are obtained using different ways of estimating the wavenumbers. For the UW method in
Figure 9a, there is only one wavenumber result from each frequency bin. The wavenumber is estimated from the nearly monocomponent wave field, which implements only directional filtering with
from Equation (3). However, the PW method in
Figure 9b shows the results from abundant wavenumbers that are implemented using different
from Equation (3). For each of the methods, we also discuss the depth estimations with and without the Kalman filter. Both
Figure 9a,b show that the Kalman-filtered wavenumbers are helpful for obtaining more reliable depth results. Compared to the results of
Figure 9a, the depth estimations using the least-squares fit of the plural wavenumber–frequency pairs can be improved. To evaluate the accuracy of depth estimation using estimated wavenumbers after Kalman filtering, we estimate different statistical parameters from the estimations and ground truths shown in
Table 1. Although the correlation coefficients of different methods are all over 0.95, the depth estimations using abundant wavenumbers still show a higher correlation with the survey depth. In addition, the root-mean-square deviation of depth estimation can be improved when the Kalman-filtered wavenumbers are applied to estimate the depth.
4. Limitations and Uncertainties
An accurate wavenumber is undoubtedly necessary to obtain the reliable depth result using wave dispersion relation.
Figure 5 shows that most of the inaccurate wavenumber estimations are derived from higher-frequency bins. According to Equation (1), the influence of depth on the wavenumber–frequency pairs is obvious at lower frequencies. In contrast, the wave–current interaction is obvious at higher frequencies. The coastal current can be highly nonstationary and inhomogeneous due to the influences of sea states and coastal bathymetry. In our study, the wave–current interaction is assumed to be neglected when using the dispersion relationship. However, the influences of sea surface currents induce wavenumbers in high-frequency bins to deviate from the dispersion relation curve without currents. Another reason for the inaccurate wavenumber is the aliasing effect. In the physical sciences, the wavenumber is the spatial frequency of a wave. The complex spectral densities at higher frequencies are easily influenced by aliasing [
29]. Due to the overlap of complex spectral densities at spatial frequencies near the Nyquist spatial frequency, the influence of phase estimation from complex spectral densities is unavoidable.
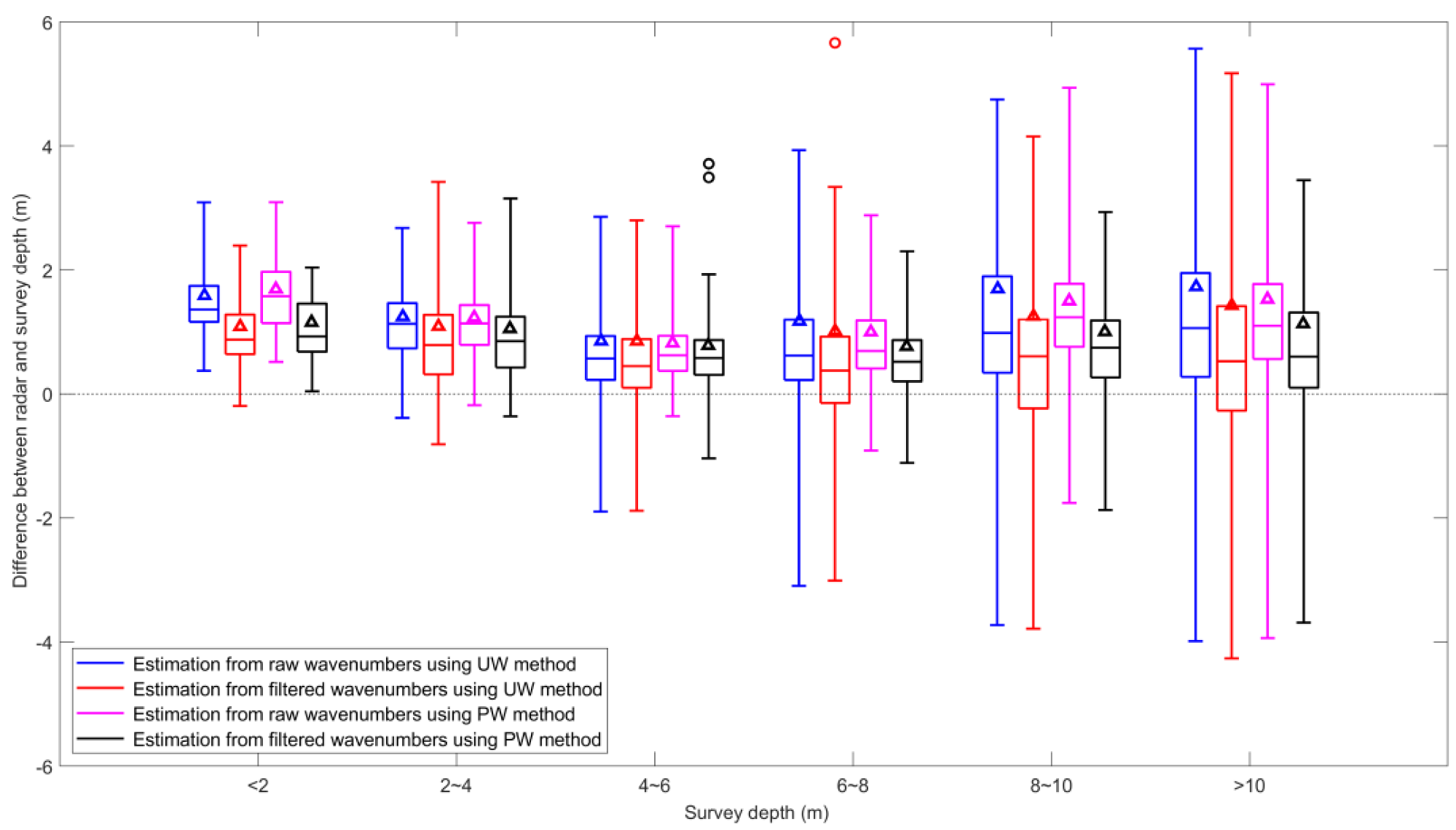
The scatter plot in
Figure 9 shows that the Kalman-filtered wavenumbers are helpful for obtaining more reliable depth results. However, the accuracy of radar estimations seems to depend on the survey depth.
Figure 10 presents the differences between radar depths and survey depths, which are classified into different conditions of survey depths. We observed that most of the radar-estimated depths are overestimated from the shallower area. As we pointed out in the data analysis section, the wavenumber–frequency pairs at higher-frequency bins, whose normalized magnitude is
, are mostly weak and are excluded from the fitting process. The nonlinear effects are often unavoidable for the wavenumber–frequency pairs at lower-frequency bins, even though we removed the estimations whose
values are too low. Large amplitude waves in shallow water are known to travel slightly faster than predicted by linear wave theory, which causes a slight overestimation of the radar depth [
30]. This finding should explain the positive bias of radar-estimated depth estimation. The cases of shallow-water areas are often overestimated, regardless of whether Kalman filtering is applied.
The overestimation of radar-estimated depths is not obvious in deeper water. However, we observe more inaccurate radar-estimated depths from the sea area where the survey depths exceed 10 m. The uncertain radar estimations in the deep-water case are related to the unclear wave patterns on the radar image. In our study site, the deep-water areas are located farther from the radar antenna. Because the radar echo intensities decay with distance, the unclear wave pattern on the radar image is unavoidable. A sufficiently clear wave pattern is important for estimating the wavenumbers.
5. Conclusions
The phase gradient (PG) has been demonstrated to be a powerful tool for extracting local wavenumbers from spatial images. Since only one local PG can be found along the horizontal or vertical direction, only one wavenumber modulus can be obtained at any given spatial location of a remotely sensed image. Although it is still possible to use a single wavenumber to estimate depth using the theory of the wave dispersion relation, the wavenumber obtained from the wave field of a remotely sensed image is sensitive to noise. The depth result can be uncertain if a single and unreliable wavenumber is used. Some studies obtain the representative wavenumber, which can be more reliable than the wavenumber from the PG method, i.e., from the 2D image spectrum. However, the resolution between the spatiotemporal domain and the wavenumber–frequency domain is the opposite of that based on the Heisenberg uncertainty principle. To obtain reliable and accurate wavenumber and frequency results from the spectrum, degeneration of the spatiotemporal resolution is unavoidable.
The depth determination in our study is based on the fit of the dispersion relationship curve to abundant frequency-dependent wavenumbers. Some previous studies extracted different wavenumber–frequency pairs from different frequency bins of the image spectrum and then best fitted all frequencies to determine the local depth. Under the same idea, we extract the features of the plural wavenumbers of each frequency bin from fixed locations within the wave field image. To extract more wavenumbers of each frequency bin from the same location, we applied directional filtering technology. Different nearly monocomponent wave images can be produced from remotely sensed images using different directional pass filters. As a result, we can estimate more wavenumbers from nearly monocomponent wave images using the PG method.
The remotely sensed images we analyzed in this study are X-band radar images. Within the area of radar monitoring, we have the in situ depth data that were measured 8 days after the radar observation. Due to the influences of ocean currents and image noise, the raw wavenumber results extracted from the nearly monocomponent wave images are highly uncertain in higher-frequency bins. The Kalman filter is confirmed to improve highly scattered wavenumbers. For the cases with lower coefficients of determination, the errors of depth estimation from deeper-water areas are higher. As a result, the coefficient of determination can be used as an index to obtain reliable depth estimations. After removing the depth estimations with low coefficients of determination, we discuss the performance of radar depths using the survey depth data. In contrast to the depth estimations from a single wavenumber of each frequency bin, the depth estimations from more wavenumbers of each frequency bin show results that are more reliable. In addition, Kalman filtering is helpful in reducing the root-mean-square deviation of depth estimations.
As stated before, the spatial resolution of bathymetry determination using the PG method can be higher than that using the spectral method. In previous studies, the application of spatial or temporal filters was common in reducing the error of bathymetry maps. In our study, there is no low-pass filter for the spatial domain in the process of depth determination from our radar images, and the spatial resolution of the bathymetry maps is the same as that of radar images. Long-term radar image sequences are also unnecessary for our image process. After checking the quality of the depth results using the coefficient of determination, 128 continuous radar images that take approximately three minutes were found to be sufficient to obtain a reliable bathymetry map. We also confirm that directional filtering can produce different nearly monocomponent wave images and then obtain plural local wavenumbers at the same location. Plural wavenumber fitting is workable in improving the reliability of depth estimation.