Pose Estimation of Non-Cooperative Space Targets Based on Cross-Source Point Cloud Fusion
Abstract
:1. Introduction
- (1)
- We propose a cross-source point cloud fusion algorithm, which uses the unified and simplified expression of geometric elements in conformal geometry algebra, breaks the traditional point-to-point correspondence, and constructs a matching relationship between points and spheres, to obtain the attitude transformation relationship of the two point clouds. We used the geometric meaning of the inner product in CGA to construct the similarity measurement function between the point and the sphere as the objective function.
- (2)
- To estimate the pose of a non-cooperative target, the contour model of the target needs to be reconstructed first. To improve its reconstruction accuracy, we propose a plane clustering method based CGA to eliminate point cloud diffusion after fusion. This method combines the shape factor concept and the plane growth algorithm.
- (3)
- We introduced a twist parameter for rigid body pose analysis in CGA and combined it with the Clohessy–Wiltshire equation to obtain the posture and other motion parameters of the non-cooperative target through the unscented Kalman filter.
- (4)
- We designed numerical simulation experiments and semi-physical experiments to verify our non-cooperative target measurement system. The results show that the proposed cross-source point cloud fusion algorithm effectively solves the problem of low point cloud overlap and large density distribution differences, and the fusion accuracy is higher than that of other algorithms. The attitude estimation of non-cooperative targets meets the requirement of measurement accuracy, and the estimation error of the angle of the rotating spindle is 30% lower than that of other methods.
2. Method
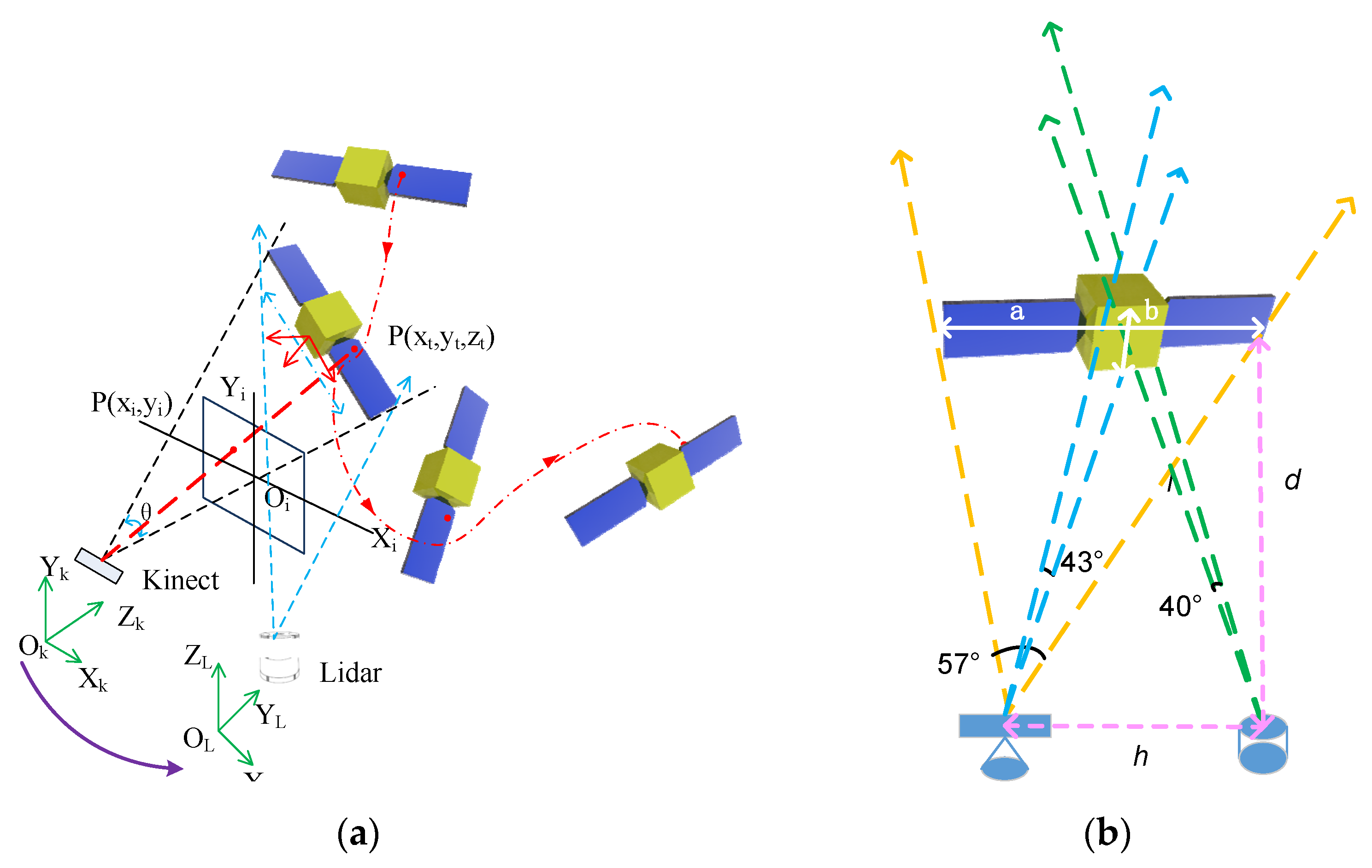
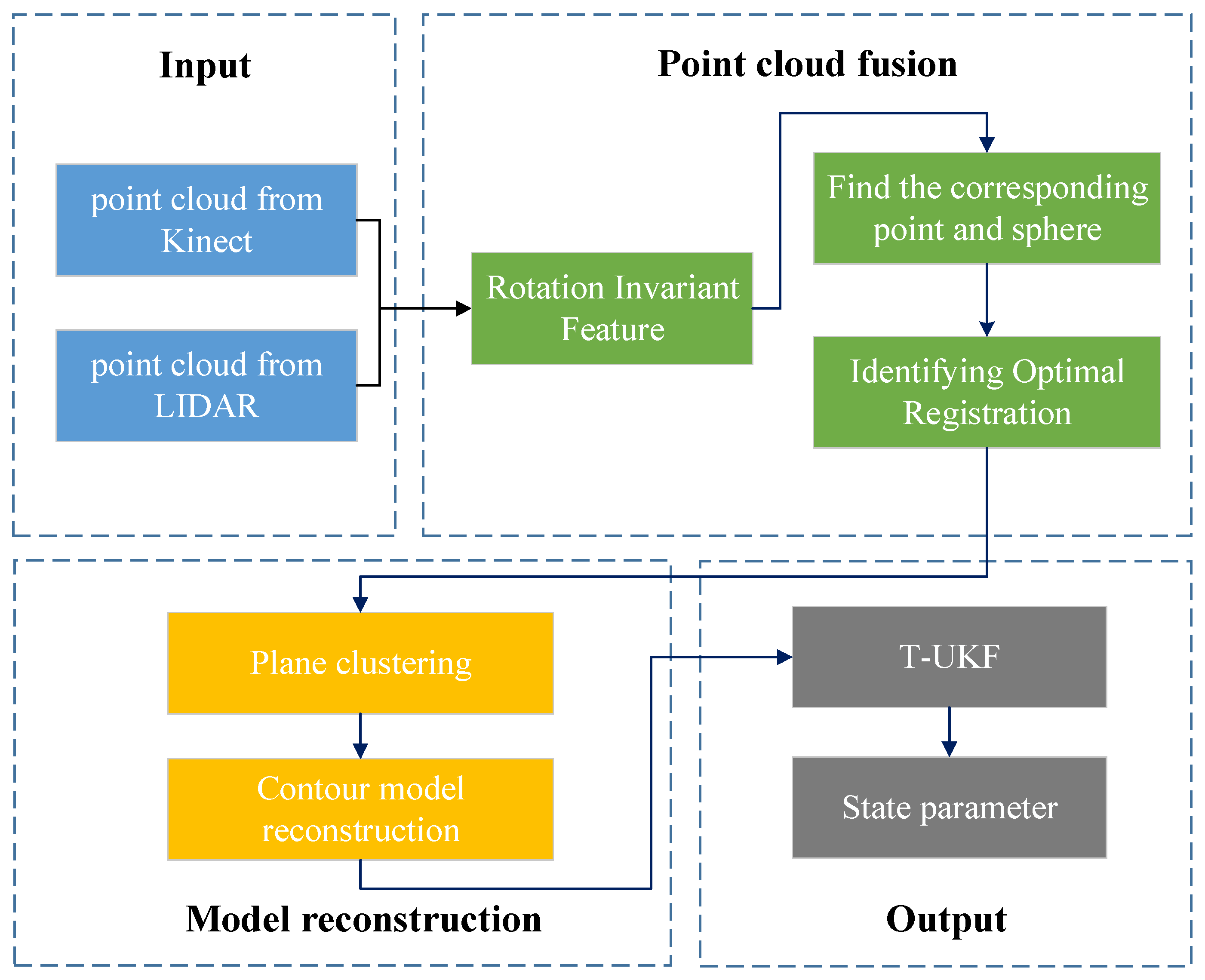
2.1. Measurement System and Algorithm Framework
2.2. Cross-Source Point Cloud Fusion
2.2.1. Rotation Invariant Features Based on CGA
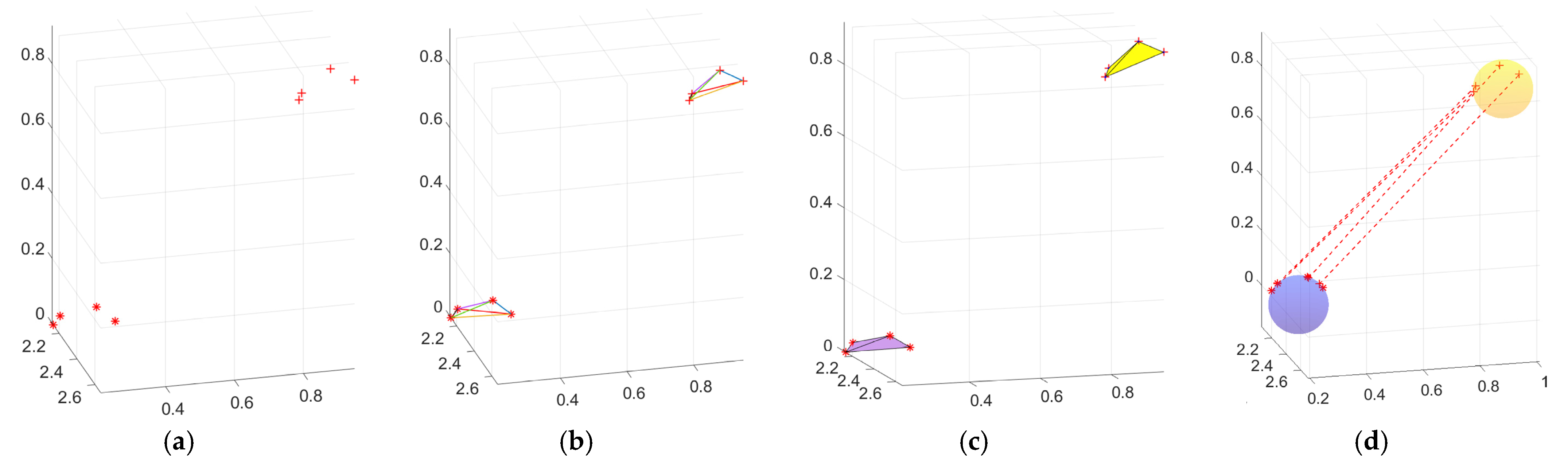
2.2.2. Find the Corresponding Point and Sphere
- Calculate the centroids of the two point clouds and move the centroids to the origins of their respective coordinate systems: , .
- Taking the centroid as the starting point and using the farthest point sampling method, uniformly sample n points in the reference point cloud.
- Given the distance from the centroid of the reference point cloud to each sampling point, {, look for the distance to the centroid in the moving point cloud to satisfy the relationship . In this paper, T is the average distance between points of the moving point cloud.
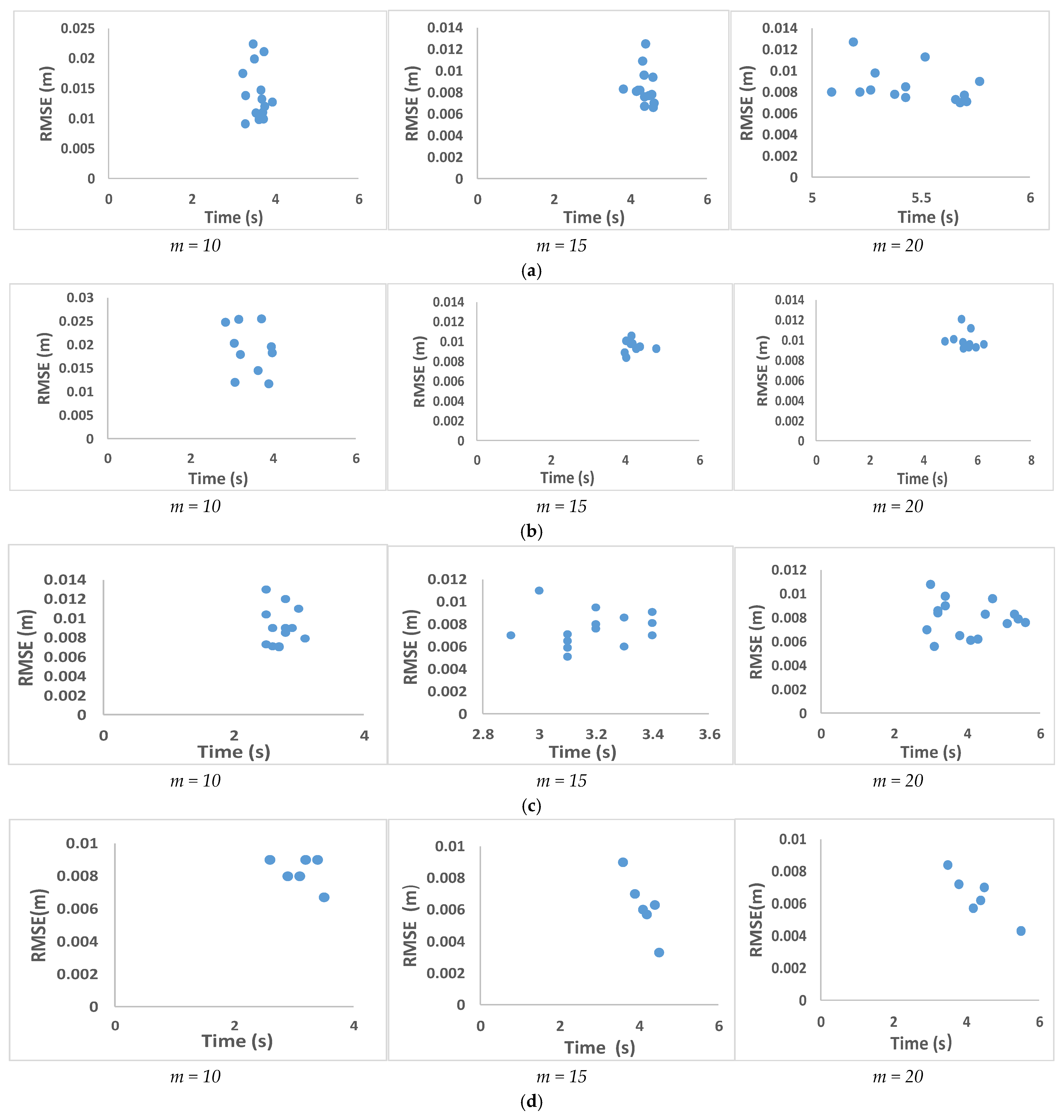
- Use the descriptor from (13) to judge the n points sampled and retain the points that satisfy (13). Otherwise, continue sampling until the final number of retained sampling points reaches m pairs. (The value of m is discussed in Section 4 of the paper).
- According to Equations (10)–(12), construct the corresponding feature sphere in the moving point cloud and calculate the center and radius of the sphere.
2.2.3. Identifying Optimal Registration
2.3. Point Cloud Model Reconstruction
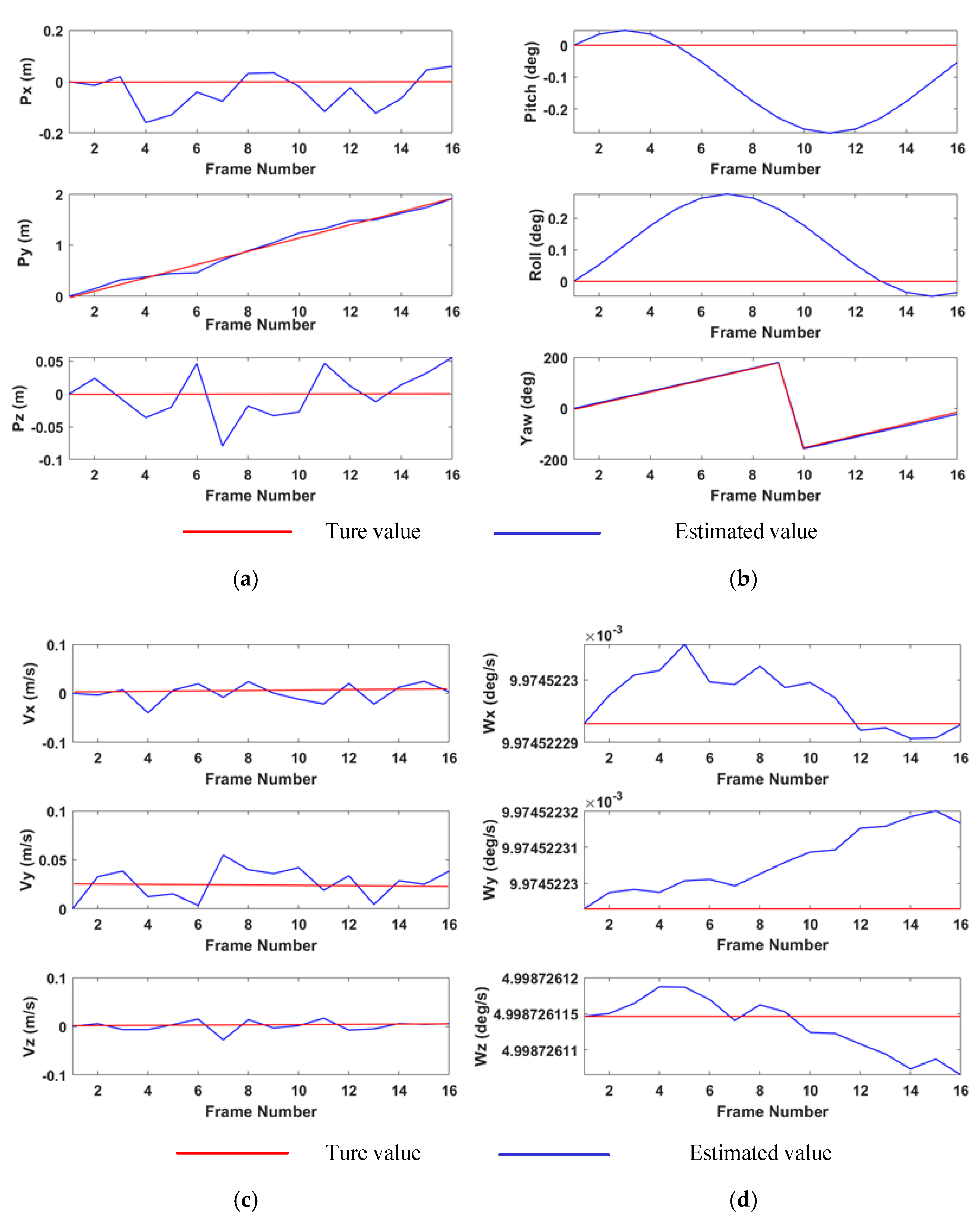
2.4. Estimation of Attitude and Motion Parameters
| Algorithm 1. UKF Algorithm | |
| Input: | State variable at time k , covariance matrix |
| Output: | At time k+1 , |
| Initial value: | , |
| Iteration process | |
| Step 1: | Convert the pose quaternion into the error twistor , and perform sigma sampling on it |
| Step 2: | Convert the sigma sample point of the error twistor into a pose dual quaternion, and obtain a new prediction point through the state equation |
| Step 3: | Determine the mean and covariance of the predicted points , , and |
| Step 4: | Obtain the new observation point mean and covariance through the observation equations , , and |
| Step 5: | Determine the Kalman gain for the UKF using and |
| Step 6: | Update the status according to and |
3. Experimental Results and Analysis
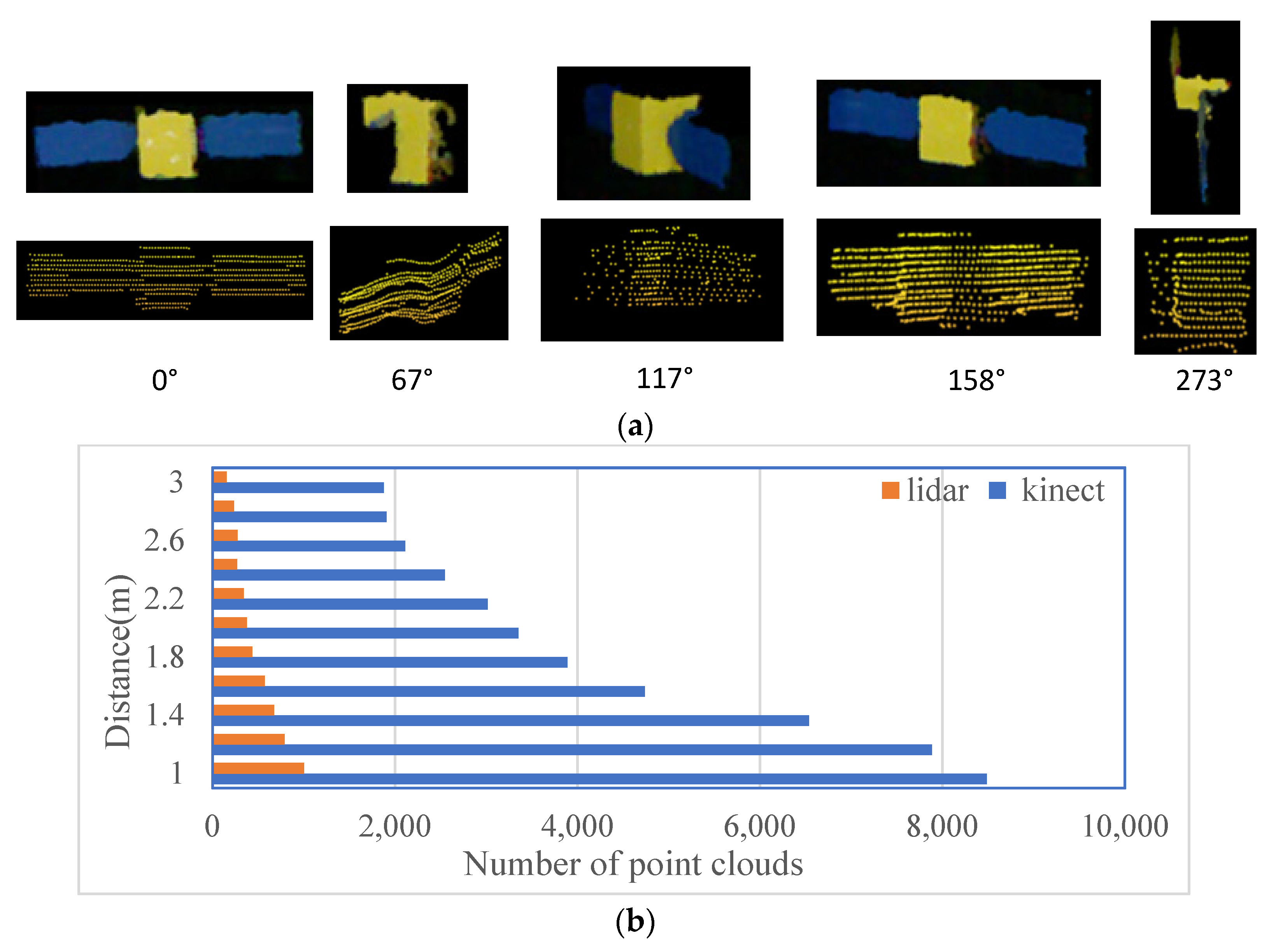
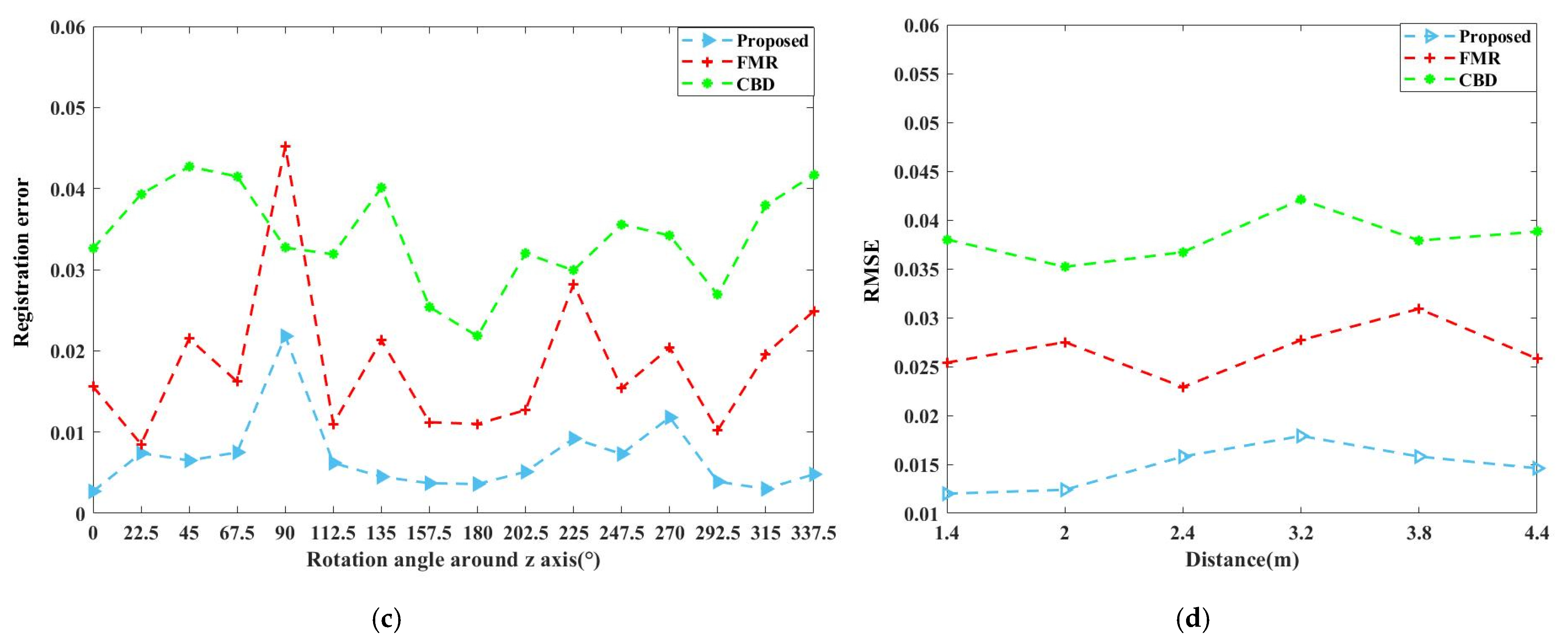
3.1. Numerical Simulation
- Step 1:
- Set the positions of the Kinect and LiDAR sensors in the Blendor software, and select the appropriate sensor parameters. Table 2 lists the sensor parameter settings for the numerical simulation in this study.
- Step 2:
- Rotate the satellite model once around the z axis (inertial coordinate system), and collect 16 frames of point cloud in 22.5° yaw angle increments.
- Step 3:
- Use the proposed fusion algorithm to register the point clouds collected by the two sensors.
- Step 4:
- Rotate the satellite model around the x axis or y axis, and repeat steps 2–4.
- Step 5:
- Adjust the distance between the two sensors and the satellite model, and repeat steps 2–5.
- Step 6:
- Use the root mean square error (RMSE) to verify the effectiveness of the algorithm.
3.1.1. Registration Results
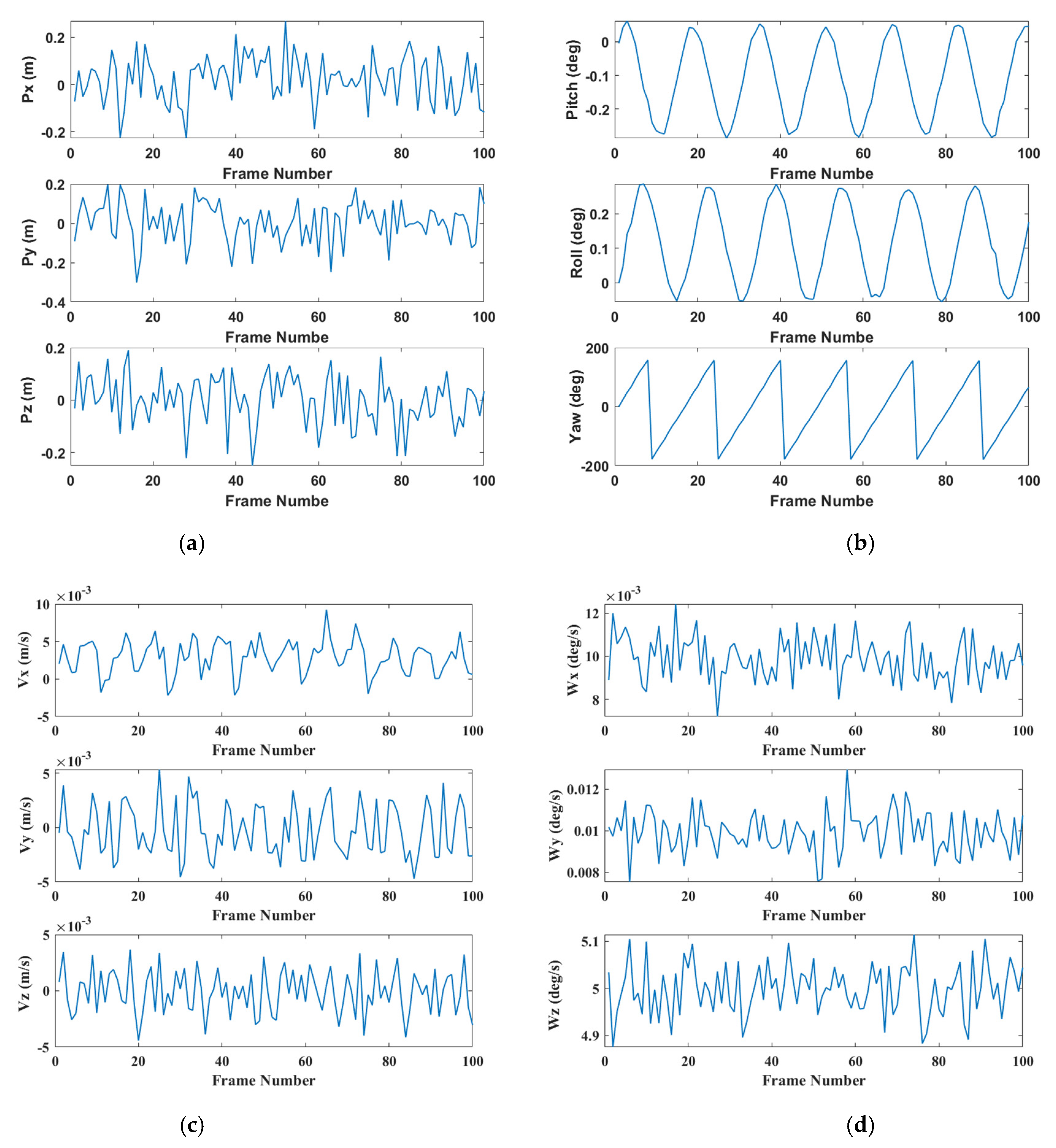
3.1.2. Pose Estimation Results of Simulated Point Clouds
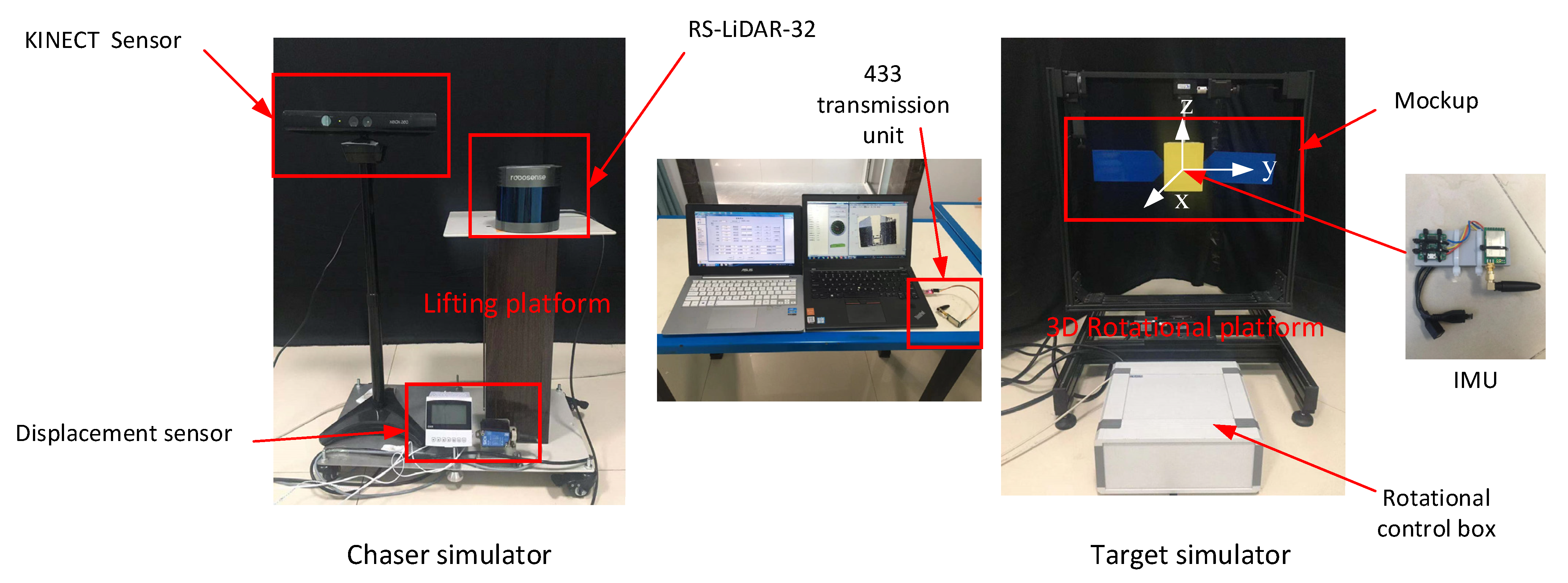
3.2. Semi-Physical Experiment and Analysis
3.2.1. Experimental Environment Setup
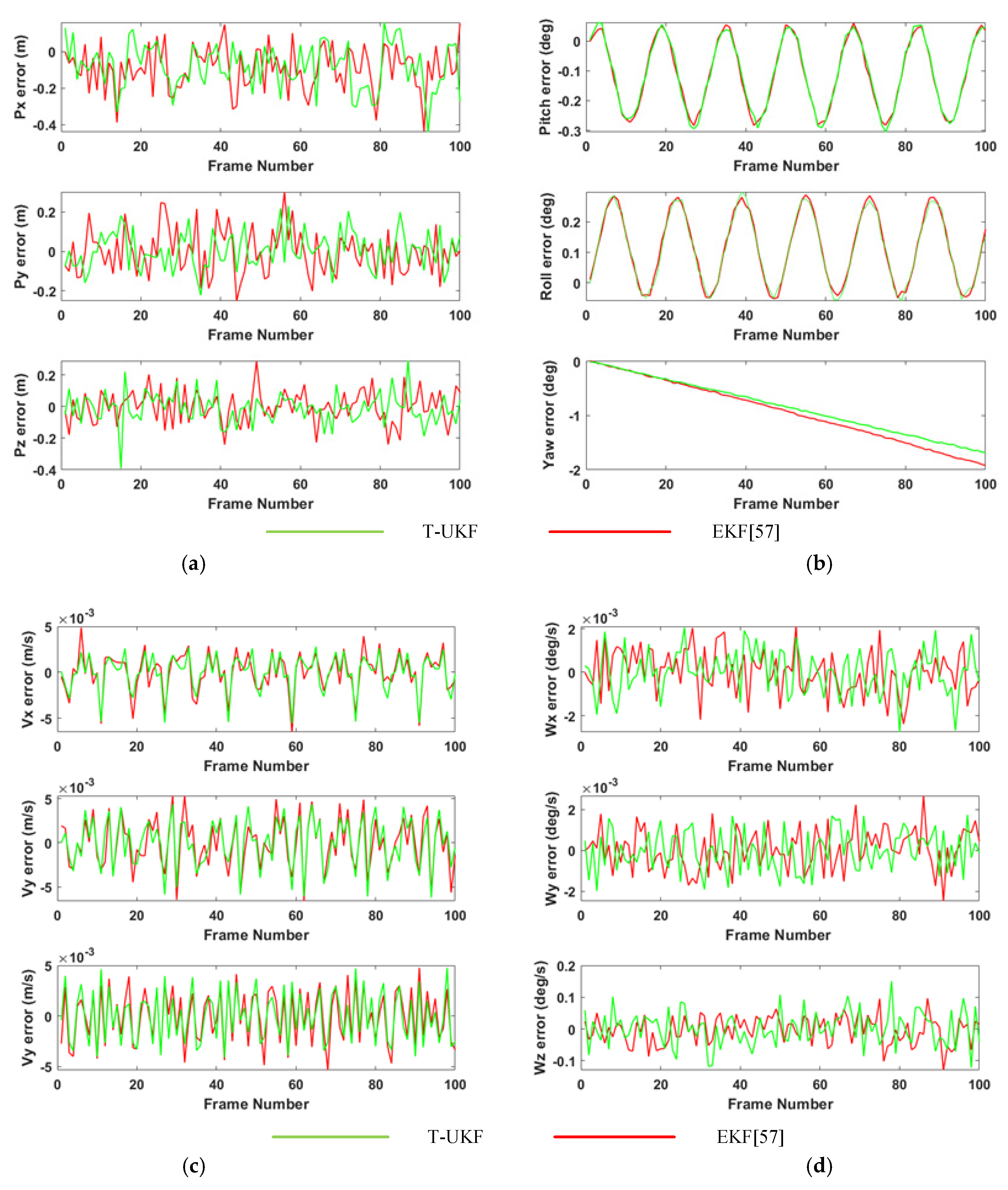
3.2.2. Results of Semi-Physical Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, P.; Liu, J.; Wu, C. Survey on research and development of on-orbit active debris removal methods. Sci. China Ser. E Technol. Sci. 2020, 63, 2188–2210. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Y.; Wang, Y.; Xu, K. A review of structures, verification, and calibration technologies of space robotic systems for on-orbit servicing. Sci. China Ser. E Technol. Sci. 2021, 64, 462–480. [Google Scholar] [CrossRef]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. A review of cooperative and uncooperative spacecraft pose determination techniques for close-proximity operations. Prog. Aerosp. Sci. 2017, 93, 53–72. [Google Scholar] [CrossRef]
- Yingying, G.; Li, W. Fast-swirl space non-cooperative target spin state measurements based on a monocular camera. Acta Astronaut. 2019, 166, 156–161. [Google Scholar] [CrossRef]
- Vincenzo, C.; Kyunam, K.; Alexei, H.; Soon-Jo, C. Monocular-based pose determination of uncooperative space objects. Acta Astronaut. 2020, 166, 493–506. [Google Scholar] [CrossRef]
- Cassinis, L.P.; Fonod, R.; Gill, E.; Ahrns, I.; Gil-Fernández, J. Evaluation of tightly- and loosely-coupled approaches in CNN-based pose estimation systems for uncooperative spacecraft. Acta Astronaut. 2021, 182, 189–202. [Google Scholar] [CrossRef]
- Yin, F.; Wusheng, C.; Wu, Y.; Yang, G.; Xu, S. Sparse Unorganized Point Cloud Based Relative Pose Estimation for Uncooperative Space Target. Sensors 2018, 18, 1009. [Google Scholar] [CrossRef]
- Lim, T.W.; Oestreich, C.E. Model-free pose estimation using point cloud data. Acta Astronaut. 2019, 165, 298–311. [Google Scholar] [CrossRef]
- Nocerino, A.; Opromolla, R.; Fasano, G.; Grassi, M. LIDAR-based multi-step approach for relative state and inertia parameters determination of an uncooperative target. Acta Astronaut. 2021, 181, 662–678. [Google Scholar] [CrossRef]
- Zhao, D.; Sun, C.; Zhu, Z.; Wan, W.; Zheng, Z.; Yuan, J. Multi-spacecraft collaborative attitude determination of space tumbling target with experimental verification. Acta Astronaut. 2021, 185, 1–13. [Google Scholar] [CrossRef]
- Masson, A.; Haskamp, C.; Ahrns, I.; Brochard, R.; Duteis, P.; Kanani, K.; Delage, R. Airbus DS Vision Based Navigation solutions tested on LIRIS experiment data. J. Br. Interplanet. Soc. 2017, 70, 152–159. [Google Scholar]
- Perfetto, D.M.; Opromolla, R.; Grassi, M.; Schmitt, C. LIDAR-based model reconstruction for spacecraft pose determination. In Proceedings of the 2019 IEEE 5th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Torino, Italy, 19–21 June 2019. [Google Scholar]
- Wang, Q.L.; Li, J.Y.; Shen, H.K.; Song, T.T.; Ma, Y.X. Research of Multi-Sensor Data Fusion Based on Binocular Vision Sensor and Laser Range Sensor. Key Eng. Mater. 2016, 693, 1397–1404. [Google Scholar] [CrossRef]
- Ordóñez, C.; Arias, P.; Herráez, J.; Rodriguez, J.; Martín, M.T. A combined single range and single image device for low-cost measurement of building façade features. Photogramm. Rec. 2008, 23, 228–240. [Google Scholar] [CrossRef]
- Wu, K.; Di, K.; Sun, X.; Wan, W.; Liu, Z. Enhanced Monocular Visual Odometry Integrated with Laser Distance Meter for Astronaut Navigation. Sensors 2014, 14, 4981–5003. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Zhao, R.; Liu, E.; Yan, K.; Ma, Y. Scale Estimation and Correction of the Monocular Simultaneous Localization and Mapping (SLAM) Based on Fusion of 1D Laser Range Finder and Vision Data. Sensors 2018, 18, 1948. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Xu, S.; Bo, Y. LiDAR-Based Non-Cooperative Tumbling Spacecraft Pose Tracking by Fusing Depth Maps and Point Clouds. Sensors 2018, 18, 3432. [Google Scholar] [CrossRef] [Green Version]
- Padial, J.; Hammond, M.; Augenstein, S.; Rock, S.M. Tumbling target reconstruction and pose estimation through fusion of monocular vision and sparse-pattern range data. In Proceedings of the 2012 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Hamburg, Germany, 13–15 September 2012; pp. 419–425. [Google Scholar]
- Zhang, Z.; Zhao, R.; Liu, E.; Yan, K.; Ma, Y.; Xu, Y. A fusion method of 1D laser and vision based on depth estimation for pose estimation and reconstruction. Robot. Auton. Syst. 2019, 116, 181–191. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, J.; Fan, L.; Wu, Q.; Yuan, C. A Systematic Approach for Cross-Source Point Cloud Registration by Preserving Macro and Micro Structures. IEEE Trans. Image Process. 2017, 26, 3261–3276. [Google Scholar] [CrossRef]
- Huang, X.; Mei, G.; Zhang, J. A comprehensive survey on point cloud registration. arXiv 2021, arXiv:2103.02690. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Tombari, F.; Salti, S.; Di Stefano, L. Unique signatures of histograms for local surface description. In Integer Programming and Combinatorial Optimization; Springer: London, UK, 2010; pp. 356–369. [Google Scholar]
- Frome, A.; Huber, D.; Kolluri, R.; Bülow, T.; Malik, J. Recognizing objects in range data using regional point descriptors. In Proceedings of the 8th European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 224–237. [Google Scholar]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Multi-scale EM-ICP: A fast and robust approach for surface registration. In Proceedings of the Computer Vision—ECCV 2002, 7th European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002.
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-ICP. In Proceedings of the Robotics: Science and Systems V, University of Washington, Seattle, WA, USA, 28 June–1 July 2009. [Google Scholar]
- He, Y.; Liang, B.; Yang, J.; Li, S.; He, J. An Iterative Closest Points Algorithm for Registration of 3D Laser Scanner Point Clouds with Geometric Features. Sensors 2017, 17, 1862. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.; Liu, T.; Han, X. Improved Iterative Closest Point (ICP) 3D point cloud registration algorithm based on point cloud filtering and adaptive fireworks for coarse registration. Int. J. Remote Sens. 2020, 41, 3197–3220. [Google Scholar] [CrossRef]
- Biber, P. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar]
- Yang, J.; Li, H.; Campbell, D.; Jiaolong, Y. Go-ICP: A Globally Optimal Solution to 3D ICP Point-Set Registration. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2241–2254. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Wang, C.; Song, Z.; Wang, M. Efficient global point cloud registration by matching rotation invariant features through translation search. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 448–463. [Google Scholar]
- Chen, S.; Nan, L.; Xia, R.; Zhao, J.; Wonka, P. PLADE: A Plane-Based Descriptor for Point Cloud Registration with Small Overlap. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2530–2540. [Google Scholar] [CrossRef]
- Huang, X.; Mei, G.; Zhang, J. Feature-metric registration: A fast semi-supervised approach for robust point cloud registration without correspondences. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–18 June 2020; pp. 11363–11371. [Google Scholar] [CrossRef]
- Cao, W.; Lyu, F.; He, Z.; Cao, G.; He, Z. Multimodal Medical Image Registration Based on Feature Spheres in Geometric Algebra. IEEE Access 2018, 6, 21164–21172. [Google Scholar] [CrossRef]
- Kleppe, A.L.; Tingelstad, L.; Egeland, O. Coarse Alignment for Model Fitting of Point Clouds Using a Curvature-Based Descriptor. IEEE Trans. Autom. Sci. Eng. 2018, 16, 811–824. [Google Scholar] [CrossRef]
- Li, J.; Zhuang, Y.; Peng, Q.; Zhao, L. Band contour-extraction method based on conformal geometrical algebra for space tumbling targets. Appl. Opt. 2021, 60, 8069. [Google Scholar] [CrossRef]
- Peng, F.; Wu, Q.; Fan, L.; Zhang, J.; You, Y.; Lu, J.; Yang, J.-Y. Street view cross-sourced point cloud matching and registration. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 2026–2030. [Google Scholar]
- Li, H.; Hestenes, D.; Rockwood, A. Generalized Homogeneous Coordinates for Computational Geometry; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2001; pp. 27–59. [Google Scholar]
- Perwass, C.; Hildenbrand, D. Aspects of Geometric Algebra in Euclidean, Projective and Conformal Space. 2004. Available online: https://www.uni-kiel.de/journals/receive/jportal_jparticle_00000165 (accessed on 24 September 2021).
- Yuan, L.; Yu, Z.; Luo, W.; Zhou, L.; Lü, G. A 3D GIS spatial data model based on conformal geometric algebra. Sci. China Earth Sci. 2011, 54, 101–112. [Google Scholar] [CrossRef]
- Duben, A.J. Geometric algebra with applications in engineering. Comput. Rev. 2010, 51, 292–293. [Google Scholar]
- Marani, R.; Renò, V.; Nitti, M.; D’Orazio, T.; Stella, E. A Modified Iterative Closest Point Algorithm for 3D Point Cloud Registration. Comput. Civ. Infrastruct. Eng. 2016, 31, 515–534. [Google Scholar] [CrossRef] [Green Version]
- Censi, A. An ICP variant using a point-to-line metric. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 19–25. [Google Scholar]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Aiger, D.; Mitra, N.J.; Cohen-Or, D. 4-points congruent sets for robust pairwise surface registration. In Proceedings of the ACM SIGGRAPH 2008 Papers on—SIGGRAPH ’08, Los Angeles, CA, USA, 11–15 August 2008; ACM Press: New York, NY, USA, 2008; Volume 27, p. 85. [Google Scholar]
- Li, H.B. Conformal geometric algebra—A new framework for computational geometry. J. Comput. Aided Des. Comput. Graph. 2005, 17, 2383. [Google Scholar] [CrossRef]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-Squares Fitting of Two 3-D Point Sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 698–700. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Umeyama, S. Least-squares estimation of transformation parameters between two point patterns. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 376–380. [Google Scholar] [CrossRef] [Green Version]
- Valkenburg, R.; Dorst, L. Estimating motors from a variety of geometric data in 3D conformal geometric algebra. In Guide to Geometric Algebra in Practice; Springer: London, UK, 2011; pp. 25–45. [Google Scholar] [CrossRef]
- Lasenby, J.; Fitzgerald, W.J.; Lasenby, A.N.; Doran, C.J. New Geometric Methods for Computer Vision. Int. J. Comput. Vis. 1998, 26, 191–216. [Google Scholar] [CrossRef]
- Alexander, A.L.; Hasan, K.; Kindlmann, G.; Parker, D.L.; Tsuruda, J.S. A geometric analysis of diffusion tensor measurements of the human brain. Magn. Reson. Med. 2000, 44, 283–291. [Google Scholar] [CrossRef]
- Ritter, M.; Benger, W.; Cosenza, B.; Pullman, K.; Moritsch, H.; Leimer, W. Visual data mining using the point distribution tensor. In Proceedings of the International Conference on Systems, Vienna, Austria, 11–13 April 2012; pp. 10–13. [Google Scholar]
- Lu, X.; Liu, Y.; Li, K. Fast 3D Line Segment Detection from Unorganized Point Cloud. arXiv 2019, arXiv:1901.02532v1. [Google Scholar]
- Lefferts, E.; Markley, F.; Shuster, M. Kalman Filtering for Spacecraft Attitude Estimation. J. Guid. Control. Dyn. 1982, 5, 417–429. [Google Scholar] [CrossRef]
- Martínez, H.G.; Giorgi, G.; Eissfeller, B. Pose estimation and tracking of non-cooperative rocket bodies using Time-of-Flight cameras. Acta Astronaut. 2017, 139, 165–175. [Google Scholar] [CrossRef]
- Kang, G.; Zhang, Q.; Wu, J.; Zhang, H. Pose estimation of a non-cooperative spacecraft without the detection and recognition of point cloud features. Acta Astronaut. 2021, 179, 569–580. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Xie, Y. Using consecutive point clouds for pose and motion estimation of tumbling non-cooperative target. Adv. Space Res. 2019, 63, 1576–1587. [Google Scholar] [CrossRef]
- De Jongh, W.; Jordaan, H.; Van Daalen, C. Experiment for pose estimation of uncooperative space debris using stereo vision. Acta Astronaut. 2020, 168, 164–173. [Google Scholar] [CrossRef]
- Opromolla, R.; Nocerino, A. Uncooperative Spacecraft Relative Navigation With LIDAR-Based Unscented Kalman Filter. IEEE Access 2019, 7, 180012–180026. [Google Scholar] [CrossRef]
- Yunli, W.; Guangren, D. Design of Luenberger function observer with disturbance decoupling for matrix second-order linear systems-a parametric approach. J. Syst. Eng. Electron. 2006, 17, 156–162. [Google Scholar] [CrossRef]
- Hestenes, D. New tools for computational geometry and rejuvenation of screw theory. In Geometric Algebra Computing; Springer-Verlag London Limited: London, UK, 2010; p. 3. ISBN 978-1-84996-107-3. [Google Scholar]
- Hestenes, D.; Fasse, E.D. Homogeneous rigid body mechanics with elastic coupling. In Applications of Geometric Algebra in Computer Science and Engineering; Birkhauser: Boston, MA, USA, 2002; ISBN 978-1-4612-6606-8. [Google Scholar]
- Deng, Y. Spacecraft Dynamics and Control Modeling Using Geometric Algebra. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2016. [Google Scholar]
- Weiss, A.; Baldwin, M.; Erwin, R.S.; Kolmanovsky, I. Model Predictive Control for Spacecraft Rendezvous and Docking: Strategies for Handling Constraints and Case Studies. IEEE Trans. Control Syst. Technol. 2015, 23, 1638–1647. [Google Scholar] [CrossRef]
- Gschwandtner, M.; Kwitt, R.; Uhl, A.; Pree, W. BlenSor: Blender sensor simulation toolbox. In Lecture Notes in Computer Science; Springer Science and Business Media LLC: London, UK, 2011; pp. 199–208. [Google Scholar]


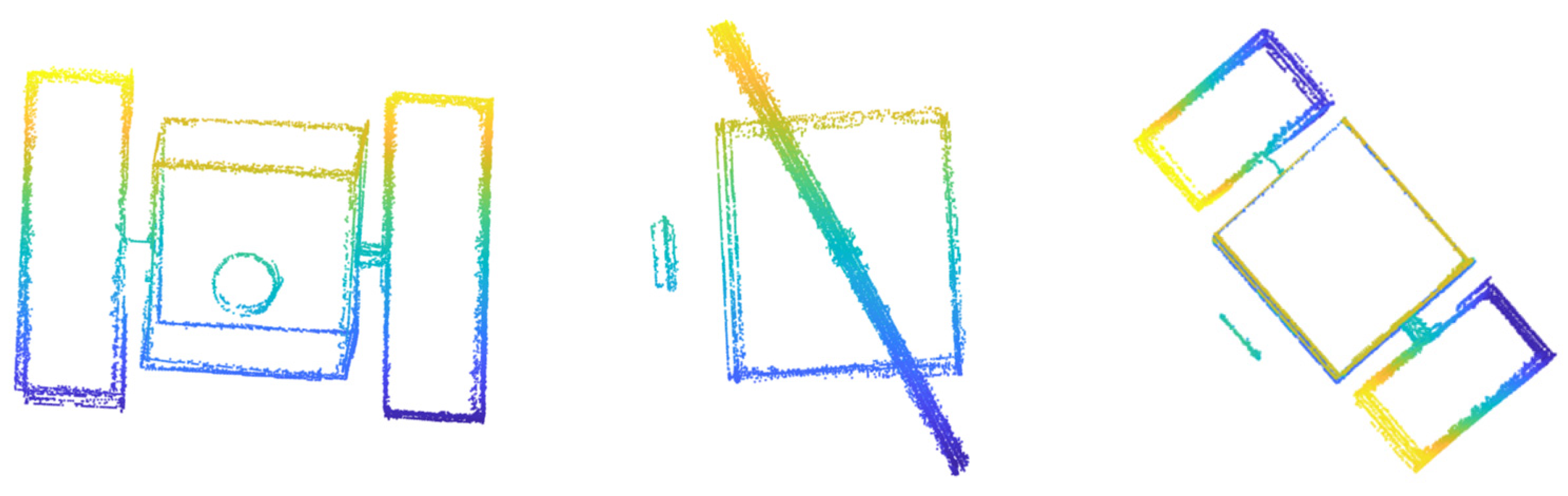



| Geometric Objects | Geometric Shape | Inner Product Representation |
|---|---|---|
| Point and point | 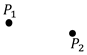 | |
| Point and plane | 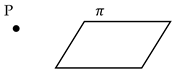 | |
| Plane and sphere | 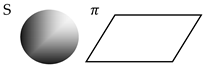 | |
| Sphere and sphere |  |
| Sensor | Parameter | Value |
|---|---|---|
| Kinect 1.0 | Resolution | 640 px × 480 px |
| Focal Length | 4.73 mm | |
| FOV (V,H) | (43°, 57°) | |
| Scan Distance | 1–6 m | |
| Velodyne HDL-64 | Scan Resolution | (0.08°–0.35°) H |
| 0.4° V | ||
| Scan Distance | 120 m | |
| FOV (V) | 26.9° |
| Parameter | Symbol | Value |
|---|---|---|
| Initial relative position | (0, 0, 0) m | |
| Initial relative velocity | (0, 0, 0) m/s | |
| Orbit altitude (circular orbit) | 0.2 m | |
| Initial Euler angle | (0, 0, 0) | |
| Initial angular velocity | (0, 0, 5) °/s | |
| Sensor acquisition frequency | 0.22 Hz | |
| Frame number | 16 |
| Cloud | Depth | Range of Detection | Depth Uncertainty | Angle | |||
|---|---|---|---|---|---|---|---|
| Resolution | FPS | Resolution | FPS | Horizontal | Vertical | ||
| 640 × 480 | 30 | 320 × 240 (16 bit) | 30 | 0.8–6.0 m | 2–30 mm | 57° | 43° |
| Channel Number | Rotation Speed | Scan Distance | FOV | Angular Resolution | ||
|---|---|---|---|---|---|---|
| Vertical | Horizontal | Vertical | Horizontal | |||
| 32 nonlinear | 300/600/1200 rpm | 0.4–200 m | −25°~+15° | 360° | 0.33° | 0.1°~0.4° |
| Average Number of Point Clouds in a Frame (Kinect/LIDAR) | Our Method (s) | FMR [34] (s) | CBD [36] (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Rotate Around x axis | Rotate Around y axis | Rotate Around z axis | Rotate Around x axis | Rotate Around y axis | Rotate Around z axis | Rotate Around x axis | Rotate Around y axis | Rotate Around z axis | |
| 1239/126 | 3.06 | 3.46 | 3.60 | 2.06 | 2.01 | 2.56 | 5.79 | 5.60 | 6.17 |
| 1724/217 | 3.18 | 3.57 | 3.91 | 2.15 | 2.96 | 2.96 | 5.41 | 6.54 | 6.29 |
| 2653/358 | 3.43 | 3.31 | 4.18 | 2.40 | 3.29 | 3.06 | 6.32 | 6.38 | 6.33 |
| 4496/641 | 4.20 | 3.78 | 3.73 | 2.43 | 3.75 | 3.76 | 6.70 | 6.25 | 7.05 |
| 7921/951 | 4.10 | 4.35 | 4.27 | 3.18 | 3.09 | 3.92 | 6.19 | 6,06 | 7.10 |
| 8105/828 | 3.99 | 3.89 | 4.51 | 3.26 | 4.56 | 4.75 | 6.82 | 6.14 | 7.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhuang, Y.; Peng, Q.; Zhao, L. Pose Estimation of Non-Cooperative Space Targets Based on Cross-Source Point Cloud Fusion. Remote Sens. 2021, 13, 4239. https://doi.org/10.3390/rs13214239
Li J, Zhuang Y, Peng Q, Zhao L. Pose Estimation of Non-Cooperative Space Targets Based on Cross-Source Point Cloud Fusion. Remote Sensing. 2021; 13(21):4239. https://doi.org/10.3390/rs13214239
Chicago/Turabian StyleLi, Jie, Yiqi Zhuang, Qi Peng, and Liang Zhao. 2021. "Pose Estimation of Non-Cooperative Space Targets Based on Cross-Source Point Cloud Fusion" Remote Sensing 13, no. 21: 4239. https://doi.org/10.3390/rs13214239
APA StyleLi, J., Zhuang, Y., Peng, Q., & Zhao, L. (2021). Pose Estimation of Non-Cooperative Space Targets Based on Cross-Source Point Cloud Fusion. Remote Sensing, 13(21), 4239. https://doi.org/10.3390/rs13214239






