Abstract
Rice is considered one of the most important crops in the world. According to the Food and Agriculture Organization of the United Nations (FAO), rice production has increased significantly (156%) during the last 50 years, with a limited increase in cultivated area (24%). With the recent advances in remote sensing technologies, it is now possible to monitor rice crop production for a better understanding of its management at field scale to ultimately improve rice yields. In this work, we monitor within-field rice production of the two main rice varieties grown in Valencia (Spain) JSendra and Bomba during the 2020 season. The sowing date of both varieties was May 22–25, while the harvesting date was September 15–17 for Bomba and October 5–8 for JSendra. Rice yield data was collected over 66.03 ha (52 fields) by harvesting machines equipped with onboard sensors that determine the dry grain yield within irregular polygons of 3–7 m width. This dataset was split in two, selecting 70% of fields for training and 30% for validation purposes. Sentinel-2 surface reflectance spectral data acquired from May until September 2020 was considered over the test area at the two different spatial resolutions of 10 and 20 m. These two datasets were combined assessing the best combination of spectral reflectance bands (SR) or vegetation indices (VIs) as well as the best timing to infer final within-field yields. The results show that SR improves the performance of models with VIs. Furthermore, the correlation of each spectral band and VIs with the final yield changes with the dates and varieties. Considering the training data, the best correlation with the yields is obtained on July 4, with R2 for JSendra of 0.72 at 10 m and 0.76 at 20 m resolution, while the R2 for Bomba is 0.87 at 10 m and 0.92 at 20 m resolution. Based on the validation dataset, the proposed models provide within-field yield modelling Mean Absolute Error (MAE) of 0.254 t⋅ha−1 (Mean Absolute Percentage Error, MAPE, of 3.73%) for JSendra at 10 m (0.240 t⋅ha−1; 3.48% at 20 m) and 0.218 t⋅ha−1 (MAPE 5.82%) for Bomba (0.223 t⋅ha−1; 5.78% at 20 m) on July 4, that is three months before harvest. At parcel level the model’s MAE is 0.176 t⋅ha−1 (MAPE 2.61%) for JSendra and 0.142 t⋅ha−1 (MAPE 4.51%) for Bomba. These results confirm the close correlation between the rice yield and the spectral information from satellite imagery. Additionally, these models provide a timeliness overview of underperforming areas within the field three months before the harvest where farmers can improve their management practices. Furthermore, it highlights the importance of optimum agronomic management of rice plants during the first weeks of rice cultivation (40–50 days after sowing) to achieve high yields.
1. Introduction
Rice (Oryza sativa L.) is one of the three most important crops in the world, being vital for the world’s food supply. Rice is grown in Asia, America, Australia, Europe, and Africa, following diverse production practices. In 2019, the global rice production was close to 755 million tons, covering an area of 162 million hectares. In Europe, its production is mostly located in the southern countries, Spain being one of the major producers and representing approximately 28% of the total production across the European Union in 2019 [1]. The Valencian Community produces 16% (125 thousand tons) of the national rice, covering an area of approximately 15 thousand hectares in 2019 [2]. During the last 50 years, world rice production has increased by 156%, while the cultivated area has only increased by 24%, resulting in a 107% increase in yield. The evolution of world population growth and the increase in rice production have been closely connected over the last 50 years [1]. According to the latest United Nations’ forecasts for the next 50 years, the world population could increase by 35% [3], which means that rice production must continue increasing. Given that the statistics of the last five decades show that the cultivated area has hardly changed, the required increase in rice production must imply an increase in yield [4].
Earth observation (EO) data allow efficient monitoring of crop growth at field scale owning to its high spatial (~10 m) and temporal (each 5 days) resolutions (e.g., [5,6,7]). The launch of the ESA optical high-resolution missions Sentinel-2A in 2015 and Sentinel-2B in 2017 and their fusion with Landsat providing free high-frequency and high-resolution data, along with the significant advances in big data analytics and high-performance computing, have revolutionized the EO uptake for agriculture applications. Recent works have shown that satellite data can be used to infer crop yields both within-field and at field scales. For instance, Skakun [8] showed that corn and soybean yield variability could be explained using Planet 3 m spatial resolution while the coarser resolution of Sentinel-2 (10 m) reduces the explained yield variability by 14%. The same study also concluded that the most important spectral bands explaining the yield variability are green, red edge and Near Infrared (NIR) but the lower correlation obtained for high yields suggested saturation of multi-spectral optical data. Kayad [9] investigated different Vegetation Indices (VI) from Sentinel-2 and machine learning techniques to assess corn yield within the field scale. Their study selected as the best VI the Green Normalized Difference Vegetation Index (GNDVI), which integrated into a Random Forest provided an R2 of 0.60 over an independent validation test. Zhao [10] tested a set of VI from Sentinel-2 to estimate wheat yield at the field scale. Deines [11] applied the Scalable Crop Yield Mapper (SCYM) [12] to over one million corn fields yield observations spanning nine states in the US Corn Belt and based on Landsat observations. Their results showed that remote sensing technology at within-field scale show coefficients of determination of 0.40 and increase to 0.45 and 0.69 when aggregated to field level and county level scales, respectively.
Focusing on rice crops, the Asia-RiCE initiative [13] is the rice monitoring component of the Group on Earth Observations Global Agricultural Monitoring initiative (GEOGLAM) [14]. Its main goal is to foster the use of EO, leveraging existing agricultural monitoring programs and initiatives for rice monitoring at national, regional and global scales as an input to the GEOGLAM Crop Monitor [15] and the Agricultural Market Information System (AMIS) Market Monitor [16]. EO technologies have proven to be useful in monitoring rice crops biophysical and biochemical properties pushing towards a more efficient farming management. The implementation of remote sensing technologies in rice farming has evident advantages in monitoring rice growth, soil fertility evaluation, detection of diseases, and yield estimation, among others. Previous works have shown that the growth of the rice crops, as well as the nitrogen content, can be inferred based on the spectral reflectance from EO sensors. For instance, Cai [17] showed that the Normalized Difference Vegetation Index (NDVI) or the Green NDVI (GDVI) can be used to monitor the nitrogen content of rice crops. Shi [18] studied the use of different VIs to map the distribution of rice diseases such as rice blast. In fact, several studies (e.g. [19,20,21]) show that the NIR spectral region is sensitive enough to detect the first symptoms produced by rice blast, and other studies show how remote sensing data can be used to monitor the nitrogen deficit in rice (e.g., [22,23]). Regarding rice yield monitoring, Gilardelli [24] assimilated Leaf Area Index (LAI) data from Landsat and Sentinel-2 at 30 m spatial resolution into the WARM rice model [25] to derive within-field rice yields in Italy with a Mean Absolute Error (MAE) of 0.66 t⋅ha−1 and Relative Root Mean Square Error (RRMSE) of 13.8%. Finally, an extensive overview on rice yield estimation or forecasting based on EO can be found in Mosleh [26]. One of the major challenges in rice monitoring over Asia is the high frequency of cloud coverage. Therefore, most of the works based on this area use synthetic aperture radar (SAR) for rice yield monitoring (e.g. [27,28,29]). Other works use optical data based on VI that are then related to forecast rice yields mostly at regional level using coarse resolution data (MODIS [30,31], SPOT-4 [32] or AVHRR [33]) or medium resolution (Landsat [34]). However, most works or rice yield monitoring are applied at regional scale or at parcel level and there are essentially no works on rice yield estimation at within-field scale. Additionally, VIs are widely used as inputs for the yield models, and Skakun [8] showed that surface reflectance-based models outperformed VI-based models highlighting the importance of incorporating surface reflectance (SR) values directly into the yield models. Therefore, in this work we aim to expand the science of rice yield monitoring at within-field scale, testing all spectral information retrieved by Sentinel-2. Particularly, the main science questions that we aim to answer in this study are: To what degree can EO data in the optical spectral region explain the rice within-field yield variability? Which spectral band or combination of bands is better correlated with the final yield? When is the most critical timing of the rice growing season when satellite imagery can explain the final yields?
In this work we present a study to monitor rice within-field yield variability. It is based on multi-spectral SR data retrieved by Sentinel-2 and rice yield maps acquired with harvesting machines over 52 fields covering a total area of 66ha in Valencia (Spain) during the 2020 season.
2. Materials and Methods
2.1. Study Area
The coastal wetland Albufera is located at the Mediterranean Spanish coast and south of Valencia city (39°20′ N, 0°21′ W). The wetland has an area of 211.2 km2 and is bordered by the Turia (north) and Jucar (south) rivers. The Albufera is the second largest lake in the Iberian Peninsula with an area of 23.2 km2. It is shallow (1.2 m of mean depth) and has a mean salinity of 1–2%. The European Commission [35] considers the Albufera a special protected area in the Natura 2000 network and restricts agriculture practices in the area to only rice crops. This area has a typical Mediterranean climate, with an annual mean air temperature and humidity of 18.3 ± 0.1 °C and 65.0 ± 0.5%, respectively [36]. Annual rainfall is usually concentrated in the spring and autumn seasons. The water level of the lake is regulated by a large network of irrigation channels that connect it to the rice fields and to the Mediterranean Sea. This area can be considered a homogeneous rice planting area of approximately 10 × 20 km2 extension.
JSendra and Bomba common japonica-type Spanish rice varieties (Oryza sativa var.japonica), were used in the experiment. The most commercial cultivar in East Spain (Valencia) is JSendra (cross between M202 and Senia in 2005 by Instituto Valenciano de Investigaciones Agrarias, IVIA), characterized by high yields (typically 7.5–8.0 t⋅ha−1) and good culinary quality. Bomba is a traditional rice variety, obtained by selection in 1929 in Valencia, and it is characterized by low yields (typically 3.5–4.0 t⋅ha−1) and excellent culinary quality. The differences in performance between the two varieties are significant: JSendra plants have a greater number of tillers, a lower height, and a longer season than Bomba plants. The planted area of JSendra in 2020 was 6716 ha (44%), while in Bomba’s planted area was 1777 ha (12%). Table 1 shows the timing of the main stages of both varieties in Valencia.

Table 1.
Timing of the main phenological stages of rice in Valencia.
2.2. Field Data Pre-Processing
Field data was collected by harvesting machines and provide dry volumetric yield in irregular polygons as shown in Figure 1A. These data were preprocessed to remove errors in the software acquisition such as turns, overlaps (keeping the first overpass) and extreme values (JSendra: >11.0 t⋅ha−1; Bomba: >7.0 t⋅ha−1) that had no biological meaning [37]. Additionally, we removed small sized polygons with extreme values compared to the neighbors [38]. Given the noise observed in the dataset, these data were aggregated to an intermediate 5 m resolution (Figure 1B) to apply a grid moving average filter of 7 × 7 pixels (Figure 1C). Finally, this dataset was aggregated to 10 m resolution removing the edge pixels (Figure 1D).
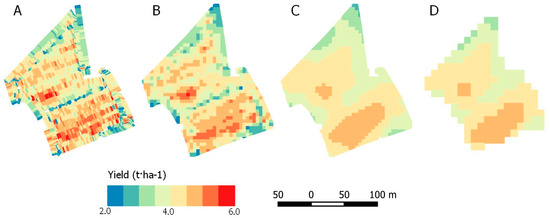
Figure 1.
Example of the harvester data curation of a Bomba rice field within the training samples being (A) the original harvester machine data, (B) the 5 m aggregated data, (C) the 5 m aggregated data after applying the grid moving average filter and (D) picture C aggregated to 10 m.
2.3. Satellite Data
We downloaded Sentinel-2A and Sentinel-2B data covering the main rice area in Valencia, that is using the tiles 30SYJ and 31SBD, from May until September 2020 and we applied the atmospheric correction algorithm LaSRC [39]. All the Sentinel-2 spectral bands at 10 m and 20 m spatial resolution were analyzed to select the best combination to infer rice crop yield. Table 2 shows the spectral response and spatial resolution of the considered bands.

Table 2.
Sentinel-2 bands analyzed in this study.
2.4. Methods
The two rice varieties were treated separately. For each variety, 70% of the data was randomly selected as training data and 30% of data was kept for validation purposes (Table 3). Additionally, Figure 2 shows the spatial distribution of the datasets.

Table 3.
Field data dissemination to build and evaluate the algorithms (the number of pixels was obtained at 10 m (20 m in parenthesis)).
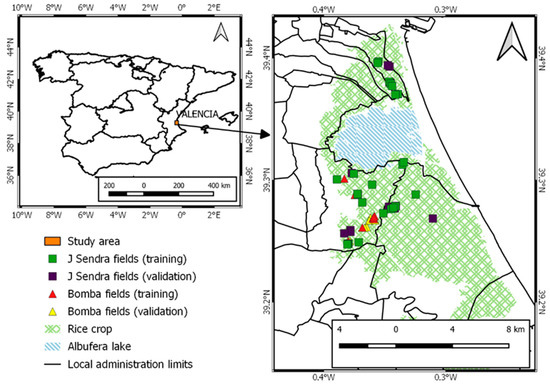
Figure 2.
Location of the rice fields analyzed in this study.
Each date and spatial resolution were analyzed independently, looking for the best combination that provided the best performance metrics against the yield values. Additionally, multivariable linear regressions were built between yields at pixel level and their corresponding surface reflectance values of a given band, interactions between bands and vegetation indices (Appendix C). Specifically, when combining all bands at each spatial resolution, the following equation was tested to derive the yield of pixel i:
where is the estimated yield; , , , , are the model coefficients; and , , , are the surface reflectance (SR) spectral bands, vegetation index (VI) or the interaction between the different SR for a given date of the growing season.
The software StatGraphics Centurion XVII (v.17.2.00) [40] was implemented to determine the best combination of SR on equation 1, using a stepwise regression method, for each date, spatial resolution, and variety.
Finally, the following performance metrics were derived based on the validation data: the coefficient of determination (R2); the Mean Absolute Error (MAE); and the Mean Absolute Percentage Error (MAPE).
These performance metrics of each model based on a spectral band or combination of bands. Finally, each of the variables were validated with a linear regression analysis to test the statistical significance of each factor with a probability p < 0.05, according to the Student’s t-test. The linear model was validated with the Snedecor statistical F-test (p < 0.05).
The processing of the yield maps and the satellite images, as well as the validation, was carried out with the QGIS 3.10.14 software [41].
3. Results
3.1. Evaluation at Within-Field Level in JSendra Rice
The JSendra fields’ coefficient of determination evolution for each Sentinel-2 spectral band at 10 m (Figure A1a) and at 20 m (Figure A1b) spatial resolution is analyzed in Appendix A. These results include the R2 temporal evolution of three simple linear regression models combining the different spectral bands (M1S in Figure A1a and M2S and M3S in Figure A1b). Note that the R2 values studied represent all within-field pixels of the JSendra training data. The models can be written as:
where the spatial resolution is specified in parenthesis and the model coefficients are different for each equation and for each date.
Figure A1a shows that at 10 m, the band that shows the highest correlation with the yield is B8 (NIR), followed by B2 (Blue) and B3 (Green), while B4 (Red) shows the lowest correlation. At 20 m (Figure A1b), B8A shows the highest correlation, followed by B8 and B7 (Red edge) whose evolution is very close to B6 (Red edge), but has a minor peak at the beginning of the season. Other bands, such B11 and B12 (SWIR), show some lower peaks of correlation, having only one significant peak on July 4. Visible bands show a similar tendency compared to 10 m resolution and B5 (Red edge) is very close to B4 (Red). The linear models combining spectral bands (M1S, M2S and M3S) show the best correlation, which is consistent with previous works utilizing remote sensing data to infer within-field maize and soybean yields [8]. The best performance (based on the coefficient of determination evolution) happens on July 4 for both spatial resolutions, that is when rice is in the tillering phase. Comparing the performance at 10 m and 20 m the coefficient of determination remains almost the same and shows an equivalent evolution.
Focusing on July 4, Figure 3 shows the average spectral response of each band, splitting all training data into nine yield ranges. Note that we preserved the spatial resolution of each band. B6, B7, B8A and specially B8 show the largest differences amongst yield ranges by increasing their reflectance values with the yield.
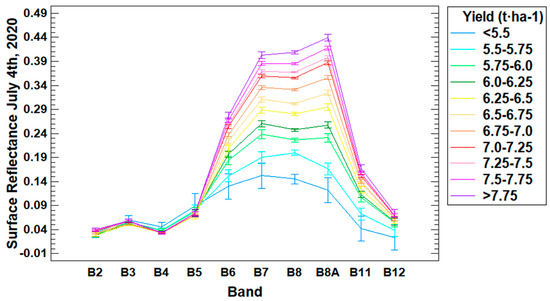
Figure 3.
Surface reflectance average values for each Sentinel-2 band grouping all pixels of the JSendra training data within the yield range specified in the legend (the vertical bars indicate the LSD interval (p < 0.05) for the separation of means).
Next, Table A1 and Table A2 (Appendix B) show the performance metrics of each model at 10 m and 20 m spatial resolution, respectively, focusing on the tillering phase and based on the training data. This phenological stage has been determined in the previous results as critical to monitor rice yield. Three Sentinel-2 acquisition dates were selected to analyze the performance metrics of each model: the date of the R2 peak (July 4), the previous date (June 29) and the next one (July 19). Note that in these tables, models consisting in bands are built based on a linear regression of said band or combination of band. Additionally, the tables show the performance metrics of three models (M1S+, M2S+ and M3S+) whose definition is based on a stepwise regression program (StatGraphics). These models are written as:
where the spatial resolution is specified in parenthesis and the model coefficients are different for each equation and for each date. As a summary of the results, Table 4 shows the evaluation of the best performing models for each date and spatial resolution.

Table 4.
JSendra best model evaluation for each date and spatial resolution with training data.
The best performing models at 10 m are M1S and M1S+, which combine the four bands (B2, B3, B4 and B8). In relation to 20 m, the best performing models are M3S, M2S+ and M3S+. Comparing the dates, July 4 observations provide the best performance metrics, showing R2 greater than 0.70, MAPEs lower than 4% (<3% at 20 m) and MAEs ranging from 0.20–0.25 t⋅ha−1. In relation to the VIs (based on visible, NIR, Red edge and SWIR regions), they do not improve considerably the spectral bands or linear combinations of bands with higher R2 (data, equations and references are shown in Appendix C). The best results for VIs are obtained with the Rice Growth Vegetation Index (RGVI) (R2 = 0.66). Appendix D shows an example at 10 m and 20 m of a reference yield map, each spectral band, and the modeled yield.
Finally, Figure 4 shows the evaluation of the best performing models (M1S and M1S+ at 10 m and M3S and M3S+ at 20 m) for the JSendra variety on July 4 considering all data from the validation fields for each spatial resolution. M1S+ and M3S+ provide a yield modelling error (MAE) of 0.254 t⋅ha−1 (3.73%) and 0.240 t⋅ha−1 (3.48%), respectively, which is aligned with the statistics shown on the training data. In fact, 60% of all pixels evaluated presented a difference between modelled and referenced yield lower than the MAE value, with a maximum difference of 1.0 t·ha−1 and with only 10% of data exceeding a difference of 0.50 t·ha−1. Additionally, Figure 4 (right) shows the performance metrics of the models without interactions at a spatial resolution of 10 m (M1S) and 20 m (M3S). The performance metrics (MAE of 0.318 t⋅ha−1 (4.71%) at 10 m and 0.305 t⋅ha−1 (4.50%) at 20 m) show worse results than on the training data modelling, which suggests that the interactions proposed in M1S+ and M3S+ models provide a better consistency and applicability. Finally, we tested a Random Forest model considering all bands from the training data as inputs and evaluating its performance with the validation data. This model provides an R2 of 0.79 and MAE of 0.292 t⋅ha−1 (4.33%) at 10 m and R2 of 0.78 and MAE of 0.302 t⋅ha−1 (4.46%) at 20 m. These statistics are equivalent to M1S+ and M3S+.
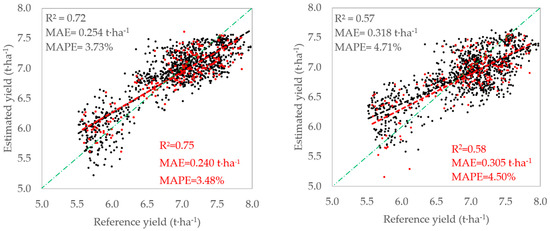
Figure 4.
Validation of the JSendra models on July 4 at validation area: M1S+ (black) and M3S+ (red) (left); M1S (black) and M3S (red) (right).
3.2. Evaluation at Within-Field Level in Bomba Rice
Focusing now on the Bomba variety, Figure A2 (Appendix A) shows the coefficient of determination evolution along the rice season for each Sentinel-2 band acquisition at 10 m (Figure A2a) and at 20 m (Figure A2b) spatial resolution considering the training data. Additionally, the figures include the R2 for three models which linearly combine all bands, following the same structure than the models described in JSendra (M1S, M2S and M3S) but changing the model coefficients. Thus, for Bomba these equations are named M1B, M2B and M3B (M1B in Figure A2a and M2B and M3B in Figure A2b). Note that Bomba rice was harvested by mid-September, thus latter dates are excluded in the plot.
In this case, there are two dates with the maximum correlation at 10 m and 20 m, July 4 and August 28, although the latter includes half the number of pixels than the former. Analogously to JSendra, the results are similar at both spatial resolutions. However, in Bomba rice the visible bands (B2, B3, B4) show the best correlation with the final yields on July 4. B5 shows a very similar performance to the visible bands, and even improves and anticipates the correlation peak with the final yield on June 29. Furthermore, these bands keep a high R2 throughout July and decrease in August (when the flowering stage happens). Additionally, B3 (Green) and B5 show an acceptable value of R2 on August 28. On the contrary, the NIR bands show poor correlation on July 4, which is improved by mid-season (end of July), and finally shows an R2 peak on August 28. Analogously to JSendra, B8, B8A and B7 present very similar results. B6 shows an equivalent evolution to these bands but with a poor correlation during mid-season. Regarding the SWIR bands, at the beginning of the season they show a small correlation peak which decreases until reaching a minimum by the end of June and then improves again, reaching a peak by the end of July which is comparable to the visible bands’ correlation. Finally, the models M1B, M2B and M3B show the best performance.
Focusing on July 4, Figure 5 shows the average spectral surface reflectance for all pixels within the training fields splitting them by yield ranges. In this variety and date, the visible bands (specially B3) have a larger separability showing lower SR values for higher yields. Otherwise, the NIR, Red edge and SWIR reflectance do not show a clear dependency with the yield.
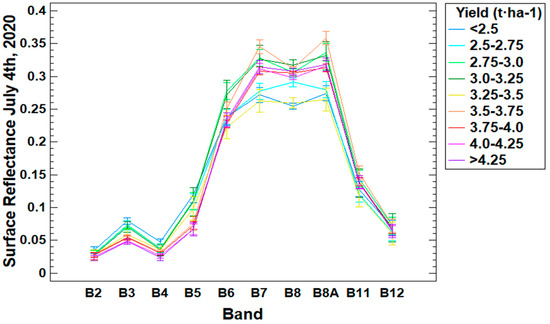
Figure 5.
Surface reflectance average values for each Sentinel-2 band grouping all pixels of the Bomba training data within the yield range specified in the legend (the vertical bars indicate the LSD interval (p < 0.05) for the separation of means).
Next, Table A3 and Table A4 (Appendix B) show the performance metrics of each model at 10 m and 20 m spatial resolution respectively, focusing on the same dates as in JSendra. These three dates are essential for a forecast, since tillering is still being defined and it is still possible to modify crop management to improve final yields. Models are built and shown based on the same principles as in the JSendra variety. The resulting models of the stepwise regression program (StatGraphics), M1B+, M2B+ and M3B+ are defined as:
where the spatial resolution is specified in parenthesis and the model coefficients are different for each equation and for each date. As a summary of the results, the Table 5 shows the evaluation of the best models for each date and spatial resolution.

Table 5.
Bomba best model evaluation for each date and spatial resolution with training data.
Comparing the dates, July 4 observations provide the best performance metrics, showing an R2 greater than 0.85, MAPEs lower than 8% (<6% at 20 m) and MAEs ranging from 0.18–0.23 t⋅ha−1. The best model at 10 m is M1B+, that is the model including B2, B3, B4 and their interactions. Note that this model does not include the NIR band. Additionally, model M1B shows similar results to the simple linear model without the NIR band (). At 20 m, M2B+ and M3B+ show the best performance metrics. Note that M2B+, which depends only on B2 and B3, shows similar performance metrics to M3B+ (that depends on B2, B3, B11 and B12) and M3B (that includes all bands). Additionally, it is important to note that B3 (Green) and B5 individually show excellent results. Regarding VIs, the best performance is obtained using the Normalized Difference Red Edge 2 (NDRE2) (R2 = 0.59). All the performance metrics of the VIs tested, their equations and references can be found in Appendix C. Analogously to the JSendra section, Appendix D shows an example at 10 m and 20 m of a reference yield map, each spectral band, and the modeled yield.
Figure 6 (left) shows the validation of the best performance models (M1B+ and M3B+) for the Bomba variety on July 4 considering the validation fields. These results show that the proposed models M1B+ and M3B+ provide a MAE of 0.218 t·ha−1 (5.82%) and 0.223 t·ha−1 (5.78%), respectively. A total of 60% of pixels presented a difference between modelled and referenced yield lower than the MAE, being the maximum difference around 0.80 t·ha−1, with only 9% of data exceeding a difference of 0.50 t·ha−1. Note that the differences in MAPE between varieties were due to their corresponding average yields, being 3.8 t⋅ha−1 for Bomba and 7.0 t⋅ha−1 for JSendra in the studied area. The validation results of M1B and M3B are shown in Figure 6 (right) (MAE of 0.261 t·ha−1 (6.93%) at 10 m and 0.273 t·ha−1 (7.17%) at 20 m) and are slightly worse than M1B+ and M3B+, respectively. The decrease in R2 when compared to the training data evaluation is caused by the limited yield variability in the validation pixels (between 2.5 and 5.0 t⋅ha−1) compared to the training pixels (between 0.8 and 5.0 t·ha−1). Note that this is not the case in JSendra, where the training and validation pixels show similar variability (5.5–8.0 t⋅ha−1). Finally, a Random Forest algorithm based on the same dataset provides a R2 of 0.71 and MAE of 0.287 t⋅ha−1 (7.67%) at 10 m and R2 of 0.67 and MAE of 0.297 t⋅ha−1 (7.69%) at 20 m. These performance metrics are worse than the previous models based on linear regressions (M1B+, M3B+, M1B and M3B).
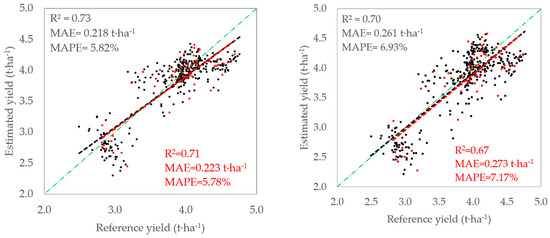
Figure 6.
Validation of the Bomba models on July 4 at validation area: M1B+ (black) and M3B+ (red) (left); M1B (black) and M3B (red) (right).
3.3. Evaluation at Parcel Level
Finally, Figure 7 shows the evaluation of the model at parcel level by aggregating at this scale the pixel level estimations at 10 m based on models M1S+ for JSendra (left) and M1B+ for Bomba (right) on July 4, and the harvester machine measurements through all validation fields. These plots show a very good agreement with a MAE of 0.176 t⋅ha−1 and 2.61% MAPE for JSendra; and a MAE of 0.142 t⋅ha−1 and 4.51% MAPE for Bomba.
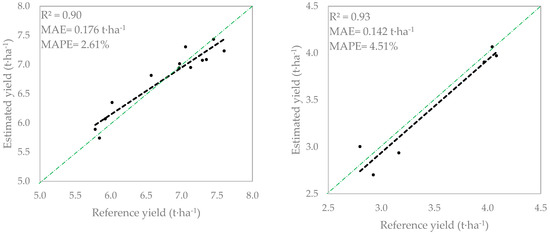
Figure 7.
Validation at parcel level of the JSendra fields (left) and Bomba fields (right).
4. Discussion
In this work we analyze the rice yield dependency on the spectral information provided by Sentinel-2 satellite image acquisitions prior to harvest. To do so, an extensive dataset of harvester machine measurements of within-field yield during the 2020 campaign is preprocessed and linked to the pixel level surface reflectance retrievals considering all Sentinel-2 spectral bands. The two major rice varieties planted in the Albufera region have been analyzed: JSendra and Bomba.
First of all, it is worth noting the high variability of within-field yields despite the limited size of the Valencian fields (areas around 1 ha). In the few examples that we show in this work, even at 10 m resolution and after applying the grid moving average filter to the harvester machine data, the variability of yields can get up to 2.5 t·ha−1, highlighting underperforming areas within the field. Given that all areas within a field are managed in the same manner, empirical models are the only feasible solution to model such variability. Looking at the plots of the coefficient of determination’s seasonal evolution of each band against the final yield, two periods with maximum values of R2 can be identified in both varieties. There is a first period, when the crop is ending the vegetation stage and a second period, when the crop is ending the maturity stage. Both periods are preceded and followed by a decrease of R2. During the first month after the start of season (until end of June) there is barely correlation of the spectral information with the final yield given the reduced size of the rice plants and their signal mixture with water (we need to keep in mind that Valencian rice remains flooded during most of the season). By the beginning of July, the highest correlation is achieved in both varieties. This might be a consequence of the higher density of vegetation and the minimization of the water background signal. During this period, rice plants are in the tillering stage. Tillering is one of the fundamental rice stages defining the final yield since it determines the number of productive tillers per plant which in turn determine the number of grains and their weight. During this phase, the importance of each spectral region is very different among both varieties. JSendra shows a stronger correlation of NIR bands with the yield while Bomba shows a larger R2 with visible bands and band 5 (red edge). This might be a consequence of the agronomic characteristics of each variety. While JSendra plants are denser but smaller in size, Bomba plants are thinner and have a lighter green color. The higher NIR importance in JSendra during this stage might be linked to the positive impact in the final yield of denser fields or areas within the field. Besides, when monitoring vegetation, visible band spectral response is linked to the leaf pigments performance. In particular, Feng [42] showed that band 5 (red edge) is correlated with the chlorophyll-a content during the rice tillering stage. Therefore, the higher importance of this spectral region in Bomba final yields might highlight the dependency of the yield with the chlorophyll-a content during tillering. From mid-July until mid-August the NDVI reaches its maximum in both varieties and remains high and stable. During this period the plant remains in the reproductive stage. By mid-August, the coefficient of determination that decreases during the reproductive stage reaches a minimum value. This could be caused by mixing different fields with different phenological stages, where some areas remain in the reproductive stage while others enter the ripening stage. It could also be a consequence of the mixing signal from the springs. By the end of August there is another R2 peak for both varieties. The JSendra variety shows a stronger correlation of visible bands (and specially the green band) with the final yield. The importance of the visible bands at the ripening stage might differ in those fields that enter the senescence phase earlier compared to those that remain green longer, which may enhance final yields. Regarding Bomba, NIR bands are predominant during this stage. However, looking at the number of pixels covered during this second peak of correlation, which is reduced to 20% in JSendra and 50% in Bomba, and considering its proximity to harvest, this second date has not been considered to build the forecast model. Finally, comparing the performance metrics of modeled rice yield with different VIs and SR data supports the findings in Skakun [8] in corn and soybean, that is SR-based models outperform VI-based models to monitor rice yields.
We also studied different models to correlate yield with the spectral surface reflectance. The simplest model is the linear regression of all bands both at 10 m and at 20 m spatial resolution. Besides, the models proposed by a stepwise regression model (StatGraphics), linearly combine the spectral bands but add some multiplicative terms or band ratios. The results show a similar performance by both models on the training samples, but when applied to the validation samples, the StatGraphics model outperform the linear regression models. Overall, and based on the available dataset and the particular year analyzed, the best statistics can be achieved on July 4 with an error of 0.254 t⋅ha−1 (3.73%) for JSendra and 0.218 t⋅ha−1 (5.82%) for Bomba rice based on the 10 m spatial resolution data. The 20 m resolution analysis, despite adding more spectral information, shows very similar performance metrics. At parcel level the proposed models provide a MAE of 0.176 t⋅ha−1 (2.61% MAPE) for JSendra and a MAE of 0.142 t⋅ha−1 (4.51% MAPE) for Bomba. More complex relationships were also tested using a Random Forest algorithm, providing equivalent results to the linear regression models in JSendra rice and worse results in Bomba rice (given the lower number of samples). Therefore, given the simplicity of linear models, which allow a better interpretation of the inputs considered, we propose using linear models to monitor within-field rice yield.
Finally, we need to highlight that despite the good performance metrics obtained, Figure 4 and Figure 6 (validation plots) and the examples in Appendix D, show that extreme yield values are smoothed out by the models, that is overestimation of low yields and underestimation of high yields. This might be a consequence of the uncertainties of the harvester machine. This is consistent with previous studies [8,9,10].
As a summary and addressing the science questions stated in the Introduction Section, the most critical timing when EO data is better correlated with the final rice yield for both varieties is the beginning of July during the rice tillering stage. The best bands that explain the within-field yield variability are the NIR bands for JSendra and visible and red edge (B5) for Bomba. The proposed models based uniquely on EO data provide accuracies of 0.22–0.25 t⋅ha−1 at within-field scale and 0.14–0.17 t⋅ha−1 at parcel level.
These models were developed considering as a reference yields from a particular year (2020) and a limited sized area where meteorological conditions can be considered constant so no meteorological data could be integrated. Therefore, these models are expected to work on those years with similar meteorological conditions. To solve this limitation, future works will integrate both EO and meteorological data of forthcoming seasons.
5. Conclusions
In this work we analyzed the use of remote sensing data to monitor rice yield. To do so we leveraged an extensive within-field rice yield dataset covering 66 ha of the two major rice varieties planted in Valencia, JSendra and Bomba. The results showed very different correlation of the spectral bands with the final yields, depending on the variety and phenology. During the vegetation stage, the NIR bands showed a stronger correlation in JSendra, whereas the visible bands showed a higher importance in Bomba rice. On the contrary, during the maturity stage, JSendra yield is better correlated with the visible bands while Bomba yields show higher R2 with the NIR bands. These results highlight the need for discriminating between the two varieties to generate EO-based yield models. The proposed model allows a within-field yield forecast error with a MAE of 0.254 t⋅ha−1 (3.73%) for JSendra and 0.218 t⋅ha−1 (5.82%) for Bomba on July 4th and parcel level MAE of 0.176 t⋅ha−1 (2.61% MAPE) for JSendra and a MAE of 0.142 t⋅ha−1 (4.51% MAPE) for Bomba. This date coincides with the rice tillering stage and underlines the importance of achieving a good performance of the plants during this stage. Therefore, agronomic decisions in crop management before this stage are critical to improve rice yield. Additionally, these estimations are about three months prior to harvest and provide enough time for improving the rice management towards more direct interventions of those areas that already show any underperformance in plant nutrition (or diseases control) during the tillering stage, thus advancing the science of precision agriculture.
Author Contributions
Conceptualization and methodology, B.F., A.S.B. and C.R.; formal analysis and investigation, D.F., D.T.-S., A.S.; resources, B.F., A.S.B.; data curation, B.F., A.S.B., C.R., S.S., E.V.; writing—original draft preparation, B.F.; writing—review and editing, B.F., A.S.B., D.F., C.R., D.T.-S., A.S., S.S., E.V., I.B.-R., A.U.; supervision, B.F., C.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the program Generacio Talent of Generalitat Valenciana (CIDEGENT/2018/009).
Informed Consent Statement
Not applicable.
Acknowledgments
We acknowledge the program Generacio Talent of Generalitat Valenciana (CIDEGENT/2018/009).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
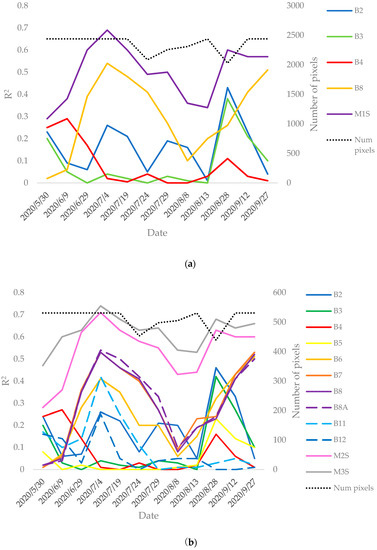
Figure A1.
Coefficient of determination timeseries evolution focusing on JSendra training data of each band at 10 m (a) and at 20 m (b) spatial resolution and the linear combination of all of them against the final yield at pixel level (M1S, M2S and M3S). Additionally, the number of pixels is added as a reference of the cloud situation.
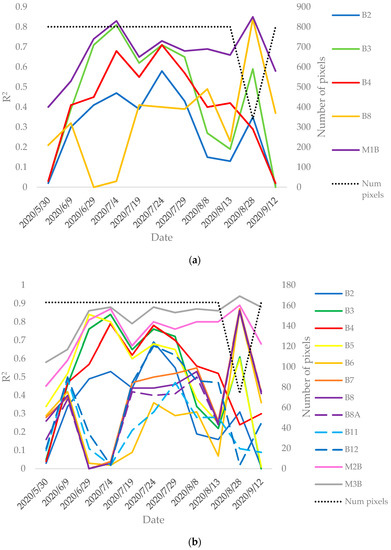
Figure A2.
Coefficient of determination timeseries evolution focusing on Bomba training data of each band at 10 m (a) and at 20 m (b) spatial resolution and the linear combination of all of them against the final yield at pixel level (M1B, M2B and M3B). Additionally, the number of pixels is added as a reference of the cloud situation.
Appendix B

Table A1.
JSendra 10 m spatial resolution model evaluation with training data (model coefficients are different for each equation).
Table A1.
JSendra 10 m spatial resolution model evaluation with training data (model coefficients are different for each equation).
| 10 m | 29 June 2020 | 04 July 2020 | 19 July 2020 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | MAE (t⋅ha−1) | MAPE (%) | R2 | MAE (t⋅ha−1) | MAPE (%) | R2 | MAE (t⋅ha−1) | MAPE (%) |
| 0.06 | 0.419 | 6.20 | 0.26 | 0.359 | 5.29 | 0.21 | 0.374 | 5.51 | |
| 0.00 | 0.437 | 6.45 | 0.04 | 0.419 | 6.20 | 0.02 | 0.428 | 6.32 | |
| 0.17 | 0.387 | 5.68 | 0.02 | 0.439 | 6.47 | 0.01 | 0.438 | 6.46 | |
| 0.39 | 0.355 | 5.16 | 0.54 | 0.295 | 4.28 | 0.48 | 0.310 | 4.50 | |
| 0.29 | 0.351 | 5.19 | 0.51 | 0.309 | 4.49 | 0.43 | 0.324 | 4.75 | |
| 0.54 | 0.285 | 4.18 | 0.61 | 0.269 | 3.90 | 0.46 | 0.320 | 4.69 | |
| 0.39 | 0.355 | 5.16 | 0.55 | 0.292 | 4.23 | 0.54 | 0.292 | 4.23 | |
| 0.41 | 0.322 | 4.73 | 0.31 | 0.352 | 5.18 | 0.15 | 0.399 | 5.88 | |
| 0.44 | 0.336 | 4.88 | 0.55 | 0.292 | 4.24 | 0.49 | 0.308 | 4.47 | |
| 0.47 | 0.320 | 4.66 | 0.55 | 0.291 | 4.22 | 0.49 | 0.308 | 4.48 | |
| 0.54 | 0.285 | 4.17 | 0.62 | 0.269 | 3.90 | 0.48 | 0.312 | 4.56 | |
| 0.58 | 0.288 | 4.17 | 0.68 | 0.257 | 3.71 | 0.60 | 0.273 | 3.96 | |
| 0.57 | 0.281 | 4.10 | 0.66 | 0.254 | 3.68 | 0.57 | 0.283 | 4.10 | |
| 0.47 | 0.315 | 4.59 | 0.55 | 0.291 | 4.21 | 0.49 | 0.308 | 4.47 | |
| M1S | 0.60 | 0.277 | 4.02 | 0.69 | 0.251 | 3.63 | 0.60 | 0.274 | 3.96 |
| M1S+ | 0.64 | 0.258 | 3.75 | 0.72 | 0.234 | 3.36 | 0.63 | 0.263 | 3.81 |

Table A2.
JSendra 20 m spatial resolution model evaluation with training data (model coefficients are different for each equation).
Table A2.
JSendra 20 m spatial resolution model evaluation with training data (model coefficients are different for each equation).
| 20 m | 29 June 2020 | 04 July 2020 | 19 July 2020 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | MAE (t⋅ha−1) | MAPE (%) | R2 | MAE (t⋅ha−1) | MAPE (%) | R2 | MAE (t⋅ha−1) | MAPE (%) |
| 0.07 | 0.401 | 5.90 | 0.26 | 0.346 | 5.07 | 0.22 | 0.355 | 5.22 | |
| 0.00 | 0.421 | 6.20 | 0.04 | 0.403 | 5.94 | 0.02 | 0.410 | 6.03 | |
| 0.14 | 0.382 | 5.60 | 0.01 | 0.424 | 6.23 | 0.00 | 0.422 | 6.21 | |
| 0.02 | 0.415 | 6.11 | 0.00 | 0.422 | 6.21 | 0.00 | 0.421 | 6.20 | |
| 0.28 | 0.374 | 5.44 | 0.41 | 0.330 | 4.79 | 0.35 | 0.338 | 4.91 | |
| 0.36 | 0.353 | 5.13 | 0.53 | 0.294 | 4.25 | 0.46 | 0.312 | 4.51 | |
| 0.35 | 0.357 | 5.19 | 0.53 | 0.293 | 4.24 | 0.46 | 0.310 | 4.48 | |
| 0.35 | 0.358 | 5.21 | 0.54 | 0.291 | 4.19 | 0.50 | 0.297 | 4.29 | |
| 0.14 | 0.392 | 5.76 | 0.42 | 0.328 | 4.75 | 0.25 | 0.372 | 5.40 | |
| 0.03 | 0.414 | 6.10 | 0.25 | 0.373 | 5.43 | 0.05 | 0.417 | 6.11 | |
| M2S | 0.62 | 0.261 | 3.78 | 0.71 | 0.232 | 3.33 | 0.63 | 0.261 | 3.77 |
| M2S+ | 0.66 | 0.240 | 3.47 | 0.74 | 0.216 | 3.09 | 0.66 | 0.246 | 3.53 |
| M3S | 0.63 | 0.259 | 3.75 | 0.74 | 0.221 | 3.18 | 0.66 | 0.247 | 3.57 |
| M3S+ | 0.69 | 0.237 | 3.41 | 0.76 | 0.204 | 2.92 | 0.70 | 0.232 | 3.35 |

Table A3.
Bomba 10 m spatial resolution model evaluation with training data (model coefficients are different for each equation).
Table A3.
Bomba 10 m spatial resolution model evaluation with training data (model coefficients are different for each equation).
| 10 m | 29 June 2020 | 04 July 2020 | 19 July 2020 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | MAE (t⋅ha−1) | MAPE (%) | R2 | MAE (t⋅ha−1) | MAPE (%) | R2 | MAE (t⋅ha−1) | MAPE (%) |
| 0.41 | 0.476 | 17.91 | 0.47 | 0.443 | 16.08 | 0.39 | 0.463 | 17.64 | |
| 0.71 | 0.317 | 11.63 | 0.81 | 0.274 | 9.87 | 0.62 | 0.365 | 14.47 | |
| 0.45 | 0.458 | 16.47 | 0.68 | 0.336 | 12.12 | 0.55 | 0.385 | 15.83 | |
| 0.00 | 0.584 | 24.49 | 0.03 | 0.587 | 24.28 | 0.41 | 0.452 | 18.32 | |
| 0.72 | 0.312 | 11.67 | 0.81 | 0.274 | 9.84 | 0.62 | 0.357 | 14.39 | |
| 0.46 | 0.448 | 16.26 | 0.68 | 0.336 | 12.19 | 0.55 | 0.372 | 15.69 | |
| 0.41 | 0.473 | 17.79 | 0.47 | 0.443 | 16.05 | 0.54 | 0.420 | 15.63 | |
| 0.71 | 0.314 | 11.43 | 0.82 | 0.261 | 9.27 | 0.62 | 0.365 | 14.36 | |
| 0.71 | 0.310 | 11.4 | 0.82 | 0.267 | 9.64 | 0.64 | 0.359 | 14.07 | |
| 0.51 | 0.414 | 14.73 | 0.72 | 0.319 | 11.32 | 0.59 | 0.378 | 15.16 | |
| 0.74 | 0.293 | 10.61 | 0.83 | 0.255 | 9.24 | 0.63 | 0.360 | 14.36 | |
| 0.73 | 0.298 | 11.21 | 0.82 | 0.268 | 9.63 | 0.64 | 0.355 | 14.04 | |
| 0.51 | 0.416 | 14.81 | 0.74 | 0.304 | 11.07 | 0.59 | 0.378 | 15.16 | |
| 0.71 | 0.311 | 11.37 | 0.82 | 0.262 | 9.28 | 0.65 | 0.358 | 13.87 | |
| M1B | 0.74 | 0.293 | 10.61 | 0.83 | 0.253 | 9.19 | 0.65 | 0.359 | 13.86 |
| M1B+ | 0.75 | 0.288 | 10.08 | 0.87 | 0.229 | 7.37 | 0.8 | 0.266 | 9.59 |

Table A4.
Bomba 20 m spatial resolution model evaluation with training data (model coefficients are different for each equation).
Table A4.
Bomba 20 m spatial resolution model evaluation with training data (model coefficients are different for each equation).
| 20 m | 29 June 2020 | 04 July 2020 | 19 July 2020 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | MAE (t⋅ha−1) | MAPE (%) | R2 | MAE (t⋅ha−1) | MAPE (%) | R2 | MAE (t⋅ha−1) | MAPE (%) |
| 0.49 | 0.464 | 17.20 | 0.53 | 0.419 | 14.93 | 0.44 | 0.470 | 17.72 | |
| 0.76 | 0.296 | 11.10 | 0.84 | 0.263 | 9.72 | 0.65 | 0.367 | 14.82 | |
| 0.57 | 0.423 | 14.59 | 0.79 | 0.265 | 9.24 | 0.62 | 0.361 | 15.23 | |
| 0.84 | 0.244 | 8.92 | 0.80 | 0.267 | 10.65 | 0.60 | 0.360 | 15.54 | |
| 0.03 | 0.591 | 25.42 | 0.02 | 0.590 | 25.46 | 0.09 | 0.558 | 24.28 | |
| 0.00 | 0.603 | 25.89 | 0.04 | 0.605 | 25.51 | 0.47 | 0.429 | 18.06 | |
| 0.00 | 0.603 | 25.89 | 0.03 | 0.604 | 25.57 | 0.44 | 0.442 | 18.62 | |
| 0.00 | 0.603 | 25.89 | 0.03 | 0.604 | 25.57 | 0.42 | 0.453 | 19.02 | |
| 0.11 | 0.612 | 24.18 | 0.02 | 0.594 | 25.49 | 0.21 | 0.528 | 21.22 | |
| 0.19 | 0.596 | 22.65 | 0.02 | 0.602 | 25.65 | 0.47 | 0.437 | 17.17 | |
| M2B | 0.81 | 0.256 | 9.10 | 0.87 | 0.215 | 7.93 | 0.67 | 0.362 | 14.16 |
| M2B+ | 0.83 | 0.251 | 8.49 | 0.90 | 0.201 | 6.48 | 0.84 | 0.247 | 8.98 |
| M3B | 0.86 | 0.228 | 7.89 | 0.88 | 0.213 | 7.74 | 0.79 | 0.285 | 10.52 |
| M3B+ | 0.87 | 0.223 | 7.67 | 0.92 | 0.175 | 5.74 | 0.88 | 0.222 | 7.77 |
Appendix C
Table A5 provides detailed information about the vegetation indices, and their mathematical formula according to [8,10,26], that have been tested in the yield models. Table A6 shows the performance metrics of these VIs on July 4 for each variety.

Table A5.
Vegetation indices used in the study.
Table A5.
Vegetation indices used in the study.
| Vegetation Index | Formula |
|---|---|
| Normalized difference vegetation index (NDVI) | |
| Difference vegetation index (DVI) | |
| Enhanced vegetation index (EVI) | |
| Enhanced vegetation index 2 (EVI2) | |
| Green NDVI (GNDVI) | |
| Green difference vegetation index (GDVI) | |
| Green chlorophyll vegetation index (GCVI) | |
| Wide dynamic range vegetation index (WDRVI) | |
| Soil-adjusted vegetation index (SAVI) | |
| Ratio vegetation index (RVI) | |
| Land surface water index (LSWI) | |
| Normalized difference built-up index (NDBI) | |
| Triangular vegetation index (TVI) | |
| Infrared percentage vegetation index (IPVI) | |
| Rice growth vegetation index (RGVI) | |
| Red edge chlorophyll index 1 (CIre1) | |
| Normalized difference red edge 1 (NDRE1) | |
| Normalized difference red edge 2 (NDRE2) |

Table A6.
Performance metrics of the VIs-based models considering the training dataset at 20 m spatial resolution.
Table A6.
Performance metrics of the VIs-based models considering the training dataset at 20 m spatial resolution.
| JSendra Rice | Bomba Rice | |||||
|---|---|---|---|---|---|---|
| R2 | MAE (t·ha−1) | MAPE (%) | R2 | MAE (t·ha−1) | MAPE (%) | |
| NDVI | 0.40 | 0.331 | 4.82 | 0.36 | 0.485 | 18.86 |
| DVI | 0.55 | 0.292 | 4.23 | 0.07 | 0.590 | 23.98 |
| EVI | 0.60 | 0.274 | 3.97 | 0.11 | 0.585 | 23.59 |
| EVI2 | 0.56 | 0.287 | 4.17 | 0.11 | 0.585 | 23.56 |
| GNDVI | 0.42 | 0.322 | 4.68 | 0.49 | 0.436 | 16.63 |
| GDVI | 0.55 | 0.292 | 4.24 | 0.11 | 0.587 | 23.57 |
| GCVI | 0.35 | 0.349 | 5.09 | 0.41 | 0.475 | 18.48 |
| WDRVI | 0.40 | 0.329 | 4.78 | 0.36 | 0.494 | 19.28 |
| SAVI | 0.56 | 0.286 | 4.15 | 0.14 | 0.578 | 23.17 |
| RVI | 0.37 | 0.339 | 4.95 | 0.33 | 0.511 | 20.11 |
| LSWI | 0.07 | 0.397 | 5.85 | 0.02 | 0.613 | 25.85 |
| NDBI | 0.07 | 0.397 | 5.85 | 0.02 | 0.613 | 25.85 |
| TVI | 0.40 | 0.334 | 4.86 | 0.36 | 0.484 | 18.85 |
| IPVI | 0.40 | 0.331 | 4.82 | 0.36 | 0.485 | 18.86 |
| RGVI | 0.66 | 0.245 | 3.54 | 0.57 | 0.394 | 16.3 |
| CIre1 | 0.40 | 0.325 | 4.71 | 0.48 | 0.446 | 17.77 |
| NDRE1 | 0.45 | 0.307 | 4.44 | 0.54 | 0.414 | 16.34 |
| NDRE2 | 0.43 | 0.313 | 4.52 | 0.59 | 0.393 | 15.29 |
Appendix D
Figure A3 shows the reference yield maps from the harvester machine (D1A and D1H) over a JSendra training field and the corresponding surface reflectance and DVI values from Sentinel-2 on July 4 (B-F at 10 m, I-M at 20 m). Furthermore, Figure A3G,N show the resulting yield estimations based on the M1S+ (left) and M3S+ model (right). Looking at the spatial distribution of the yield measurements, there are two areas with larger yield in the center of the field while the left and right edges show lower yield values. This pattern is very close to the NIR (B8) and DVI distribution across the parcel whereas the other bands hardly show any similarity. This provides a visual idea of how each spectral band or VI intervenes and how it affects the change of spatial resolution (10 m, left and 20 m, right). The models can identify high and low yield zones. However, extreme values are smoothed.
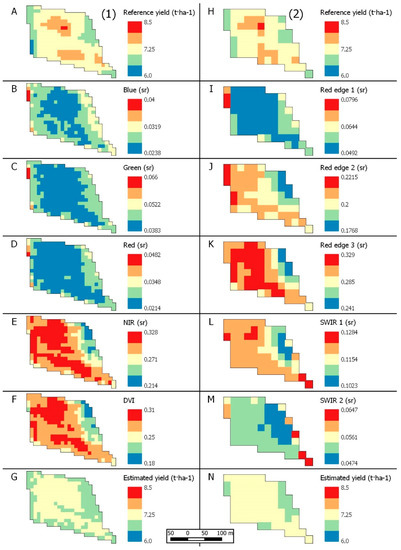
Figure A3.
Example of one training JSendra field at 10 m (left, (1)) and 20 m (right, (2)) spatial resolution, being: (A,H) the reference yield map; (B–F) and (I–M) the SR or VI indicated at legend; (G,N) the modelling result (M1S+ for G and M3S+ for N).
Figure A4 shows an example of a Bomba training field where D2A and D2H show the reference yields at 10 m and 20 m, respectively, other images show the corresponding pixel level reflectance and DVI values (D2B-F at 10 m, D2I-M at 20 m). D2G and D2N show the yield resulting maps after implementing M1B+ and M3B+ respectively. The yield maps show two clusters with high within-field yields, while the top edge shows the lowest yields. Looking at the surface reflectance and the DVI images, the green (B3) and red (B4) bands show the highest correspondence with said distribution. Moreover, the maps give a visual validation of the effect of spatial resolution. From these figures, NIR, Red edge and SWIR should have better results in the modelling. However, those bands do not explain the yield variability between fields well. Finally, the estimated yield maps present a good agreement with the reference yield map identifying high and low yield zones, although extreme values are smoothed out.
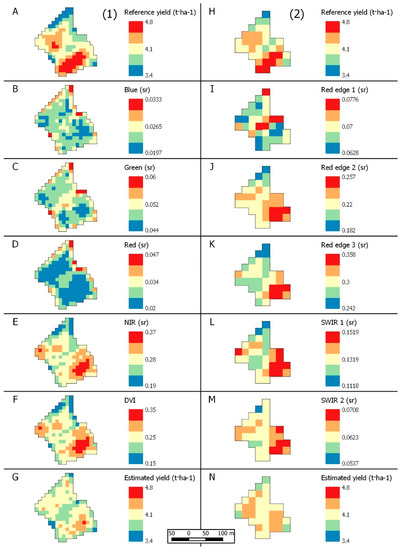
Figure A4.
Example of one training Bomba field at 10 m (left, (1)) and 20 m (right, (2)) spatial resolution, being: (A,H) the reference yield map; (B–F) and (I–M) the SR or VI indicated at legend; (G,N) the modelling result (M1B+ for G and M3B+ for N).
References
- FAOSTAT. Food and Agriculture Statistics. Available online: htttp://www.fao.org/faostat (accessed on 15 June 2021).
- MAPA. Ministerio de Agricultura, Pesca y Alimentación. Available online: https://www.mapa.gob.es (accessed on 15 June 2021).
- United Nations. Available online: https://www.un.org/en (accessed on 15 June 2021).
- La Agricultura Mundial en la Perspectiva del Año 2050. Available online: http://www.fao.org/fileadmin/templates/wsfs/docs/Issues_papers/Issues_papers_SP/La_agricultura_mundial.pdf (accessed on 15 June 2021).
- Johnson, D.M. A comprehensive assessment of the correlations between field crop yields and commonly used MODIS products. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 65–81. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Skakun, S.; Roger, J.C.; Becker-Reshef, I.; Murphy, E.; Justice, C. Remote sensing based yield monitoring: Application to winter wheat in United States and Ukraine. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 112–127. [Google Scholar] [CrossRef]
- Skakun, S.; Vermote, E.; Franch, B.; Roger, J.C.; Kussul, N.; Ju, J.; Masek, J. Winter wheat yield assessment from Landsat 8 and Sentinel-2 data: Incorporating surface reflectance, through phenological fitting, into regression yield models. Remote Sens. 2019, 11, 1768. [Google Scholar] [CrossRef]
- Skakun, S.; Kalecinski, N.I.; Brown, M.G.; Johnson, D.M.; Vermote, E.F.; Roger, J.C.; Franch, B. Assessing within-Field Corn and Soybean Yield Variability from WorldView-3, Planet, Sentinel-2, and Landsat 8 Satellite Imagery. Remote Sens. 2021, 130, 872. [Google Scholar] [CrossRef]
- Kayad, A.; Sozzi, M.; Gatto, S.; Marinello, F.; Pirotti, F. Monitoring within-field variability of corn yield using Sentinel-2 and machine learning techniques. Remote Sens. 2019, 11, 2873. [Google Scholar] [CrossRef]
- Zhao, Y.; Potgieter, A.B.; Zhang, M.; Bingfang, W.; Hammer, G.L. Predicting wheat yield at the field scale by combining high-resolution Sentinel-2 satellite imagery and crop modelling. Remote Sens. 2020, 12, 1024. [Google Scholar] [CrossRef]
- Deines, J.M.; Patel, R.; Liang, S.Z.; Dado, W.; Lobell, D.B. A million kernels of truth: Insights into scalable satellite maize yield mapping and yield gap analysis from an extensive ground dataset in the US Corn Belt. Remote Sens. Environ. 2021, 253, 112174. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- RICA: A Rice Crop Calendar for Asia Based on MODIS Multi-Year Data. Available online: http://asia-rice.org (accessed on 1 June 2021).
- GEOGLAM. Available online: https://www.earthobservations.org/geoglam.php (accessed on 3 June 2021).
- Open, Timely, and Science-Driven Information on Crop Conditions in Support of Market Transparency and Early Warning of Production Shortfalls. Available online: https://cropmonitor.org (accessed on 3 June 2021).
- Agricultural Market Information System. Available online: http://www.amis-outlook.org// (accessed on 3 June 2021).
- Cai, Y.; Guan, K.; Nafziger, E.; Chowdhary, G.; Peng, B.; Jin, Z.; Wang, S.; Wang, S. Detecting in-season crop nitrogen stress of corn for field trials using UAV-and CubeSat-based multispectral sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 5153–5166. [Google Scholar] [CrossRef]
- Shi, Y.; Huang, W.; Ye, H.; Ruan, C.; Xing, N.; Geng, Y.; Dong, Y.; Peng, D. Partial least square discriminant analysis based on normalized two-stage vegetation indices for mapping damage from rice diseases using PlanetScope datasets. Sensors 2018, 18, 1901. [Google Scholar] [CrossRef]
- Kobayashi, T.; Sasahara, M.; Kanda, E.; Ishiguro, K.; Hase, S.; Torigoe, Y. Assessment of rice panicle blast disease using airborne hyperspectral imagery. Open Agric. J. 2016, 10, 28–34. [Google Scholar] [CrossRef]
- Yang, Y.; Chai, R.; He, Y. Early detection of rice blast (Pyricularia) at seedling stage in Nipponbare rice variety using near-infrared hyper-spectral image. Afr. J. Biotechnol. 2012, 11, 6809–6817. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, T.; Tian, Y.; Xu, H.; Song, J.; Lan, Y. Assessment of rice leaf blast severity using hyperspectral imaging during late vegetative growth. Australas. Plant Pathol. 2020, 49, 571–578. [Google Scholar] [CrossRef]
- Bacenetti, J.; Paleari, L.; Tartarini, S.; Vesely, F.M.; Foi, M.; Movedi, E.; Ravasi, R.A.; Bellopede, V.; Durello, S.; Ceravolo, C.; et al. May smart technologies reduce the environmental impact of nitrogen fertilization? A case study for paddy rice. Sci. Total Environ. 2020, 715, 136956. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Garcia, B.; Casterad, M.; Guillén, M.; Quílez, D. Agronomic and Economic Potential of Vegetation Indices for Rice N Recommendations under Organic and Mineral Fertilization in Mediterranean Regions. Remote Sens. 2018, 10, 1908. [Google Scholar] [CrossRef]
- Gilardelli, C.; Stella, T.; Confalonieri, R.; Ranghetti, L.; Campos-Taberner, M.; García-Haro, F.J.; Boschetti, M. Downscaling rice yield simulation at sub-field scale using remotely sensed LAI data. Eur. J. Agron. 2019, 103, 108–116. [Google Scholar] [CrossRef]
- Confalonieri, R.; Rosenmund, A.S.; Baruth, B. An improved model to simulate rice yield. Agron. Sustain. Dev. 2009, 29, 463–474. [Google Scholar]
- Mosleh, M.K.; Hassan, Q.K.; Chowdhury, E.H. Application of remote sensors in mapping rice area and forecasting its production: A review. Sensors 2015, 15, 769–791. [Google Scholar] [CrossRef]
- Shao, Y.; Fan, X.; Liu, H.; Xiao, J.; Ross, S.; Brisco, B.; Brown, R.; Staples, G. Rice monitoring and production estimation using multi-temporal RADARSAT. Remote Sens. Environ. 2001, 76, 310–325. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Q.; Li, X.; Liao, S.; Chi, G.; Peng, S. Towards an operational system for regional-scale rice yield estimation using a time-series of RADARSAT ScanSAR images. Int. J. Remote Sens. 2003, 24, 4207–4220. [Google Scholar] [CrossRef]
- Chen, C.; McNairn, H. A neural network integrated approach for rice crop monitoring. Int. J. Remote Sens. 2006, 27, 1367–1393. [Google Scholar] [CrossRef]
- Nuarsa, I.W.; Nishio, F.; Hongo, C. Relationship between rice spectral and rice yield using MODIS data. J. Agric. Sci. 2011, 2, 80–88. [Google Scholar] [CrossRef][Green Version]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Chang, L.Y.; Due, H.N.; Nguyen, L.D. Prediction of rice crop yield using MODIS EVI-LAI data in the Mekong Delta, Vietnam. Int. J. Remote Sens. 2013, 34, 7275–7292. [Google Scholar] [CrossRef]
- Noureldin, N.A.; Aboelghar, M.A.; Saudy, H.S.; Ali, A.M. Rice yield forecasting models using satellite imagery in Egypt. Egypt. J. Remote Sens. Space Sci. 2013, 16, 125–131. [Google Scholar] [CrossRef]
- Rahman, A.; Khan, K.; Krakauer, N.Y.; Roytman, L.; Kogan, F. Use of remote sensing data for estimation of Aman rice yield. Int. J. Agric. For. 2012, 2, 101–107. [Google Scholar] [CrossRef]
- Nuarsa, I.W.; Nishio, F.; Hongo, C. Rice yield estimation using Landsat ETM+ data and field observation. J. Agric. Sci. 2012, 3, 45–56. [Google Scholar] [CrossRef]
- Natura 2000. Available online: https://ec.europa.eu/environment/nature/natura2000/index_en.htm (accessed on 4 June 2021).
- Romo, S.; Soria, J.; Fernandez, F.; Ouahid, Y.; Barón-Solá, Á. Water residence time and the dynamics of toxiccyanobacteria. Freshw. Biol. 2013, 58, 513–522. [Google Scholar] [CrossRef]
- Kharel, T.P.; Swink, S.N.; Maresma, A.; Youngerman, C.; Kharel, D.; Czymmek, K.J.; Ketterings, Q.M. Yield monitor data cleaning is essential for accurate corn grain and silage yield determination. Agron. J. 2019, 111, 509–516. [Google Scholar] [CrossRef]
- Dobermann, A.; Ping, J.L. Geostatistical integration of yield monitor data and remote sensing improves yield maps. Agron. J. 2004, 96, 285–297. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Statgraphics 19® Centurion. Available online: https://www.statgraphics.com/centurion-overview (accessed on 10 June 2021).
- Un Sistema de Información Geográfica Libre y de Código Abierto. Available online: https://www.qgis.org/es/site/ (accessed on 10 June 2021).
- Feng, H.; Chen, G.; Xiong, L.; Liu, Q.; Yang, W. Accurate digitization of the chlorophyll distribution of individual rice leaves using hyperspectral imaging and an integrated image analysis pipeline. Front. Plant Sci. 2017, 8, 1238. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).