Abstract
It has been reported that global warming results in the increase of globally averaged wave heights. What happened to the global-averaged wave heights during the global warming slowdown period (1999–2013)? Using reanalysis products, together with remote sensing and in situ observational data, it was found that the temporal variation pattern of the globally averaged wave heights was similar to the slowdown trend in the increase in global mean surface temperature during the same period. The analysis of the spatial distribution of trends in wave height variation revealed different rates in global oceans: a downward trend in the northeastern Pacific and southern Indian Ocean, and an upward trend in other regions. The decomposition of waves into swells and wind waves demonstrates that swells dominate global wave height variations, which indicates that local sea surface winds indirectly affect the slowdown in the rate of wave height growth.
1. Introduction
Coastal and offshore engineering projects are significantly affected by wind-generated waves. When waves travel from deep to shallow waters, they often carry sediment, resulting in coastal change, erosion and siltation, especially in ports, channels, and estuaries. Wave heights in the open ocean play an important role in safe and efficient ship transportation. High wave heights affect the speed of the transportation of goods and may cause ship accidents. Moreover, ocean surface waves are the media for air–sea exchanges, such as energy budgets and upper ocean mixing. Changes in ocean wave conditions influence air–sea interaction mechanisms, thus playing an important role in determining the simulation accuracy of climate models [1,2,3].
The global warming trend, characterized by global mean surface temperature (GMST), exhibited a slowdown between two large El Niño events in 1997/98 and 2015/16 [4,5,6,7,8,9,10]. The Intergovernmental Panel on Climate Change’s Fifth Assessment Report states that there was a significant reduction in GMST over the 15 years from 1998 to 2012 compared with the 60 years from 1951 to 2012 [11]. Debates are ongoing concerning this finding [12,13,14].
What has happened to global waves in recent decades? On a regional scale, a downward trend in wave height in the mid-latitude North Pacific has been reported [15]. On a global scale, trends in mean wave direction, significant wave height (SWH), mean wave period, and wave energy flux between 1979 and 2010 have been assessed: they all varied in time and space. Among them, the mean wave period and the mean wave direction showed the most and least significant changes, respectively [16]. Furthermore, changes in global waves before 2008, and global winds and waves from 1985 to 2018, have been examined using satellite data. These studies showed that both values increased slightly, especially in extreme conditions, with the largest growth in the Southern Ocean [1,17]. A proposed mechanism for these changes is that ocean warming was a crucial factor affecting global winds and, hence, the waves they generate. Ocean warming in different basins may affect wind conditions through sea surface temperature (SST), thus leading to an increase in global wave energy [18].
Although the above-mentioned studies used multi-source data to analyze wave trends in different ocean regions over different periods, none of them, focused on the characteristics of the global wave climate during the global warming slowdown period. We seek to fill this gap by investigating changes in the global wave climate in response to the global warming slowdown between two large El Niño events from 1999 to 2013 through the integrated use of buoy, satellite altimeter, and reanalysis datasets.
2. Materials and Methods
2.1. Data
To investigate the climatic characteristics and long-term trends in the global wave field, reliable and extended time series of data are required. Almost all previous studies used satellite altimeter data [1,17,19], numerical hindcast outputs [20,21], buoy data [22,23], ship observations [24], and/or reanalysis data [25,26,27] to investigate the trend in ocean wave conditions. We used ERA5 [28] and ERA-Interim [29] reanalysis datasets produced by the European Center for Medium-Range Weather Forecast (ECMWF), satellite altimeter data from the French Research Institute for the Exploitation of the Sea (IFREMER), and National Data Buoy Center (NDBC) buoy data to statistically analyze global wave trends [30].
In this study, we used the ERA5 global wave (wind) reanalysis data at a spatial resolution of 0.5° × 0.5° (0.25° × 0.25°) and at monthly intervals from January 1979 to December 2019. The ECMWF regularly uses its models and data assimilation systems to re-analyze archived observations, creating global datasets describing the recent history of the atmosphere, land surface, and oceans. ERA5 is the fifth generation ECMWF reanalysis of the global climate and weather for the past four to seven decades, and contains detailed records from 1950 onwards. It is a relatively high-resolution, long-duration time series, and offers a wide spatial coverage. The SWH from ERA5 is approximately equal to the average height of the highest third of the surface ocean waves generated by wind and swell. The SWH can be partitioned into remotely generated swell (swell wave height) and locally generated wind-sea (wind wave height). The wind speed is usually characterized by measurements at a reference height of 10 m. The surface ocean wave field consists of a combination of waves with different heights, lengths, and directions (known as the two-dimensional wave spectrum). The wave spectrum can be decomposed into wind-sea waves, which are directly affected by local winds, and swell, waves that are generated by wind at a different location and time. More strictly, the significant wave height is four times the square root of the integral in all directions and all frequencies of the two-dimensional wave spectrum [28].
The ERA-Interim wave reanalysis from the ECMWF is at a spatial resolution of 1° × 1° and covers the whole globe. The data are available from January 1979 to December 2017 at 6-hourly intervals. The ECMWF periodically uses its forecast models and data assimilation systems to re-analyze archived observations, creating global datasets describing the recent history of the atmosphere, land surface, and oceans.
The National Data Buoy Center (NDBC) is part of the National Oceanic and Atmospheric Administration’s (NOAA) National Weather Service (NWS). It provides hourly observations from a network of approximately 90 buoys and 60 Coastal Marine Automated Network (C-MAN) stations.
The monthly mean altimeter data of SWH have a spatial resolution of 2° × 2°, and are available from January 1993 to December 2016. Continuous altimeter measurements of SWH are available over 24 years (1993–2016) from the nine altimeter missions: ERS-1&2, TOPEX-Poseidon, GEOSAT Follow-On (GFO), Jason-1, Jason-2, ENVISAT, Cryosat, and SARAL.
The global annual mean surface air (land and ocean) temperature (GMST) from 1979 to 2019 is provided by the NOAA. These two datasets are blended into a single product to produce combined global land and ocean temperature anomalies. The available time series of global-scale temperature anomalies are calculated with respect to the 20th-Century average, while the mapping tool displays global-scale temperature anomalies with respect to the base period of 1981–2010.
2.2. Calculation of Global Time Series
The monthly SWH time series are aggregated by years to calculate the globally averaged time series. The global signals for both SWH and 10-m sea surface wind speed (SSW) anomalies are obtained by spatially averaging as follows:
where Vi represents an annual mean variable at each location at grid i and S is the surface area of the grid cell at the specified latitude and longitude.
2.3. Mann–Kendall test for Monotonic Trend
The Mann–Kendall (MK) time series trend analysis method proposed by Mann and Kendall [31,32] is used to statistically assess a monotonic trend in a variable of interest. In the MK test, for a time series of x over length n, an indicator function can be calculated by:
where S is the test statistics and n is the number of observations in the set. The parameter is used to determine the trend:
signifies an upward trend, and signifies a downward trend.
All the estimates of trend are associated with statistical variability. The most common way to address such issues is by determining whether the trends are statistically significant. In this study, all the spatial distributions of trends were used in this way and regions where the trend is significant at the 95% level were shaded.
2.4. Swell Index
The swell index [33,34] is used to quantitatively analyze whether the swell is dominant in global waves:
where Si is the swell index, hs is swell-wave height, Ts is the mean wave period of swells, hm is SWH, and Tm is the mean wave period of mixed waves.
3. Results
3.1. Slowdown in Trend of Global Average SWH from 1999 to 2013
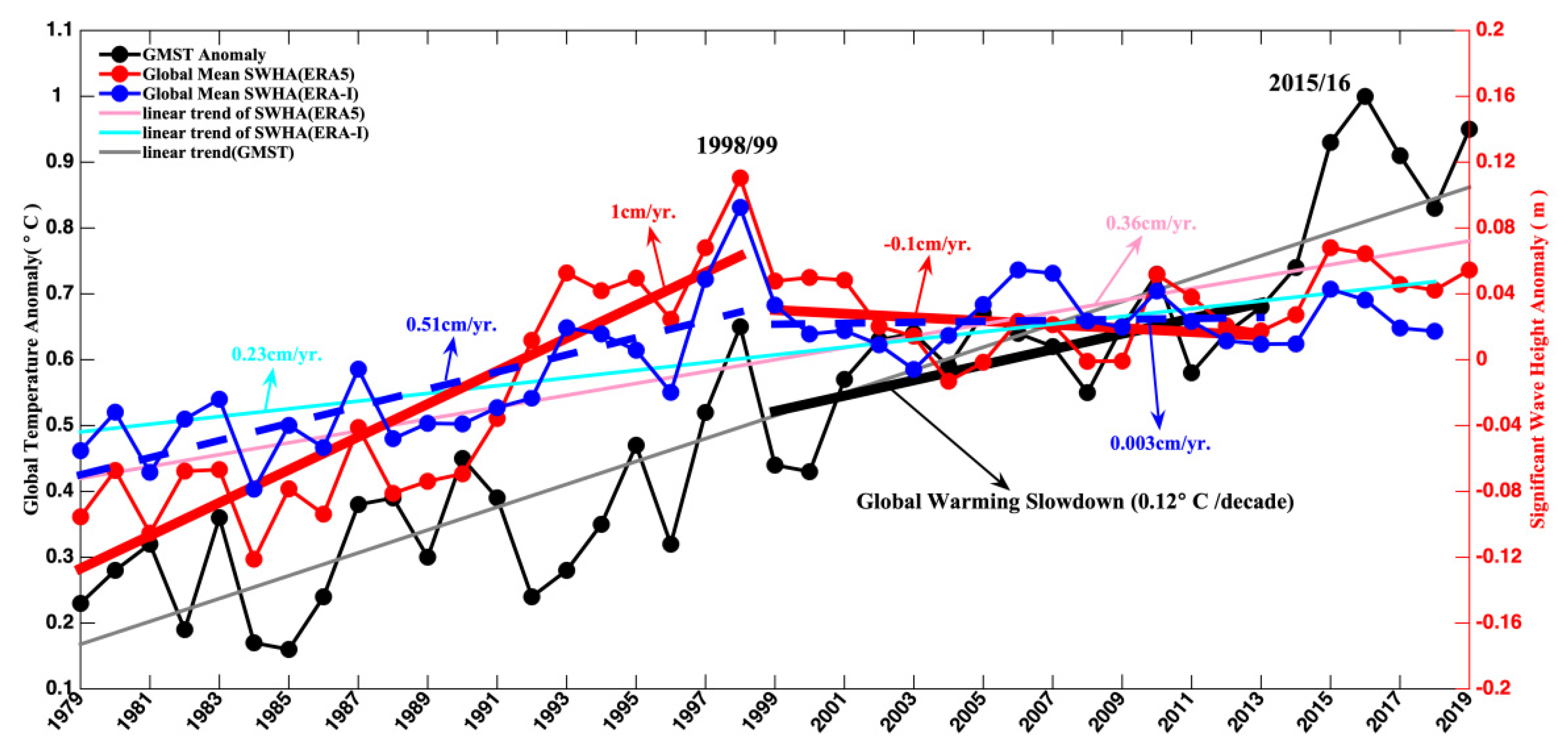
Both observations and model simulations suggested that the rate of increase in the annual GMST anomaly slowed down over the 15 years from 1998 to 2012, with the ocean being widely viewed as an important element in this phenomenon [6]. Waves are an important player in air–sea interactions, and wave characteristics are greatly affected by the climate. Figure 1 shows the time series of the global mean SWH anomaly (SWHA) and GMST [35] from 1979 to 2019 (41 years). The wave data is from the ECMWF (ERA5 and ERA-Interim), and the GMST data was obtained from the National Oceanic and Atmospheric Administration (NOAA) (see Methods and Data availability). The GMST time series was correlated with the ERA5 (0.68) and ERA-Interim (0.71) global mean SWHA time series. The long-term time series trends for GMST and SWHA were first calculated using the Mann-Kendall (MK) test (see Methods) and linear fitting. It was found that the growth rate of the GMST slowed down significantly after 1998, and accelerated again after 2013. Figure 1 shows that SWHs increased by 0.36 cm per year from 1979 to 2019 (ERA5) and by 0.23 cm per year from 1979 to 2018 (ERA-interim). SWH exhibited a slowdown between the two large El-Niño events (1999–2013). The slope of SWHA from the ERA5 was −0.100 cm per year, and that from the ERA-Interim was 0.003 cm per year over this period. Over the first 20 years (1979–1998), SWHs increased by 1.00 cm per year (ERA5) and by 0.51 cm per year (ERA-interim). In other words, the SWH growth rate for the first 20 years of data was much larger than that for the global warming slowdown period.
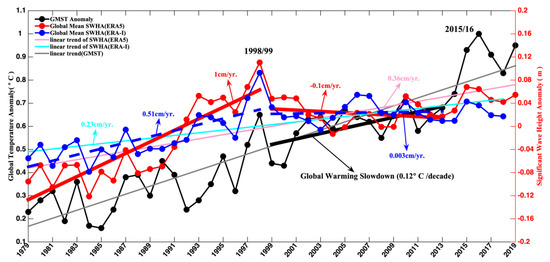
Figure 1.
Significant wave height annual anomalies (with respect to the 1979–2019 average of 2.47 m) averaged over the global oceans using ERA5 reanalysis data (solid red line; units: m), (with respect to the 1979–2018 average of 2.36 m) from ERA-Interim reanalysis data (solid blue line) and global mean surface temperature with respect to the 1981–2010 average (solid black line; units: °C). The blue dotted line is the linear trend of global SWH anomalies. The two thick red lines (ERA5) and two blue dotted lines (ERA-Interim) represent the slopes of global SWH anomalies during 1979–1998 and 1999–2013, respectively. The thick black line is the slope of the global mean surface temperature during the global warming slowdown period. The years corresponding to strong El-Niño events in 1998/99 and 2015/16 are annotated on the graph. The solid lines represent the linear trends of SWHA from ERA5 (light red), SWHA from ERA-Interim (light blue) and global mean surface temperature from NOAA (grey).
3.2. Uneven Geographical Distribution in SWH Trends from 1999 to 2013
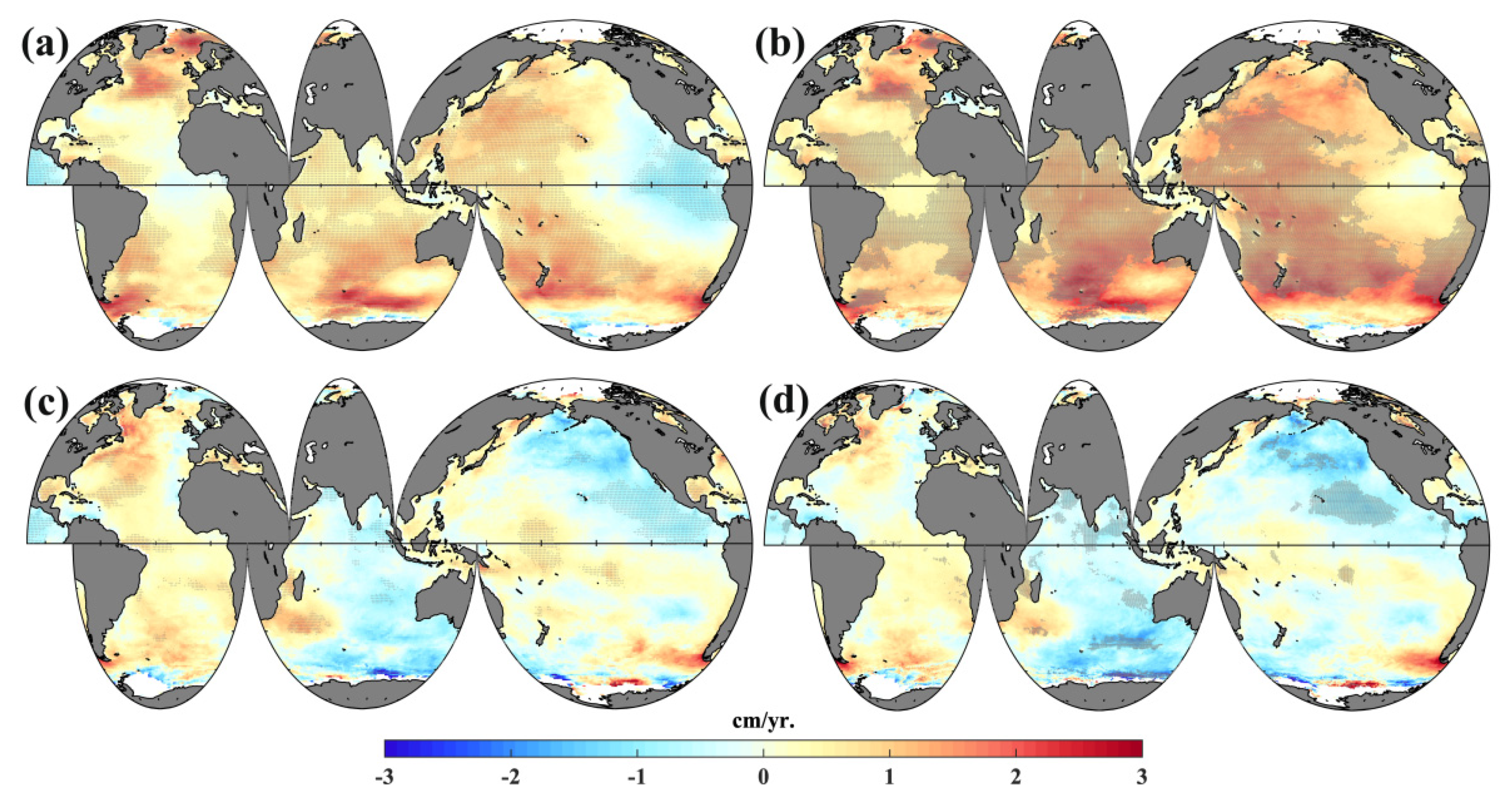
To better understand the global SWH trend, the global spatial distribution of the annually averaged SWH trend from 1979 to 2013 was investigated. Figure 2a (ERA-interim) and Figure 2b (ERA5) display global distributions of SWH variation from 1979 to 1998, showing a clear global upward trend. The SWH in the Southern Ocean and high-latitude northern Atlantic showed a stronger positive trend (2.5 cm per year) than the other oceans. The SWH increase in the northwestern Pacific and Arabian Sea was approximately 1.5 cm per year. However, the eastern equatorial Pacific Ocean demonstrated a weak negative trend, and the regions of decreasing wave height in the ERA-interim data were larger than those for ERA5. Figure 2c (ERA-interim) and Figure 2d (ERA5) show the spatial distributions of the SWH slowdown over the period from 1999 to 2013. Weaker SWH-increasing trends can be found in the high latitudes of the northern Atlantic (1.5 cm per year), and a weak negative trend can be observed near Greenland (1.0 cm per year). Large regions of the Indian Ocean and high latitudes of the northern Pacific demonstrated a stronger decreasing trend, reaching a maximum of −1.5 cm per year. There was a clearly increasing trend of approximately 0.5 cm per year in the equatorial east Pacific, the southern Atlantic, and south of Madagascar. Similar negative trend distributions occurred in the southern Indian Ocean and the high latitudes of the northern Pacific, as also observed by the altimeter (Figure A1).
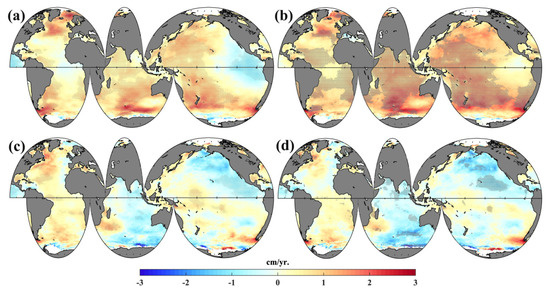
Figure 2.
Spatial distribution of global annual mean SWH trend (units: cm/yr.) from ERA-Interim (a: 1979–1998; c: 1999–2013) and ERA5 (b: 1979–1998; d: 1999–2013). The grey shaded areas represent points that are statistically significant at a 95% confidence level.
3.3. Reliability of Reanalysis Data for Estimating SWH Trends
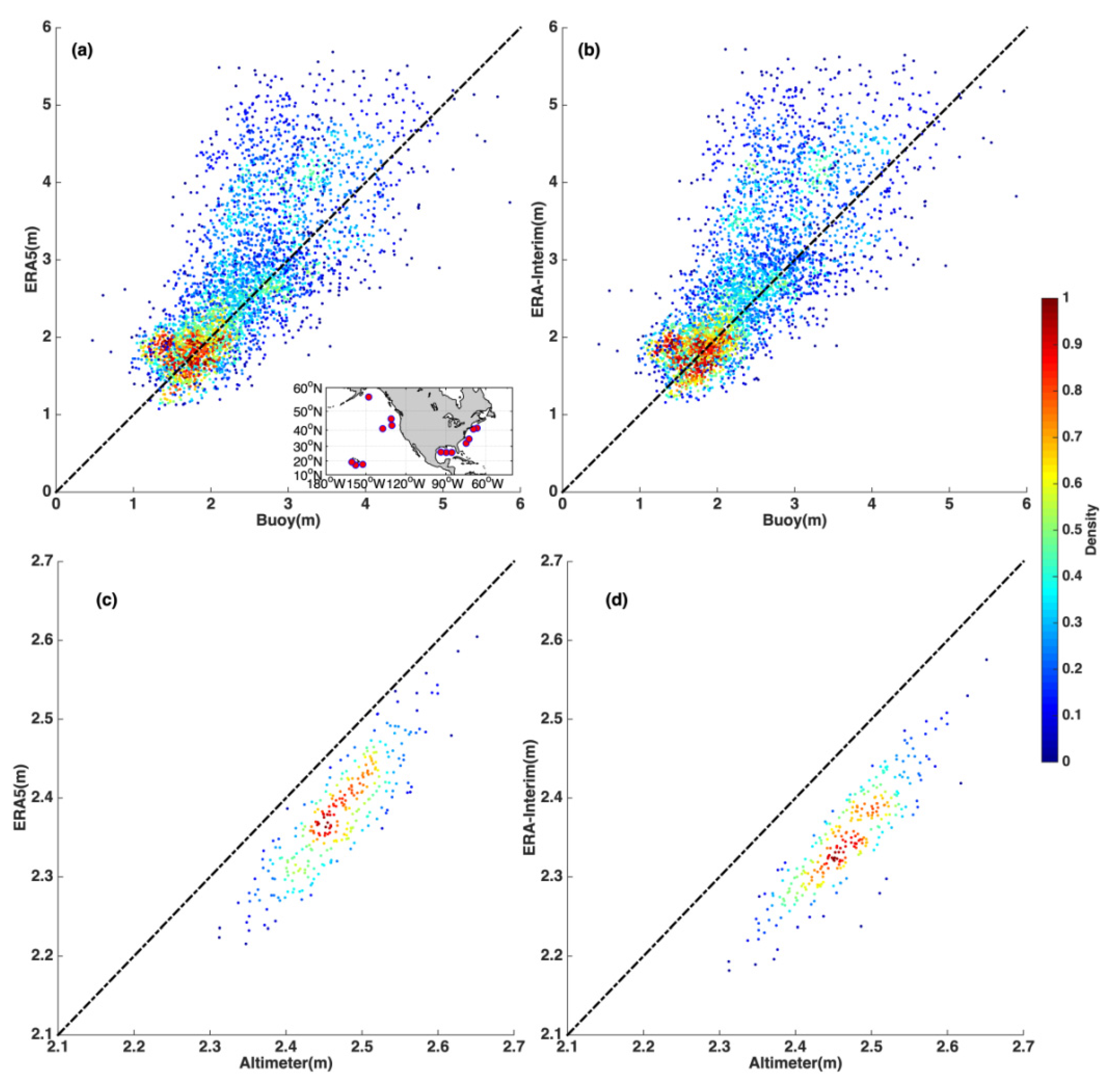
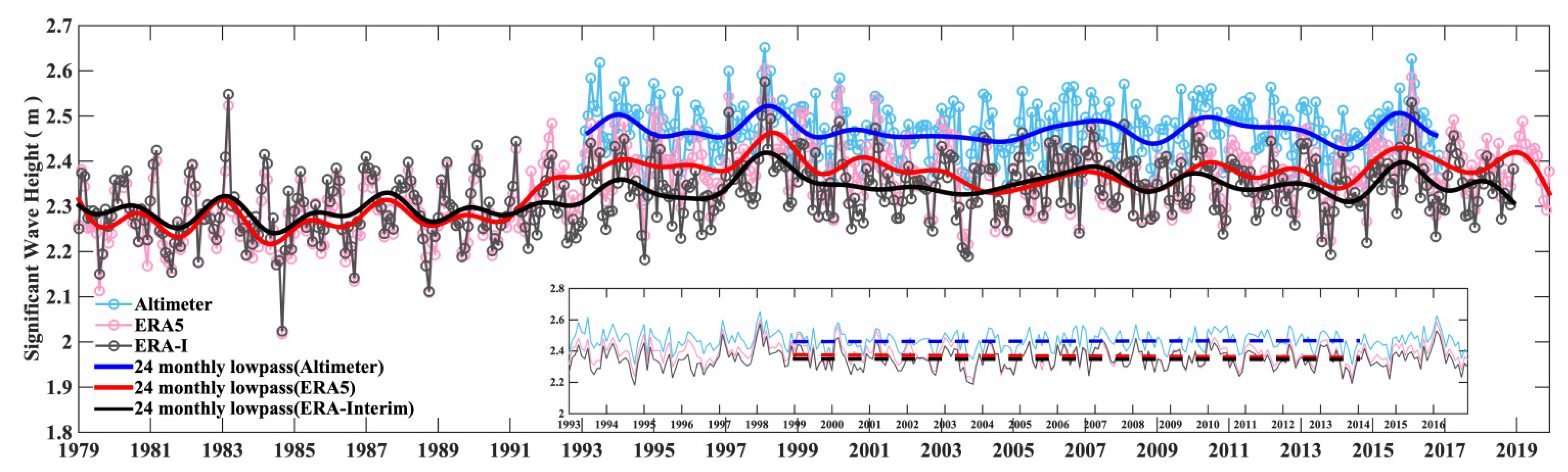
Figure 3 shows scatter plots comparing the monthly values of the two reanalysis datasets compared to those from the NDBC buoys and satellite altimeters. These comparisons were in good agreement, although they demonstrated differences in spatial averaging and temporal mis-matches. Globally averaged changes in wave climate, as suggested by the reanalysis data, were confirmed by comparison of time series with the remotely sensed altimeter data, as shown in Figure 4. The comparison shows that the differences between the reanalysis and observations were small. While the wave height fields from the reanalysis datasets (ERA5 and ERA-Interim) were slightly underestimated compared to those from the buoy observations, the overall trends were consistent, and the statistical relative error was measured at 0.18 m between the two reanalysis datasets. The root-mean-square (rms) error of monthly averages between ERA5 (ERA-Interim) and the altimeter data was 0.09 m (0.12 m). The rate of increase in the annually averaged SWH from the altimeter data was 0.045 cm per year during the global warming slowdown period (Figure 4). These results demonstrate that the reanalysis data produced comparable results to buoys for the absolute SWH and to altimeters for globally averaged trends.
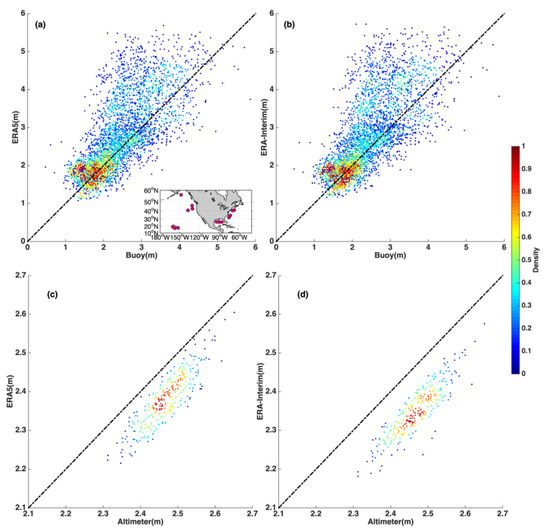
Figure 3.
Correlation scatter plots of monthly SWH (units: m) with density from (a) ERA5 and buoy, (b) ERA-Interim and buoy, (c) ERA5 and altimeter, and (d) ERA-Interim and altimeter data. The ordinate represents the observed wave height, and the abscissa represents the reanalysis wave height. The small insert in the lower right corner of (a) shows the buoys’ geographical locations. The 14 buoys were provided by the NDBC. The root-mean-square error between the ERA5 and altimeter data was 0.09 m. The rms error of monthly averages between the ERA-I and altimeter data was 0.12 m. There were 288 monthly mean global SWH values from the altimeter and the reanalysis. Each buoy had 468 monthly mean SWH records.
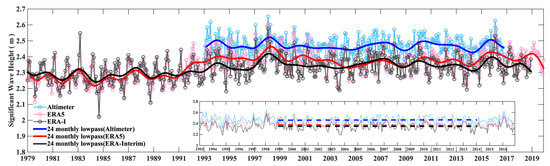
Figure 4.
Time series of monthly-averaged SWH measured by altimeter, ERA5 and ERA-Interim (the solid lines are 24-month low-pass-filtered values). The root-mean-square error of monthly averages between ERA5 and altimeter was 0.09 m. The rms error of monthly averages between the ERA-I and the altimeter was 0.12 m. The small insert in the lower right corner shows the monthly average time series from 1993 to 2016. The three dotted lines represent the linear fittings of SWH measured by altimeter, ERA5 and ERA-Interim from 1999 to 2013, respectively. The SWH slope from the altimeter was 0.04 cm/month; the SWH slope from ERA5 was −0.1 cm/month; and the SWH slope from ERA-Interim was −0.02 cm/month.
To validate the trends obtained from the reanalysis data, the same analysis was applied to the data from the 14 deep-water buoys. Based on their geographical positions, the following areas were identified: the western Atlantic, the Gulf of Mexico, the northeast of the United States, Alaska Bight, the northwest of the United States, and the seas surrounding Hawaii. Table 1 presents the annual rate of change in SWH and SSW from the buoys. We can see that after 1998, these areas, which are normally characterized by wave-height-increasing trends, demonstrated reduced trends, and those areas normally featuring downward trends demonstrated accelerated trends. The buoys located in the Pacific Ocean were notable in this regard. The SSWs at each buoy location showed decreased trends during the global warming slowdown period (1999–2013).

Table 1.
Trend estimates for the annual mean SWH and SSW at buoy locations from NDBC data.
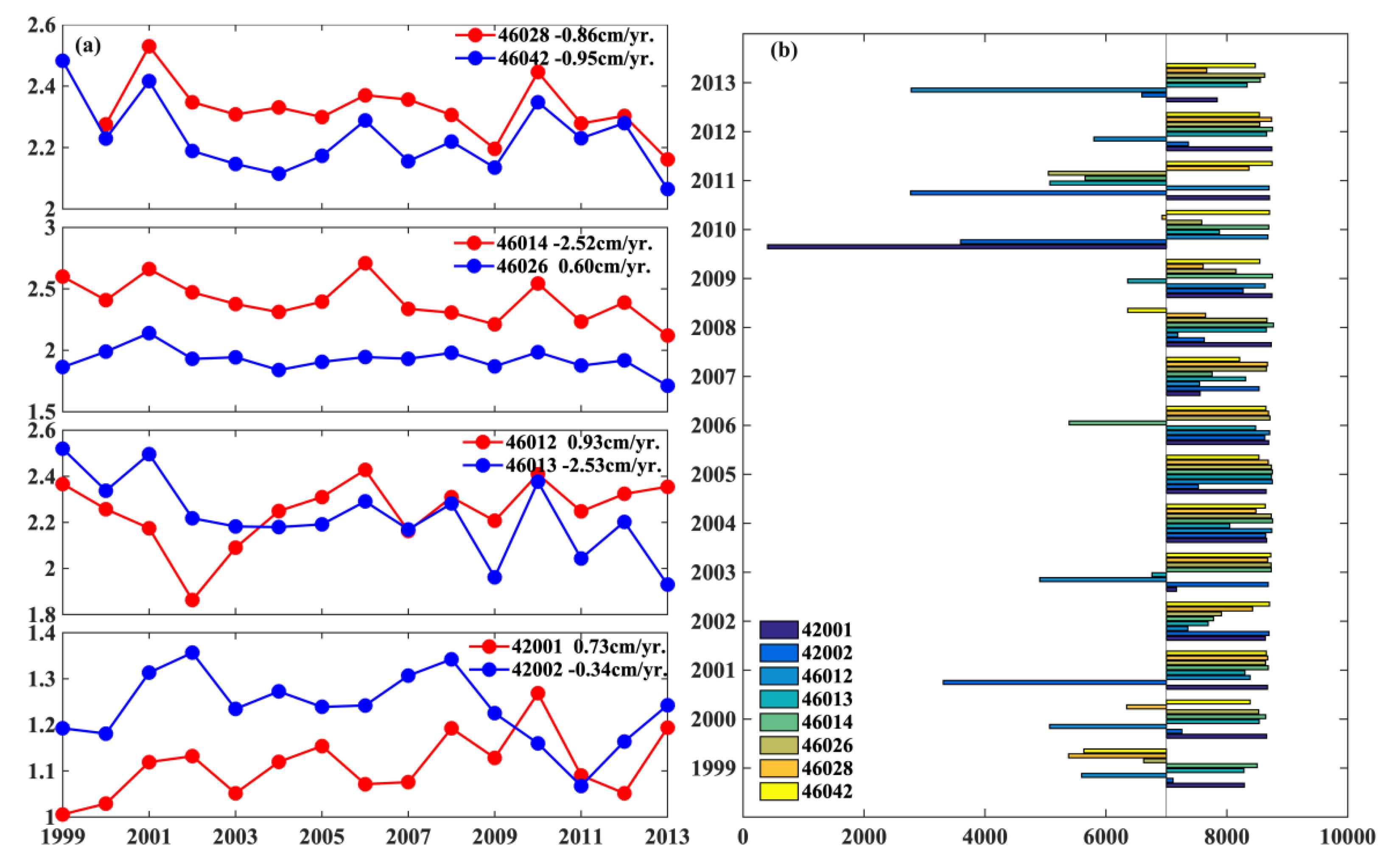
The trends in SWHs for another set of six coastal buoys near the USA-Northeast and two buoys in the Gulf of Mexico were examined (Figure 5a). The detailed information from these stations is listed in Table 2. Increasing SWH trends were apparent at Station 46026, Station 46012, and Station 42001. The other stations exhibited a negative trend from 1999 to 2013. The annual numbers of null values of the hourly measured wave height data were lower during this period (Figure 5b).
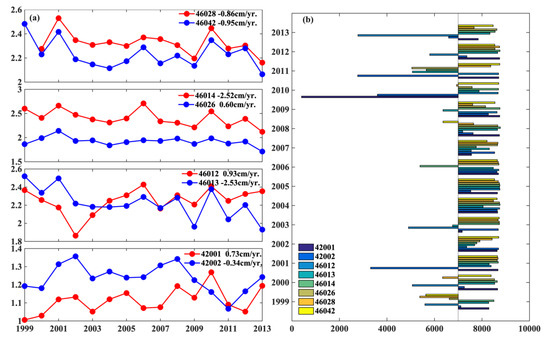
Figure 5.
(a) Time series of annual average SWH measured by eight buoy stations. (b) Histogram of annual number of wave data at each station.

Table 2.
Information on the data of buoys located near USA-Northeast and the Gulf of Mexico.
Although the buoy comparisons described above generally supported the observed trends form the reanalysis datasets, these buoy data should be treated with some caution. As pointed out by Gemmrich et al. [36], buoy data can be non-homogeneous due to changes in buoy hull types and the processing methods of long time series.
3.4. Different Trends in Wind-Generated Waves and Swell
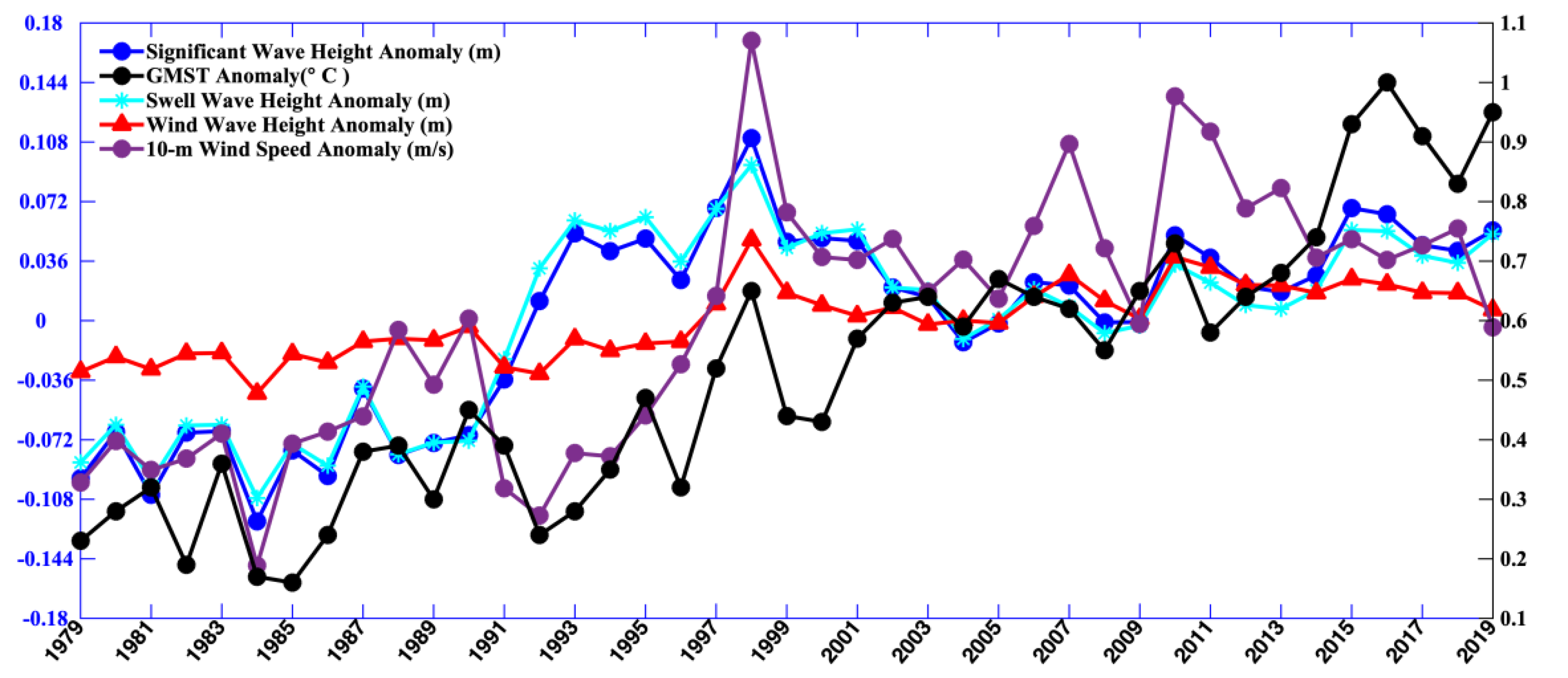
Global warming has an impact on the sea surface wind field [37]. Furthermore, the spatio-temporal changes of the sea surface wind field can affect the wave field. When directly generated and affected by local winds, waves are called wind sea. After the wind ceases to blow, waves propagate away from their areas of generation and experience changes in their properties, becoming swells. Figure 6 shows a comparison of globally averaged SSW, SWH, swell wave height, and wind sea wave height over the study period. The correlation coefficient between the mean SSW and SWH was 0.67. The correlation coefficient between SSW and wind sea wave height was 0.97, as expected. There was also a good agreement between the wind speed anomalies and the wind-wave height anomalies.
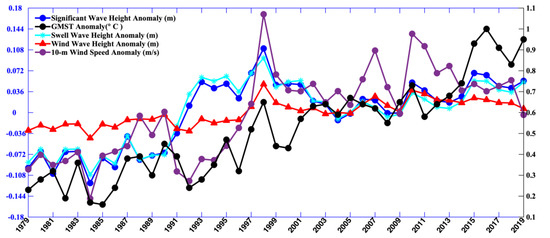
Figure 6.
Time series of annual anomalies of global mean SWH (solid blue line; units: m), global mean surface wind speed (solid purple line; units: m/s), global mean swell wave height (solid cyan line; units: m), and global mean wind wave height (solid red line; units: m) from the ERA5 reanalysis data. The black line is the global mean surface temperature anomalies with respect to the years 1981–2010. The wave height anomaly quantities are represented on the left axis and the wind speed anomalies are represented on the right axis.
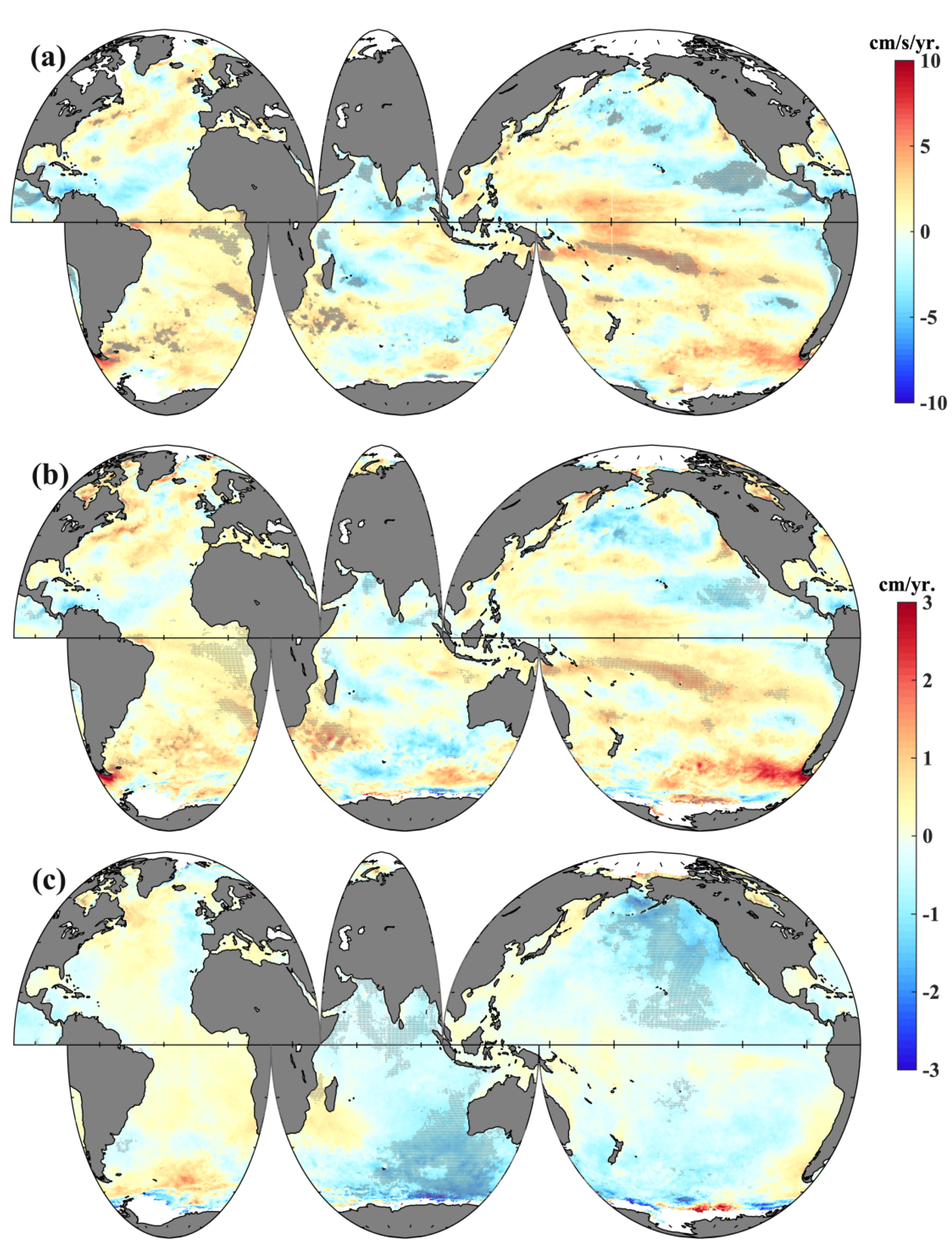
Figure 7a displays the spatial trend of global 10-m SSW speed from 1999 to 2013. The variations of SWH in the northern Indian Ocean, the area south of the Aleutian Islands, the eastern equatorial Pacific, and the waters surrounding Hawaii were positively correlated with SSW speed, and their trends were similar. Decreasing trends of 10-m SSW speed were found in the Arabian Sea and the Bay of Bengal (−6 cm/s per year). The negative patterns in these seas were the same as those of SWH, as shown in Figure 2d. In the equatorial Pacific Ocean, large regions of the northern Pacific, Indian Ocean near Australia, and the mid-latitudes of the southern Atlantic Ocean demonstrated negative trends. The surface wind trend grew more slowly or even reversed in the northern Pacific, the Indian Ocean, the Caribbean Sea, the Scotia Sea, and the waters surrounding Hawaii compared to the first 20 years (1979–1998) of the study period (Figure A2a).
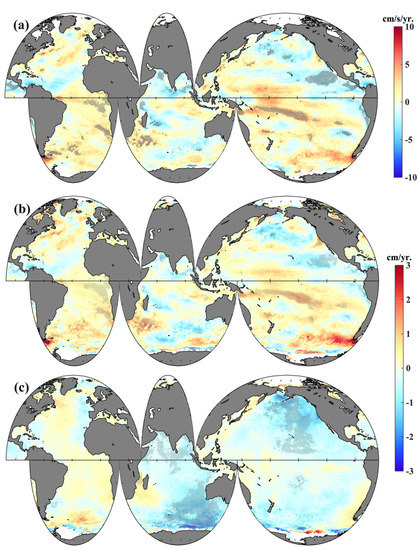
Figure 7.
The linear trends in surface wind speed and significant wave height and its components during the global warming slowdown period: (a) spatial distributions of global annual mean surface wind speed trend, (b) wind wave height trend, and (c) swell wave height trend from ERA5. The grey shaded areas represent points that are statistically significant at ae 95% confidence level.
Surface gravity waves in the open ocean are complex, and they are classified into two categories: locally generated wind sea waves and swell [1,38]. In every area of the ocean, a mixture of both wind sea waves (Figure A2b) and swells (Figure A2c) can be observed. The global wave field is dominated by swells, especially in the low latitudes [39,40] (see Figure A3 and Figure A4). For swell wave height, the strong positive trends across the majority of the global oceans were statistically significant (2 cm per year), and the trends were similar to those of the SWH during the period 1979–1998. Statistically significant trends in wind-wave height (Figure 7b) and swell-wave height (Figure 7c) in the global warming slowdown period were identified. Decreasing trends in significant wind sea wave height and wind speed were found in the same seas, and their spatial correlation reached 0.71. The decreasing trend in the waters surrounding Hawaii was about 1 cm per year. Large high-latitude regions in the northern Pacific demonstrated a stronger decreasing trend, reaching a maximum of 2 cm per year. Some regions of the global oceans nonetheless demonstrated positive trends in wind-generated waves for the period 1999–2013. By contrast, there were more regions characterized by negative trends in swell-wave height. The decreasing trend in swell in large regions of the Pacific and Indian Oceans was 1.5 cm per year. The trend in swells in the Indian Ocean was in good agreement with that of SWH (Figure 2d), because swells play a dominant role in mixed waves throughout most of the Indian Ocean, especially in the tropical waters. The swell-wave height in the Roaring Forties of the Indian Ocean is generated by local winds and propagates to the tropical waters [41]. The increasing trend in swell wave height slowed down over most of the Atlantic during the global warming slowdown period.
4. Discussion and Conclusions
We examined global trends in SWH through a comprehensive analysis of reanalysis, satellite altimeter, and buoy data. We found clear effects of the global warming slowdown on the global wave climate. The global mean SWH trend was similar to that of the global mean surface (land and ocean) temperature: the increasing trend of the mean SWH slowed down during the global warming slowdown period (Figure 1). Large regions of the Pacific and Indian oceans showed rapidly decreasing trends in mean SWH from 1999 to 2013 (Figure 2). Changes in wave height caused by sea surface wind energy transfer and sea surface temperature have an important influence on the global wind pattern [18]. Surface winds are influenced by surface pressure patterns and it has been demonstrated that changes in surface temperature are altering these surface pressure patterns. For instance, high-latitude, low pressure systems are strengthening and moving closer to the poles. In addition, warmer oceans provide a greater source of energy for storms. Hence, there is growing evidence of more frequent and more intense storm systems [42].
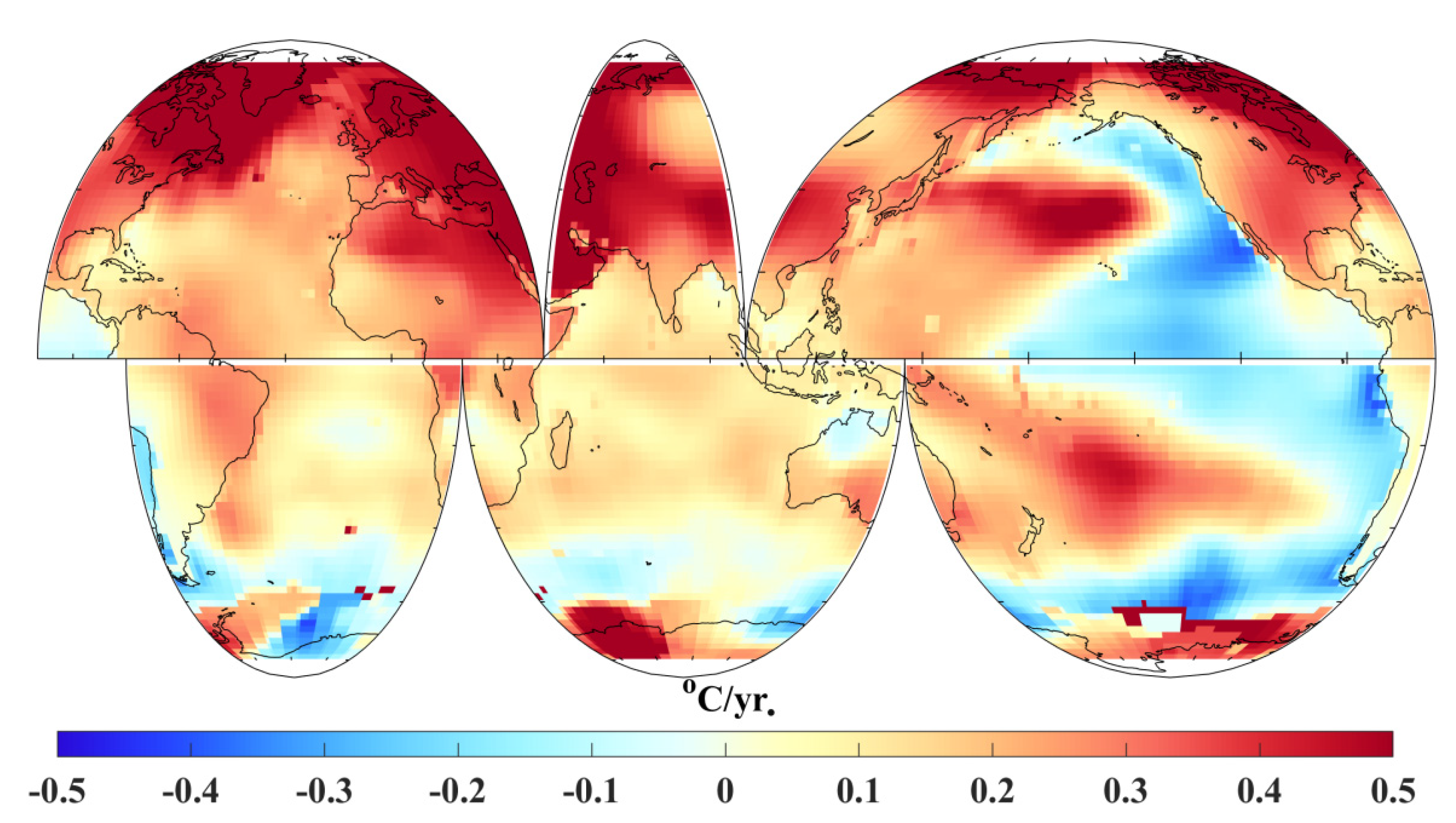
The spatial distributions of the GMST trend during the global warming slowdown period are shown in Figure 8. GMST-decreasing trends were found in the eastern Pacific and Southern Ocean. The SWH and GMST showed a negative correlation in the Indian Ocean and a positive correlation in the eastern tropical Pacific. Figure A4 shows that swells were the dominant wave component in the Indian Ocean. Given that the variation of wave height was generally affected by SSW, the wind-generated wave followed the trend in wind speed, but swell variation showed more complex patterns in the study period (Figure 6 and Figure 7). Reguero et al. [18] found that SWH and GMST are linked by atmospheric teleconnections and pointed out that wave power is affected by upper-ocean warming. The global warming slowdown between 1998 and 2013 left its footprint in many ways. This study focused on how global surface waves adjusted during the slowdown.
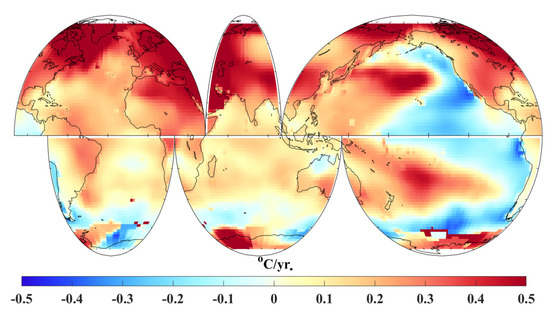
Figure 8.
Spatial distributions of GMST linear trend with respect to the 1979–2013 average during the global warming slowdown period (data source: the land surface air temperature is from GHCNv4 [43] and the sea surface temperature is from ERSSTv5 [44]).
It should be noted that there was a slight jump from 1991 to 1992 in the time series of SWH anomalies from ERA5 and ERA-Interim, shown in Figure 1, which might have been caused by the start of the data assimilation of the altimeter products into the reanalysis datasets. After the adjustment period, the trend in global SWH provided by ERA5 is similar to that of the altimeter data during 1993–2016 (Figure 4). The spatial patterns in SWH trends between the ERA5 and altimeter data were similar from 1999 to 2013 (Figure A1). Moreover, the slight jump did not affect the slopes of the trend before or after 1999; therefore, the effect of the data assimilation on the reanalysis did not appear to change the conclusions obtained in the present study.
Author Contributions
Conceptualization: C.D.; methodology: Y.C., C.D., I.R.Y.; investigation: Y.C.; visualization: Y.C.; supervision: C.D., J.Y.; writing—original draft: Y.C.; writing—review and editing: Y.C., C.D., I.R.Y., J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by The National Key Research and Development Program of China under contract No.2017YFA0604100, 2016YFA0601803, and 2016YFC1401407; the Guangdong Basic and Applied Basic Research Foundation, contract 2019A1515110840; the Key Program of Marine Economy Development (Six Marine Industries), Special Foundation of the Department of Natural Resources of Guangdong Province (GDNRC [2020]049).
Data Availability Statement
The ERA-Interim wave reanalysis from the ECMWF used in this study can be accessed online (https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/). The ERA5 global wave (wind) reanalysis data from the ECMWF were downloaded in July 2020, and can be accessed at https://cds.climate.copernicus.eu/cdsapp#!/search?type=dataset. The in situ wave data were downloaded from the National Data Buoy Center, and can be accessed at https://www.ndbc.noaa.gov/. The altimeter data were obtained from the IFREMER, and can be accessed at http://globwave.ifremer.fr/products/demo-products/item/417-merged-altimeter-wave-height-product. The global annual mean surface (land and ocean) temperature (GMST) data were downloaded in July 2020, and can be accessed at https://www.ncdc.noaa.gov/cag/.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
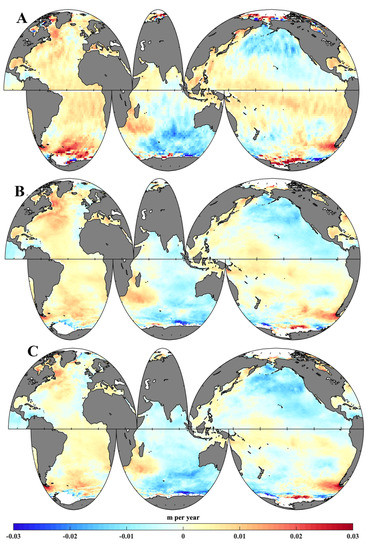
Figure A1.
Spatial distributions of global annual SWH trends for 1999–2013 from (A) altimeter, (B) ERA-Interim and (C) ERA5.
Figure A1.
Spatial distributions of global annual SWH trends for 1999–2013 from (A) altimeter, (B) ERA-Interim and (C) ERA5.
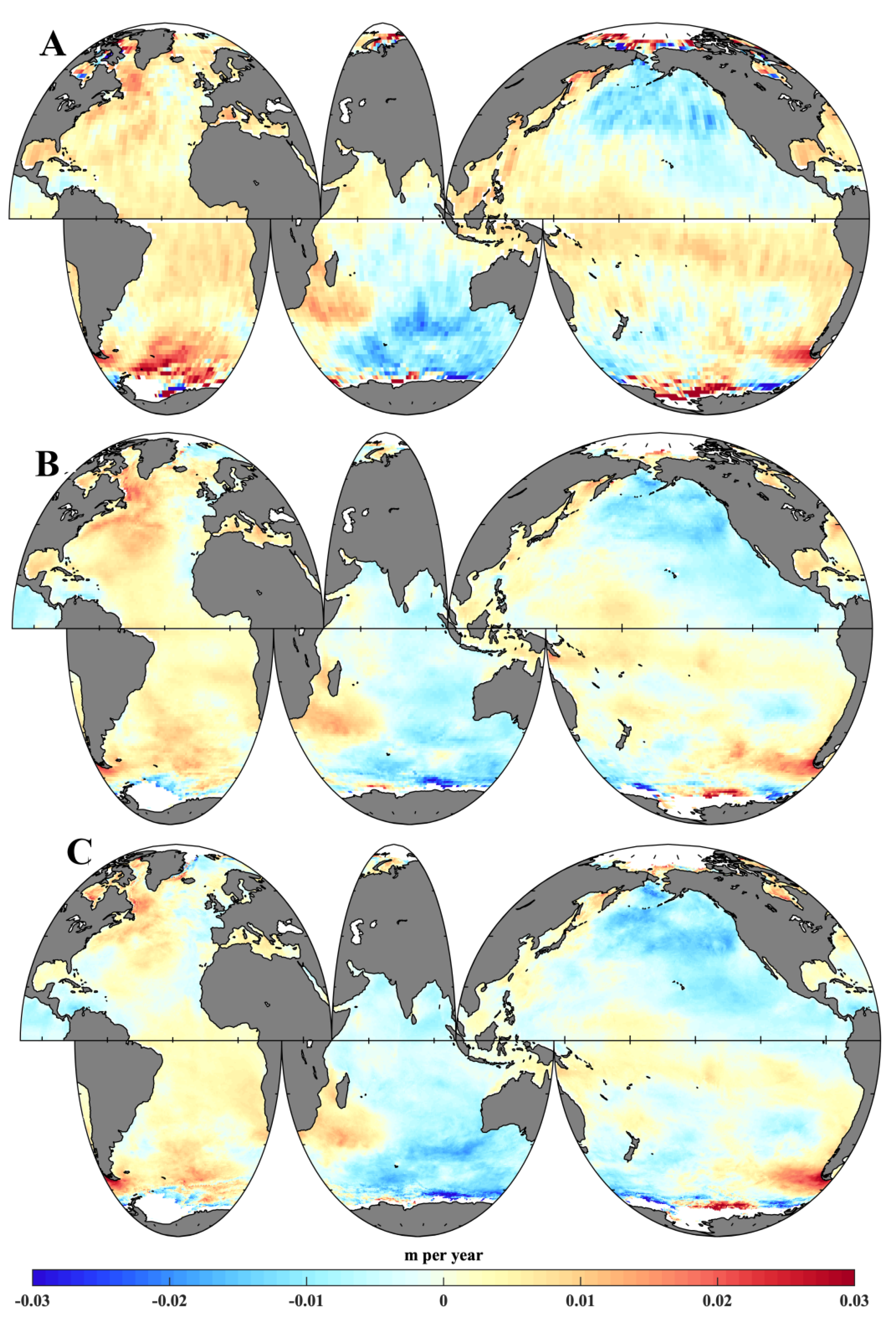
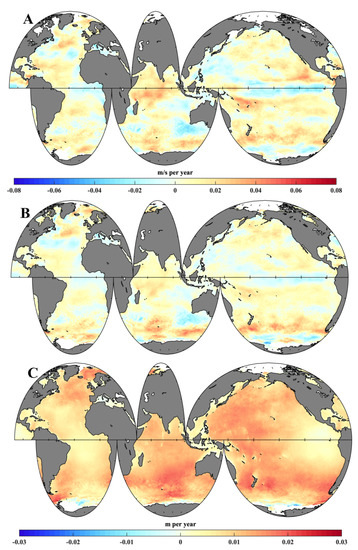
Figure A2.
Spatial distributions of (A) global annual mean surface wind speed trends, (B) wind wave height trend and (C) swell wave height trend, for 1979–1998 from ERA5.
Figure A2.
Spatial distributions of (A) global annual mean surface wind speed trends, (B) wind wave height trend and (C) swell wave height trend, for 1979–1998 from ERA5.
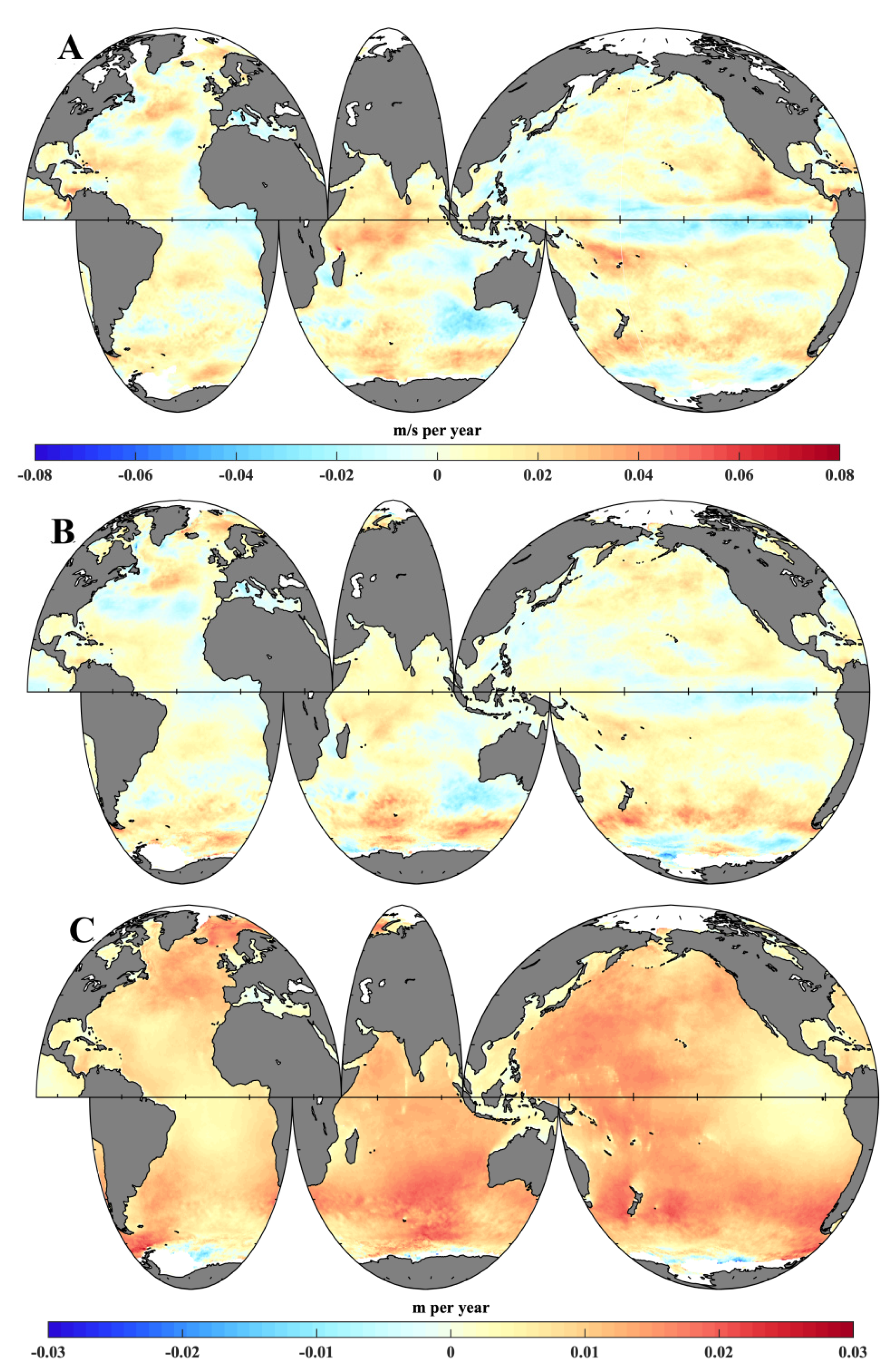
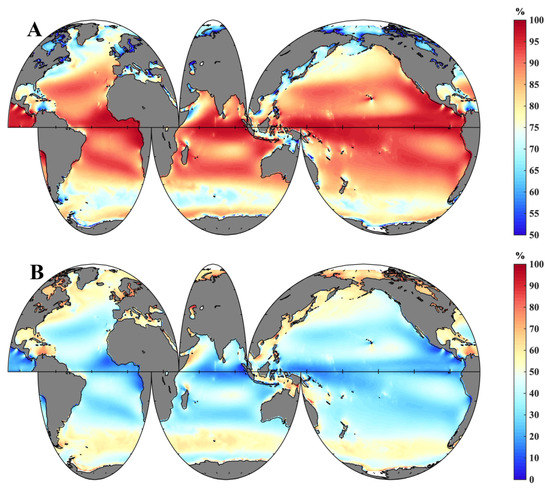
Figure A3.
Percentage of (A) wind wave height and (B) swell wave height in mixed wave heights from by ERA5.
Figure A3.
Percentage of (A) wind wave height and (B) swell wave height in mixed wave heights from by ERA5.
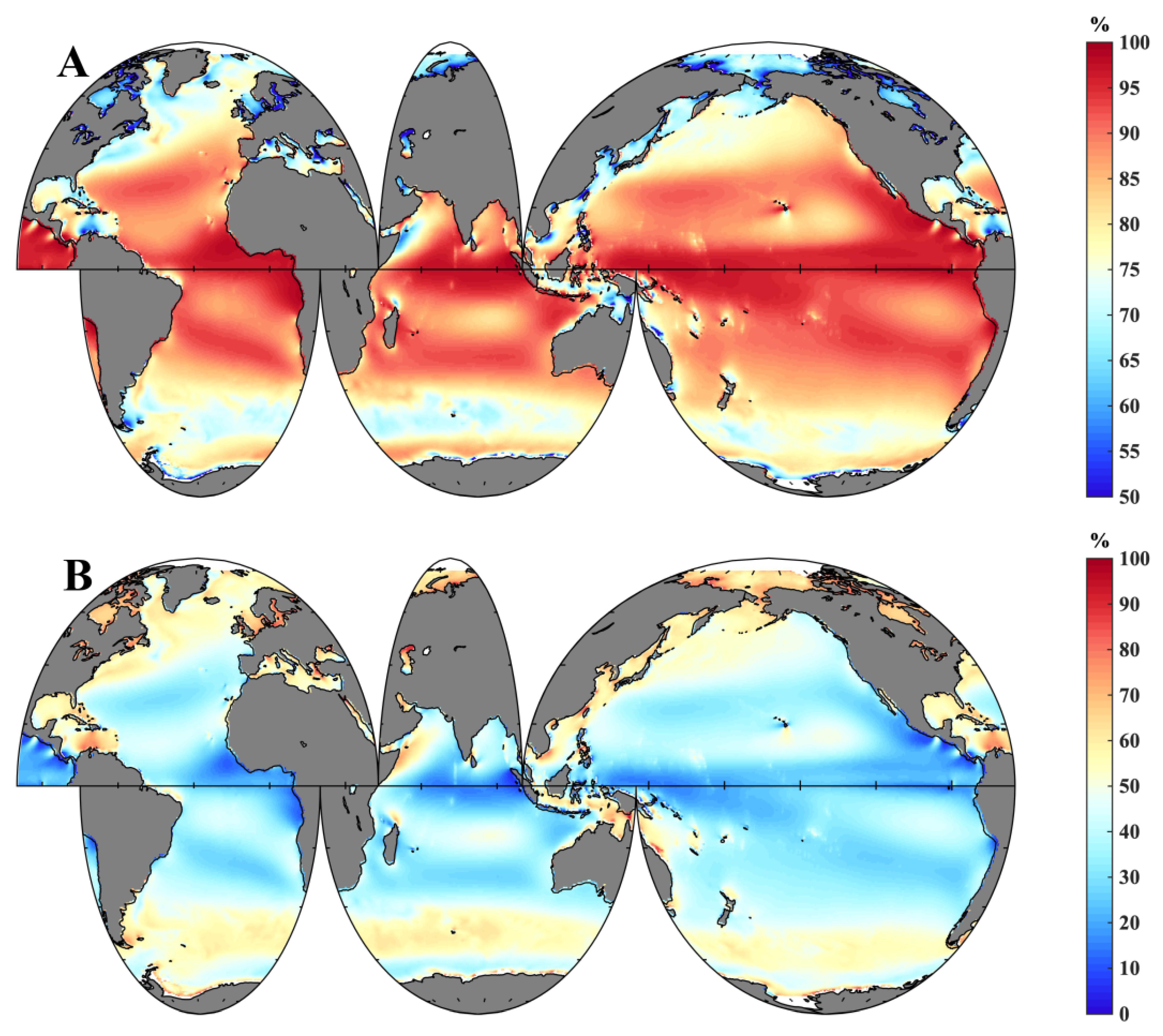
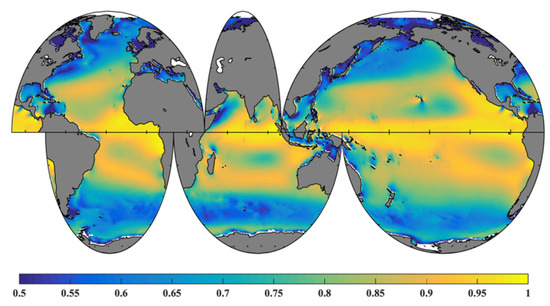
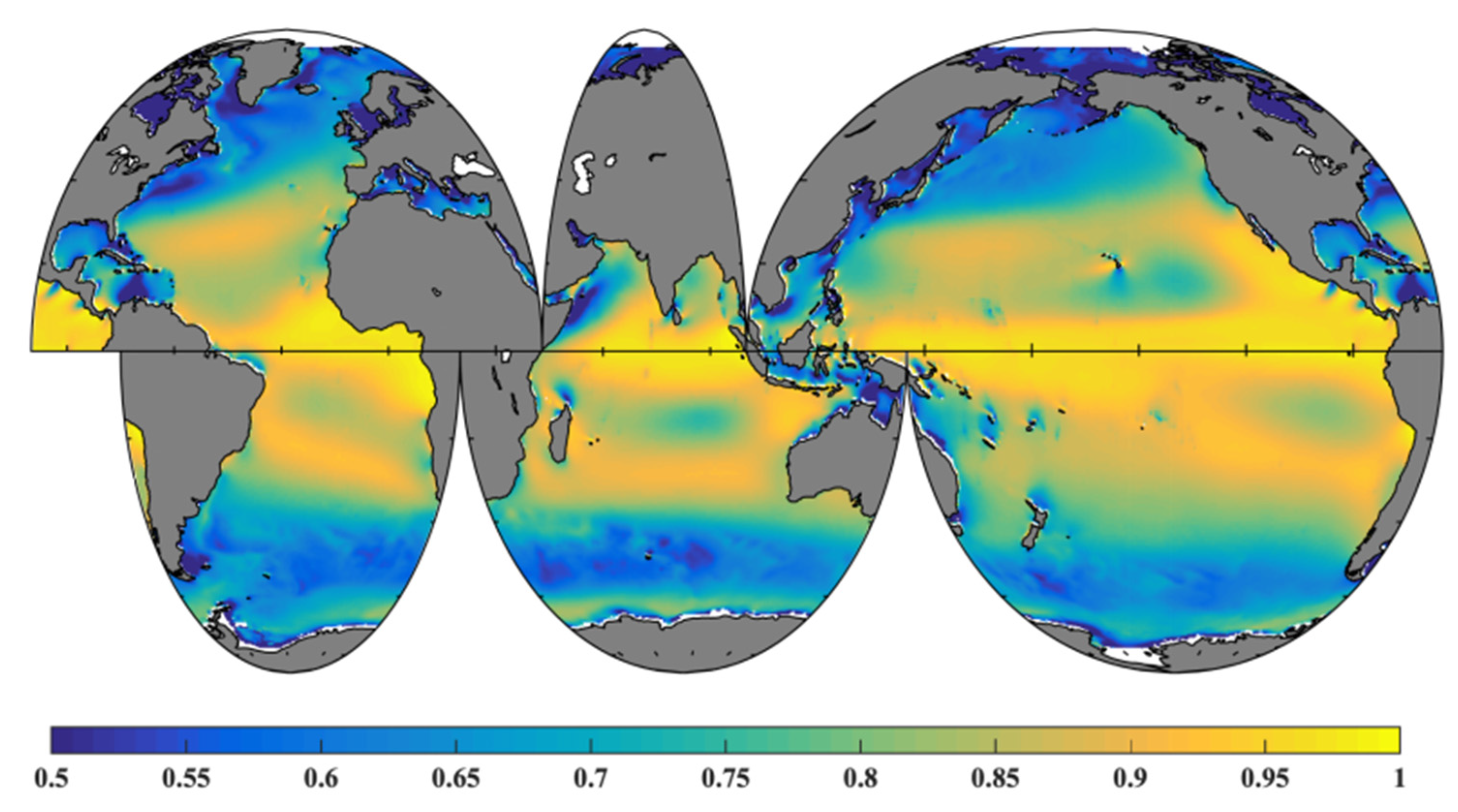
Figure A4.
Swell index (1979–2019) for the global oceans from ERA5.
Figure A4.
Swell index (1979–2019) for the global oceans from ERA5.
References
- Young, I.R.; Zieger, S.; Babanin, A.V. Global trends in wind speed and wave height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef]
- Kumar, P.; Min, S.K.; Weller, E.; Lee, H.; Wang, X.L. Influence of climate variability on extreme ocean surface wave heights assessed from ERA-Interim and ERA-20C. J. Clim. 2016, 29, 4031–4046. [Google Scholar] [CrossRef]
- Morim, J.; Hemer, M.; Wang, X.L.; Cartwright, N.; Trenham, C.; Semedo, A.; Young, I.; Bricheno, L.; Camus, P.; Casas-Prat, M.; et al. Robustness and uncertainties in global multivariate wind-wave climate projections. Nat. Clim. Chang. 2019, 9, 711–718. [Google Scholar] [CrossRef]
- Knight, J.; Kenneby, J.; Folland, C.; Harris, G.; Jones, G.S.; Palmer, M.; Stott, P. Do global temperature trends over the last decade falsify climate predictions? Bull. Am. Meteorol. Soc. 2009, 90, 22–23. [Google Scholar]
- Kerr, R.A. What happened to global warming? Scientists say just wait a bit. Science 2009, 326, 28–29. [Google Scholar] [CrossRef][Green Version]
- Kosaka, Y.; Xie, S.-P. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 2013, 501, 403–407. [Google Scholar] [CrossRef]
- Yan, X.H.; Boyer, T.; Trenberth, K.; Karl, T.R.; Xie, S.; Nieves, V.; Tung, K.; Roemmich, D. The global warming hiatus: Slowdown or redistribution? Earths Future 2016, 4, 472–482. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.P.; Kosaka, Y. What caused the global surface warming hiatus of 1998–2013? Curr. Clim. Chang. Rep. 2017, 3, 128–140. [Google Scholar] [CrossRef]
- Roberts, C.; Palmer, M.; McNeall, D.; Collins, M. Quantifying the likelihood of a continued hiatus in global warming. Nat. Clim. Chang. 2015, 5, 337–342. [Google Scholar] [CrossRef]
- Fyfe, J.C.; Gillett, N.P.; Zwiers, F.W. Overestimated global warming over the past 20 years. Nat. Clim. Chang. 2013, 3, 767–769. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Alexander, L.V.; Allen, S.K.; Bindoff, N.L.; Bréon, F.M.; Church, J.A.; Cubasch, U.; Emori, S.; et al. Technical summary. In Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Cowtan, K.; Way, R.G. Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Q. J. R. Meteorol. Soc. 2014, 140, 1935–1944. [Google Scholar] [CrossRef]
- Karl, T.R.; Arguez, A.; Huang, B.; Lawrimore, J.H.; McMahon, J.R.; Menne, M.J.; Peterson, T.C.; Vose, R.S.; Zhang, H.-M. Possible artifacts of data biases in the recent global surface warming hiatus. Science 2015, 348, 1469–1472. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, X.; Zhang, Q.; Lin, Y.; Hao, M.; Luo, Y.; Zhao, Z.; Yao, Y.; Chen, X.; Wang, L.; et al. Recently amplified arctic warming has contributed to a continual global warming trend. Nat. Clim. Chang. 2017, 7, 875–879. [Google Scholar] [CrossRef]
- Sasaki, W. Changes in the North Pacific wave climate since the mid-1990s. Geophys. Res. Lett. 2014, 41, 7854–7860. [Google Scholar] [CrossRef]
- Wu, L.; Qin, J.; Wu, T.; Li, X. Trends in global ocean surface wave characteristics as represented in the ERA-Interim wave reanalysis for 1979–2010. J. Mar. Sci. Technol. 2018, 23, 2–9. [Google Scholar] [CrossRef]
- Young, I.R.; Ribal, A. Multiplatform evaluation of global trends in wind speed and wave height. Science 2019, 364, 548–552. [Google Scholar] [CrossRef]
- Reguero, B.G.; Losada, I.J.; Méndez, F.J. A recent increase in global wave power as a consequence of oceanic warming. Nat. Commun. 2019, 10, 1–14. [Google Scholar] [CrossRef]
- Hemer, M.A.; Church, J.A.; Hunter, J.R. Variability and trends in the directional wave climate of the Southern Hemisphere. Int. J. Climatol. J. R. Meteorol. Soc. 2010, 30, 475–491. [Google Scholar] [CrossRef]
- Alvarez-Ellacuria, A.; Orfila, A.; Gómez-Pujol, L.; Simarro, G.; Obregon, N. Decoupling spatial and temporal patterns in short-term beach shoreline response to wave climate. Geomorphology 2011, 128, 199–208. [Google Scholar] [CrossRef]
- Semedo, A.; Weisse, R.; Behrens, A.; Sterl, A.; Bengtsson, L.; Gunther, H. Projection of global wave climate change toward the end of the twenty-first century. J. Clim. 2012, 26, 8269–8288. [Google Scholar] [CrossRef]
- Zieger, S.; Vinoth, J.; Young, I.R. Joint calibration of multiplatform altimeter measurements of wind speed and wave height over the past 20 years. J. Atmos. Ocean. Technol. 2009, 26, 2549–2564. [Google Scholar] [CrossRef]
- Timmermans, B.W.; Gommenginger, C.P.; Dodet, G.; Bidlot, J.R. Global Wave Height Trends and Variability from New Multimission Satellite Altimeter Products, Reanalyses, and Wave Buoys. Geophys. Res. Lett. 2020, 47, e2019GL086880. [Google Scholar] [CrossRef]
- Feng, X.; Tsimplis, M.N.; Yelland, M.J.; Quartly, G. Changes in significant and maximum wave heights in the Norwegian Sea. Glob. Planet. Chang. 2014, 113, 68–76. [Google Scholar] [CrossRef]
- Aarnes, O.J.; Abdalla, S.; Bidlot, J.R.; Breivik, O. Marine wind and wave height trends at different ERA-Interim forecast ranges. J. Clim. 2015, 28, 819–837. [Google Scholar] [CrossRef]
- Zheng, C.; Pan, J.; Tan, Y.; Gap, Z.; Rui, Z.; Chen, C. The seasonal variations in the significant wave height and sea surface wind speed of the China’s seas. Acta Oceanol. Sin. 2015, 34, 58–64. [Google Scholar] [CrossRef]
- Zheng, C.; Zhou, L.; Huang, C.; Shi, T.; Li, J. The long-termtrend of the sea surface wind speed and the wave height (wind wave, swell, mixed wave) in global ocean during the last 44 a. Acta Oceanol. Sin. 2013, 32, 1–4. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Munoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balsmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Meindl, E.A. Hamilton G D. Programs of the national data buoy center. Bull. Am. Meteorol. Soc. 1992, 73, 985–994. [Google Scholar] [CrossRef]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 163–171. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Chen, G.; Chapron, B.; Ezraty, R.; Vandemark, D. A global view of swell and wind sea climate in the ocean by satellite altimeter and scatterometer. J. Atmos. Ocean. Technol. 2002, 19, 1849–1859. [Google Scholar] [CrossRef]
- Deng, Z.; Wu, K.; Yu, T. The wave transport of the eastern area of the Pacific. Acta Oceanol. Sin. 2007, 29, 1–9. [Google Scholar]
- NOAA National Centers for Environmental Information. Climate at a Glance: Global Time Series. July 2020. Available online: https://www.ncdc.noaa.gov/cag/ (accessed on 18 July 2020).
- Gemmrich, J.; Thomas, B.; Bouchard, R. Observational changes and trends in northeast Pacific wave records. Geophys. Res. Lett. 2011, 38, L22601. [Google Scholar] [CrossRef]
- Ma, J.; Foltz, G.R.; Soden, B.J.; Huang, G.; He, J.; Dong, C. Will surface winds weaken in response to global warming? Environ. Res. Lett. 2016, 11, 124012. [Google Scholar] [CrossRef]
- Thomson, J.; Rogers, W.E. Swell and sea in the emerging Arctic Ocean. Geophys. Res. Lett. 2014, 41, 3136–3140. [Google Scholar] [CrossRef]
- Semedo, A.; Sušelj, K.; Rutgersson, A.; Sterl, A. A global view on the wind sea and swell climate and variability from ERA-40. J. Clim. 2011, 24, 1461–1479. [Google Scholar] [CrossRef]
- Zheng, K.; Sun, J.; Guan, C.; Shao, W. Analysis of the global swell and wind sea energy distribution using WAVEWATCH III. Adv. Meteorol. 2016, 2016, 8419580. [Google Scholar] [CrossRef]
- Zheng, C.W.; Li, C.Y. Analysis of temporal and spatial characteristics of waves in the Indian Ocean based on ERA-40 wave reanalysis. Appl. Ocean Res. 2017, 63, 217–228. [Google Scholar] [CrossRef]
- Meucci, A.; Young, I.R.; Hemer, M.; Kirezci, E.; Ranasinghe, R. Projected 21st Century changes in extreme wind-wave events. Sci. Adv. 2020, 6, eaaz7295. [Google Scholar] [CrossRef]
- Menne, M.J.; Williams, C.N.; Gleason, B.E.; Rennie, J.J.; Lawrimore, J.H. The global historical climatology network monthly temperature dataset, version 4. J. Clim. 2018, 31, 9835–9854. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended reconstructed sea surface temperature, version 5 (ERSSTv5): Upgrades, validations, and intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).