Change Detection Using a Texture Feature Space Outlier Index from Mono-Temporal Remote Sensing Images and Vector Data
Abstract
1. Introduction
2. Methods
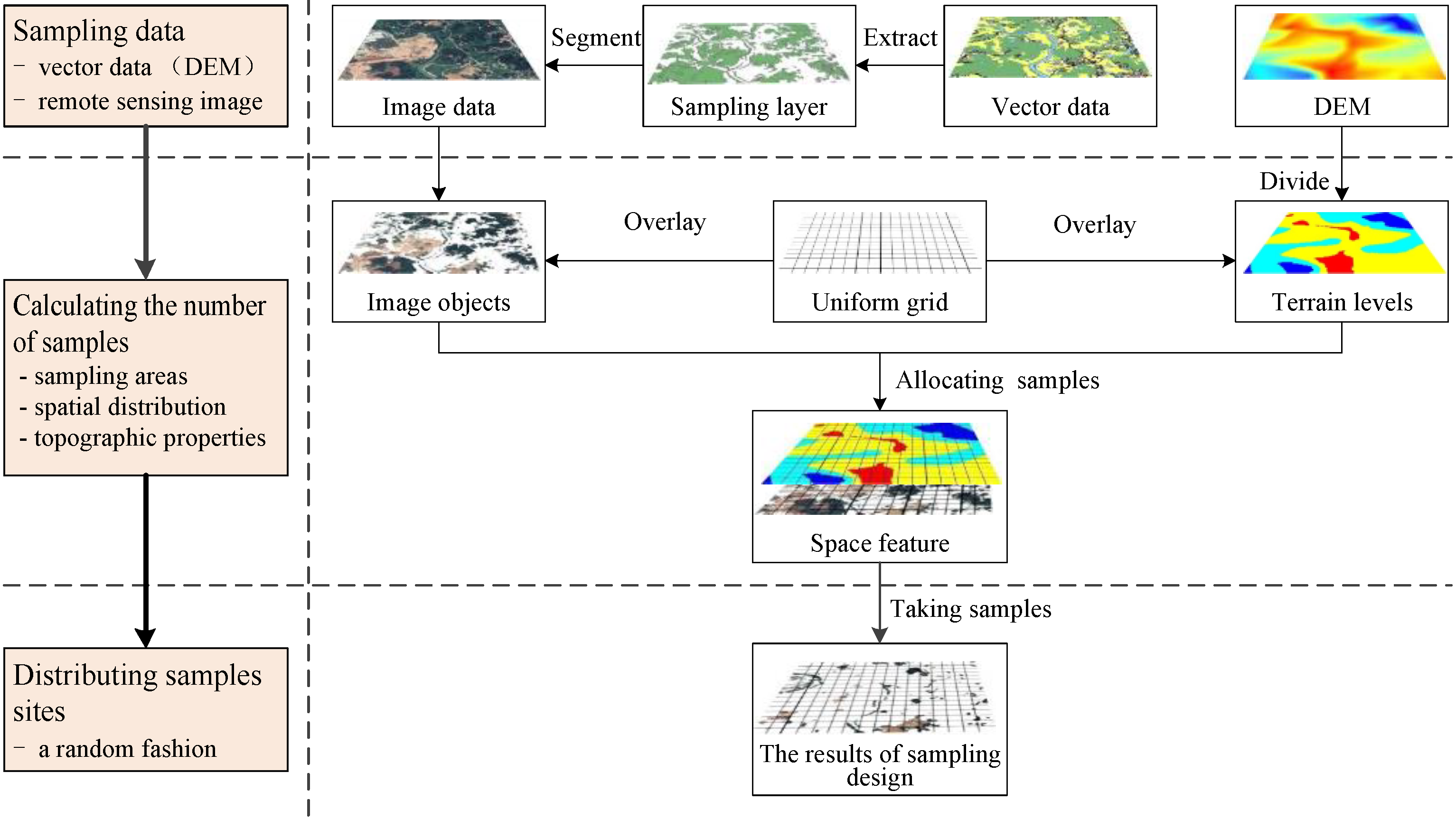
2.1. Sampling Design with a Priori Information from Vector Data and DEM
2.2. Refining Samples by Iteration of Texture Feature Selection and Outlier Sample Elimination
2.2.1. TFCI Computation Based on Information Gain
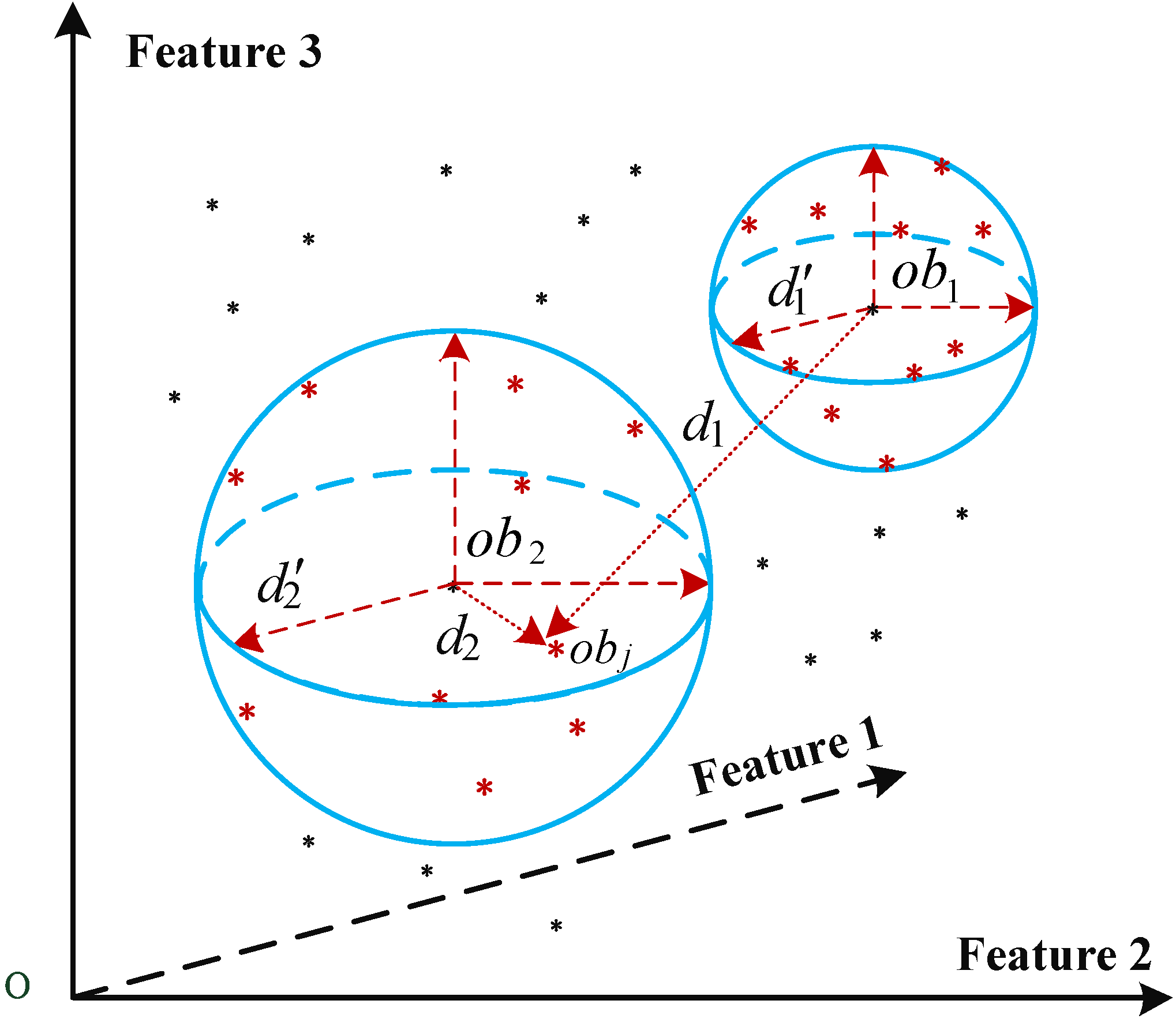
2.2.2. FSOI Computation Based on Local Reachability Density
2.2.3. Refining Samples and Selecting the Optimal Texture Features for Each Category
- 1.
- Calculate the TFCI values using the a priori categories of the initial samples based on Equation (4), and establish the first TFSV by texture feature selection.
- 2.
- Calculate the FSOI values of the initial samples in the TFSV established in step (1) based on Equation (8). Compared with unchanged samples, outlier samples (i.e., the changed samples in the initial sample sets) have higher FSOI values. Thus, outlier samples can be identified by setting an appropriate FSOI threshold. In general, a higher FSOI threshold may misjudge outlier samples as unchanged samples. On the contrary, a lower FSOI threshold may misjudge unchanged samples as outlier samples. In outlier sample detection, it is crucial that all outlier samples must be able to be identified. Accordingly, it is reasonable that each outlier sample can be identified by setting a relatively lower FSOI threshold. Then, eliminate outlier samples by comparing the size of FSOI values with the FSOI threshold, and update sample sets.
- 3.
- Calculate TFCI values using the updated samples in step (2) based on Equation (4), and establish the second TFSV by texture feature selection.
- 4.
- Calculate the FSOI values of samples in the TFSV established in step (3) based on Equation (8). Detect and eliminate outlier samples, and update sample sets.
- 5.
- Repeat steps (3) and (4) until the results of texture feature selection are the same for each category in the last two iterations.
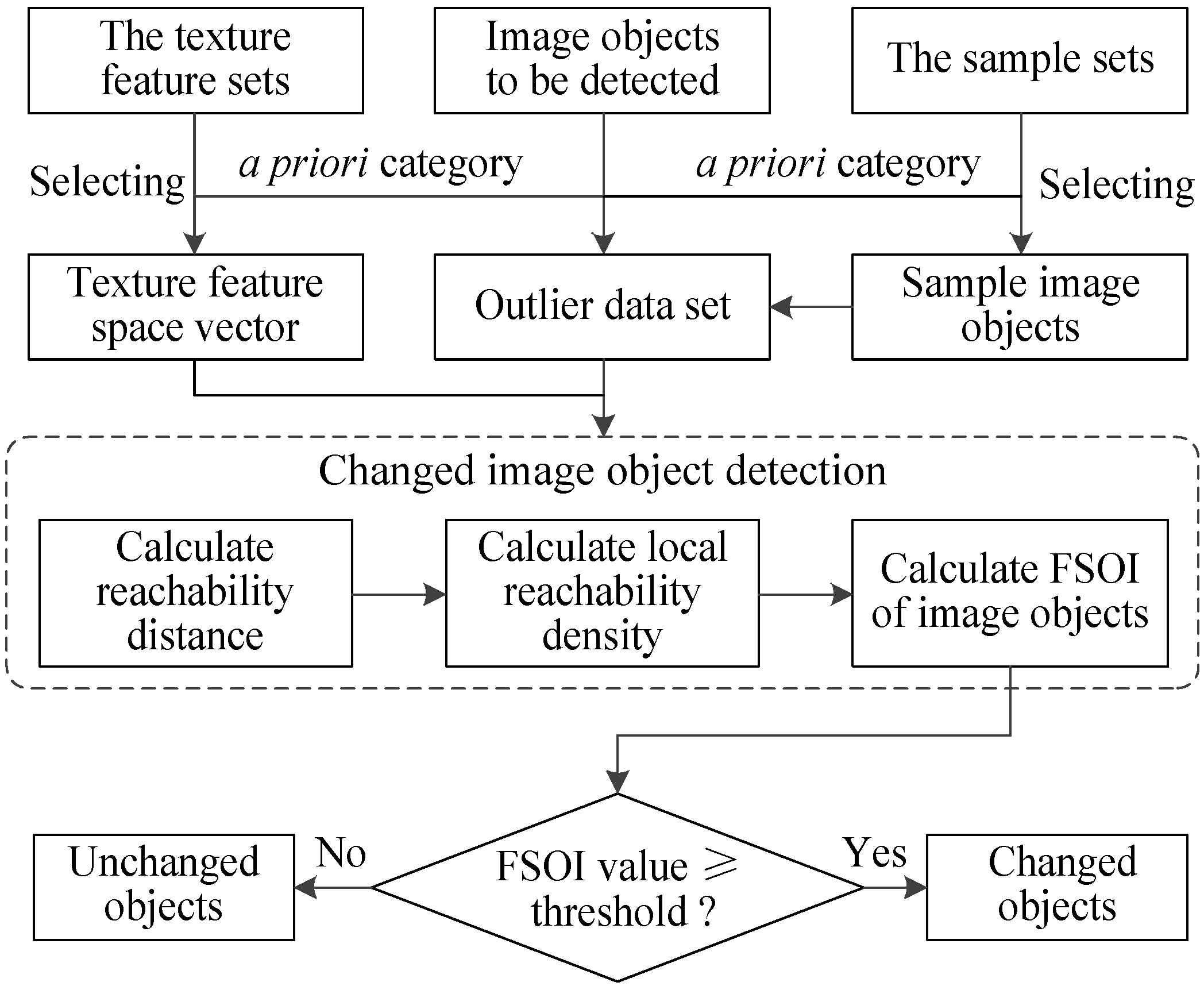
2.3. Changed Object Detection Based on the FSOI
- 1.
- First, according to the a priori category of an image object to be detected, the data set used for outlier detection with the samples and the object is established, and the is determined by the optimal texture features. Let S be the data set used for outlier detection. S can be written as:where denotes the set of objects used for outlier detection, and t is the number of samples with the same categories .
- 2.
- Second, the reachability distance between image objects in S is calculated in the based on Equation (6).
- 3.
- Third, the local reachability density of the image objects in S is calculated by Equation (7).
- 4.
- Then, the FSOI value of the image object can be achieved based on Equation (8). Compared with unchanged image objects, changed image objects have higher FSOI values. Thus, changed image objects can be identified by setting an appropriate FSOI threshold.
- 5.
- Finally, a determination is made whether the object has changed or not by comparing the FSOI value of the object with FSOI threshold. If the FSOI value of the object is greater than FSOI threshold, the object should be identified as changed objects. On the contrary, if the FSOI value of the object is smaller than FSOI threshold, the object . should be identified as unchanged objects.
3. Experiments and Results
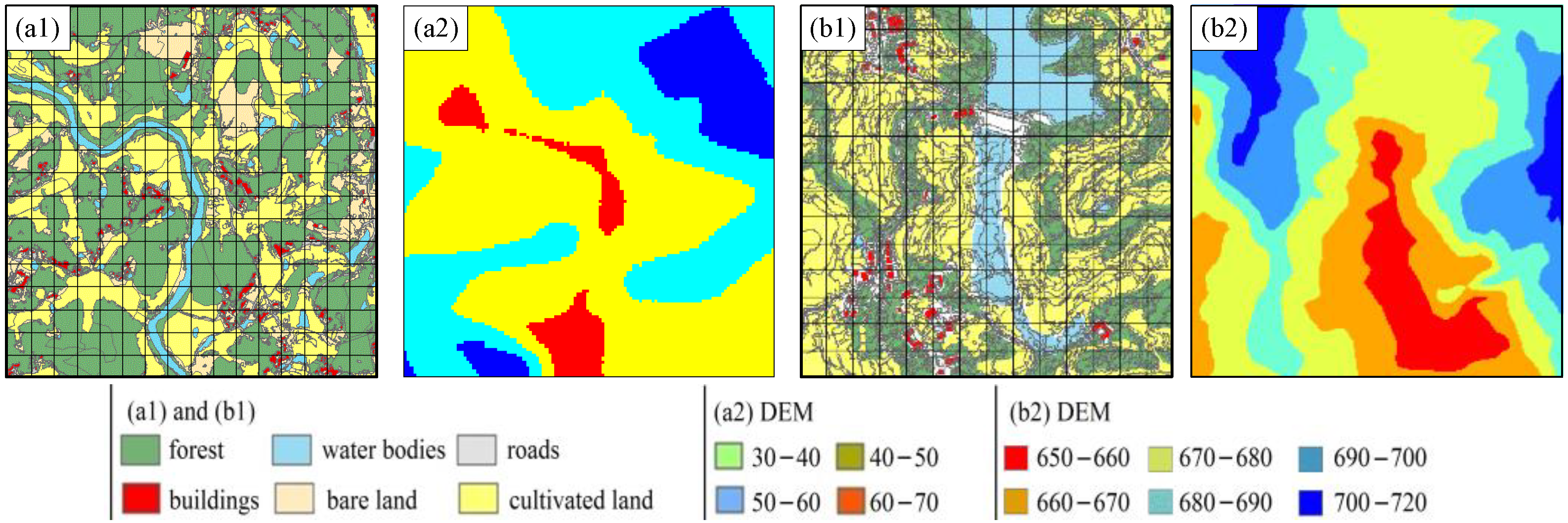
3.1. Study Areas and Data
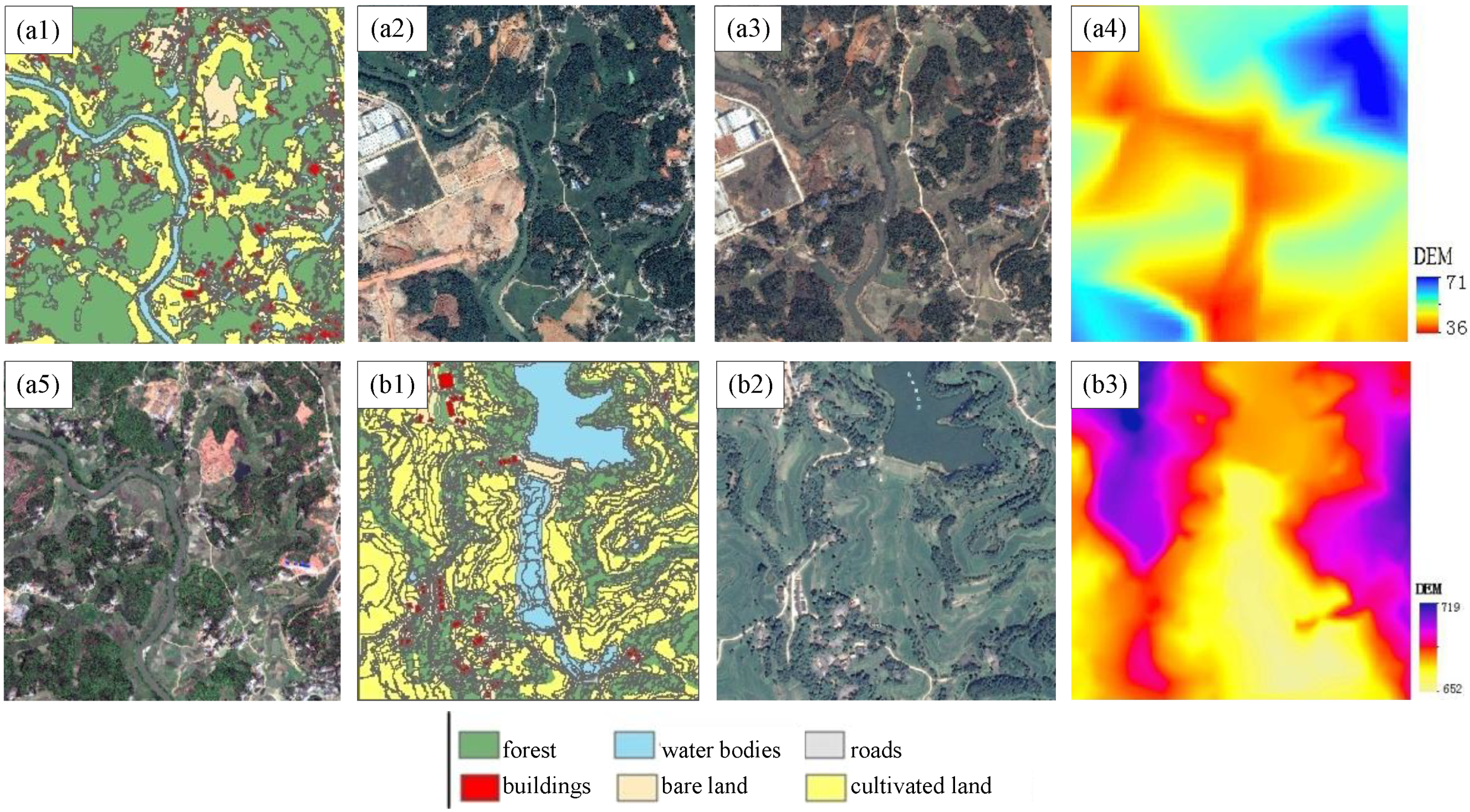
3.1.1. Study Area A
3.1.2. Study Area B
3.2. Results
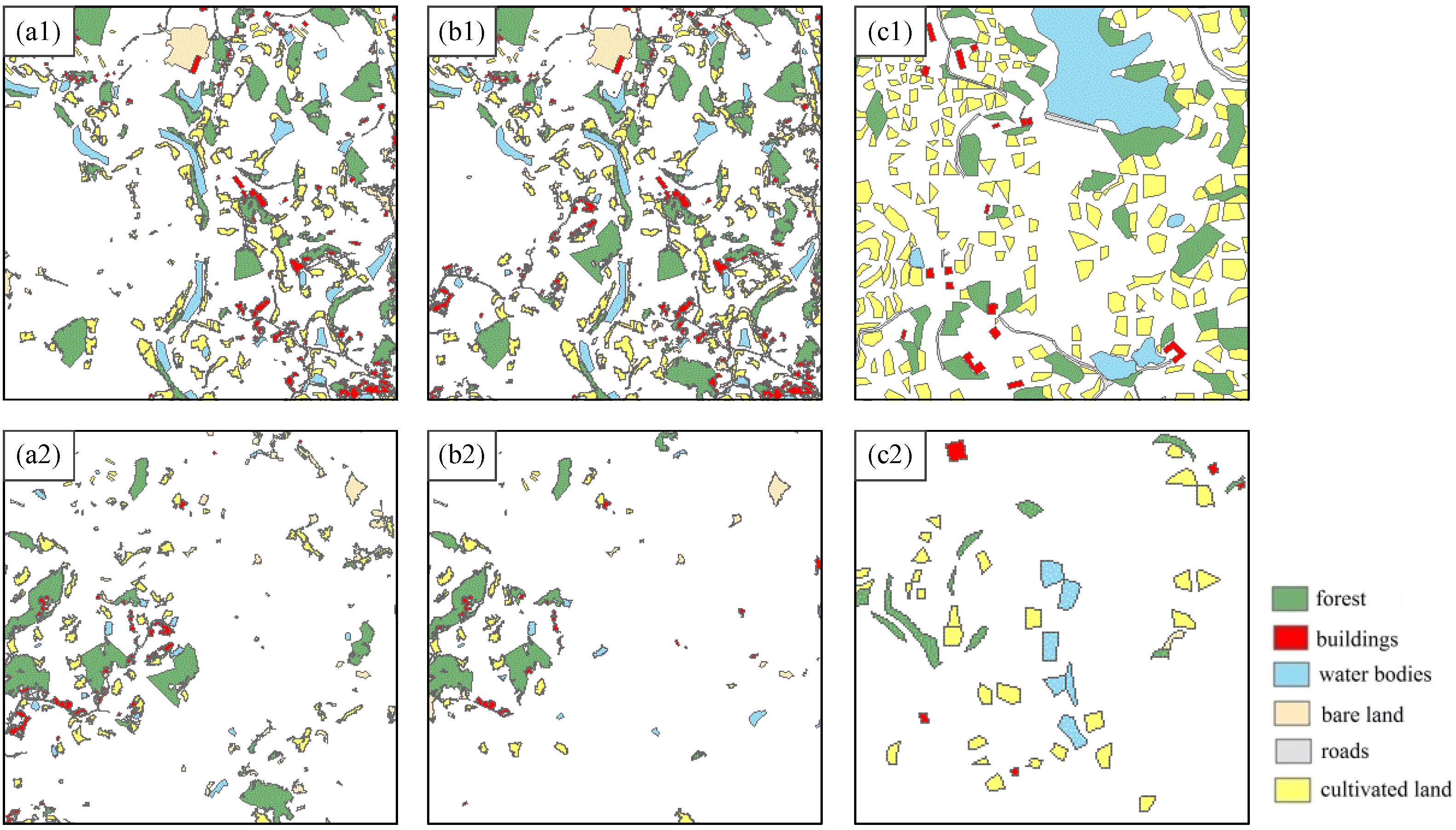
3.2.1. Results of Sampling Design
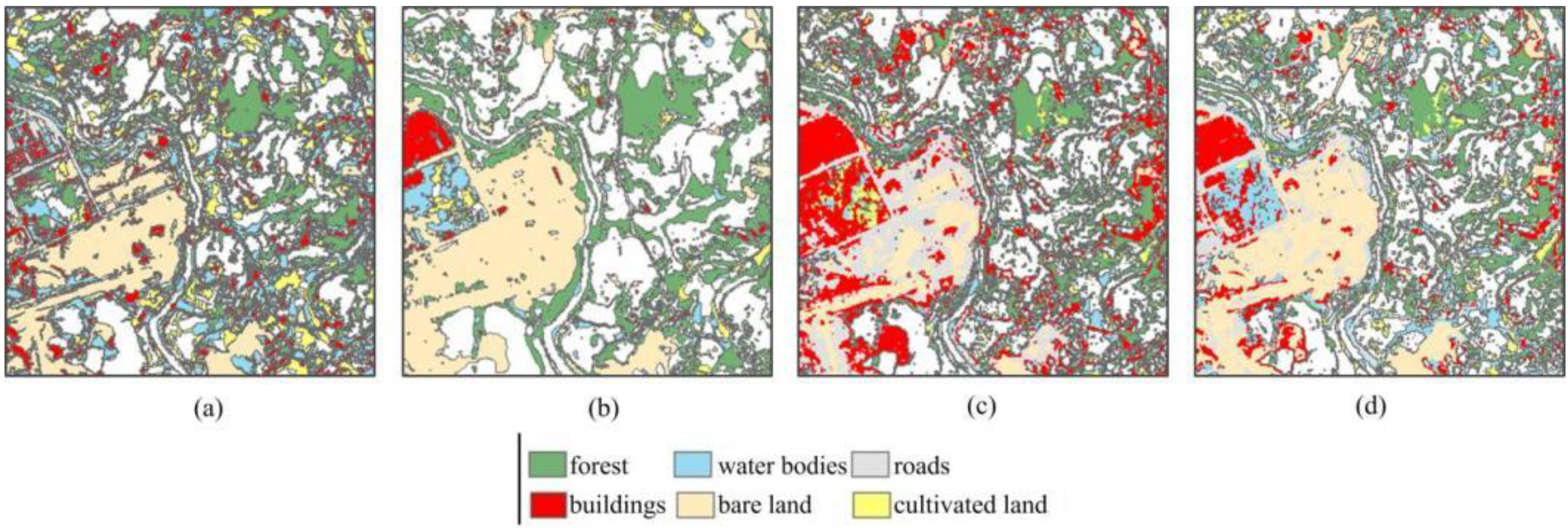
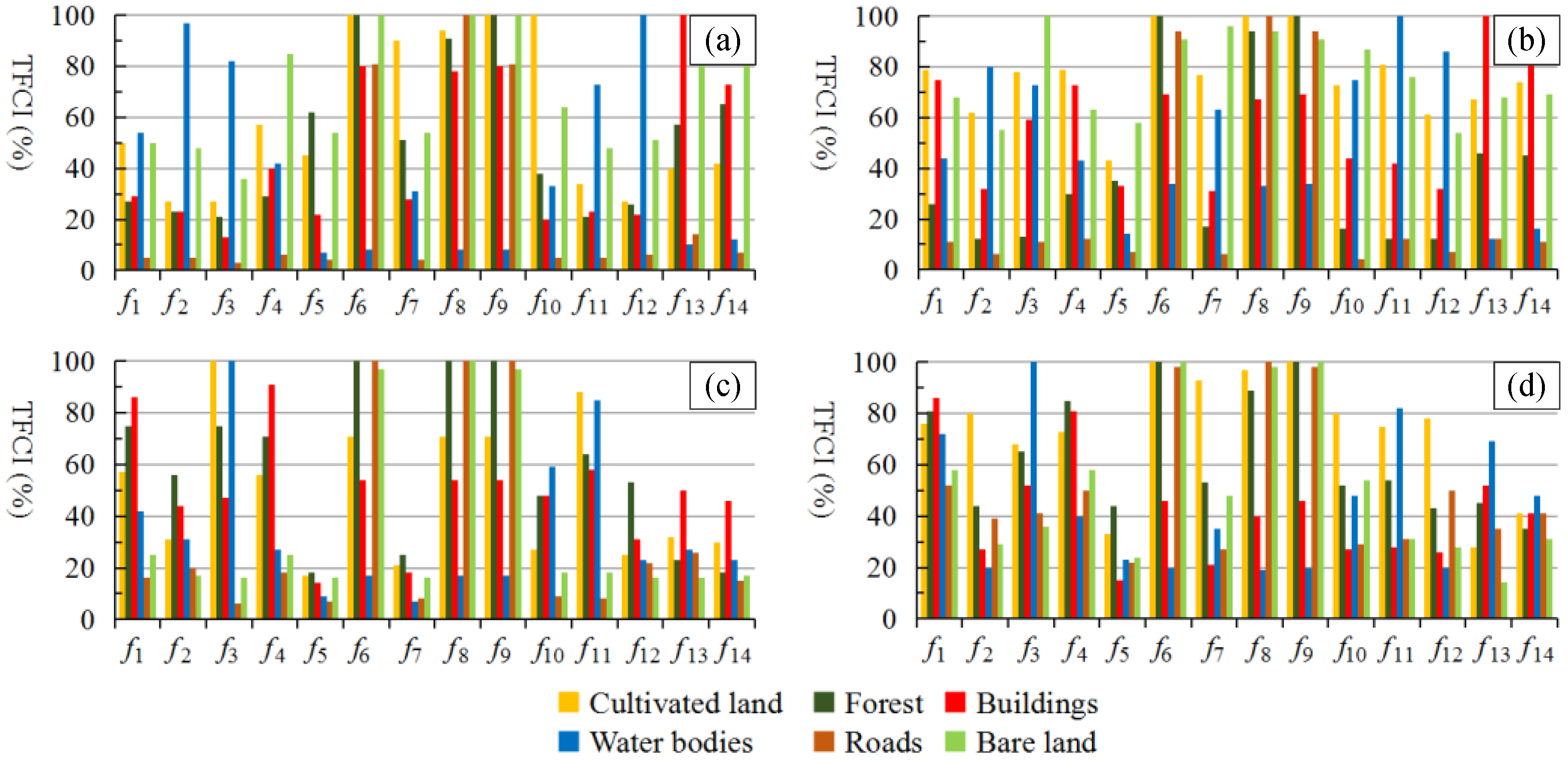
3.2.2. Texture Feature Selection and Outlier Sample Detection
3.2.3. Change Detection and Validation
3.3. Comparison of the Proposed OTO-Based Method with Other Change Detection Methods
4. Discussion
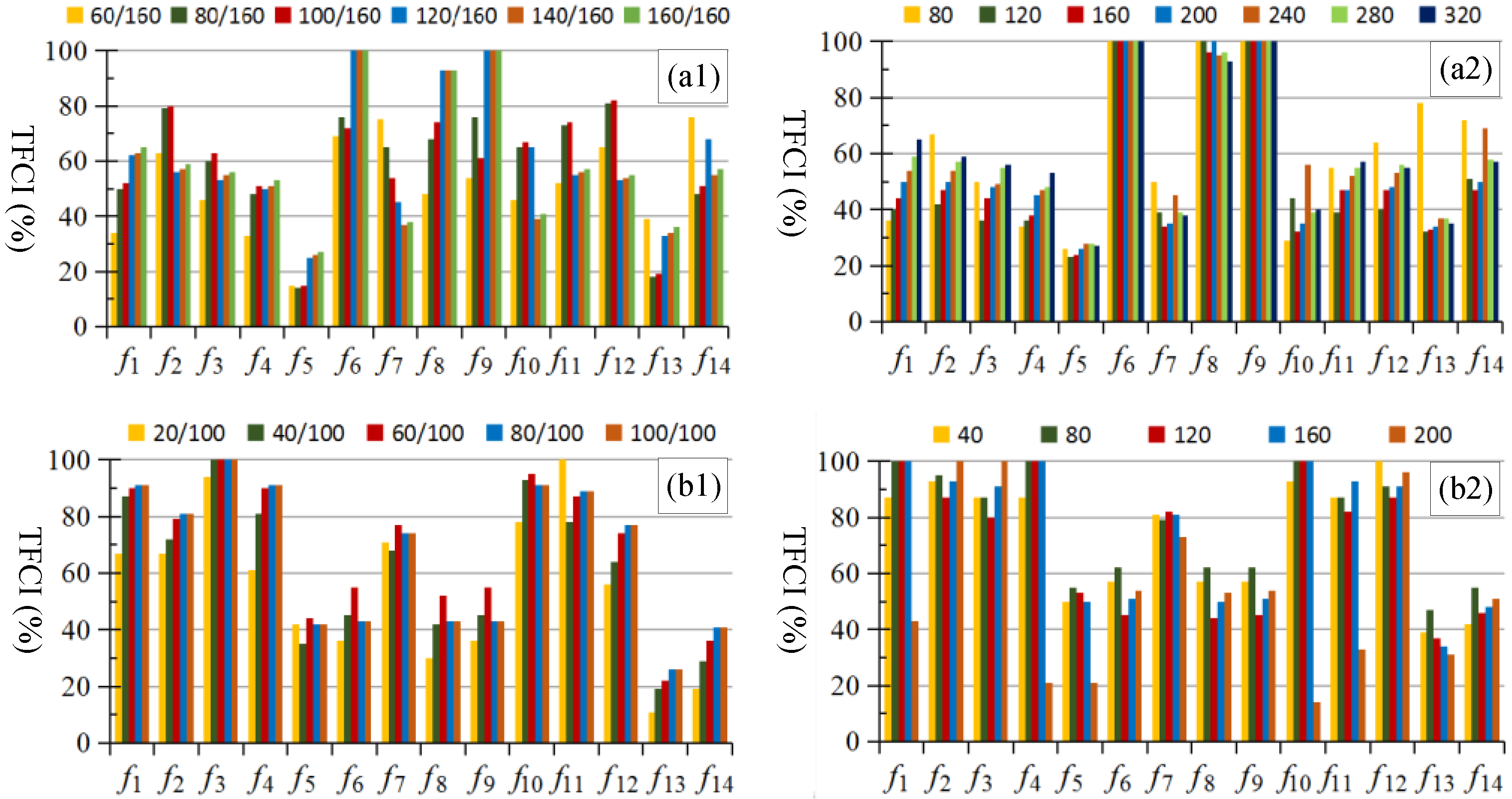
4.1. Influence of Sample Proportions and Sizes on the Texture Feature Selection of Surface Objects
4.2. Influence of Image Data Source on the Texture Feature Selection of Surface Objects
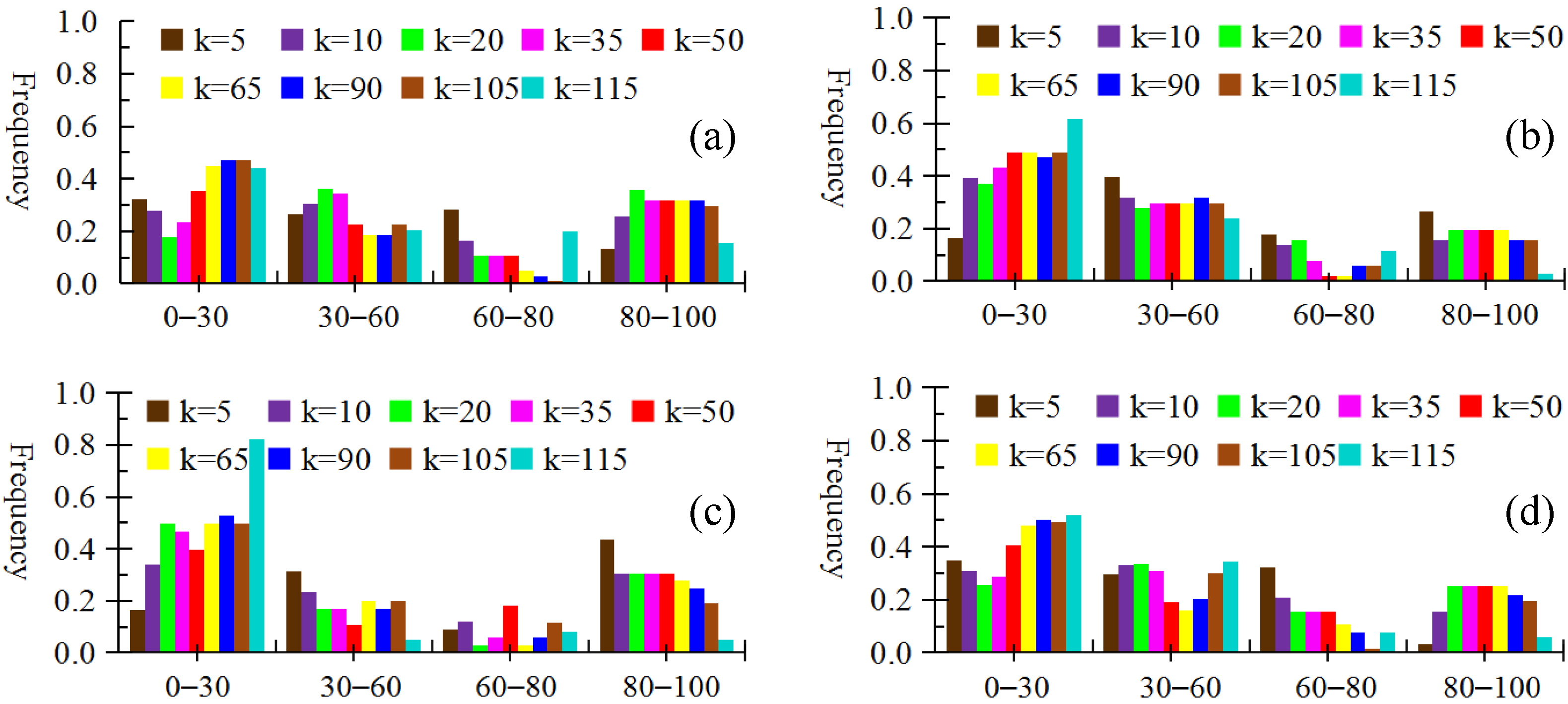
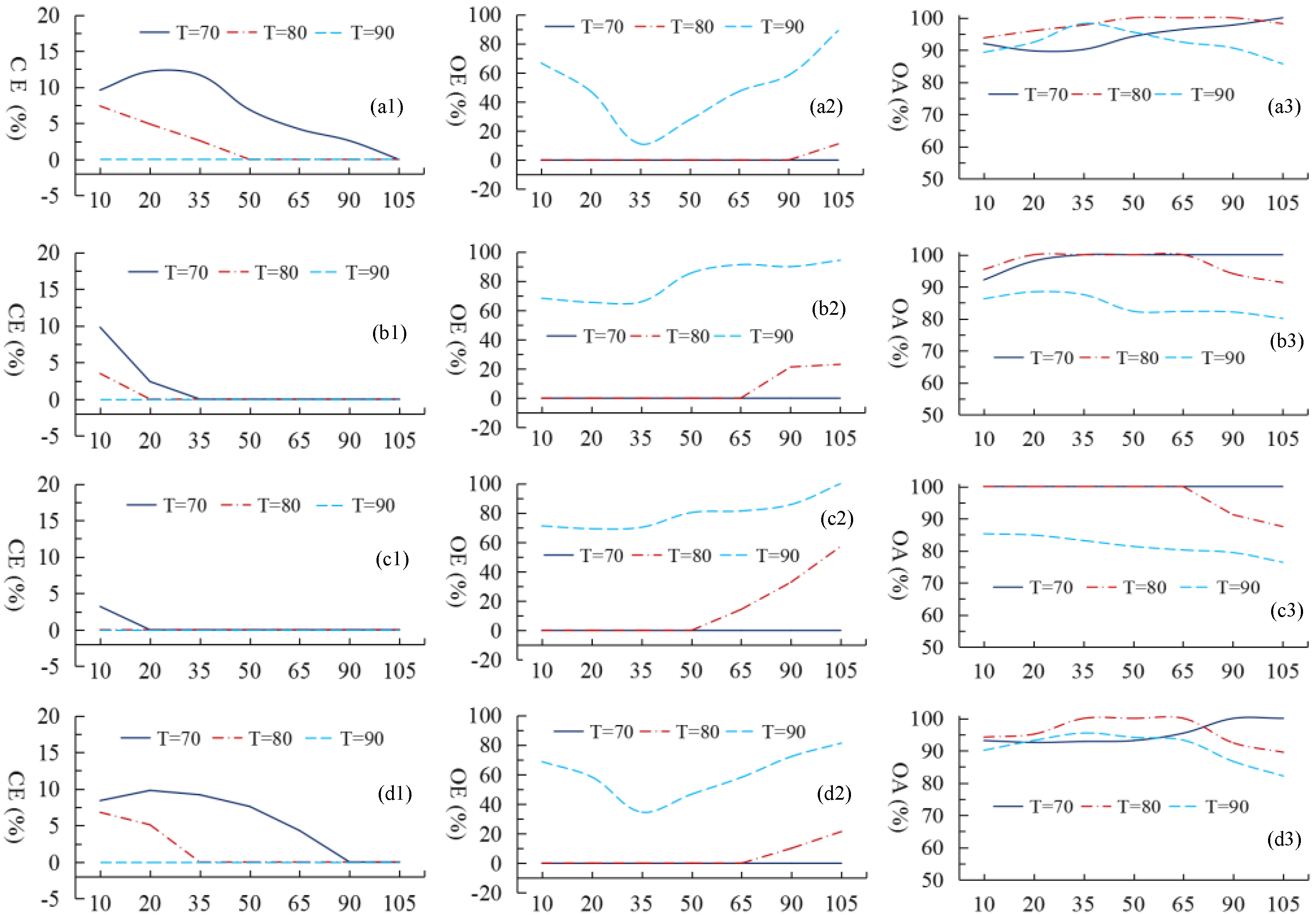
4.3. Role of Neighborhood Parameter k and FSOI Threshold in Outlier Detection
4.4. Role of Texture Feature Selection in Outlier Detection
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, C.; Du, B.; Zhang, L. Hyperspectral anomalous change detection based on joint sparse representation. ISPRS J. Photogramm. Remote Sens. 2018, 146, 137–150. [Google Scholar] [CrossRef]
- Coppin, P.; Jonckheere, I.; Nackaerts, K.; Muys, B.; Lambin, E. Review ArticleDigital change detection methods in ecosystem monitoring: A review. Int. J. Remote Sens. 2004, 25, 1565–1596. [Google Scholar] [CrossRef]
- Singh, A. Digital change detection techniques using remotely sensed data. Int. J. Remote Sens. 1988, 10, 989–1003. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Global land cover mapping at 30 m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Sterling, S.M.; Ducharne, A.; Polcher, J. The impact of global land-cover change on the terrestrial water cycle. Nat. Clim. Chang. 2012, 3, 385–390. [Google Scholar] [CrossRef]
- Foley, J.A.; DeFries, R.; Asner, G.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.; Daily, G.C.; Gibbs, H.K.; et al. Global Consequences of Land Use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef] [PubMed]
- Bruzzone, L.; Serpico, S. An iterative technique for the detection of land-cover transitions in multitemporal remote-sensing images. IEEE Trans. Geosci. Remote Sens. 1997, 35, 858–867. [Google Scholar] [CrossRef]
- Lambin, E.F.; Ehrlich, D. Land-cover changes in sub-saharan Africa (1982–1991): Application of a change index based on remotely sensed surface temperature and vegetation indices at a continental scale. Remote Sens. Environ. 1997, 61, 181–200. [Google Scholar] [CrossRef]
- Varma, S.; Shah, V.; Banerjee, B.; Buddhiraju, K.M. Change Detection of Desert Sand Dunes: A Remote Sensing Approach. Adv. Remote Sens. 2014, 3, 10–22. [Google Scholar] [CrossRef][Green Version]
- Chen, X.; Chen, J.; Shi, Y.; Yamaguchi, Y. An automated approach for updating land cover maps based on integrated change detection and classifi-cation methods. ISPRS J. Photogramm. Remote Sens. 2012, 71, 86–95. [Google Scholar] [CrossRef]
- Rogan, J.; Chen, D. Remote sensing technology for mapping and monitoring land-cover and land-use change. Prog. Plan. 2004, 61, 301–325. [Google Scholar] [CrossRef]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Alphan, H.; Derse, M.A. Change detection in Southern Turkey using normalized difference vegetation index (NDVI). J. Environ. Eng. Landsc. Manag. 2012, 21, 12–18. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L. A Theoretical Framework for Unsupervised Change Detection Based on Change Vector Analysis in the Polar Domain. IEEE Trans. Geosci. Remote Sens. 2006, 45, 218–236. [Google Scholar] [CrossRef]
- FAN, H.; MA, A.; LI, J. Case Study on Image Differencing Method for Land Use Change Detection Using Thematic Data in Renhe District of Panzhi-hua. J. Remote Sens. 2001, 5, 75–80. [Google Scholar]
- Townshend, J.R.G.; Justice, C.O. Spatial variability of images and the monitoring of changes in the Normalized Difference Vegetation Index. Int. J. Remote Sens. 1995, 16, 2187–2195. [Google Scholar] [CrossRef]
- Alphan, H.; Doygun, H.; Unlukaplan, Y.I. Post-classification comparison of land cover using multitemporal Landsat and ASTER imagery: The case of Kahramanmaraş, Turkey. Environ. Monit. Assess. 2008, 151, 327–336. [Google Scholar] [CrossRef] [PubMed]
- Manandhar, R.; Odeh, I.O.A.; Ancev, T. Improving the Accuracy of Land Use and Land Cover Classification of Landsat Data Using Post-Classification Enhancement. Remote Sens. 2009, 1, 330–344. [Google Scholar] [CrossRef]
- Dronova, I.; Gong, P.; Wang, L. Object-based analysis and change detection of major wetland cover types and their classification uncertainty during the low water period at Poyang Lake, China. Remote Sens. Environ. 2011, 115, 3220–3236. [Google Scholar] [CrossRef]
- Vidal, A.; Moreno, M.R. Change detection of isolated housing using a new hybrid approach based on object classification with optical and Ter-raSAR-X data. Int. J. Remote Sens. 2011, 32, 9621–9635. [Google Scholar] [CrossRef]
- Duro, D.; Franklin, S.; Dubé, M. Hybrid Object-based Change Detection and Hierarchical Image Segmentation for Thematic Map Updating. Photogramm. Eng. Remote Sens. 2013, 79, 259–268. [Google Scholar] [CrossRef]
- Eisavi, V.; Homayouni, S. Performance evaluation of random forest and support vector regressions in natural hazard change detection. J. Appl. Remote Sens. 2016, 10, 46030. [Google Scholar] [CrossRef]
- Cao, G.; Li, Y.; Liu, Y.; Shang, Y. Automatic change detection in high-resolution remote-sensing images by means of level set evolution and support vector machine classification. Int. J. Remote Sens. 2014, 35, 6255–6270. [Google Scholar] [CrossRef]
- Woodcock, C.; Macomber, S.; Pax-Lenney, M.; Cohen, W.B. Monitoring large areas for forest change using Landsat: Generalization across space, time and Landsat sensors. Remote Sens. Environ. 2001, 78, 194–203. [Google Scholar] [CrossRef]
- De, S.; Pirrone, D.; Bovolo, F.; Bruzzone, L.; Bhattacharya, A. A novel change detection framework based on deep learning for the analysis of mul-ti-temporal polarimetric SAR images. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5193–5196. [Google Scholar]
- Zhang, P.; Gong, M.; Su, L.; Liu, J.; Li, Z. Change detection based on deep feature representation and mapping transformation for mul-ti-spatial-resolution remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 116, 24–41. [Google Scholar] [CrossRef]
- Bouziani, M.; Goïta, K.; He, D.-C. Automatic change detection of buildings in urban environment from very high spatial resolution images using exist-ing geodatabase and prior knowledge. ISPRS J. Photogramm. Remote Sens. 2010, 65, 143–153. [Google Scholar] [CrossRef]
- Bayarjargal, Y.; Karnieli, A.; Bayasgalan, M.; Khudulmur, S.; Gandush, C.; Tucker, C. A comparative study of NOAA–AVHRR derived drought indi-ces using change vector analysis. Remote Sens. Environ. 2006, 105, 9–22. [Google Scholar] [CrossRef]
- Nackaerts, K.; Vaesen, K.; Muys, B.; Coppin, P. Comparative performance of a modified change vector analysis in forest change detection. Int. J. Remote Sens. 2005, 26, 839–852. [Google Scholar] [CrossRef]
- Ghosh, A.; Mishra, N.S.; Ghosh, S. Fuzzy clustering algorithms for unsupervised change detection in remote sensing images. Inf. Sci. 2011, 181, 699–715. [Google Scholar] [CrossRef]
- Yuan, F.; Sawaya, K.E.; Loeffelholz, B.C.; Bauer, M.E. Land cover classification and change analysis of the Twin Cities (Minnesota) Metropolitan Area by multitemporal Landsat remote sensing. Remote Sens. Environ. 2005, 98, 317–328. [Google Scholar] [CrossRef]
- Habib, T.; Inglada, J.; Mercier, G.; Chanussot, J. Support Vector Reduction in SVM Algorithm for Abrupt Change Detection in Remote Sensing. IEEE Geosci. Remote Sens. Lett. 2009, 6, 606–610. [Google Scholar] [CrossRef]
- Huang, C.; Song, K.; Kim, S.; Townshend, J.R.; Davis, P.; Masek, J.G.; Goward, S.N. Use of a dark object concept and support vector machines to automate forest cover change analysis. Remote Sens. Environ. 2008, 112, 970–985. [Google Scholar] [CrossRef]
- Zhang, H.; Gong, M.; Zhang, P.; Su, L.; Shi, J. Feature-Level Change Detection Using Deep Representation and Feature Change Analysis for Multispectral Imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1666–1670. [Google Scholar] [CrossRef]
- Gong, M.; Zhao, J.; Liu, J.; Miao, Q.; Jiao, L. Change Detection in Synthetic Aperture Radar Images Based on Deep Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 125–138. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z. Change detection using landsat time series: A review of frequencies, preprocessing, algorithms, and applications. ISPRS J. Photogramm. Remote Sens. 2017, 130, 370–384. [Google Scholar] [CrossRef]
- Sofina, N.; Ehlers, M. Building Change Detection Using High Resolution Remotely Sensed Data and GIS. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3430–3438. [Google Scholar] [CrossRef]
- Guo, Z.; Du, S. Mining parameter information for building extraction and change detection with very high-resolution imagery and GIS data. GIScience Remote Sens. 2016, 54, 38–63. [Google Scholar] [CrossRef]
- Hegazy, I.R.; Kaloop, M.R. Monitoring urban growth and land use change detection with GIS and remote sensing techniques in Daqahlia governorate Egypt. Int. J. Sustain. Built Environ. 2015, 4, 117–124. [Google Scholar] [CrossRef]
- Li, D. Remotely sensed images and GIS data fusion for automatic change detection. Int. J. Image Data Fusion 2010, 1, 99–108. [Google Scholar] [CrossRef]
- Baltsavias, E. Object extraction and revision by image analysis using existing geodata and knowledge: Current status and steps towards operational systems. ISPRS J. Photogramm. Remote Sens. 2004, 58, 129–151. [Google Scholar] [CrossRef]
- Turker, M.; Cetinkaya, B. Automatic detection of earthquake-damaged buildings using DEMs created from pre-and post-earthquake stereo aerial photographs. Int. J. Remote Sens. 2005, 26, 823–832. [Google Scholar] [CrossRef]
- De Alwis, D.A.; So, E. Enhanced change detection index for disaster response, recovery assessment and monitoring of accessibility and open spaces (camp sites). Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 49–60. [Google Scholar] [CrossRef]
- Lopez, C.V.; Kempf, T.; Speck, R.; Anglberger, H.; Stilla, U. Automatic change detection using very high-resolution SAR images and prior knowledge about the scene. Radar Sens. Technol. XXI 2017, 10188, 1018805. [Google Scholar] [CrossRef]
- Tian, J.; Chen, D.-M. Optimization in multi-scale segmentation of high-resolution satellite images for artificial feature recognition. Int. J. Remote Sens. 2007, 28, 4625–4644. [Google Scholar] [CrossRef]
- Witharana, C.; Civco, D.L. Optimizing multi-resolution segmentation scale using empirical methods: Exploring the sensitivity of the supervised dis-crepancy measure Euclidean distance 2 (ED2). ISPRS J. Photogramm. Remote Sens. 2014, 87, 108–121. [Google Scholar] [CrossRef]
- Lillesand, T.; Kiefer, R.W.; Chipman, J. Remote Sensing and Image Interpretation, 7th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Masjedi, A.; Zoej, M.J.V.; Maghsoudi, Y. Classification of Polarimetric SAR Images Based on Modeling Contextual Information and Using Texture Features. IEEE Trans. Geosci. Remote Sens. 2015, 54, 932–943. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Eichkitz, C.G.; Amtmann, J.; Schreilechner, M.G. Calculation of grey level co-occurrence matrix-based seismic attributes in three dimensions. Comput. Geosci. 2013, 60, 176–183. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Kouyate, F.; Brisco, B.; Williams, T.H.L. Textural Infornation in SAR Images. IEEE Trans. Geosci. Remote Sens. 1986, GE-24, 235–245. [Google Scholar] [CrossRef]
- Białynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 129–132. [Google Scholar] [CrossRef]
- Kent, J.T. Information gain and a general measure of correlation. Biometrika 1983, 70, 163–173. [Google Scholar] [CrossRef]
- Mohammad, A.H. Comparing two feature selections methods (Information gain and gain ratio) on three different classification algorithms using ara-bic dataset. J. Theor. Appl. Inf. Technol. 2018, 96, 1561–1568. [Google Scholar]
- Fariza, A.; Rusydi, I.; Hasim, J.A.N.; Basofi, A. Spatial flood risk mapping in east Java, Indonesia, using analytic hierarchy process—Natural breaks classification. In Proceedings of the 2017 2nd International Conferences on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 1–3 November 2017; pp. 406–411. [Google Scholar]
- Rezaeian, M.; Dunn, G.; Leger, S.S.; Appleby, L. The production and interpretation of disease maps. Soc. Psychiatry Psychiatr. Epidemiol. 2004, 39, 947–954. [Google Scholar] [CrossRef] [PubMed]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIG-MOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104. [Google Scholar]
- Bartnett, V.; Lewis, T. Outliers in Statistical Data, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Hoaglin, D.C.; Kempthorne, P.J. [Influential Observations, High Leverage Points, and Outliers in Linear Regression]: Comment. Stat. Sci. 1986, 1, 408–412. [Google Scholar] [CrossRef]
- Ro, K.; Zou, C.; Wang, Z.; Yin, G. Outlier detection for high-dimensional data. Biometrika 2015, 102, 589–599. [Google Scholar] [CrossRef]
- Hawkins, D.M. Identification of Outliers; Springer: Dordrecht, The Netherlands, 1980; Volume 11. [Google Scholar]
- Tang, J.; Chen, Z.; Fu, A.W.-C.; Cheung, D.W. Enhancing Effectiveness of Outlier Detections for Low Density Patterns. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Seoul, Korea, 30 April–2 May 2003; pp. 535–548. [Google Scholar]
- Ramaswamy, S.; Rastogi, R.; Shim, K. Efficient algorithms for mining outliers from large data sets. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 427–438. [Google Scholar]
- Bai, T.; Sun, K.; Deng, S.; Li, D.; Li, W.; Chen, Y. Multi-scale hierarchical sampling change detection using Random Forest for high-resolution satellite imagery. Int. J. Remote Sens. 2018, 39, 7523–7546. [Google Scholar] [CrossRef]
- Anniballe, R.; Noto, F.; Scalia, T.; Bignami, C.; Stramondo, S.; Chini, M.; Pierdicca, N. Earthquake damage mapping: An overall assessment of ground surveys and VHR image change detection after L’Aquila 2009 earthquake. Remote Sens. Environ. 2018, 210, 166–178. [Google Scholar] [CrossRef]




| Serial Number | Texture Features |
|---|---|
| f1 | Angular Second Moment (ASM) |
| f2 | Contrast (CON) |
| f3 | Inverse Difference Moment (IDM) |
| f4 | Entropy (ENT) |
| f5 | Correlation (COR) |
| f6 | Mean (MEAN) |
| f7 | Variance (VAR) |
| f8 | Sum Variance (SVAR) |
| f9 | Sum Average (SAVE) |
| f10 | Sum Entropy (SENT) |
| f11 | Difference Entropy (DENT) |
| f12 | Difference Variance (DVAR) |
| f13 | Information Measures of Correlation (IMC) |
| f14 | Maximal Correlation Coefficient (MCC) |
| Hierarchy Number | TFCI Value | Contribution Level |
|---|---|---|
| I | [0, 20] | Very low contribution |
| II | (20, 40] | Low contribution |
| III | (40, 60] | Moderate contribution |
| IV | (60, 80] | High contribution |
| V | (80, 100] | Very high contribution |
| Types | Experiment One | Experiment Two | Experiment Three | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Texture Features | Texture Features | Texture Features | ||||||||||||||
| TFCI (%) | TFCI (%) | TFCI (%) | ||||||||||||||
| Forest | f6 | f9 | f8 | f4 | f1 | f6 | f8 | f9 | f1 | f3 | f4 | f3 | f2 | f12 | ||
| 100 | 100 | 89 | 85 | 81 | 100 | 100 | 100 | 75 | 75 | 71 | 100 | 86 | 79 | |||
| Water bodies | f3 | f11 | f1 | f11 | f3 | f11 | f12 | f2 | f11 | |||||||
| 100 | 82 | 72 | 82 | 100 | 85 | 100 | 82 | 76 | ||||||||
| Buildings | f1 | f4 | f4 | f1 | f13 | f11 | f14 | |||||||||
| 86 | 81 | 91 | 86 | 100 | 64 | 64 | ||||||||||
| Cultivated land | f6 | f9 | f8 | f7 | f2 | f10 | f3 | f11 | f6 | f8 | f9 | f6 | f9 | f8 | f1 | |
| 100 | 100 | 97 | 93 | 80 | 80 | 100 | 88 | 71 | 71 | 71 | 100 | 100 | 89 | 67 | ||
| Roads | f8 | f6 | f9 | f6 | f8 | f9 | f6 | f8 | f9 | |||||||
| 100 | 98 | 98 | 100 | 100 | 100 | 100 | 100 | 100 | ||||||||
| Bare land | f6 | f9 | f8 | f8 | f6 | f9 | f6 | f8 | f9 | |||||||
| 100 | 100 | 98 | 100 | 97 | 97 | 100 | 100 | 100 | ||||||||
| Type | Experiment One | Experiment Two | Experiment Three | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Omission Errors (%) | Commission Errors (%) | Overall Accuracy (%) | Omission Errors (%) | Commission Errors (%) | Overall Accuracy (%) | Omission Errors (%) | Commission Errors (%) | Overall Accuracy (%) | |
| Forest | 0 | 0 | 100 | 0 | 4 | 96 | 0 | 0 | 100 |
| Buildings | 0 | 0 | 100 | 0 | 0 | 100 | 0 | 5 | 95 |
| Roads | 0 | 16 | 84 | 0 | 12 | 88 | 0 | 14 | 86 |
| Water bodies | 0 | 8 | 92 | 0 | 7 | 93 | 0 | 0 | 100 |
| Bare land | 0 | 19 | 81 | 0 | 18 | 82 | 0 | 8 | 92 |
| Cultivated land | 0 | 6 | 94 | 0 | 0 | 100 | 0 | 2 | 98 |
| Types in 2017 (m2) | Types in 2009 (m2) | Total | Changes in 2017 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Forest | Cultivated Land | Bare Land | Water Bodies | Roads | Buildings | (m2) | % | ||
| Forest | 837,083 | 167,831 | 34,919 | 7976 | 4639 | 9202 | 1,061,650 | −414,256 | −28.07 |
| Cultivated land | 76,106 | 447,706 | 53,150 | 3814 | 4459 | 37,204 | 622,439 | −384,266 | −38.17 |
| Bare land | 188,669 | 122,642 | 59,071 | 380 | 1280 | 24,151 | 396,193 | 188,508 | 90.77 |
| Water bodies | 12,922 | 6312 | 17,953 | 131,840 | 1951 | 22,787 | 193,765 | 30,294 | 18.53 |
| Roads | 115,424 | 91,192 | 9587 | 6259 | 60,057 | 57,646 | 340,165 | 247,975 | 268.98 |
| Buildings | 245,702 | 171,022 | 33,005 | 13,202 | 19,804 | 75,727 | 558,462 | 331,745 | 146.33 |
| Total | 1,475,906 | 1,006,705 | 207,685 | 163,471 | 92,190 | 226,717 | 3,172,674 | ||
| Types in 2016 (m2) | Types in 2009 (m2) | Total | Changes in 2016 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Forest | Cultivated Land | Bare Land | Water Bodies | Roads | Buildings | (m2) | % | ||
| Forest | 1,258,007 | 51,013 | 56,558 | 0 | 0 | 50,198 | 1,415,776 | −60,130 | −4.07 |
| Cultivated land | 0 | 821,399 | 0 | 11,975 | 0 | 10,727 | 844,101 | −162,604 | −16.15 |
| Bare land | 200,206 | 45,897 | 50,292 | 0 | 0 | 20,845 | 317,240 | 109,555 | 52.75 |
| Water bodies | 0 | 21,937 | 0 | 135,724 | 0 | 0 | 157,661 | −5810 | −3.55 |
| Roads | 0 | 20,061 | 0 | 15,772 | 61,415 | 38,657 | 135,905 | 43,715 | 47.41 |
| Buildings | 17,693 | 46,398 | 100,835 | 0 | 30,775 | 106,290 | 301,991 | 75,274 | 33.20 |
| Total | 1,475,906 | 1,006,705 | 207,685 | 163,471 | 92,190 | 226,717 | 3,172,674 | ||
| Types in 2016 (m2) | Types in 2014 (m2) | Total | Changes in 2016 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Forest | Cultivated Land | Bare Land | Water Bodies | Roads | Buildings | (m2) | % | ||
| Forest | 522,527 | 94,714 | 0 | 1223 | 2693 | 4998 | 626,154 | 73,058 | 13.21 |
| Cultivated land | 14,206 | 839,465 | 0 | 61,932 | 1963 | 3366 | 920,932 | −74,078 | −7.44 |
| Bare land | 4943 | 4881 | 78,195 | 1289 | 947 | 1319 | 91,575 | 6015 | 7.03 |
| Water bodies | 674 | 2015 | 0 | 164,088 | 0 | 733 | 167,510 | −71,787 | −29.99 |
| Roads | 3851 | 48,694 | 3409 | 10,766 | 106,950 | 5810 | 179,479 | 64,012 | 55.44 |
| Buildings | 6896 | 5241 | 3956 | 0 | 2914 | 22,380 | 41,386 | 2780 | 7.20 |
| Total | 553,095 | 995,010 | 85,560 | 239,297 | 115,467 | 38,606 | 2,027,036 | ||
| Type | Experiment One | Experiment Two | Experiment Three | |||
|---|---|---|---|---|---|---|
| Omission Errors (%) | Commission Errors (%) | Omission Errors (%) | Commission Errors (%) | Omission Errors (%) | Commission Errors (%) | |
| Forest | 3.85 | 6.25 | 2.56 | 5.00 | 2.13 | 1.28 |
| Cultivated land | 3.53 | 3.53 | 2.35 | 3.49 | 2.36 | 2.30 |
| Bare land | 3.95 | 7.59 | 3.95 | 8.75 | 3.92 | 5.19 |
| Water bodies | 3.89 | 1.33 | 2.67 | 0.00 | 1.30 | 1.56 |
| Roads | 4.11 | 2.78 | 6.85 | 2.86 | 4.32 | 2.69 |
| Buildings | 5.06 | 2.59 | 3.80 | 1.29 | 2.62 | 2.53 |
| Overall accuracy | 95.94% | 96.36% | 96.28% | |||
| Kappa coefficient | 0.951 | 0.956 | 0.953 | |||
| Object-Based Methods (OBMs) | Deep-Learning-Based Method (DLMs) | Random Forest (RF) | Support Vector Machine (SVM) | Proposed Method | |
|---|---|---|---|---|---|
| Overall accuracy (%) | 79.23 | 90.16 | 78.50 | 80.50 | 95.94 |
| Omission errors (%) | 9.68 | 4.12 | 8.04 | 9.47 | 1.87 |
| Commission errors (%) | 11.09 | 5.72 | 13.46 | 10.03 | 2.19 |
| Omission Errors (%) | Commission Errors (%) | Overall Accuracy (%) | |
|---|---|---|---|
| with texture feature selection | 4.52 | 0.72 | 94.76 |
| without texture feature selection | 35.00 | 7.22 | 57.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, D.; Hou, D.; Zhou, X.; Chen, J. Change Detection Using a Texture Feature Space Outlier Index from Mono-Temporal Remote Sensing Images and Vector Data. Remote Sens. 2021, 13, 3857. https://doi.org/10.3390/rs13193857
Wei D, Hou D, Zhou X, Chen J. Change Detection Using a Texture Feature Space Outlier Index from Mono-Temporal Remote Sensing Images and Vector Data. Remote Sensing. 2021; 13(19):3857. https://doi.org/10.3390/rs13193857
Chicago/Turabian StyleWei, Dongsheng, Dongyang Hou, Xiaoguang Zhou, and Jun Chen. 2021. "Change Detection Using a Texture Feature Space Outlier Index from Mono-Temporal Remote Sensing Images and Vector Data" Remote Sensing 13, no. 19: 3857. https://doi.org/10.3390/rs13193857
APA StyleWei, D., Hou, D., Zhou, X., & Chen, J. (2021). Change Detection Using a Texture Feature Space Outlier Index from Mono-Temporal Remote Sensing Images and Vector Data. Remote Sensing, 13(19), 3857. https://doi.org/10.3390/rs13193857








