Approaching Global Instantaneous Precise Positioning with the Dual- and Triple-Frequency Multi-GNSS Decoupled Clock Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Uncombined Dual- and Triple-Frequency Multi-GNSS Decoupled Clock Model
2.1.1. PPP Observation Equations
2.1.2. Uncombined Dual- and Triple-Frequency DCM
- Two receiver clock terms are present in the equation: a pseudorange clock, defined as: and a carrier-phase clock defined as: . This decoupling of the clocks is a consequence of using the DCM, as both terms are biased versions of and , the pseudorange and carrier-phase clocks, respectively. Both state terms are affected by receiver biases, with the carrier-phase clock being affected by the reference satellite’s ambiguity as well, which is discussed in more detail later.
- The ionospheric delay term absorbs the ionosphere-free combination of the receiver pseudorange biases in the form: . When trying to use external ionospheric corrections, either global or regional corrections, the biases have to be separated from the ionospheric delay state term. The biases can be estimated as separate state terms, as long as additional observations of the ionospheric delays are present.
- are the integer single-differenced ambiguities relative to the reference satellite. The single-differencing is performed implicitly without having to explicitly difference the measurements or ambiguities from different satellites. The implicit single-difference is a consequence of the decoupling of the clocks, as the phase measurements lose their datum—typically set by the pseudorange measurements through the receiver clock. The new datum is set by the reference satellite, as its ambiguities are fixed to arbitrary integers and they are not estimated. Doing so not only leads to all ambiguities being single-differenced, but also recovers the datum in the phase measurements, as each frequency’s datum is being set by the reference satellite’s ambiguity on that frequency.
- An interfrequency bias term appears in the third frequency’s pseudorange measurement equation, expressed as: . The term arises from the fact that the other state terms cannot absorb the additional receiver bias that comes with the third pseudorange measurement, as opposed to the first and second frequency receiver pseudorange biases, which are absorbed by the receiver pseudorange clock and ionospheric delay. Ignoring this state term leads to it appearing in the pseudorange residuals, and potentially affecting the estimation of other states.
- Equation (2) also contains two state terms which are specific to the DCM, referred to here as the receiver L2 phase bias , and the receiver L3 phase bias . The two state terms are defined as: and . Both state terms contain receiver biases, as well as the reference satellite’s ambiguities.
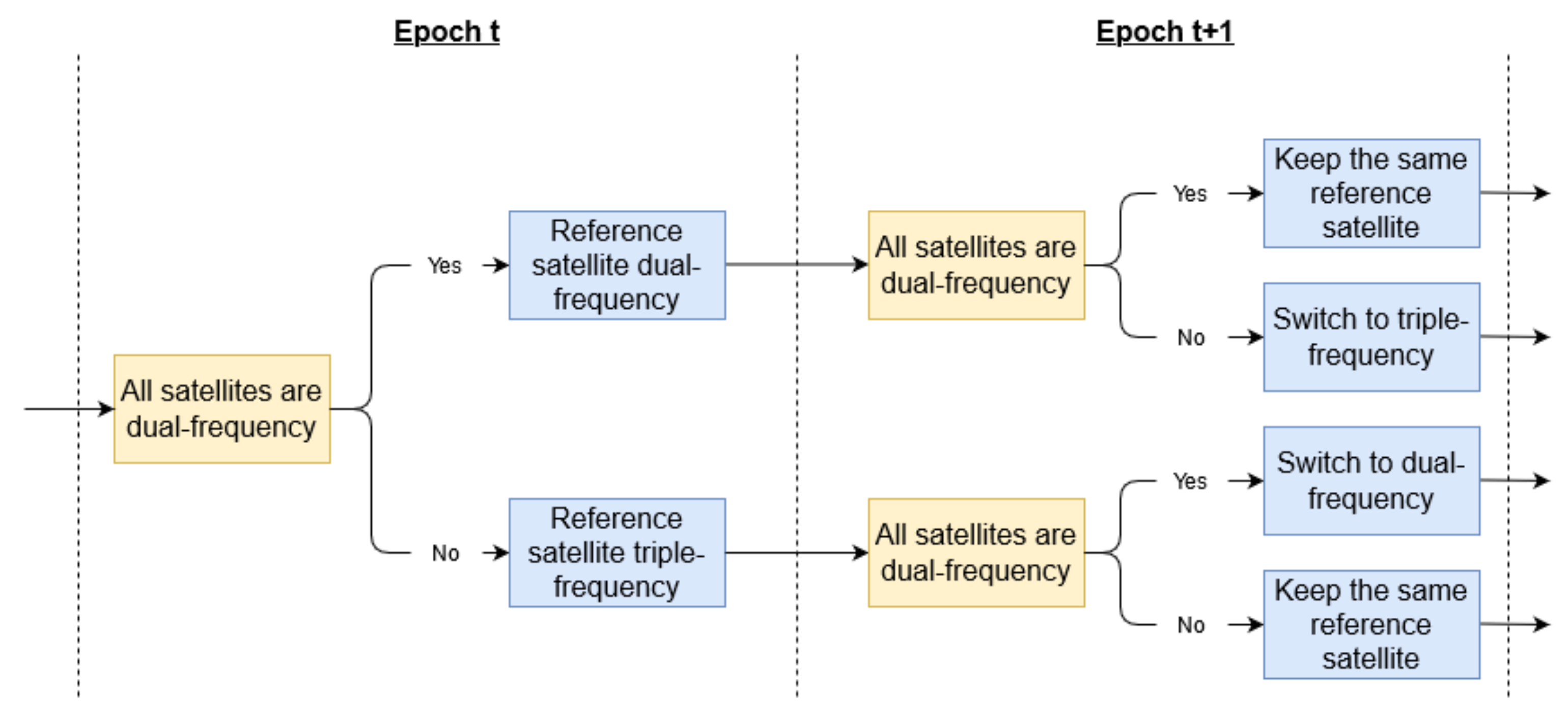
2.1.3. Reference Satellite and Multi-GNSS Considerations
2.2. Data and Processing
3. Results
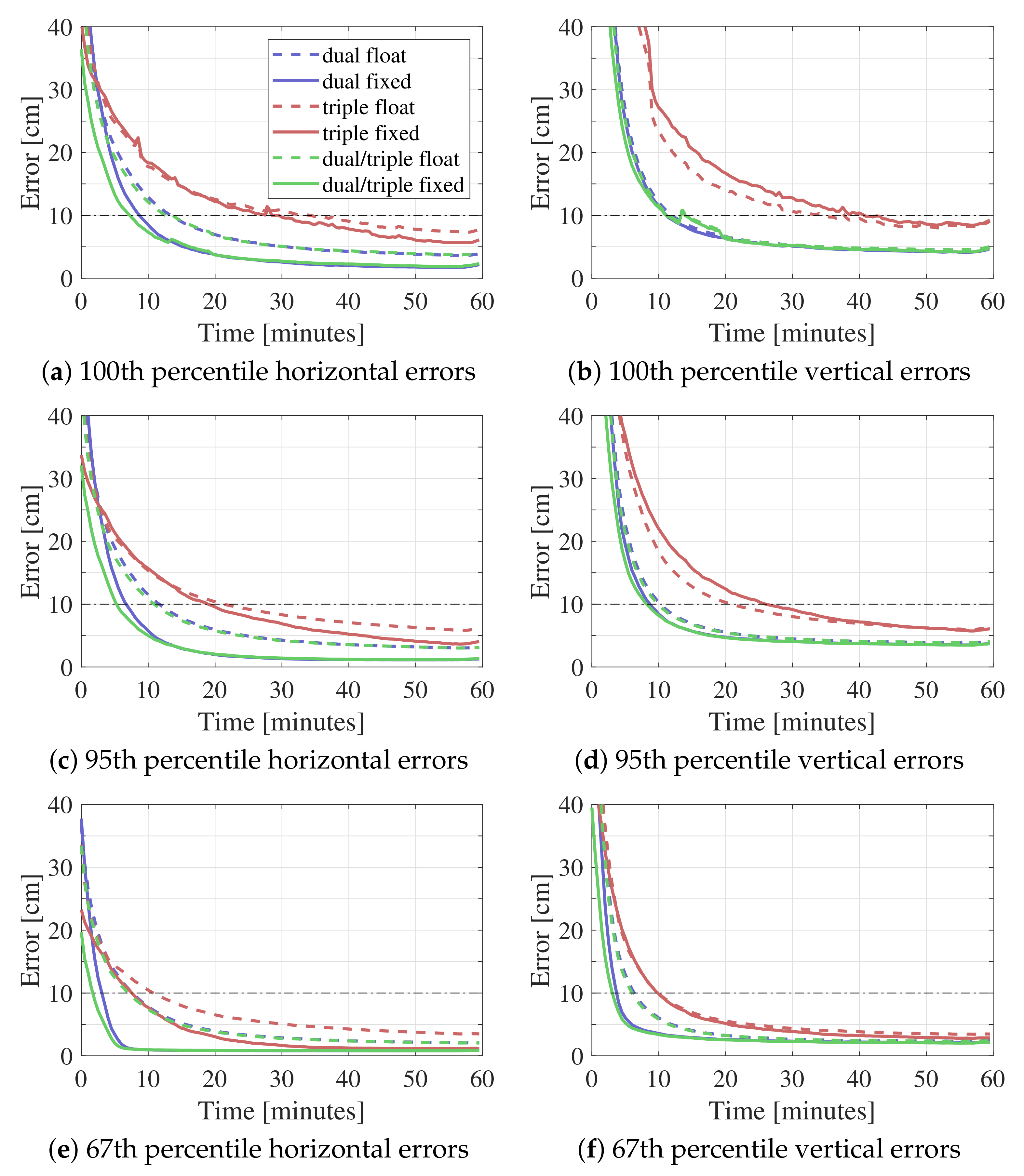
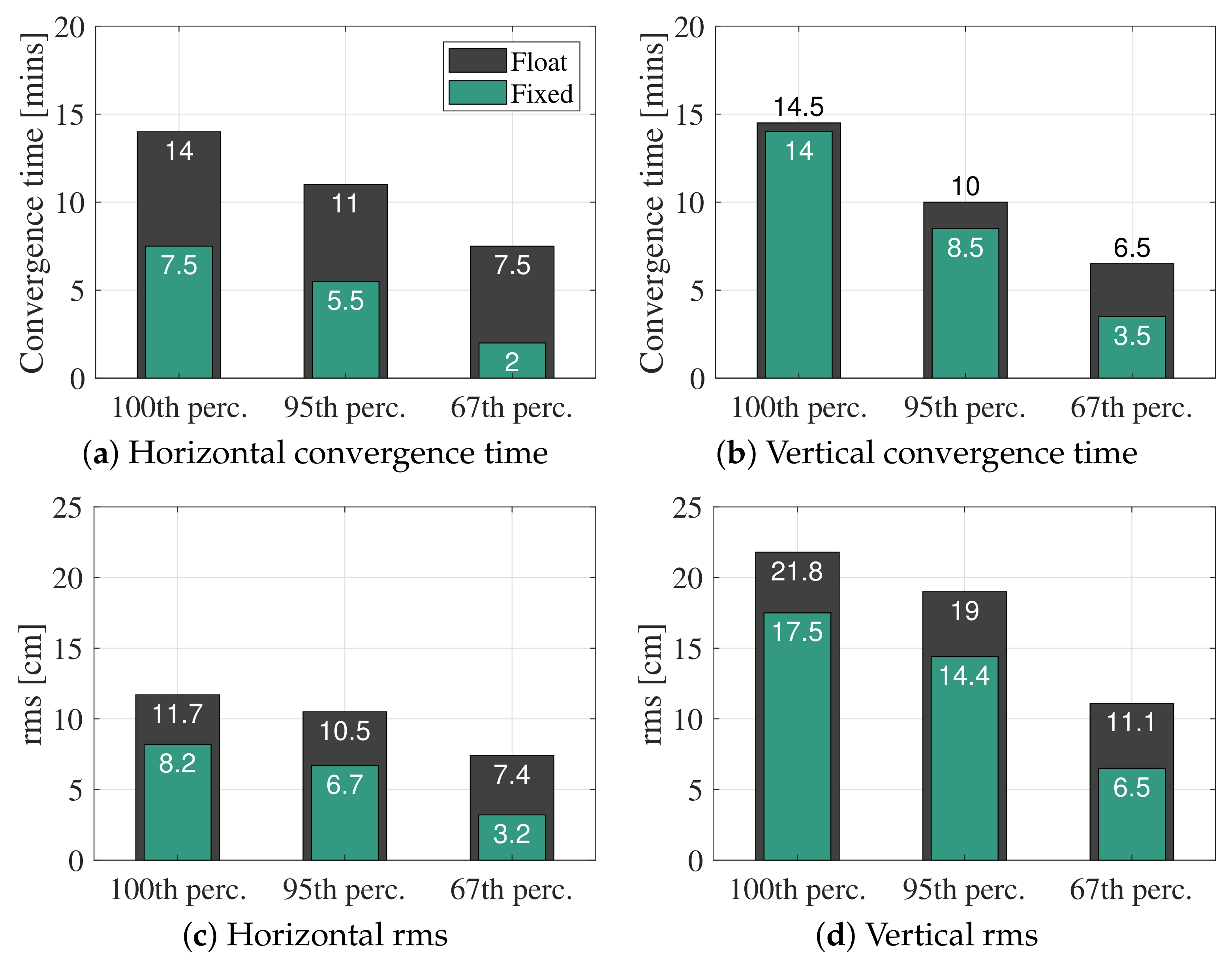
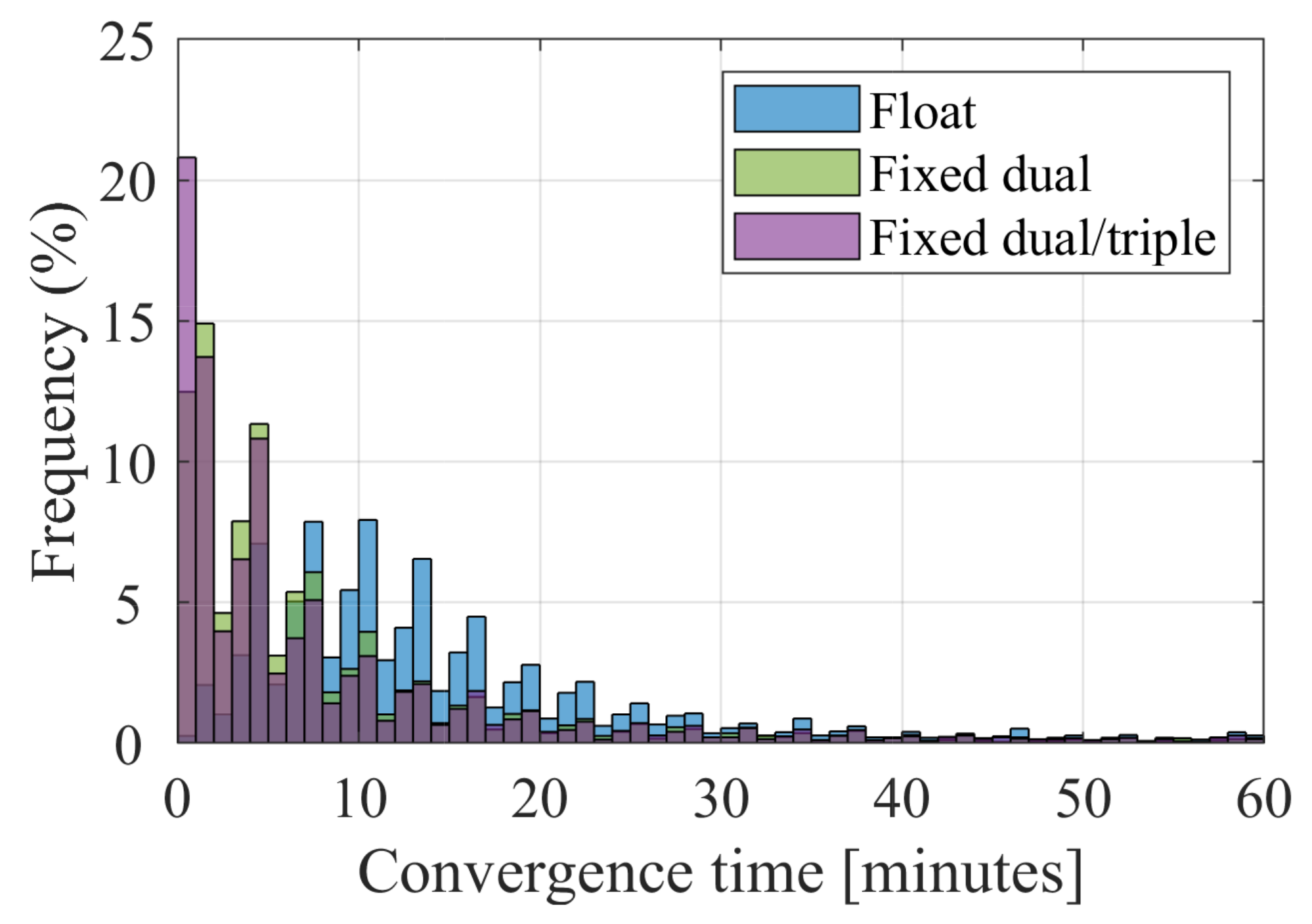
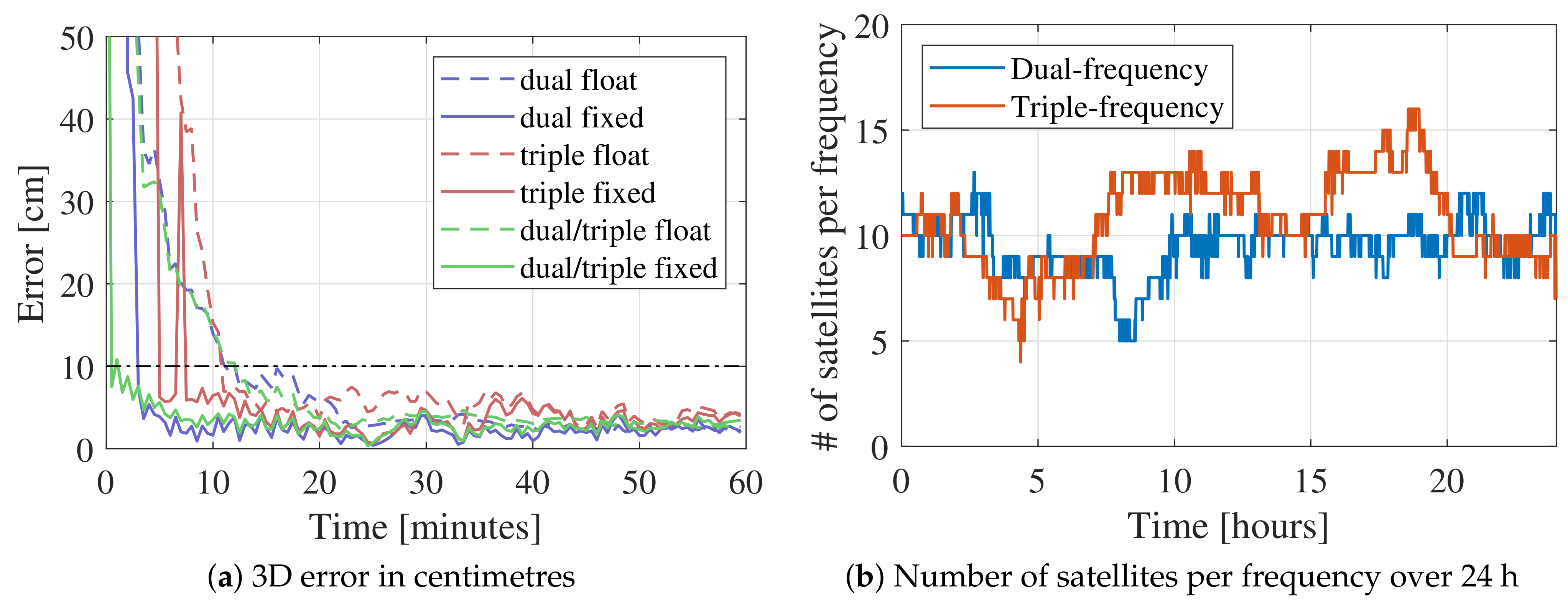
3.1. Performance Comparison with Dual-, Triple-, and Mixed Dual-/Triple-Frequency Processing
3.2. Mixed Dual-/Triple-Frequency Performance Analysis
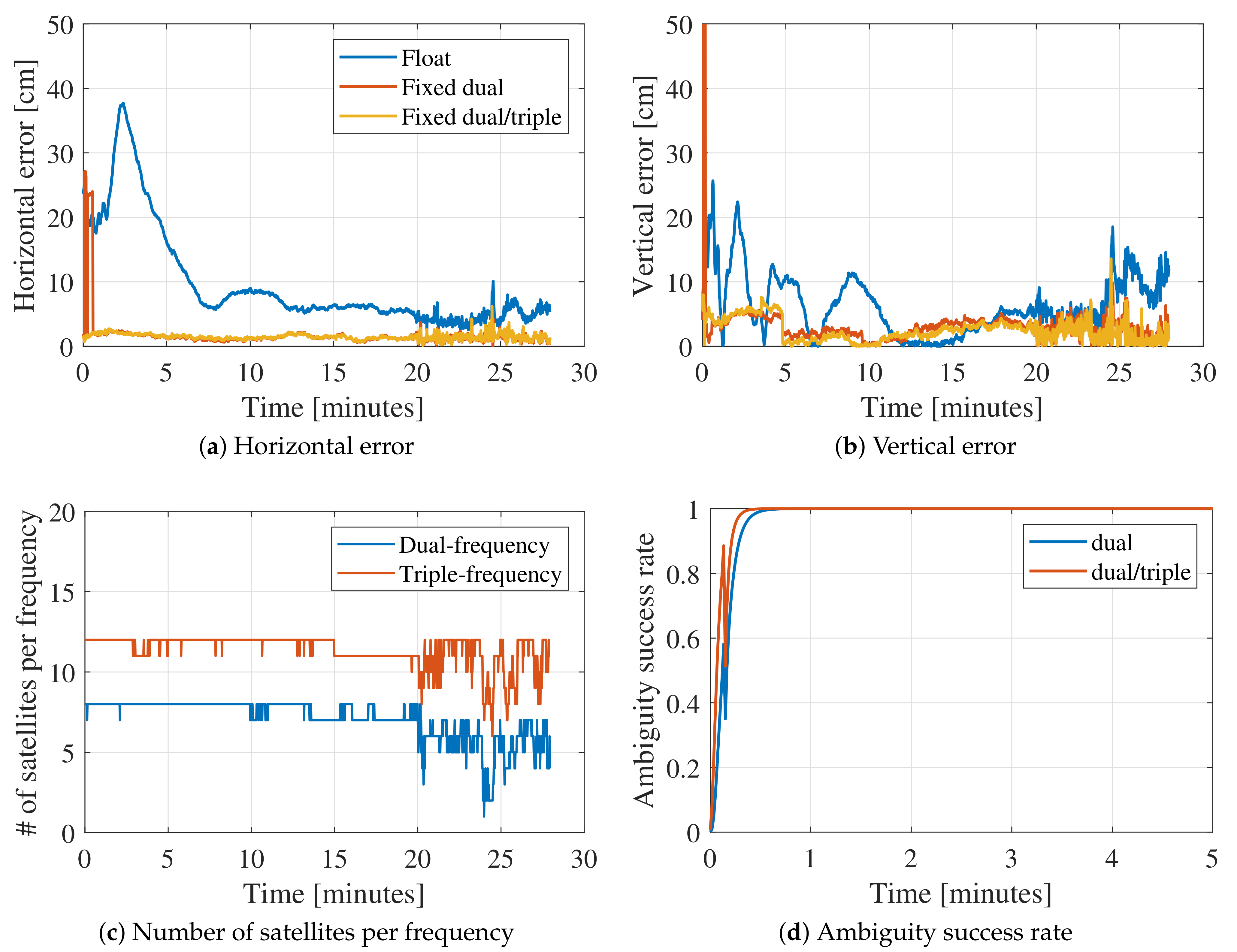
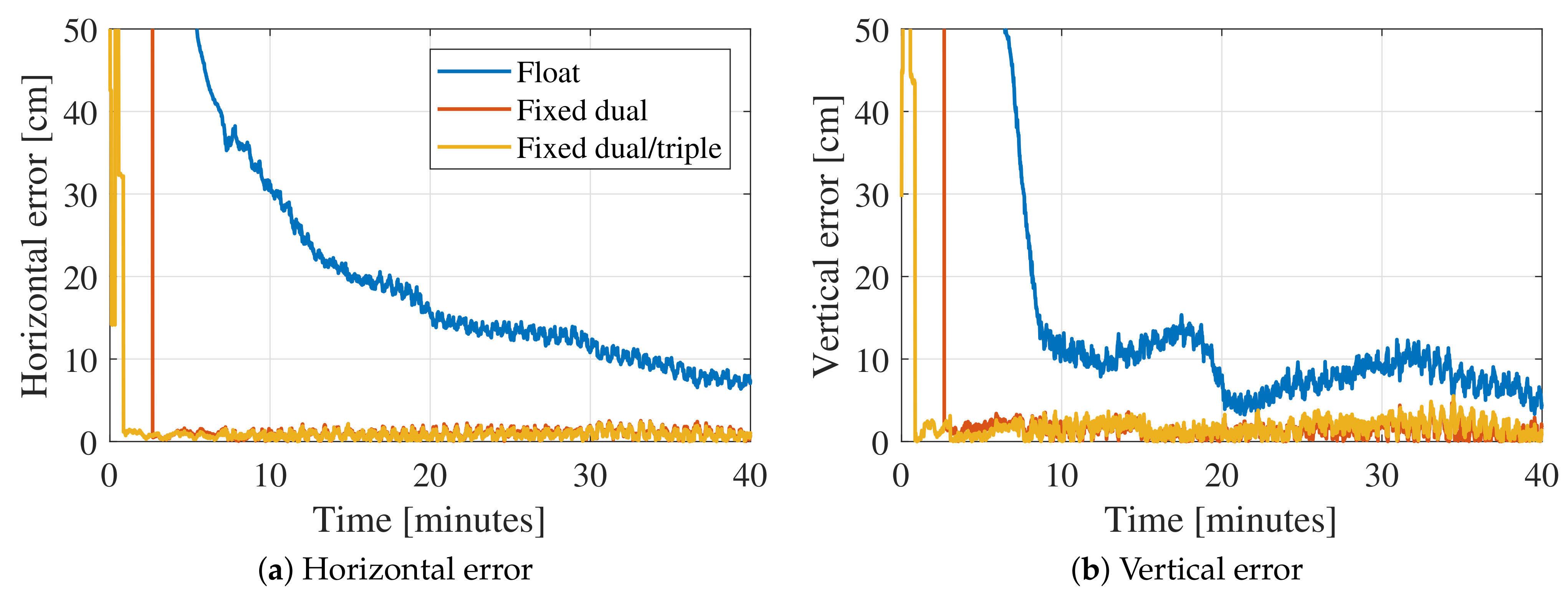
3.3. Kinematic Automotive Data Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Takasu, T.; Yasuda, A. Kalman-filter-based integer ambiguity resolution strategy for long-baseline RTK with ionosphere and troposphere estimation. In Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2010), Portland, OR, USA, 21–24 September 2010; pp. 161–171. [Google Scholar]
- Odolinski, R.; Teunissen, P.; Odijk, D. Combined GPS+ BDS for short to long baseline RTK positioning. Meas. Sci. Technol. 2015, 26, 045801. [Google Scholar] [CrossRef]
- Bisnath, S. PPP: Perhaps the natural processing mode for precise GNSS PNT. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 419–425. [Google Scholar]
- Bisnath, S.; Gao, Y. Precise point positioning a powerful technique with a promising future. GPS World 2009, 20, 43–50. [Google Scholar]
- Nadarajah, N.; Khodabandeh, A.; Wang, K.; Choudhury, M.; Teunissen, P.J. Multi-GNSS PPP-RTK: From large-to small-scale networks. Sensors 2018, 18, 1078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Collins, P.; Lahaye, F.; Heroux, P.; Bisnath, S. Precise point positioning with ambiguity resolution using the decoupled clock model. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 1315–1322. [Google Scholar]
- Geng, J.; Guo, J.; Meng, X.; Gao, K. Speeding up PPP ambiguity resolution using triple-frequency GPS/BeiDou/Galileo/QZSS data. J. Geod. 2020, 94, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Naciri, N.; Bisnath, S. Multi-GNSS Ambiguity Resolution as a Substitute to Obstructed Satellites in Precise Point Positioning Processing. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2020), Virtual, 21–25 September 2020; pp. 2960–2971. [Google Scholar]
- Collins, P. Isolating and estimating undifferenced GPS integer ambiguities. In Proceedings of the Institute of Navigation, National Technical Meeting, San Diego, CA, USA, 28–30 January 2008; Volume 2, pp. 720–732. [Google Scholar]
- Collins, P.; Lahaye, F.; Bisnath, S. External ionospheric constraints for improved PPP-AR initialisation and a generalised local augmentation concept. In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 3055–3065. [Google Scholar]
- Banville, S.; Collins, P.; Zhang, W.; Langley, R.B. Global and regional ionospheric corrections for faster PPP convergence. Navig. J. Inst. Navig. 2014, 61, 115–124. [Google Scholar] [CrossRef]
- Aggrey, J.; Bisnath, S. Improving GNSS PPP convergence: The case of atmospheric-constrained, multi-GNSS PPP-AR. Sensors 2019, 19, 587. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naciri, N.; Hauschild, A.; Bisnath, S. Exploring Signals on L5/E5a/B2a for Dual-Frequency GNSS Precise Point Positioning. Sensors 2021, 21, 2046. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y.; Pan, L.; Zhu, J. Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo. Adv. Space Res. 2015, 56, 133–143. [Google Scholar] [CrossRef]
- Li, X.; Liu, G.; Li, X.; Zhou, F.; Feng, G.; Yuan, Y.; Zhang, K. Galileo PPP rapid ambiguity resolution with five-frequency observations. GPS Solut. 2020, 24, 1–13. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J. Beyond three frequencies: An extendable model for single-epoch decimeter-level point positioning by exploiting Galileo and BeiDou-3 signals. J. Geod. 2020, 94, 1–15. [Google Scholar] [CrossRef]
- Naciri, N.; Bisnath, S. An uncombined triple-frequency user implementation of the decoupled clock model for PPP-AR. J. Geod. 2021, 95, 1–17. [Google Scholar] [CrossRef]
- El-Mowafy, A.; Deo, M.; Rizos, C. On biases in precise point positioning with multi-constellation and multi-frequency GNSS data. Meas. Sci. Technol. 2016, 27, 035102. [Google Scholar] [CrossRef]
- Håkansson, M.; Jensen, A.B.; Horemuz, M.; Hedling, G. Review of code and phase biases in multi-GNSS positioning. GPS Solut. 2017, 21, 849–860. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Dong, D.; Li, P.; Li, X.; Schuh, H. Influence of stochastic modeling for inter-system biases on multi-GNSS undifferenced and uncombined precise point positioning. GPS Solut. 2019, 23, 1–13. [Google Scholar] [CrossRef]
- Abdelazeem, M.; Çelik, R.N.; El-Rabbany, A. MGR-DCB: A precise model for multi-constellation GNSS receiver differential code bias. J. Navig. 2016, 69, 698–708. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Teunissen, P.; Yuan, Y. On the short-term temporal variations of GNSS receiver differential phase biases. J. Geod. 2017, 91, 563–572. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Teunissen, P.; Yuan, Y.; Zhang, X.; Li, M. A modified carrier-to-code leveling method for retrieving ionospheric observables and detecting short-term temporal variability of receiver differential code biases. J. Geod. 2018, 93, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08. atx: Status and potential improvements. J. Geod. 2016, 90, 343–364. [Google Scholar] [CrossRef] [Green Version]
- Aggrey, J. Precise Point Positioning Augmentation for Various Grades of Global Navigation Satellite System Hardware. Ph.D. Thesis, York University, Toronto, ON, Canada, 2019. [Google Scholar]
- Seepersad, G. Reduction of Initial Convergence Period in GPS PPP Data Processing. Ph.D. Thesis, York University, Toronto, ON, Canada, 2012. [Google Scholar]
- Kouba, J. Testing of global pressure/temperature (GPT) model and global mapping function (GMF) in GPS analyses. J. Geod. 2009, 83, 199–208. [Google Scholar] [CrossRef]
- Laurichesse, D.; Blot, A. Fast PPP convergence using multi-constellation and triple-frequency ambiguity resolution. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation, ION GNSS+ 2016, Portland, OR, USA, 12–16 September 2016; Volume 3, pp. 2082–2088. [Google Scholar] [CrossRef] [Green Version]
- Chang, X.W.; Yang, X.; Zhou, T. MLAMBDA: A modified LAMBDA method for integer least-squares estimation. J. Geod. 2005, 79, 552–565. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, J. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Xiao, G.; Li, P.; Gao, Y.; Heck, B. A unified model for multi-frequency PPP ambiguity resolution and test results with Galileo and BeiDou triple-frequency observations. Remote Sens. 2019, 11, 116. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Gao, Y. A troposphere constraint method to improve PPP ambiguity-resolved height solution. J. Navig. 2014, 67, 249–262. [Google Scholar] [CrossRef]
- Teunissen, P. Influence of ambiguity precision on the success rate of GNSS integer ambiguity bootstrapping. J. Geod. 2007, 81, 351–358. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.; Zhang, X.; Wang, J.; Ren, X. Modeling and assessment of triple-frequency BDS precise point positioning. J. Geod. 2016, 90, 1223–1235. [Google Scholar] [CrossRef]
- Geng, J.; Bock, Y. Triple-frequency GPS precise point positioning with rapid ambiguity resolution. J. Geod. 2013, 87, 449–460. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J.; Chang, H.; Li, X. Toward global instantaneous decimeter-level positioning using tightly coupled multi-constellation and multi-frequency GNSS. J. Geod. 2019, 93, 977–991. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhu, F.; Zhang, Y.; Mohamed, F.; Zhou, W. The improvement in integer ambiguity resolution with INS aiding for kinematic precise point positioning. J. Geod. 2019, 93, 993–1010. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Liu, G.; Yuan, Y.; Freeshah, M.; Zhang, K.; Zhou, F. BDS multi-frequency PPP ambiguity resolution with new B2a/B2b/B2a+ b signals and legacy B1I/B3I signals. J. Geod. 2020, 94, 1–15. [Google Scholar] [CrossRef]



| State Term Dependency (One Per …) | Measurement Type | Frequency Band | ||||||
|---|---|---|---|---|---|---|---|---|
| Receiver | Constellation | Satellite | Code | Phase | 1 | 2 | 3 | |
| Receiver coordinates | X | X | X | X | X | X | ||
| Wet tropospheric delay | X | X | X | X | X | X | ||
| Receiver pseudorange clock | X | X | X | X | X | |||
| Receiver carrier-phase clock | X | X | X | X | X | |||
| Receiver L2 phase bias | X | X | X | |||||
| Receiver L3 phase bias | X | X | X | |||||
| Receiver IFB | X | X | X | |||||
| Slant ionospheric delay | X | X | X | X | X | X | ||
| L1 ambiguity | X | X | X | |||||
| L2 ambiguity | X | X | X | |||||
| L3 ambiguity | X | X | X | |||||
| Parameter | Strategy |
|---|---|
| Receiver coordinates | Kinematic mode: estimated with process noise equivalent to 100 km/h |
| Static mode: estimated as constants | |
| Receiver reference coordinates | IGS SINEX positions |
| Receiver code and phase clocks | Estimated as white noise processes |
| Receiver L2 and L3 phase biases and IFB | Estimated as white noise processes |
| Tropospheric delay | Dry: GMF model and mapping function [29]. |
| Wet: estimated as a random walk process with process noise of 0.05 mm/ | |
| Ionospheric delays | Estimated as white noise processes |
| Ambiguities | Estimated as constants on each continuous arc |
| Elevation angle cut-off | 7 |
| Satellite orbits and clocks | Corrected for using CNES ultra-rapid products [30] |
| Code and phase biases | Corrected for using CNES ultra-rapid observable-specific bias (OSB) products |
| Weighting strategy | Elevation dependent weighting: with equal to |
| 0.3 m and 0.003 m for the pseudorange and carrier-phase measurements, | |
| respectively, and being the elevation angle. a and b were determined | |
| based on a residual and measurement quality analysis. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naciri, N.; Bisnath, S. Approaching Global Instantaneous Precise Positioning with the Dual- and Triple-Frequency Multi-GNSS Decoupled Clock Model. Remote Sens. 2021, 13, 3768. https://doi.org/10.3390/rs13183768
Naciri N, Bisnath S. Approaching Global Instantaneous Precise Positioning with the Dual- and Triple-Frequency Multi-GNSS Decoupled Clock Model. Remote Sensing. 2021; 13(18):3768. https://doi.org/10.3390/rs13183768
Chicago/Turabian StyleNaciri, Nacer, and Sunil Bisnath. 2021. "Approaching Global Instantaneous Precise Positioning with the Dual- and Triple-Frequency Multi-GNSS Decoupled Clock Model" Remote Sensing 13, no. 18: 3768. https://doi.org/10.3390/rs13183768
APA StyleNaciri, N., & Bisnath, S. (2021). Approaching Global Instantaneous Precise Positioning with the Dual- and Triple-Frequency Multi-GNSS Decoupled Clock Model. Remote Sensing, 13(18), 3768. https://doi.org/10.3390/rs13183768






