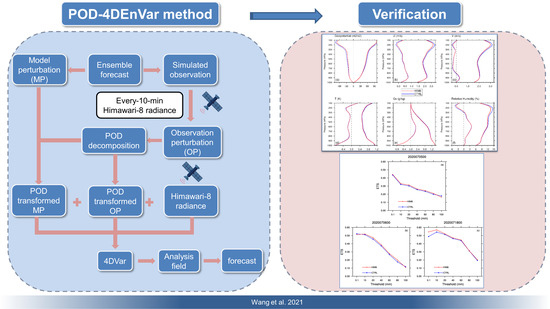
Potential Impacts of Assimilating Every-10-Minute Himawari-8 Satellite Radiance with the POD-4DEnVar Method
Abstract
:1. Introduction
2. Methodology
2.1. POD-4DEnVar Algorithm
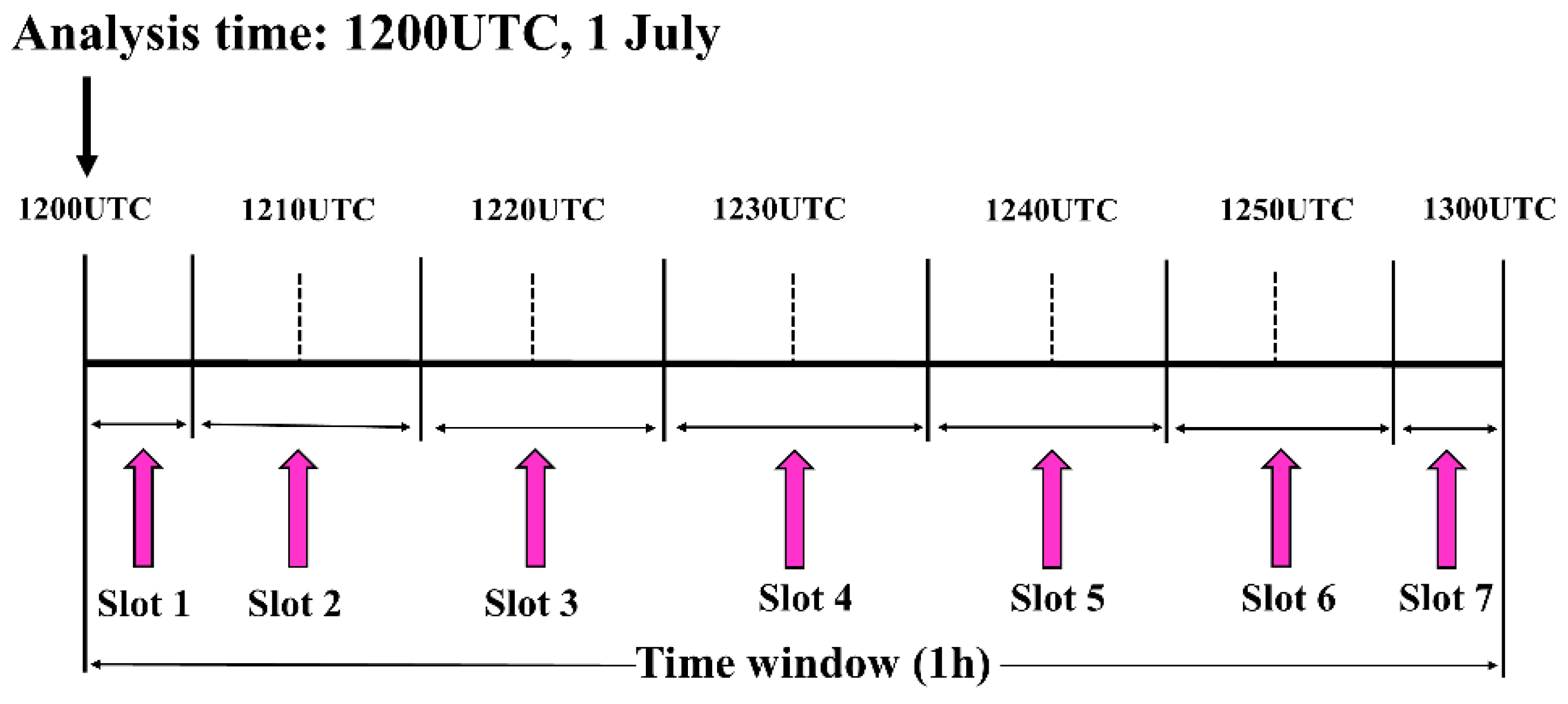
2.2. Four-Dimensional Ensemble Sample Construction
2.3. Himawari-8 Observations Quality Control
3. Experiment Design
4. Results and Discussion
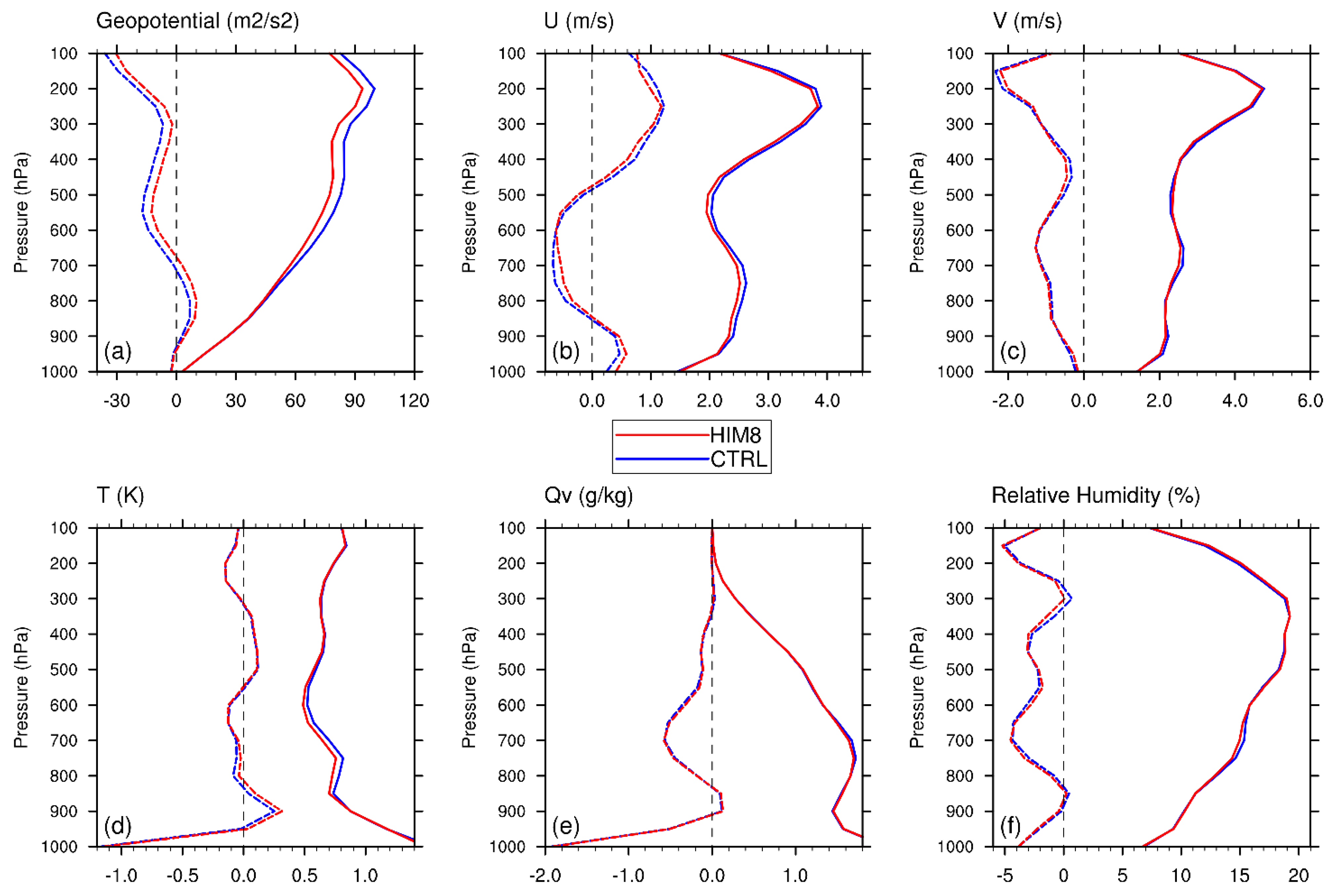
4.1. RMSE Verification against ERA-5 Data
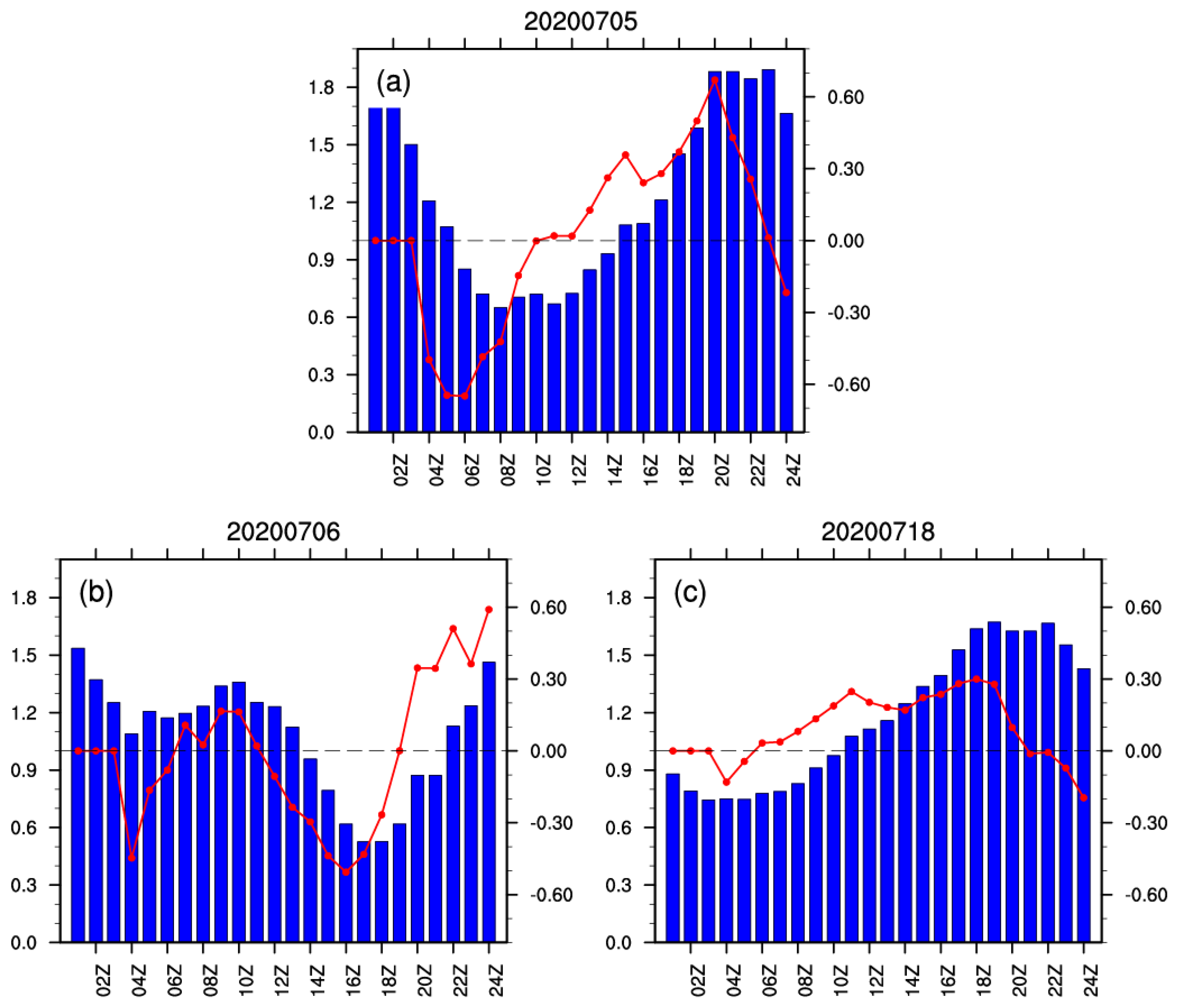
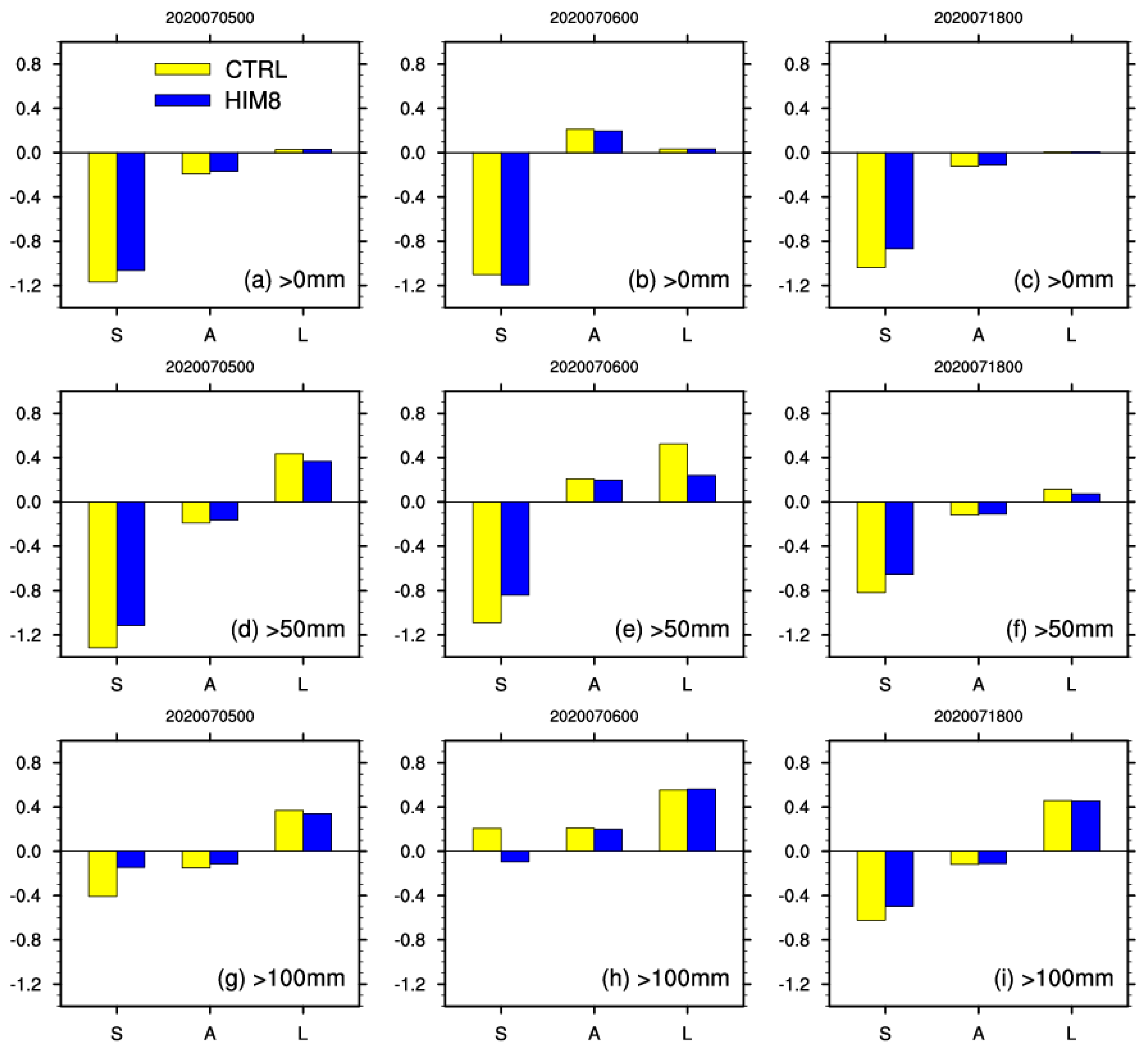
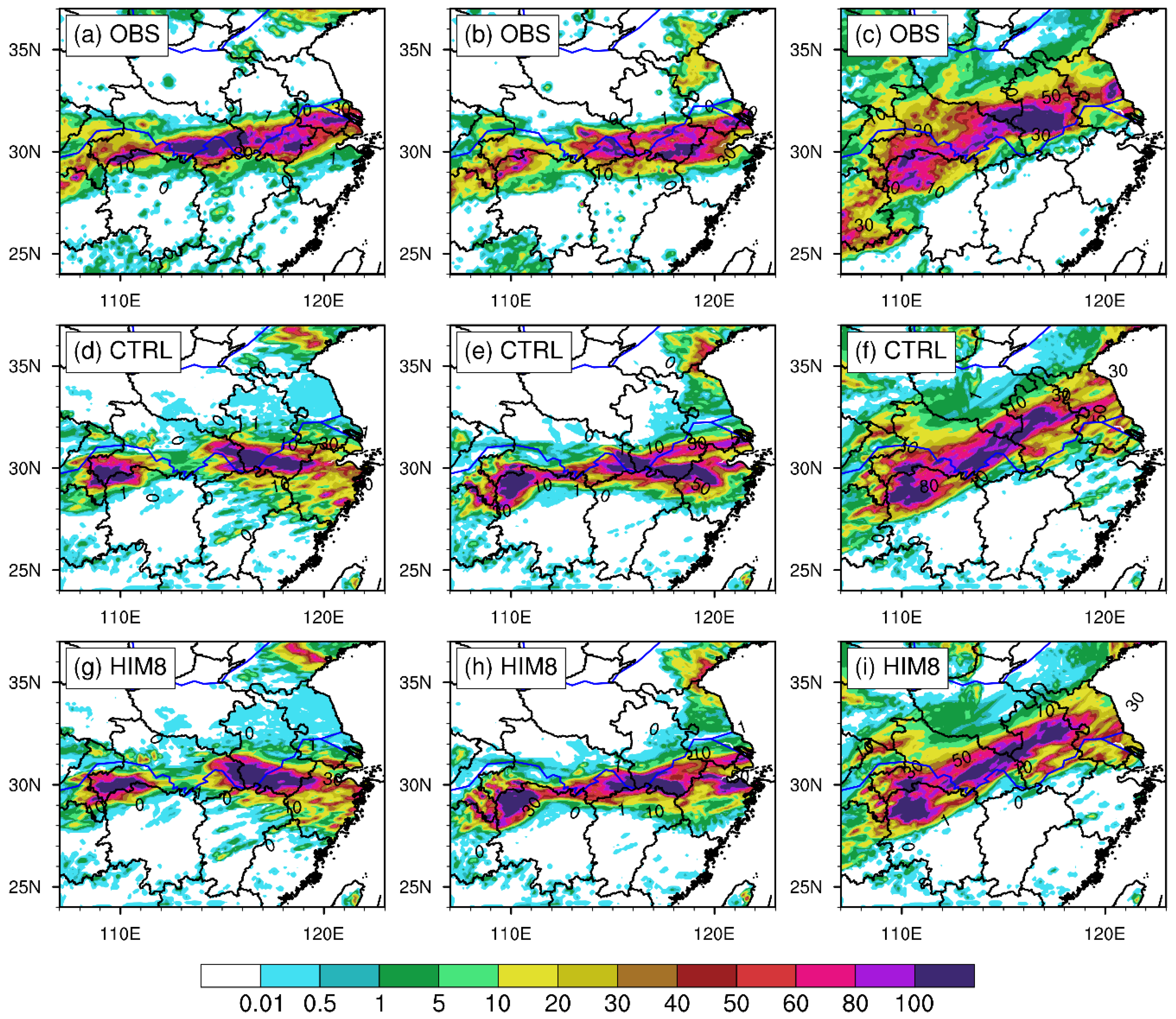
4.2. Impacts on Rainfall Forecasts
4.3. Discussion
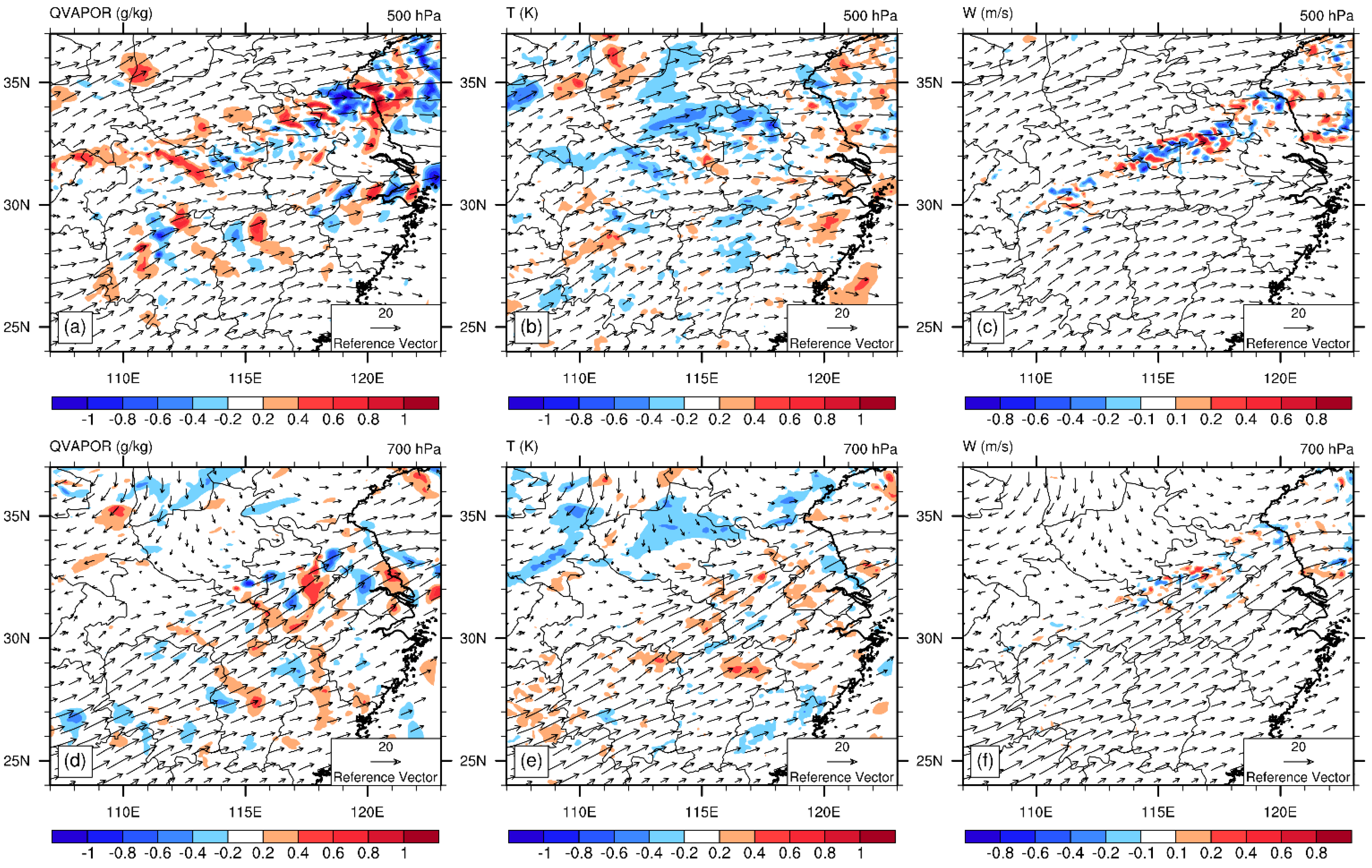
4.3.1. The Initial Increments
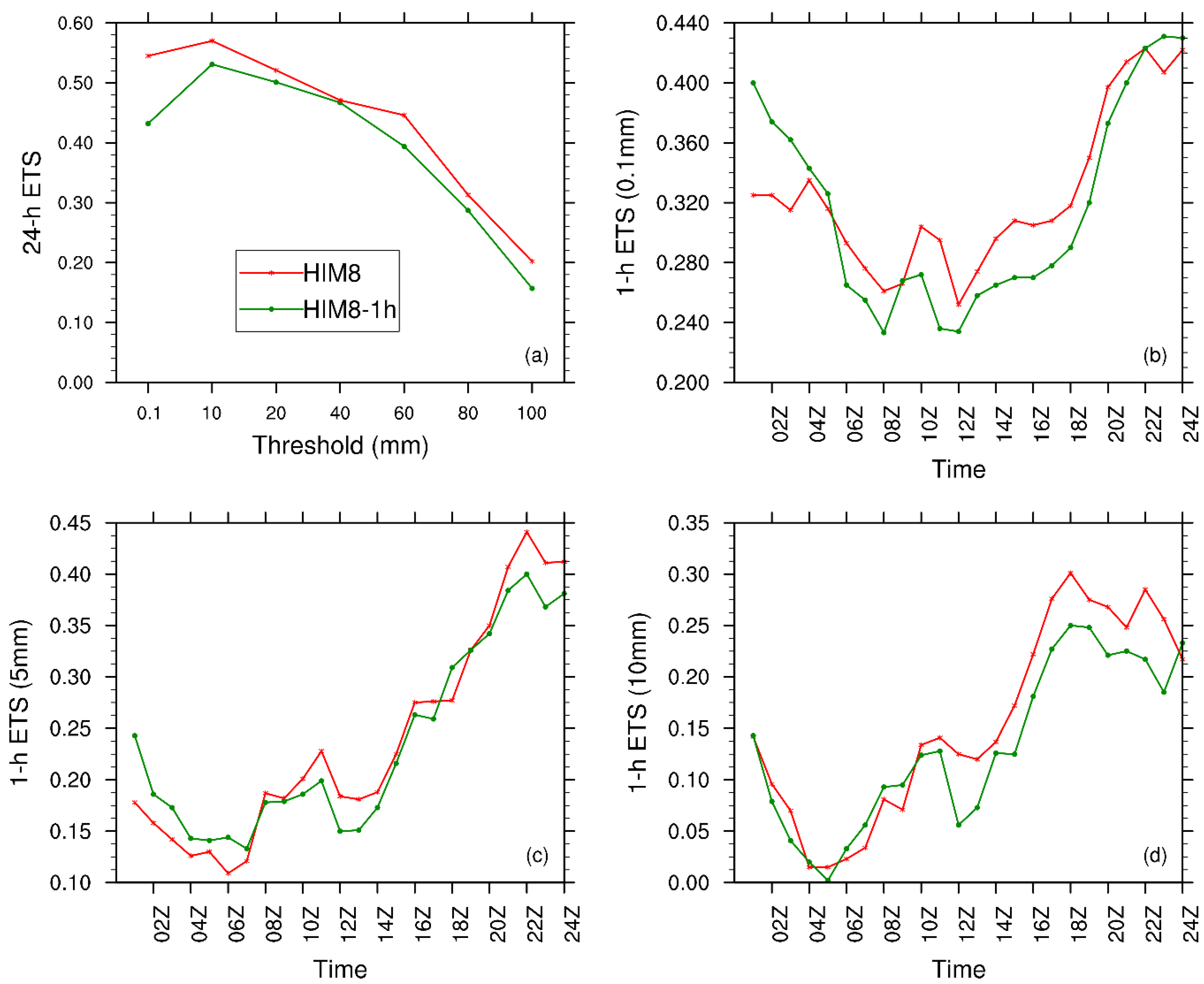
4.3.2. The Effect of Observation Frequency
4.3.3. The Effect of the Assimilation Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic. J. Geophys. Res. 1994, 99, 20. [Google Scholar]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Hamill, T.M. Ensemble-based atmospheric data assimilation. In Predictability of Weather and Climate; Palmer, T., Hagedorn, R., Eds.; Cambridge University Press: Cambridge, UK, 2006; pp. 124–156. [Google Scholar]
- Derber, J.C.; Wu, W.-S. The Use of TOVS Cloud-Cleared Radiances in the NCEP SSI Analysis System. Mon. Weather Rev. 1998, 126, 2287–2290. [Google Scholar] [CrossRef]
- Chen, D.; Xue, J. An Overview on Recent Progresses of the Operational Numerical Weather Prediction Models. Acta Meteorol. Sin. 2004, 62, 623–633. [Google Scholar]
- Barker, D.M.; Huang, W.; Guo, Y.-R.; Bourgeois, A.J.; Xiao, Q.N. A Three-Dimensional Variational Data Assimilation System for MM5_ Implementation and Initial Results. Mon. Weather Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef] [Green Version]
- Bouttier, G.K.F. Observing-system experiments in the ECMWF 4D-Var data assimilation system. Q. J. R. Meteorol. Soc. 2001, 127, 1469–1488. [Google Scholar] [CrossRef]
- Huang, X.Y.; Xiao, Q.; Barker, D.M.; Zhang, X.; Michalakes, J.; Huang, W.; Henderson, T.; Bray, J.; Chen, Y.; Ma, Z.; et al. Four-Dimensional Variational Data Assimilation for WRF: Formulation and Preliminary Results. Mon. Weather Rev. 2009, 137, 299–314. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Huang, X.Y.; Liu, J.; Poterjoy, J.; Weng, Y.; Zhang, F.; Wang, H. Development of an Efficient Regional Four-Dimensional Variational Data Assimilation System for WRF. J. Atmos. Ocean Technol. 2014, 31, 2777–2794. [Google Scholar] [CrossRef] [Green Version]
- Pellerin, S.; Laroche, S.; Tanguay, M.; Gauthier, P.; Morneau, J. Extension of 3DVAR to 4DVAR: Implementation of 4DVAR at the Meteorological Service of Canada. Mon. Weather Rev. 2007, 135, 2339–2354. [Google Scholar]
- Houtekamer, P.L.; Mitchell, H.L. Data Assimilation Using an Ensemble Kalman Filter Technique. Mon. Weather Rev. 1998, 126, 796. [Google Scholar] [CrossRef]
- Wang, X.; Barker, D.M.; Snyder, C.; Hamill, T.M. A Hybrid ETKF–3DVAR Data Assimilation Scheme for the WRF Model. Part I: Observing System Simulation Experiment. Mon. Weather Rev. 2008, 136, 5116–5131. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Barker, D.M.; Snyder, C.; Hamill, T.M. A Hybrid ETKF–3DVAR Data Assimilation Scheme for the WRF Model. Part II: Real Observation Experiments. Mon. Weather Rev. 2008, 136, 5132–5147. [Google Scholar] [CrossRef] [Green Version]
- Lorenc, A.C. The potential of the ensemble Kalman filter for NWP—A comparison with 4D-Var. Q. J. R. Meteorol. Soc. 2003, 129, 3183–3203. [Google Scholar] [CrossRef]
- Geer, A.J.; Lonitz, K.; Weston, P.; Kazumori, M.; Okamoto, K.; Zhu, Y.; Liu, E.H.; Collard, A.; Bell, W.; Migliorini, S.; et al. All-sky satellite data assimilation at operational weather 2018. Q. J. R. Meteorol. Soc. 2018, 114, 1191–1217. [Google Scholar] [CrossRef]
- Xiong, C.; Zhang, L.; Guan, J.; Tao, H.; Su, J. Development and application of ensemble-variational data assimilation methods. Adv. Earth Sci. 2013, 28, 648–656. [Google Scholar]
- Hamill, T.M.; Snyder, C. A Hybrid Ensemble Kalman Filter–3D Variational Analysis Scheme. Mon. Weather Rev. 2000, 128, 2905–2919. [Google Scholar] [CrossRef]
- Wang, X. Application of the WRF Hybrid ETKF–3DVAR data assimilation system for hurricane track forecasts. Weather Forecast. 2011, 26, 868–884. [Google Scholar] [CrossRef]
- Poterjoy, J.; Zhang, M.; Zhang, F. E3DVar: Coupling an Ensemble Kalman Filter with Three-Dimensional Variational Data Assimilation in a Limited-Area Weather Prediction Model and Comparison to E4DVar. Mon. Weather Rev. 2013, 141, 900–917. [Google Scholar]
- Zhang, M.; Zhang, F. E4DVar: Coupling an Ensemble Kalman Filter with Four-Dimensional Variational Data Assimilation in a Limited-Area Weather Prediction Model. Mon. Weather Rev. 2012, 140, 587–600. [Google Scholar] [CrossRef] [Green Version]
- Buehner, M.; McTaggart-Cowan, R.; Beaulne, A.; Charette, C.; Garand, L.; Heilliette, S.; Lapalme, E.; Laroche, S.; Macpherson, S.R.; Morneau, J.; et al. Implementation of Deterministic Weather Forecasting Systems Based on Ensemble–Variational Data Assimilation at Environment Canada. Part I: The Global System. Mon. Weather Rev. 2015, 143, 2532–2559. [Google Scholar] [CrossRef]
- Qiu, C.; Shao, A.; Xu, Q.; Wei, L. Fitting model fields to observations by using singular value decomposition: An ensemble-based 4DVar approach. J. Geophys. Res. 2007, 112, D11105. [Google Scholar] [CrossRef]
- Wang, B.; Liu, J.; Wang, S.; Cheng, W.; Juan, L.; Liu, C.; Xiao, Q.; Kuo, Y.H. An economical approach to four-dimensional variational data assimilation. Adv. Atmos. Sci. 2010, 27, 715–727. [Google Scholar] [CrossRef] [Green Version]
- Tian, X.; Xie, Z.; Dai, A. An ensemble-based explicit four-dimensional variational assimilation method. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Tian, X.; Xie, Z. An explicit four-dimensional variational data assimilation method based on the proper orthogonal decomposition: Theoretics and evaluation. Sci. China Ser. D 2009, 52, 279–286. [Google Scholar] [CrossRef]
- Tian, X.; Xie, Z.; Sun, Q. A POD-based ensemble four-dimensional variational assimilation method. Tellus 2011, 63, 805–816. [Google Scholar] [CrossRef]
- Tian, X.; Xie, Z.; Liu, Y.; Cai, Z.; Fu, Y.; Zhang, H.; Feng, L. A joint data assimilation system (Tan-Tracker) to simultaneously estimate surface CO2 fluxes and 3-D atmospheric CO2 concentrations from observations. Atmos. Chem. Phys. 2014, 14, 13281–13293. [Google Scholar] [CrossRef] [Green Version]
- Collard, A.; Hilton, F.; Forsythe, M.; Candy, B. From Observations to Forecasts—Part 8: The use of satellite observations in numerical weather prediction. Q. J. R. Meteorol. Soc. 2011, 66, 31–36. [Google Scholar] [CrossRef] [Green Version]
- Köpken, C.; Kelly, G.; Thépaut, J.-N. Assimilation of Meteosat radiance data within the 4D-Var system at ECMWF: Assimilation experiments and forecast impact. Q. J. R. Meteorol. Soc. 2004, 130, 2277–2292. [Google Scholar] [CrossRef]
- Ha, S.-Y.; Snyder, C.; Schwartz, C.S.; Liu, Z. Impact of Assimilating AMSU-A Radiances on Forecasts of 2008 Atlantic Tropical Cyclones Initialized with a Limited-Area Ensemble Kalman Filter. Mon. Weather Rev. 2012, 140, 4017–4034. [Google Scholar]
- Zou, X.; Weng, F.; Zhang, B.; Lin, L.; Qin, Z.; Tallapragada, V. Impacts of assimilation of ATMS data in HWRF on track and intensity forecasts of 2012 four landfall hurricanes. J. Geophys. Res. 2013, 118, 11–558. [Google Scholar] [CrossRef]
- Shen, F.; Min, J. Assimilating AMSU-a radiance data with the WRF hybrid En3DVAR system for track predictions of Typhoon Megi (2010). Adv. Atmos. Sci. 2015, 32, 1231–1243. [Google Scholar] [CrossRef]
- Lu, Q.; Bell, W.; Bauer, P.; Bormann, N.; Peubey, C. An evaluation of FY-3A satellite data for numerical weather prediction. Q. J. R. Meteorol. Soc. 2011, 137, 1298–1311. [Google Scholar] [CrossRef]
- Chen, K.; English, S.; Bormann, N.; Zhu, J. Assessment of FY-3A and FY-3B MWHS observations. Weather Forecast. 2015, 30, 1280–1290. [Google Scholar] [CrossRef]
- Li, J.; Liu, G. Direct assimilation of Chinese FY-3C Microwave Temperature Sounder-2radiances in the global GRAPES system. Atmos. Meas. Tech. 2016, 9, 3095–3113. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, H.; Bormann, N.; Geer, A.J.; Lu, Q.; English, S.J. Evaluation and Assimilation of the Microwave Sounder MWHS-2 Onboard FY-3C in the ECMWF Numerical Weather Prediction System. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3333–3349. [Google Scholar] [CrossRef]
- Zou, X.; Qin, Z.; Weng, F. Improved Coastal Precipitation Forecasts with Direct Assimilation of GOES-11/12 Imager Radiances. Mon. Weather Rev. 2011, 139, 3711–3729. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Minamide, M.; Clothiaux, E.E. Potential impacts of assimilating all-sky infrared satellite radiances from GOES-R on convection-permitting analysis and prediction of tropical cyclones. Geophys. Res. Lett. 2016, 43, 2954–2963. [Google Scholar] [CrossRef] [Green Version]
- Qin, Z.; Zou, X. Direct Assimilation of ABI Infrared Radiances in NWP Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2022–2033. [Google Scholar] [CrossRef]
- Szyndel, M.D.E.; Kelly, G.; Thépaut, J.N. Evaluation of potential benefit of assimilation of SEVIRI water vapour radiance data from Meteosat-8 into global numerical weather prediction analyses. Atmos. Sci. Lett. 2005, 6, 105–111. [Google Scholar] [CrossRef]
- Stengel, M.; Undén, P.; Lindskog, M.; Dahlgren, P.; Gustafsson, N.; Bennartz, R. Assimilation of SEVIRI infrared radiances with HIRLAM 4D-Var. Q. J. R. Meteorol. Soc. 2009, 135, 2100–2109. [Google Scholar] [CrossRef]
- Wang, Y.; He, J.; Chen, Y.; Min, J. The Potential Impact of Assimilating Synthetic Microwave Radiances Onboard a Future Geostationary Satellite on the Prediction of Typhoon Lekima Using the WRF Model. Remote Sens. 2021, 13, 886. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An Introduction to Himawari-8/9—Japan’s New-Generation Geostationary Meteorological Satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Maddy, E.S.; Zhang, B.; Zhu, T.; Boukabara, S.A. Impact Assessment of Himawari-8 AHI Data Assimilation in NCEP GDAS/GFS with GSI. J. Atmos. Ocean Technol. 2017, 34, 797–815. [Google Scholar] [CrossRef]
- Kazumori, M. Assimilation of Himawari-8 Clear Sky Radiance Data in JMA’s Global and Mesoscale NWP Systems. J. Meteorol. Soc. Jpn. Ser. II 2018, 96, 173–192. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Yang, S.; Min, J.; Chen, L.; Chen, Y.; Zhang, T. Added Value of Assimilating Himawari-8 AHI Water Vapor Radiances on Analyses and Forecasts for “7.19” Severe Storm Over North China. J. Geophys. Res. 2018, 123, 3374–3394. [Google Scholar] [CrossRef]
- Sawada, Y.; Okamoto, K.; Kunii, M.; Miyoshi, T. Assimilating every-10-minute Himawari-8 infrared radiances to improve convective predictability. J. Geophys. Res. Atmos. 2019, 124, 2546–2561. [Google Scholar] [CrossRef]
- Honda, T.; Miyoshi, T.; Lien, G.; Nishizawa, S.; Yoshida, R.; Adachi, S.A.; Terasaki, K.; Okamoto, K.; Tomita, H.; Bessho, K. Assimilating All-Sky Himawari-8 Satellite Infrared Radiances: A Case of Typhoon Soudelor (2015). Mon. Weather Rev. 2018, 146, 213–229. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, L.; Zhang, B. FY-3A Microwave Data Assimilation Based on the POD-4DEnVar Method. Atmosphere 2018, 9, 189. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Zhang, L.; Zhang, B.; Guan, J.; You, W. Assimilation of MWHS and MWTS radiance data from the FY-3A satellite with the POD-3DEnVar method for forecasting heavy rainfall. Atmos. Res. 2019, 219, 95–105. [Google Scholar] [CrossRef]
- Xu, Q.; Wei, L.; Lu, H.; Qiu, C.; Zhao, Q. Time-expanded sampling for ensemble-based filters: Assimilation experiments with a shallow-water equation model. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Radhakrishnan, C.; Balaji, C. Impact of physics parameterization and 3DVAR data assimilation on prediction of tropical cyclones in the Bay of Bengal region. Nat. Hazards 2016, 80, 223–247. [Google Scholar]
- Aksoy, A.; Meng, Z.; Zhang, F. Tests of an Ensemble Kalman Filter for Mesoscale and Regional-Scale Data Assimilation. Part I: Perfect Model Experiments. Mon. Weather Rev. 2006, 134, 722–736. [Google Scholar]
- Lan, W.; Zhu, J.; Xue, M.; Lei, T.; Gao, J. Storm-scale ensemble Kalman filter data assimilation experiments using simulated Doppler radar data. Part II: Imperfect model tests. Chin. J. Atmos. Sci. 2010, 34, 737–753. (In Chinese) [Google Scholar]
- Yang, Y.; Zhang, L.; Zhang, B.; You, W.; Zhang, M.; Xie, B. Application of a Physical Ensemble Method in the POD-4DEnVar. Weather Forecast. 2018, 33, 1567–1585. [Google Scholar] [CrossRef]
- Ishida, H.; Nakajima, T.Y. Development of an unbiased cloud detection algorithm for a spaceborne multispectral imager. J. Geophys. Res. 2009, 114, D07206. [Google Scholar] [CrossRef]
- Auligné, T.; McNally, A.P.; Dee, D.P. Adaptive bias correction for satellite data in a numerical weather prediction system. Q. J. R. Meteorol. Soc. 2007, 133, 631–642. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.; Duda, M.G.; Powers, J.G. A Description of the Advanced Research WRF Version 3. NCAR Tech. No. 2008, 113. [Google Scholar] [CrossRef]
- Yesubabu, V.; Islam, S.; Sikka, D.R.; Kaginalkar, A.; Kashid, S.; Srivastava, A.K. Impact of variational assimilation technique on simulation of a heavy rainfall event over Pune, India. Nat. Hazards 2014, 71, 639–658. [Google Scholar] [CrossRef]
- Han, Y.; van Delst, P.; Liu, Q.; Weng, F.; Yan, B.; Han, Y. JCSDA Community radiative Transfer Model (CRTM)-Version 1. NOAA Tech. Rep. NESDIS 2006, 122, 33. [Google Scholar]
- CRTM. Available online: https://github.com/JCSDA/crtm (accessed on 7 October 2020).
- Singh, R.; Kumar, P.; Pal, P.K. Assimilation of Oceansat-2-Scatterometer-Derived Surface Winds in the Weather Research and Forecasting Model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1015–1021. [Google Scholar] [CrossRef]
- Yang, C.; Liu, Z.; Bresch, J.; Rizvi, S.; Huang, X.; Min, J. AMSR2 all-sky radiance assimilation and its impact on the analysis and forecast of Hurricane Sandy with a limited-area data assimilation system. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 30917. [Google Scholar] [CrossRef] [Green Version]
- Xian, Z.; Chen, K.; Zhu, J. All-sky assimilation of the MWHS-2 observations and evaluation the impacts on the analyses and forecasts of binary typhoons. J. Geophys. Res. Atmos. 2019, 124, 6359–6378. [Google Scholar] [CrossRef]
- Wang, C.C. On the calculation and correction of equitable threat score for model quantitative precipitation forecasts for small verification areas: The example of Taiwan. Weather Forecast. 2014, 29, 788–798. [Google Scholar] [CrossRef]
- Paulat, M.; Wernli, H.; Hagen, M.; Frei, C. SAL—A Novel Quality Measure for the Verification of Quantitative Precipitation Forecasts. Mon. Weather Rev. 2008, 136, 4470–4487. [Google Scholar]








| Physics | Schemes |
|---|---|
| Microphysics | Ensembles 1-31: Kessler scheme Ensembles 32-62: New Thompson scheme |
| Cumulus parameterization (not used in inner domain) | Ensembles 1-31: Kain–Fritsch scheme Ensembles 32-62: Betts–Miller–Janjic scheme |
| Planetary boundary layer | Yonsei University scheme |
| Surface layer | Revised MM5 Monin–Obukhov scheme |
| Longwave radiation | RRTM scheme |
| Shortwave radiation | Dudhia scheme |
| Pressure (hPa) | 1000 | 950 | 900 | 850 | 800 | 700 | 600 | 500 | 400 | 300 | 200 | 100 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | CRTL | −2.151 | −10.83 | −16.43 | −19.07 | −20.32 | −21.98 | −24.60 | −27.64 | −30.51 | −36.18 | −65.74 | −69.98 |
| HIM8 | −2.198 | −10.87 | −16.26 | −18.57 | −19.48 | −20.41 | −22.23 | −24.21 | −26.24 | −31.96 | −60.59 | −64.28 | |
| Improvement (%) | −2.14 | −0.35 | 1.02 | 2.61 | 4.16 | 7.13 | 9.65 | 12.39 | 14.00 | 11.67 | 7.83 | 8.16 | |
| RMSE | CRTL | 2.864 | 16.32 | 26.34 | 33.16 | 38.48 | 46.91 | 53.43 | 57.86 | 61.76 | 69.36 | 92.69 | 103.8 |
| HIM8 | 2.914 | 16.38 | 26.22 | 32.79 | 37.83 | 45.59 | 51.31 | 54.94 | 58.66 | 66.75 | 88.53 | 97.79 | |
| Improvement (%) | −1.74 | −0.33 | 0.45 | 1.13 | 1.69 | 2.81 | 3.97 | 5.06 | 5.01 | 3.76 | 4.49 | 5.84 |
| Pressure (hPa) | 1000 | 950 | 900 | 850 | 800 | 700 | 600 | 500 | 400 | 300 | 200 | 100 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | CRTL | −2.589 | −1.662 | 2.733 | 6.759 | 6.765 | −7.836 | −14.138 | −16.09 | −11.04 | −6.797 | −19.67 | −36.02 |
| HIM8 | −2.554 | −1.169 | 4.118 | 9.224 | 10.14 | −3.353 | −9.498 | −11.57 | −6.490 | −2.126 | −15.68 | −30.50 | |
| Improvement (%) | 1.36 | 29.65 | −50.64 | −36.45 | −49.93 | 57.20 | 32.82 | 28.07 | 41.26 | 68.71 | 20.29 | 15.34 | |
| RMSE | CRTL | 2.967 | 14.20 | 25.98 | 36.38 | 44.44 | 59.85 | 73.97 | 82.83 | 84.51 | 87.76 | 99.80 | 82.58 |
| HIM8 | 2.913 | 14.06 | 25.82 | 36.06 | 43.68 | 57.18 | 68.93 | 77.27 | 78.57 | 81.87 | 93.81 | 77.09 | |
| Improvement (%) | 1.84 | 0.94 | 0.59 | 0.87 | 1.72 | 4.46 | 6.81 | 6.72 | 7.03 | 6.71 | 6.00 | 6.65 |
| 5 July | 6 July | 18 July | Average | |
|---|---|---|---|---|
| 0.1 mm | 2.09% | 5.40% | 4.20% | 3.90% |
| 5 mm | 3.96% | 9.0% | 7.90% | 6.95% |
| 10 mm | 15.52% | 11.20% | 11.40% | 12.71% |
| Average | 7.19% | 8.53% | 7.83% | 7.85% |
| 0.1 mm | 10 mm | 20 mm | 40 mm | 60 mm | 80 mm | 100 mm | |
|---|---|---|---|---|---|---|---|
| POD-4DEnVar | 0.545 | 0.57 | 0.521 | 0.471 | 0.446 | 0.313 | 0.202 |
| 3DVar | 0.487 | 0.453 | 0.471 | 0.442 | 0.385 | 0.289 | 0.194 |
| 0.1 mm | 5 mm | 10 mm | ||||
|---|---|---|---|---|---|---|
| POD-4DEnVar | 3DVar | POD-4DEnVar | 3DVar | POD-4DEnVar | 3DVar | |
| 01Z | 0.325 | 0.294 | 0.178 | 0.177 | 0.142 | 0.148 |
| 02Z | 0.325 | 0.323 | 0.158 | 0.19 | 0.096 | 0.103 |
| 03Z | 0.315 | 0.334 | 0.142 | 0.18 | 0.07 | 0.103 |
| 04Z | 0.335 | 0.353 | 0.126 | 0.179 | 0.015 | 0.092 |
| 05Z | 0.316 | 0.331 | 0.13 | 0.165 | 0.015 | 0.067 |
| 06Z | 0.293 | 0.286 | 0.109 | 0.136 | 0.023 | 0.052 |
| 07Z | 0.276 | 0.256 | 0.121 | 0.125 | 0.034 | 0.072 |
| 08Z | 0.261 | 0.234 | 0.187 | 0.143 | 0.081 | 0.042 |
| 09Z | 0.266 | 0.213 | 0.182 | 0.161 | 0.071 | 0.064 |
| 10Z | 0.304 | 0.233 | 0.201 | 0.167 | 0.134 | 0.08 |
| 11Z | 0.295 | 0.224 | 0.228 | 0.159 | 0.141 | 0.096 |
| 12Z | 0.252 | 0.202 | 0.184 | 0.117 | 0.125 | 0.072 |
| 13Z | 0.274 | 0.218 | 0.181 | 0.133 | 0.12 | 0.08 |
| 14Z | 0.296 | 0.245 | 0.188 | 0.175 | 0.137 | 0.118 |
| 15Z | 0.308 | 0.277 | 0.225 | 0.224 | 0.172 | 0.123 |
| 16Z | 0.305 | 0.284 | 0.275 | 0.262 | 0.222 | 0.165 |
| 17Z | 0.308 | 0.285 | 0.276 | 0.266 | 0.276 | 0.209 |
| 18Z | 0.318 | 0.277 | 0.277 | 0.258 | 0.301 | 0.216 |
| 19Z | 0.35 | 0.301 | 0.326 | 0.282 | 0.275 | 0.235 |
| 20Z | 0.397 | 0.333 | 0.35 | 0.304 | 0.268 | 0.216 |
| 21Z | 0.414 | 0.345 | 0.407 | 0.319 | 0.248 | 0.205 |
| 22Z | 0.423 | 0.386 | 0.441 | 0.352 | 0.285 | 0.255 |
| 23Z | 0.407 | 0.396 | 0.411 | 0.364 | 0.256 | 0.226 |
| 24Z | 0.422 | 0.409 | 0.412 | 0.41 | 0.217 | 0.188 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, L.; Guan, J.; Wang, X.; Zhang, M.; Wang, Y. Potential Impacts of Assimilating Every-10-Minute Himawari-8 Satellite Radiance with the POD-4DEnVar Method. Remote Sens. 2021, 13, 3765. https://doi.org/10.3390/rs13183765
Wang J, Zhang L, Guan J, Wang X, Zhang M, Wang Y. Potential Impacts of Assimilating Every-10-Minute Himawari-8 Satellite Radiance with the POD-4DEnVar Method. Remote Sensing. 2021; 13(18):3765. https://doi.org/10.3390/rs13183765
Chicago/Turabian StyleWang, Jingnan, Lifeng Zhang, Jiping Guan, Xiaodong Wang, Mingyang Zhang, and Yuan Wang. 2021. "Potential Impacts of Assimilating Every-10-Minute Himawari-8 Satellite Radiance with the POD-4DEnVar Method" Remote Sensing 13, no. 18: 3765. https://doi.org/10.3390/rs13183765
APA StyleWang, J., Zhang, L., Guan, J., Wang, X., Zhang, M., & Wang, Y. (2021). Potential Impacts of Assimilating Every-10-Minute Himawari-8 Satellite Radiance with the POD-4DEnVar Method. Remote Sensing, 13(18), 3765. https://doi.org/10.3390/rs13183765