An Improved Method of Soil Moisture Retrieval Using Multi-Frequency SNR Data
Abstract
:1. Introduction
2. Methods
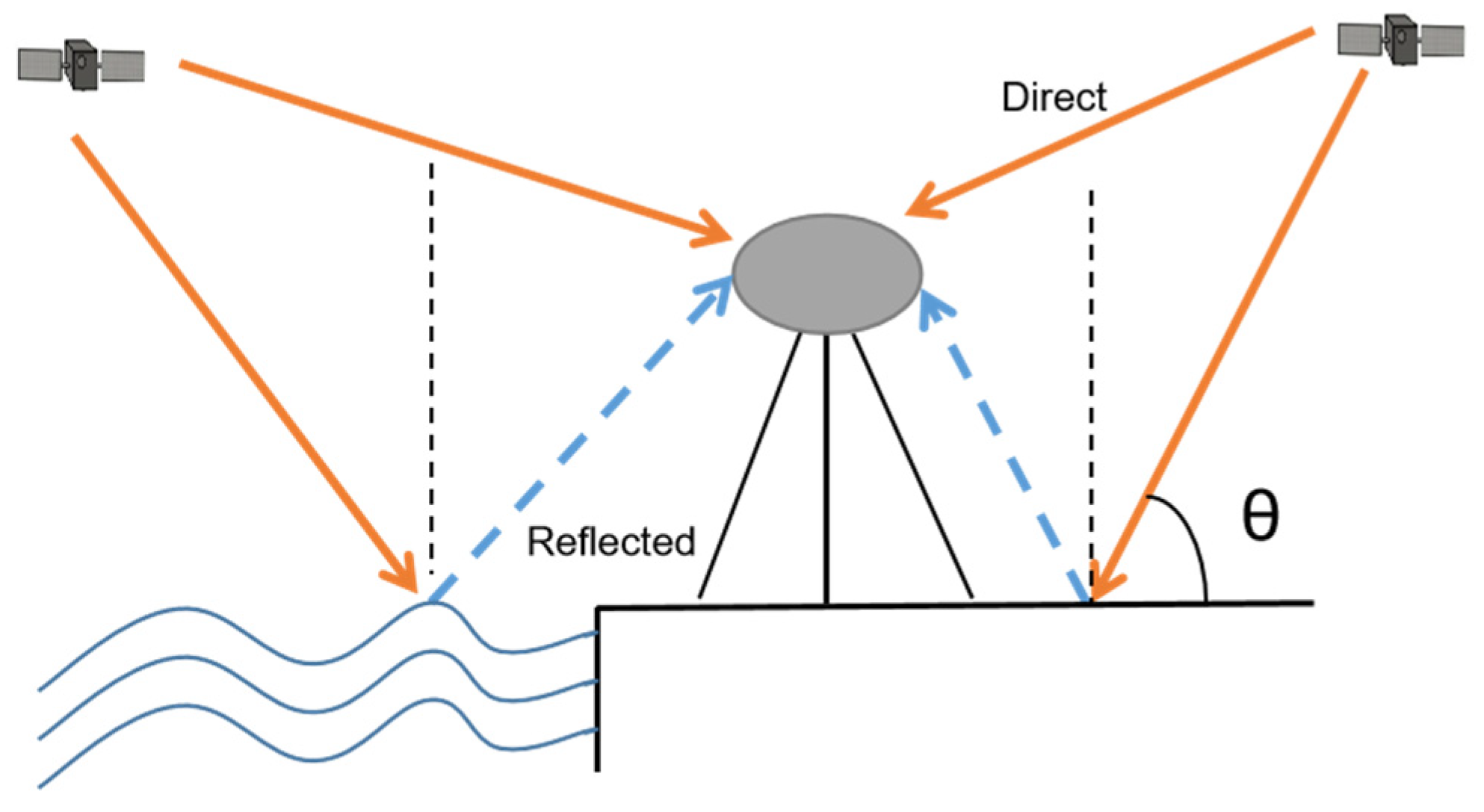
2.1. The Traditional Single-Frequency Retrieval Method of GNSS-IR
2.2. An Improved Method
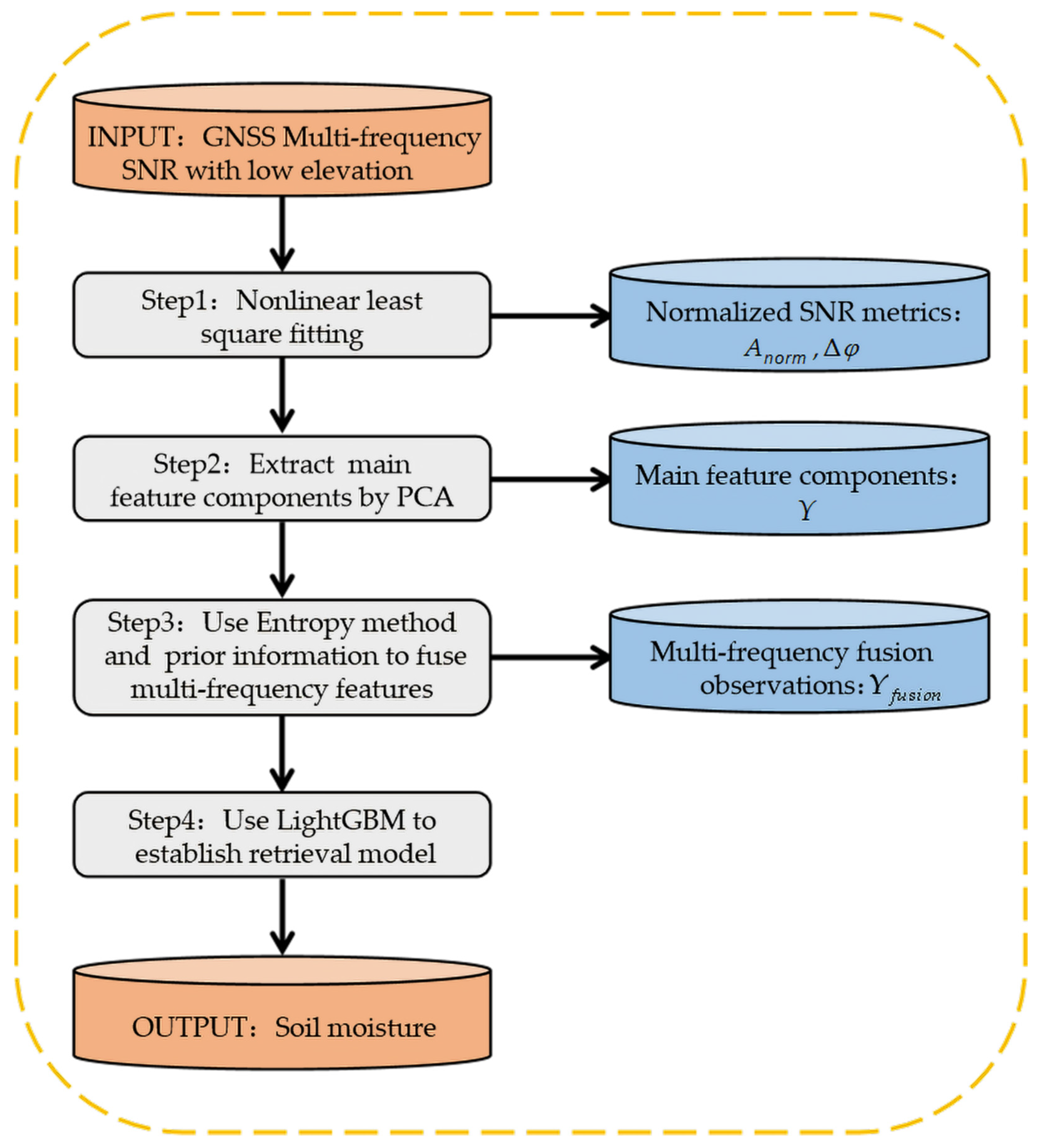
2.2.1. Multi-Frequency Fusion Retrieval Procedure
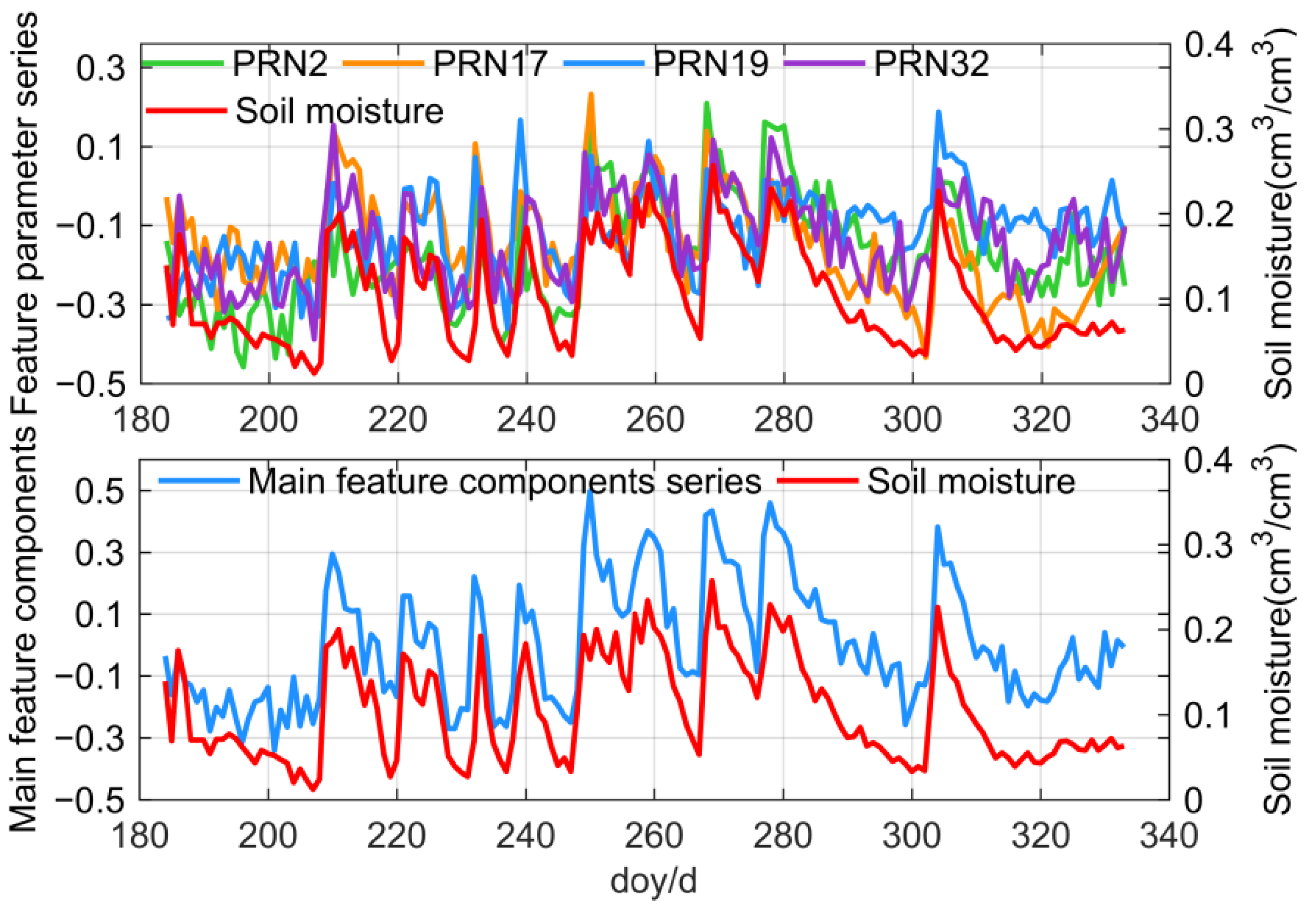
2.2.2. Use PCA to Extract Main Feature Components of Single-Frequency
2.2.3. Use Entropy Method and Priori Information to Fuse Multi-Frequency Features
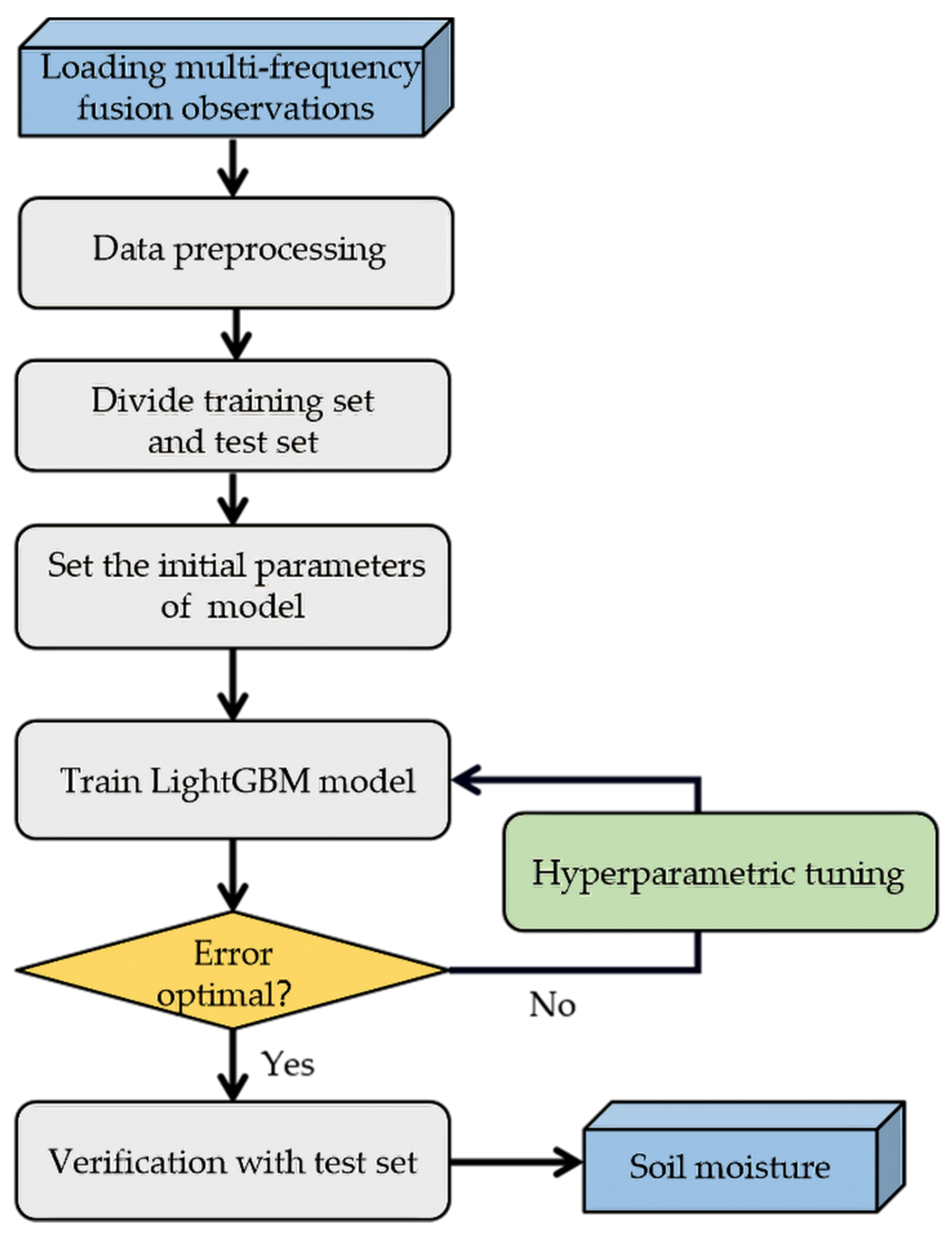
2.2.4. Use LightGBM to Establish a Retrieval Model
3. Experiments
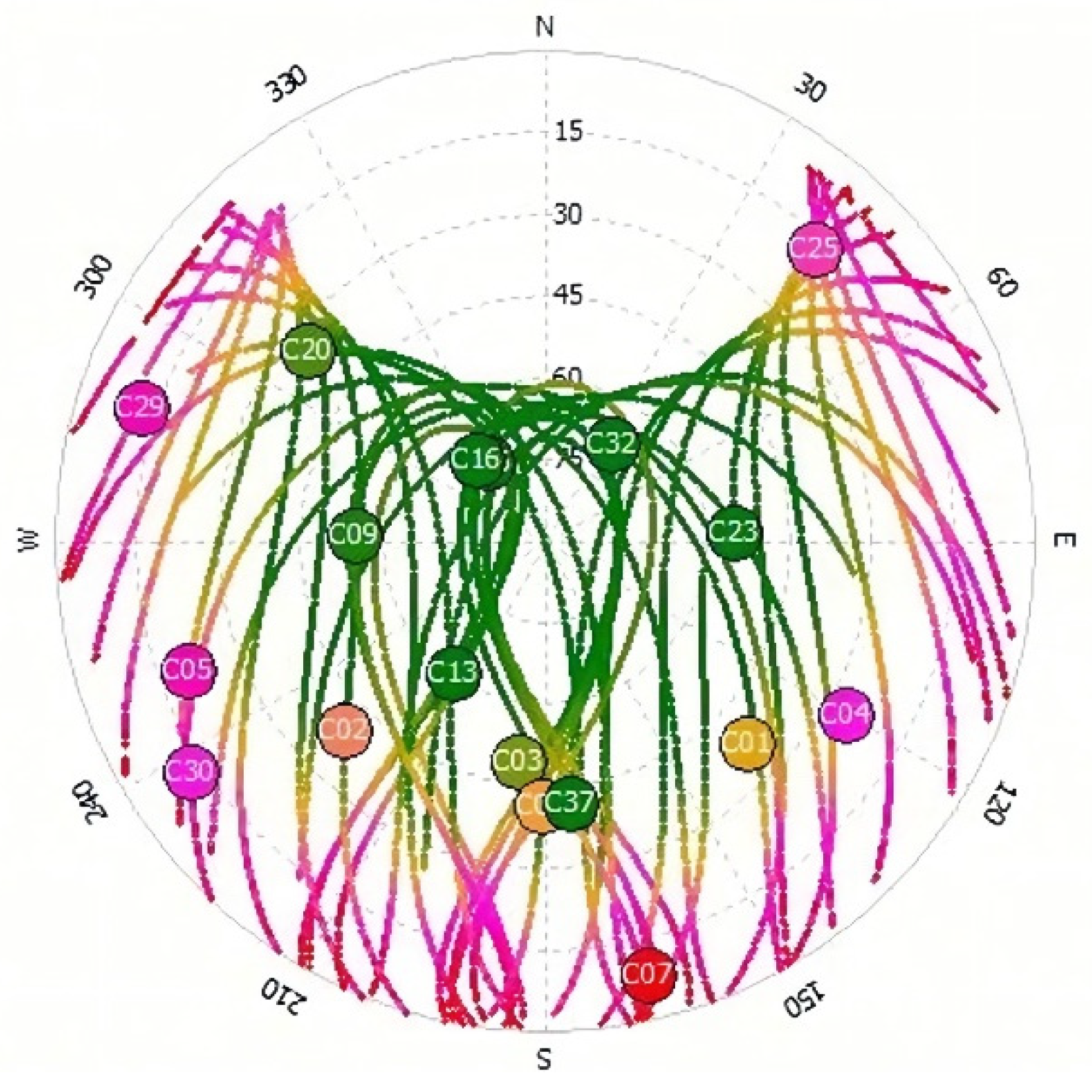
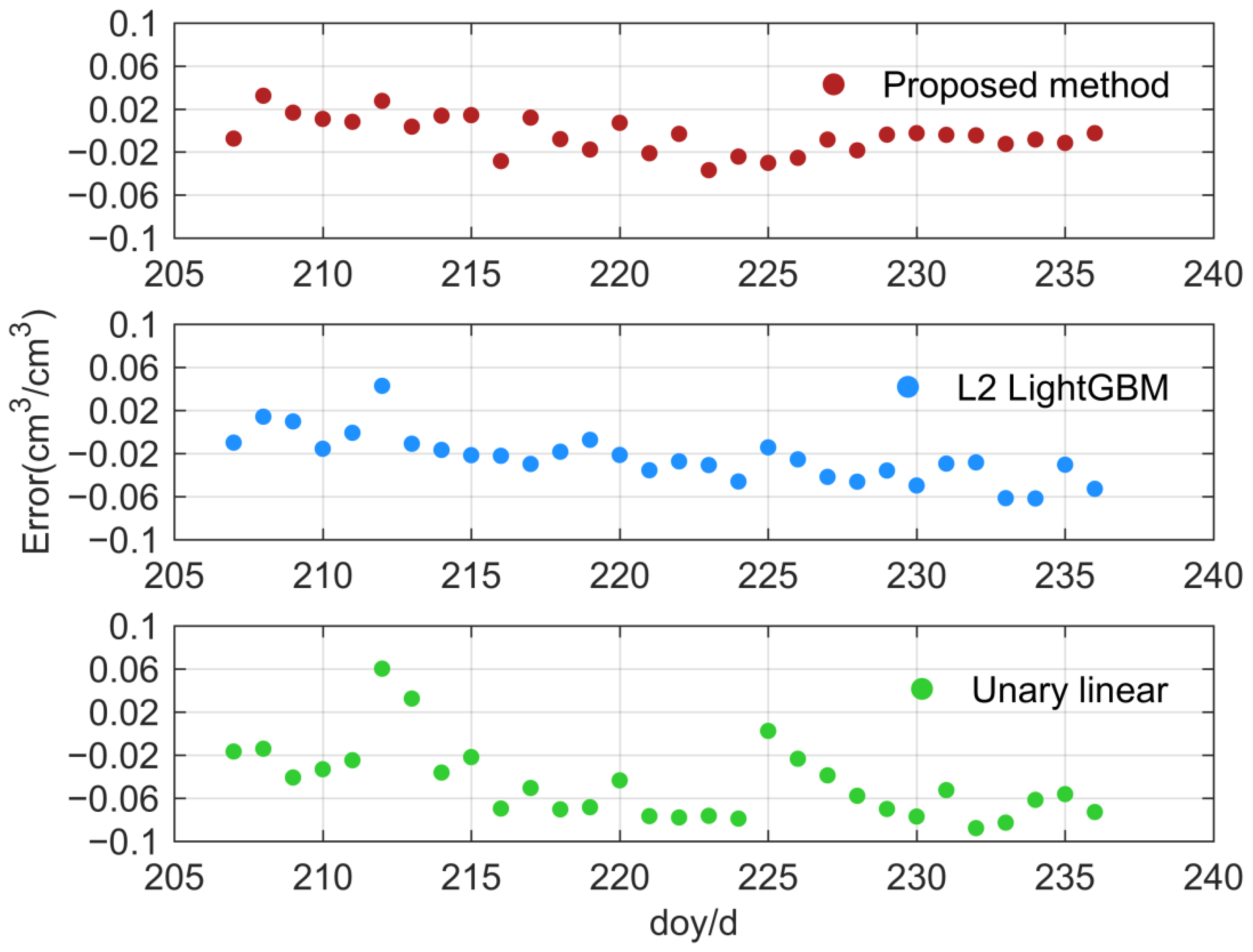
3.1. PBO H2O Network Experiments
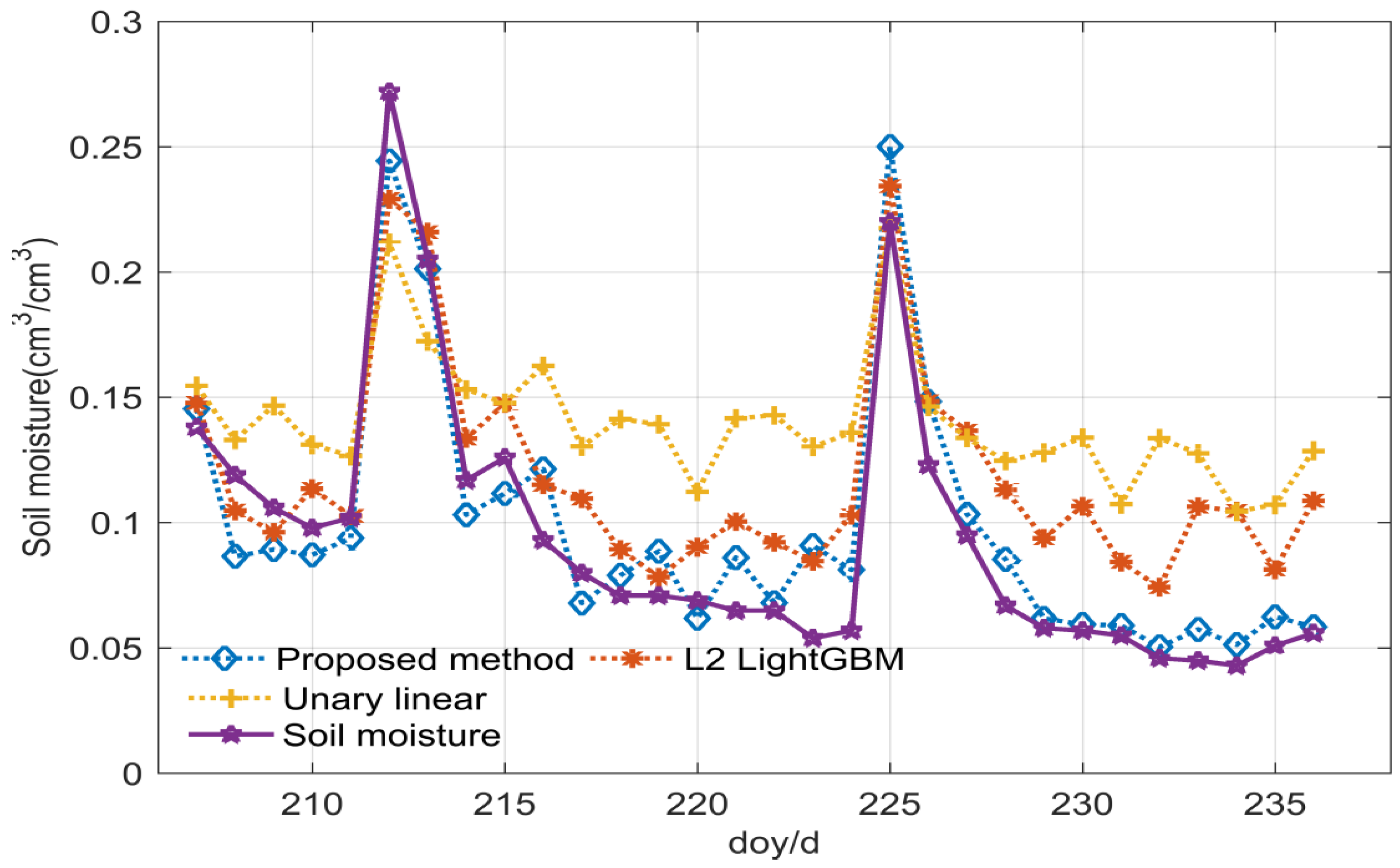
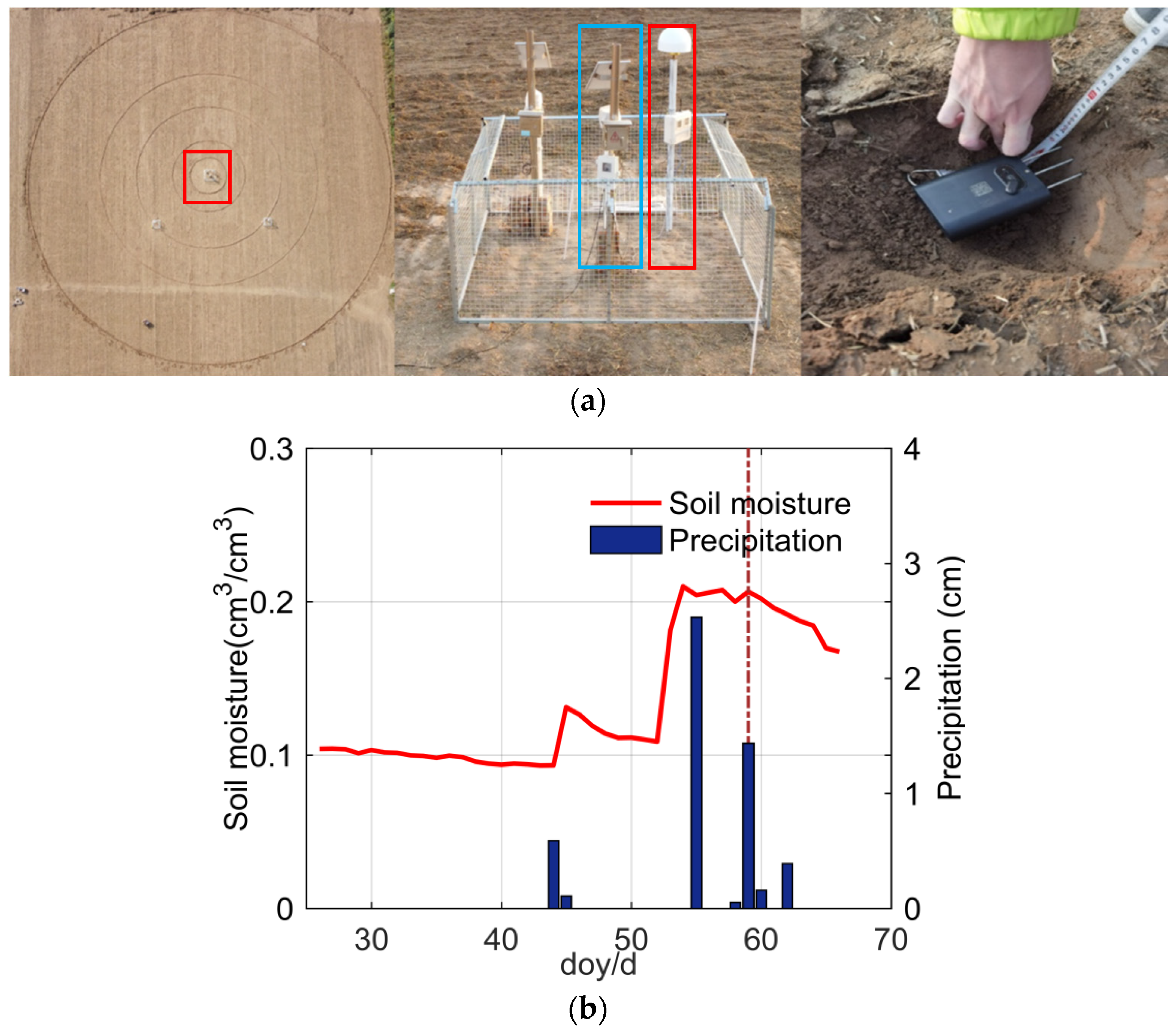
3.2. Henan Experiment
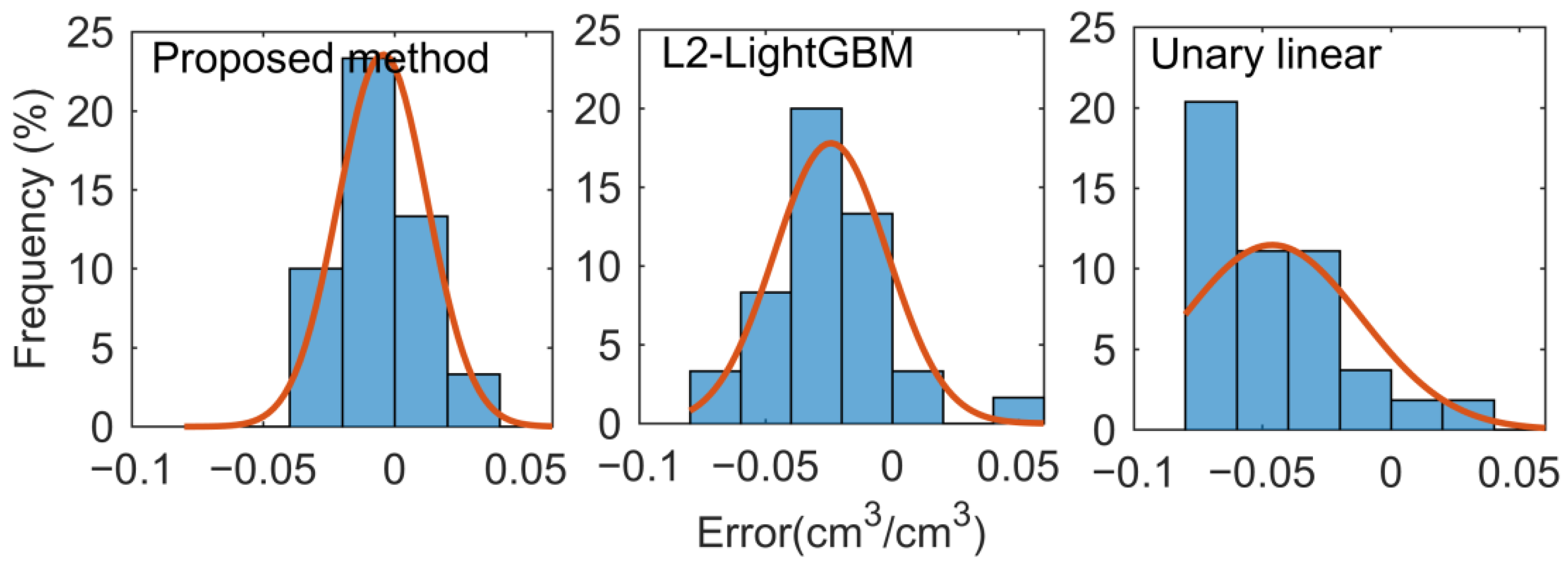
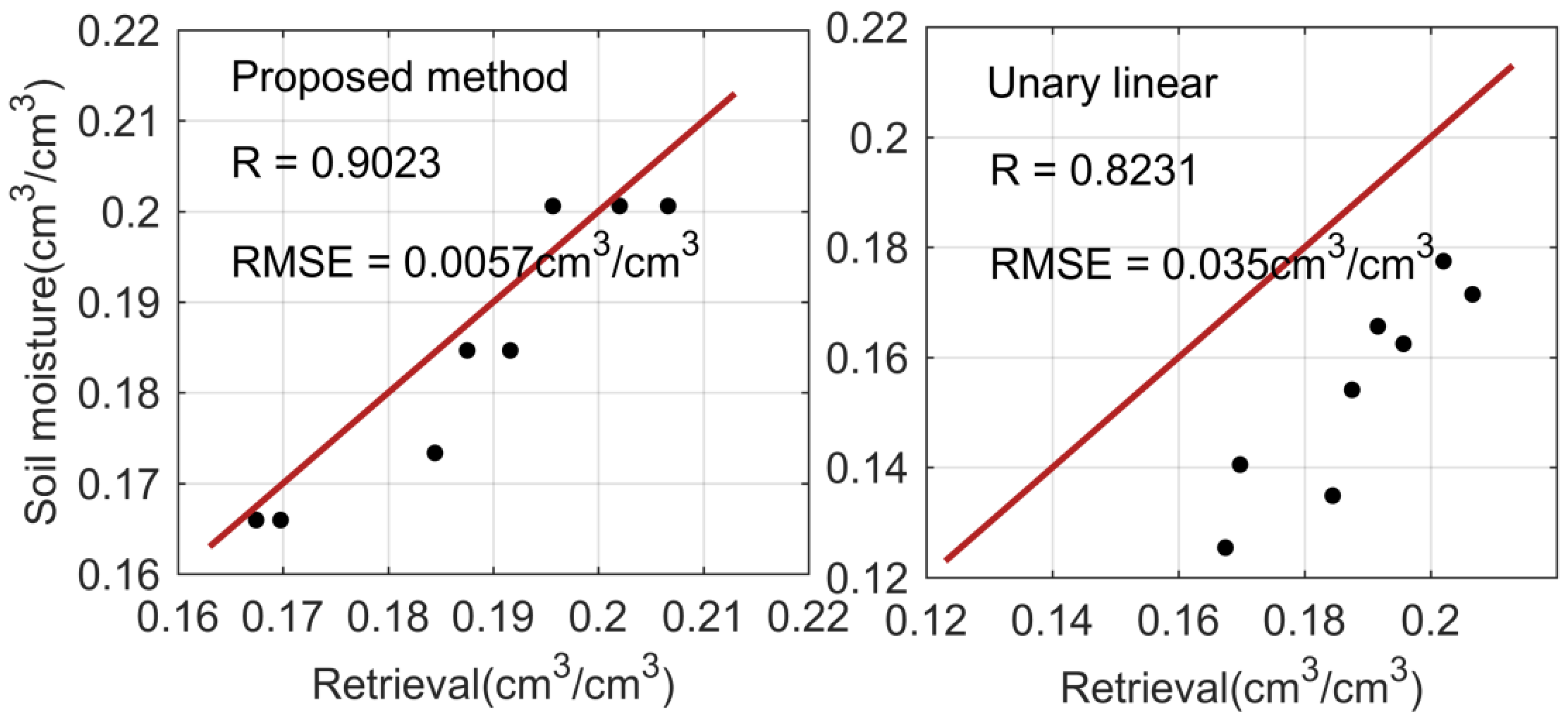
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hall, C.D.; Cordey, R.A. Multistatic Scatterometry. In Proceedings of the International Geoscience & Remote Sensing Symposium, Edinburgh, UK, 12–16 September 1988. [Google Scholar]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Ramos-Perez, I.; Valencia, E.; Park, H.; Vall-Llossera, M. Vegetation Water Content Estimation Using GNSS Measurements. IEEE Geosci. Remote Sens. Lett. 2012, 9, 282–286. [Google Scholar] [CrossRef]
- Jia, Y.; Jin, S.; Savi, P.; Gao, Y.; Tang, J.; Chen, Y.; Li, W. GNSS-R Soil Moisture Retrieval Based on a XGboost Machine Learning Aided Method: Performance and Validation. Remote Sens. 2019, 11, 1655. [Google Scholar] [CrossRef] [Green Version]
- Alonso-Arroyo, A.; Camps, A.; Park, H.; Pascual, D.; Onrubia, R.; Martín, F. Retrieval of Significant Wave Height and Mean Sea Surface Level Using the GNSS-R Interference Pattern Technique: Results From a Three-Month Field Campaign. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3198–3209. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Alvarez, N.; Aguasca, A.; Valencia, E.; Bosch-Lluis, X.; Ramos-Pérez, I.; Park, H.; Vall-Llossera, M. Snow monitoring using GNSS-R techniques. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 4375–4378. [Google Scholar]
- Jin, S.; Najibi, N. Sensing snow height and surface temperature variations in Greenland from GPS reflected signals. Adv. Space Res. 2014, 53, 1623–1633. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G.; Clarizia, M.P.; Comite, D.; Floury, N. Remote Sensing of Forest Biomass Using GNSS Reflectometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2351–2368. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Guerriero, L.; Pierdicca, N.; Rahmoune, R. Forest biomass monitoring with GNSS-R: Theoretical simulations. Adv. Space Res. 2011, 47, 1823–1832. [Google Scholar] [CrossRef]
- Gao, H.; Yang, D.; Zhang, B.; Wang, Q.; Wang, F. Remote Sensing of Sea Ice Thickness with GNSS Reflected Signal. J. Electron. Inf. Technol. 2017, 39, 1096–1100. [Google Scholar]
- Strandberg, J.; Hobiger, T.; Haas, R. Coastal Sea Ice Detection Using Ground-Based GNSS-R. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1552–1556. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A.; Axelrad, P.; Braun, J. Using GPS Multipath to Measure Soil Moisture Fluctuations: Initial Results. GPS Solut. 2008, 12, 173–177. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.D.; Bilich, A.L. Use of gps receivers as a soil moisture network for water cycle studies. Geophys. Res. Lett. 2008, 35, 851–854. [Google Scholar] [CrossRef] [Green Version]
- Ban, W.; Yu, K.; Zhang, X. GEO-Satellite-Based Reflectometry for Soil Moisture Estimation: Signal Modeling and Algorithm Development. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1829–1838. [Google Scholar] [CrossRef]
- Yan, S.; Li, Z.; Yu, K.; Zhang, K. GPS-R L1 interference signal processing for soil moisture estimation: An experimental study. Eurasip J. Adv. Signal Process. 2014, 2014, 107. [Google Scholar] [CrossRef] [Green Version]
- Wan, W.; Larson, K.M.; Small, E.E.; Chew, C.C.; Braun, J.J. Using geodetic GPS receivers to measure vegetation water content. GPS Solut. 2015, 19, 237–248. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E. Normalized Microwave Reflection Index: A Vegetation Measurement Derived From GPS Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1501–1511. [Google Scholar] [CrossRef]
- Yuan, Q.; Li, S.; Yue, L.; Li, T.; Shen, H.; Zhang, L. Monitoring the Variation of Vegetation Water Content with Machine Learning Methods: Point–Surface Fusion of MODIS Products and GNSS-IR Observations. Remote Sens. 2019, 11, 1440. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Gutmann, E.D.; Zavorotny, V.U.; Braun, J.J.; Williams, M.W.; Nievinski, F.G. Can we measure snow depth with GPS receivers? Geophys. Res. Lett. 2009, 36, L17502. [Google Scholar] [CrossRef] [Green Version]
- Gutmann, E.D.; Larson, K.M.; Williams, M.W.; Nievinski, F.G.; Zavorotny, V.U. Snow measurement by GPS interferometric reflectometry: An evaluation at Niwot Ridge, Colorado. Hydrol. Process. 2012, 26, 2951–2961. [Google Scholar] [CrossRef]
- Tabibi, S.; Geremia-Nievinski, F.; Dam, T.V. Statistical Comparison and Combination of GPS, GLONASS, and Multi-GNSS Multipath Reflectometry Applied to Snow Depth Retrieval. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3773–3785. [Google Scholar] [CrossRef]
- Larson, K.M.; Braun, J.J.; Small, E.E.; Zavorotny, V.U.; Gutmann, E.D.; Bilich, A.L. GPS Multipath and Its Relation to Near-Surface Soil Moisture Content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 91–99. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E.; Larson, K.M. Effects of Near-Surface Soil Moisture on GPS SNR Data: Development of a Retrieval Algorithm for Soil Moisture. IEEE Trans. Geosci. Remote Sens. 2013, 52, 537–543. [Google Scholar] [CrossRef]
- Vey, S.; Güntner, A.; Wickert, J.; Blume, T.; Ramatschi, M. Long-term soil moisture dynamics derived from GNSS interferometric reflectometry: A case study for Sutherland, South Africa. GPS Solut. 2016, 20, 641–654. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Larson, K.M.; Braun, J.J.; Small, E.E.; Gutmann, E.D.; Bilich, A.L. A Physical Model for GPS Multipath Caused by Land Reflections: Toward Bare Soil MoistureRetrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 100–110. [Google Scholar] [CrossRef]
- Yang, T.; Wan, W.; Chen, X.; Chu, T.; Hong, Y. Using BDS SNR Observations to Measure Near-Surface Soil Moisture Fluctuations: Results From Low Vegetated Surface. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1308–1312. [Google Scholar] [CrossRef]
- Feng, Q.; Zheng, N. Retrieving Soil Moisture Using Signal-to-noise Ratio of GPS Signal by Assisted Machine Learning Algorithm. Bull. Surv. Mapp. 2018, 7, 106–111. [Google Scholar]
- Jin, L.; Yang, L.; Han, M.; Hong, X.; Sun, B.; Liang, Y. Soil moisture inversion method based on GNSS-IR dual frequency data fusion. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 1248. [Google Scholar]
- Sun, B.; Liang, Y.; Han, M.; Yang, L.; Jin, L.; Hong, X. A method for GNSS-IR soil moisture inversion based on GPS multi-satellite and triple-frequency data fusion. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1089–1096. [Google Scholar]
- Chew, C.C. Soil Moisture Remote Sensing using GPS-Interferometric Reflectometry. Dissertations & Theses—Gradworks. In 2017 Forum on Cooperative Positioning and Service (CPGPS); IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Small, E.E.; Larson, K.M.; Chew, C.C.; Dong, J.; Ochsner, T.E. Validation of GPS-IR Soil Moisture Retrievals: Comparison of Different Algorithms to Remove Vegetation Effects. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4759–4770. [Google Scholar] [CrossRef]
- Zribi, M.; Gorrab, A.; Baghdadi, N.; Lili-Chabaane, Z.; Mougenot, B. Influence of Radar Frequency on the Relationship Between Bare Surface Soil Moisture Vertical Profile and Radar Backscatter. IEEE Geosci. Remote Sens. Lett. 2013, 11, 848–852. [Google Scholar] [CrossRef] [Green Version]
- Qi, X. Technology Research of Face Recognition Based on PCA; Wuhan University of Technology: Wuhan, China, 2007. [Google Scholar]
- Asante-Okyere, S.; Shen, C.; Ziggah, Y.Y.; Rulegeya, M.M.; Zhu, X. Principal Component Analysis (PCA) Based Hybrid Models for the Accurate Estimation of Reservoir Water Saturation. Comput. Geosci. 2020, 145, 104555. [Google Scholar] [CrossRef]
- Qiao, J. Application of Improved Entropy Method in Henan Sustainable Development Evaluation. Resour. Sci. 2004, 26, 113–119. [Google Scholar]
- Wang, F.; Mao, A.; Li, H.; Jia, M. Quality Measurement and Regional Difference of Urbanization in Shandong Province Based on the Entropy Method. Sci. Geogr. Sin. 2013, 33, 1323–1329. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 3147–3155. [Google Scholar]
- Zhang, Y.; Zhu, C.; Wang, Q. LightGBM-based model for metro passenger volume forecasting. IET Intelligent Transport Systems 2020, 14, 1815–1823. [Google Scholar] [CrossRef]
- Wang, F.; Cheng, H.; Dai, H.; Han, H. Freeway Short-Term Travel Time Prediction Based on LightGBM Algorithm. In IOP Conference Series: Earth Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 638, pp. 12–29. [Google Scholar]
- Gurtner, W.; Estey, L. Rinex: The Receiver Independent Exchange Format Version 3.04; Astronomical Institute, University of Bern and UNAVCO: Bolulder, CO, USA, 2007. [Google Scholar]




| Station | Latitude and Longitude | Location | Year | Time Span/Days of Year |
|---|---|---|---|---|
| P037 | 38.42°N,105.10°W | Canon, Colorado | 2014 | 145–294 |
| P041 | 39.95°N,105.19°W | Boulder, Colorado | 2012 | 87–236 |
| P043 | 43.88°N,104.49°W | Newcastle, Wyoming | 2016 | 184–333 |
| Item | Revisit Period (Days) |
|---|---|
| GPS | 1 |
| BDS(GEO and IGSO satellites) | 1 |
| BDS(MEO satellites) | 7 |
| Station | Method | Correlation Coefficient | Root-Mean-Square-Error (cm3/cm3) | Mean-Absolute-Error (cm3/cm3) |
|---|---|---|---|---|
| P037 | Proposed | 0.9007 | 0.0217 | 0.0190 |
| L2-LightGBM | 0.8493 | 0.0270 | 0.0237 | |
| Linear | 0.7403 | 0.0364 | 0.0319 | |
| P041 | Proposed | 0.9045 | 0.0172 | 0.0142 |
| L2-LightGBM | 0.8596 | 0.0327 | 0.0286 | |
| Linear | 0.7677 | 0.0568 | 0.0525 | |
| P043 | Proposed | 0.9524 | 0.0120 | 0.0100 |
| L2-LightGBM | 0.8896 | 0.0149 | 0.0116 | |
| Linear | 0.8033 | 0.0209 | 0.0168 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Cao, X.; Shen, F.; Ge, Y. An Improved Method of Soil Moisture Retrieval Using Multi-Frequency SNR Data. Remote Sens. 2021, 13, 3725. https://doi.org/10.3390/rs13183725
Chen K, Cao X, Shen F, Ge Y. An Improved Method of Soil Moisture Retrieval Using Multi-Frequency SNR Data. Remote Sensing. 2021; 13(18):3725. https://doi.org/10.3390/rs13183725
Chicago/Turabian StyleChen, Kun, Xinyun Cao, Fei Shen, and Yulong Ge. 2021. "An Improved Method of Soil Moisture Retrieval Using Multi-Frequency SNR Data" Remote Sensing 13, no. 18: 3725. https://doi.org/10.3390/rs13183725
APA StyleChen, K., Cao, X., Shen, F., & Ge, Y. (2021). An Improved Method of Soil Moisture Retrieval Using Multi-Frequency SNR Data. Remote Sensing, 13(18), 3725. https://doi.org/10.3390/rs13183725






