Retrieval of Daily Mean Top-of-Atmosphere Reflected Solar Flux Using the Advanced Very High Resolution Radiometer (AVHRR) Instruments
Abstract
:1. Introduction
2. Input Data
2.1. External Input Data
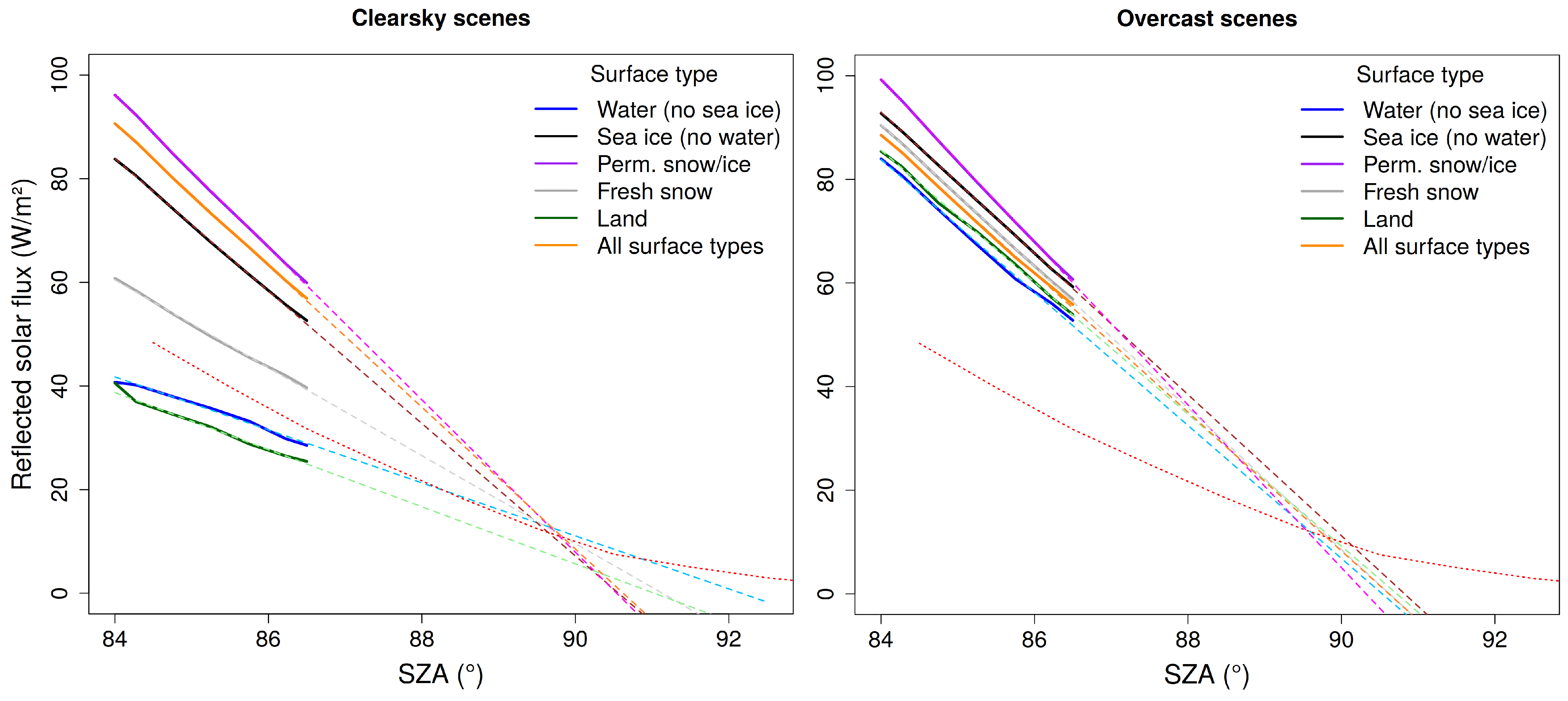
2.2. Twilight Model and Coefficients
2.3. Narrowband-to-Broadband Coefficients
3. Method
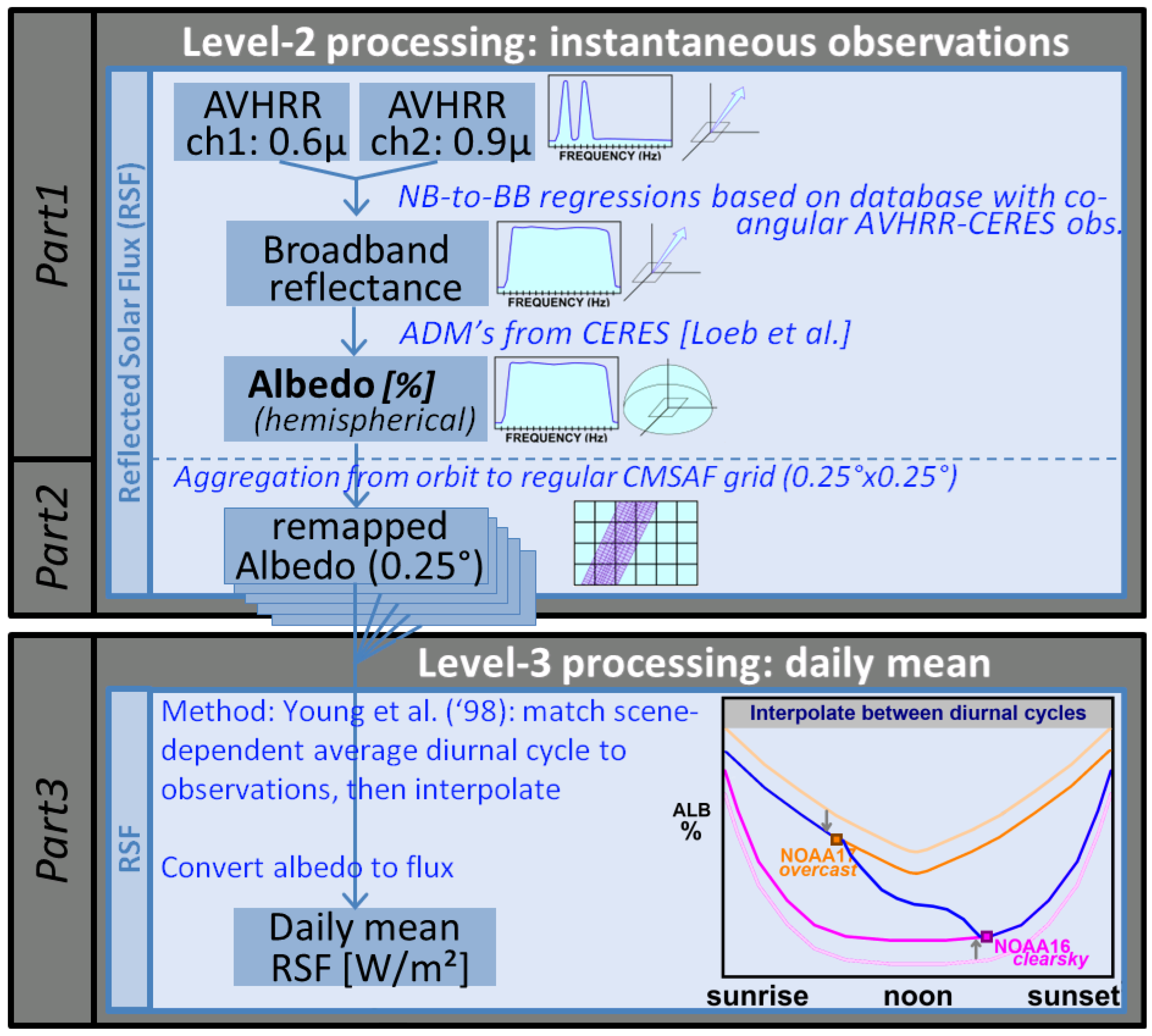
3.1. Part 1: Retrieval Algorithm for Instantaneous TOA Albedo (Level-2)
3.1.1. Data Pre-Processing
3.1.2. Sunglint Treatment
3.1.3. Narrowband-to-Broadband (NTB) Conversion
3.1.4. Angular Distribution Modeling
3.2. Part 2: Spatial Aggregation from GAC Orbit Grid to Regular CM SAF Grid (Level-2b)
3.3. Part 3: Processing of Instantaneous Albedo to Daily Mean RSF (Level-3)
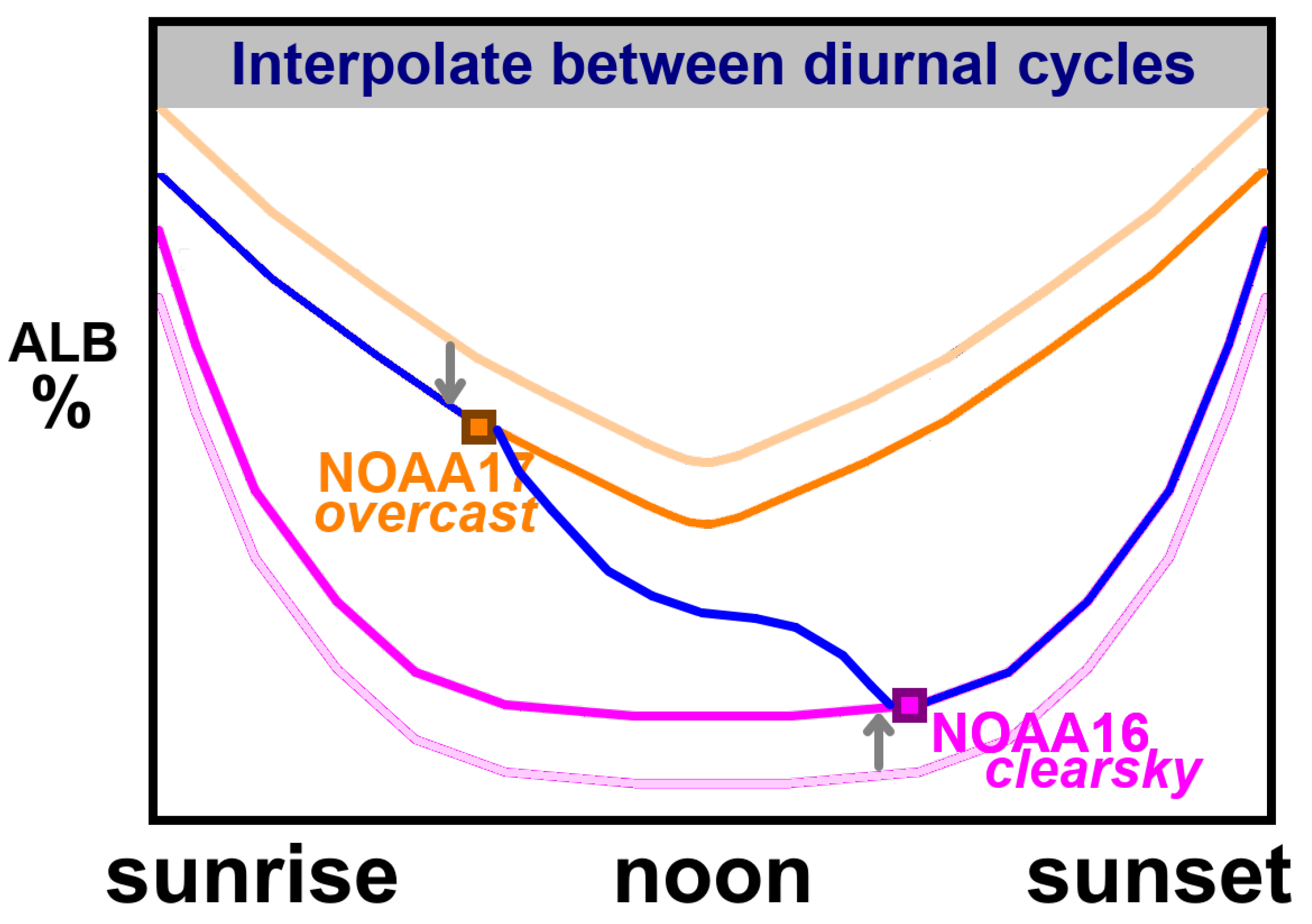
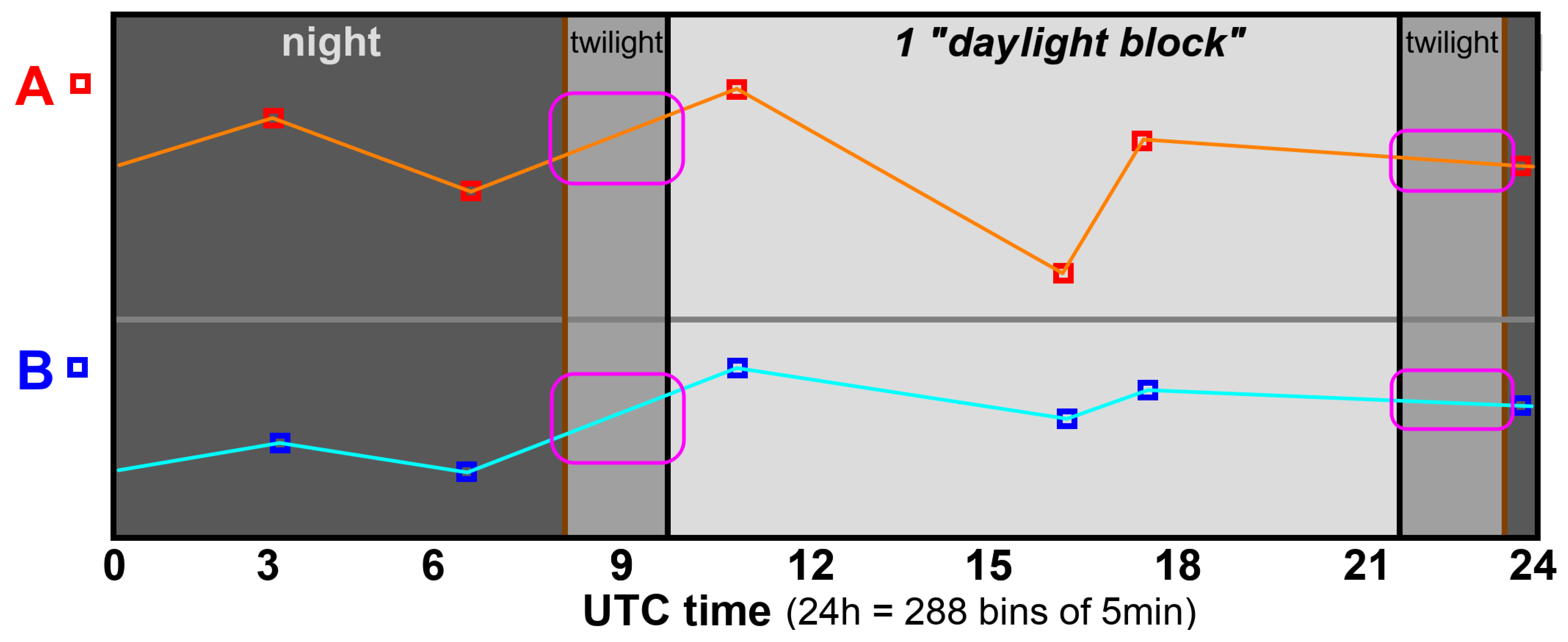
3.3.1. Daylight Conditions (): Modeling Albedo Diurnal Cycle
3.3.2. Twilight Conditions ()
3.3.3. Nighttime Conditions ()
3.3.4. Daily Integral
4. Results and Validation
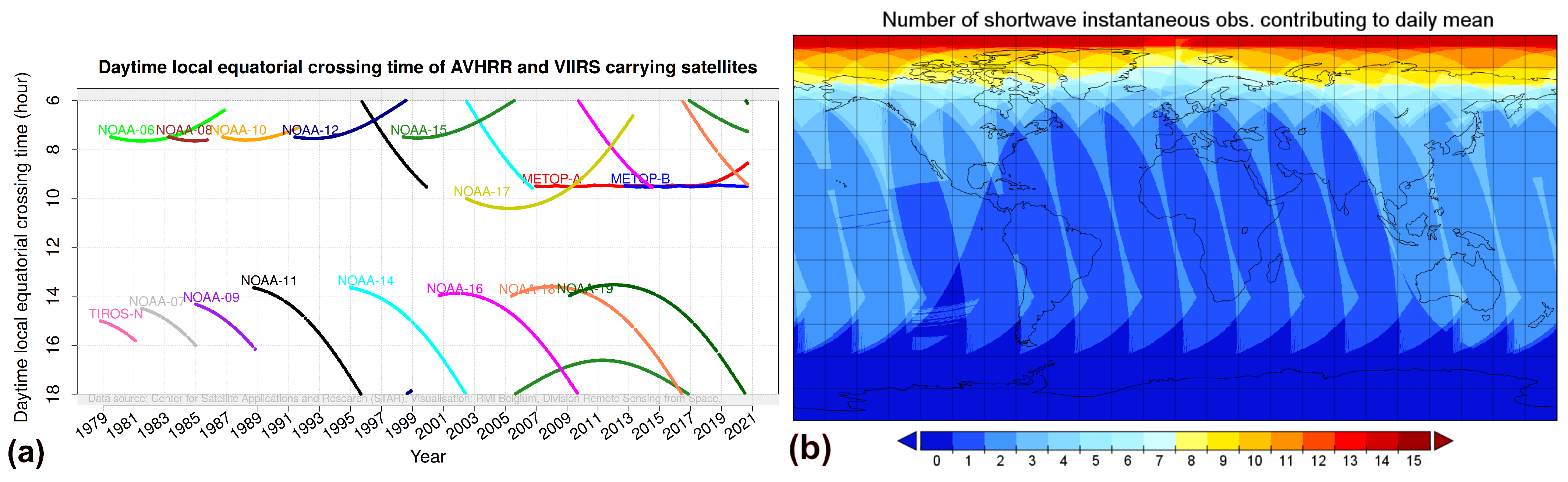
4.1. Orbital Configurations
4.2. Validation Approach and Performance Indicators
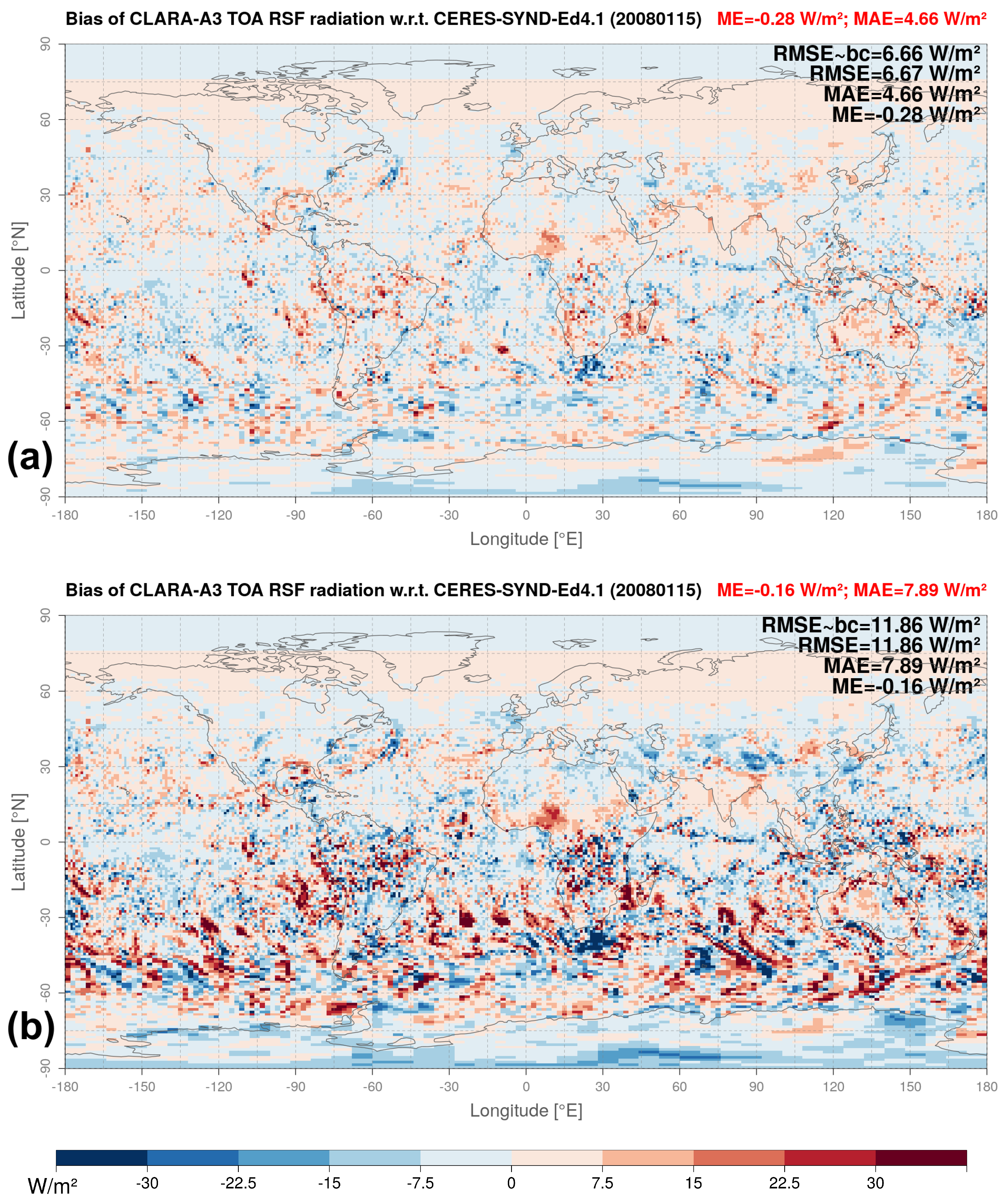
4.3. Validation on Daily Time Scale
| Orbital Configurations | Annual Average of Daily Statistics (Wm) | |||||||
|---|---|---|---|---|---|---|---|---|
| Early/Late | Midmorning | Aftern. | ||||||
| N15 | N16 | Met | N17 | N18 | *** | *** | Daily ** | Hourly ** |
| x | x | x | x | x | −0.27 | 6.93 | 4.83 | 9.47 |
| x | x | x | −0.14 | 7.20 | 4.91 | 9.24 | ||
| x | x | x | x | −0.15 | 7.59 | 5.24 | 9.97 | |
| x | x | x | x | −0.31 | 7.18 | 5.01 | 9.76 | |
| x | x | x | x | −0.31 | 11.92 | 8.05 | 12.56 | |
| x | x | x | −0.76 | 14.63 | 9.62 | 14.42 | ||
| x | −0.33 | 15.56 | 10.01 | 14.40 | ||||
| x | 0.28 | 17.32 | 11.14 | 15.41 | ||||
| x | 0.65 | 18.50 | 11.87 | 16.11 | ||||
| x * | −2.45 | 28.86 | 19.28 | 24.13 | ||||
| x * | 0.39 | 30.40 | 20.02 | 25.07 | ||||
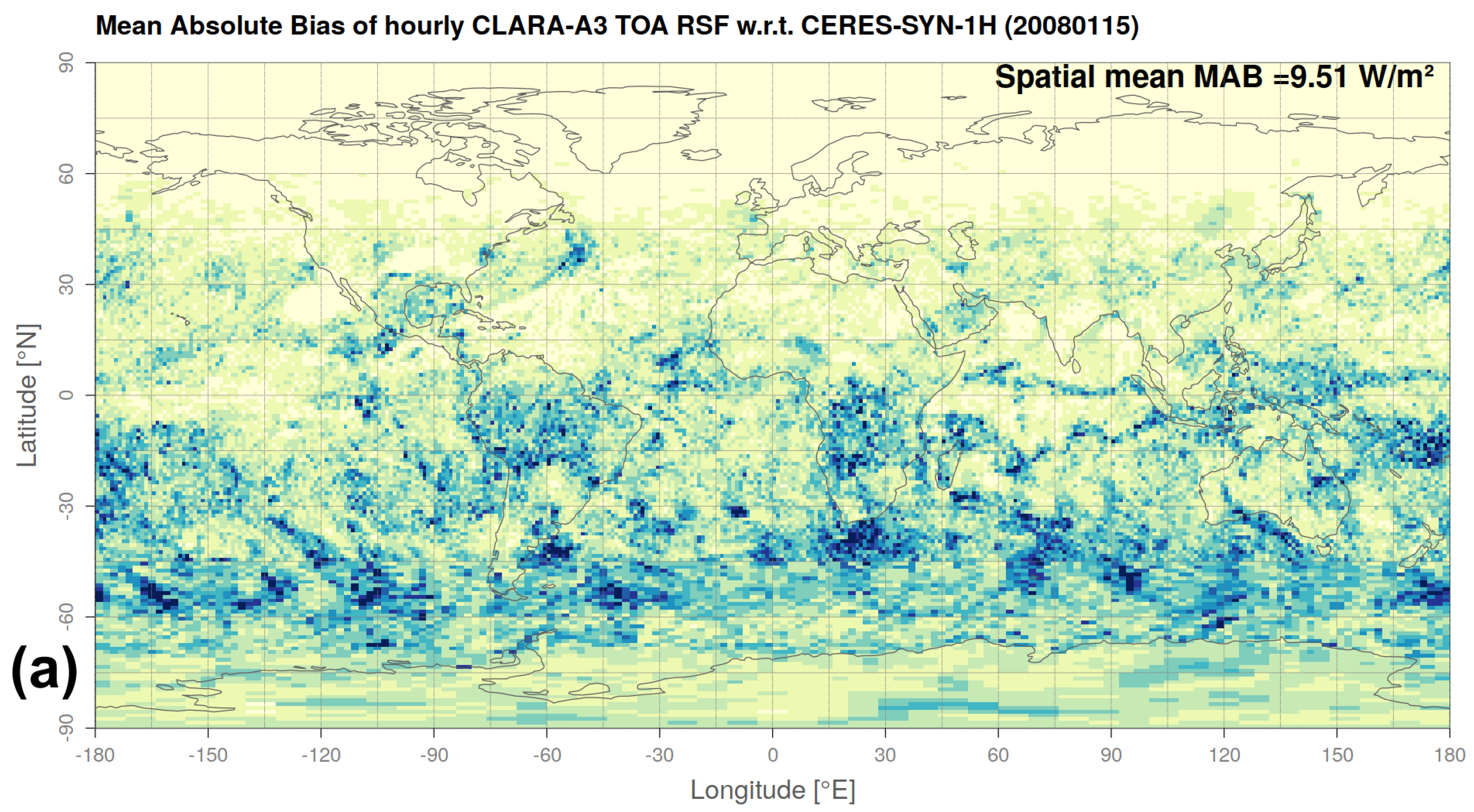
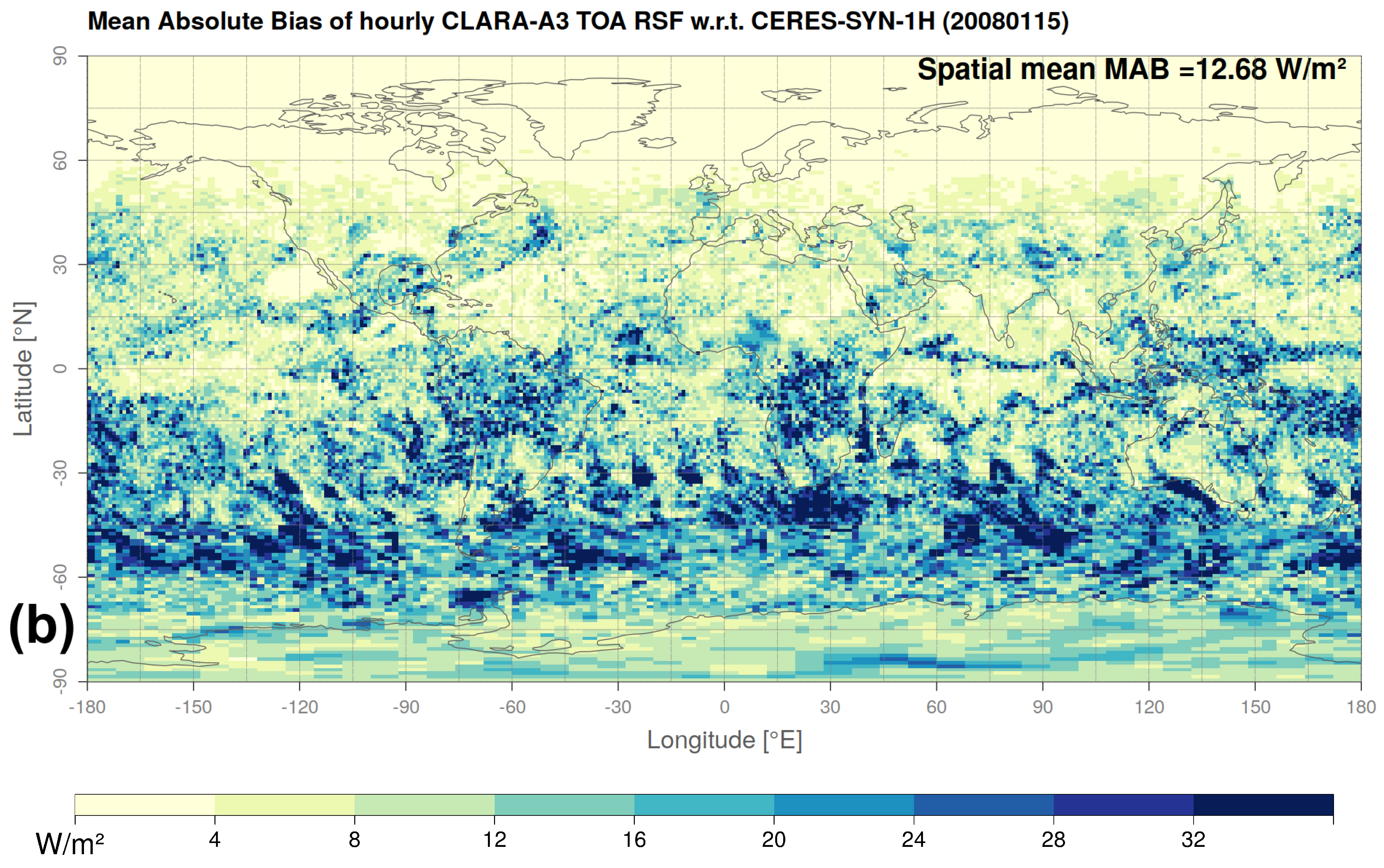
4.4. Validation on Hourly Time Scale
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADM | Angular Distribution Model |
| AVHRR | Advanced Very High Resolution Radiometer |
| CPP | Cloud Physical Properties |
| Ch1, Ch2 | Channel 1, Channel 2 |
| CDR | Climate Data Record |
| CDS | Climate Data Store, from the Copernicus Climate Change Service (C3S) |
| CERES | Clouds and the Earth’s Radiant Energy System (instrument and mission) |
| CM SAF | Climate Monitoring Satellite Application Facility |
| CLARA-A3 | CM SAF Cloud, Albedo And Surface Radiation dataset from AVHRR data, 3rd edition |
| Cloud_cci | Cloud component in the ESA’s Climate Change Initiative (CCI) programme |
| COT | Cloud Optical Thickness |
| CPP | Cloud Physical Properties |
| DLB | Daylight block |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ERA5 | ECMWF Reanalysis 5th Generation |
| ERB | Earth Radiation Budget |
| EUMETSAT | European Organisation for the Exploitation of Meteorological Satellites |
| CDR | Climate Data Record |
| FDR | Fundamental Data Record |
| FOV | Field of View |
| GAC | Global Area Coverage |
| GERB | Geostationary Earth Radiation Budget |
| GCOS | Global Observing System for Climate |
| GLCC | Global Land Cover Characterization |
| IGBP | International Geosphere-Biosphere Programme |
| ISCCP | International Satellite Cloud Climatology Project |
| LECT | Local Equator Crossing Time |
| MAB | (Global) Mean absolute bias calculated from daily RSF |
| MABH | (Global) Mean absolute bias calculated from hourly RSF |
| MB | (Global) Mean bias |
| MetOp-A | Meteorological Operational satellite, Satellite A (ESA) |
| Met | MetOp-A |
| NOAA-X | National Oceanic and Atmospheric Administration, Satellite X |
| N15, N16, ⋯ | NOAA-15, NOAA-16, ⋯ |
| NTB | Narrowband-to-Broadband |
| NWC SAF | Nowcasting Satellite Application Facility |
| OSI SAF | Ocean and Sea Ice Satellite Application Facility |
| PPS | Polar Platform System |
| RAA () | Relative Azimuth Angle |
| RMSB | Root Mean Square of Bias |
| RSF | Reflected Solar Flux |
| SR | Scaled Radiance (spectral) |
| SYN1deg | Synoptic gridded 1 product (from CERES) |
| SZA () | Solar zenith angle |
| TOA | Top of Atmosphere |
| TSI | Total Solar Irradiance |
| TWL | Twilight |
| VZA () | Viewing zenith angle |
References
- GCOS. Systematic Observation Requirements for Satellite-Based Products for Climate (2011 Update): Supplemental Details to the Satellite-Based Component of the “Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC”. Reference Document GCOS-154. WMO. 2011. Available online: www.wmo.int (accessed on 1 August 2021).
- Dewitte, S.; Clerbaux, N. Measurement of the earth radiation budget at the top of the atmosphere—A review. Remote Sens. 2017, 9, 1143. [Google Scholar] [CrossRef] [Green Version]
- Barkstrom, B.R. The earth radiation budget experiment (ERBE). Bull. Am. Meteorol. Soc. 1984, 65, 1170–1185. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B., III; Smith, G.L.; Cooper, J.E. Clouds and the Earth’s Radiant Energy System (CERES): An earth observing system experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef] [Green Version]
- Harries, J.E.; Russell, J.; Hanafin, J.; Brindley, H.; Futyan, J.; Rufus, J.; Kellock, S.; Matthews, G.; Wrigley, R.; Last, A.; et al. The geostationary earth radiation budget project. Bull. Am. Meteorol. Soc. 2005, 86, 945–960. [Google Scholar] [CrossRef] [Green Version]
- Kandel, R.; Viollier, M.; Raberanto, P.; Duvel, J.P.; Pakhomov, L.; Golovko, V.; Trishchenko, A.; Mueller, J.; Raschke, E.; Stuhlmann, R.; et al. The ScaRaB earth radiation budget dataset. Bull. Am. Meteorol. Soc. 1998, 79, 765–784. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hogan, R.J.; Bozzo, A. A flexible and efficient radiation scheme for the ECMWF model. J. Adv. Model. Earth Syst. 2018, 10, 1990–2008. [Google Scholar] [CrossRef] [Green Version]
- Young, A.H.; Knapp, K.R.; Inamdar, A.; Hankins, W.; Rossow, W.B. The international satellite cloud climatology project H-Series climate data record product. Earth Syst. Sci. Data 2018, 10, 583–593. [Google Scholar] [CrossRef] [Green Version]
- Stengel, M.; Stapelberg, S.; Sus, O.; Finkensieper, S.; Würzler, B.; Philipp, D.; Hollmann, R.; Poulsen, C.; Christensen, M.; McGarragh, G. Cloud_cci Advanced Very High Resolution Radiometer post meridiem (AVHRR-PM) dataset version 3: 35-year climatology of global cloud and radiation properties. Earth Syst. Sci. Data 2020, 12, 41–60. [Google Scholar] [CrossRef] [Green Version]
- Poulsen, C.A.; McGarragh, G.R.; Thomas, G.E.; Stengel, M.; Christensen, M.W.; Povey, A.C.; Proud, S.R.; Carboni, E.; Hollmann, R.; Grainger, R.G. Cloud_cci ATSR-2 and AATSR data set version 3: A 17-year climatology of global cloud and radiation properties. Earth Syst. Sci. Data 2020, 12, 2121–2135. [Google Scholar] [CrossRef]
- Lee, H.T.; Gruber, A.; Ellingson, R.G.; Laszlo, I. Development of the HIRS outgoing longwave radiation climate dataset. J. Atmos. Ocean. Technol. 2007, 24, 2029–2047. [Google Scholar] [CrossRef] [Green Version]
- Urbain, M.; Clerbaux, N.; Ipe, A.; Tornow, F.; Hollmann, R.; Baudrez, E.; Velazquez Blazquez, A.; Moreels, J. The CM SAF TOA radiation data record using MVIRI and SEVIRI. Remote Sens. 2017, 9, 466. [Google Scholar] [CrossRef] [Green Version]
- Heidinger, A.K.; Straka III, W.C.; Molling, C.C.; Sullivan, J.T.; Wu, X. Deriving an inter-sensor consistent calibration for the AVHRR solar reflectance data record. Int. J. Remote Sens. 2010, 31, 6493–6517. [Google Scholar] [CrossRef]
- Hollman, R.; Schlundt, C.; Finkensieper, S.; Raspaud, M.; Karlsson, K.G.; Stengel, M. Technical Report on AVHRR GAC FCDR Generation. Technical Report Issue 1, Revision 0, ESA Cloud cci. 2017. Available online: http://www.esa-cloud-cci.org/sites/default/files/upload/Cloud_cci_RAFCDR_v1.0.pdf (accessed on 1 August 2021).
- Abel, P.; Gruber, A. An Improved Model for the Calculation of Longwave Flux at 11 um. NOAA Technical Memorandum NESS 106. 1979. Available online: https://repository.library.noaa.gov/view/noaa/18548 (accessed on 1 August 2021).
- Akkermans, T.; Clerbaux, N. Narrowband-to-broadband conversions for top-of-atmosphere reflectance from the Advanced Very High Resolution Radiometer (AVHRR). Remote Sens. 2020, 12, 305. [Google Scholar] [CrossRef] [Green Version]
- Karlsson, K.G.; Riihelä, A.; Müller, R.; Meirink, J.; Sedlar, J.; Stengel, M.; Lockhoff, M.; Trentmann, J.; Kaspar, F.; Hollmann, R.; et al. CLARA-A1: A cloud, albedo, and radiation dataset from 28 yr of global AVHRR data. Atmos. Chem. Phys. 2013, 13, 5351–5367. [Google Scholar] [CrossRef] [Green Version]
- Karlsson, K.G.; Anttila, K.; Trentmann, J.; Stengel, M.; Fokke Meirink, J.; Devasthale, A.; Hanschmann, T.; Kothe, S.; Jääskeläinen, E.; Sedlar, J.; et al. CLARA-A2: The second edition of the CM SAF cloud and radiation data record from 34 years of global AVHRR data. Atmos. Chem. Phys. 2017, 17, 5809–5828. [Google Scholar] [CrossRef] [Green Version]
- Clerbaux, N.; Akkermans, T.; Baudrez, E.; Velazquez Blazquez, A.; Moutier, W.; Moreels, J.; Aebi, C. The Climate Monitoring SAF Outgoing Longwave Radiation from AVHRR. Remote Sens. 2020, 12, 929. [Google Scholar] [CrossRef] [Green Version]
- Akkermans, T.; Clerbaux, N.; Karlsson, K.G.; Hollman, R. CM SAF Algorithm Theoretical Basis Document for Top-of-Atmosphere Products from the CMSAF Cloud, Albedo, Radiation Data Record, AVHRR-Based, Edition 3 (CLARA-A3). SAF/CM/RMIB/ATBD/GAC/TOA, Issue 1, Rev 0. 27 April 2021. EUMETSAT Satellite Application Facility on Climate Monitoring (CM SAF); Prepared by Royal Meteorological Institute Belgium (RMIB). 2021. Available online: www.cmsaf.eu; ftp://gerb.oma.be/tomakker/ATBD-TOA.pdf (accessed on 1 August 2021).
- Devasthale, A.; Raspaud, M.; Schlundt, C.; Hanschmann, T.; Finkensieper, S.; Dybbroe, A.; Hörnquist, S.; Håkansson, N.; Stengel, M.; Karlsson, K. PyGAC: An open-source, community-driven Python interface to preprocess more than 30-year AVHRR Global Area Coverage (GAC) data. GSICS Quartherly Newsl. 2018, 11, 3–5. [Google Scholar]
- Dybbroe, A.; Karlsson, K.G.; Thoss, A. NWCSAF AVHRR cloud detection and analysis using dynamic thresholds and radiative transfer modeling. Part I: Algorithm description. J. Appl. Meteorol. 2005, 44, 39–54. [Google Scholar] [CrossRef]
- Dybbroe, A.; Karlsson, K.G.; Thoss, A. NWCSAF AVHRR cloud detection and analysis using dynamic thresholds and radiative transfer modeling. Part II: Tuning and validation. J. Appl. Meteorol. 2005, 44, 55–71. [Google Scholar] [CrossRef]
- Roebeling, R.; Feijt, A.; Stammes, P. Cloud property retrievals for climate monitoring: Implications of differences between Spinning Enhanced Visible and Infrared Imager (SEVIRI) on METEOSAT-8 and Advanced Very High Resolution Radiometer (AVHRR) on NOAA-17. J. Geophys. Res. Atmos. 2006, 111, D20210. [Google Scholar] [CrossRef]
- CMSAF. CM SAF Algorithm Theoretical Basis Document for the Cloud Probability Product of the NWC/PPS Package. NWC/CDOP3/PPS/SMHI/SCI/ATBD/CloudProbability, Issue 2, Rev 0; 26 April 2021. EUMETSAT Satellite Application Facility on Climate Monitoring (CM SAF); Prepared by Swedish Meteorological and Hydrological Institute (SMHI). 2021. Available online: www.cmsaf.eu (accessed on 1 August 2021).
- Karlsson, K.G.; Johansson, E.; Håkansson, N.; Sedlar, J.; Eliasson, S. Probabilistic Cloud Masking for the Generation of CM SAF Cloud Climate Data Records from AVHRR and SEVIRI Sensors. Remote Sens. 2020, 12, 713. [Google Scholar] [CrossRef] [Green Version]
- CMSAF. CM SAF Algorithm Theoretical Basis Document for the Cloud Mask of the NWC/PPS. NWC/CDOP3/PPS/SMHI/SCI/ ATBD/CloudMask, Issue 3, Rev 0. 26 April 2021. EUMETSAT Satellite Application Facility on Climate Monitoring (CM SAF); Prepared by Swedish Meteorological and Hydrological Institute (SMHI). 2021. Available online: www.cmsaf.eu (accessed on 1 August 2021).
- CMSAF. CM SAF Algorithm Theoretical Basis Document for Cloud Micro Physics of the NWC/PPS. NWC/CDOP3/PPS/SMHI/ SCI/ATBD/CMIC, Issue 3, Rev 0e; 26 April 2021. EUMETSAT Satellite Application Facility on Climate Monitoring (CM SAF); Prepared by Swedish Meteorological and Hydrological Institute (SMHI). 2021. Available online: www.cmsaf.eu (accessed on 1 August 2021).
- Tonboe, R.; Lavelle, J.; Pfeiffer, R.H.; Howe, E. Product user Manual for Osi Saf Global Sea Ice Concentration; Danish Meteorological Institute: Copenhagen, Denmark, 2016. [Google Scholar]
- Dewitte, S.; Nevens, S. The total solar irradiance climate data record. Astrophys. J. 2016, 830, 25. [Google Scholar] [CrossRef]
- Loeb, N.G.; Doelling, D.R.; Wang, H.; Su, W.; Nguyen, C.; Corbett, J.G.; Liang, L.; Mitrescu, C.; Rose, F.G.; Kato, S. Clouds and the earth’s radiant energy system (CERES) energy balanced and filled (EBAF) top-of-atmosphere (TOA) edition-4.0 data product. J. Clim. 2018, 31, 895–918. [Google Scholar] [CrossRef]
- Townshend, J.; Justice, C.; Skole, D.; Malingreau, J.P.; Cihlar, J.; Teillet, P.; Sadowski, F.; Ruttenberg, S. The 1 km resolution global data set: Needs of the International Geosphere Biosphere Programme. Int. J. Remote Sens. 1994, 15, 3417–3441. [Google Scholar] [CrossRef]
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a global land cover characteristics database and IGBP DISCover from 1 km AVHRR data. Int. J. Remote Sens. 2000, 21, 1303–1330. [Google Scholar] [CrossRef]
- Loeb, N.G.; Manalo-Smith, N.; Kato, S.; Miller, W.F.; Gupta, S.K.; Minnis, P.; Wielicki, B.A. Angular distribution models for top-of-atmosphere radiative flux estimation from the Clouds and the Earth’s Radiant Energy System instrument on the Tropical Rainfall Measuring Mission satellite. Part I: Methodology. J. Appl. Meteorol. 2003, 42, 240–265. [Google Scholar] [CrossRef]
- Loeb, N.G.; Kato, S.; Loukachine, K.; Manalo-Smith, N. Angular distribution models for top-of-atmosphere radiative flux estimation from the Clouds and the Earth’s Radiant Energy System instrument on the Terra satellite. Part I: Methodology. J. Atmos. Ocean. Technol. 2005, 22, 338–351. [Google Scholar] [CrossRef]
- Kato, S.; Loeb, N.G. Twilight irradiance reflected by the earth estimated from Clouds and the Earth’s Radiant Energy System (CERES) measurements. J. Clim. 2003, 16, 2646–2650. [Google Scholar] [CrossRef]
- De Rosnay, P.; Isaksen, L.; Dahoui, M. Snow data assimilation at ECMWF. ECMWF Newsl. 2015, 143, 26–31. [Google Scholar]
- Dutra, E.; Balsamo, G.; Viterbo, P.; Miranda, P.M.; Beljaars, A.; Schär, C.; Elder, K. An improved snow scheme for the ECMWF land surface model: Description and offline validation. J. Hydrometeorol. 2010, 11, 899–916. [Google Scholar] [CrossRef]
- Young, D.F.; Wong, T.; Wielicki, B.A.; Minnis, P.; Gibson, G.G.; Barkstrom, B.R.; Charlock, T.P.; Doelling, D.R.; Miller, A.J.; Mitchum, M.V.; et al. Clouds and the Earth’s Radiant Energy System (CERES) Algorithm Theoretical Basis Document; Atmospheric Sciences Division, NASA Langley Research Center: Hampton, Virginia, 1997. [Google Scholar]
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary enhanced temporal interpolation for CERES flux products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Young, D.; Minnis, P.; Doelling, D.; Gibson, G.; Wong, T. Temporal interpolation methods for the Clouds and the Earth’s Radiant Energy System (CERES) experiment. J. Appl. Meteorol. 1998, 37, 572–590. [Google Scholar] [CrossRef] [Green Version]
- Bretagnon, P.; Simon, J.L. Planetary Programs and Tables from −4000 to +2800; Willmann-Bell: Richmond, VA, USA, 1986. [Google Scholar]
- Rutan, D.A.; Kato, S.; Doelling, D.R.; Rose, F.G.; Nguyen, L.T.; Caldwell, T.E.; Loeb, N.G. CERES synoptic product: Methodology and validation of surface radiant flux. J. Atmos. Ocean. Technol. 2015, 32, 1121–1143. [Google Scholar] [CrossRef]
- Gueymard, C.A. A review of validation methodologies and statistical performance indicators for modeled solar radiation data: Towards a better bankability of solar projects. Renew. Sustain. Energy Rev. 2014, 39, 1024–1034. [Google Scholar] [CrossRef]







| Data Type | Data Source | Data Accessibility |
|---|---|---|
| FDR AVHRR radiances | EUMETSAT * | PPS (v2018-patch5) L1c output |
| Cloud products | CMSAF CLARA-A3 | PPS (v2018-patch5) L2 output |
| Snow depth | ERA5 reanalysis [7] | C3S Climate Data Store ** |
| Wind speed | ERA5 reanalysis [7] | C3S Climate Data Store ** |
| Sea ice conc. | OSI SAF [30] | Archive HL FTP server ** |
| TSI | C3S/RMIB [2,31] | C3S Climate Data Store |
| COT climatology | CERES EBAF [32] | https://ceres.larc.nasa.gov/ (accessed on 1 August 2021) |
| Land cover map (30” res.) | IGBP classification applied | USGS Earth Explorer |
| on GLCC database [33,34] | ||
| Land cover map (10’ res.) | CERES surface type map | pers.comm. N.Loeb [21] |
| ADMs | CERES [35,36] | https://ceres.larc.nasa.gov/ (accessed on 1 August 2021) |
| Cloud Class | Clear-Sky | Overcast | ||||
|---|---|---|---|---|---|---|
| TWL Surface Type | ||||||
| Water | 34,283 | 41.749 | −5.114 | 4,969,304 | 83.833 | −12.835 |
| Sea ice 100% | 141,835 | 83.897 | −12.784 | 375,797 | 92.968 | −13.628 |
| Perm.snow/ice | 1,626,464 | 96.117 | −14.699 | 1,879,264 | 99.274 | −15.704 |
| Fresh snow | 86,142 | 60.456 | −8.476 | 652,909 | 90.565 | −13.671 |
| Land | 7902 | 38.724 | −5.501 | 102,852 | 85.617 | −12.739 |
| Clear-Sky | Overcast | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NTB Surface Type | ||||||||||
| Ocean | 1.811 | 1.148 | −0.523 | −0.043 | 0.390 | 4.013 | 0.313 | 0.447 | 0.709 | 1.286 |
| Forests | 1.471 | 0.480 | 0.377 | 1.358 | 1.211 | 3.622 | 0.366 | 0.395 | 0.905 | 1.542 |
| Savannas | 1.421 | 0.463 | 0.382 | 2.696 | 0.769 | 3.328 | 0.403 | 0.355 | 4.127 | 1.059 |
| Grass/crop | 2.575 | 0.443 | 0.339 | 1.101 | 1.430 | 3.704 | 0.393 | 0.368 | 1.093 | 1.893 |
| Dark deserts | 2.384 | 0.367 | 0.376 | 1.279 | 0.724 | 3.031 | 0.291 | 0.473 | 1.377 | 1.597 |
| Bright deserts | 3.225 | 0.365 | 0.335 | 1.467 | 1.291 | 1.305 | 0.462 | 0.317 | 2.648 | 1.419 |
| Perm. snow/ice | 7.511 | 0.202 | 0.479 | −0.507 | 1.612 | 15.075 | 0.164 | 0.463 | −1.231 | 6.254 |
| Fresh snow | 1.598 | 0.310 | 0.412 | 1.627 | 3.213 | 2.487 | 0.334 | 0.430 | 1.223 | 3.272 |
| Sea ice 100% | 7.214 | 0.212 | 0.460 | −0.163 | 4.139 | 8.590 | 0.270 | 0.423 | 0.029 | 4.896 |
| Sea ice 95–99% | 8.486 | 0.220 | 0.437 | −0.424 | 3.847 | 9.553 | 0.238 | 0.449 | −0.266 | 4.424 |
| Sea ice 90–95% | 6.376 | 0.253 | 0.430 | −0.209 | 3.320 | 10.353 | 0.214 | 0.466 | −0.466 | 4.176 |
| Sea ice 80–90% | 3.619 | 0.345 | 0.367 | 0.191 | 2.635 | 9.456 | 0.207 | 0.484 | −0.218 | 3.879 |
| Sea ice 60–80% | 2.922 | 0.410 | 0.296 | 0.562 | 2.734 | 6.188 | 0.275 | 0.455 | 0.455 | 3.148 |
| Sea ice 10–60% | 2.540 | 0.458 | 0.227 | 0.492 | 4.172 | 4.259 | 0.290 | 0.472 | 0.444 | 2.518 |
| Sea ice 0–10% | 1.868 | 0.806 | −0.121 | 0.382 | 2.267 | 4.195 | 0.326 | 0.436 | 0.392 | 2.839 |
| IGBP Class | NTB Surface Type | CERES Surface Type (ADM, Albedo Model) | TWL Surface Type |
|---|---|---|---|
| Water | WATER | OCEAN | WATER |
| Evergreen Needleleaf Forest | |||
| Evergreen Broadleaf Forest | |||
| Deciduous Needleleaf Forest | FOREST | ||
| Deciduous Broadleaf Forest | VEGETATION-DARK | ||
| Mixed Forest | |||
| Woody Savannas | SAVANNA | ||
| Savannas | |||
| Grasslands | |||
| Croplands | VEGETATION-BRIGHT | LAND | |
| Cropland/Natural Vegetation Mosaic | GRASS-CROP | ||
| Closed Shrublands | |||
| Wetlands | VEGETATION-DARK | ||
| Urban and Built-Up | |||
| Open Shrubland | DESERT-DARK | DESERT-DARK | |
| Tundra | or * | ||
| Barren or Sparsely Vegetated | DESERT-BRIGHT | DESERT-BRIGHT | |
| Permanent Snow and Ice | PERM-SNOW-ICE | SNOW | PERM-SNOW-ICE |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akkermans, T.; Clerbaux, N. Retrieval of Daily Mean Top-of-Atmosphere Reflected Solar Flux Using the Advanced Very High Resolution Radiometer (AVHRR) Instruments. Remote Sens. 2021, 13, 3695. https://doi.org/10.3390/rs13183695
Akkermans T, Clerbaux N. Retrieval of Daily Mean Top-of-Atmosphere Reflected Solar Flux Using the Advanced Very High Resolution Radiometer (AVHRR) Instruments. Remote Sensing. 2021; 13(18):3695. https://doi.org/10.3390/rs13183695
Chicago/Turabian StyleAkkermans, Tom, and Nicolas Clerbaux. 2021. "Retrieval of Daily Mean Top-of-Atmosphere Reflected Solar Flux Using the Advanced Very High Resolution Radiometer (AVHRR) Instruments" Remote Sensing 13, no. 18: 3695. https://doi.org/10.3390/rs13183695
APA StyleAkkermans, T., & Clerbaux, N. (2021). Retrieval of Daily Mean Top-of-Atmosphere Reflected Solar Flux Using the Advanced Very High Resolution Radiometer (AVHRR) Instruments. Remote Sensing, 13(18), 3695. https://doi.org/10.3390/rs13183695






