High Resolution Apparent Thermal Inertia Mapping on Mars
Abstract
:1. Introduction
2. Method and Datasets
2.1. Albedo
or i = arccos (M) if t > 12
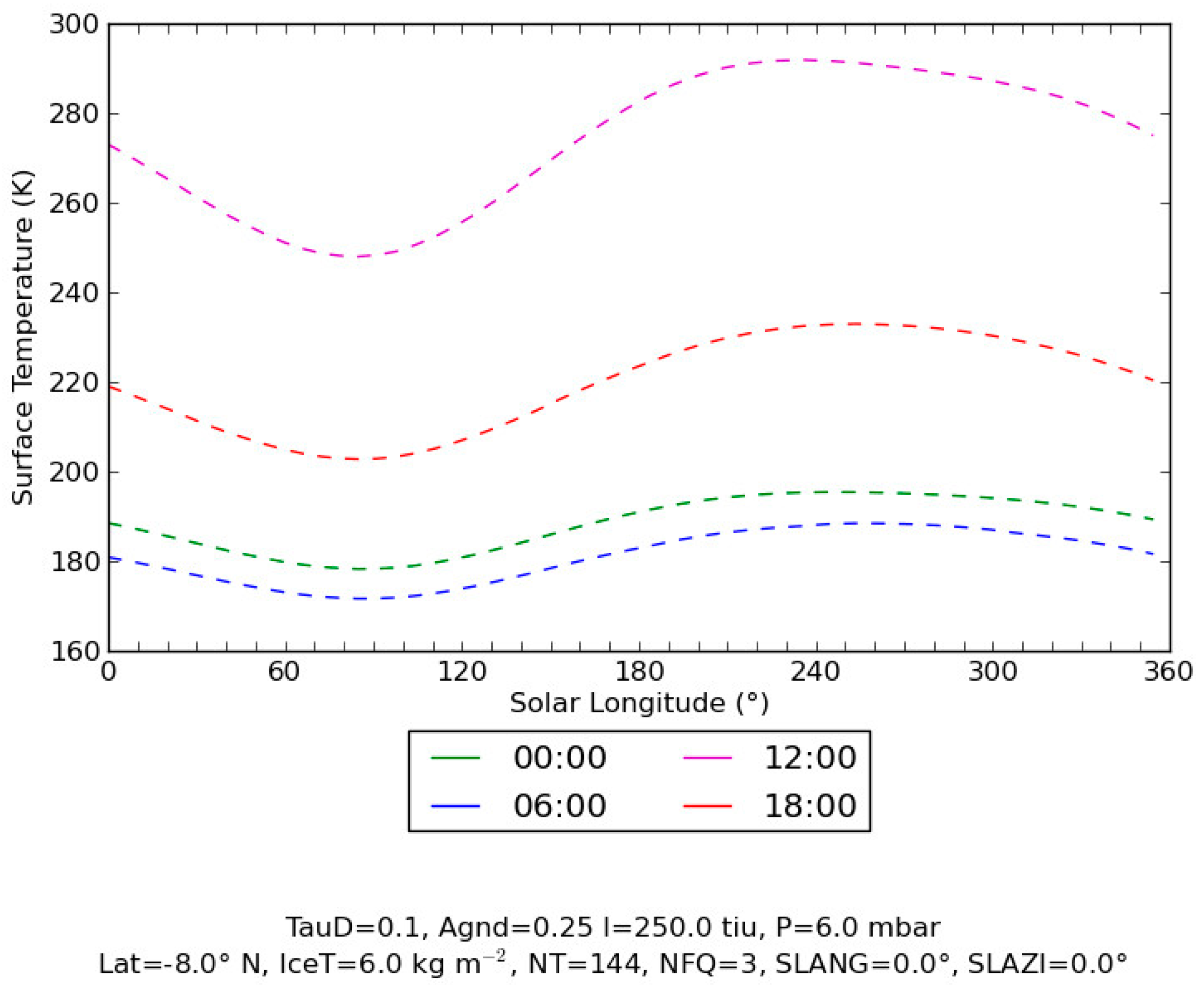
2.2. Surface Temperature
2.3. Solar Longitude
2.4. Dust Opacity
2.5. Topography
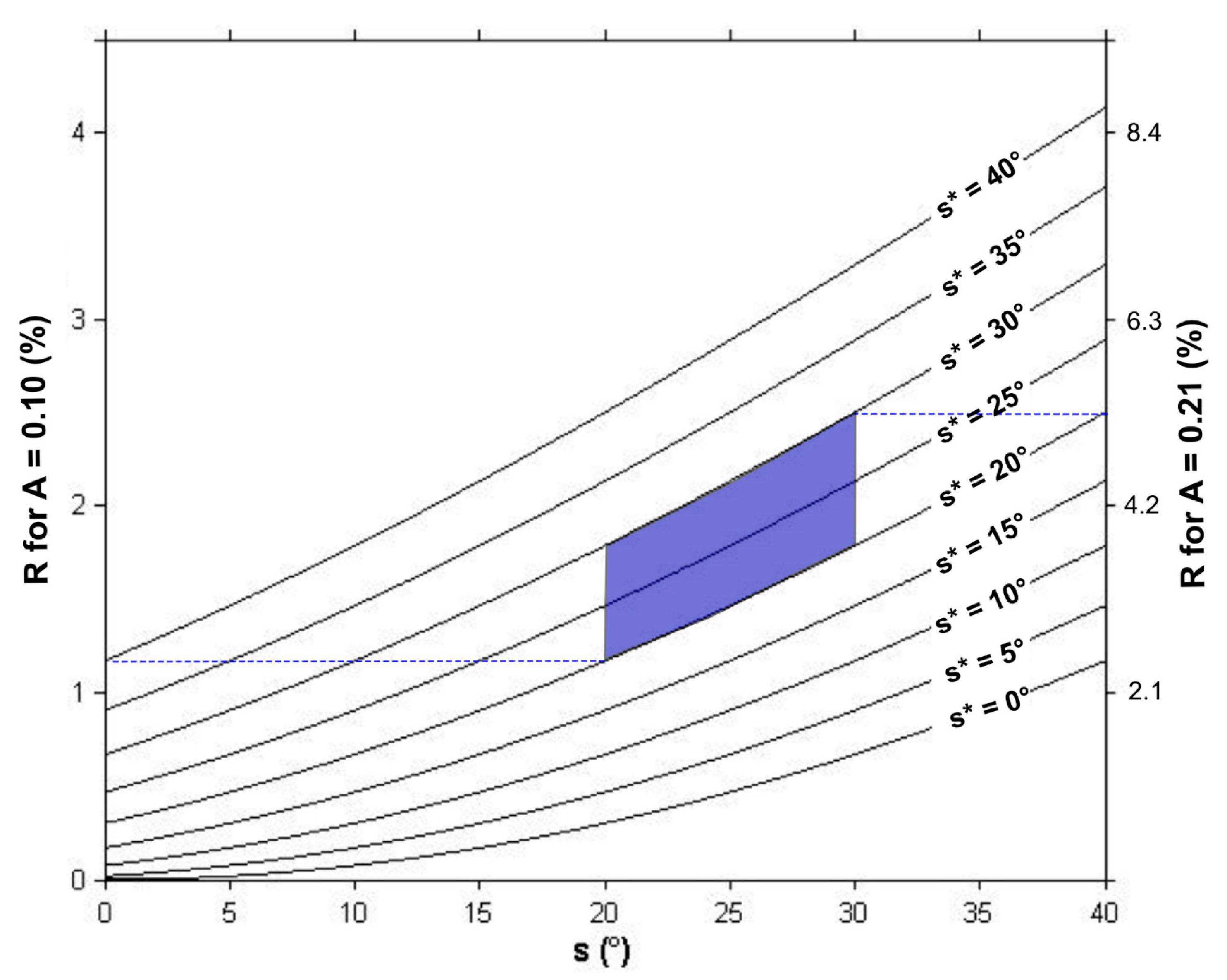
2.6. Errors and Total Uncertainty
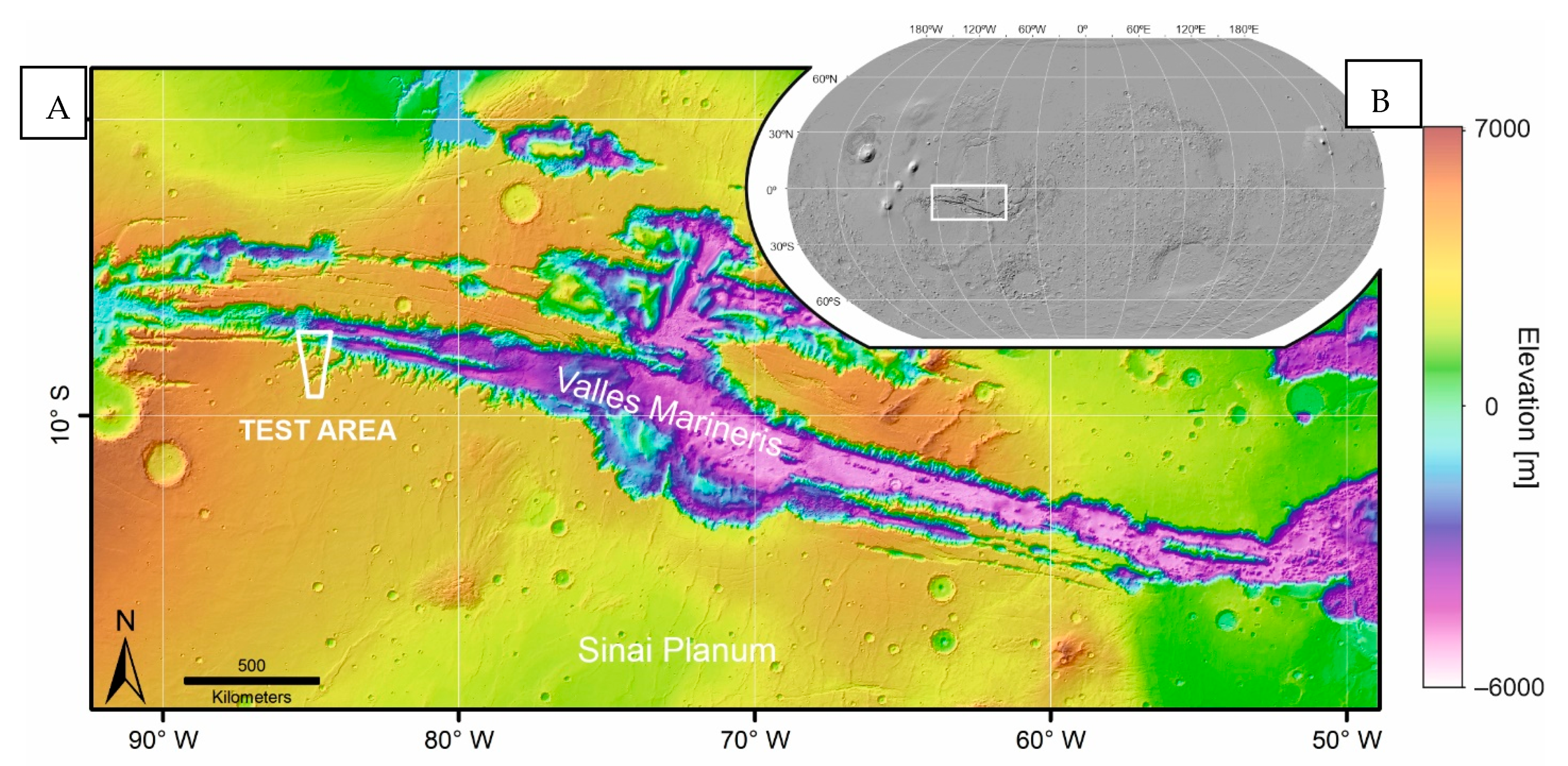
3. Application
3.1. Albedo
3.2. Surface Temperature
3.3. Apparent Thermal Inertia
4. Analysis of Results
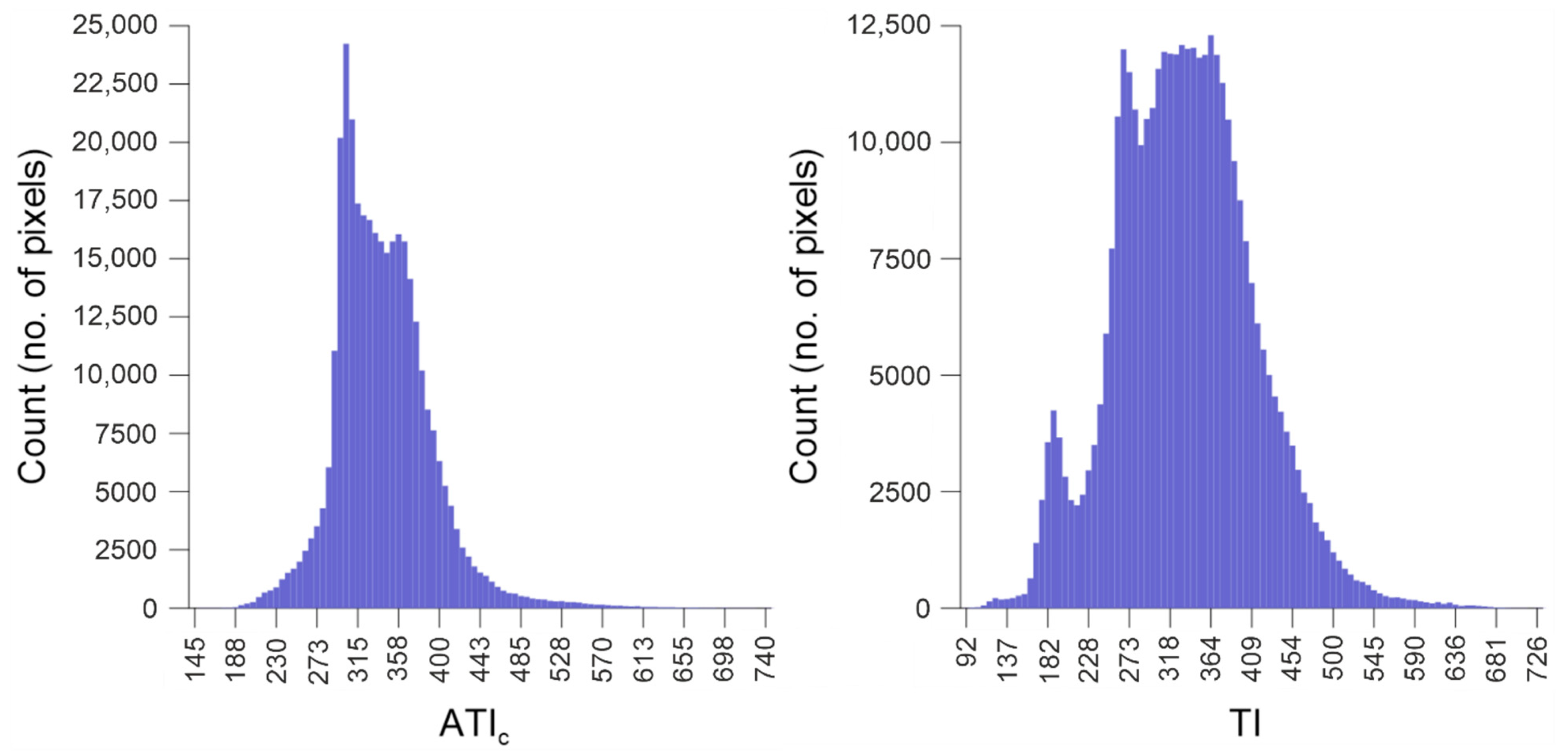
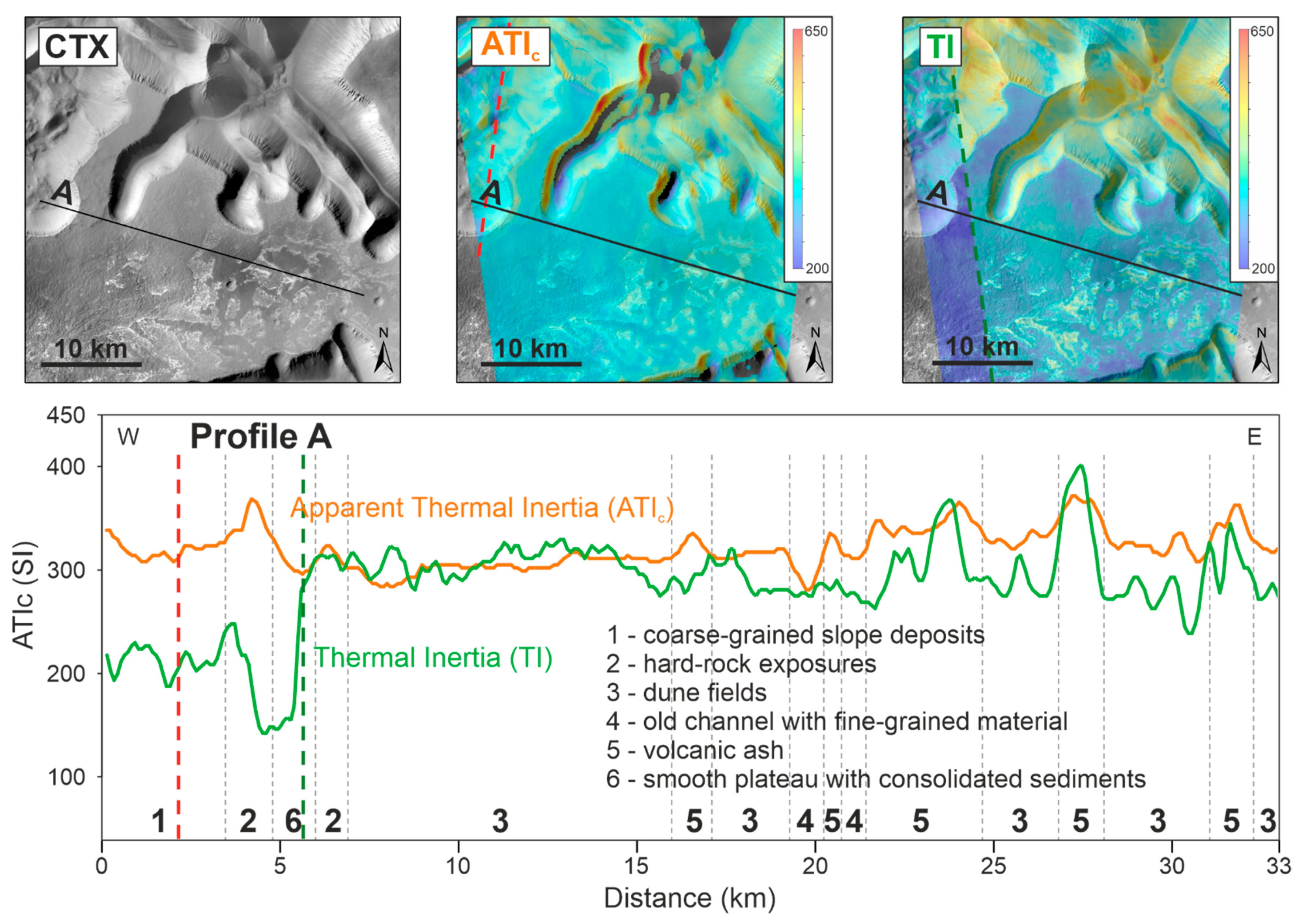
4.1. Overview
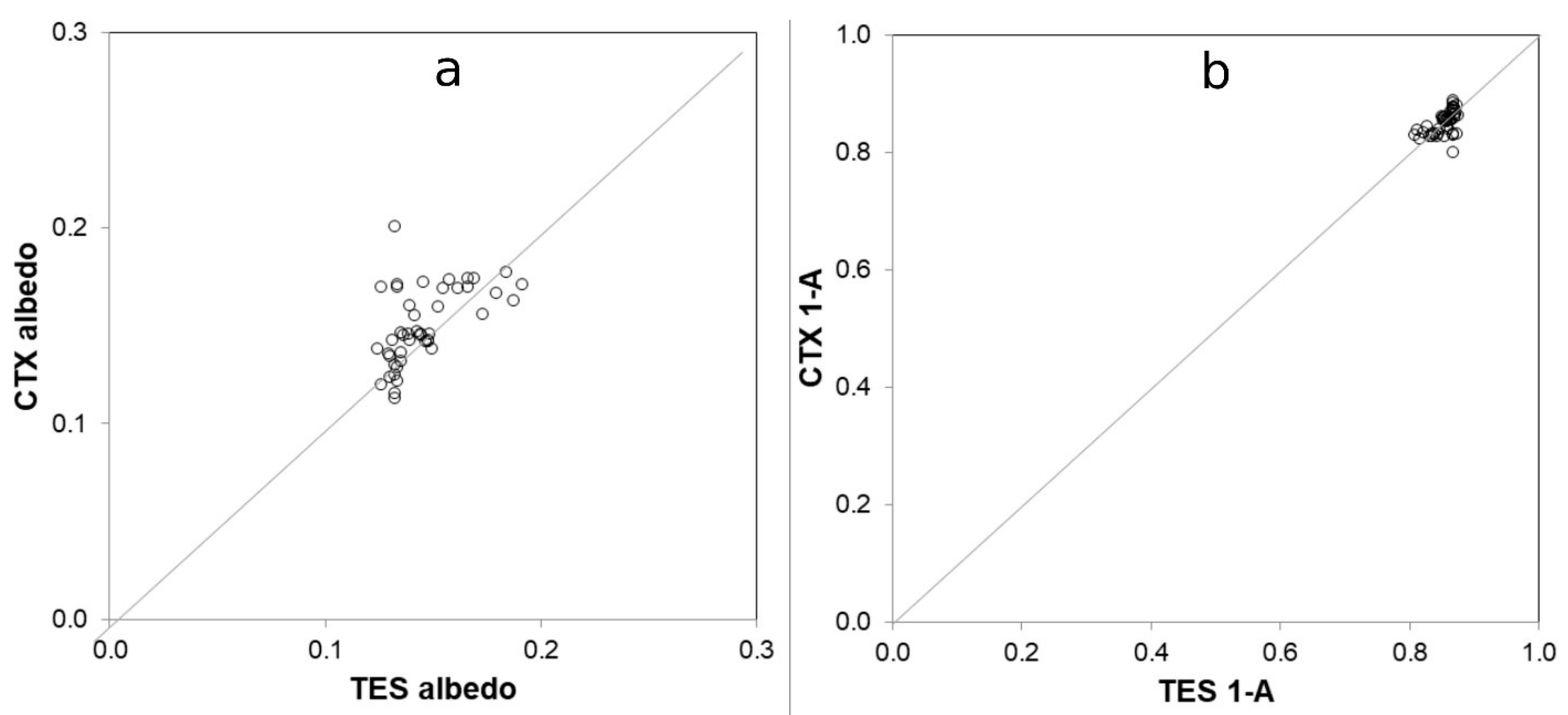
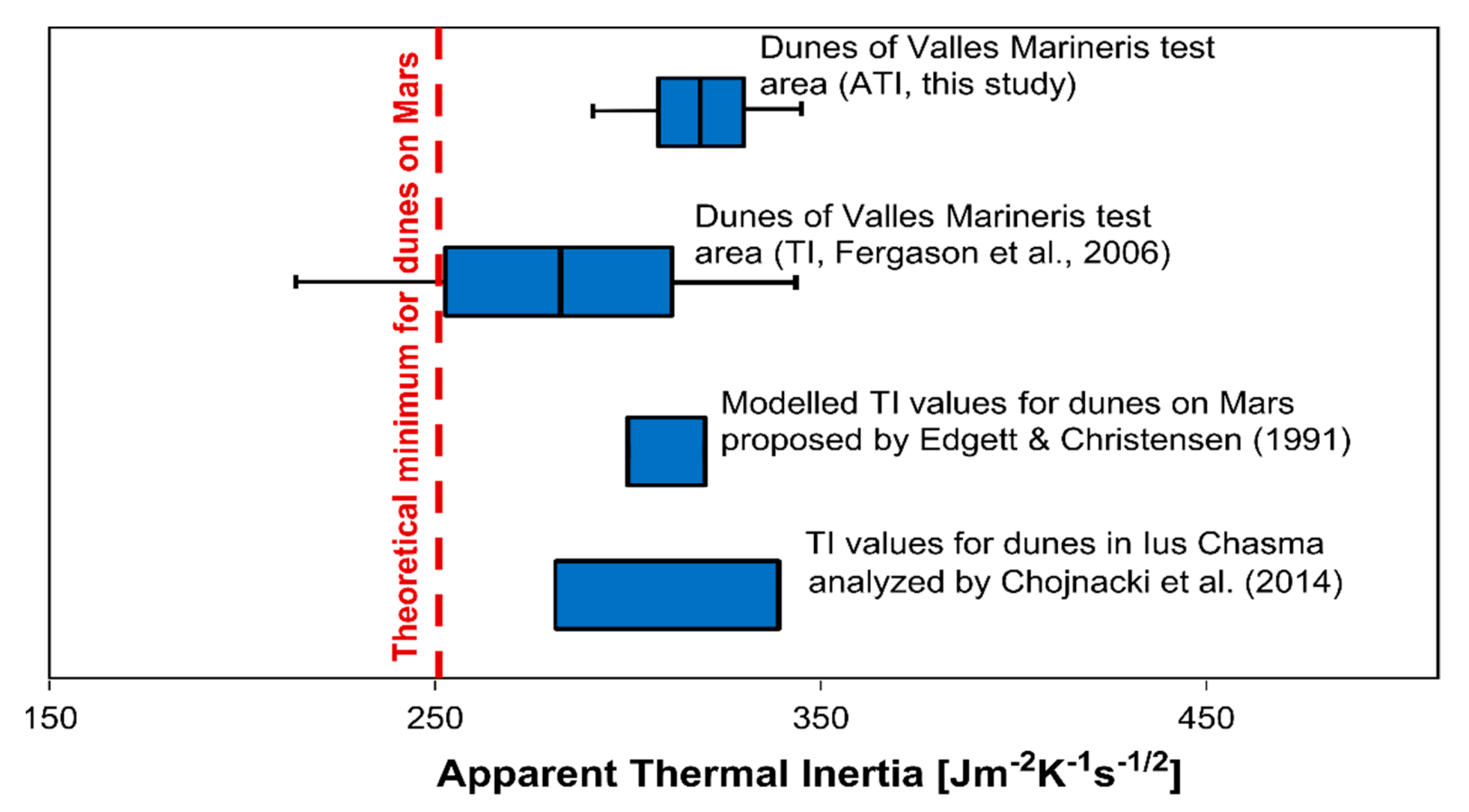
4.2. Method Validation
5. Discussion
5.1. Model Strengths and Applicability
5.2. Model Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Piqueux, S.; Christensen, P.R. Temperature-dependent thermal inertia of homogeneous Martian regolith. J. Geophys. Res. Planets 2011, 116. [Google Scholar] [CrossRef]
- Fergason, R.L.; Christensen, P.R.; Kieffer, H.H. High-resolution thermal inertia derived from the Thermal Emission Imaging System (THEMIS): Thermal model and applications. J. Geophys. Res. Planets 2006, 111. [Google Scholar] [CrossRef]
- Neugebauer, G.; Münch, G.; Kieffer, H.; Chase Jr, S.C.; Miner, E. Mariner 1969 infrared radiometer results: Temperatures and thermal properties of the Martian surface. Astron. J. 1971, 76, 719–749. [Google Scholar] [CrossRef] [Green Version]
- Morrison, D.; Sagan, C.; Pollack, J.B. Martian temperatures and thermal properties. Icarus 1969, 11, 36–45. [Google Scholar] [CrossRef]
- Kieffer, H.H.; Chase, S.C., Jr.; Miner, E.; Münch, G.; Neugebauer, G. Preliminary report on infrared radiometric measurements from the Mariner 9 spacecraft. J. Geophys. Res. 1973, 78, 4291–4312. [Google Scholar] [CrossRef] [Green Version]
- Kieffer, H.H.; Martin, T.Z.; Peterfreund, A.R.; Jakosky, B.M.; Miner, E.D.; Palluconi, F.D. Thermal and albedo mapping of Mars during the Viking primary mission. J. Geophys. Res. 1977, 82, 4249–4291. [Google Scholar] [CrossRef]
- Kieffer, H.H. Thermal model for analysis of Mars infrared mapping. J. Geophys. Res. Planets 2013, 118, 451–470. [Google Scholar] [CrossRef]
- Vdovin, V.V.; Zhegulev, V.S.; Ksanfomaliti, L.V.; Moroz, V.I.; Petrova, E.V. Some characteristics of the soil in the equatorial zone of Mars according to the thermal radiometry data from Mars 5. Cosm. Res. 1981, 18, 609–622. [Google Scholar]
- Palluconi, F.D.; Kieffer, H.H. Thermal inertia mapping of Mars from 60 S to 60 N. Icarus 1981, 45, 415–426. [Google Scholar] [CrossRef]
- Haberle, R.M.; Jakosky, B.M. Atmospheric effects on the remote determination of thermal inertia on Mars. Icarus 1991, 90, 187–204. [Google Scholar] [CrossRef]
- Christensen, P.; Moore, H.J. The Martian surface layer. In Mars; Kieffer, H.H., Ed.; University of Arizona Press: Tucson, AZ, USA, 1992; pp. 686–729. [Google Scholar]
- Dollfus, A.; Deschamps, M.; Zimbelman, J.R. Soil texture and granulometry at the surface of Mars. J. Geophys. Res. Planets 1993, 98, 3413–3429. [Google Scholar] [CrossRef] [Green Version]
- Zent, A.P.; Haberle, R.M.; Houben, H.C.; Jakosky, B.M. A coupled subsurface-boundary layer model of water on Mars. J. Geophys. Res. Planets 1993, 98, 3319–3337. [Google Scholar] [CrossRef]
- Jakosky, B.M.; Mellon, M.T.; Kieffer, H.H.; Christensen, P.R.; Varnes, E.S.; Lee, S.W. The thermal inertia of Mars from the Mars global surveyor thermal emission spectrometer. J. Geophys. Res. Planets 2000, 105, 9643–9652. [Google Scholar] [CrossRef]
- Mellon, M.T.; Jakosky, B.M.; Kieffer, H.H.; Christensen, P.R. High-resolution thermal inertia mapping from the Mars global surveyor thermal emission spectrometer. Icarus 2000, 148, 437–455. [Google Scholar] [CrossRef]
- Putzig, N.E.; Mellon, M.T.; Kretke, K.A.; Arvidson, R.E. Global thermal inertia and surface properties of Mars from the MGS mapping mission. Icarus 2005, 173, 325–341. [Google Scholar] [CrossRef]
- Price, J.C. On the analysis of thermal infrared imagery: The limited utility of apparent thermal inertia. Remote Sens. Environ. 1985, 18, 59–73. [Google Scholar] [CrossRef]
- Xue, Y.; Cracknell, A.P. Advanced thermal inertia modelling. Remote Sens. 1995, 16, 431–446. [Google Scholar] [CrossRef]
- Cracknell, A.P.; Xue, Y. Thermal inertia determination from space—a tutorial review. Int. J. Remote Sens. 1996, 17, 431–461. [Google Scholar] [CrossRef]
- Edwards, C.S.; Piqueux, S. The water content of recurring slope lineae on Mars. Geophys. Res. Lett. 2016, 43, 8912–8919. [Google Scholar] [CrossRef]
- Hamilton, V.E.; Vasavada, A.R.; Sebastián, E.; de la Torre Juárez, M.; Ramos, M.; Armiens, C.; Arvidson, R.E.; Carrasco, I.; Christensen, P.R.; De Pablo, M.A. Observations and preliminary science results from the first 100 sols of MSL Rover Environmental Monitoring Station ground temperature sensor measurements at Gale Crater. J. Geophys. Res. Planets 2014, 119, 745–770. [Google Scholar] [CrossRef] [Green Version]
- Sabol, D.E.; Gillespie, A.R.; McDonald, E.; Danillina, I. Differential thermal inertia of geological surfaces. In Proceedings of the 2nd Annual International Symposium of Recent Advances in Quantitative Remote Sensing, Torrent, Spain, 25–29 September 2006; pp. 25–29. [Google Scholar]
- Putzig, N.E.; Mellon, M.T. Apparent thermal inertia and the surface heterogeneity of Mars. Icarus 2007, 191, 68–94. [Google Scholar] [CrossRef]
- Scheidt, S.; Ramsey, M.; Lancaster, N. Determining soil moisture and sediment availability at White Sands Dune Field, New Mexico, from apparent thermal inertia data. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Kubiak, M.; Stach, A. The use of motor-glider in topoclimatic studies. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 186–198. [Google Scholar] [CrossRef]
- Kubiak, M.; Mège, D.; Gurgurewicz, J.; Ciazela, J. Thermal mapping of mountain slopes on Mars by application of a Differential Apparent Thermal Inertia technique. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 12–17 April 2015; p. 1030. [Google Scholar]
- Price, J.C. Thermal inertia mapping: A new view of the earth. J. Geophys. Res. 1977, 82, 2582–2590. [Google Scholar] [CrossRef]
- Kahle, A.B. Geologic Application of Thermal Inertia Imaging Using HCMM Data; National Aeronautics and Space Administration, Jet Propulsion Laboratory: Pasadena, CA, USA, 1981. [Google Scholar]
- Kahle, A.B. A simple thermal model of the Earth’s surface for geologic mapping by remote sensing. J. Geophys. Res. 1977, 82, 1673–1680. [Google Scholar] [CrossRef]
- Coakley, J.A., Jr. Reflectance and Albedo, Surface. In Encyclopedia of the Atmosphere; Holton, J.R., Curry, J.A., Eds.; Academic Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Malin, M.C.; Bell, J.F.; Cantor, B.A.; Caplinger, M.A.; Calvin, W.M.; Clancy, R.T.; Edgett, K.S.; Edwards, L.; Haberle, R.M.; James, P.B. Context camera investigation on board the Mars Reconnaissance Orbiter. J. Geophys. Res. Planets 2007, 112. Available online: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2006JE002808 (accessed on 14 September 2021).
- Christensen, P.R.; Bandfield, J.L.; Hamilton, V.E.; Ruff, S.W.; Kieffer, H.H.; Titus, T.N.; Malin, M.C.; Morris, R.V.; Lane, M.D.; Clark, R.L.; et al. Mars Global Surveyor Thermal Emission Spectrometer experiment: Investigation description and surface science results. J. Geophys. Res. Planets 2001, 106, 23823–23871. [Google Scholar] [CrossRef]
- Bell, J.F.; Malin, M.C.; Caplinger, M.A.; Fahle, J.; Wolff, M.J.; Cantor, B.A.; James, P.B.; Ghaemi, T.; Posiolova, L.V.; Ravine, M.A.; et al. Calibration and Performance of the Mars Reconnaissance Orbiter Context Camera (CTX). Int. J. Mars Sci. Explor. 2013, 8, 1–14. [Google Scholar] [CrossRef]
- Becker, K.J.; Anderson, J.A.; Weller, L.A.; Becker, T.L. ISIS support for NASA mission instrument ground data processing systems. In Proceedings of the Lunar and Planetary Science Conference, The Woodlands, TX, USA, 18–22 March 2013; Volume 44, p. 2829. [Google Scholar]
- Montabone, L.; Forget, F.; Millour, E.; Wilson, R.J.; Lewis, S.R.; Cantor, B.; Kass, D.; Kleinböhl, A.; Lemmon, M.T.; Smith, M.D. Eight-year climatology of dust optical depth on Mars. Icarus 2015, 251, 65–95. [Google Scholar] [CrossRef] [Green Version]
- Montabone, L.; Cantor, B.; Forget, F.; Kass, D.; Kleinboehl, A.; Smith, M.D.; Wolff, M.J. On the Dustiest Locations on Mars from Observations. In Proceedings of the Sixth International Workshop on The Mars Atmosphere: Modelling and Observations, Granada, Spain, 17 January 2017; pp. 17–20. [Google Scholar]
- Forget, F.; Montabone, L. Atmospheric dust on Mars: A review. In Proceedings of the 47th International Conference on Environmental Systems, Charleston, SC, USA, 16–20 July 2017. [Google Scholar]
- Gwinner, K.; Scholten, F.; Spiegel, M.; Schmidt, R.; Giese, B.; Oberst, J.; Heipke, C.; Jaumann, R.; Neukum, G. Derivation and validation of high-resolution digital terrain models from Mars Express HRSC data. Photogramm. Eng. Remote Sens. 2009, 75, 1127–1142. [Google Scholar] [CrossRef] [Green Version]
- Zevenbergen, L.W.; Thorne, C.R. Quantitative analysis of land surface topography. Earth Surf. Process. Landf. 1987, 12, 47–56. [Google Scholar] [CrossRef]
- Heipke, C.; Oberst, J.; Albertz, J.; Attwenger, M.; Dorninger, P.; Dorrer, E.; Ewe, M.; Gehrke, S.; Gwinner, K.; Hirschmüller, H. Evaluating planetary digital terrain models—The HRSC DTM test. Planet. Space Sci. 2007, 55, 2173–2191. [Google Scholar] [CrossRef]
- Tanaka, K.L.; Skinner, J.A., Jr.; Dohm, J.M.; Irwin, R.P., III; Kolb, E.J.; Fortezzo, C.M.; Platz, T.; Michael, G.G.; Hare, T.M. Geologic map of Mars. Sci. -Investig. Map 2014. [Google Scholar] [CrossRef]
- Edgett, K.S.; Christensen, P.R. The particle size of Martian aeolian dunes. J. Geophys. Res. Planets 1991, 96, 22765–22776. [Google Scholar] [CrossRef]
- Presley, M.A.; Christensen, P.R. The effect of bulk density and particle size sorting on the thermal conductivity of particulate materials under Martian atmospheric pressures. J. Geophys. Res. Planets 1997, 102, 9221–9229. [Google Scholar] [CrossRef]
- Bell, J.F.; Rice, M.S.; Johnson, J.R.; Hare, T.M. Surface albedo observations at Gusev Crater and Meridiani Planum, Mars. J. Geophys. Res. E Planets 2008, 113, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Ball, G.H.; Hall, D.J. ISODATA, A Novel Method of Data Analysis and Pattern Classification; Stanford Research Institute: Menlo Park, CA, USA, 1965. [Google Scholar]
- Eastman, J.R. IDRISI Selva; Clark Labs-Clark University: Worcester, MA, USA, 2012. [Google Scholar]
- Minacapilli, M.; Cammalleri, C.; Ciraolo, G.; D’Asaro, F.; Iovino, M.; Maltese, A. Thermal Inertia Modeling for Soil Surface Water Content Estimation: A Laboratory Experiment; Thermal Inertia Modeling for Soil Surface Water Content Estimation: A Laboratory Experiment. Soil Sci. Soc. Am. J. 2012, 76, 92–100. [Google Scholar] [CrossRef]
- Le Deit, L.; Bourgeois, O.; Mège, D.; Hauber, E.; Le Mouélic, S.; Massé, M.; Jaumann, R.; Bibring, J.-P. Morphology, stratigraphy, and mineralogical composition of a layered formation covering the plateaus around Valles Marineris, Mars: Implications for its geological history. Icarus 2010, 208, 684–703. [Google Scholar] [CrossRef]
- Lucchitta, B.K.; McEwen, A.S.; Clow, G.D.; Geissler, P.E.; Singer, R.B.; Schultz, R.A.; Squyres, S.W. Valles Marineris. In Mars; University of Arizona Press: Tuscon, AZ, USA, 1992; pp. 453–492. [Google Scholar]
- Beyer, R.A.; McEwen, A.S. Layering stratigraphy of eastern Coprates and northern Capri Chasmata, Mars. Icarus 2005, 179, 1–23. [Google Scholar] [CrossRef]
- Flahaut, J.; Quantin, C.; Clenet, H.; Allemand, P.; Mustard, J.F.; Thomas, P. Pristine Noachian crust and key geologic transitions in the lower walls of Valles Marineris: Insights into early igneous processes on Mars. Icarus 2012, 221, 420–435. [Google Scholar] [CrossRef]
- Mellon, M.T.; Fergason, R.L.; Putzig, N.E. The thermal inertia of the surface of Mars. Martian Surf.-Compos. Mineral. Phys. Prop. 2008, 399, 399–427. [Google Scholar] [CrossRef]
- Edgett, K.S.; Christensen, P.R. Mars aeolian sand: Regional variations among dark-hued crater floor features. J. Geophys. Res. Planets 1994, 99, 1997–2018. [Google Scholar] [CrossRef]
- Wentworth, C.K. A scale of grade and class terms for clastic sediments. J. Geol. 1922, 30, 377–392. [Google Scholar] [CrossRef]
- Leszek, C.; Natalia, Z.; Anita, Z.; Marta, C.; Witek Piotr, K.J. The mechanisms of formation of some small cones in Chryse Planitia on Mars. In Proceedings of the EGU General Assembly 2021, Online event, 19–30 April 2021. [Google Scholar]
- Brož, P.; Bernhardt, H.; Conway, S.J.; Parekh, R. An overview of explosive volcanism on Mars. J. Volcanol. Geotherm. Res. 2021, 409, 107125. [Google Scholar] [CrossRef]
- Hauber, E.; Bleacher, J.; Gwinner, K.; Williams, D.; Greeley, R. The topography and morphology of low shields and associated landforms of plains volcanism in the Tharsis region of Mars. J. Volcanol. Geotherm. Res. 2009, 185, 69–95. [Google Scholar] [CrossRef]
- Brož, P.; Čadek, O.; Hauber, E.; Rossi, A.P. Scoria cones on Mars: Detailed investigation of morphometry based on high-resolution digital elevation models. J. Geophys. Res. Planets 2015, 120, 1512–1527. [Google Scholar] [CrossRef] [Green Version]
- Brož, P.; Čadek, O.; Hauber, E.; Rossi, A.P. Shape of scoria cones on Mars: Insights from numerical modeling of ballistic pathways. Earth Planet. Sci. Lett. 2014, 406, 14–23. [Google Scholar] [CrossRef] [Green Version]
- Rivera-Hernández, F.; Sumner, D.Y.; Mangold, N.; Banham, S.G.; Edgett, K.S.; Fedo, C.M. Grain Size Variations in the Murray Formation: Stratigraphic Evidence for Changing Depositional Environments in Gale Crater. Mars. J. Geophys. Res. 2020, 125, e2019JE006230. [Google Scholar] [CrossRef] [Green Version]
- Jerolmack, D.J.; Mohrig, D.; Grotzinger, J.P.; Fike, D.A.; Watters, W.A.; Jerolmack, C.; Mohrig, D.; Grotzinger, J.P.; Fike, D.A.; Watters, W.A. Spatial grain size sorting in eolian ripples and estimation of wind conditions on planetary surfaces: Application to Meridiani Planum, Mars. J. Geophys. Res. 2006, 111, 12–14. [Google Scholar] [CrossRef] [Green Version]
- Di Pietro, I.; Séjourné, A.; Costard, F.; Ciążela, M.; Rodriguez, J.A.P. Evidence of mud volcanism due to the rapid compaction of martian tsunami deposits in southeastern Acidalia Planitia, Mars. Icarus 2021, 354, 114096. [Google Scholar] [CrossRef]
- Hay, J.E.; McKAY, D.C. Estimating solar irradiance on inclined surfaces: A review and assessment of methodologies. Int. J. Sol. Energy 1985, 3, 203–240. [Google Scholar] [CrossRef]
- Hay, J.E. Calculating solar radiation for inclined surfaces: Practical approaches. Renew. Energy 1993, 3, 373–380. [Google Scholar] [CrossRef]
- Spiga, A.; Forget, F. Fast and accurate estimation of solar irradiance on Martian slopes. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Hay, J.E. Computation model for radiative fluxes. J. Hydrol. 1971, 10, 36–48. [Google Scholar]

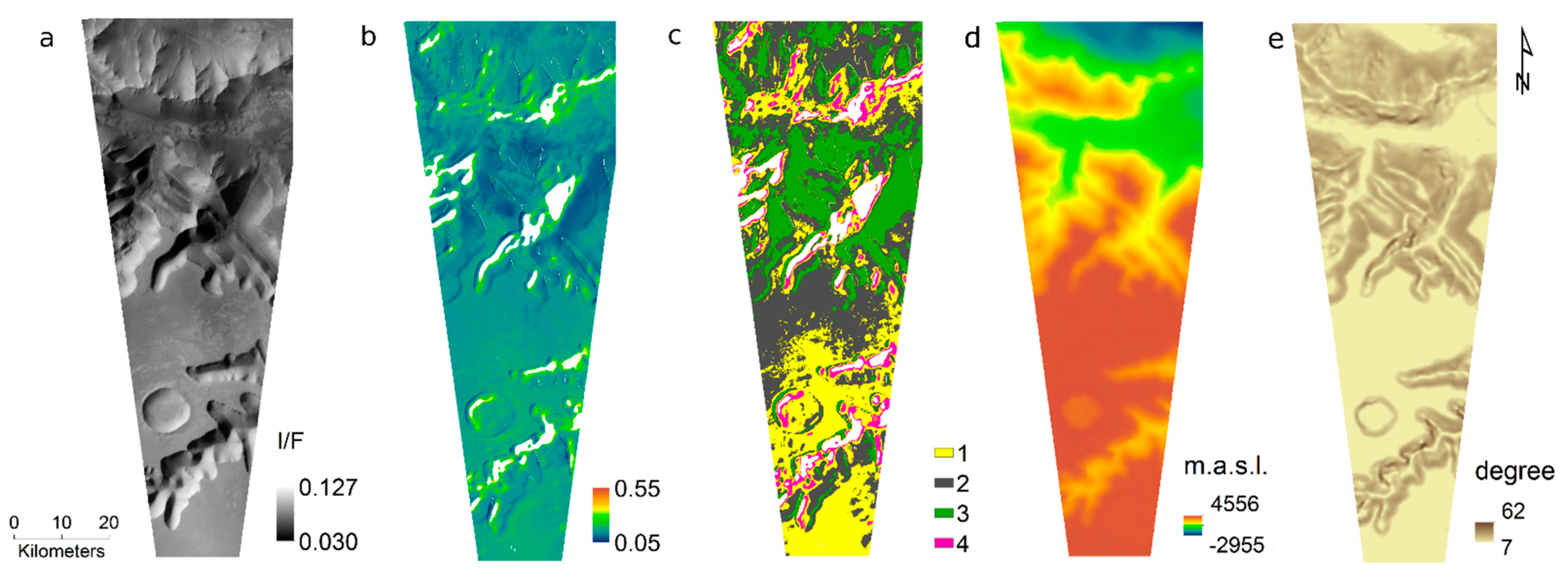



| Isodata Class | Average Albedo | Average ΔT |
|---|---|---|
| 1 | 0.17 | 94.2 |
| 2 | 0.14 | 91.5 |
| 3 | 0.11 | 87.4 |
| 4 | 0.25 | 91.2 |
| THEMIS Image ID | Local Solar Time (t) | Solar Longitude (Ls) | Mars Year |
|---|---|---|---|
| Day | |||
| I17277013 | 16.16 | 319.1 | 27 |
| I07967021 | 16.73 | 271.2 | 26 |
| Night | |||
| I16872020 | 4.34 | 299.6 | 27 |
| I08186009 | 4.57 | 282.5 | 26 |
| Grain Classification | Grain Size Range (µm) | ATIc Range (J m−2 K−1s−1/2) |
|---|---|---|
| Clay (clay) | 0–3.9 | 13.8–99.6 |
| Silt (silt) | 3.9–62.5 | 99.6–190.4 |
| Very fine sand (vfs) | 62.5–125 | 190.4–223.9 |
| Fine sand (fs) | 125–250 | 224–263 |
| Medium sand (ms) | 250–500 | 263–310 |
| Coarse sand (cs) | 500–1000 | 310–364 |
| Very coarse sand (vcs) | 1000–2000 | 364–428 |
| Granules (g) | 2000–4000 | 428–503 |
| Pebbles (p) | 4000–64,000 | 503–961 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciazela, M.; Ciazela, J.; Pieterek, B. High Resolution Apparent Thermal Inertia Mapping on Mars. Remote Sens. 2021, 13, 3692. https://doi.org/10.3390/rs13183692
Ciazela M, Ciazela J, Pieterek B. High Resolution Apparent Thermal Inertia Mapping on Mars. Remote Sensing. 2021; 13(18):3692. https://doi.org/10.3390/rs13183692
Chicago/Turabian StyleCiazela, Marta, Jakub Ciazela, and Bartosz Pieterek. 2021. "High Resolution Apparent Thermal Inertia Mapping on Mars" Remote Sensing 13, no. 18: 3692. https://doi.org/10.3390/rs13183692
APA StyleCiazela, M., Ciazela, J., & Pieterek, B. (2021). High Resolution Apparent Thermal Inertia Mapping on Mars. Remote Sensing, 13(18), 3692. https://doi.org/10.3390/rs13183692







