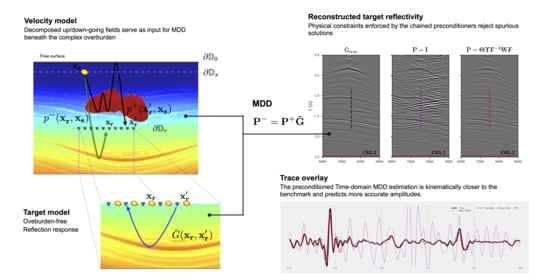
Time-Domain Multidimensional Deconvolution: A Physically Reliable and Stable Preconditioned Implementation
Abstract
1. Introduction
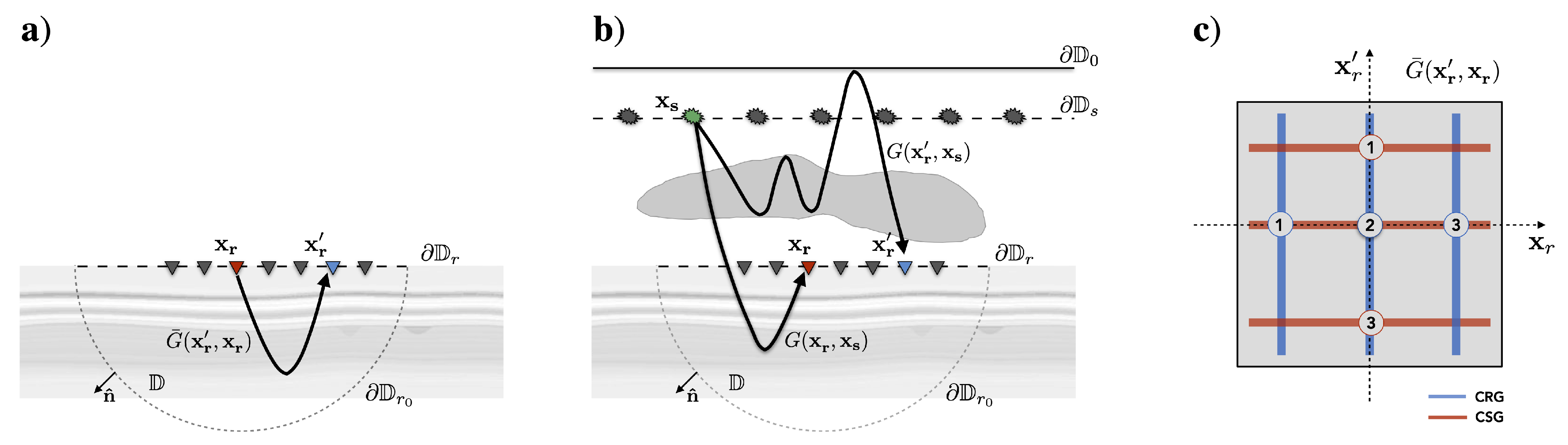
2. Seismic Wavefield Redatuming
2.1. Two-Way Multidimensional Deconvolution
2.2. One-Way Multidimensional Deconvolution
2.3. Frequency Domain MDD—Regularized Least Squares
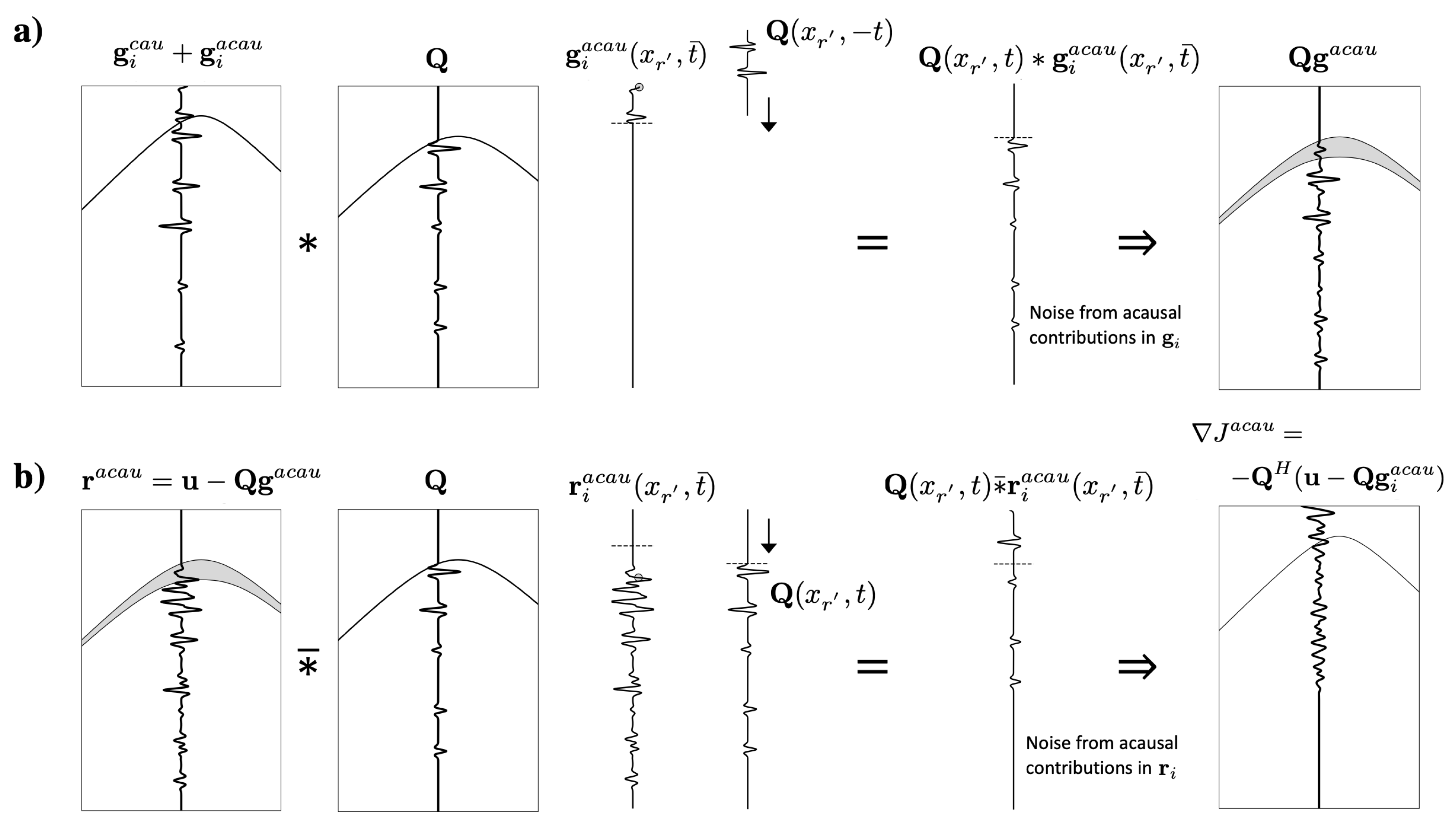
2.4. Time Domain MDD—Constrained Least Squares
2.5. Physics-Inspired Preconditioners
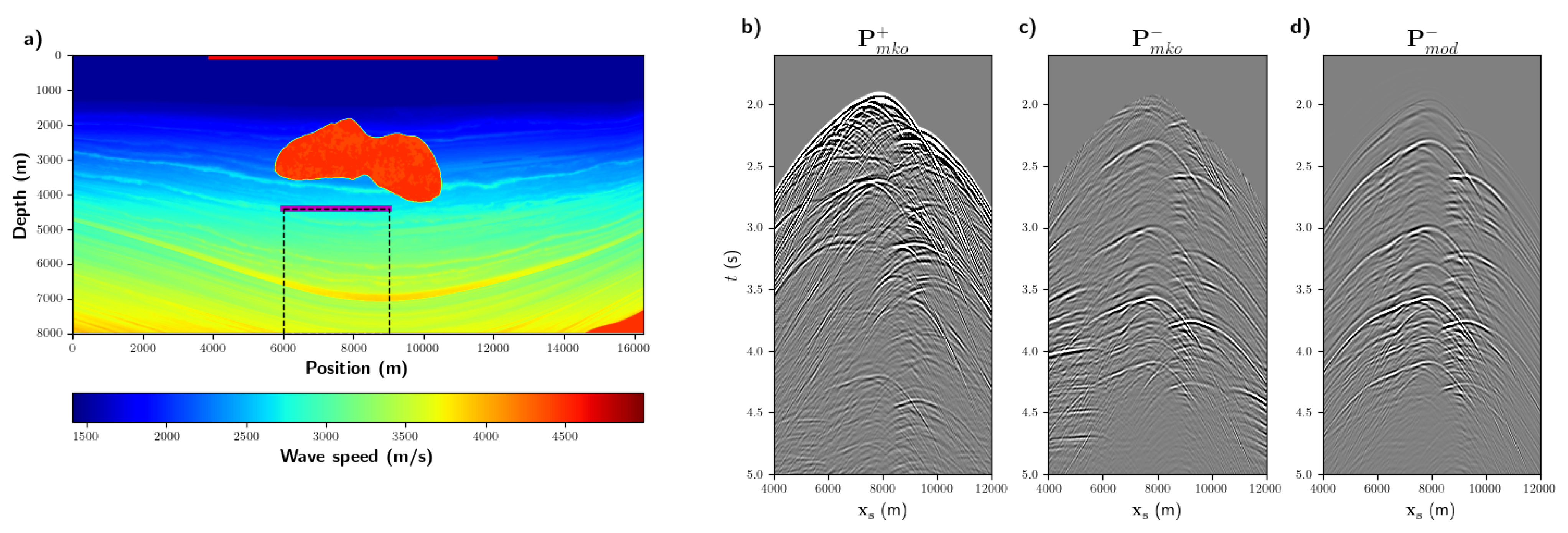
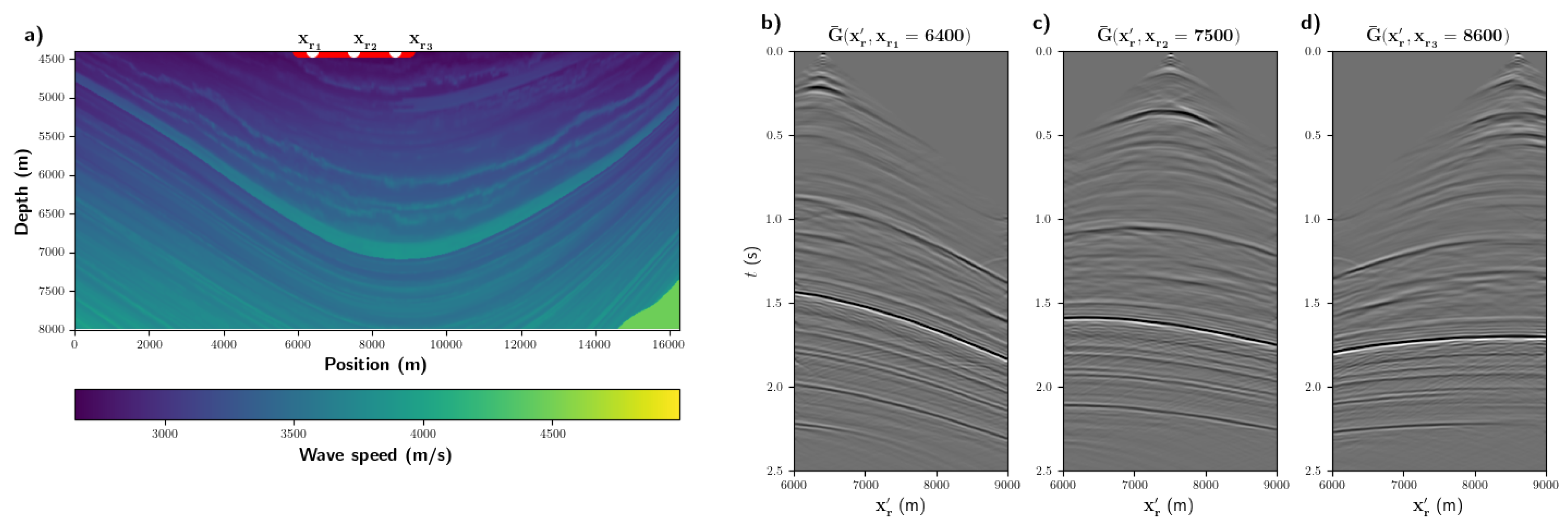
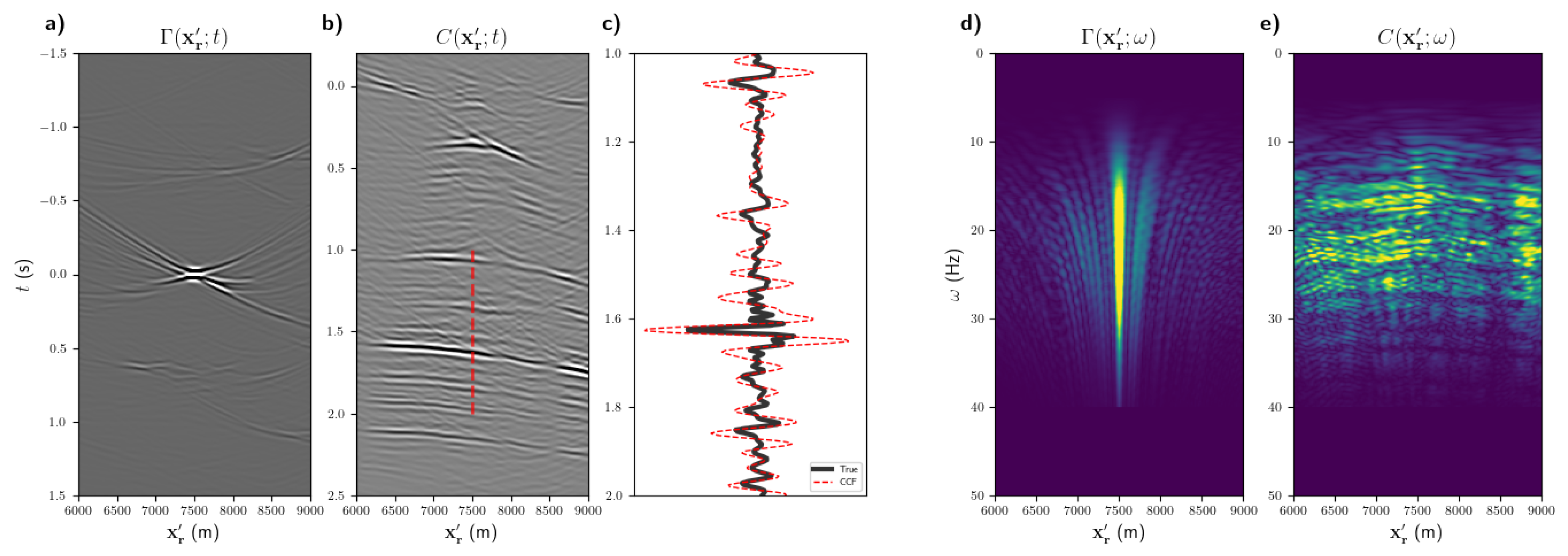
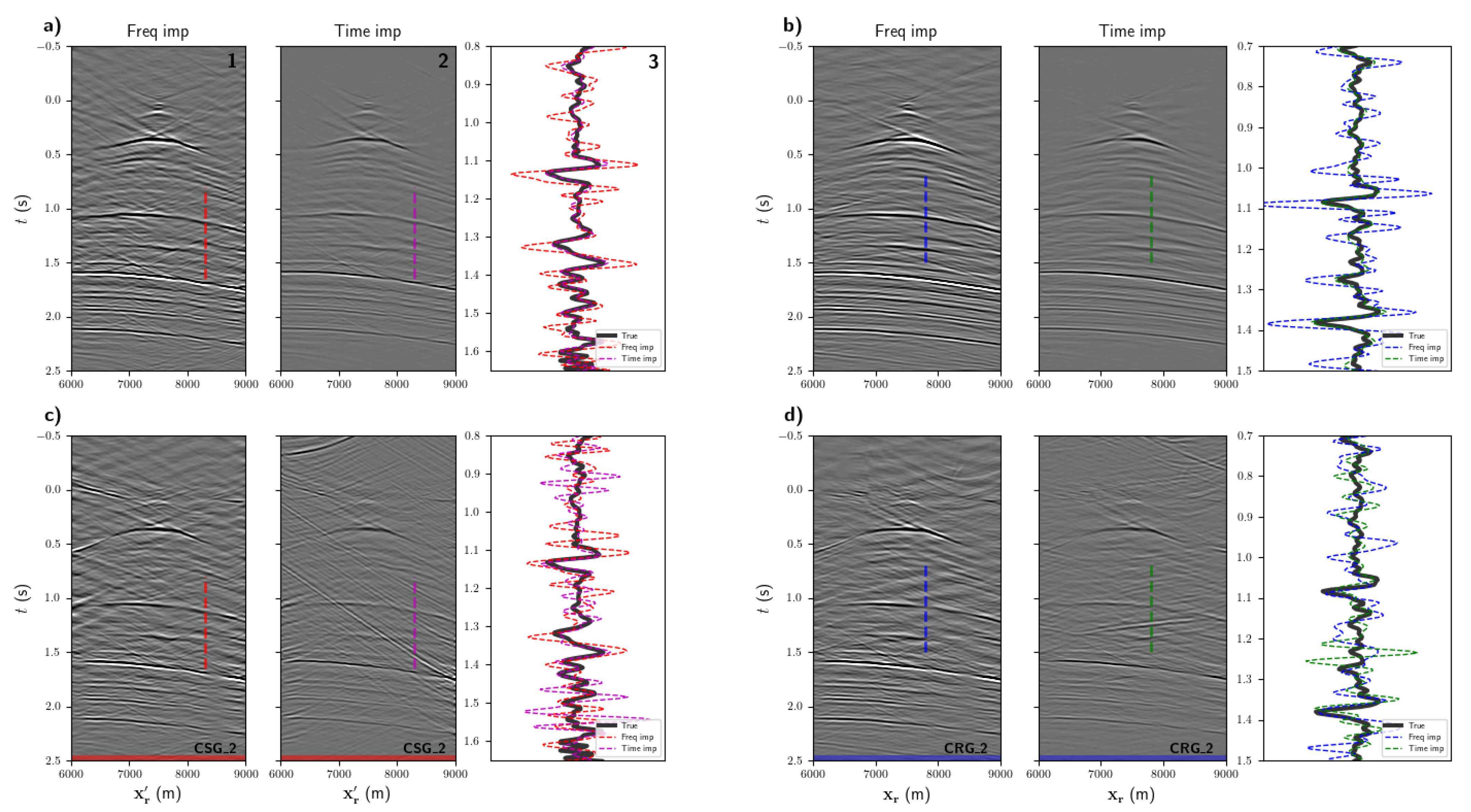
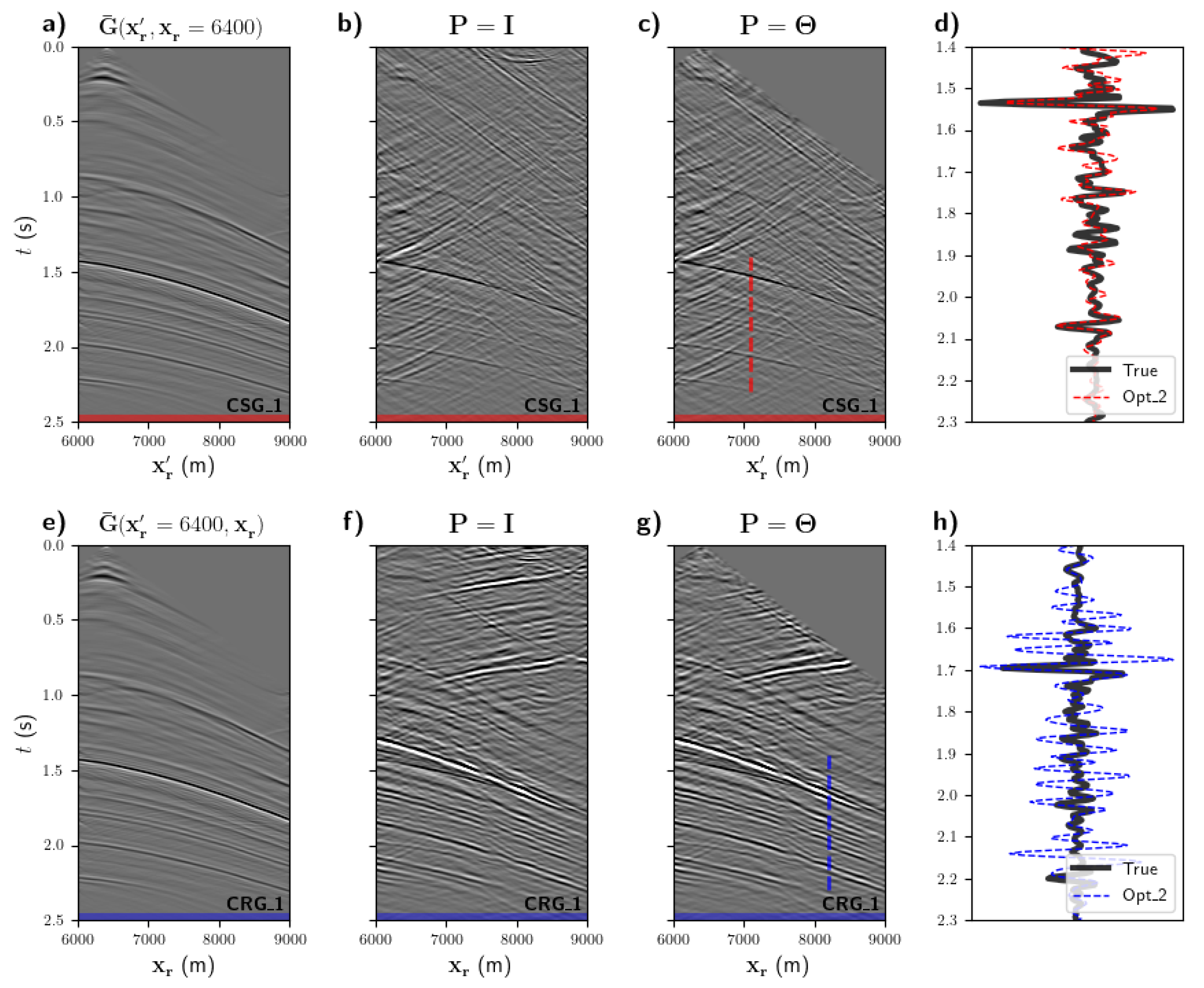
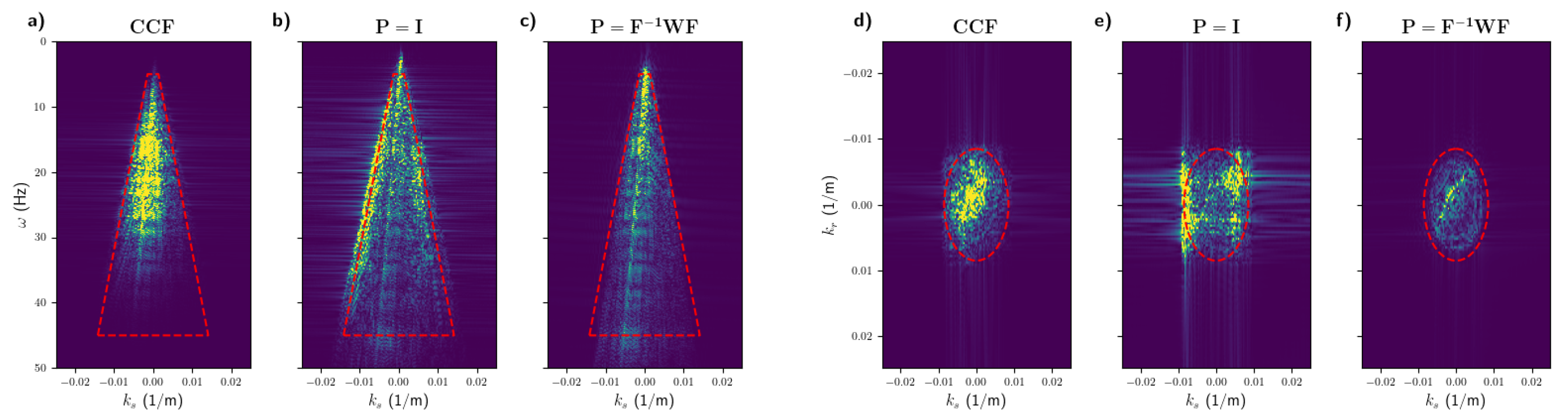
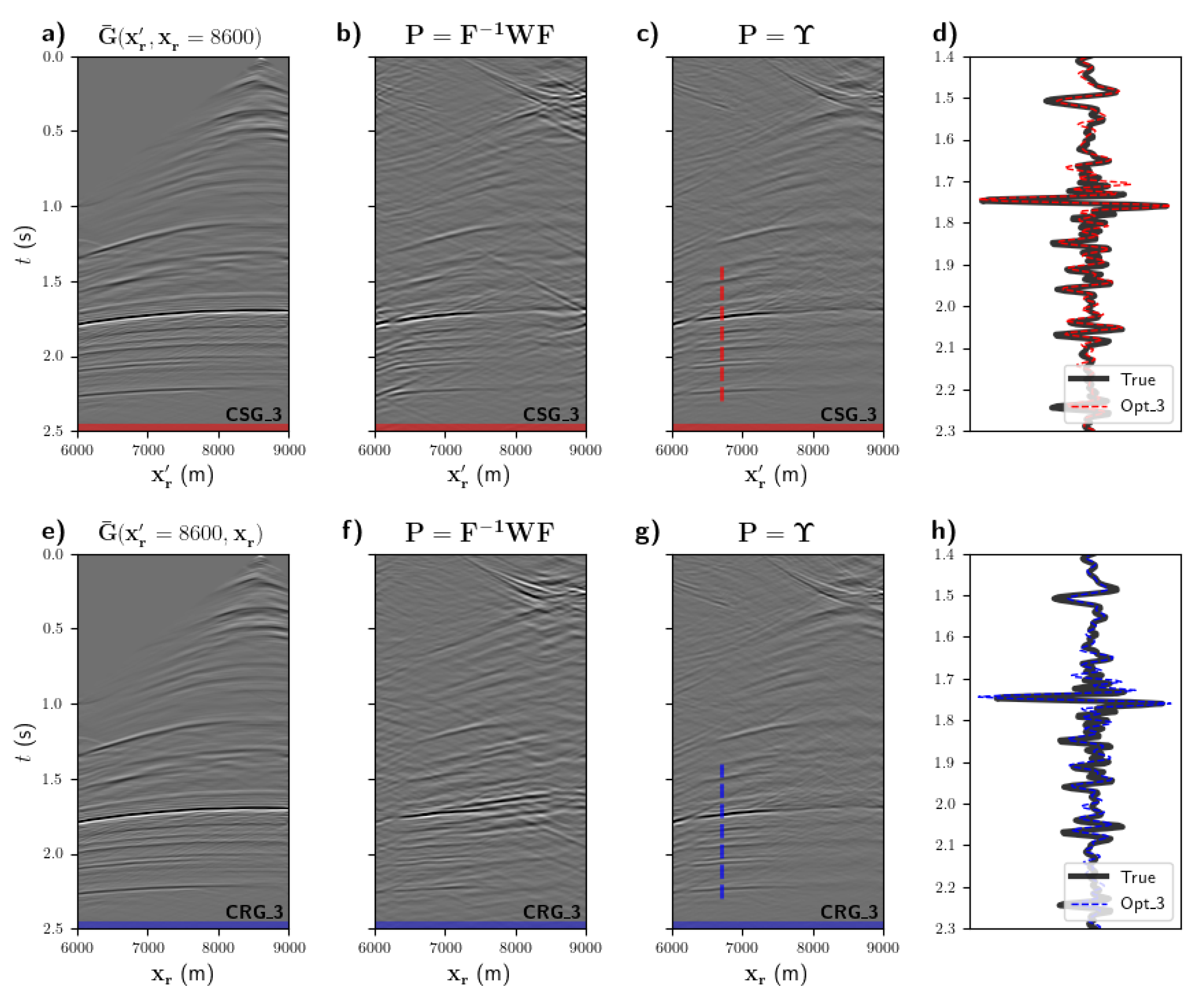
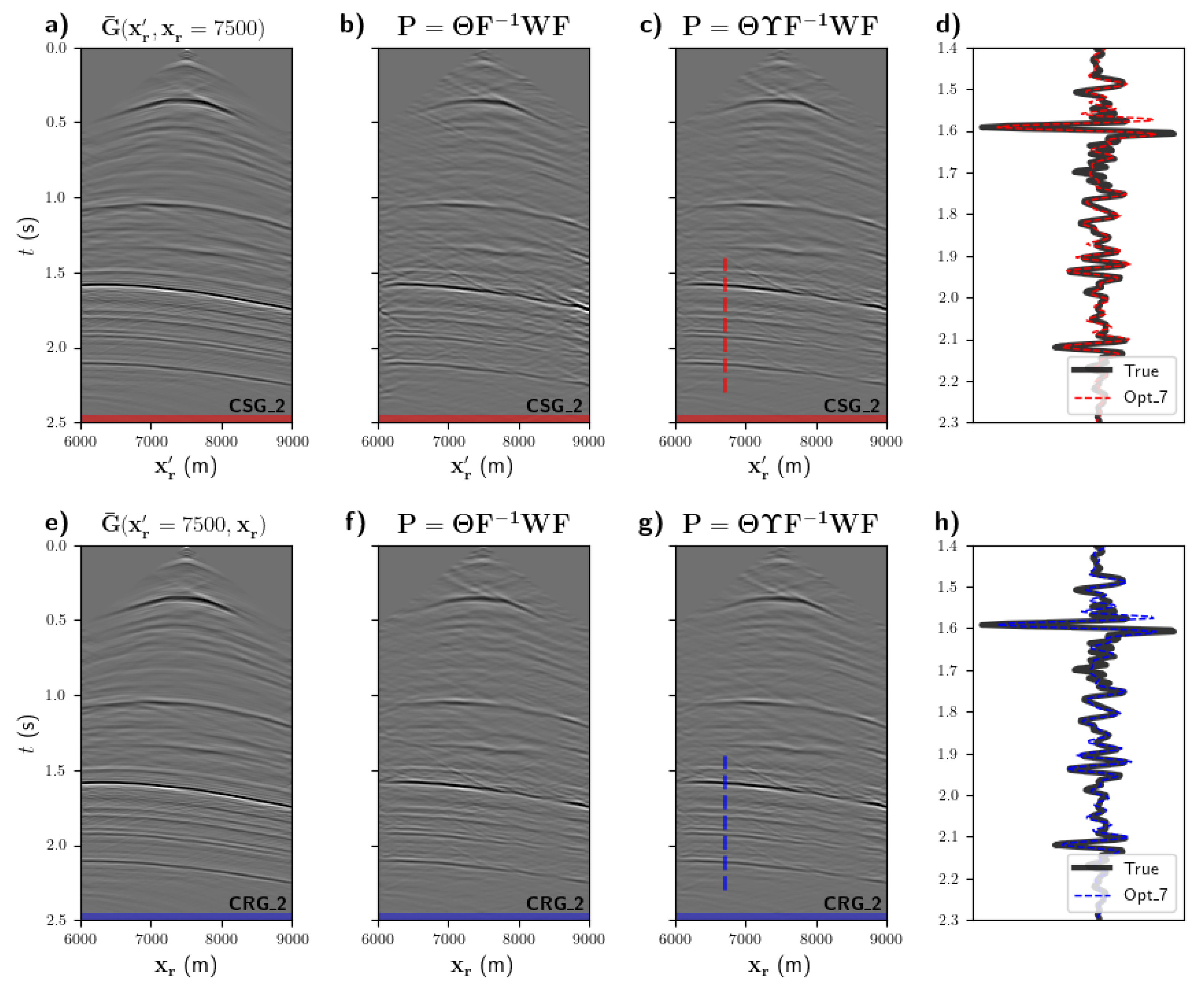
3. Numerical Examples
3.1. Noise-Free Modelled Wavefields
3.2. Noise-Contaminated Marchenko Wavefields
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OBS | Ocean-bottom seismic |
| MDC | Multidimensional convolution |
| MDD | Multidimensional deconvolution |
| CCF | Cross correlation function |
| PSF | Point spread function |
| CSG | Common shot gathers |
| CRG | Common receiver gathers |
| SVD | Singular-value decomposition |
| SRM | Surface related multiples |
| SRME | Surface related multiples elimination |
| FWM | Full-Wavefield Migration |
| RMSE | Root means square error |
| SSIM | Structural similarity index measure |
| FISTA | Fast Iterative Shrinkage-Thresholding Algorithm |
| SPGL1 | Spectral projected gradient 1-norm Algorithm |
| HPC | High-performance computing |
References
- Fokkema, J.; van den Berg, P. Seismic Applications of Acoustic Reciprocity; Elsevier Science: Amsterdam, The Netherlands, 1993. [Google Scholar] [CrossRef]
- Schuster, G.T.; Yu, J.; Sheng, J.; Rickett, J. Interferometric/daylight seismic imaging. Geophys. J. Int. 2004, 157, 838–852. [Google Scholar] [CrossRef]
- Bakulin, A.; Calvert, R. The virtual source method: Theory and case study. Geophysics 2006, 71, SI139–SI150. [Google Scholar] [CrossRef]
- Wapenaar, K.; van der Neut, J.; Ruigrok, E.; Draganov, D.; Hunziker, J.; Slob, E.; Thorbecke, J.; Snieder, R. Seismic interferometry by crosscorrelation and by multidimensional deconvolution: A systematic comparison. Geophys. J. Int. 2011, 185, 1335–1364. [Google Scholar] [CrossRef]
- Ruigrok, E.; Campman, X.; Draganov, D.; Wapenaar, K. High-resolution lithospheric imaging with seismic interferometry. Geophys. J. Int. 2010, 183, 339–357. [Google Scholar] [CrossRef]
- Draganov, D.; Campman, X.; Thorbecke, J.; Verdel, A.; Wapenaar, K. Reflection images from ambient seismic noise. Geophysics 2009, 74, A63–A67. [Google Scholar] [CrossRef]
- Li, X.; Becker, T.; Ravasi, M.; Robertsson, J.; van Manen, D.J. Closed-aperture unbounded acoustics experimentation using multidimensional deconvolution. J. Acoust. Soc. Am. 2021, 149, 1813–1828. [Google Scholar] [CrossRef]
- Berryhill, J.R. Wave-equation datuming. Geophysics 1979, 44, 1329–1344. [Google Scholar] [CrossRef]
- Schuster, G.T.; Zhou, M. A theoretical overview of model-based and correlation-based redatuming methods. Geophysics 2006, 71, SI103–SI110. [Google Scholar] [CrossRef]
- Vasconcelos, I.; Snieder, R. Interferometry by deconvolution: Part 1—Theory for acoustic waves and numerical examples. Geophysics 2008, 73, S115–S128. [Google Scholar] [CrossRef]
- Van der Neut, J.; Thorbecke, J.; Mehta, K.; Slob, E.; Wapenaar, K. Controlled-source interferometric redatuming by crosscorrelation and multidimensional deconvolution in elastic media. Geophysics 2011, 76, SA63–SA76. [Google Scholar] [CrossRef]
- Wapenaar, K.; Slob, E.; Snieder, R. Seismic and electromagnetic controlled-source interferometry in dissipative media. Geophys. Prospect. 2008, 56, 419–434. [Google Scholar] [CrossRef]
- Soubaras, R. Deghosting by joint deconvolution of a migration and a mirror migration. In Proceedings of the 80th Annual International Meeting, Denver, CO, USA, 17–22 October 2010; Expanded Abstracts. SEG: Tulsa, OK, USA, 2010; pp. 3406–3410. [Google Scholar] [CrossRef]
- Wapenaar, K.; Thorbecke, J.; van der Neut, J.; Broggini, F.; Slob, E.; Snieder, R. Marchenko imaging. Geophysics 2014, 79, WA39–WA57. [Google Scholar] [CrossRef]
- Mildner, C.; Broggini, F.; de Vos, K.; Robertsson, J.O.A. Accurate source wavelet estimation using Marchenko focusing functions. Geophysics 2019, 84, Q73–Q88. [Google Scholar] [CrossRef]
- Verschuur, D.J.; Berkhout, A.J.; Wapenaar, C.P.A. Adaptive surface-related multiple elimination. Geophysics 1992, 57, 1166–1177. [Google Scholar] [CrossRef]
- Dragoset, B.; Verschuur, E.; Moore, I.; Bisley, R. A perspective on 3D surface-related multiple elimination. Geophysics 2010, 75, 75A245–75A261. [Google Scholar] [CrossRef]
- Beasley, C.J.; Chambers, R.E.; Jiang, Z. A new look at simultaneous sources. In SEG Technical Program Expanded Abstracts 1998, Proceedings of the 68th Annual International Meeting, New Orleans, LA, USA, 13–18 September 1998; SEG: Tulsa, OK, USA, 1998; pp. 133–135. [Google Scholar] [CrossRef]
- Berkhout, A.J. Changing the mindset in seismic data acquisition. Lead. Edge 2008, 27, 924–938. [Google Scholar] [CrossRef]
- Schuster, G.T.; Wang, X.; Huang, Y.; Dai, W.; Boonyasiriwat, C. Theory of multisource crosstalk reduction by phase-encoded statics. Geophys. J. Int. 2011, 184, 1289–1303. [Google Scholar] [CrossRef]
- Wapenaar, K.; van der Neut, J.; Thorbecke, J. On the relation between seismic interferometry and the simultaneous-source method. Geophys. Prospect. 2012, 60, 802–823. [Google Scholar] [CrossRef]
- Backus, M.M. Water reverberations, their nature and elimination. Geophysics 1959, 24, 233–261. [Google Scholar] [CrossRef]
- Riley, D.C.; Claerbout, J.F. 2D multiple reflections. Geophysics 1976, 41, 592–620. [Google Scholar] [CrossRef]
- Amundsen, L. Elimination of free-surface related multiples without need of the source wavelet. Geophysics 2001, 66, 327–341. [Google Scholar] [CrossRef]
- Minato, S.; Matsuoka, T.; Tsuji, T. Singular-value decomposition analysis for seismic interferometry by multidimensional deconvolution. In SEG Technical Program Expanded Abstracts 2011, Proceedings of the 81st Annual International Meeting, San Antonio, TX, USA, 18–23 September 2011; SEG: Tulsa, OK, USA, 2011; pp. 2694–2699. [Google Scholar] [CrossRef]
- Boiero, D.; Bagaini, C. Up and down deconvolution in complex geological scenarios. Geophysics 2020, 86, 1–46. [Google Scholar] [CrossRef]
- van der Neut, J.; Herrmann, F.J. Interferometric redatuming by sparse inversion. Geophys. J. Int. 2012, 192, 666–670. [Google Scholar] [CrossRef][Green Version]
- van der Neut, J.; Ravasi, M.; Liu, Y.; Vasconcelos, I. Target-enclosed seismic imaging. Geophysics 2017, 82, Q53–Q66. [Google Scholar] [CrossRef]
- Luiken, N.; van Leeuwen, T. Seismic wavefield redatuming with regularized multi-dimensional deconvolution. Inverse Probl. 2020, 36, 095010. [Google Scholar] [CrossRef]
- Ravasi, M.; Vasconcelos, I. An open-source framework for the implementation of large-scale integral operators with flexible, modern HPC solutions—Enabling 3D Marchenko imaging by least squares inversion. Geophysics 2021, 86, 1–74. [Google Scholar] [CrossRef]
- van der Neut, J.; Vasconcelos, I.; Wapenaar, K. On Green’s function retrieval by iterative substitution of the coupled Marchenko equations. Geophys. J. Int. 2015, 203, 792–813. [Google Scholar] [CrossRef]
- Ravasi, M. Rayleigh-Marchenko redatuming for target-oriented, true-amplitude imaging. Geophysics 2017, 86, S439–S452. [Google Scholar] [CrossRef]
- Berkhout, A.G. Review Paper: An outlook on the future of seismic imaging, Part I: Forward and reverse modelling. Geophys. Prospect. 2014, 62, 911–930. [Google Scholar] [CrossRef]
- Garg, A.; Sharma, S.; Verschuur, D. Reservoir Elastic Parameters Estimation from Surface Seismic Data Using JMI-res: A Full-Wavefield Approach. In Proceedings of the 80th Annual International Conference and Exhibition, Copenhagen, Denmark, 11–14 June 2018; Extended Abstracts. EAGE: Houten, The Netherlands, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ziolkowski, A.M.; Taylor, D.B.; Johnston, R.J.K. Marine seismic wavefield measurement to remove sea-surface multiples. Geophys. Prospect. 1999, 47, 841–870. [Google Scholar] [CrossRef]
- Wapenaar, K.; Fokkema, J.; Dillen, M.; Scherpenhuijsen, P. One-way acoustic reciprocity and its applications in multiple elimination and time-lapse seismics. In Proceedings of the 70th Annual International Meeting, Calgary, AB, CA, 6–11 August 2000; Expanded Abstracts. SEG: Tulsa, OK, USA, 2000; pp. 2377–2380. [Google Scholar] [CrossRef]
- Wapenaar, K.; van der Neut, J.; Ruigrok, E. Passive seismic interferometry by multidimensional deconvolution. Geophysics 2008, 73, A51–A56. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.; Bale, R.; Grion, S.; Holden, J. The ups and downs of ocean-bottom seismic processing: Applications of wavefield separation and up-down deconvolution. Lead. Edge 2010, 29, 1258–1265. [Google Scholar] [CrossRef]
- Hartstra, I.; Almagro Vidal, C.; Wapenaar, K. Full-field multidimensional deconvolution to retrieve body-wave reflections from sparse passive sources. Geophys. J. Int. 2017, 210, 609–620. [Google Scholar] [CrossRef]
- Boiero, D.; Bagaini, C.; Banerjee, S.; Bloor, R.; Kostov, C.; Caprioli, P.; Zarkhidze, A. What to Do When Up-Down Deconvolution Breaks Down. In Proceedings of the 82th Annual International Conference and Exhibition, Online, 8–11 December 2020; Extended Abstracts. EAGE: Houten, The Netherlands, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Lokshtanov, D. Fast and efficient up-down decomposition and deconvolution for OBS data. In Proceedings of the 82th Annual International Conference and Exhibition, Online, 8–11 December 2020; Extended Abstracts. EAGE: Houten, The Netherlands, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- de Hoop, A.T. Handbook of Radiation and Scattering of Waves: Acoustic Waves in Fluids, Elastic Waves in Solids, Electromagnetic Waves; Academic Press: London, UK, 1995. [Google Scholar]
- Ravasi, M.; Meles, G.; Curtis, A.; Rawlinson, Z.; Yikuo, L. Seismic interferometry by multidimensional deconvolution without wavefield separation. Geophys. J. Int. 2015, 202, 1–16. [Google Scholar] [CrossRef]
- Fishman, L. One-way wave propagation methods in direct and inverse scalar wave propagation modeling. Radio Sci. 1993, 28, 865–876. [Google Scholar] [CrossRef]
- Wapenaar, K. One-way representations of seismic data. Geophys. J. Int. 1996, 127, 178–188. [Google Scholar] [CrossRef][Green Version]
- Wapenaar, K. Reciprocity and Representation Theorems for Flux- and Field-Normalised Decomposed Wave Fields. Adv. Math. Phys. 2020, 2020, 9540135. [Google Scholar] [CrossRef]
- Wapenaar, K.; Fokkema, J. Green’s function representations for seismic interferometry. Geophysics 2006, 71, SI33–SI46. [Google Scholar] [CrossRef]
- Gutknecht, M.H. Block Krylov Space Methods for Linear Systems with Multiple Right-Hand Sides: An Introduction. 2006. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.189.5036 (accessed on 9 July 2021).
- Luiken, N.; van Leeuwen, T.; Garg, A. Block-Krylov methods for multi-dimensional deconvolution. In Proceedings of the 89th Annual International Meeting, San Antonio, TX, USA, 15–20 September 2019; Expanded Abstracts. SEG: Tulsa, OK, USA, 2019; pp. 5070–5074. [Google Scholar] [CrossRef]
- Bauer, F.; Lukas, M.A. Comparing parameter choice methods for regularization of ill-posed problems. Math. Comput. Simul. 2011, 81, 1795–1841. [Google Scholar] [CrossRef]
- Paige, C.C.; Saunders, M.A. LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares. ACM Trans. Math. Softw. 1982, 8, 43–71. [Google Scholar] [CrossRef]
- Ravasi, M.; Vasconcelos, I. PyLops—A linear-operator Python library for scalable algebra and optimization. SoftwareX 2020, 11, 100361. [Google Scholar] [CrossRef]
- Vargas, D.; Vasconcelos, I.; Sripanich, Y.; Ravasi, M. Scattering-based focusing for imaging in highly complex media from band-limited, multi-component data. Geophysics 2021, 86, 1–64. [Google Scholar] [CrossRef]
- Wapenaar, K. Reciprocity properties of one-way propagators. Geophysics 1998, 63, 1795–1798. [Google Scholar] [CrossRef][Green Version]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Kuijpers, D.; Vasconcelos, I.; Putzky, P. Reconstructing missing seismic data using Deep Learning. arXiv 2021, arXiv:2101.09554. [Google Scholar]
- Snieder, R.; Sheiman, J.; Calvert, R. Equivalence of the virtual-source method and wave-field deconvolution in seismic interferometry. Phys. Rev. E 2006, 73, 066620. [Google Scholar] [CrossRef]
- Nakata, N.; Snieder, R. Near-surface weakening in Japan after the 2011 Tohoku-Oki earthquake. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Nakata, N.; Snieder, R. Estimating near-surface shear wave velocities in Japan by applying seismic interferometry to KiK-net data. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Vinnik, L. Detection of waves converted from P to SV in the mantle. Phys. Earth Planet. Inter. 1977, 15, 39–45. [Google Scholar] [CrossRef]
- Ammon, C.J. The isolation of receiver effects from teleseismic P waveforms. Bull.-Seismol. Soc. Am. 1991, 81, 2504–2510. [Google Scholar]
- Galetti, E.; Curtis, A. Generalised receiver functions and seismic interferometry. Tectonophysics 2012, 532–535, 1–26. [Google Scholar] [CrossRef]
- Hennenfent, G.; Herrmann, F.J. Simply denoise: Wavefield reconstruction via jittered undersampling. Geophysics 2008, 73, V19–V28. [Google Scholar] [CrossRef]
- Natterer, F. The Mathematics of Computerized Tomography; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar] [CrossRef]
- Starck, J.L.; Candes, E.; Donoho, D. The curvelet transform for image denoising. IEEE Trans. Image Process. 2002, 11, 670–684. [Google Scholar] [CrossRef] [PubMed]
- Candès, E.; Demanet, L.; Donoho, D.; Ying, L. Fast Discrete Curvelet Transforms. Multiscale Model. Simul. 2006, 5, 861–899. [Google Scholar] [CrossRef]
- Guo, K.; Labate, D. Optimally Sparse Multidimensional Representation Using Shearlets. SIAM J. Math. Anal. 2007, 39, 298–318. [Google Scholar] [CrossRef]
- Fomel, S.; Liu, Y. Seislet transform and seislet frame. Geophysics 2010, 75, V25–V38. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling theory—Part I: Complex signal and scattering in multilayered media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
- Stéphane, M. A Wavelet Tour of Signal Processing, 3rd ed.; Academic Press: Boston, MA, USA, 2009. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- van den Berg, E.; Friedlander, M.P. Probing the Pareto Frontier for Basis Pursuit Solutions. SIAM J. Sci. Comput. 2009, 31, 890–912. [Google Scholar] [CrossRef]

| MDD | U | Q | G | C | Equation | |
|---|---|---|---|---|---|---|
| Two-way | (3) | |||||
| One-way | (4) | |||||
| (5) |
| Opt | Causality | Reciprocity | f-k Filtering | Preconditioner |
|---|---|---|---|---|
| 1 | ||||
| 2 | ∗ | |||
| 3 | ∗ | |||
| 4 | ∗ | |||
| 5 | ∗ | ∗ | ||
| 6 | ∗ | ∗ | ||
| 7 | ∗ | ∗ | ∗ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargas, D.; Vasconcelos, I.; Ravasi, M.; Luiken, N. Time-Domain Multidimensional Deconvolution: A Physically Reliable and Stable Preconditioned Implementation. Remote Sens. 2021, 13, 3683. https://doi.org/10.3390/rs13183683
Vargas D, Vasconcelos I, Ravasi M, Luiken N. Time-Domain Multidimensional Deconvolution: A Physically Reliable and Stable Preconditioned Implementation. Remote Sensing. 2021; 13(18):3683. https://doi.org/10.3390/rs13183683
Chicago/Turabian StyleVargas, David, Ivan Vasconcelos, Matteo Ravasi, and Nick Luiken. 2021. "Time-Domain Multidimensional Deconvolution: A Physically Reliable and Stable Preconditioned Implementation" Remote Sensing 13, no. 18: 3683. https://doi.org/10.3390/rs13183683
APA StyleVargas, D., Vasconcelos, I., Ravasi, M., & Luiken, N. (2021). Time-Domain Multidimensional Deconvolution: A Physically Reliable and Stable Preconditioned Implementation. Remote Sensing, 13(18), 3683. https://doi.org/10.3390/rs13183683