Abstract
We develop a linear inversion technique for measuring the modal composition and directionality of ambient seismic noise. The technique draws from similar techniques used in astrophysics and gravitational-wave physics, and relies on measuring cross-correlations between different seismometer channels in a seismometer array. We characterize the sensitivity and the angular resolution of this technique using a series of simulations and real-world tests. We then apply the technique to data acquired by the three-dimensional seismometer array at the Homestake mine in Lead, SD, to estimate the composition and directionality of the seismic noise at microseism frequencies. We show that, at times of low-microseism amplitudes, noise is dominated by body waves (P and S), while at high-microseism times, the noise is dominated by surface Rayleigh waves.
1. Introduction
There has been much effort in recent decades to understand and exploit the ambient seismic noise wavefield. For example, efforts have been made to understand the generation of noise in the primary and secondary microseims (0.05–0.2 Hz) [1,2,3]. While Rayleigh waves usually dominate observations at these periods, several studies have also specifically observed the generation of Love and body phases [4,5,6,7,8]. These various wavetypes can all be used in the extraction of travel times between two seismic stations, through the calculation of a noise correlation function (NCF) [9,10,11]. While this correlation would result in a true Green’s function between any two stations if the background noise wavefield were perfectly equipartitioned and stationary, this is clearly not the case in the real Earth [9,10,11].
Most studies have located these sources of noise through classic beamforming techniques [12,13]. Such methods perform a grid search over possible incident plane waves, testing different directions and slownesses by applying a time shift to observed signals and then either summing or correlating. Although exceptions exist [14], these methods are generally not posed as a misfit-reduction inverse problem and thus uncertainties can be difficult to quantify. Additionally, generally, only the vertical component of motion is used, though some more recent works have incorporated three-component observations and added constraints on polarization and ellipticity to distinguish wavetypes [5,15,16,17,18,19]. Such a separation is ultimately necessary to understand how the ambient noise wavefield is actually excited and generated, but understanding the content of the seismic wavefield is important in other contexts as well. For example, knowing the appropriate ratios of wave energy is needed for proper modeling of horizontal-to-vertical ratios in certain near-surface tomography methods [20], and the local amplification of seismic waves from strong earthquakes can also be quite different for various wavetypes [21,22,23]. Similarly, understanding the energy distribution across different modes is critical for estimating the fluctuations in the local gravitational field, which is relevant for multiple applications including the development of gravitational-wave detectors [24].
While the beamforming methods above search for possible plane waves from distant sources, some authors have employed Backprojection or Matched Field Processing methods to test for noise sources distributed on some defined spatial domain (i.e., the Earth’s surface) [25,26]. Again, these methods are based on a grid search and the application of timeshifts to the raw data, and may incorporate three-component data to constrain the wavetype [27]. Concurrently, methods have been explored which solve for the spatial distribution of noise sources in a mathematically rigorous inverse problem [28,29,30,31], again potentially including multicomponent information [32]. While promising, these methods require significant computational power, as the problem is nonlinear and synthetic noise-correlation waveforms must be calculated for each realization of a noise model.
Linear inversion of the NCF has been explored in the past—for example, in [33,34,35,36]. Here, we expand on this approach, allowing it to be used in three-dimensional seismometer array configurations and enabling simultaneous recovery of multiple wave-mode contributions such as P and S body waves and Rayleigh and Love surface waves. Specifically, we follow the radiometer formalism that has proven successful in astrophysics and gravitational-wave physics [37] and adjust it to the framework of seismic wave fields and to observations by (3D or 2D) seismometer arrays. The ability to use 3D arrays allows us to take advantage of the depth dependence of surface wave modes, hence improving the ability to distinguish between different mode contributions. However, the method and formalism are still complete for the case of a 2D array. The technique is based on computing the cross-correlations between different seismometer channels in the seismometer array. The phase information in the cross-correlation and its dependence on the depths of the seismometers can then be used to decompose the field into a superposition of body (P and S) and surface (Rayleigh, Love) waves. We develop a Bayesian inference framework to perform this decomposition (or inversion) and we conduct a series of synthetic and real-world tests of the technique to assess its sensitivity and angular resolution. We then apply the technique to the data acquired by the three-dimensional seismometer array operated in the Homestake mine in Lead, SD, in 2014–2016, to answer a specific question: what is the composition and directionality of the microseism and its temporal variation? We find that, at quiet times, the microseism noise at Homestake is dominated by body waves, while at loud times, it is dominated by surface waves.
The remainder of this paper is organized as follows: in Section 2, we introduce the mathematical formalism for the linear inversion technique; in Section 3, we discuss the performance of the technique using a series of simulations and a real-world test of our technique using an anthropogenic signal observed by the Homestake Seismic Array; in Section 4, we apply the technique to the Homestake data to understand the composition of the microseism noise at Homestake; in Section 5, we offer our concluding remarks.
2. Formalism
The radiometer formalism has been used in different fields when attempting to estimate the directional structure in a wave field. We start from the formalism developed for measuring anisotropy (directionality) in the gravitational-wave energy density, and adjust it to account for the different modal composition of the seismic wave field and for the different response of the measuring instruments (seismometers in our case) [37,38,39,40,41]. While the formalism is general enough to treat all wave modes (primary pressure (P), secondary shear (S), Rayleigh (R), Love (L)), there are differences in the implementation that we discuss here. Our analysis follows the development presented in [40,41].
2.1. Body-Wave Formalism
We begin by assuming that seismic sources are far away from the measurement locations and that they are constant in power during the measurement period. Under the additional assumption that the seismic structure is homogeneous and isotropic, the seismic displacement field can be modeled as a plane-wave expansion:
Here, m specifies the body-wave component of the seismic field (i.e., P or S waves), A denotes the polarization of the wave, is a unit vector (on the unit sphere) that denotes the wave propagation direction, and is a polarization vector for a wave of polarization A traveling in the direction , as depicted in Figure 1. Note that for a longitudinal P wave, , and there is only one polarization. For S waves, the displacement is perpendicular to and there are two polarization vectors. The phase velocity of mode m is given by . We denote the Fourier amplitude in mode m at frequency f traveling in direction with . We use f throughout, although it also common to formulate such methods in terms of the angular frequency as well. Equation (1) thus modestly generalizes the framework of [34] to include polarizations. We note that this formalism does not account for free-surface effects [42,43] but could be modified to do so.
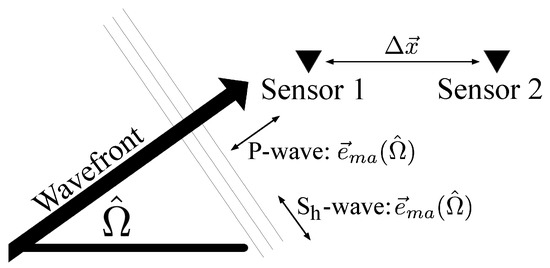
Figure 1.
Plane waves from a possible source direction, , arrive at two sensors shown in 2D. The plane wave is described for a given wave type, m, and polarization, A, with polarization vector . This is a simplified 2D example meant to illustrate the notation that we use in Section 2.1; in 3D, two angles are needed to describe the propagation direction, .
We then define a two-point frequency-domain correlation function, assuming that waves of different modes, directions, polarizations, and frequencies are uncorrelated [34,35]
Here, denotes complex conjugation, denotes the Kronecker delta function (=1 if , and 0 otherwise), while denotes the Dirac delta function. In particular, denotes a two-dimensional Dirac delta function on the sphere, which, in spherical coordinates, can be written as . Further, is the displacement power spectrum of mode m, polarization A, at linear frequency f propagating in the direction . It therefore has units of . The brackets denote taking the expectation value, i.e., averaging over many realizations of the seismic wave field. As discussed below, this assumption may fail in real-world situations—for example, due to surface reflection that may introduce correlations between different wave modes/directions. Furthermore, the assumption may also fail for transient events, such as earthquakes and mine blasts.
The displacement time series observed in channel (denoting East, North, or vertical) of a seismometer i located at is given by
where denotes the unit vector in the -direction. We then define the time-domain cross-correlation between the displacement time-series of two channels of two physically separated seismometers as
where T is the duration of data considered. Inserting Equation (1) for the plane-wave expansion of each channel and then using the delta functions in Equation (2) to evaluate some of the sums and integrals yields
Here, we adopt the notation where Latin indices denote seismometers and Greek indices denote seismometer channels, and denotes the vector pointing between the two seismometers.
Defining as the Fourier coefficient of then
This expression allows us to explicitly measure the frequency dependence of the seismic displacement power spectrum. Note that is included on both sides of Equation (6) to account for integrating over a small but finite frequency band centered at f, and that is the cross-correlation evaluated at zero time lag.
In practice, we calculate by taking the complex cross-correlation between the two data streams:
where is calculated using a fast Fourier transform over duration T. The assumption that is constant, which we have made throughout, is reasonable as long as is sufficiently small.
To measure the directional content of the power spectrum, we expand it into a set of basis vectors . One common choice that is suitable for describing extended structures is the spherical harmonics basis, . In this paper, we will use the pixel basis on the sphere, a set of Dirac delta functions in different directions corresponding to seismic point sources: . The displacement power spectrum can then be written as
Our objective will therefore be to estimate the coefficients , which, in the pixel basis, have units of (because the basis functions carry units of ). Substituting this expansion into Equation (6) yields
where repeated indices are summed over and we have defined the “overlap reduction functions” between different seismometer channels, and , for basis vectors a, seismic modes m, and polarizations A, as
These factors, , are purely geometrical and codify how seismic waves of specific direction, mode, polarization, and frequency are mapped into the cross-correlation between two channels of two spatially separated seismometers. If we view Equation (9) as a linear algebra problem, the task of estimating the amplitude coefficients is reduced to inverting the matrix of factors. It is therefore possible to simultaneously estimate the contributions of body wave modes with different polarizations, which represents a departure from past work on methods of this kind [14,34,35]. If the matrix does not have full column rank, which will be common in practical applications, approximate solutions are necessary. We discuss these practical issues in Section 2.3 and Section 3, including the effects that aperture size, array design, and cross-talk between wave-modes have on our ability to carry out the method in practice.
2.2. Surface-Wave Formalism
The formalism for seismic surface waves is similar to the body wave case, but it takes into account the depth dependence of the surface-wave amplitude. To describe the decay of amplitude with depth, we follow the approach of [44,45], where the fundamental-mode depth dependence is described by a bi-exponential model for the horizontal and vertical components of the Rayleigh waves ( and , respectively) and by a single-exponential model for the Love waves ().
The plane-wave expansion for Rayleigh and Love waves is then:
Note that the factor of imposes the retrograde motion that is characteristic of Rayleigh waves, and the sign between the horizontal and vertical Rayleigh components follows the same convention as in [45]. The wave propagation direction, , is assumed to be confined to the horizontal plane, and the Love displacement is assumed to be in the horizontal direction perpendicular to , denoted by .
Following similar steps as in the body wave case, we can again relate the cross-correlation between two channels of two seismometers and the Rayleigh or Love seismic displacement power spectra expanded in the pixel basis, similar to Equation (9). The corresponding Rayleigh and Love overlap reduction functions are:
where and are used to indicate the depth at which the i and j sensors are located, respectively. Because the functions and are normalized such that , the interpretation of the recovered Rayleigh-wave (henceforth ‘R-wave’) maps shown below should be that they represent the longitudinal (horizontal) amplitude induced by the R wave at the surface. Other directions and other depths can then be inferred using the Rayleigh-wave eigenfunctions themselves.
Throughout the rest of this paper, we use the bi-exponential models, and , and the single-exponential model, , that were measured explicitly for the Homestake seismometer array using mine-blast studies [45]. In the situation where all stations are located on the surface, this reduces to specifying the horizontal-to-vertical displacement ratio.
2.3. Inversion Approach and Map Making
Equation (9) relates the cross-correlation expectation values for seismometer channel pairs to the seismic displacement power at a given frequency, mode, polarization, and direction: . Our objective is to estimate the coefficients from the cross-correlation measurements for different seismometer channel pairs. To do so, we will develop a Bayesian parameter estimation framework, which, to our knowledge, is a novel approach in seismic interferometry (NCF) inversion studies. We follow the approach used in gravitational-wave astrophysics [38,39] and construct a log-likelihood function, starting with a single mode for simplicity and assuming pairs of seismometer channels:
Here, is a matrix containing the frequency-domain complex cross-correlation for each pair of channels, calculated using Equation (7). is a matrix of overlap reduction function values for a single wave mode (we discuss the case of multiple wave modes below), where stands for the number of basis elements used in the pixel decomposition. is a matrix whose elements represent the displacement power associated with a specific basis element (pixel) for a seismic field mode m that we aim to estimate (i.e., this is a matrix representation of the coefficients). is the instrument noise covariance matrix. Under the assumption that the instrument noise level in each channel is the same and is uncorrelated between different instruments and channels, then is proportional to the identity matrix. Note that we use the superscript “†” to indicate the hermitian conjugate of a matrix. In our analysis below, we will assume uniform prior distributions for coefficients so that finding the maximum of the posterior distributions reduces to the problem of likelihood maximization. Maximizing this likelihood function leads to the following estimator for :
We can also rewrite Equation (15) using a Cholesky decomposition on , i.e., we write where is a lower-triangular matrix. We can then define and and rewrite our maximum likelihood expression
where we have defined the pseudo-inverse of , denoted by . If the Fisher information matrix is invertible, this expression is exact. However, it is very likely that is singular. This indicates that does not have full column rank, and so there are either fewer data points (pairs of channels) than the basis elements that we are trying to measure or there are directions to which we are not sensitive.
There are many ways of finding approximate solutions to this expression when is not invertible [46,47]. We opt to construct a regularized pseudo-inverse matrix using a singular value decomposition (SVD) [41]. The SVD approach allows us to regularize the inverse matrix by manually setting to zero any singular values that are smaller than some minimum . The choice of is important: small values of will increase the variance of the estimator while large values of will reduce the variance but increase the number of null directions and the spread of a point source on the two-sphere.
It will also be useful to define the “model resolution matrix,” :
quantifies the bias due to the regularized pseudo-inverse that we have constructed (and is the identity matrix when is invertible). The columns of depict the spread on the two-sphere corresponding to a single-pixel seismic source of unity amplitude [41].
The formalism can be extended to recover multiple modes of the seismic field simultaneously by stacking the matrices for different modes. For example, if we want to recover maps for P and R waves simultaneously, then our new matrix in Equation (15) becomes
and becomes a column matrix of length with maps for each mode stacked on top of one another ( in our example of P and R waves only).
All calculations in this paper use the HEALPix [48] formalism for pixelating the two-sphere—in particular, using the healpy (https://github.com/healpy/healpy accessed on 30 July 2021) python package. As such, the number of pixels is constrained to , where is an integer power of two.
3. Performance Assessment
3.1. Performance Assessment Using Simulations
To assess the performance of the formalism presented above, we first conduct a series of illustrative simulations which are meant to test the method, but not necessarily mimic realistic situations. We assume a seismometer array with station distribution identical to that of the Homestake array. The Homestake seismometer array was introduced in detail in [49]. The array consisted of 24 seismic stations, 15 underground and 9 surface stations, deployed in and around the old Homestake mine in Lead, South Dakota. The underground stations were operated between December 2014 and December 2016, while surface stations were operated between May 2015 and September 2016. The horizontal span of the array was approximately 5 km, while the vertical span was approximately 1.5 km. A map of the array can be found in Figure 1 of [49], and a 3D rendering of the array can be found in the electronic Supplementary Material of that work.
The underground stations were scattered across several levels: one at a depth of 300 ft (91 m), one at 800 ft (244 m), one at 1700 ft (518 m), five at 2000 ft (610 m), three at 4100 ft (1250 m), and four at 4850 ft (1478 m). The locations of these stations were chosen to maximize the horizontal aperture of the underground part of the array within the constraints imposed by safe access, availability of power, and access to the fiber optic network. The horizontal aperture size for the sensors deployed underground was roughly 1 km. Six of the surface stations were located directly above the underground extent of the mine, while the remaining three were located several km away to enlarge the horizontal extent of the array.
Most stations operated Streckheisen STS-2 high-sensitivity broadband seismometers. The exceptions were the underground station on the 300 ft level and three surface stations, where the more water-resistant Guralp CMG-3T seismometers were deployed. Each underground station was oriented using Octans instruments and synchronized through the fiber optic network to a master GPS signal from the surface, while the surface stations were oriented and synchronized using the GPS. The seismic equipment was provided by the Portable Array Seismic Studies of the Continental Lithosphere (PASSCAL) instrument center, which is a part of the Incorporated Research Institutions for Seismology (IRIS). Further details on the installation and operation of the Homestake seismometer array can be found in [49].
For synthetic performance tests, we generate a 1 Hz sinusoidal time-series with amplitude m for different components of the seismic field (i.e., for different wave modes and propagation directions). The simulations do not include seismometer instrument noise or other potential confusion noise, such as scattering or inelastic processes within the array itself, as we expect these sources of noise to be at least an order of magnitude lower than the ambient seismic field. For each station and for each simulated signal, we apply a phase delay consistent with the travel time to that station from the respective propagation direction. Finally, at each station, we compute the displacement projections of each simulated wave to the N, E, and vertical channels of the seismometer.
We simulate 200 s of data and divide them into four 50 s segments. We compute Fourier transforms of each seismometer channel in each segment, multiply the transforms for any two channel pairs, average the products over the four segments, and finally multiply by the frequency bin width (0.02 Hz) to obtain units of . This represents our estimates of the cross-correlation spectra between channel pairs, which we use in Equation (17).
Likelihood maximization then produces the maps of the directionality of seismic wave sources for each wave mode. To estimate the recovered amplitude, we identify peaks in the map and sum up the power in all pixels associated with each peak.
To start, we investigate the importance of , which is used in constructing the pseudo-inverse in Equation (18). We simulate a single-plane P wave, for simplicity, chosen to propagate in the direction corresponding to the center of the recovery map—its true decomposition is given by , which contains a single non-zero entry associated with the propagation direction of the wave. Figure 2 shows and the corresponding P-wave maximum likelihood recovery map, , as a function of . For small values of , the noise in the recovery map is high and we cannot recover the signal. This is because very small values of allow the inclusion of null or near-null directions, hence contributing noise in the recovered map. This noise does not exist when multiplying by because, outside of a single pixel, all other values of are zero. As we increase , the simulated signal emerges, the recovered spot size increases, and its significance with respect to the other pixels in the map grows as well. This exemplifies the trade-off between the covariance and the angular resolution of the recovery, originating from the fact that our system is underdetermined (i.e., ).
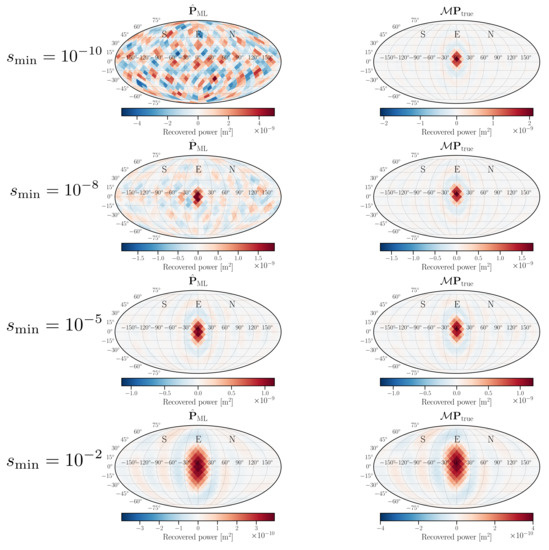
Figure 2.
Left column shows the maximum likelihood recovery for a simulated P-wave injection, . Right column shows the model resolution matrix of the P-wave overlap reduction function, plotted as a map, . Each row represents a different choice of . We see that as the spot size in the model resolution plots increases, the covariance in each pixel decreases. In these maps, 0 in the azimuthal coordinate corresponds to eastward propagation, while 90 corresponds to northward propagation.
We note that in this simple, single-mode simulation and recovery, the position is recovered correctly, and the simulated signal power is within 5%. For this example, the value of makes a negligible difference in the recovered total power in the map. In general, the choice of is dependent upon the frequency at which the recovery is performed, and the wave modes included in the recovery. For this reason, we do not offer a systematic study for a general choice of .
The angular resolution is ultimately limited by the diffraction limit of the array (instrument) used in the measurement, roughly given by:
where d is the projected distance between stations and is the wavelength. More accurately, we can estimate the resolution for our array by producing , where corresponds to an east-propagating wave for wave type m. The SVD cutoff in this case is for all cases. We draw a contour around the region containing 95% of the total map power and find the maximum extent in the azimuthal and polar angles of the contour. The resolution as a function of wavelength, along with the diffraction limit estimate, is shown in Figure 3. We observe better resolution in the azimuthal angle than in the polar angle because the Homestake array is only ∼1.5 deep but is ∼5 wide. Figure 3 shows that for small wavelengths, the angular resolution is well approximated by Equation (21). At relatively long wavelengths, the angular resolution is better than that predicted by Equation (21)—this is because the polarization information of the recovered wave also carries directional information (in addition to time delays between stations, which ultimately define the diffraction limit).
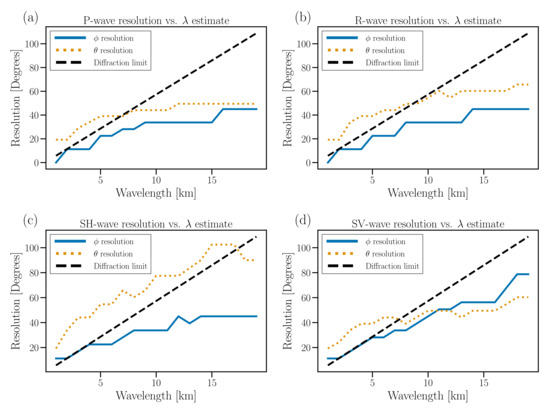
Figure 3.
An estimate of the angular resolution for the different components of the seismic field based on (see text) for P, R , and waves (a–d). The resolution is estimated by drawing a contour around the region containing 95% of the total map power and finding the extent in the azimuth () and polar () angle that this contour encompasses. We also show the diffraction limit estimate on each plot.
While the angular resolution is determined by the interplay of the aperture of the seismic array, wavelength, and modal content of the wave, the situation is further complicated in situations when multiple waves are present. Figure 4 shows the recovery of two point sources of P waves. When simulating each of the two waves alone, our method recovers correctly both the direction and the amplitude of the wave (c.f. Figure 2). However, when simulating the two waves simultaneously, the method recovers successfully both wave directions, but the total recovered power is , which is larger than what one would naively expect if the waves from different directions were uncorrelated. This comes from the fact that the formalism assumes waves of different modes and directions to be uncorrelated (c.f. Equation (2)), which is not the case in our simulation: we have simulated two sinusoidal waves with different propagation directions and with a fixed phase difference between them, making the two waves highly correlated (the level of correlation between them is direction-dependent). This simulation hence illustrates a limitation of our inversion technique, i.e., its assumption that seismic waves from different directions and of different modes are uncorrelated. If one takes into account the total coherent power from the two waves in each channel, then 95% of the total injected power in the map would be , which is very close to what is recovered.
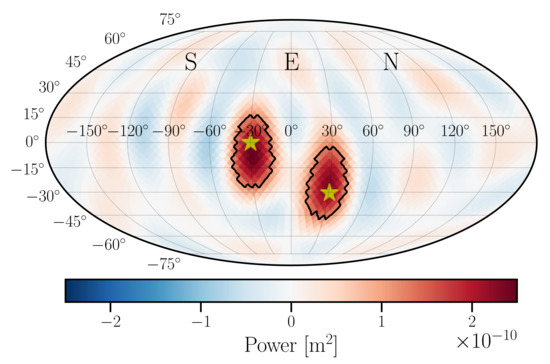
Figure 4.
Recovery of two pressure waves is shown, with their true propagation directions indicated by stars. The contours, defined to enclose 95% of the total power, amount to the total recovered power of , as compared to the simulated . This discrepancy is caused by the coherence between the two signals, breaking one of the underlying assumptions of our inversion technique.
Finally, in Figure 5, we show recovery in the case where we have simulated P, , and R waves in different directions, and try to recover all three at once ( wave mode was not simulated, but it was included in the recovery analysis). We successfully identify the presence of each of the three modes, with correct propagation direction. The total recovered power is biased, however, due to “cross-talk” between the different modes. The simulated power was uniform for all three signals, while the total power in the R-wave map was ; for the P-wave map, it is , and for the S-wave map, it is . These biases once again stem from the violation of the assumption of uncorrelated waves of different modes and directions: each of the three simulated signals is a sine-wave, and their phase differences are constant in time. While realistic wave fields are likely to be more complex, with different modes generally characterized with different wavelength compositions and with non-stationary phase differences, hence better obeying the underlying assumptions of our inversion technique, it is important to keep these limitations in mind when applying the formalism to real data.
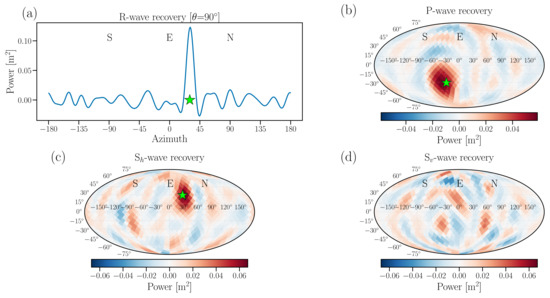
Figure 5.
(a–d) R-, P-, -, -wave recoveries. R, P, and S waves are simultaneously simulated with different propagation directions and are successfully recovered (no wave was simulated). The total recovered power is biased: the simulated power was uniform for all three signals, while the total power in the R-wave map was ; for the P-wave map, it is , and for the S-wave map, it is . Adding the power across all four maps yields a total amplitude of , which is larger than what one would expect if all injections were uncorrelated. We assumed , , and .
3.2. Performance Assessment Using Homestake Data
We now study the performance of our inversion method using the data acquired by the Homestake array. A strong source of seismic waves at 1.4–1.6 is observed by multiple stations in the Homestake seismometer array, most prominently in the surface stations. The source is on intermittently during the day, lasting for several hours at a time, suggesting an anthropogenic source. The phase between the vertical and horizontal channels for these stations suggests that this signal is dominated by Rayleigh waves, as shown in Figure 6.
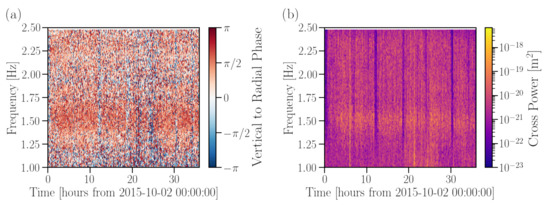
Figure 6.
(a) Vertical-to-horizontal phase between the east and the vertical channels of the YATES station is shown for 36 h starting from 2 October 2015. (b) Cross-power between the vertical and east channels of YATES station. The signal at 1.4–1.6 Hz appears at the 1 h mark, and its phase hovers near radians, consistent with the retrograde motion in Rayleigh waves. This signal is clearly a peak in the spectrum, as seen on the right.
We use the surface stations YATES, ROSS, ORO, DEAD, TPK, and the station at 300 ft depth to perform a simple phase delay analysis to determine the direction of the incoming Rayleigh wave. We use 1 h of data starting from 2 October 2015 03:00 UTC, split into 100 s segments, and compute the phase of the complex cross-correlation between each channel pair of these stations at 1.5 Hz. We then compare the phase to the modeled phase:
where depicts the wave propagation direction (with corresponding to eastward propagation), are the locations of the two stations, and v is the Rayleigh wave speed that was studied and measured in [45,50]. The comparison is performed using a likelihood maximization method, yielding the preferred wave propagation direction , i.e., nearly eastward propagation.
We next apply our inversion technique to the cross-correlations averaged over the same data period. Figure 7 shows the results of the recovery assuming R and P waves only. We observe clear evidence for R waves propagating in the eastward direction, consistent with the above timing-only analysis. The total power in each map is for P waves, and for R waves, providing strong evidence for R waves. Additional snapshots from a day with particularly strong background noise and particularly weak background noise are shown in the Supplementary Material.
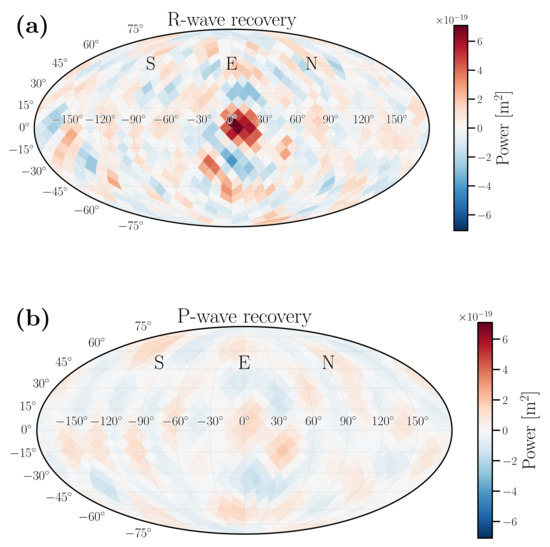
Figure 7.
Recovery of 1.5 Hz source from 2 October 03:00–04:00 UTC for Rayleigh waves (a), and P waves (b). We see that there is a strong peak between 0 and 30 for R waves, while for P waves, there is no obviously preferred direction. Note that we plot the R-wave recovery in 2D, even though only one (azimuthal) angle defines the wave propagation direction. This is done as a cross-check—if incorrect R-wave phase velocity is used in the recovery, the recovered spot could appear off the x-axis in this plot.
4. Microseism Noise Composition at Homestake
We now apply our formalism to study the seismic noise field at Homestake. In particular, we will examine the modal composition and directionality of oceanic microseism. In a past publication, we have shown evidence based on coherence across different seismic stations that when microseism is weak, the seismic field at low frequencies (0.2–0.4 Hz) appears to be dominated by body waves, while when microseism is strong, Rayleigh waves appear to dominate [50]. However, the evidence provided was indirect, as it was based on evaluating how quickly the coherence between stations drops off as a function of distance (i.e., more quickly for Rayleigh waves, less quickly for body waves), and did not attempt to directly estimate the various noise amplitudes. We now apply our linear inversion technique to measure the contribution of each mode and to estimate its propagation direction, with a specific goal of confirming or rejecting the previous suggestion. For this study, we only perform recoveries using R waves, P waves, and S waves. In future analyses, we plan to include Love waves as well.
We analyze 256 days of data between 2 June 2015 and 23 February 2016. We calculate 128 s Hanning-windowed Fourier transforms and use these to generate inter-station and inter-channel cross-spectral densities, which we evaluate at 0.2 Hz. For the inversion, we assume velocities of for R waves, for P waves, and for S waves, based on past studies of velocities and Rayleigh eigenfunctions [45,50]. We average together 45 of the 128 s cross-spectral densities and use the resulting spectrum estimated from 1.6 h worth of data as when performing the recoveries. We assume that the instrument noise covariance matrix, , is proportional to the identity matrix, and thus drops out of Equation (16). We repeat this process for all available chunks of data. We choose , although we repeated the same procedure with , 0.001, and 0.0005, over a 30-day period and, when considering total map power for each wave mode, found nearly identical results to those found with . We are interested in the long-term properties of the oceanic microseism, as opposed to the directionality of the seismic field at any individual time. Therefore, we sum over all directions in the R-wave maps and body-wave maps separately, to estimate the total power in R waves and body waves at each time. To give an idea of what the directional recoveries look like, we show examples of recovery maps for R, P, and S waves for a time period dominated by R waves in Figure S1 and for a time period dominated by body waves in Figure S2.
In Figure 8a, we compare the ratio of total recovered power in body waves to recovered power in R waves (blue, solid) to the total power across all recovered maps (orange, dashed) for all available data. Both curves show clear seasonal trends. The total power is larger in winter than in summer, while the opposite is true for the ratio of body to R waves. During the summer, the oceanic microseism is dominated by body waves, while in winter, the contribution of R waves is comparable. In Figure 8b, we show the same as Figure 8a, for only days 100–150 (roughly September through October 2015). There is clear anti-correlation between the total power and the ratio of body waves to R waves, as well as variability on a roughly 7-day timescale. The variability is present in the recovered power for both R waves and body waves, but is more pronounced in R waves than in body waves (leading to the anti-correlation in their ratio shown in Figure 8b). This variability is likely caused by storms or other weather variability that occur on 5–10-day timescales [51]. There is no corresponding trend when comparing the individual S- and P-wave contributions over the course of these data.
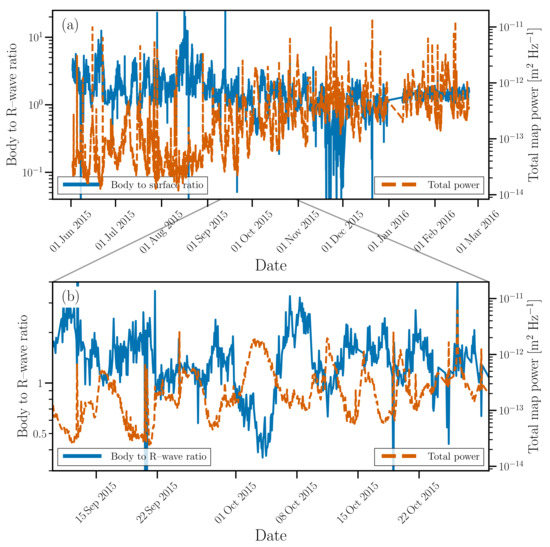
Figure 8.
(a) Ratio of body-wave to R-wave power (blue solid) and total map power (orange, dashed). There is an obvious seasonal shift in total map power that corresponds to a decrease in the ratio of body waves to surface waves. In (b), we zoom in on fifty days. There is evident variability on a ∼7-day time-scale, and anti-correlation between total map power and the ratio of body waves to R waves. The variability is likely due to storms, which cause an increase in surface wave amplitude and hence an increase in total power and corresponding decrease in the ratio of body waves to R waves.
These results demonstrate that there is strong temporal variability in the relative contributions of body waves and surface waves at Homestake. Surface waves generally dominate the total power when the 0.2 Hz microseism is strongly observed at Homestake, as is expected based on other studies of ocean microseism using ambient noise correlations (e.g., [1,31,52]). However, unexpectedly, body waves dominate the total power when the 0.2 Hz microseism is weak, potentially because the 0.2 Hz surface waves during such times are sufficiently damped by attenuation along the long continental path to Homestake, located in the continental interior in South Dakota. (The Great Lakes, to the northeast, and do not contribute to the signals we observe, as they are not large enough and do not support wind-generated lake microseism at the 5 s period that we are considering [53].) This dominance of body waves that anti-correlates with short-period microseism power is consistent with previous indirect inferences that body waves may dominate during quiet times at Homestake [50]. Our findings suggest that body waves may be more prevalent at short-period microseism periods than previously expected, particularly in interior continental settings with long attenuation distances for ocean microseism sources. This in turn has significant implications for the wave-field content of ambient noise correlations in such locales and how such data should be interpreted. With short-period microseism in the continental interior, the common assumption that correlations are dominated by fundamental-mode surface waves (e.g., [54]) may need to be reconsidered.
5. Conclusions
In this paper, we have introduced a linear inversion technique to study the modal composition and the directionality of the ambient seismic field. The technique is based on measuring cross-correlations between seismometer channels in a three-dimensional seismometer array, and uses the phase, polarization, and depth information in the cross-correlations to disentangle contributions from different wave modes propagating in different directions.
We have shown that the technique can be used to measure the contribution of all (body, surface) wave modes simultaneously. While, for short wavelengths, the angular resolution of this technique is limited by the diffraction limit of the seismometer array, for long wavelengths, it is possible to surpass the diffraction limit by taking advantage of the polarization and depth information in the data.
It is also important to emphasize some of the limitations of this technique. First, the technique is based on plane-wave decomposition of the seismic wave field, and is therefore applicable in situations when the seismic sources are far away (far relative to the wavelength). In the presence of local seismic sources (that emit, e.g., spherically outgoing waves), the technique may lead to misestimates of the seismic field content. Second, the technique also assumes that waves of different modes propagating in different directions are uncorrelated. In practice, this assumption could be broken due to scattering and reflection. As indicated in our simulations, this effect is likely to lead to leakage in the estimates from one wave mode to another. The severity of this effect will depend on the complexity of the noise field that is being measured, and on the level of scattering and reflection in the observed environment. On the other hand, the formalism introduced here allows for the inclusion of more complex seismic field models that may accommodate the complexities of the local environment. As a concrete example, introducing the depth-dependent Rayleigh/Love seismic field model has boosted the sensitivity of our analysis and enabled us to better separate the body and surface wave contributions.
We have demonstrated the technique using the data acquired by the three-dimensional Homestake seismometer array. We have shown that the technique can be used to study both anthropogenic noise sources and to understand the composition of the microseism as a function of time. For short-period (0.2 Hz) microseism, our linear inversion results clearly indicate that body waves dominate surface waves when the total microseism power is weak in South Dakota, consistent with previous indirect inferences [50]. This result suggests that short-period microseism in interior continental settings may generally be more strongly dominated by body waves than previously thought. While our analyses have focused on using a single frequency bin, there is potential to improve on the overall sensitivity of the technique by combining measurements from multiple frequency bins.
We anticipate the technique to be of broader use in a variety of studies involving seismic noise, including its temporal variability and microseismicity and its composition, anthropogenic contributions, site amplification effects, and many others.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs13163097/s1, Figure S1: Recovery of seismic field during time period dominated by R waves, Figure S2: Recovery of seismic field during time period dominated by body waves.
Author Contributions
Conceptualization, P.M.M., T.P., V.M., V.C.T. and D.C.B.; Data curation, P.M.M., T.P., V.M., V.C.T., D.C.B., G.P. and R.C.; Formal analysis, P.M.M., T.P., V.M., V.C.T., and D.C.B.; Funding acquisition, V.M., V.C.T. and G.P.; Methodology, P.M.M., T.P., V.M., V.C.T., D.C.B. and A.M.; Software, P.M.M., T.P., D.C.B., and A.M.; Writing—original draft, P.M.M., V.M., V.C.T. and D.C.B.; Writing—review & editing, P.M.M., T.P., V.M., V.C.T., D.C.B., A.M., G.P. and R.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Science Foundation INSPIRE grant PHY1344265. Parts of this research were conducted by the Australian Research Council Centre of Excellence for Gravitational Wave Discovery (OzGrav), through project number CE170100004.
Data Availability Statement
Data used in this project are available from the Incorporated Research Institutions for Seismology (IRIS) [49]. Software that implements the formalism we have presented can be found at https://github.com/meyers-academic/seismic_radiometer (accessed on 30 July 2021).
Acknowledgments
Data used in this project are available from the Incorporated Research Institutions for Seismology (IRIS) [49]. The seismic instruments used for this array were provided by IRIS through the PASSCAL Instrument Center at New Mexico Tech. We thank the staff at the Sanford Underground Research Facility and PASSCAL for assistance, particularly the help of Tom Regan, Jaret Heise, Jamey Tollefson, and Bryce Pietzyk. This work was supported by National Science Foundation INSPIRE grant PHY1344265. This paper has been assigned LIGO document number LIGO-P2000219. Parts of this research were conducted by the Australian Research Council Centre of Excellence for Gravitational Wave Discovery (OzGrav), through project number CE170100004.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Gerstoft, P.; Tanimoto, T. A year of microseisms in southern California. Geophys. Res. Lett. 2007, 34, 2–7. [Google Scholar] [CrossRef] [Green Version]
- Kedar, S.; Longuet-Higgins, M.; Webb, F.; Graham, N.; Clayton, R.; Jones, C. The origin of deep ocean microseisms in the North Atlantic Ocean. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 777–793. [Google Scholar] [CrossRef]
- Ardhuin, F.; Herbers, T.H. Noise generation in the solid Earth, oceans and atmosphere, from nonlinear interacting surface gravity waves in finite depth. J. Fluid Mech. 2013, 716, 316–348. [Google Scholar] [CrossRef] [Green Version]
- Landés, M.; Hubans, F.; Shapiro, N.M.; Paul, A.; Campillo, M. Origin of deep ocean microseisms by using teleseismic body waves. J. Geophys. Res. Solid Earth 2010, 115, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Juretzek, C.; Hadziioannou, C. Where do ocean microseisms come from? A study of Love-to-Rayleigh wave ratios. J. Geophys. Res. Solid Earth 2016, 121, 6741–6756. [Google Scholar] [CrossRef] [Green Version]
- Nishida, K.; Takagi, R. Teleseismic S Wave Microseisms. Science 2016, 353, 919–921. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Koper, K.D.; Burlacu, R.; Ni, S.; Wang, F.; Zou, C.; Wei, Y.; Gal, M.; Reading, A.M. Source locations of teleseismic P, SV, and SH waves observed in microseisms recorded by a large aperture seismic array in China. Earth Planet. Sci. Lett. 2016, 449, 39–47. [Google Scholar] [CrossRef]
- Ward Neale, J.; Harmon, N.; Srokosz, M. Improving Microseismic P Wave Source Location With Multiple Seismic Arrays. J. Geophys. Res. Solid Earth 2018, 123, 476–492. [Google Scholar] [CrossRef] [Green Version]
- Lobkis, O.I.; Weaver, R.L. On the emergence of the Green’s function in the correlations of a diffuse field. J. Acoust. Soc. Am. 2001, 110, 3011. [Google Scholar] [CrossRef] [Green Version]
- Shapiro, N.M.; Campillo, M.; Stehly, L.; Ritzwoller, M.H. High-resolution surface-wave tomography from ambient seismic noise. Science 2005, 307, 1615–1618. [Google Scholar] [CrossRef] [Green Version]
- Tsai, V.C. On establishing the accuracy of noise tomography travel-time measurements in a realistic medium. Geophys. J. Int. 2009, 178, 1555–1564. [Google Scholar] [CrossRef] [Green Version]
- Van Veen, B.D.; Buckley, K.M. Beamforming: A Versatile Approach to Spatial Filtering. IEEE ASSP Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef]
- Rost, S.; Thomas, C. Array seismology: Methods and applications. Rev. Geophys. 2002, 40, 2-1–2-27. [Google Scholar] [CrossRef] [Green Version]
- Lehujeur, M.; Maggi, A.; Schmittbuhl, J. Ambient noise tomography with non-uniform noise sources and low aperture networks: Case study of deep geothermal reservoirs in northern Alsace, France. Geophys. J. Int. 2017, 208, 193–210. [Google Scholar] [CrossRef]
- Esmersoy, C.; Cormier, V.F.; Toksoz, M.N. Three-component array processing. VELA Program Twenty-Five Year Rev. Basic Res. 1985, 78, 1725–1743. [Google Scholar]
- Jurkevics, A. Polarization analysis of three-component array data. Bull. Seismol. Soc. Am. 1988, 78, 1725–1743. [Google Scholar]
- Wagner, G.S. Resolving diversely polarized, superimposed signals in three-component seismic array data. Geophys. Res. Lett. 1996, 23, 1837–1840. [Google Scholar] [CrossRef]
- Riahi, N.; Bokelmann, G.; Sala, P.; Saenger, E.H. Time-lapse analysis of ambient surface wave anisotropy: A three-component array study above an underground gas storage. J. Geophys. Res. Solid Earth 2013, 118, 5339–5351. [Google Scholar] [CrossRef]
- Löer, K.; Riahi, N.; Saenger, E.H. Three-component ambient noise beamforming in the Parkfield area. Geophys. J. Int. 2018, 213, 1478–1491. [Google Scholar] [CrossRef]
- Sánchez-Sesma, F.J.; Rodríguez, M.; Iturrarán-Viveros, U.; Luzón, F.; Campillo, M.; Margerin, L.; García-Jerez, A.; Suarez, M.; Santoyo, M.A.; Rodríguez-Castellanos, A. A theory for microtremor H/V spectral ratio: Application for a layered medium. Geophys. J. Int. 2011, 186, 221–225. [Google Scholar] [CrossRef] [Green Version]
- Bard, P.Y.; Bouchon, M. The seismic response of sediment-filled valleys. Part 2. The case of incident P and SV waves. Bull. Seismol. Soc. Am. 1980, 70, 1921–1941. [Google Scholar] [CrossRef]
- Bard, P.y.; Bouchon, M. The seismic response of sediment-filled valleys. Part 1. The case of incident SH waves. Bull. Seismol. Soc. Am. 1980, 70, 1263–1286. [Google Scholar] [CrossRef]
- Bowden, D.C.; Tsai, V.C. Earthquake ground motion amplification for surface waves. Geophys. Res. Lett. 2017, 43, 121–127. [Google Scholar] [CrossRef] [Green Version]
- Harms, J. Terrestrial gravity fluctuations. Living Rev. Relativ. 2019, 22, 6. [Google Scholar] [CrossRef] [Green Version]
- Baggeroer, A.B.; Kuperman, W.A.; Schmidt, H.; Baggeroer, A.B. Matched field processing: Source localization in correlated noise as an optimum parameter estimation problem. J. Acoust. Soc. Am. 1988, 83, 571–587. [Google Scholar] [CrossRef]
- Corciulo, M.; Roux, P.; Campillo, M.; Dubucq, D.; Kuperman, W.A. Multiscale matched-field processing for noise-source localization in exploration geophysics. Geophysics 2012, 77, KS33–KS41. [Google Scholar] [CrossRef]
- Gal, M.; Reading, A.M.; Rawlinson, N.; Schulte-Pelkum, V. Matched Field Processing of Three-Component Seismic Array Data Applied to Rayleigh and Love Microseisms. J. Geophys. Res. Solid Earth 2018, 123, 6871–6889. [Google Scholar] [CrossRef]
- Tromp, J.; Luo, Y.; Hanasoge, S.; Peter, D. Noise cross-correlation sensitivity kernels. Geophys. J. Int. 2010, 183, 791–819. [Google Scholar] [CrossRef] [Green Version]
- Sager, K.; Ermert, L.; Boehm, C.; Fichtner, A. Towards full waveform ambient noise inversion. Geophys. J. Int. 2018, 212, 566–590. [Google Scholar] [CrossRef]
- Sager, K.; Boehm, C.; Ermert, L.; Krischer, L.; Fichtner, A. Global-Scale Full-Waveform Ambient Noise Inversion. J. Geophys. Res. Solid Earth 2020, 125, 1–17. [Google Scholar] [CrossRef]
- Igel, J.K.H.; Ermert, L.A.; Fichtner, A. Rapid finite-frequency microseismic noise source inversion at regional to global scales. Geophys. J. Int. 2021, 227, 169–183. [Google Scholar] [CrossRef]
- Xu, Z.; Mikesell, T.D.; Gribler, G.; Mordret, A. Rayleigh-wave multicomponent cross-correlation-based source strength distribution inversion. Part 1: Theory and numerical examples. Geophys. J. Int. 2019, 218, 1761–1780. [Google Scholar] [CrossRef]
- Aki, K. Space and time spectra of stationary stochastic waves, with special reference to microtremors. Bull. Earthq. Res. Inst. 1957, 35, 415–457. [Google Scholar]
- Cox, H. Spatial correlation in arbitrary noise fields with application to ambient sea noise. J. Acoust. Soc. Am. 2010, 54, 1973. [Google Scholar] [CrossRef]
- Harmon, N.; Rychert, C.; Gerstoft, P. Distribution of noise sources for seismic interferometry. Geophys. J. Int. 2010, 183, 1470. [Google Scholar] [CrossRef] [Green Version]
- Haney, M.M.; Mikesell, T.D.; van Wijk, K.; Nakahara, H. Extension of the spatial autocorrelation (SPAC) method to mixed-component correlations of surface waves. Geophys. J. Int. 2012, 191, 189–206. [Google Scholar] [CrossRef] [Green Version]
- Ballmer, S.W. A radiometer for stochastic gravitational waves. Class. Quantum Gravity 2006, 23, S179. [Google Scholar] [CrossRef] [Green Version]
- Thrane, E.; Ballmer, S.; Romano, J.; Mitra, S.; Talukder, D.; Bose, S.; Mandic, V. Probing the anisotropies of a stochastic gravitational-wave background using a network of ground-based laser interferometers. Phys. Rev. D 2009, 80, 122002. [Google Scholar] [CrossRef] [Green Version]
- Romano, J.; Taylor, S.; Cornish, N.; Gair, J.; Mingarelli, C.; van Haasteren, R. Phase-coherent mapping of gravitational-wave backgrounds using ground-based laser interferometers. Phys. Rev. D 2015, 92, 042003. [Google Scholar] [CrossRef] [Green Version]
- Prestegard, T. Unmodeled Searches for Long-Lasting Gravitational-Wave Signals with LIGO and Studies of Underground Seismic Noise for Future Gravitational-Wave Detectors. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2016. [Google Scholar]
- Meyers, P. Cross-Correlation Searches for Persistent Gravitational Waves with Advanced LIGO and Noise Studies for Current and Future Ground-Based Gravitational-Wave Detectors. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2018. [Google Scholar]
- Park, S.; Ishii, M. Near-surface compressional and shear wave speeds constrained by body-wave polarization analysis. Geophys. J. Int. 2018, 213, 1559–1571. [Google Scholar] [CrossRef]
- Park, S.; Tsai, V.C.; Ishii, M. Frequency-dependent P wave polarization and its subwavelength near-surface depth sensitivity. Geophys. Res. Lett. 2019, 46, 14377–14384. [Google Scholar] [CrossRef]
- Haney, M.M.; Tsai, V.C. Nonperturbational surface-wave inversion: A Dix-type relation for surface waves. Geophysics 2015, 80, EN167–EN177. [Google Scholar] [CrossRef] [Green Version]
- Meyers, P.; Bowden, D.C.; Prestegard, T.; Tsai, V.C.; Mandic, V.; Pavlis, G.; Caton, R. Direct Observations of Surface-Wave Eigenfunctions at the Homestake 3D Array. Bull. Seismol. Soc. Am. 2019, 109, 1194–1202. [Google Scholar] [CrossRef]
- Paige, C.C.; Saunders, M.A. LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares. ACM Trans. Math. Softw. 1982, 8, 43–71. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E. Methods of Conjugate Gradients for Solving Linear Systems. J. Res. Natl. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Gorski, K.M.; Hivon, E.; Banday, A.J.; Wandelt, B.D.; Hansen, F.K.; Reinecke, M.; Bartelmann, M. HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere. Astrophys. J. 2005, 622, 759–771. [Google Scholar] [CrossRef]
- Mandic, V.; Tsai, V.C.; Pavlis, G.L.; Prestegard, T.; Bowden, D.C.; Meyers, P.; Caton, R. A 3D Broadband Seismometer Array Experiment at the Homestake Mine. Seismol. Res. Lett. 2018, 89, 2420–2429. [Google Scholar] [CrossRef]
- Coughlin, M.; Harms, J.; Bowden, D.C.; Meyers, P.; Tsai, V.C.; Mandic, V.; Pavlis, G.; Prestegard, T. Coherence-Based Approaches for Estimating the Composition of the Seismic Wavefield. J. Geophys. Res. Solid Earth 2019, 124, 2941–2956. [Google Scholar] [CrossRef]
- Lovejoy, S. What Is Climate? Eos Trans. Am. Geophys. Union 2013, 94, 1–2. [Google Scholar] [CrossRef]
- Stehly, L.; Campillo, M.; Shapiro, N.M. A study of the seismic noise from its long-range correlation properties. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Xu, Y.; Koper, K.D.; Burlacu, R. Lakes as a Source of Short-Period (0.5–2 s) Microseisms. J. Geophys. Res. Solid Earth 2017, 122, 8241–8256. [Google Scholar] [CrossRef]
- Bensen, G.D.; Ritzwoller, M.H.; Shapiro, N.M. Broadband ambient noise surface wave tomography across the United States. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).