Hyperspectral Dimensionality Reduction Based on Inter-Band Redundancy Analysis and Greedy Spectral Selection †
Abstract
:1. Introduction
- We propose a filter-based method called interband redundancy analysis (IBRA) that works as a preselection method to remove redundant bands and reduce the search space dramatically;
- We present a two-step band selection method that first applies IBRA to obtain a reduced set of candidate bands and then selects the desired number of bands using a wrapper-based method called greedy spectral selection (GSS);
- We show that IBRA can be used as part of a more general two-step feature extraction framework where any dimensionality reduction method can be applied following IBRA to obtain the desired number of feature channels;
- Since one of the objectives of this work is to aid in the design of multispectral imaging systems based on the wavelengths recommended by a band selection method, we also present an extensive set of experiments that use the original hyperspectral data cube to enable simulating the process of using actual filters in a multispectral imager.
2. Related Work
3. Materials and Methods
3.1. Dataset Descriptions
3.2. Data Preprocessing
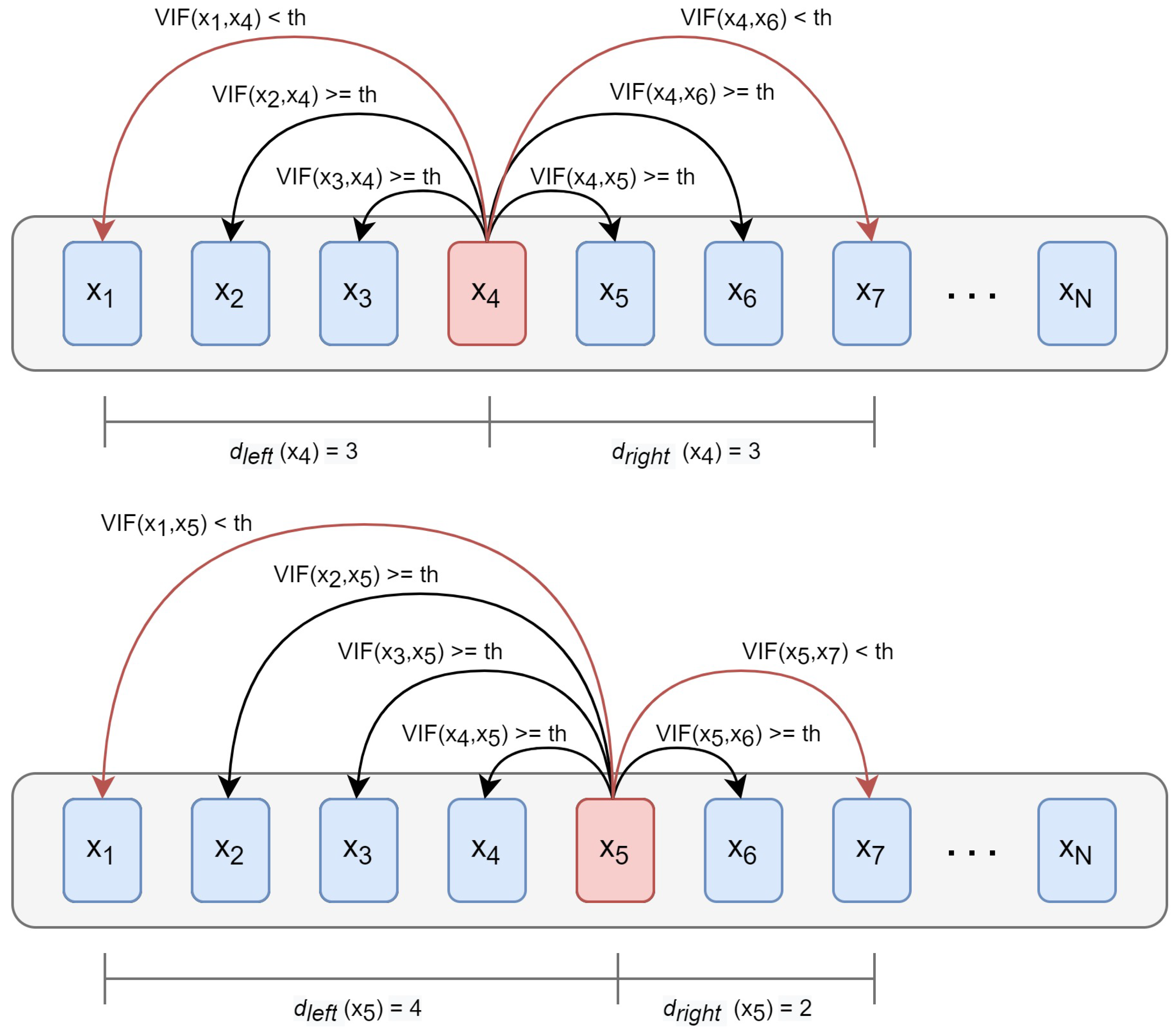
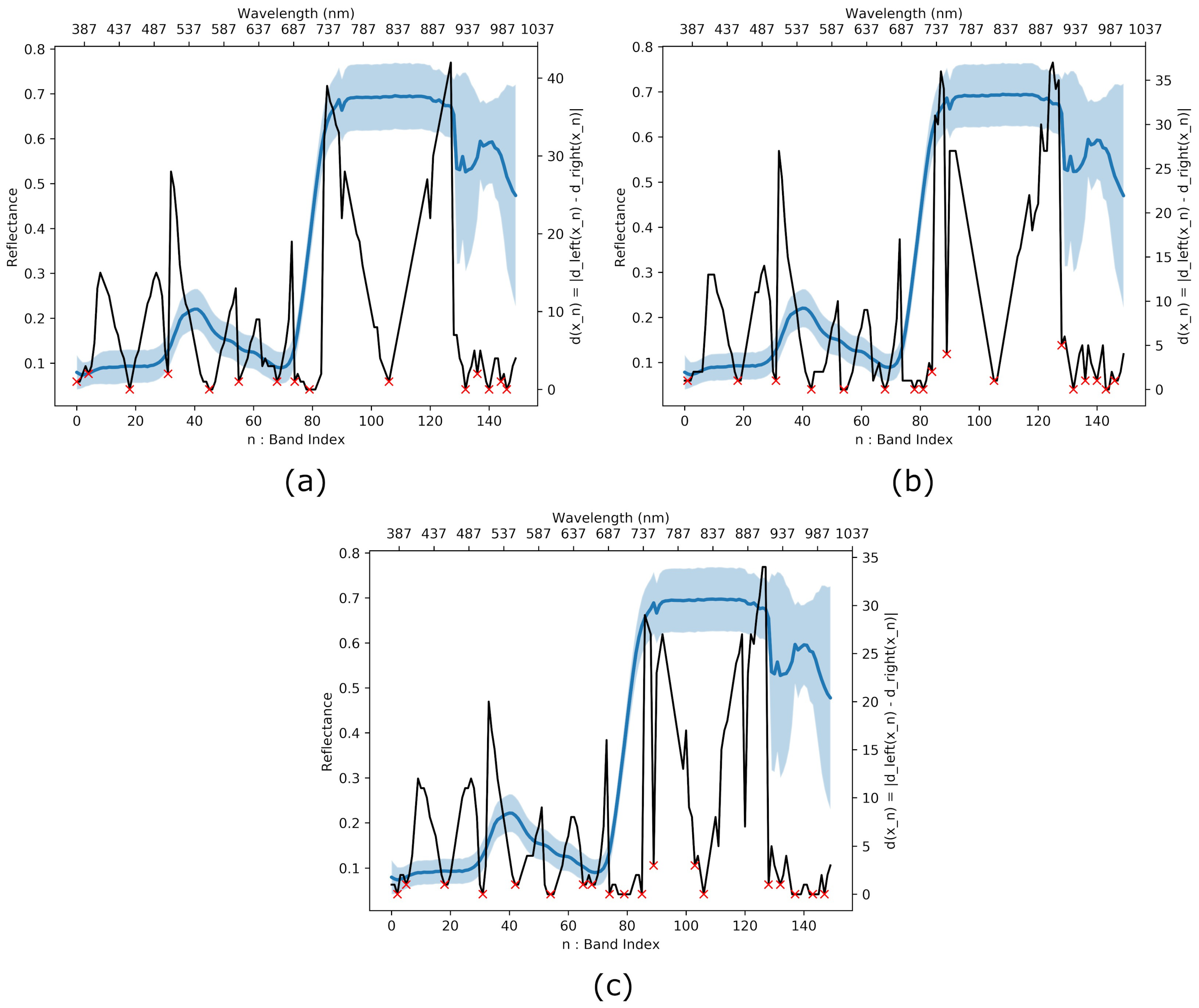
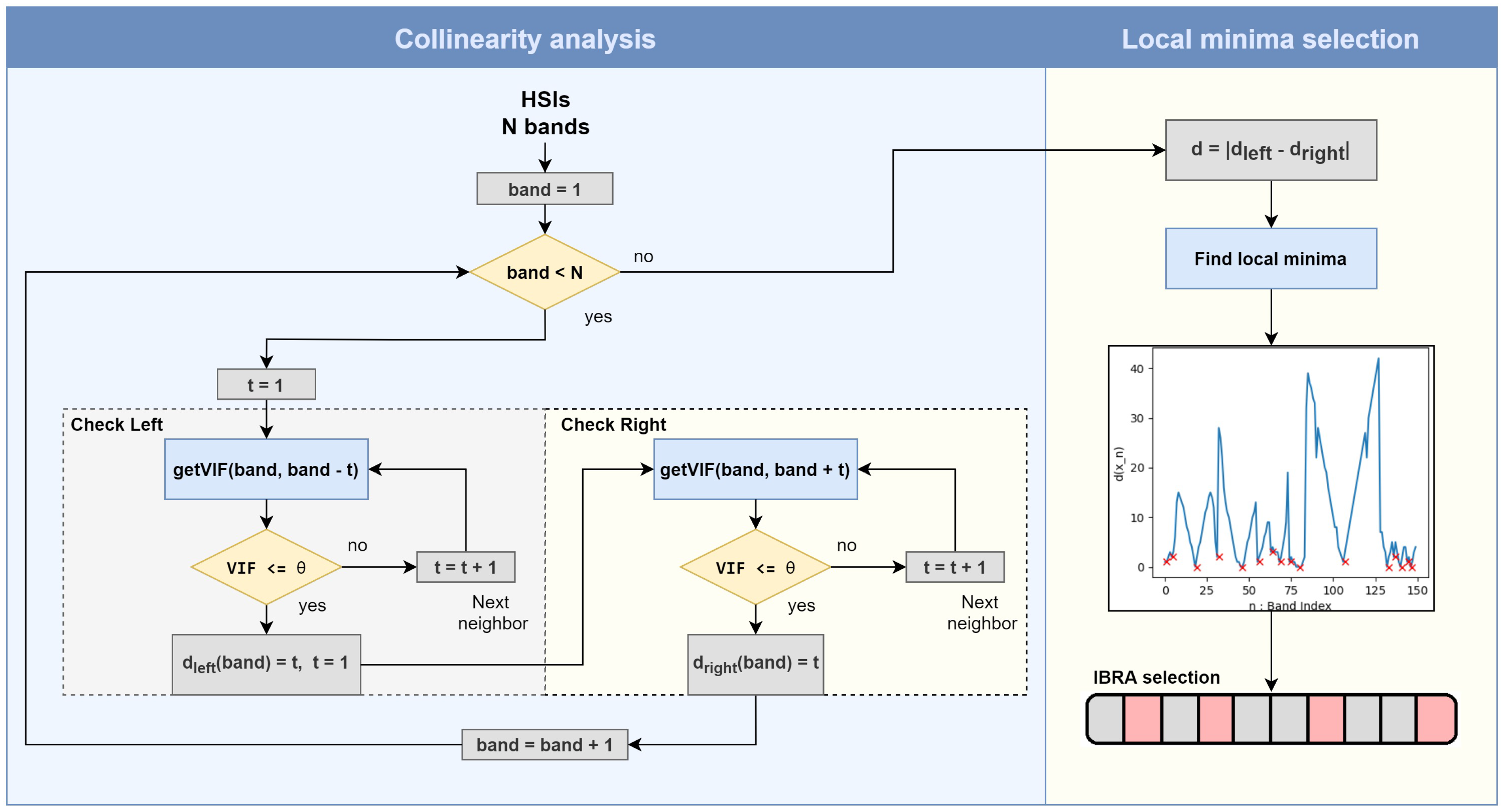
3.3. Interband Redundancy Analysis
| Algorithm 1 Calculating the interband redundancy. |
|
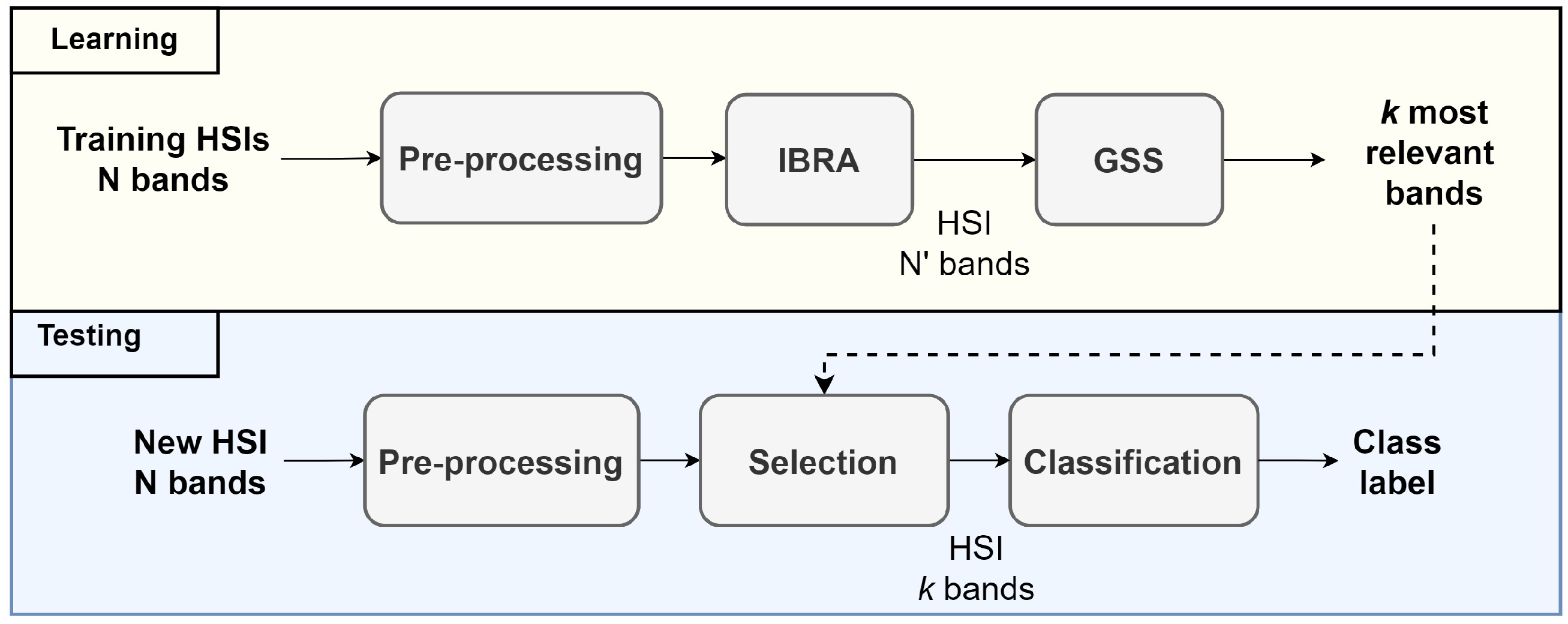
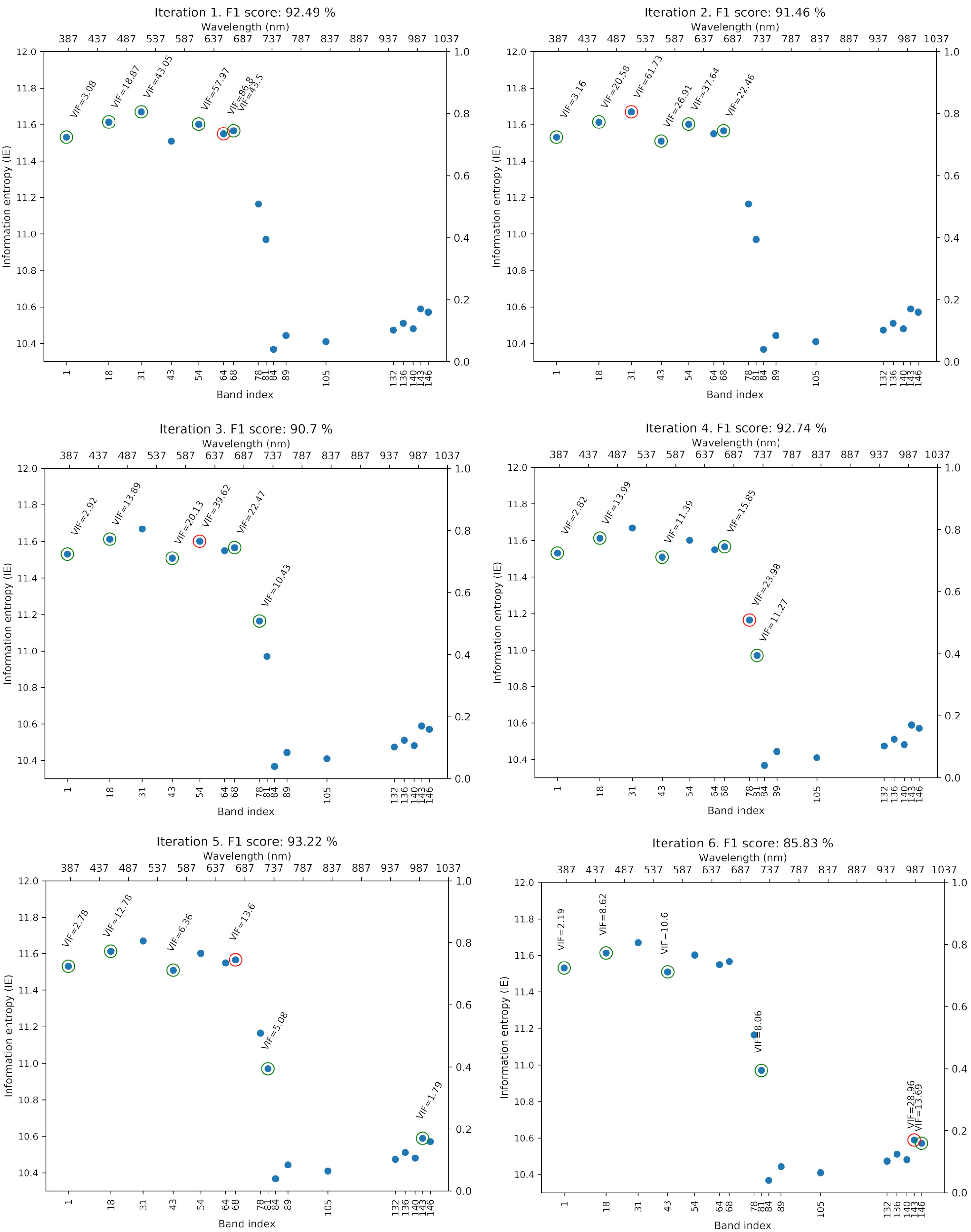
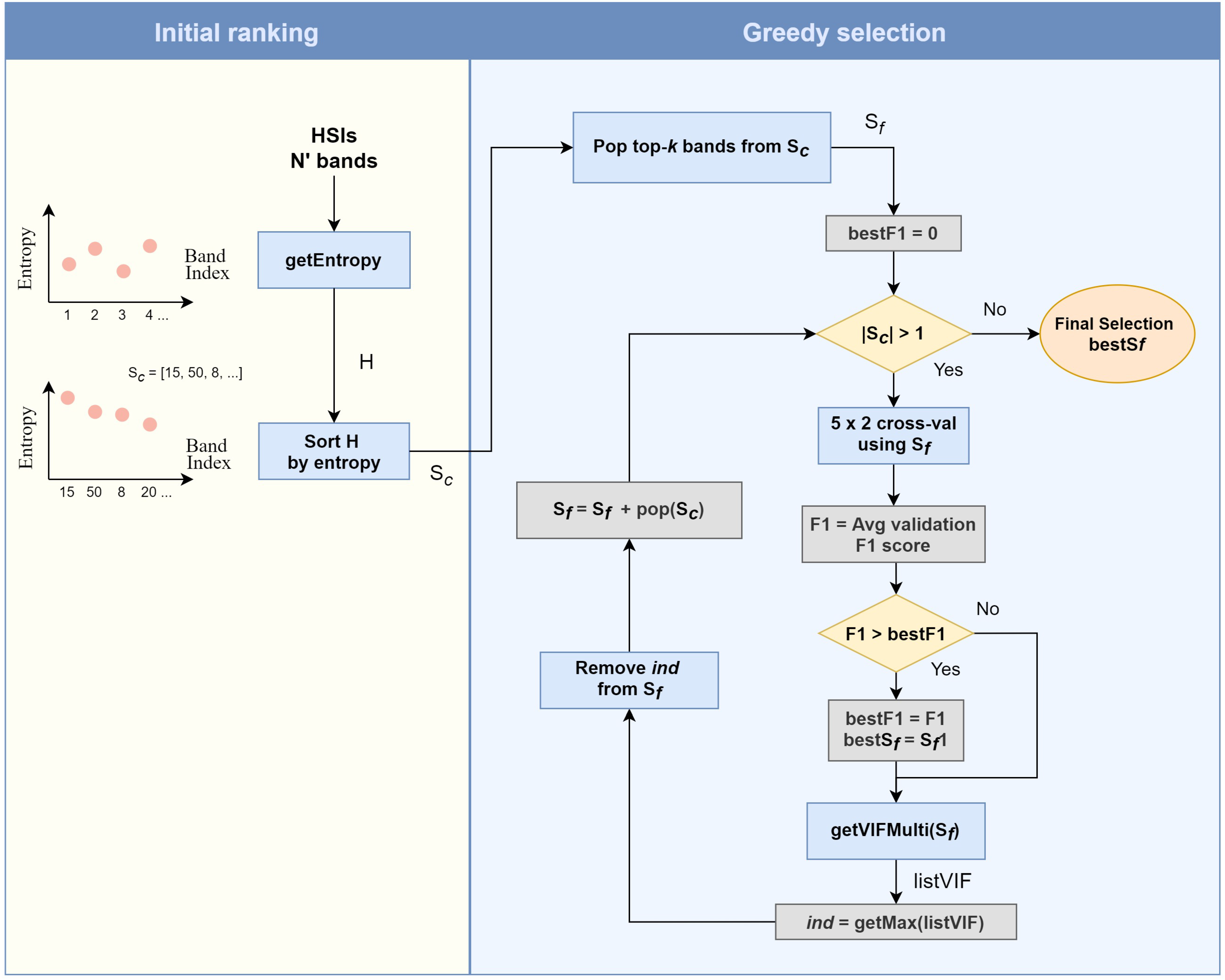
3.4. Band Selection Using Pre-Selected Bands
| Algorithm 2 Greedy spectral selection. |
|
3.5. Convolutional Neural Network Architecture
3.6. Multispectral Imager Design
3.7. Feature Extraction Framework
4. Experimental Results
4.1. Training with Preselected Bands Alone
4.2. Greedy Spectral Selection
4.3. Comparative Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scherrer, B.; Sheppard, J.; Jha, P.; Shaw, J.A. Hyperspectral imaging and neural networks to classify herbicide-resistant weeds. J. Appl. Remote Sens. 2019, 13, 044516. [Google Scholar] [CrossRef]
- Davenport, G. Remote sensing applications in forensic investigations. Hist. Archaeol. 2001, 35, 87–100. [Google Scholar] [CrossRef]
- Mathews, S.A. Design and fabrication of a low-cost, multispectral imaging system. Appl. Opt. 2008, 47, F71–F76. [Google Scholar] [CrossRef] [Green Version]
- Yang, C. A high-resolution airborne four-camera imaging system for agricultural remote sensing. Comput. Electron. Agric. 2012, 88, 13–24. [Google Scholar] [CrossRef]
- Wu, D.; Sun, D.W. Advanced applications of hyperspectral imaging technology for food quality and safety analysis and assessment: A review—Part I: Fundamentals. Innov. Food Sci. Emerg. Technol. 2013, 19, 1–14. [Google Scholar] [CrossRef]
- Goetz, A.F. Three decades of hyperspectral remote sensing of the Earth: A personal view. Remote Sens. Environ. 2009, 113, S5–S16. [Google Scholar] [CrossRef]
- Hook, S.J. NASA 2014 the Hyperspectral Infrared Imager (HyspIRI)–Science Impact of Deploying Instruments on Separate Platforms; White Paper 14-13; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar]
- Guo, X.; Zhang, H.; Wu, Z.; Zhao, J.; Zhang, Z. Comparison and Evaluation of Annual NDVI Time Series in China Derived from the NOAA AVHRR LTDR and Terra MODIS MOD13C1 Products. Sensors 2017, 17, 1298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- González-Betancourt, M.; Liceth Mayorga-Ruíz, Z. Normalized difference vegetation index for rice management in El Espinal, Colombia. DYNA 2018, 85, 47–56. [Google Scholar] [CrossRef]
- Martínez-Usó, A.; Pla, F.; Sotoca, J.M.; Garcia-Sevilla, P. Clustering-Based Hyperspectral Band Selection Using Information Measures. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4158–4171. [Google Scholar] [CrossRef]
- Ghojogh, B.; Samad, M.N.; Mashhadi, S.A.; Kapoor, T.; Ali, W.; Karray, F.; Crowley, M. Feature Selection and Feature Extraction in Pattern Analysis: A Literature Review. arXiv 2019, arXiv:1905.02845. [Google Scholar]
- Deng, L.; Mao, Z.; Li, X.; Hu, Z.; Duan, F.; Yan, Y. UAV-based multispectral remote sensing for precision agriculture: A comparison between different cameras. ISPRS J. Photogramm. Remote Sens. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- Vasefi, F.; MacKinnon, N.; Farkas, D. Hyperspectral and Multispectral Imaging in Dermatology. In Imaging in Dermatology; Academic Press: Boston, MA, USA, 2016; pp. 187–201. [Google Scholar]
- Morales, G.; Sheppard, J.; Logan, R.; Shaw, J. Hyperspectral Band Selection for Multispectral Image Classification with Convolutional Networks. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN2021), virtual event, 18–22 July 2021. [Google Scholar]
- Bellman, R. Adaptive Control Processes: A Guided Tour; Princeton University Press: Princeton, NJ, USA, 1961. [Google Scholar]
- Sun, W.; Du, Q. Hyperspectral Band Selection: A Review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.P.; Mamun, M.A.; Hossain, M.A. Feature extraction for hyperspectral image classification. In Proceedings of the IEEE Region 10 Humanitarian Technology Conference (R10-HTC), Dhaka, Bangladesh, 21–23 December 2017; pp. 379–382. [Google Scholar]
- Prasad, S.; Bruce, L. Limitations of Principal Components Analysis for Hyperspectral Target Recognition. IEEE Geosci. Remote Sens. Lett. 2008, 5, 625–629. [Google Scholar] [CrossRef]
- Jayaprakash, C.; Damodaran, B.B.; Sowmya, V.; Soman, K.P. Dimensionality Reduction of Hyperspectral Images for Classification using Randomized Independent Component Analysis. In Proceedings of the 2018 5th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 22–23 February 2018; pp. 492–496. [Google Scholar]
- Du, Q.; Younan, N. Dimensionality Reduction and Linear Discriminant Analysis for Hyperspectral Image Classification. In Knowledge-Based Intelligent Information and Engineering Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 392–399. [Google Scholar]
- Sugiyama, M. Dimensionality Reduction of Multimodal Labeled Data by Local Fisher Discriminant Analysis. J. Mach. Learn. Res. 2007, 8, 1027–1061. [Google Scholar]
- Fordellone, M.; Bellincontro, A.; Mencarelli, F. Partial Least Squares Discriminant Analysis: A Dimensionality Reduction Method to Classify Hyperspectral Data. Stat. Appl.-Ital. J. Appl. Stat. 2019, 31, 181–200. [Google Scholar]
- Hong, D.; Yokoya, N.; Zhu, X.X. Learning a Robust Local Manifold Representation for Hyperspectral Dimensionality Reduction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2960–2975. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, L.; Gao, L.; Zhang, B.; Fu, X.; Bioucas-Dias, J.M. Hyperspectral Image Denoising and Anomaly Detection Based on Low-Rank and Sparse Representations. IEEE Trans. Geosci. Remote Sens. 2020, 1–17. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Q.; Li, X. A Fast Neighborhood Grouping Method for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5028–5039. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F.; Li, X. Optimal Clustering Framework for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5910–5922. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Xia, Z.; Zhang, C. Sensitive Wavelengths Selection in Identification of Ophiopogon japonicus Based on Near-Infrared Hyperspectral Imaging Technology. Int. J. Anal. Chem. 2017, 2017, 6018769. [Google Scholar]
- Walton, N.; Sheppard, J.; Shaw, J. Using a Genetic Algorithm with Histogram-Based Feature Selection in Hyperspectral Image Classification. In Proceedings of the ACM Genetic and Evolutionary Computation Conference (GECCO’19), Prague, Czech Republic, 13–17 July 2019; pp. 1364–1372. [Google Scholar]
- Pirgazi, J.; Alimoradi, M.; Abharian, T.; Olyaee, M. An Efficient hybrid filter-wrapper metaheuristic-based gene selection method for high dimensional datasets. Sci. Rep. 2019, 9, 18580. [Google Scholar] [CrossRef] [PubMed]
- Taherkhani, F.; Dawson, J.; Nasrabadi, N. Deep Sparse Band Selection for Hyperspectral Face Recognition. arXiv 2019, arXiv:1908.09630. [Google Scholar]
- Tschannerl, J.; Ren, J.; Zabalza, J.; Marshall, S. Segmented Autoencoders for Unsupervised Embedded Hyperspectral Band Selection. In Proceedings of the 2018 7th European Workshop on Visual Information Processing (EUVIP), Tampere, Finland, 26–28 November 2018; pp. 1–6. [Google Scholar]
- Chang, C.; Du, Q.; Sun, T.; Althouse, M. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef] [Green Version]
- Frenich, A.G.; Jouan-Rimbaud, D.; Massart, D.L.; Kuttatharmmakul, S.; Galera, M.M.; Vidal, J.L.M. Wavelength selection method for multicomponent spectrophotometric determinations using partial least squares. Analyst 1995, 120, 2787–2792. [Google Scholar] [CrossRef]
- Barbin, D.F.; Sun, D.W.; Su, C. NIR hyperspectral imaging as non-destructive evaluation tool for the recognition of fresh and frozen–thawed porcine longissimus dorsi muscles. Innov. Food Sci. Emerg. Technol. 2013, 18, 226–236. [Google Scholar] [CrossRef]
- Preet, P.; Batra, S.S. Feature Selection for classification of hyperspectral data by minimizing a tight bound on the VC dimension. arXiv 2015, arXiv:1509.08112. [Google Scholar]
- Vapnik, V.; Chervonenkis, A. On the Uniform Convergence of Relative Frequencies of Events to their Probabilities. Theory Probab. Its Appl. 1971, 16, 264–280. [Google Scholar] [CrossRef]
- Castaldi, F.; Castrignanò, A.; Casa, R. A data fusion and spatial data analysis approach for the estimation of wheat grain nitrogen uptake from satellite data. Int. J. Remote Sens. 2016, 37, 4317–4336. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Li, X.; Hou, W.; Wang, Y.; Wei, Y. A Similarity-Based Ranking Method for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Medjahed, S.A.; Ouali, M. Band selection based on optimization approach for hyperspectral image classification. Egypt. J. Remote Sens. Space Sci. 2018, 21, 413–418. [Google Scholar] [CrossRef]
- Wallays, C.; Missotten, B.; De Baerdemaeker, J.; Saeys, W. Hyperspectral waveband selection for on-line measurement of grain cleanness. Biosyst. Eng. 2009, 104, 1–7. [Google Scholar] [CrossRef]
- Feng, L.; Zhu, S.; Liu, F.; He, Y.; Bao, Y.; Zhang, C. Hyperspectral imaging for seed quality and safety inspection: A review. Plant Methods 2019, 15, 2631–2641. [Google Scholar] [CrossRef] [Green Version]
- Fang, B.; Li, Y.; Zhang, H.; Chan, J. Hyperspectral Images Classification Based on Dense Convolutional Networks with Spectral-Wise Attention Mechanism. Remote Sens. 2019, 11, 159. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Zhao, Y.; Dudziak, L.; Mullins, R.; Xu, C.Z. Dynamic channel pruning: Feature boosting and suppression. In Proceedings of the 7th International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Pasa, F.; Golkov, V.; Pfeiffer, F.; Cremers, D.; Pfeiffer, D. Efficient Deep Network Architectures for Fast Chest X-Ray Tuberculosis Screening and Visualization. Sci. Rep. Vis. 2019, 9, 6268. [Google Scholar] [CrossRef] [Green Version]
- Pan, J.; Ferrer, C.; McGuinness, K.; O’Connor, N.; Torres, J.; Sayrol, E.; Giro-i-Nieto, X. SalGAN: Visual Saliency Prediction with Generative Adversarial Networks. arXiv 2017, arXiv:1701.01081. [Google Scholar]
- Nagasubramanian, K.; Jones, S.; Singh, A.K.; Sarkar, S.; Singh, A.; Ganapathysubramanian, B. Plant disease identification using explainable 3D deep learning on hyperspectral images. Plant Methods 2019, 15, 98. [Google Scholar] [CrossRef] [PubMed]
- Baumgardner, M.F.; Biehl, L.L.; Landgrebe, D.A. 220 Band AVIRIS Hyperspectral Image Data Set: June 12, 1992 Indian Pine Test Site 3; Purdue University Research Repository: West Lafayette, IN, USA, 2015. [Google Scholar] [CrossRef]
- Gualtieri, A.G.; Chettri, S.; Cromp, R.F.; Johnson, L.F. Support Vector Machine Classifiers as Applied to AVIRIS Data. In Proceedings of the Summaries of the Eighth JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 9–11 February 1999. [Google Scholar]
- Dexter, A.G.; Luecke, J.L. Survey of Weed Control and Production Practices on Sugarbeet in Eastern North Dakota and Minnesota-2000. Sugarbeet Res. Ext. Rep 2001, 32, 35–63. [Google Scholar]
- Mengistu, L.W.; Messersmith, C.G. Genetic diversity of Kochia. Weed Sci. 2002, 50, 498–503. [Google Scholar] [CrossRef]
- Waite, J.C. Glyphosate Resistance in Kochia (Kochia scoparia). Master’s Thesis, Department of Agronomy, College of Agriculture, Kansas State University, Manhattan, KS, USA, 2010. [Google Scholar]
- Porter, W.M.; Enmark, H.T. A System Overview of the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). In Imaging Spectroscopy II; Vane, G., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 1987; Volume 0834, pp. 22–31. [Google Scholar]
- Tadjudin, S. Classification of High Dimensional Data with Limited Training Samples. Ph.D. Thesis, School of Electrical and Computer Engineering, Purdue University, West Lafayette, IN, USA, 1998. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning with Applications in R; Springer Science + Business Media: New York, NY, USA, 2013. [Google Scholar]
- Belsley, D.; Kuh, E.; Welsch, R.; Wells, R. Regression Diagnostics: Identifying Influential Data and Sources of Collinearity; Wiley Series in Probability and Statistics—Applied Probability and Statistics Section Series; Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Hair, J.; Anderson, R.; Babin, B. Multivariate Data Analysis, 7th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Morales, G.; Sheppard, J.; Scherrer, B.; Shaw, J. Reduced-Cost Hyperspectral Convolutional Neural Networks. J. Appl. Remote Sens. 2020, 14, 036519. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar]
- Howard, A.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Zeiler, M. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Marker, M.; Rayens, W. Partial Least Squares for Discrimination. J. Chemom. 2003, 17, 166–173. [Google Scholar]


| Layer Name | Kernel Size | Stride Size | Output Size |
|---|---|---|---|
| Input | — | — | (25, 25, N, 1) |
| Conv3D + ReLU | (3, 3, 3) | (1, 1, 1) | (25, 25, N, 16) |
| Conv3D + ReLU | (3, 3, 3) | (1, 1, 1) | (25, 25, N, 16) |
| Reshape | — | — | (25, 25, ) |
| SepConv2D + ReLU | (3, 3) | (1, 1) | (25, 25, 320) |
| SepConv2D + ReLU | (3, 3) | (2, 2) | (13, 13, 256) |
| SepConv2D + ReLU | (3, 3) | (2, 2) | (7, 7, 256) |
| GlobalAveragePooling | — | — | 256 |
| Dense + Softmax | — | — | # classes |
| Dataset | # of Bands | Accuracy | Precision | Recall | F1 | # of Parameters |
|---|---|---|---|---|---|---|
| Kochia | 150 | 98.46 ± 0.29 | 98.66 ± 0.26 | 98.55 ± 0.31 | 98.60 ± 0.28 | 561,475 |
| 17 | 97.05 ± 0.47 | 97.25 ± 0.45 | 97.17 ± 0.46 | 97.21 ± 0.44 | 258,035 | |
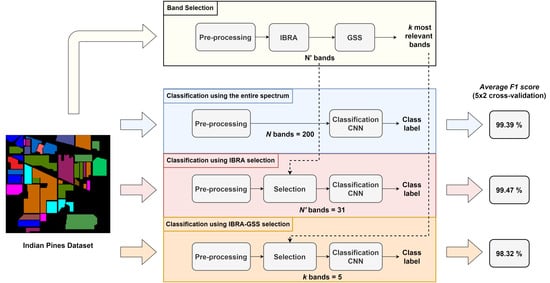
| Indian Pines | 200 | 99.42 ± 0.18 | 99.32 ± 0.29 | 99.47 ± 0.28 | 99.39 ± 0.27 | 1,274,464 |
| 31 | 99.49 ± 0.14 | 99.38 ± 0.34 | 99.56 ± 0.19 | 99.47 ± 0.23 | 338,880 | |
| Salinas | 204 | 99.92 ± 0.04 | 99.93 ± 0.05 | 99.94 ± 0.03 | 99.94 ± 0.04 | 1,296,608 |
| 14 | 99.43 ± 0.13 | 99.75 ± 0.08 | 99.72 ± 0.08 | 99.73 ± 0.08 | 244,768 |
| k | VIF | Selected Bands (nm) | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|---|---|
| 6 | 12 | [395.5, 463.3, 565.1, 700.8, 722.0, 993.3] | 92.44 ± 0.71 | 92.76 ± 0.80 | 92.79 ± 0.67 | 92.76 ± 0.72 |
| 11 | [395.5, 408.2, 463.3, 586.3, 662.6, 700.8] | 90.74 ± 1.05 | 91.56 ± 0.97 | 91.54 ± 1.06 | 91.54 ± 1.01 | |
| 10 | [391.2, 463.3, 569.3, 675.3, 730.4, 993.3] | 92.69 ± 0.53 | 93.24 ± 0.52 | 93.08 ± 0.49 | 93.15 ± 0.49 | |
| 9 | [391.2, 463.3, 569.3, 700.8, 730.4, 993.3] | 92.40 ± 0.63 | 92.67 ± 0.63 | 92.77 ± 0.59 | 92.71 ± 0.59 | |
| 8 | [387.0, 404.0, 463.3, 577.8, 700.8, 722.0] | 92.58 ± 0.63 | 93.05 ± 0.65 | 93.08 ± 0.57 | 93.06 ± 0.59 | |
| 7 | [387.0, 404.0, 463.3, 569.3, 700.8, 722.0] | 92.07 ± 0.89 | 92.52 ± 0.89 | 92.55 ± 0.79 | 92.53 ± 0.83 | |
| 6 | [387.0, 404.0, 463.3, 586.3, 700.8, 717.7] | 92.00 ± 0.61 | 92.57 ± 0.54 | 92.52 ± 0.64 | 92.53 ± 0.57 | |
| 5 | [387.0, 463.3, 586.3, 645.6, 700.8, 722.0] | 91.03 ± 1.04 | 91.79 ± 1.14 | 91.75 ± 0.91 | 91.76 ± 1.01 | |
| 8 | 12 | [395.5, 408.2, 463.3, 565.1, 675.3, 700.8, 722.0, 993.3] | 93.96 ± 0.68 | 94.47 ± 0.65 | 94.34 ± 0.68 | 94.39 ± 0.66 |
| 11 | [395.5, 408.2, 463.3, 565.1, 675.3, 700.8, 726.2, 993.3] | 94.18 ± 0.70 | 94.74 ± 0.65 | 94.47 ± 0.67 | 94.59 ± 0.66 | |
| 10 | [391.2, 463.3, 569.3, 675.3, 730.4, 963.6, 993.3, 1006.0] | 93.95 ± 0.62 | 94.48 ± 0.56 | 94.13 ± 0.68 | 94.29 ± 0.61 | |
| 9 | [391.2, 463.3, 569.3, 671.1, 700.8, 730.4, 963.6, 993.3] | 94.33 ± 0.41 | 94.81 ± 0.48 | 94.60 ± 0.47 | 94.69 ± 0.47 | |
| 8 | [387.0, 404.0, 463.3, 518.4, 577.8, 654.1, 675.32, 700.8] | 94.79 ± 0.65 | 95.28 ± 0.55 | 95.20 ± 0.67 | 95.23 ± 0.61 | |
| 7 | [387.0, 404.0, 463.3, 569.3, 675.3, 700.8, 722.0, 1006.0] | 94.48 ± 0.77 | 95.05 ± 0.72 | 94.85 ± 0.73 | 94.93 ± 0.73 | |
| 6 | [387.0, 404.0, 463.3, 586.3, 679.6, 700.8, 730.4, 1001.8] | 94.65 ± 0.45 | 95.21 ± 0.38 | 94.89 ± 0.48 | 95.04 ± 0.42 | |
| 5 | [387.0, 463.3, 586.3, 645.6, 700.8, 722.0, 980.6, 1001.8] | 93.68 ± 0.75 | 94.25 ± 0.65 | 93.95 ± 0.68 | 94.08 ± 0.66 | |
| 10 | 12 | [395.5, 408.2, 463.3, 518.4, 565.1, 616.0, 675.3, 700.8, 722.0, 993.3] | 96.31 ± 0.69 | 96.57 ± 0.55 | 96.49 ± 0.73 | 96.53 ± 0.64 |
| 11 | [395.5, 408.2, 463.3, 565.1, 662.6, 675.3, 700.8, 713.5, 726.2, 993.3] | 96.18 ± 0.41 | 96.48 ± 0.29 | 96.31 ± 0.46 | 96.39 ± 0.36 | |
| 10 | [391.2, 463.3, 518.4, 569.3, 658.4, 675.3, 717.7, 730.4, 993.3, 1006.] | 95.83 ± 0.36 | 96.10 ± 0.38 | 96.06 ± 0.32 | 96.08 ± 0.34 | |
| 9 | [391.2, 463.3, 518.4, 569.3, 616.0, 671.1, 700.8, 717.7, 730.4, 993.3] | 96.16 ± 0.56 | 96.48 ± 0.50 | 96.37 ± 0.54 | 96.42 ± 0.52 | |
| 8 | [387.0, 404.0, 463.3, 518.4, 577.8, 654.1, 675.3, 700.8, 722.0, 1006.0] | 96.47 ± 0.38 | 96.79 ± 0.36 | 96.66 ± 0.37 | 96.72 ± 0.35 | |
| 7 | [387.0, 404.0, 463.3, 518.4, 569.3, 654.1, 675.3, 700.8, 722.0, 1006.0] | 96.69 ± 0.35 | 96.92 ± 0.38 | 96.95 ± 0.34 | 96.93 ± 0.35 | |
| 6 | [387.0, 404.0, 463.3, 586.3, 649.9, 679.6, 700.8, 717.7, 730.4, 1001.8] | 95.91 ± 0.50 | 96.34 ± 0.44 | 96.12 ± 0.47 | 96.22 ± 0.45 | |
| 5 | [387.0, 463.3, 586.3, 645.6, 700.8, 722.0, 832.2, 946.7, 980.6, 1001.8] | 95.06 ± 0.54 | 95.44 ± 0.52 | 95.33 ± 0.56 | 95.38 ± 0.53 |
| VIF | Selected Bands (nm) | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|---|
| 12 | [498.3, 646.7, 706.2, 754.4, 1023.7] | 97.96 ± 0.33 | 98.21 ± 0.43 | 98.32 ± 0.33 | 98.25 ± 0.35 |
| 11 | [557.5, 587.2, 706.2, 754.4, 1023.7] | 97.55 ± 0.29 | 98.05 ± 0.29 | 97.95 ± 0.29 | 97.98 ± 0.22 |
| 10 | [498.3, 626.9, 706.2, 754.4, 1023.7] | 98.08 ± 0.43 | 98.26 ± 0.42 | 98.39 ± 0.43 | 98.32 ± 0.39 |
| 9 | [557.5, 626.9, 706.2, 821.8, 1023.7] | 98.28 ± 0.35 | 98.24 ± 0.47 | 98.06 ± 0.59 | 98.11 ± 0.43 |
| 8 | [607.0, 646.7, 706.2, 821.8, 1023.7] | 98.04 ± 0.30 | 98.19 ± 0.46 | 98.06 ± 0.46 | 98.10 ± 0.35 |
| 7 | [567.4, 587.2, 706.2, 821.8, 1023.7] | 98.01 ± 0.24 | 98.29 ± 0.18 | 98.36 ± 0.42 | 98.31 ± 0.26 |
| 6 | [577.3, 706.2, 821.8, 918.0, 1023.7] | 97.06 ± 0.49 | 97.49 ± 0.58 | 97.63 ± 0.48 | 97.53 ± 0.48 |
| 5 | [577.3, 715.8, 812.2, 918.0, 1023.7] | 96.73 ± 0.55 | 97.46 ± 0.53 | 97.00 ± 0.61 | 97.19 ± 0.49 |
| VIF | Selected Bands (nm) | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|---|
| 12 | [532.1, 731.8, 950.5, 1368.9, 2224.7] | 98.70 ± 0.11 | 99.40 ± 0.05 | 99.48 ± 0.04 | 99.44 ± 0.04 |
| 11 | [541.7, 731.8, 950.5, 1368.9, 2224.7] | 98.68 ± 0.11 | 99.36 ± 0.10 | 99.45 ± 0.05 | 99.40 ± 0.07 |
| 10 | [541.7, 731.8, 950.5, 1359.4, 2224.7] | 98.62 ± 0.14 | 99.38 ± 0.07 | 99.45 ± 0.04 | 99.41 ± 0.05 |
| 9 | [541.7, 731.8, 950.5, 1359.4, 2224.7] | 98.62 ± 0.14 | 99.38 ± 0.07 | 99.45 ± 0.04 | 99.41 ± 0.05 |
| 8 | [731.8, 950.5, 1159.7, 1254.8, 2224.7] | 99.05 ± 0.05 | 99.56 ± 0.04 | 99.55 ± 0.03 | 99.56 ± 0.03 |
| 7 | [731.8, 950.5, 1159.7, 1254.8, 2215.2] | 99.02 ± 0.10 | 99.54 ± 0.07 | 99.53 ± 0.06 | 99.54 ± 0.06 |
| 6 | [570.2, 950.5, 1245.3, 1368.9, 2215.2] | 99.02 ± 0.05 | 99.54 ± 0.04 | 99.56 ± 0.02 | 99.55 ± 0.03 |
| 5 | [560.7, 950.5, 1245.3, 1368.9, 2215.2] | 98.99 ± 0.06 | 99.52 ± 0.09 | 99.56 ± 0.05 | 99.54 ± 0.07 |
| k | Method | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|---|
| 6 | FNGBS | 84.32 ± 1.78 | 84.85 ± 1.77 | 84.37 ± 1.72 | 84.59 ± 1.73 |
| 86.98 ± 0.84 | 87.35 ± 0.80 | 86.91 ± 0.91 | 87.10 ± 0.83 | ||
| PLS-DA | 84.77 ± 1.83 | 85.15 ± 1.89 | 84.69 ± 1.82 | 84.89 ± 1.82 | |
| 88.41 ± 0.79 | 88.85 ± 0.62 | 88.37 ± 0.96 | 88.59 ± 0.78 | ||
| SR-SSIM | 86.42 ± 1.07 | 87.66 ± 1.02 | 87.31 ± 1.06 | 87.47 ± 1.03 | |
| 88.73 ± 0.90 | 89.55 ± 0.81 | 89.30 ± 0.99 | 89.41 ± 0.89 | ||
| OCF | 90.48 ± 0.57 | 90.92 ± 0.62 | 90.81 ± 0.44 | 90.86 ± 0.49 | |
| 92.42 ± 0.67 | 92.75 ± 0.66 | 92.66 ± 0.66 | 92.70 ± 0.65 | ||
| HAGRID | 91.71 ± 0.83 | 92.25 ± 0.78 | 92.17 ± 0.84 | 92.20 ± 0.80 | |
| 92.48 ± 0.62 | 92.91 ± 0.53 | 92.89 ± 0.58 | 92.89 ± 0.54 | ||
| IBRA-PCA | 83.04 ± 2.23 | 83.44 ± 2.16 | 82.96 ± 2.40 | 83.17 ± 2.29 | |
| 91.31 ± 0.74 | 91.81 ± 0.67 | 91.18 ± 0.71 | 91.46 ± 0.68 | ||
| IBRA-PLS-DA | 90.81 ± 0.96 | 91.68 ± 1.04 | 91.33 ± 0.86 | 91.48 ± 0.94 | |
| 92.29 ± 0.63 | 92.98 ± 0.58 | 92.57 ± 0.72 | 92.76 ± 0.65 | ||
| IBRA-GSS | 92.69 ± 0.53 | 93.24 ± 0.52 | 93.08 ± 0.50 | 93.15 ± 0.49 | |
| 93.32 ± 0.68 | 93.80 ± 0.64 | 93.74 ± 0.66 | 93.76 ± 0.64 | ||
| 8 | FNGBS | 92.88 ± 0.55 | 93.63 ± 0.55 | 93.10 ± 0.46 | 93.34 ± 0.50 |
| 93.12 ± 0.32 | 93.69 ± 0.28 | 93.13 ± 0.46 | 93.39 ± 0.34 | ||
| PLS-DA | 90.53 ± 1.65 | 91.70 ± 1.37 | 91.01 ± 1.72 | 91.32 ± 1.57 | |
| 91.92 ± 0.81 | 92.69 ± 0.71 | 92.21 ± 0.87 | 92.43 ± 0.79 | ||
| SR-SSIM | 91.01 ± 1.37 | 91.97 ± 1.28 | 91.54 ± 1.35 | 91.75 ± 1.31 | |
| 92.31 ± 0.83 | 93.00 ± 0.81 | 92.73 ± 0.89 | 92.86 ± 0.83 | ||
| OCF | 93.05 ± 0.90 | 93.86 ± 0.80 | 93.43 ± 0.84 | 93.62 ± 0.83 | |
| 92.89 ± 0.71 | 93.45 ± 0.64 | 93.21 ± 0.67 | 93.32 ± 0.65 | ||
| HAGRID | 91.59 ± 1.25 | 92.52 ± 1.05 | 91.88 ± 1.24 | 92.17 ± 1.16 | |
| 92.82 ± 0.79 | 93.41 ± 0.69 | 92.92 ± 0.91 | 93.15 ± 0.80 | ||
| IBRA-PCA | 83.75 ± 2.40 | 84.33 ± 2.48 | 83.77 ± 2.43 | 84.02 ± 2.45 | |
| 95.04 ± 0.70 | 95.35 ± 0.60 | 95.21 ± 0.81 | 95.27 ± 0.70 | ||
| IBRA-PLS-DA | 95.46 ± 0.53 | 95.91 ± 0.46 | 95.63 ± 0.49 | 95.76 ± 0.47 | |
| 95.42 ± 0.60 | 95.85 ± 0.52 | 95.62 ± 0.57 | 95.72 ± 0.53 | ||
| IBRA-GSS | 94.79 ± 0.65 | 95.28 ± 0.55 | 95.20 ± 0.67 | 95.23 ± 0.61 | |
| 94.08 ± 0.60 | 94.67 ± 0.57 | 94.54 ± 0.54 | 94.60 ± 0.54 | ||
| 10 | FNGBS | 93.78 ± 0.77 | 94.17 ± 0.84 | 93.99 ± 0.73 | 94.08 ± 0.78 |
| 94.19 ± 0.47 | 94.54 ± 0.47 | 94.27 ± 0.51 | 94.39 ± 0.48 | ||
| PLS-DA | 94.36 ± 0.51 | 94.86 ± 0.55 | 94.67 ± 0.47 | 94.76 ± 0.49 | |
| 95.10 ± 0.68 | 95.44 ± 0.59 | 95.18 ± 0.67 | 95.30 ± 0.63 | ||
| OCF | 94.87 ± 0.51 | 95.23 ± 0.52 | 95.11 ± 0.46 | 95.16 ± 0.47 | |
| 94.62 ± 0.73 | 95.00 ± 0.65 | 94.80 ± 0.64 | 94.89 ± 0.64 | ||
| SR-SSIM | 93.84 ± 0.62 | 94.50 ± 0.57 | 94.27 ± 0.64 | 94.37 ± 0.59 | |
| 94.36 ± 0.51 | 94.86 ± 0.55 | 94.67 ± 0.47 | 94.76 ± 0.50 | ||
| HAGRID | 94.50 ± 0.81 | 94.81 ± 0.78 | 94.69 ± 0.72 | 94.74 ± 0.74 | |
| 95.14 ± 0.51 | 95.49 ± 0.48 | 95.18 ± 0.51 | 95.33 ± 0.47 | ||
| IBRA-PCA | 95.69 ± 0.44 | 96.13 ± 0.44 | 95.92 ± 0.38 | 96.02 ± 0.39 | |
| 96.74 ± 0.30 | 96.96 ± 0.29 | 96.85 ± 0.28 | 96.91 ± 0.27 | ||
| IBRA-PLS-DA | 96.51 ± 0.46 | 96.78 ± 0.43 | 96.67 ± 0.44 | 96.72 ± 0.42 | |
| 96.82 ± 0.50 | 97.08 ± 0.44 | 96.86 ± 0.54 | 96.97 ± 0.48 | ||
| IBRA-GSS | 96.69 ± 0.35 | 96.92 ± 0.38 | 96.95 ± 0.34 | 96.93 ± 0.35 | |
| 96.21 ± 0.49 | 96.51 ± 0.45 | 96.40 ± 0.44 | 96.45 ± 0.44 |
| Method | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|
| PLS-DA | 96.68 ± 0.86 | 96.83 ± 0.99 | 95.62 ± 0.94 | 96.11 ± 0.74 |
| 97.17 ± 0.60 | 97.30 ± 0.79 | 96.66 ± 1.03 | 96.90 ± 0.84 | |
| OCF | 96.68 ± 0.56 | 97.34 ± 0.76 | 96.34 ± 0.98 | 96.77 ± 0.82 |
| 97.02 ± 0.58 | 97.73 ± 0.51 | 97.14 ± 0.63 | 97.39 ± 0.48 | |
| HAGRID | 96.74 ± 0.54 | 97.06 ± 0.75 | 96.34 ± 1.03 | 96.65 ± 0.88 |
| 97.03 ± 0.75 | 97.24 ± 0.86 | 96.72 ± 1.45 | 96.91 ± 1.21 | |
| SR-SSIM | 97.28 ± 0.37 | 97.74 ± 0.44 | 97.34 ± 0.80 | 97.49 ± 0.57 |
| 96.83 ± 0.77 | 97.14 ± 1.02 | 96.82 ± 1.95 | 96.86 ± 1.47 | |
| FNGBS | 97.49 ± 0.34 | 97.86 ± 0.36 | 97.64 ± 0.71 | 97.72 ± 0.5 |
| 97.34 ± 0.65 | 97.94 ± 0.52 | 97.75 ± 0.46 | 97.82 ± 0.44 | |
| IBRA-PCA | 94.70 ± 0.65 | 96.12 ± 0.71 | 94.45 ± 1.52 | 95.10 ± 1.02 |
| 96.99 ± 0.97 | 97.84 ± 0.77 | 97.60 ± 0.39 | 97.70 ± 0.55 | |
| IBRA-PLS-DA | 96.11 ± 1.37 | 97.10 ± 1.04 | 96.60 ± 0.98 | 96.70 ± 1.01 |
| 97.19 ± 0.67 | 97.77 ± 0.67 | 97.67 ± 1.03 | 97.64 ± 0.95 | |
| IBRA-GSS | 98.08 ± 0.43 | 98.26 ± 0.42 | 98.39 ± 0.43 | 98.32 ± 0.39 |
| 98.24 ± 0.39 | 98.56 ± 0.38 | 98.43 ± 0.42 | 98.48 ± 0.36 |
| Method | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|
| PLS-DA | 97.89 ± 0.18 | 98.99 ± 0.09 | 99.10 ± 0.10 | 99.04 ± 0.09 |
| 98.46 ± 0.10 | 99.24 ± 0.04 | 99.33 ± 0.03 | 99.28 ± 0.03 | |
| OCF | 98.37 ± 0.14 | 99.20 ± 0.07 | 99.29 ± 0.07 | 99.24 ± 0.07 |
| 98.51 ± 0.12 | 99.27 ± 0.08 | 99.34 ± 0.06 | 99.30 ± 0.07 | |
| HAGRID | 98.47 ± 0.11 | 99.26 ± 0.09 | 99.36 ± 0.05 | 99.31 ± 0.06 |
| 98.51 ± 0.12 | 99.29 ± 0.08 | 99.37 ± 0.05 | 99.33 ± 0.06 | |
| SR-SSIM | 97.89 ± 0.22 | 99.11 ± 0.11 | 99.07 ± 0.09 | 99.09 ± 0.09 |
| 98.14 ± 0.21 | 99.18 ± 0.12 | 99.18 ± 0.09 | 99.18 ± 0.10 | |
| FNGBS | 98.44 ± 0.14 | 99.34 ± 0.08 | 99.37 ± 0.06 | 99.35 ± 0.07 |
| 98.51 ± 0.10 | 99.37 ± 0.05 | 99.39 ± 0.04 | 99.38 ± 0.04 | |
| IBRA-PCA | 96.10 ± 0.78 | 98.23 ± 0.34 | 98.14 ± 0.49 | 98.16 ± 0.45 |
| 98.49 ± 0.16 | 99.39 ± 0.07 | 99.39 ± 0.07 | 99.39 ± 0.06 | |
| IBRA-PLS-DA | 96.26 ± 0.21 | 98.33 ± 0.14 | 98.36 ± 0.11 | 98.34 ± 0.10 |
| 98.14 ± 0.20 | 99.25 ± 0.08 | 99.23 ± 0.09 | 99.24 ± 0.08 | |
| IBRA-GSS | 99.05 ± 0.05 | 99.56 ± 0.04 | 99.55 ± 0.03 | 99.56 ± 0.03 |
| 99.07 ± 0.09 | 99.53 ± 0.06 | 99.55 ± 0.03 | 99.54 ± 0.04 |
| Compared Method | Kochia, | Kochia, | Kochia, | |||
|---|---|---|---|---|---|---|
| t-Test | Perm. | t-Test | Perm. | t-Test | Perm. | |
| FNGBS | 7.4 × (↑) | 2 × (↑) | 4.2 × (↑) | 1.7 × (↑) | 1 × (↑) | 2 × (↑) |
| 1.8 × (↑) | 2 × (↑) | 5.9 × (↑) | 1.7 × (↑) | 3.7 × (↑) | 2 × (↑) | |
| PLS-DA | 6.5 × (↑) | 2.6 × (↑) | 2.1 × (↑) | 2.6 × (↑) | 1.4 × (↑) | 2.6 × (↑) |
| 1.2 × (↑) | 2.6 × (↑) | 3.9 × (↑) | 2.6 × (↑) | 3.6 × (↑) | 2.6 × (↑) | |
| SR-SSIM | 1 × (↑) | 2 × (↑) | 2.6 × (↑) | 2 × (↑) | 9.9 × (↑) | 2 × (↑) |
| 1 × (↑) | 2 × (↑) | 4.2 × (↑) | 2 × (↑) | 9.9 × (↑) | 2 × (↑) | |
| OCF | 3 × (↑) | 1.9 × (↑) | 6.3 × (↑) | 3.5 × (↑) | 8 × (↑) | 1.9 × (↑) |
| 2 × (↑) | 5.4 × (↑) | 1.2 × (↑) | 1.9 × (↑) | 1.2 × (↑) | 1.9 × (↑) | |
| HAGRID | 9.1 × (↑) | 1.6 × (↑) | 5.3 × (↑) | 1.6 × (↑) | 2.1 × (↑) | 1.6 × (↑) |
| 2.8 × (↑) | 3.3 × (↑) | 5.5 × (↑) | 1.6 × (↑) | 1.6 × (↑) | 1.6 × (↑) | |
| IBRA-PCA | 3.8 × (↑) | 1.8 × (↑) | 1.9 × (↑) | 1.8 × (↑) | 9 × (↑) | 1.8 × (↑) |
| 2.9 × (↑) | 1.8 × (↑) | 1.6 (↓) | 2.3 (↓) | 5.6 (=) | 5.9 × (=) | |
| IBRA-PLS-DA | 1.8 × (↑) | 1.7 × (↑) | 2.1 (↓) | 1.2 (↓) | 0.18 (=) | 0.18 (=) |
| 7 × (↑) | 0.012 (↑) | 5.1 (↓) | 1.7 (↓) | 1.3 (↓) | 1.9 (↓) | |
| Compared Method | IP, | SA, | ||
|---|---|---|---|---|
| t-Test | Perm. | t-Test | Perm. | |
| FNGBS | 1 × (↑) | 5.7 × (↑) | 4.1 × (↑) | 2 × (↑) |
| 1.2 × (↑) | 0.014 (↑) | 2.8 × (↑) | 1.7 × (↑) | |
| PLS-DA | 1 × (↑) | 2.6 × (↑) | 3.4 × (↑) | 2.6 × (↑) |
| 5.2 × (↑) | 2.6 × (↑) | 1.4 × (↑) | 1.8 × (↑) | |
| SR-SSIM | 2.5 × (↑) | 3.6 × (↑) | 1.9 × (↑) | 2 × (↑) |
| 2.5 × (↑) | 3.6 × (↑) | 1.9 × (↑) | 2 × (↑) | |
| OCF | 3 × (↑) | 1.9 × (↑) | 3.3 × (↑) | 1.9 × (↑) |
| 4.7 × (↑) | 1.9 × (↑) | 4.2 × (↑) | 1.6 × (↑) | |
| HAGRID | 3 × (↑) | 1.6 × (↑) | 2.8 × (↑) | 1.6 × (↑) |
| 2.5 × (↑) | 3.4 × (↑) | 3.6 × (↑) | 1.9 × (↑) | |
| IBRA-PCA | 7.9 × (↑) | 1.8 × (↑) | 5.4 × (↑) | 1.8 × (↑) |
| 1 × (↑) | 1.8 × (↑) | 5.3 × (↑) | 2.6 × (↑) | |
| IBRA-PLS-DA | 2.7 × (↑) | 1.7 × (↑) | 2.9 × (↑) | 1.7 × (↑) |
| 2.5 × (↑) | 1.3 × (↑) | 1.4 × (↑) | 1.7 × (↑) | |
| # Bands | ||||
|---|---|---|---|---|
| Metric | ||||
| Mean | 88.48 | 92.15 | 95.18 | |
| 91.08 | 93.84 | 95.58 | ||
| Std | 3.93 | 3.68 | 1.43 | |
| 2.38 | 1.31 | 1.13 | ||
| F statistic | 75.99 | 69.29 | 34.05 | |
| 102.65 | 29.1 | 38.98 | ||
| p-value | 1.1 × | 1.9 × | 2 × | |
| 7.2 × | 1.3 × | 4.8 × | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morales, G.; Sheppard, J.W.; Logan, R.D.; Shaw, J.A. Hyperspectral Dimensionality Reduction Based on Inter-Band Redundancy Analysis and Greedy Spectral Selection. Remote Sens. 2021, 13, 3649. https://doi.org/10.3390/rs13183649
Morales G, Sheppard JW, Logan RD, Shaw JA. Hyperspectral Dimensionality Reduction Based on Inter-Band Redundancy Analysis and Greedy Spectral Selection. Remote Sensing. 2021; 13(18):3649. https://doi.org/10.3390/rs13183649
Chicago/Turabian StyleMorales, Giorgio, John W. Sheppard, Riley D. Logan, and Joseph A. Shaw. 2021. "Hyperspectral Dimensionality Reduction Based on Inter-Band Redundancy Analysis and Greedy Spectral Selection" Remote Sensing 13, no. 18: 3649. https://doi.org/10.3390/rs13183649
APA StyleMorales, G., Sheppard, J. W., Logan, R. D., & Shaw, J. A. (2021). Hyperspectral Dimensionality Reduction Based on Inter-Band Redundancy Analysis and Greedy Spectral Selection. Remote Sensing, 13(18), 3649. https://doi.org/10.3390/rs13183649