Modifications of the Multi-Layer Perceptron for Hyperspectral Image Classification
Abstract
:1. Introduction
- (1)
- Instead of simply applying the traditional MLP for HSI classification, a modified MLP is investigated for HSI classification with ingenious architecture in a unified framework (i.e., normalization layer, residual connections, and gaussian error linear unit operations). The Modified-MLP not only extracts discriminative features independently through spectral–spatial feature mapping, but also captures interactions with each patch by spectral–spatial information mixing for effective HSI classification.
- (2)
- To obtain the spectral–spatial information in each sample sufficiently, a simple yet effective Multiscale-MLP is proposed to classify HSI with various scales, which divides an HSI sample into various equal-sized patches without overlapping to aggregate multiple spectral–spatial interactions of different patches in HSI sample.
- (3)
- Another method, flexible Soft-MLP, is proposed with soft split operation to solve the limitations caused by the predefined patch size in MLP-based methods, which transforms a single sample of HSI with different orders and sizes with overlapping by applying soft split operation. Therefore, the Soft-MLP can model the global spectral–spatial relations of different patches to further boost the HSI classification performance.
- (4)
- Finally, label smoothing has been used for HSI classification combined with the proposed Soft-MLP, which leads to higher accuracies and indicates that the proposed MLP-based methods can be improved as CNN-based methods.
2. The MLP-Based Methods for HSI Classification
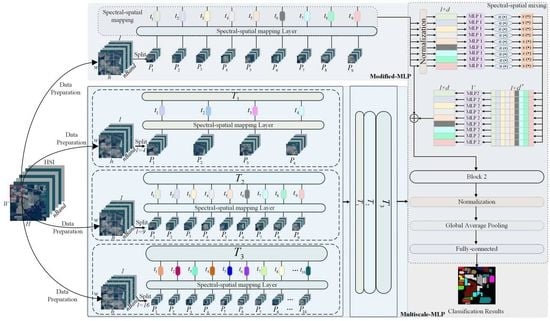
2.1. The Proposed Modified-MLP for HSI Classification
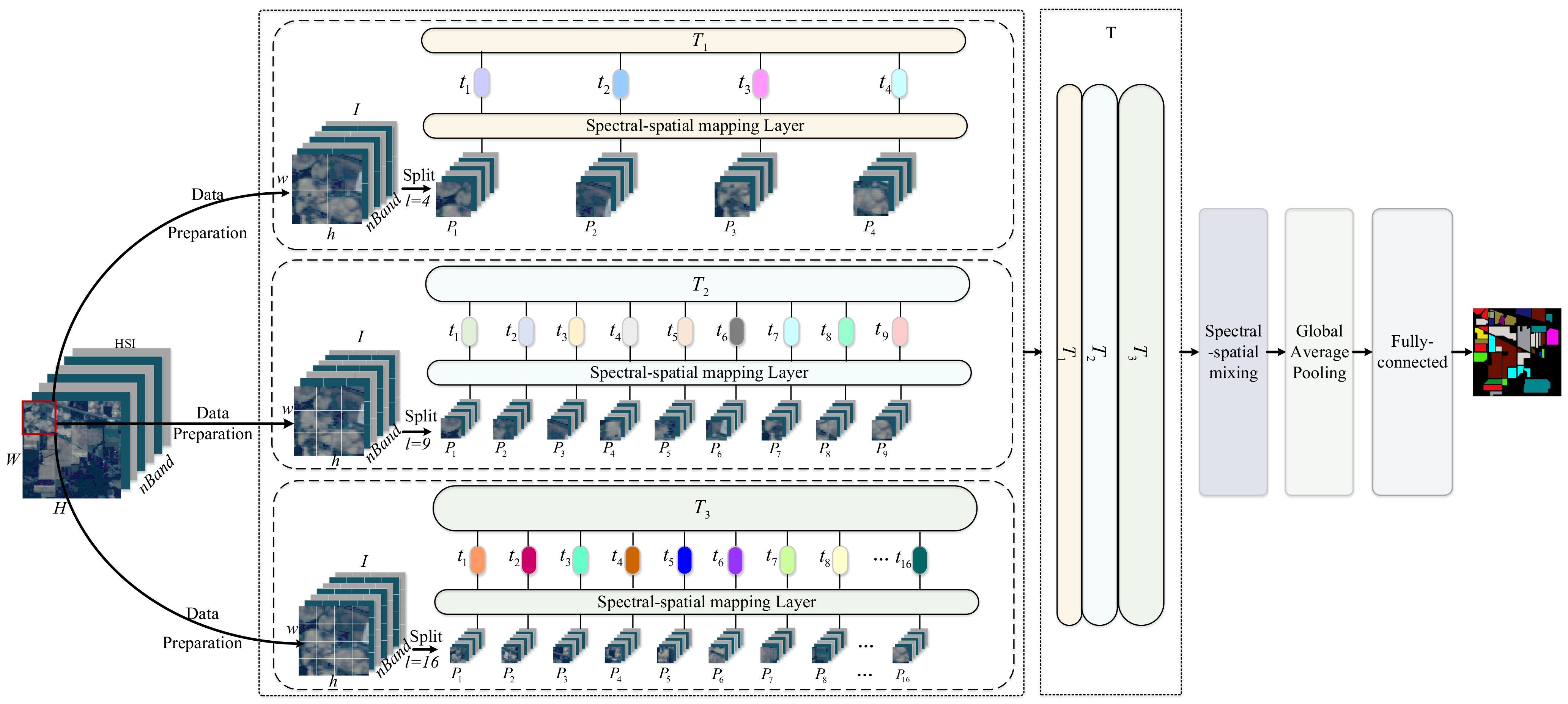
2.2. The Proposed Multiscale-MLP for HSI Classification
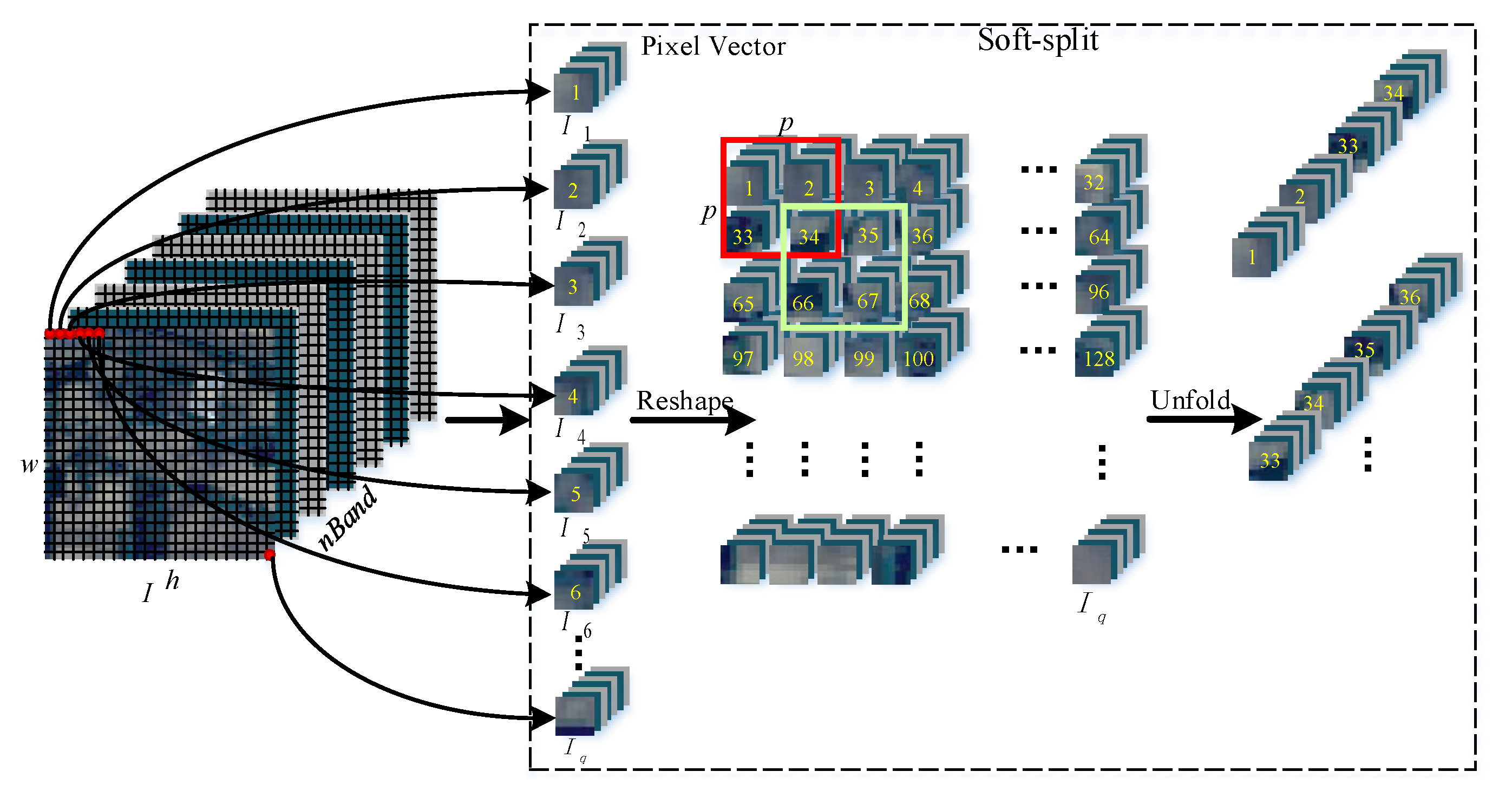
2.3. The Proposed Soft-MLP for HSI Classification
2.4. The Proposed Soft-MLP-L for HSI Classification
3. Experimental Results
3.1. Data Description
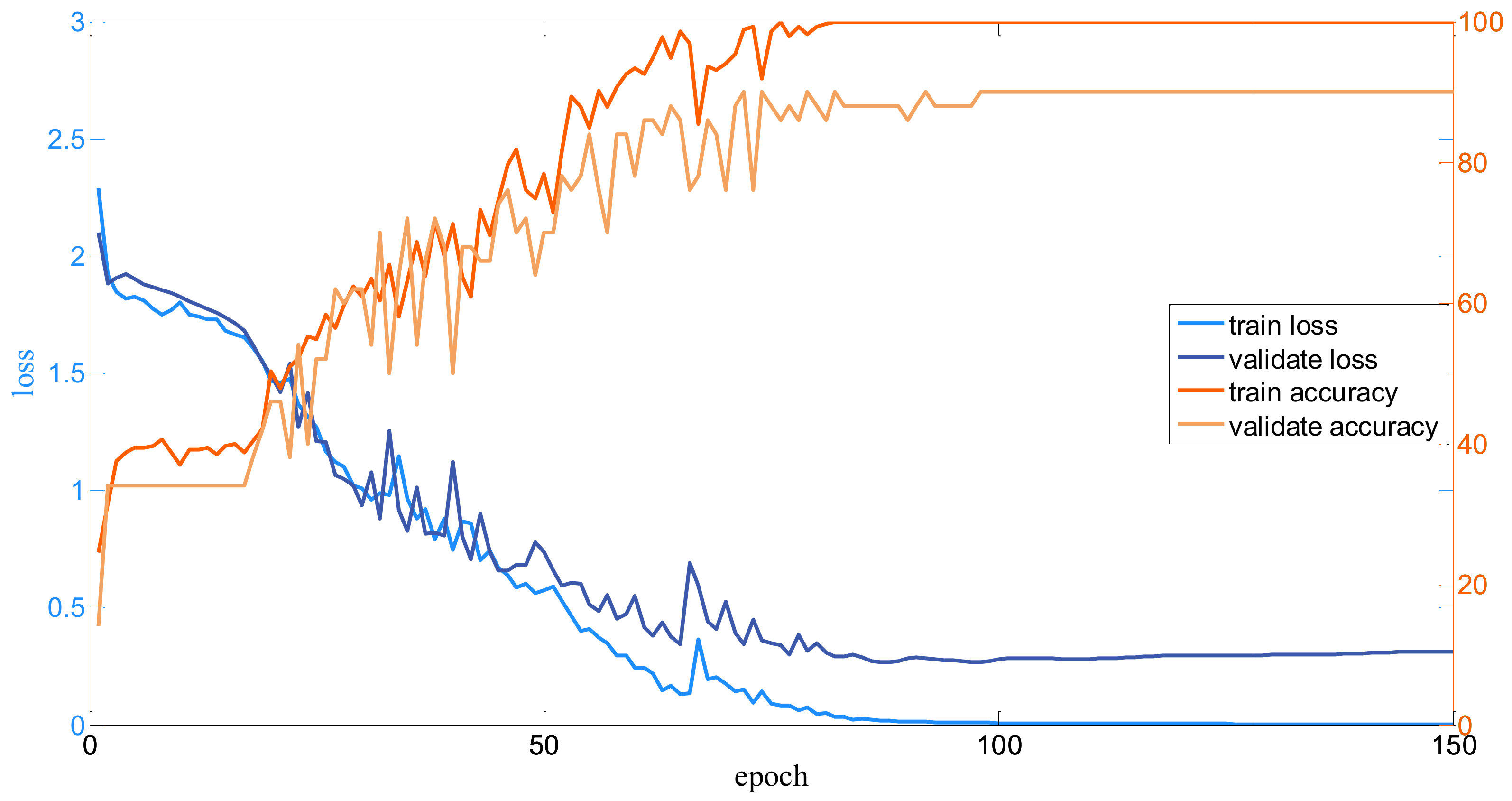
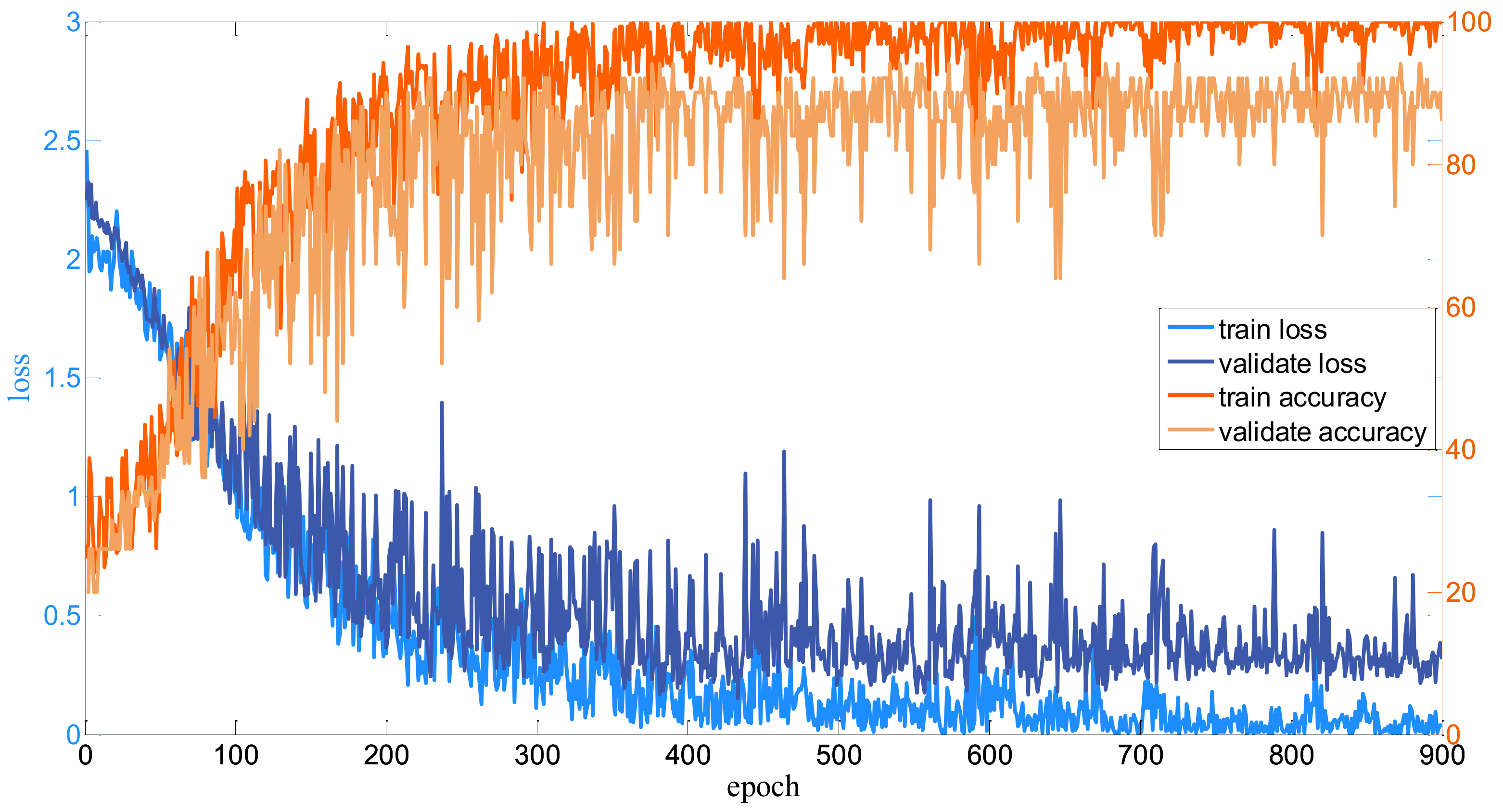
3.2. Implementation Details
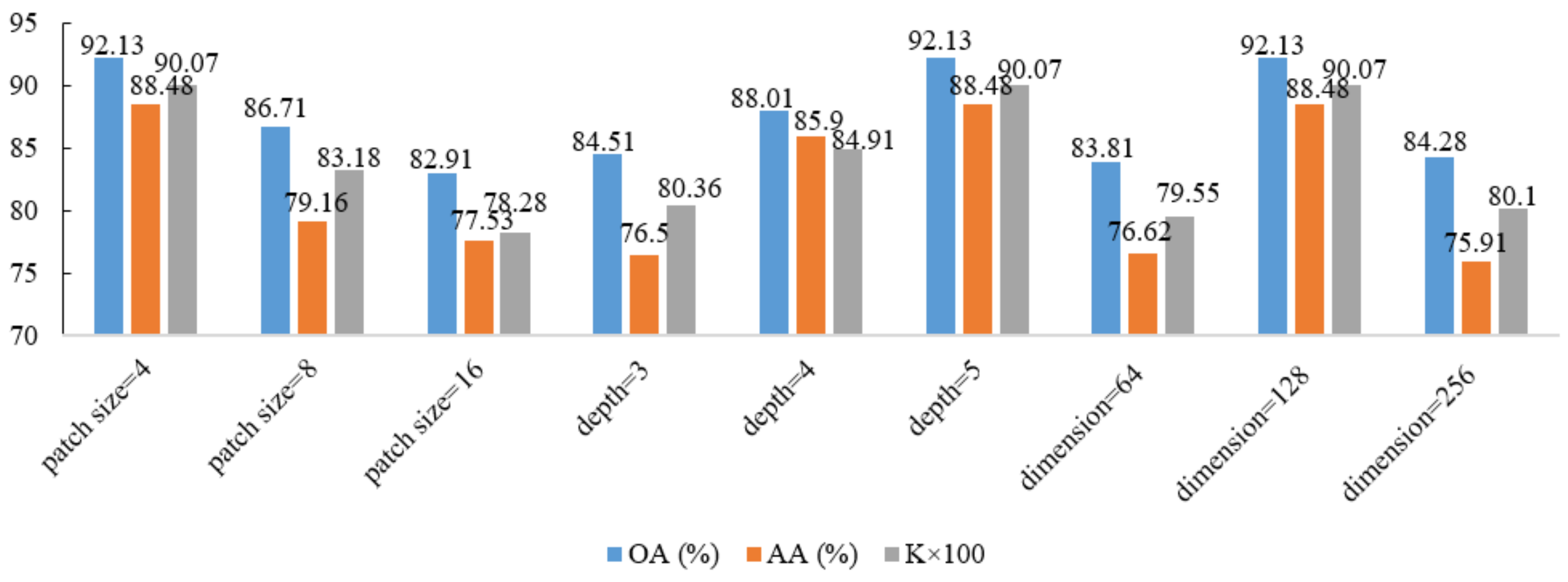
3.3. Parameter Analysis
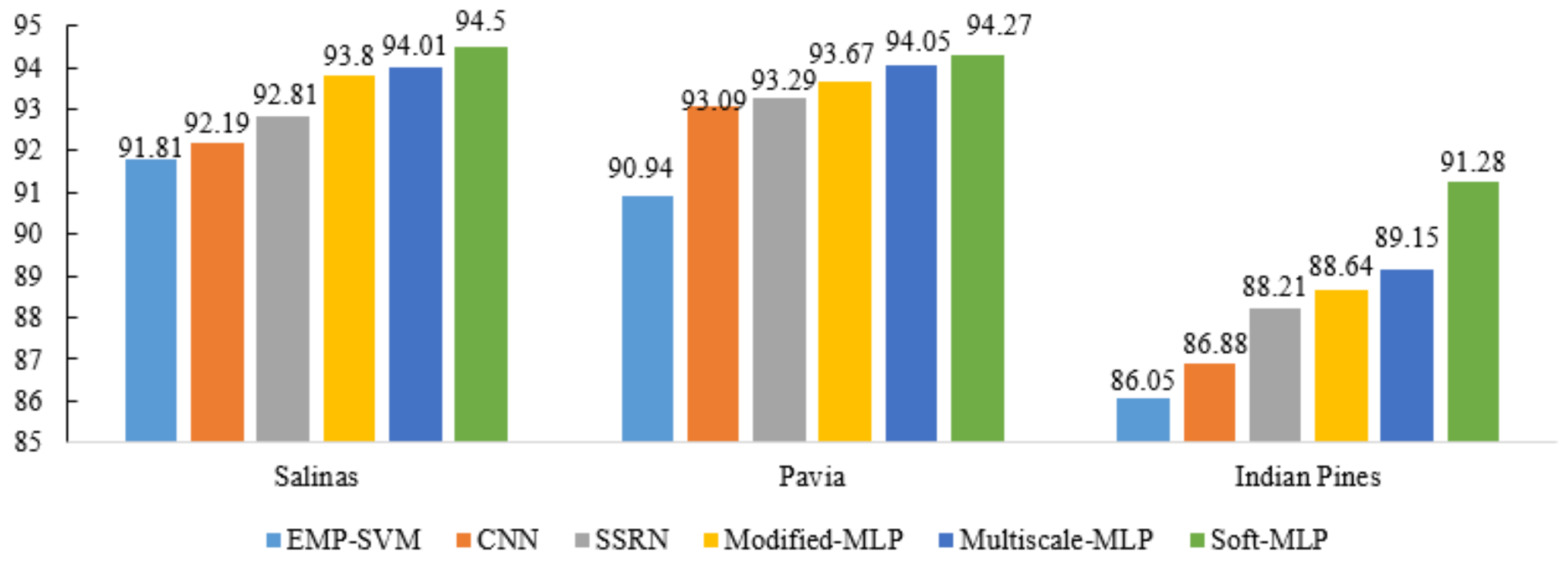
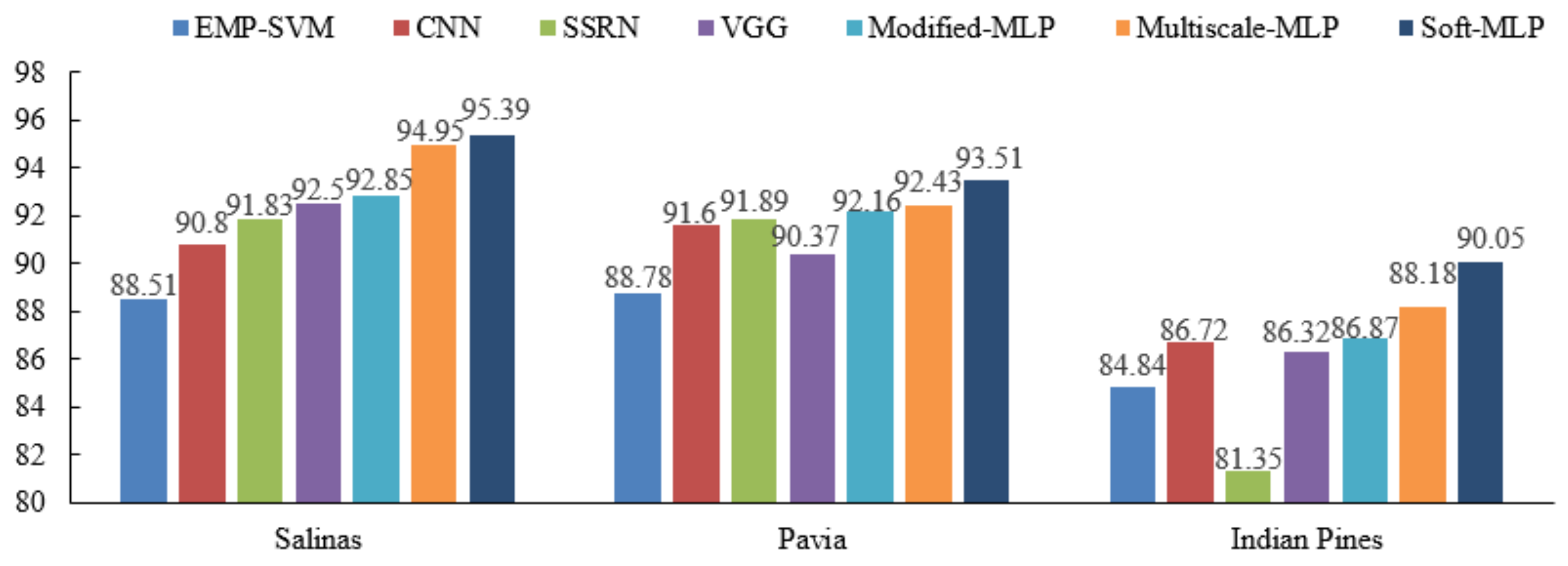
3.4. Comparison of the Proposed Methods with the State-of-the-Art Methods
3.5. Comparison with Different Methods with Cross-Validation Strategy
3.6. Comparison the Running Time and Computational Complexity of the Proposed Methods with the State-of-the-Art Methods
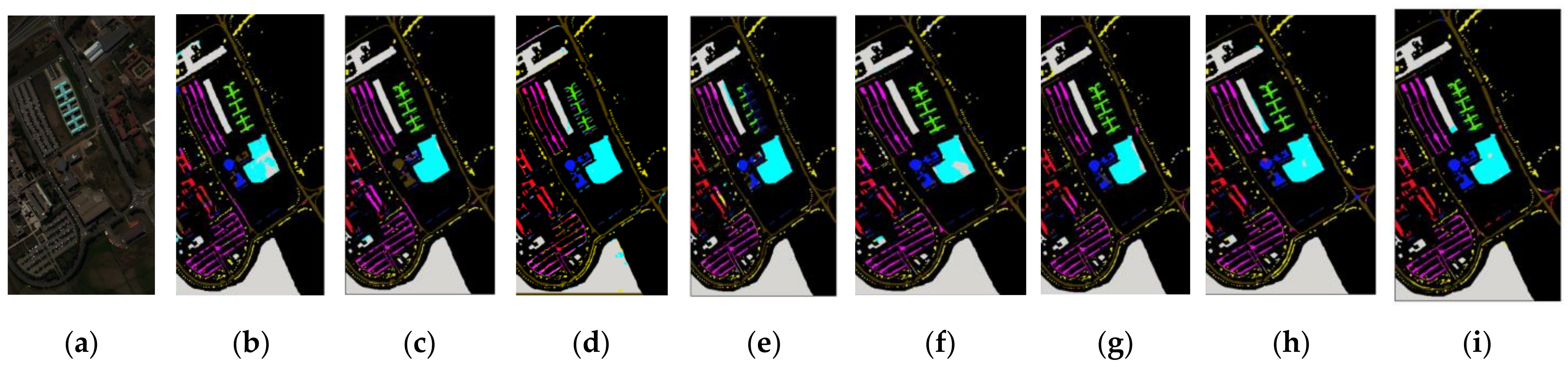
3.7. Classification Maps
3.8. Experimental Summary
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rußwurm, M.; Körner, M. Temporal vegetation modelling using long short-term memory networks for crop identification from medium-resolution multi-spectral satellite images. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1496–1504. [Google Scholar]
- El-Magd, I.A.; El-Zeiny, A. Quantitative hyperspectral analysis for characterization of the coastal water from Damietta to Port Said, Egypt. Egypt. J. Remote Sens. Space Sci. 2014, 17, 61–76. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Chen, M.; Wang, C.; Luo, L.; Li, J.; Lian, G.; Zou, X. Recognition and localization methods for vision-based fruit picking robots: A review. Front. Plant Sci. 2020, 11, 510. [Google Scholar] [CrossRef]
- Hestir, E.; Brando, V.; Bresciani, M.; Giardino, C.; Matta, E.; Villa, P.; Dekker, A. Measuring freshwater aquatic ecosystems: The need for a hyperspectral global mapping satellite mission. Remote Sens. Environ. 2015, 167, 181–195. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Li, J.; Zhang, Y.; Hong, Z.; Wang, J. Sea ice detection based on an improved similarity measurement method using hyperspectral data. Sensors 2017, 17, 1124. [Google Scholar] [CrossRef] [Green Version]
- Shang, X.; Chisholm, L. Classification of Australian native forest species using hyperspectral remote sensing and ma-chine-learning classification algorithms. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 2481–2489. [Google Scholar] [CrossRef]
- Peerbhay, K.; Mutanga, O.; Ismail, R. Random Forests Unsupervised Classification: The Detection and Mapping of Solanum mauritianum Infestations in Plantation Forestry Using Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3107–3122. [Google Scholar] [CrossRef]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hypersectral imaging for military and security applications: Combining myriad processing and sensing techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Chen, M.; Tang, Y.; Zou, X.; Huang, Z.; Zhou, H.; Chen, S. 3D global mapping of large-scale unstructured orchard integrating eye-in-hand stereo vision and SLAM. Comput. Electron. Agric. 2021, 187, 106237. [Google Scholar] [CrossRef]
- Chen, M.; Tang, Y.; Zou, X.; Huang, K.; Li, L.; He, Y. High-accuracy multi-camera reconstruction enhanced by adaptive point cloud correction algorithm. Opt. Lasers Eng. 2019, 122, 170–183. [Google Scholar] [CrossRef]
- Audebert, N.; Le Saux, B.; Lefevre, S. Deep Learning for Classification of Hyperspectral Data: A Comparative Review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 159–173. [Google Scholar] [CrossRef] [Green Version]
- Rasti, B.; Hong, D.; Hang, R.; Ghamisi, P.; Kang, X.; Chanussot, J.; Benediktsson, J.A. Feature Extraction for Hyperspectral Imagery: The Evolution From Shallow to Deep: Overview and Toolbox. IEEE Geosci. Remote Sens. Mag. 2020, 8, 60–88. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and Spatial Classification of Hyperspectral Data Using SVMs and Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef] [Green Version]
- Benediktsson, J.A.; Palmason, J.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Mura, M.D.; Villa, A.; Benediktsson, J.A.; Chanussot, J.; Bruzzone, L. Classification of Hyperspectral Images by Using Extended Morphological Attribute Profiles and Independent Component Analysis. IEEE Geosci. Remote Sens. Lett. 2011, 8, 542–546. [Google Scholar] [CrossRef] [Green Version]
- Fang, L.; He, N.; Li, S.; Ghamisi, P.; Benediktsson, J.A. Extinction Profiles Fusion for Hyperspectral Images Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1803–1815. [Google Scholar] [CrossRef]
- Gualtieri, J.A.; Cromp, R.F. Support vector machines for hyperspectral remote sensing classification. In Proceedings of the Inter-National Society for Optical Engineering, Santa Clara, CA, USA, 8–10 February 1999; Volume 3584, pp. 221–232. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.-B. Learning to diversify deep belief networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- He, N.; Paoletti, M.; Haut, J.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature extraction with multiscale covariance maps for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 202–216. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H.-C. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2016, 55, 844–853. [Google Scholar] [CrossRef]
- Kang, X.; Zhuo, B.; Duan, P. Dual-path network-based hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 16, 447–451. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Li, J. Visual Attention-Driven Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8065–8080. [Google Scholar] [CrossRef]
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, A.J. Advanced spectral classifiers for hyperspectral images: A review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Yang, Q.; Wu, Y.; Zhao, W.; Zhang, X. Double-branch multi-attention mechanism network for hyperspectral image classification. Remote Sens. 2019, 11, 1307. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Zheng, S.; Duan, C.; Yang, Y.; Wang, X. Classification of Hyperspectral Image Based on Double-Branch Dual-Attention Mechanism Network. Remote Sens. 2020, 12, 582. [Google Scholar] [CrossRef] [Green Version]
- Alam, F.; Zhou, J.; Liew, A.; Jia, X.; Chanussot, J.; Gao, Y. Conditional random field and deep feature learning for hyper-spectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8065–8080. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral-spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Song, M.; Shang, X.; Chang, C.-I. 3-D receiver operating characteristic analysis for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8093–8115. [Google Scholar] [CrossRef]
- Tang, X.; Meng, F.; Zhang, X.; Cheung, Y.-M.; Ma, J.; Liu, F.; Jiao, L. Hyperspectral image classification based on 3-D octave convolution with spatial-spectral attention network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2430–2447. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef] [Green Version]
- Lu, W.; Wang, X. Overview of hyperspectral image classification. J. Sens. 2020, 2020, 4817234. [Google Scholar]
- Oquab, M.; Bottou, L.; Laptev, I.; Sivic, J. Learning and transferring mid-level image representations using convolutional neural networks. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1717–1724. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.; Mathias, M.; Rio, A.; Sennrich, R. Why self-attention? A targeted evaluation of neural machine translation architectures. arXiv 2018, arXiv:1808.08946v3. Available online: https://arxiv.org/pdf/1808.08946v3.pdf (accessed on 11 November 2020).
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation. In Readings in Cognitive Science; Elsevier: Amsterdam, The Netherlands, 1985. [Google Scholar] [CrossRef]
- Thakur, A.; Mishra, D. Hyper spectral image classification using multilayer perceptron neural network & functional link ANN. In Proceedings of the 2017 7th International Conference on Cloud Computing, Data Science & Engineering—Confluence, Noida, India, 12–13 January 2017; pp. 639–642. [Google Scholar] [CrossRef]
- Garcia, B.; Ponomaryov, V.; Robles, M. Parallel multilayer perceptron neural network used for hyperspectral image classification. In Proceedings of the Real-Time Image and Video Processing 2016 International Society for Optics and Photonics, Boulder, CO, USA, 25–28 September 2016; pp. 1–14. [Google Scholar]
- Kalaiarasi, G.; Maheswari, S. Frost filtered scale-invariant feature extraction and multilayer perceptron for hyperspectral image classification. arXiv 2020, arXiv:2006.12556. Available online: https://arxiv.org/ftp/arxiv/papers/2006/2006.12556.pdf (accessed on 2 November 2012).
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (GELUs). arXiv 2020, arXiv:1606.08415. Available online: https://arxiv.org/pdf/1606.08415.pdf (accessed on 8 July 2020).
- Ba, J.; Kiros, J.; Hinton, G. Layer normalization. arXiv 2016, arXiv:1607.06450. Available online: https://arxiv.org/pdf/1607.06450v1.pdf (accessed on 21 July 2016).
- Dauphin, Y.; Fan, A.; Auli, M.; Grangier, D. Language modeling with gated convolutional networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 10–19. [Google Scholar]
- Muller, R.; Kornblith, S.; Hinton, G. When does label smoothing help? In Proceedings of the NeurIPS, Vancouver, BC, Canada, 8–14 December 2019; pp. 4696–4705. [Google Scholar]
- Aurelio, Y.S.; Almeida, G.; De Castro, C.L.; Braga, A.P. Learning from imbalanced data sets with weighted cross-entropy function. Neural Process. Lett. 2019, 50, 1937–1949. [Google Scholar] [CrossRef]
- Melgani, F.; Lorenzo, B. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhu, L.; Ghamisi, P.; Jia, X.; Li, G.; Tang, L. Hyperspectral Images Classification With Gabor Filtering and Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2355–2359. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the Interna-tional Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef] [Green Version]
- Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning convolutional neural networks for resource efficient inference. arXiv 2017, arXiv:1611.06440. Available online: https://arxiv.org/pdf/1611.06440.pdf (accessed on 8 June 2017).











| Class | Sample Numbers | ||
|---|---|---|---|
| No. | Color | Name | |
| 1 |  | Brocoli_green_weeds_1 | 1977 |
| 2 |  | Brocoli_green_weeds_2 | 3726 |
| 3 |  | Fallow | 1976 |
| 4 |  | Fallow_rough_plow | 1394 |
| 5 |  | Fallow_smooth | 2678 |
| 6 |  | Stubble | 3959 |
| 7 |  | Celery | 3579 |
| 8 |  | Grapes_untrained | 11,213 |
| 9 |  | Soil_vinyard_develop | 6197 |
| 10 |  | Corn_senesced_green_weeds | 3249 |
| 11 |  | Lettuce_romaine_4wk | 1058 |
| 12 |  | Lettuce_romaine_5wk | 1908 |
| 13 |  | Lettuce_romaine_6wk | 909 |
| 14 |  | Lettuce_romaine_7wk | 1061 |
| 15 |  | Vinyard_untrained | 7164 |
| 16 |  | Vinyard_vertical_trellis | 1737 |
| Total | 53,785 | ||
| Class | Sample Numbers | ||
|---|---|---|---|
| No. | Color | Name | |
| 1 |  | Asphalt | 6851 |
| 2 |  | Meadows | 18,686 |
| 3 |  | Gravel | 2207 |
| 4 |  | Trees | 3436 |
| 5 |  | Metal sheets | 1378 |
| 6 |  | Bare soil | 5104 |
| 7 |  | Bitumen | 1356 |
| 8 |  | Bricks | 3878 |
| 9 |  | Shadow | 1026 |
| Total | 43,922 | ||
| Class | Sample Numbers | ||
|---|---|---|---|
| No. | Color | Name | |
| 1 |  | Alfalfa | 46 |
| 2 |  | Corn-notill | 1428 |
| 3 |  | Corn-min | 830 |
| 4 |  | Corn | 237 |
| 5 |  | Grass-pasture | 483 |
| 6 |  | Grass-trees | 730 |
| 7 |  | Grass-pasture-mowed | 28 |
| 8 |  | Hay-windrowed | 478 |
| 9 |  | Oats | 20 |
| 10 |  | Soybean-notill | 972 |
| 11 |  | Soybean-mintill | 2455 |
| 12 |  | Soybean-clean | 593 |
| 13 |  | Wheat | 205 |
| 14 |  | Woods | 1265 |
| 15 |  | Buildings-Grass-Trees | 386 |
| 16 |  | Stone-Steel-Towers | 93 |
| Total | 10,249 | ||
| Method | RBF-SVM | EMP-SVM | CNN | SSRN | VGG | HybridSN | Modified-MLP | Multiscale-MLP | Soft- MLP | Soft- MLP-L |
|---|---|---|---|---|---|---|---|---|---|---|
| OA (%) | 83.09 ± 1.08 | 87.59 ± 2.39 | 88.40 ± 2.13 | 88.73 ± 2.06 | 89.25 ± 5.20 | 90.81 ± 2.87 | 91.92 ± 2.45 | 92.25 ± 2.57 | 93.48 ± 1.30 | 94.16 ± 0.71 |
| AA (%) | 85.46 ± 2.06 | 88.65 ± 1.93 | 92.48 ± 2.79 | 92.63 ± 1.47 | 90.16 ± 4.81 | 90.77 ± 3.27 | 92.05 ± 3.41 | 93.50 ± 2.22 | 94.21 ± 2.76 | 93.94 ± 1.43 |
| K × 100 | 81.07 ± 1.19 | 86.15 ± 2.75 | 88.27 ± 2.73 | 87.51 ± 2.26 | 88.05 ± 5.82 | 89.90 ± 3.25 | 90.96 ± 2.74 | 91.33 ± 2.51 | 92.70 ± 1.46 | 93.46 ± 0.81 |
| Brocoli_ green_weeds_1 | 94.15 ± 0.50 | 95.28 ± 4.21 | 81.75 ± 5.36 | 100.00 ± 0.00 | 82.46 ± 17.94 | 99.53 ± 0.68 | 87.56 ± 17.77 | 93.31 ± 17.69 | 99.87 ± 21.95 | 95.24 ± 6.23 |
| Brocoli_ green_weeds_2 | 98.57 ± 0.89 | 98.49 ± 0.28 | 88.89 ± 7.69 | 100.00 ± 0.00 | 88.85 ± 2.11 | 99.88 ± 0.21 | 91.52 ± 4.04 | 91.75 ± 4.98 | 87.27 ± 6.53 | 85.46 ± 6.82 |
| Fallow | 90.56 ± 0.50 | 70.53 ± 22.58 | 89.35 ± 3.85 | 72.85 ± 13.98 | 92.04 ± 1.61 | 87.06 ± 16.91 | 87.03 ± 15.21 | 95.73 ± 4.71 | 97.21 ± 5.23 | 95.20 ± 2.69 |
| Fallow_rough_plow | 98.93 ± 0.40 | 99.80 ± 0.12 | 80.01 ± 5.86 | 99.78 ± 2.15 | 89.86 ± 0.37 | 86.68 ± 14.06 | 97.15 ± 3.94 | 93.14 ± 8.40 | 99.68 ± 1.71 | 97.27 ± 2.17 |
| Fallow_smooth | 95.23 ± 0.63 | 93.34 ± 4.40 | 88.40 ± 2.57 | 98.68 ± 0.54 | 98.32 ± 3.18 | 92.29 ± 9.29 | 95.19 ± 4.88 | 95.46 ± 5.57 | 97.68 ± 5.41 | 96.96 ± 1.50 |
| Stubble | 99.25 ± 0.91 | 99.36 ± 0.22 | 90.45 ± 6.38 | 99.85 ± 0.89 | 99.97 ± 1.53 | 98.26 ± 2.48 | 99.53 ± 0.98 | 99.86 ± 0.18 | 99.89 ± 0.50 | 99.67 ± 0.40 |
| Celery | 98.82 ± 0.33 | 97.48 ± 1.84 | 97.96 ± 2.79 | 99.43 ± 0.43 | 96.98 ± 3.36 | 97.66 ± 2.51 | 96.42 ± 3.54 | 96.65 ± 3.15 | 99.68 ± 0.32 | 95.09 ± 3.84 |
| Grapes_untrained | 78.50 ± 0.57 | 90.09 ± 7.83 | 69.63 ± 9.62 | 62.90 ± 14.95 | 75.66 ± 11.52 | 88.21 ± 4.01 | 88.51 ± 6.99 | 84.56 ± 10.12 | 88.34 ± 4.30 | 92.70 ± 0.63 |
| Soil_vinyard_develop | 94.11 ± 0.50 | 98.89 ± 0.08 | 89.33 ± 9.79 | 97.87 ± 3.96 | 98.44 ± 0.13 | 99.73 ± 0.56 | 99.32 ± 0.67 | 99.93 ± 0.20 | 100.00 ± 0.00 | 99.87 ± 0.18 |
| Corn_senesced _green_weeds | 85.56 ± 0.36 | 90.74 ± 2.23 | 85.75 ± 9.08 | 88.08 ± 5.20 | 96.76 ± 13.29 | 85.54 ± 12.82 | 98.22 ± 1.50 | 98.78 ± 2.23 | 97.05 ± 2.76 | 97.49 ± 4.22 |
| Lettuce_romaine_4wk | 90.63 ± 0.78 | 93.06 ± 2.02 | 88.92 ± 9.72 | 86.54 ± 7.17 | 95.72 ± 28.25 | 78.36 ± 11.74 | 98.54 ± 2.18 | 94.25 ± 12.50 | 97.85 ± 3.56 | 99.08 ± 1.62 |
| Lettuce_romaine_5wk | 99.48 ± 0.03 | 99.98 ± 0.04 | 82.07 ± 9.37 | 99.41 ± 5.75 | 97.41± 1.01 | 90.06 ± 8.95 | 96.43 ± 2.46 | 98.58 ± 1.97 | 95.59 ± 3.70 | 98.53 ± 1.07 |
| Lettuce_romaine_6wk | 20.08 ± 2.47 | 77.91 ± 39.03 | 82.65 ± 8.30 | 84.74 ± 7.69 | 96.82 ± 37.37 | 79.08 ± 16.67 | 93.21 ± 6.55 | 88.29 ± 13.54 | 95.54 ± 11.66 | 92.43 ± 6.93 |
| Lettuce_romaine_7wk | 66.29 ± 1.67 | 98.34 ± 0.99 | 85.41 ± 9.25 | 99.33 ± 1.18 | 98.23 ± 1.40 | 91.44 ± 8.47 | 85.59 ± 19.38 | 95.49 ± 4.83 | 84.14 ± 8.47 | 92.73 ± 9.19 |
| Vinyard_untrained | 59.14 ± 1.06 | 35.73 ± 30.40 | 76.80 ± 18.48 | 93.40 ± 12.17 | 84.13 ± 35.13 | 83.29 ± 7.32 | 79.57 ± 11.79 | 83.28 ± 19.88 | 85.40 ± 7.80 | 88.17 ± 5.88 |
| Vinyard_vertical_ trellis | 66.96 ± 0.78 | 79.35 ± 6.22 | 56.06 ± 12.02 | 98.71 ± 2.58 | 50.94 ± 41.64 | 90.23 ± 11.11 | 78.98 ± 18.37 | 87.00 ± 15.40 | 82.20 ± 36.36 | 77.18 ± 20.27 |
| Method | RBF-SVM | EMP-SVM | CNN | SSRN | VGG | HybridSN | Modified-MLP | Multiscale-MLP | Soft- MLP | Soft- MLP-L |
|---|---|---|---|---|---|---|---|---|---|---|
| OA (%) | 80.06 ± 1.52 | 89.43 ± 1.20 | 91.41 ± 1.44 | 91.59 ± 3.57 | 91.72 ± 2.12 | 91.81 ± 1.35 | 92.13 ± 2.76 | 92.22 ± 1.32 | 93.02 ± 1.64 | 93.96 ± 2.11 |
| AA (%) | 69.48 ± 3.03 | 80.37 ± 3.60 | 81.03 ± 4.99 | 87.56 ± 3.57 | 84.13 ± 5.41 | 84.73 ± 1.81 | 88.48 ± 3.94 | 87.15 ± 2.09 | 88.38 ± 3.36 | 88.77 ± 3.76 |
| K × 100 | 74.19 ± 2.02 | 85.81 ± 1.64 | 89.12 ± 1.83 | 88.96 ± 1.56 | 89.53 ± 2.70 | 89.22 ± 1.82 | 90.07 ± 3.48 | 90.17 ± 1.66 | 91.13 ± 1.70 | 92.39 ± 2.70 |
| Asphalt | 88.75 ± 2.70 | 91.84 ± 1.75 | 92.36 ± 5.62 | 99.62 ± 2.57 | 89.85 ± 2.05 | 89.34 ± 3.64 | 92.68 ± 4.40 | 91.52 ± 4.18 | 93.11 ± 3.75 | 91.55 ± 6.27 |
| Meadows | 94.94 ± 1.47 | 98.02 ± 0.68 | 98.85 ± 1.04 | 98.85 ± 4.91 | 98.68 ± 1.23 | 99.55 ± 1.36 | 97.20 ± 1.62 | 98.06 ± 1.57 | 97.04 ± 1.43 | 98.48 ± 1.89 |
| Gravel | 34.89 ± 15.46 | 66.63 ± 14.10 | 42.94 ± 22.88 | 90.99 ± 25.41 | 68.99 ± 11.70 | 71.10 ± 9.07 | 79.84 ± 6.59 | 77.87 ± 10.70 | 73.10 ± 11.29 | 89.19 ± 16.83 |
| Trees | 64.11 ± 9.76 | 92.10 ± 5.14 | 93.52 ± 3.53 | 94.13 ± 8.55 | 86.72 ± 2.18 | 91.08 ± 6.13 | 94.53 ± 1.02 | 84.05 ± 5.60 | 84.72 ± 6.67 | 91.39 ± 6.78 |
| Metal sheets | 89.35 ± 8.20 | 86.26 ± 21.92 | 99.33 ± 0.72 | 99.63 ± 2.74 | 99.71 ± 0.21 | 99.93 ± 0.67 | 98.49 ± 1.11 | 97.40 ± 5.49 | 98.15 ± 3.55 | 90.80 ± 3.07 |
| Bare soil | 66.54 ± 6.15 | 78.66 ± 7.12 | 98.62 ± 1.54 | 77.72 ± 8.91 | 91.36 ± 3.23 | 99.09 ± 1.90 | 86.72 ± 3.97 | 91.20 ± 2.98 | 90.21 ± 6.43 | 96.23 ± 5.64 |
| Bitumen | 55.77 ± 22.79 | 74.43 ± 10.12 | 45.56 ± 27.30 | 59.63 ± 15.34 | 75.24 ± 22.87 | 73.33 ± 5.83 | 88.23 ± 11.54 | 90.16 ± 5.96 | 90.69 ± 8.28 | 88.34 ± 14.86 |
| Bricks | 73.39 ± 7.31 | 90.92 ± 3.70 | 90.60 ± 5.68 | 67.52 ± 23.28 | 97.24 ± 1.59 | 71.74 ± 13.24 | 88.25 ± 6.61 | 92.94 ± 2.84 | 91.50 ± 6.19 | 93.59 ± 7.51 |
| Shadow | 57.61 ± 21.51 | 74.11 ± 22.21 | 67.52 ± 33.51 | 99.90 ± 2.89 | 49.41 ± 26.69 | 67.38 ± 14.03 | 70.38 ± 14.97 | 61.16 ± 16.23 | 40.67 ± 28.98 | 48.73 ± 20.27 |
| Method | RBF-SVM | EMP-SVM | CNN | SSRN | VGG | HybridSN | Modified-MLP | Multiscale-MLP | Soft-MLP | Soft- MLP-L |
|---|---|---|---|---|---|---|---|---|---|---|
| OA (%) | 79.75 ± 1.89 | 81.53 ± 2.39 | 86.81 ± 1.28 | 83.21 ± 1.25 | 86.80 ± 1.08 | 83.08 ± 2.85 | 87.18 ± 1.53 | 87.59 ± 1.75 | 88.37 ± 1.31 | 89.31 ± 0.78 |
| AA (%) | 60.11 ± 2.56 | 72.43 ± 6.35 | 68.30 ± 4.82 | 62.88 ± 7.12 | 63.18 ± 1.98 | 70.38 ± 5.17 | 72.27 ± 4.54 | 67.26 ± 5.07 | 72.17 ± 5.29 | 76.23 ± 3.22 |
| K × 100 | 75.82 ± 2.35 | 78.87 ± 2.78 | 84.20 ± 1.57 | 80.86 ± 1.39 | 84.10 ± 1.29 | 81.65 ± 2.60 | 84.65 ± 1.85 | 85.09 ± 2.14 | 86.07 ± 1.59 | 87.20 ± 0.90 |
| Alfalfa | 38.67 ± 26.66 | 50.27 ± 41.37 | 38.70 ± 32.39 | 25.00 ± 35.08 | 35.56 ± 9.07 | 36.89 ± 13.20 | 60.69 ± 40.45 | 46.15 ± 31.40 | 50.45 ± 37.67 | 54.54 ± 50.43 |
| Corn-notill | 80.01 ± 9.17 | 72.43 ± 7.51 | 84.64 ± 6.07 | 87.16 ± 12.44 | 90.74 ± 1.98 | 73.12 ± 6.58 | 89.16 ± 4.33 | 88.03 ± 3.60 | 88.26 ± 5.39 | 92.14 ± 3.11 |
| Corn-min | 52.50 ± 11.83 | 80.77 ± 5.42 | 63.15 ± 22.10 | 95.61 ± 20.25 | 38.80 ± 20.66 | 72.04 ± 5.73 | 59.89 ± 17.34 | 53.83 ± 21.43 | 60.24 ± 22.20 | 47.85 ± 18.06 |
| Corn | 23.85 ± 22.71 | 74.44 ± 19.28 | 55.37 ± 45.79 | 20.60 ± 17.82 | 55.32 ± 27.30 | 59.01 ± 9.70 | 44.68 ± 38.53 | 50.63 ± 35.28 | 49.90 ± 38.15 | 82.94 ± 14.47 |
| Grass-pasture | 61.00 ± 16.10 | 77.04 ± 8.10 | 56.41 ± 10.40 | 84.93 ± 21.91 | 51.24 ± 11.62 | 79.04 ± 12.82 | 65.29 ± 12.39 | 55.64 ± 27.08 | 71.06 ± 15.30 | 71.60 ± 14.29 |
| Grass-trees | 91.76 ± 4.49 | 95.27 ± 3.54 | 96.90 ± 3.94 | 99.71 ± 6.22 | 94.21 ± 2.60 | 96.12 ± 3.01 | 93.30 ± 3.13 | 93.56 ± 3.66 | 89.95 ± 7.86 | 95.46 ± 2.50 |
| Grass-pasture-mowed | 16.58 ± 23.12 | 49.63 ± 49.64 | 42.54 ± 38.16 | 28.70 ± 48.04 | 13.58 ± 19.21 | 59.99 ± 23.05 | 21.28 ± 39.84 | 3.09 ± 10.69 | 42.07 ± 45.77 | 51.76 ± 48.25 |
| Hay-windrowed | 87.89 ± 8.56 | 97.43 ± 2.90 | 85.84 ± 27.28 | 97.65 ± 2.15 | 73.44 ± 18.42 | 99.87 ± 0.28 | 90.05 ± 7.87 | 94.40 ± 6.84 | 91.50 ± 10.38 | 82.75 ± 20.05 |
| Oats | 42.21 ± 37.64 | 28.95 ± 39.68 | 12.75 ± 18.33 | 9.28 ± 43.22 | 24.07 ± 34.05 | 15.79 ± 35.30 | 44.01 ± 47.16 | 13.96 ± 32.61 | 12.11 ± 25.79 | 35.79 ± 39.28 |
| Soybean-notill | 74.57 ± 8.69 | 74.92 ± 7.72 | 90.33 ± 6.48 | 80.77 ± 8.61 | 85.78 ± 4.08 | 85.56 ± 1.95 | 86.01 ± 9.06 | 89.57 ± 3.49 | 87.91 ± 2.85 | 92.81 ± 3.63 |
| Soybean-mintill | 92.74 ± 3.23 | 85.30 ± 4.85 | 94.21 ± 3.32 | 83.09 ± 6.57 | 95.70 ± 1.82 | 92.04 ± 3.49 | 91.82 ± 2.53 | 95.10 ± 1.57 | 94.85 ± 0.95 | 93.69 ± 1.85 |
| Soybean-clean | 48.60 ± 13.61 | 60.49 ± 10.01 | 58.07 ± 12.47 | 70.77 ± 21.72 | 69.35 ± 8.91 | 60.89 ± 14.47 | 65.56 ± 17.23 | 71.56 ± 20.86 | 75.11 ± 16.39 | 73.89 ± 13.50 |
| Wheat | 61.59 ± 25.50 | 75.54 ± 37.88 | 85.99 ± 14.62 | 98.48 ± 12.96 | 96.75 ± 2.72 | 77.88 ± 13.08 | 83.02 ± 16.25 | 77.20 ± 22.52 | 90.13 ± 9.74 | 83.77 ± 22.68 |
| Woods | 94.26 ± 2.15 | 96.56 ± 3.24 | 96.63 ± 2.53 | 96.99 ± 3.86 | 98.02 ± 1.93 | 96.30 ± 2.68 | 96.30 ± 2.46 | 96.67 ± 3.15 | 96.50 ± 2.68 | 94.39 ± 4.84 |
| Buildings-Grass-Trees | 52.78 ± 28.23 | 73.77 ± 9.55 | 67.38 ± 28.38 | 38.76 ± 18.17 | 58.04 ± 42.38 | 65.92 ± 17.24 | 84.59 ± 23.84 | 79.38 ± 18.41 | 77.92 ± 29.59 | 89.03 ± 19.96 |
| Stone-Steel-Towers | 42.78 ± 34.42 | 66.09 ± 43.03 | 63.96 ± 33.59 | 53.85 ± 44.51 | 30.22 ± 12.73 | 55.70 ± 12.43 | 66.36 ± 30.98 | 67.44 ± 36.81 | 75.20 ± 28.75 | 77.29 ± 31.60 |
| Datasets | Methods | Training Time (s) | Test Time (s) | FLOPs (M) | Total Parameters (M) |
|---|---|---|---|---|---|
| Salinas | CNN | 28.99 | 82.52 | 13.25 | 0.13 |
| SSRN | 141.57 | 66.69 | 47.13 | 0.24 | |
| VGG | 63.62 | 88.43 | 442.65 | 14.85 | |
| Modified-MLP | 64.02 | 63.24 | 45.62 | 0.72 | |
| Multiscale-MLP | 105.4 | 63.81 | 121.51 | 9.17 | |
| Soft-MLP | 164.57 | 93.92 | 524.45 | 9.27 | |
| Soft-MLP-L | 169.93 | 94.56 | 524.45 | 9.27 | |
| Pavia | CNN | 18.52 | 28.77 | 9.726 | 0.13 |
| SSRN | 76.82 | 20.58 | 29.12 | 0.14 | |
| VGG | 26.56 | 30.61 | 379.29 | 14.79 | |
| Modified-MLP | 59.45 | 49.23 | 38.67 | 0.61 | |
| Multiscale-MLP | 51.34 | 21.77 | 81.79 | 4.93 | |
| Soft-MLP | 206.97 | 65.41 | 317.61 | 4.99 | |
| Soft-MLP-L | 230.95 | 61.88 | 317.61 | 5.01 | |
| Indian Pines | CNN | 23.50 | 9.23 | 13.11 | 0.13 |
| SSRN | 132.51 | 3.68 | 46.19 | 0.23 | |
| VGG | 32.28 | 10.32 | 440.14 | 14.85 | |
| Modified-MLP | 126.09 | 5.43 | 57.67 | 0.91 | |
| Multiscale-MLP | 80.40 | 7.27 | 119.93 | 8.89 | |
| Soft-MLP | 116.41 | 11.23 | 516.26 | 9.00 | |
| Soft-MLP-L | 153.54 | 13.64 | 516.26 | 9.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Chen, Y. Modifications of the Multi-Layer Perceptron for Hyperspectral Image Classification. Remote Sens. 2021, 13, 3547. https://doi.org/10.3390/rs13173547
He X, Chen Y. Modifications of the Multi-Layer Perceptron for Hyperspectral Image Classification. Remote Sensing. 2021; 13(17):3547. https://doi.org/10.3390/rs13173547
Chicago/Turabian StyleHe, Xin, and Yushi Chen. 2021. "Modifications of the Multi-Layer Perceptron for Hyperspectral Image Classification" Remote Sensing 13, no. 17: 3547. https://doi.org/10.3390/rs13173547
APA StyleHe, X., & Chen, Y. (2021). Modifications of the Multi-Layer Perceptron for Hyperspectral Image Classification. Remote Sensing, 13(17), 3547. https://doi.org/10.3390/rs13173547