Observations of Surface Currents and Tidal Variability Off of Northeastern Taiwan from Shore-Based High Frequency Radar
Abstract
1. Introduction
2. Background
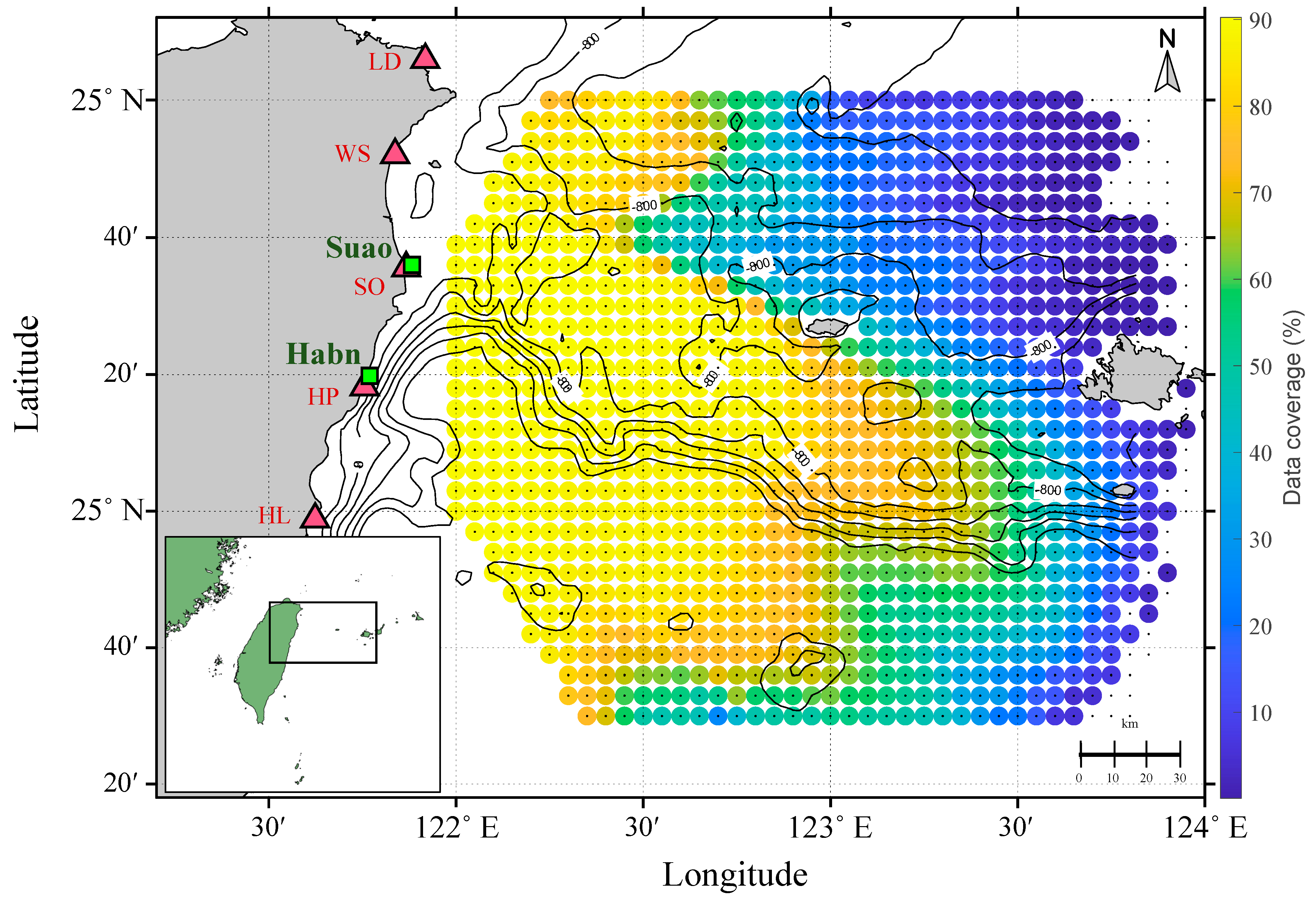
2.1. Remote Sensing Data
2.1.1. High-Frequency Radar
2.1.2. Aviso+
2.1.3. CCMP Ocean Surface Wind Components
3. Methodology
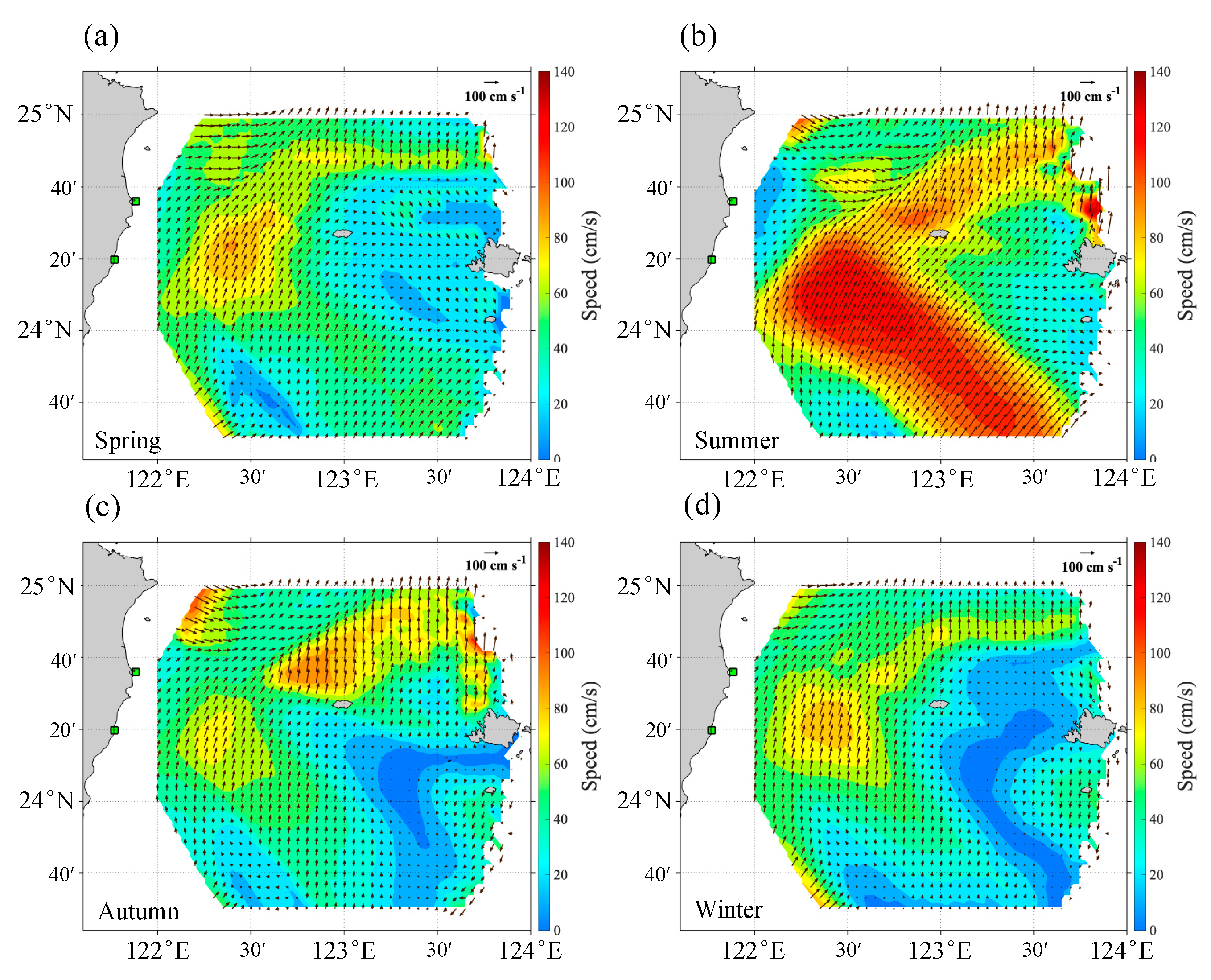
3.1. Eddy Kinetic Energy Distribution
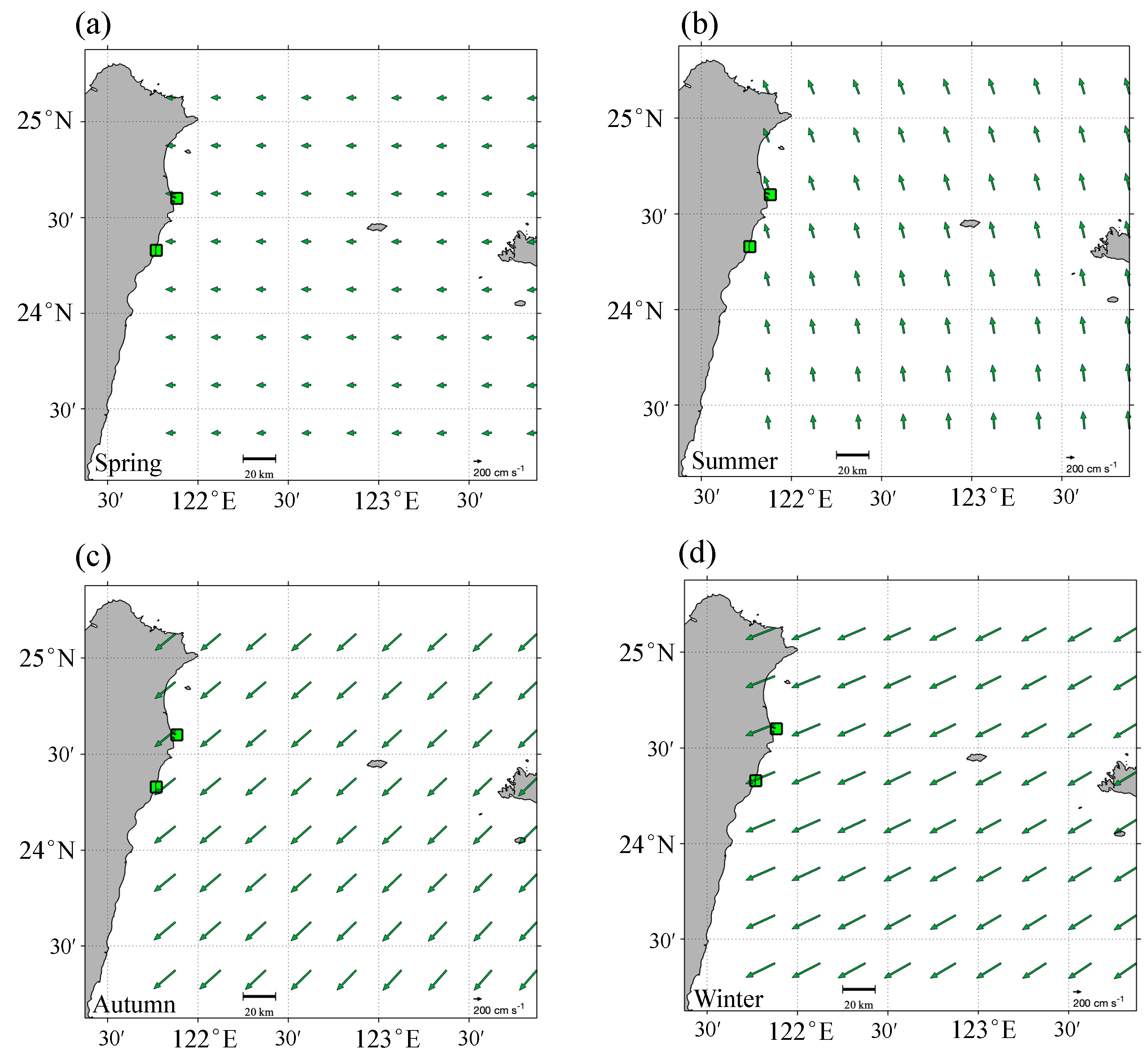
3.2. Complex Correlation of Veering
3.3. Harmonic Analysis
4. Experimental Results
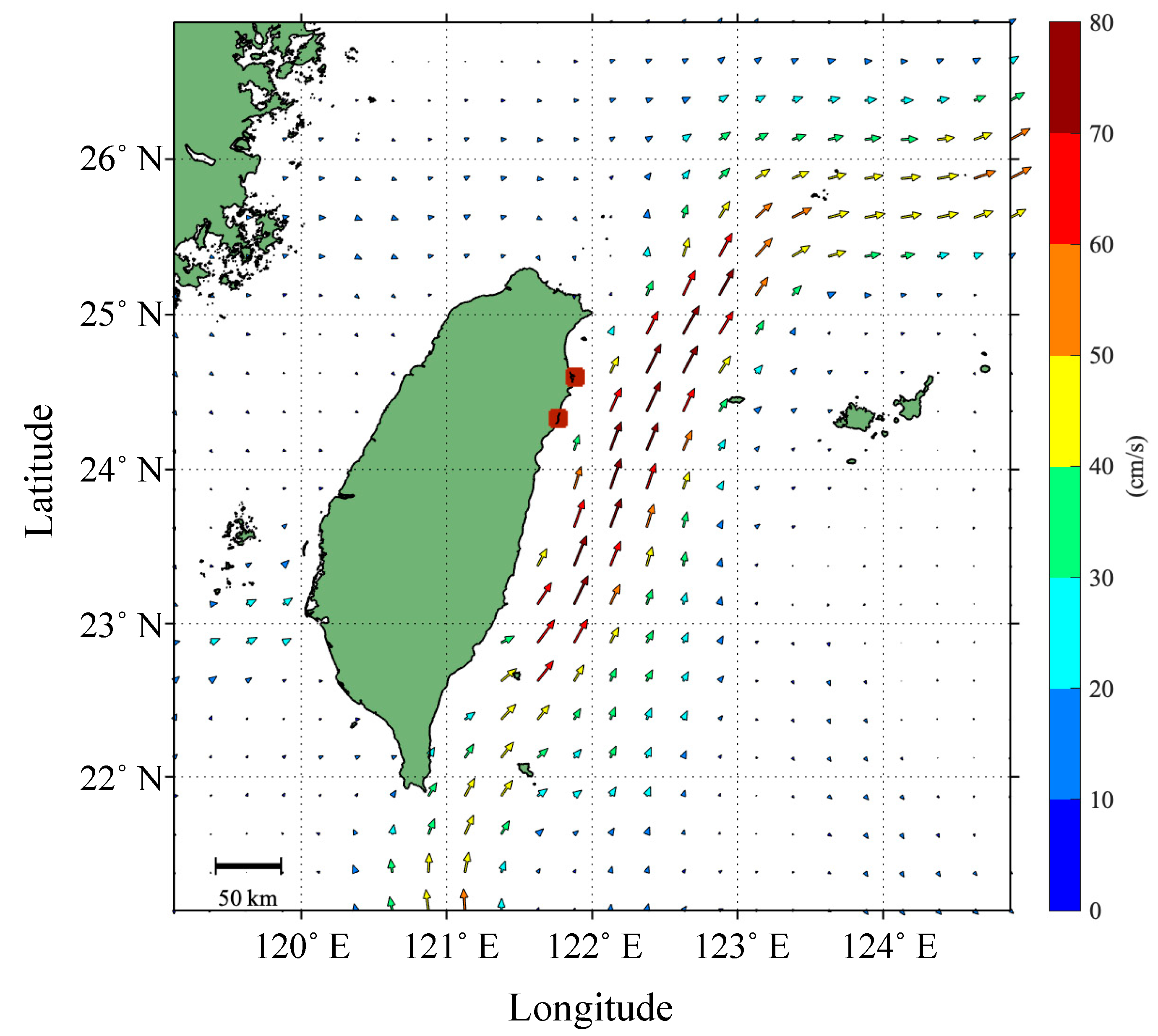
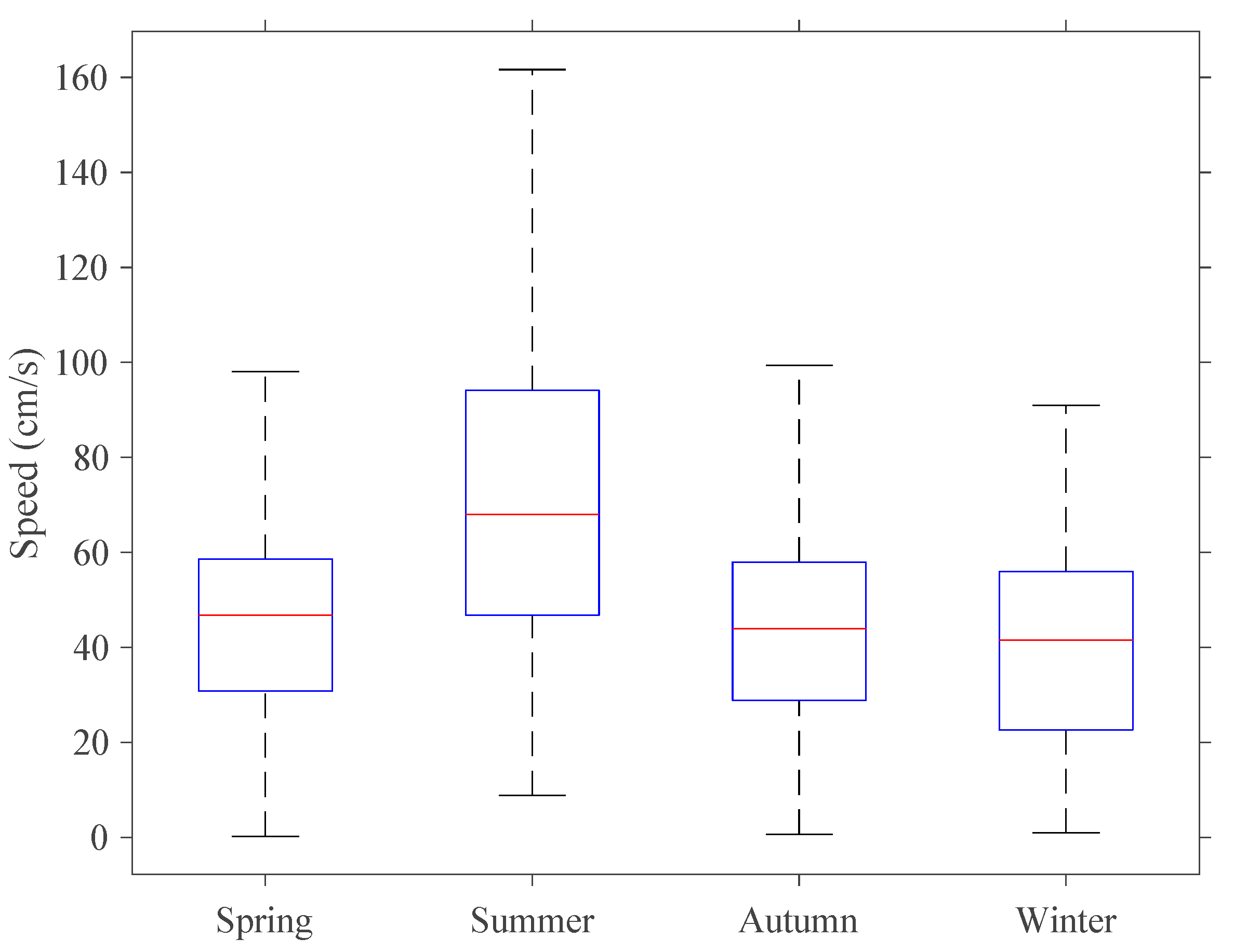
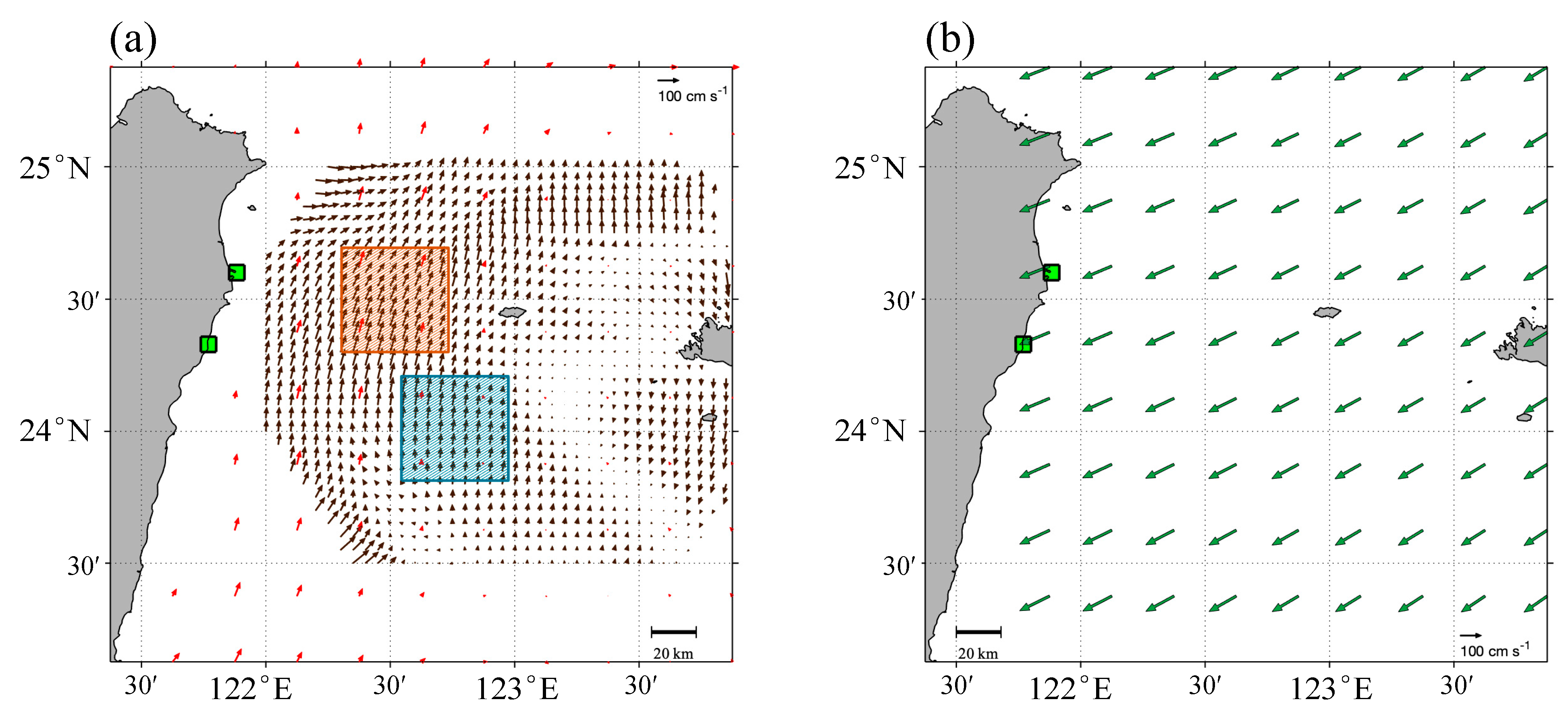
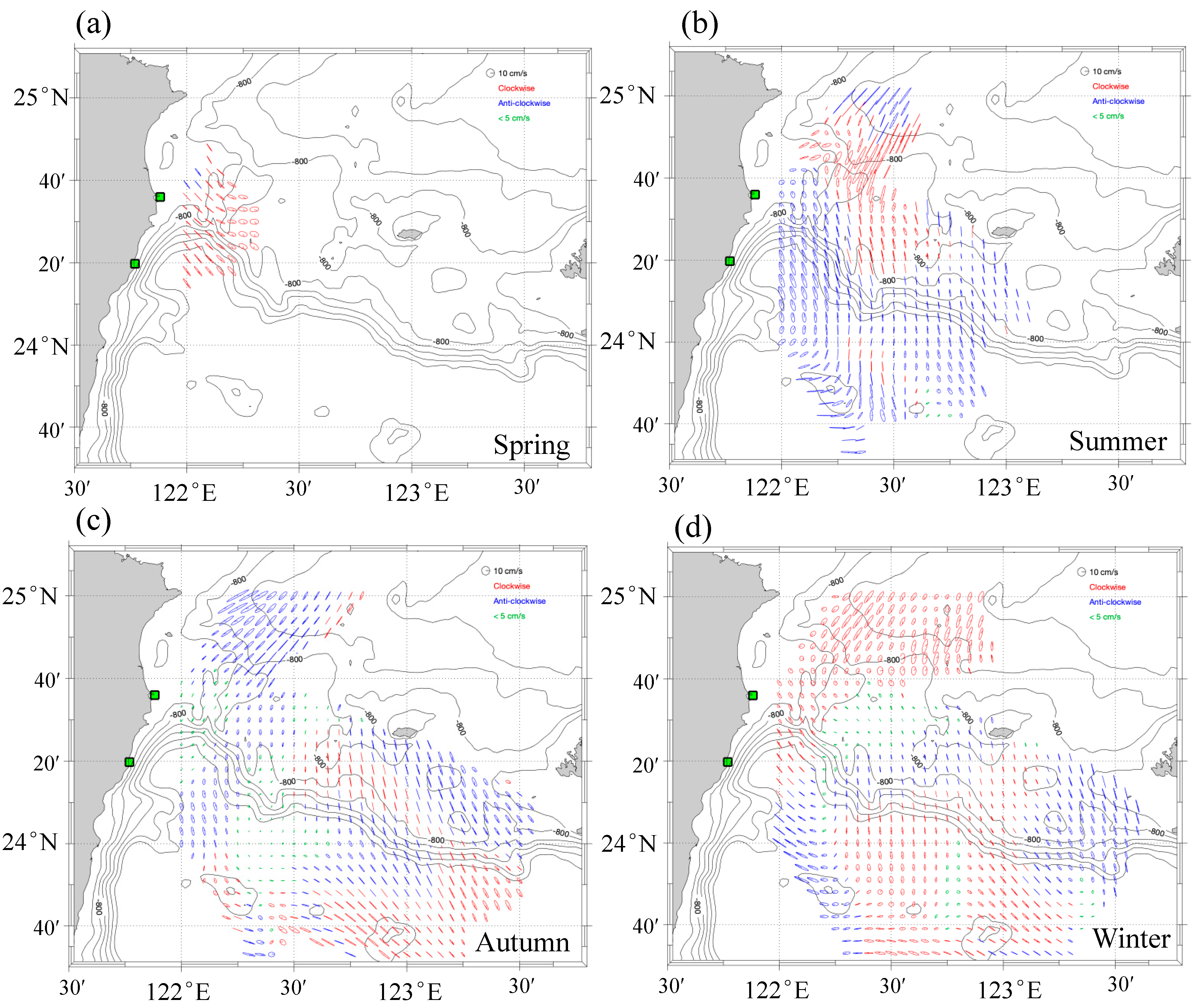
4.1. The Flow of Ocean Currents and Circulation
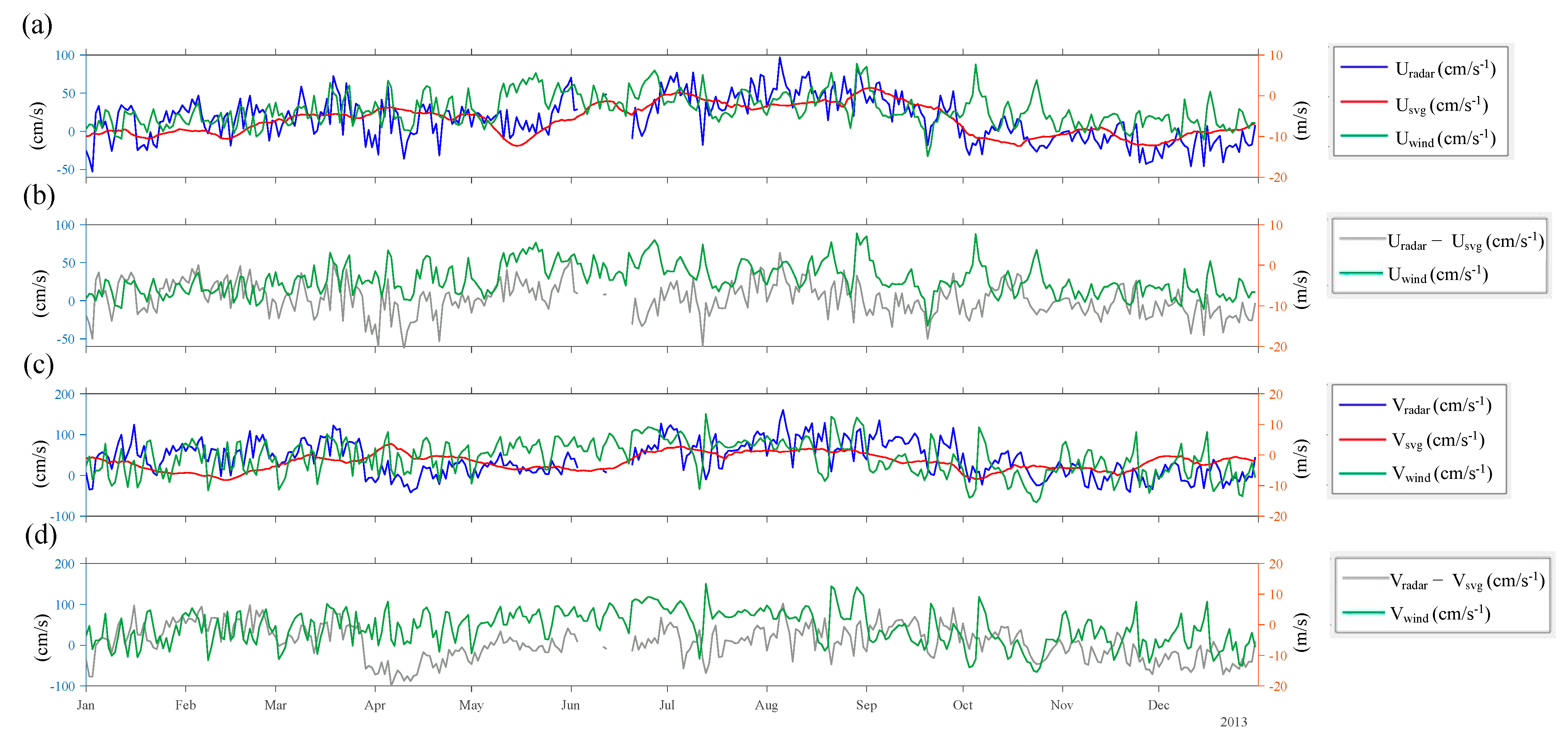
4.2. Comparison of Various Spatial Data
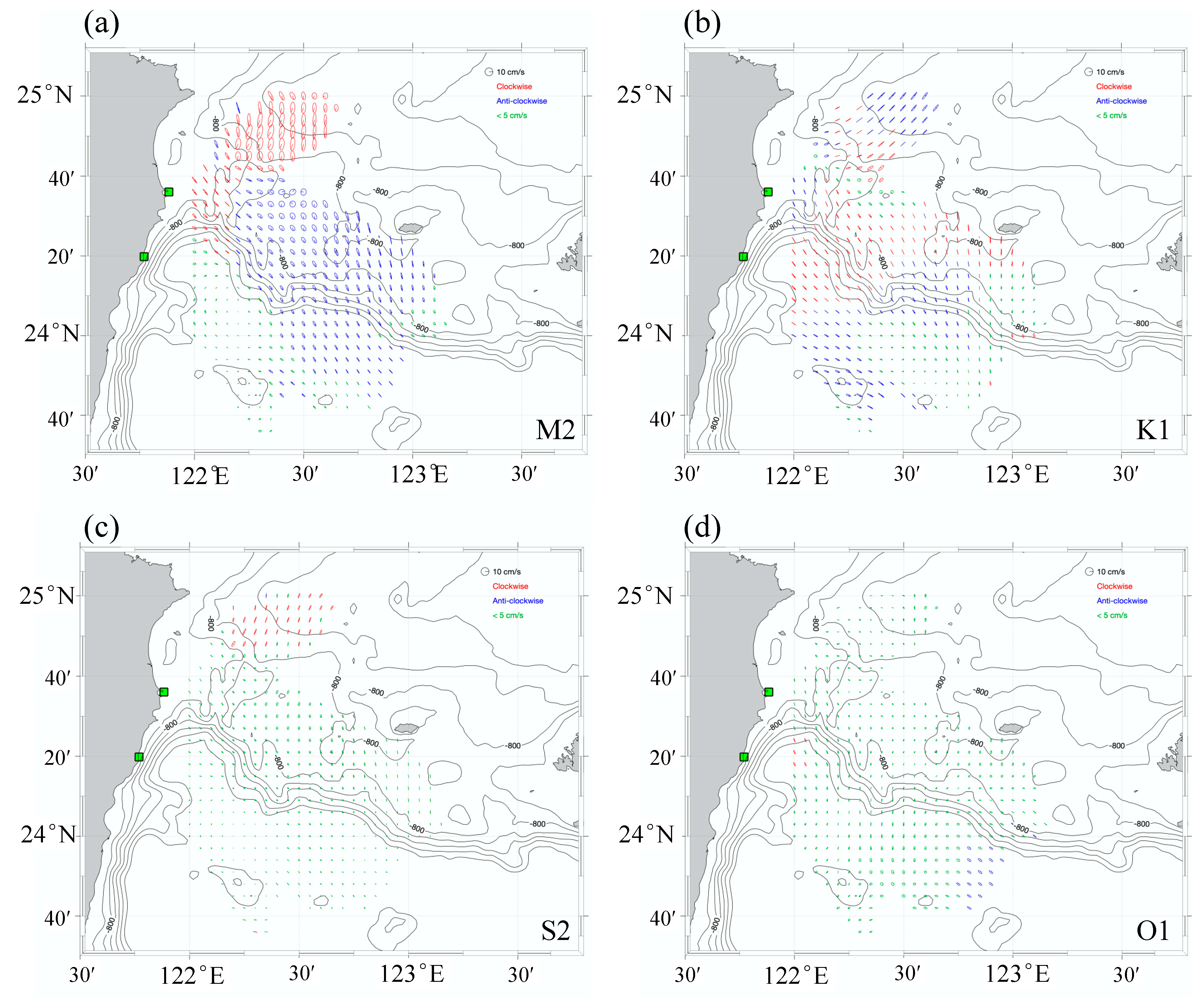
4.3. Tidal Flow
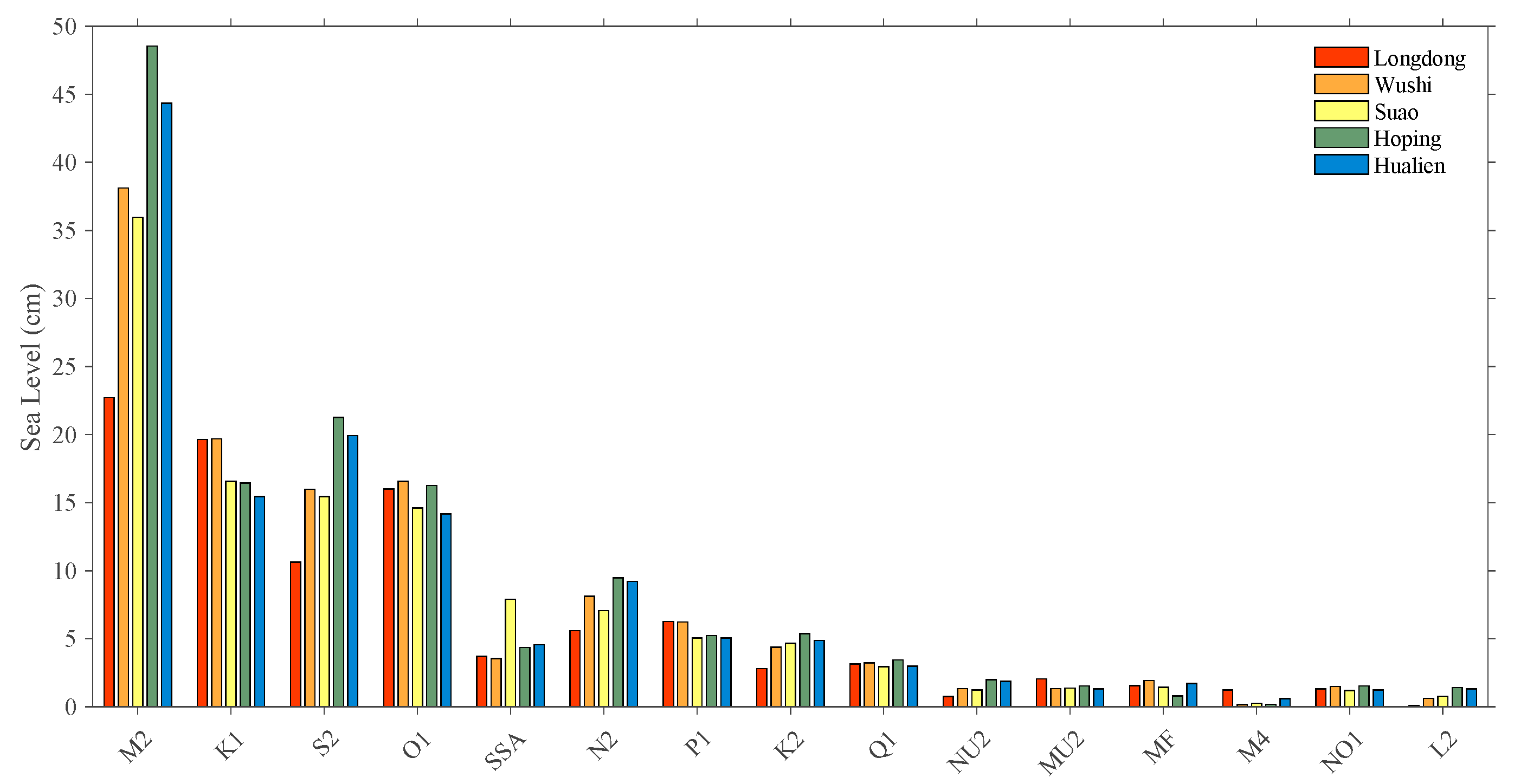
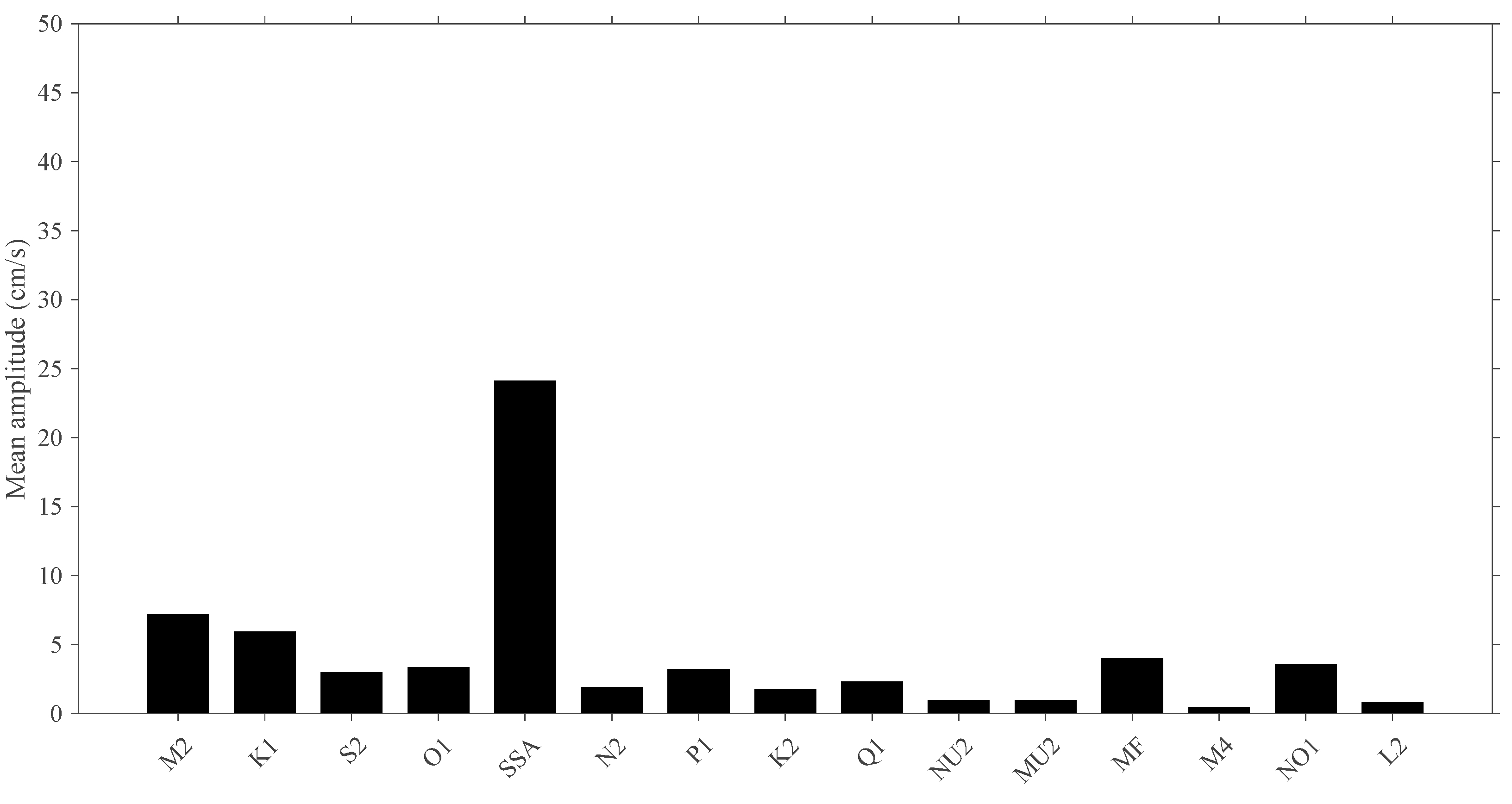
4.3.1. Validation of Tidal Constituents
4.3.2. Tide Type Classification
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Liu, C.-T.; Hu, J.-H.; Koga, M. Taiwan Current (Kuroshio) and impinging eddies. J. Oceanogr. 1999, 55, 609–617. [Google Scholar] [CrossRef]
- Liang, W.-D.; Tang, T.; Yang, Y.; Ko, M.; Chuang, W.-S. Upper-ocean currents around Taiwan. Deep Sea Res. Part II Top. Stud. Oceanogr. 2003, 50, 1085–1105. [Google Scholar] [CrossRef]
- Paduan, J.D.; Washburn, L. High-frequency radar observations of ocean surface currents. Annu. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef] [PubMed]
- Paduan, J.D.; Cook, M.S. Mapping surface currents in Monterey Bay with CODAR-type HF radar. Oceanography 1997, 10, 49–52. [Google Scholar] [CrossRef][Green Version]
- Lee, B.C.; Fan, Y.M.; Doong, D.J.; Kao, C.C. A study on the homogeneity of tides around coasts of Taiwan. J. Mar. Eng. 2005, 5, 67–83. [Google Scholar]
- Yoshikawa, Y.; Masuda, A.; Marubayashi, K.; Ishibashi, M. Seasonal variations of the surface currents in the Tsushima Strait. J. Oceanogr. 2010, 66, 223–232. [Google Scholar] [CrossRef]
- Yoshikawa, Y.; Masuda, A. Seasonal variations in the speed factor and deflection angle of the wind-driven surface flow in the Tsushima Strait. J. Geophys. Res. Oceans 2009, 114. [Google Scholar] [CrossRef]
- Fang, Y.C.; Wang, J.; Yang, Y.J. Surface Current Measurement Using HF-Radar off Northeastern Taiwan: Preliminary Result and Validation. In Proceedings of the 1st Ocean Radar Conference for Asia, Seoul, Korea, 17–19 May 2012; pp. 45–48. [Google Scholar]
- Chen, Y.-W.; Yang, Y.J.; Wang, J. A study on data filling from incomplete dataset of HF radar measured ocean currents—A case study of the flow field Northeast of Taiwan: Data filling from incomplete ocean currents dataset. In Proceedings of the OCEANS 2014, Taipei, Taiwan, 7–10 April 2014; pp. 1–4. [Google Scholar]
- Picot, N.; Case, K.; Desai, S.; Vincent, P.; Bronner, E. AVISO and PODAAC User Handbook. IGDR and GDR Jason Products; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2003. [Google Scholar]
- Hsin, Y.C.; Qiu, B.; Chiang, T.L.; Wu, C.R. Seasonal to interannual variations in the intensity and central position of the surface Kuroshio east of Taiwan. J. Geophys. Res. Oceans 2013, 118, 4305–4316. [Google Scholar] [CrossRef]
- Chao, S.-Y. Circulation of the East China Sea, a numerical study. J. Oceanogr. 1990, 46, 273–295. [Google Scholar] [CrossRef]
- Roesler, C.J.; Emery, W.; Kim, S.Y. Evaluating the use of high-frequency radar coastal currents to correct satellite altimetry. J. Geophys. Res. Oceans 2013, 118, 3240–3259. [Google Scholar] [CrossRef]
- Scott, J.; Wentz, F.; Hoffman, R.; Atlas, R. Improvements and Advances to the Cross-Calibrated Multi-Platform (CCMP) Ocean Vector Wind Analysis (V2. 0 release). Am. Geophys. Union 2016, 2016, PO54F-3322. Available online: https://www.researchgate.net/publication/298552723_Improvements_and_Advances_to_the_Cross-Calibrated_Multi-Platform_CCMP_Ocean_Vector_Wind_Analysis_V20_release (accessed on 27 August 2021).
- Richardson, P.L. Eddy kinetic energy in the North Atlantic from surface drifters. J. Geophys. Res. Oceans 1983, 88, 4355–4367. [Google Scholar] [CrossRef]
- Sikhakolli, R.; Sharma, R.; Basu, S.; Gohil, B.; Sarkar, A.; Prasad, K. Evaluation of OSCAR ocean surface current product in the tropical Indian Ocean using in situ data. J. Earth Syst. Sci. 2013, 122, 187–199. [Google Scholar] [CrossRef]
- Reyes Suarez, N.C.; Cook, M.S.; Gačić, M.; Paduan, J.D.; Drago, A.; Cardin, V. Sea Surface Circulation Structures in the Malta-Sicily Channel from Remote Sensing Data. Water 2019, 11, 1589. [Google Scholar] [CrossRef]
- Kim, S.Y.; Cornuelle, B.D.; Terrill, E.J. Anisotropic response of surface currents to the wind in a coastal region. J. Phys. Oceanogr. 2009, 39, 1512–1533. [Google Scholar] [CrossRef]
- Kohut, J.T.; Glenn, S.M.; Paduan, J.D. Inner shelf response to tropical storm Floyd. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- Paduan, J.D.; Rosenfeld, L.K. Remotely sensed surface currents in Monterey Bay from shore-based HF radar (Coastal Ocean Dynamics Application Radar). J. Geophys. Res. Oceans 1996, 101, 20669–20686. [Google Scholar] [CrossRef]
- Kundu, P.K. Ekman veering observed near the ocean bottom. J. Phys. Oceanogr. 1976, 6, 238–242. [Google Scholar] [CrossRef]
- Kohut, J.T.; Glenn, S.M.; Chant, R.J. Seasonal current variability on the New Jersey inner shelf. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Rosenfeld, L.; Shulman, I.; Cook, M.; Paduan, J.; Shulman, L. Methodology for a regional tidal model evaluation, with application to central California. Deep Sea Res. Part II Top. Stud. Oceanogr. 2009, 56, 199–218. [Google Scholar] [CrossRef]
- de Beurs, K.M.; Henebry, G.M. Spatio-temporal statistical methods for modelling land surface phenology. In Phenological Research; Springer: Berlin/Heidelberg, Germany, 2010; pp. 177–208. [Google Scholar]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Britannica, T. Harmonic Analysis. Available online: https://www.britannica.com/science/harmonic-analysis (accessed on 27 August 2021).
- Scharffenberg, M.G.; Stammer, D. Seasonal variations of the large-scale geostrophic flow field and eddy kinetic energy inferred from the TOPEX/Poseidon and Jason-1 tandem mission data. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Madah, F.; Mayerle, R.; Bruss, G.; Bento, J. Characteristics of tides in the Red Sea region, a numerical model study. Open J. Mar. Sci. 2015, 5, 193. [Google Scholar] [CrossRef]
- Subeesh, M.; Unnikrishnan, A.; Fernando, V.; Agarwadekar, Y.; Khalap, S.; Satelkar, N.; Shenoi, S. Observed tidal currents on the continental shelf off the west coast of India. Cont. Shelf Res. 2013, 69, 123–140. [Google Scholar] [CrossRef]
- Ponte, R.M.; Chaudhuri, A.H.; Vinogradov, S.V. Long-period tides in an atmospherically driven, stratified ocean. J. Phys. Oceanogr. 2015, 45, 1917–1928. [Google Scholar] [CrossRef]
- Crawford, W. Analysis of fortnightly and monthly tides. Int. Hydrogr. Rev. 1982, LIX, 132–141. [Google Scholar]
- Schureman, P. Manual of Harmonic Analysis and Prediction of Tides; US Government Printing Office: Washington, DC, USA, 1958; Volume 4. [Google Scholar]
- Stewart, R.H. Introduction to Physical Oceanography; Texas A&M University: College Station, TX, USA, 2008. [Google Scholar]
- Lin, S.F.; Yang, Y.J.; Tang, T.Y. Coastal Tidal Current Phenomena on Northern Taiwan. In Proceedings of the 27th Ocean Engineering Conference, Taichung, Taiwan, 1–2 December 2005. [Google Scholar]
- Dietrich, G.; Kalle, K. General Oceanography; An Introduction; Interscience Pub.: New York, NY, USA, 1957. [Google Scholar]
- Courtier, A. Classification of tides in four types. Int. Hydrogr. Rev. 1939. Available online: https://journals.lib.unb.ca/index.php/ihr/article/download/27428/1882520184 (accessed on 27 August 2021).
- Hicks, S.D. Tidal wave characteristics of Chesapeake Bay. Chesap. Sci. 1964, 5, 103–113. [Google Scholar] [CrossRef]
- Dai, C.F. Regional Oceanography of Taiwan Version II; National Taiwan University Press: Taipei, Taiwan, 2018. [Google Scholar]
| HFR | Altimeter (Aviso+) | CCMP | ETOPO1 | Tide Gauge | |
|---|---|---|---|---|---|
| Variable | Sea surface velocities | Geostrophic current | Wind stress | Bathymetry | Sea level |
| Temporal resolution | Hourly | Daily | 6-hourly | Hourly | |
| Spatial resolution | 1/13° | 1/8° | 1/4° | 1/60° | |
| Vertical integration | 1 m under the surface | Surface | 10 m above sea level | Degree of depth | Instrument reference level |
| Parameter | Value |
|---|---|
| Radar frequency (fc) | 4.4 MHz |
| Sweep bandwidth (B) | 18.38 kHz |
| Sweep period or sweep repetition time (Ts) | 1 s |
| Range resolution (c/2B) | 8.16 km |
| Maximum range | 292 km |
| Sampling time | 243.2 μs |
| 2013 | Geostrophic to Wind | Radar to Wind | Residual to Wind | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ1 | ρ2 | θ1 | θ2 | ρ1 | ρ2 | θ1 | θ2 | ρ1 | ρ2 | θ1 | θ2 | |
| Spring | 0.35 | 0.34 | −111.76 | −128.99 | 0.42 | 0.44 | −151.33 | −87.26 | 0.46 | 0.48 | 110.46 | −12.35 |
| Summer | 0.40 | 0.37 | −47.57 | −45.76 | 0.50 | 0.50 | −81.79 | −45.46 | 0.51 | 0.48 | −178.66 | −60.90 |
| Autumn | 0.32 | 0.37 | −163.51 | −140.08 | 0.67 | 0.45 | 177.87 | −132.29 | 0.46 | 0.40 | 72.99 | −100.76 |
| Winter | 0.40 | 0.39 | −130.21 | −110.70 | 0.69 | 0.55 | −138.33 | −105.91 | 0.48 | 0.50 | 112.58 | −99.79 |
| Mean | 0.37 | 0.37 | −113.26 | −106.38 | 0.57 | 0.49 | −48.40 | −92.73 | 0.48 | 0.47 | 29.34 | −68.45 |
| STD | 0.03 | 0.02 | 42.22 | 36.54 | 0.11 | 0.04 | 133.22 | 31.63 | 0.02 | 0.04 | 121.12 | 31.16 |
| Form Ratio | Type |
|---|---|
| 0.00–0.25 | Semidiurnal tide |
| 0.25–1.50 | Mixed mainly semidiurnal tide |
| 1.50–3.00 | Mixed mainly diurnal tide |
| 3.00–∞ | Diurnal tide |
| LD | WS | SO | HP | HL | CODAR | |
|---|---|---|---|---|---|---|
| Form ratio | 1.0690 | 0.67024 | 0.60599 | 0.46849 | 0.46057 | 0.91193 |
| Tidal types | Mixed mainly semidiurnal tide | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-R.; Paduan, J.D.; Cook, M.S.; Chuang, L.Z.-H.; Chung, Y.-J. Observations of Surface Currents and Tidal Variability Off of Northeastern Taiwan from Shore-Based High Frequency Radar. Remote Sens. 2021, 13, 3438. https://doi.org/10.3390/rs13173438
Chen Y-R, Paduan JD, Cook MS, Chuang LZ-H, Chung Y-J. Observations of Surface Currents and Tidal Variability Off of Northeastern Taiwan from Shore-Based High Frequency Radar. Remote Sensing. 2021; 13(17):3438. https://doi.org/10.3390/rs13173438
Chicago/Turabian StyleChen, Yu-Ru, Jeffrey D. Paduan, Michael S. Cook, Laurence Zsu-Hsin Chuang, and Yu-Jen Chung. 2021. "Observations of Surface Currents and Tidal Variability Off of Northeastern Taiwan from Shore-Based High Frequency Radar" Remote Sensing 13, no. 17: 3438. https://doi.org/10.3390/rs13173438
APA StyleChen, Y.-R., Paduan, J. D., Cook, M. S., Chuang, L. Z.-H., & Chung, Y.-J. (2021). Observations of Surface Currents and Tidal Variability Off of Northeastern Taiwan from Shore-Based High Frequency Radar. Remote Sensing, 13(17), 3438. https://doi.org/10.3390/rs13173438






