Accurate Prediction of Earthquake-Induced Landslides Based on Deep Learning Considering Landslide Source Area
Abstract
:1. Introduction
2. Methods and Methods
2.1. Background
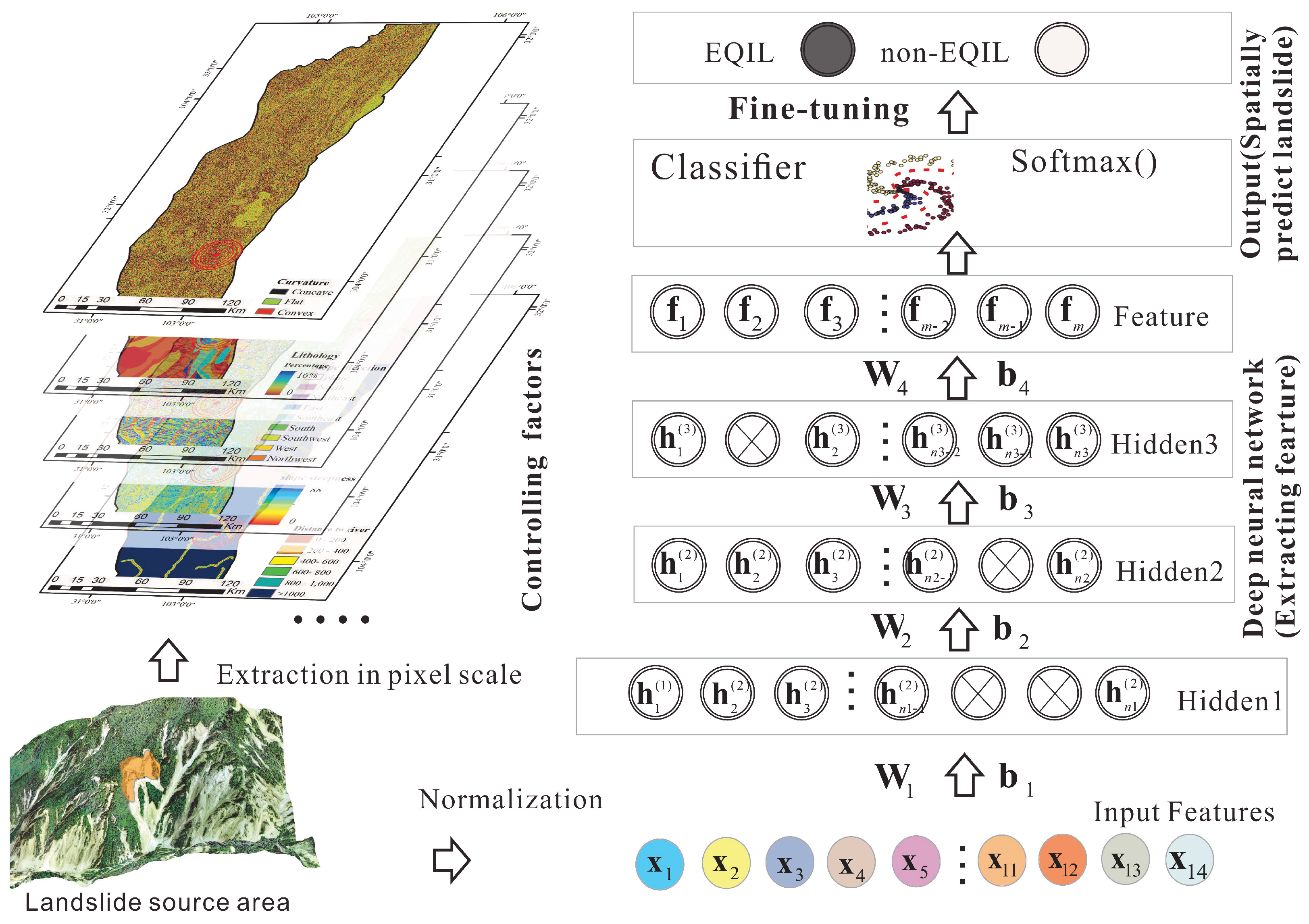
2.2. Prediction Framework
2.3. Model Evaluation
3. EQIL Inventory
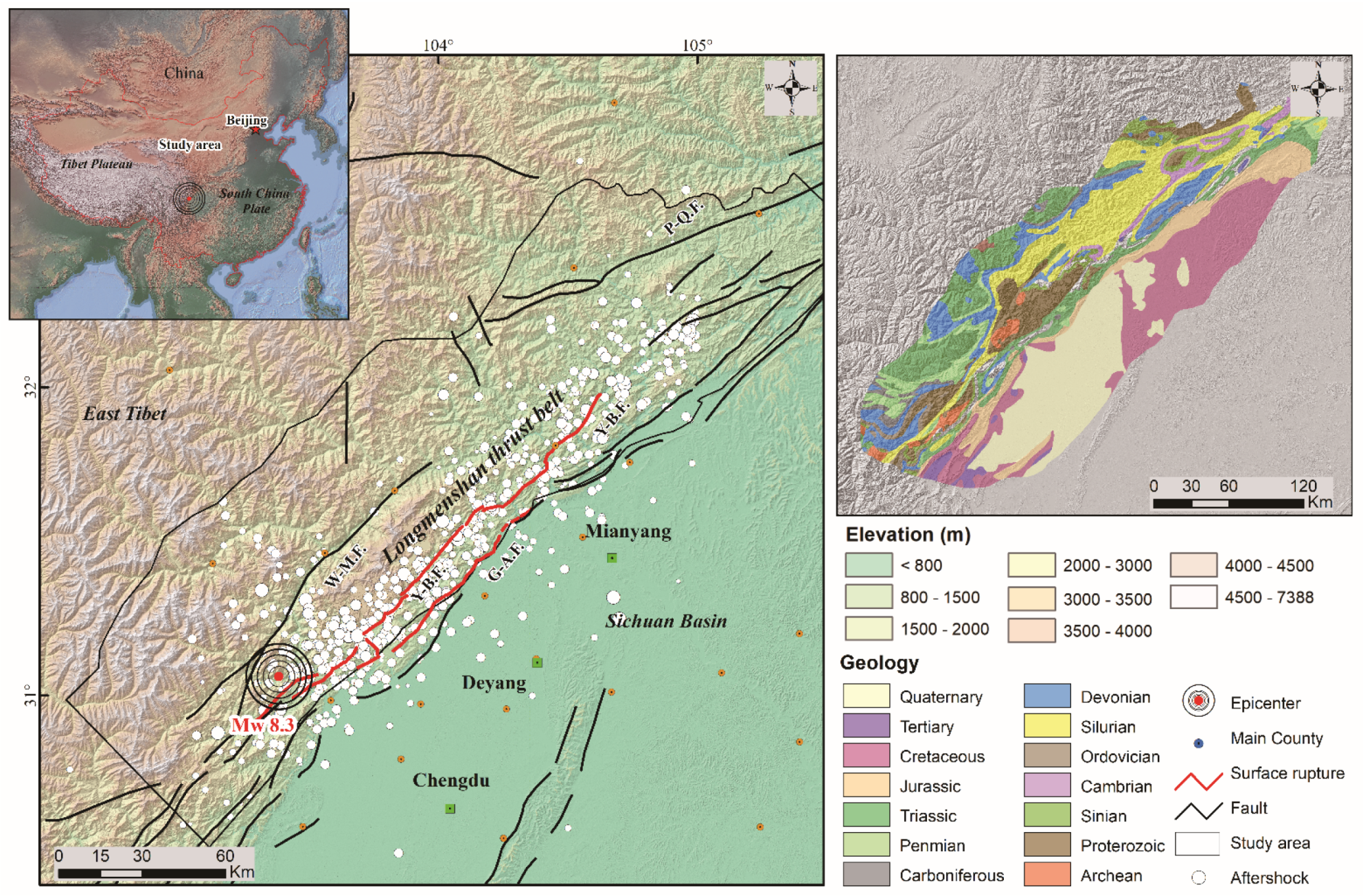
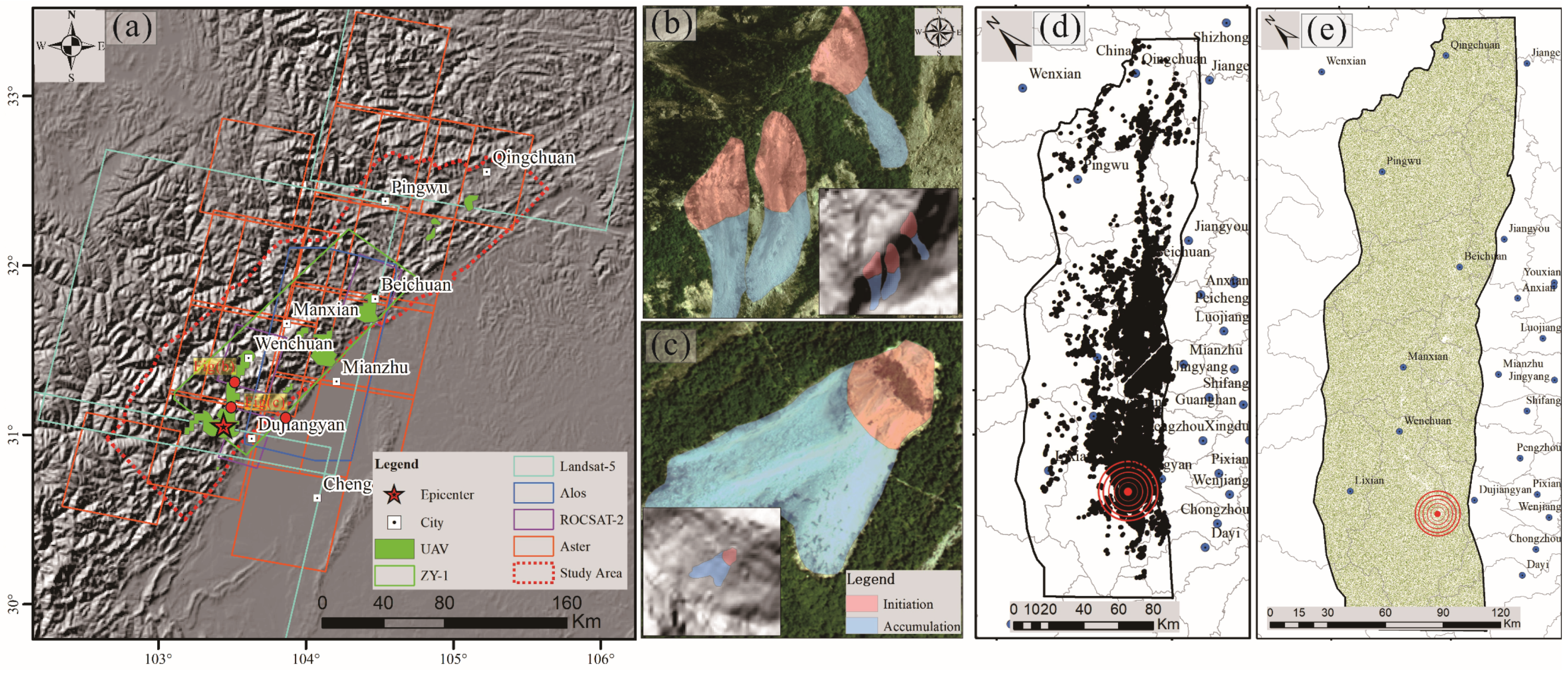
3.1. Study Area
3.2. Training and Testing Samples
3.3. Training and Testing Samples
4. Experiment and Results
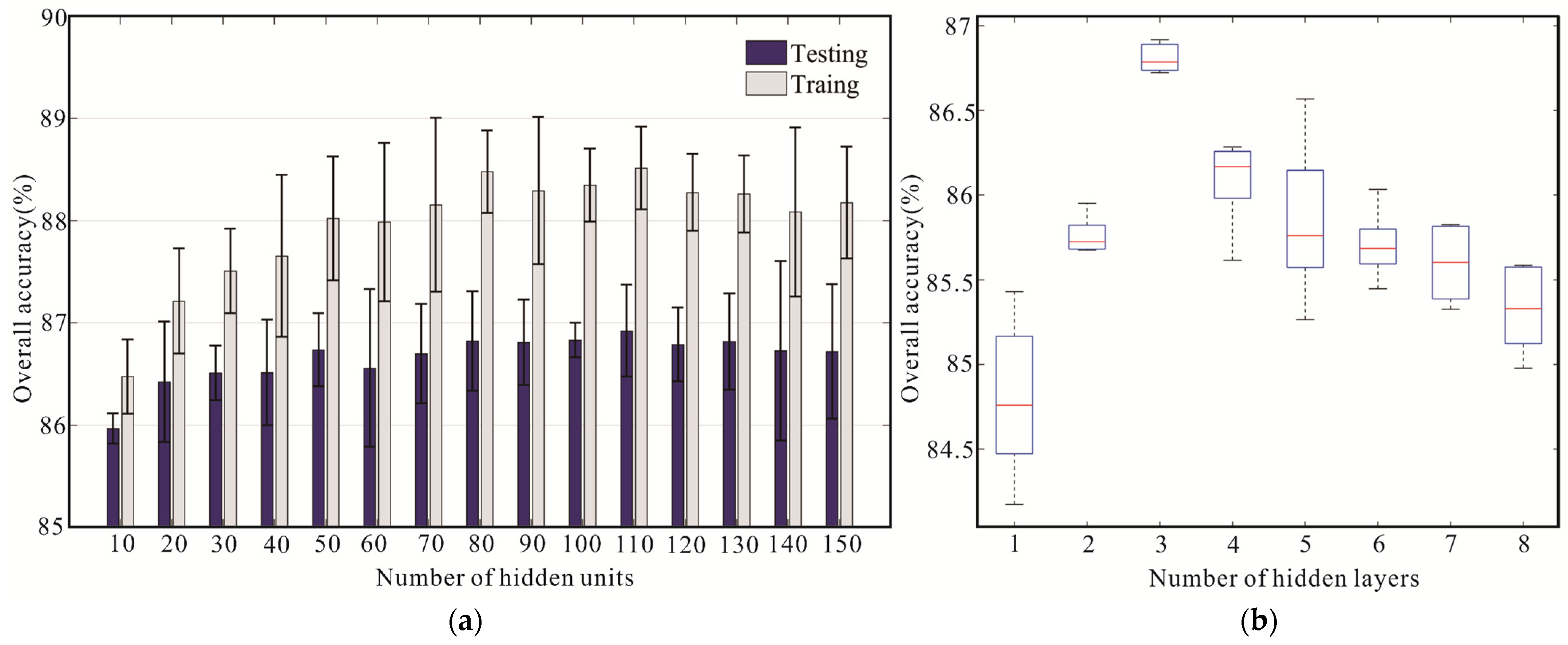
4.1. Framework Setting
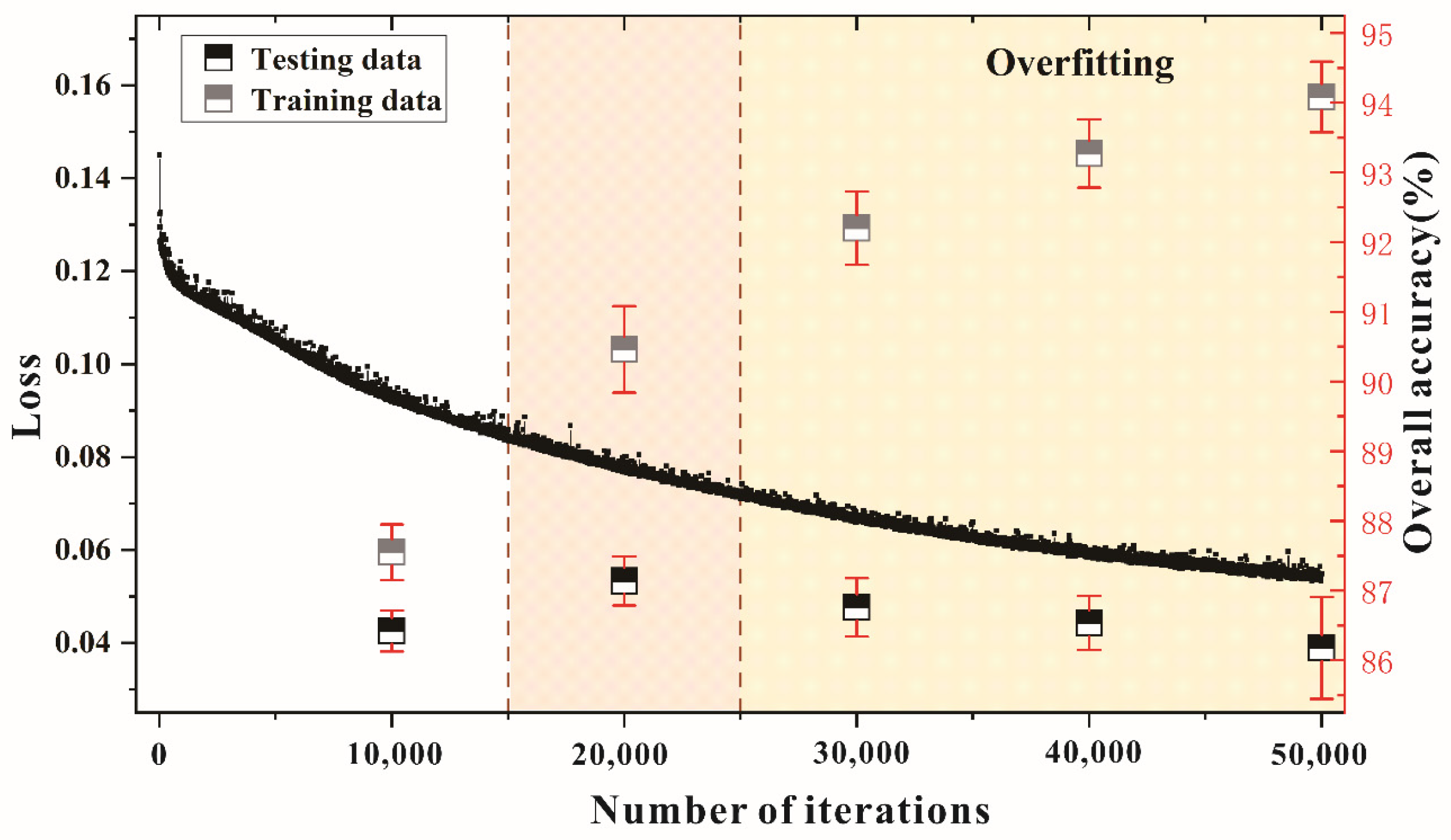
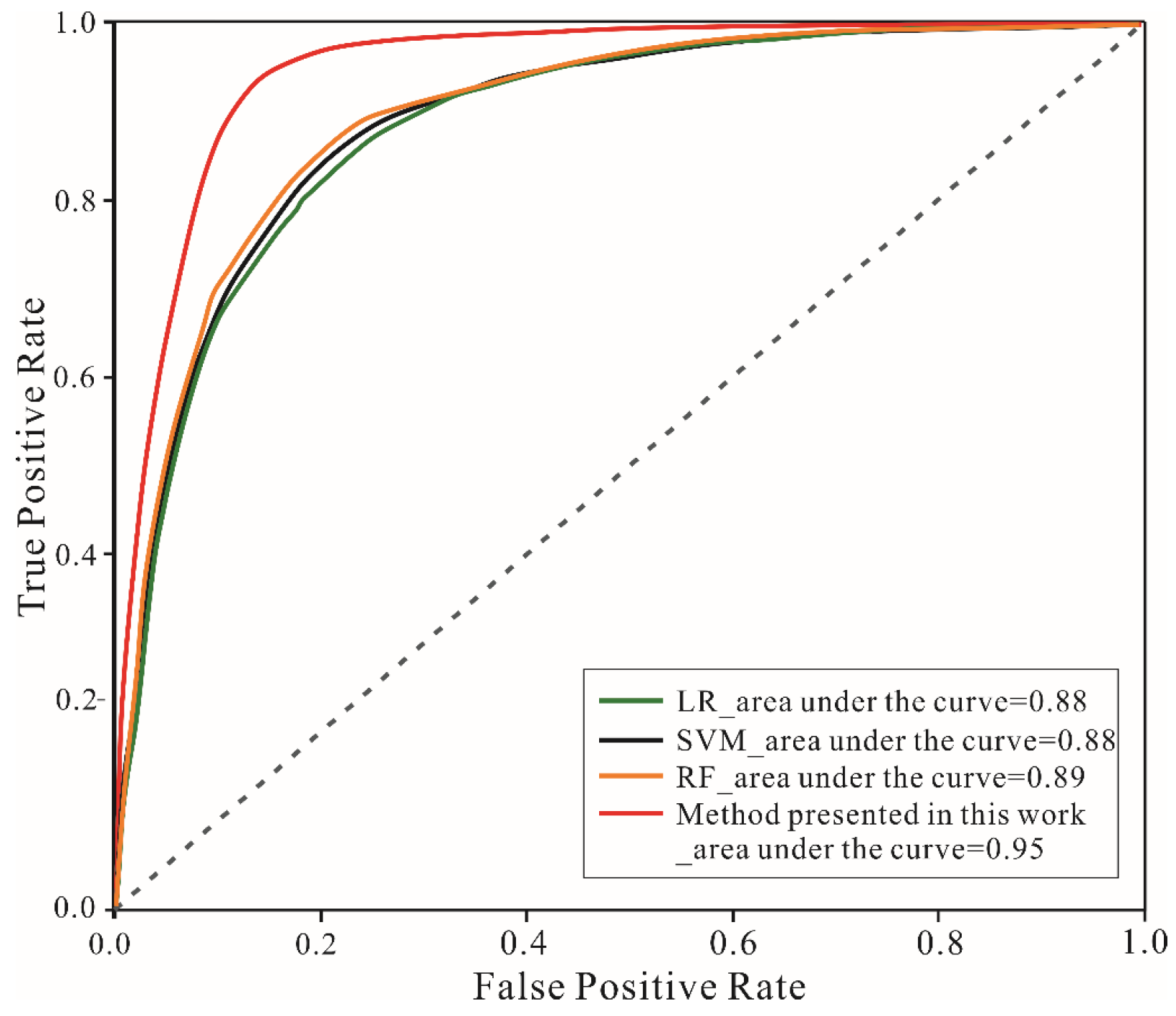
4.2. Visualizing Result and Performance Assessment
5. Discussion
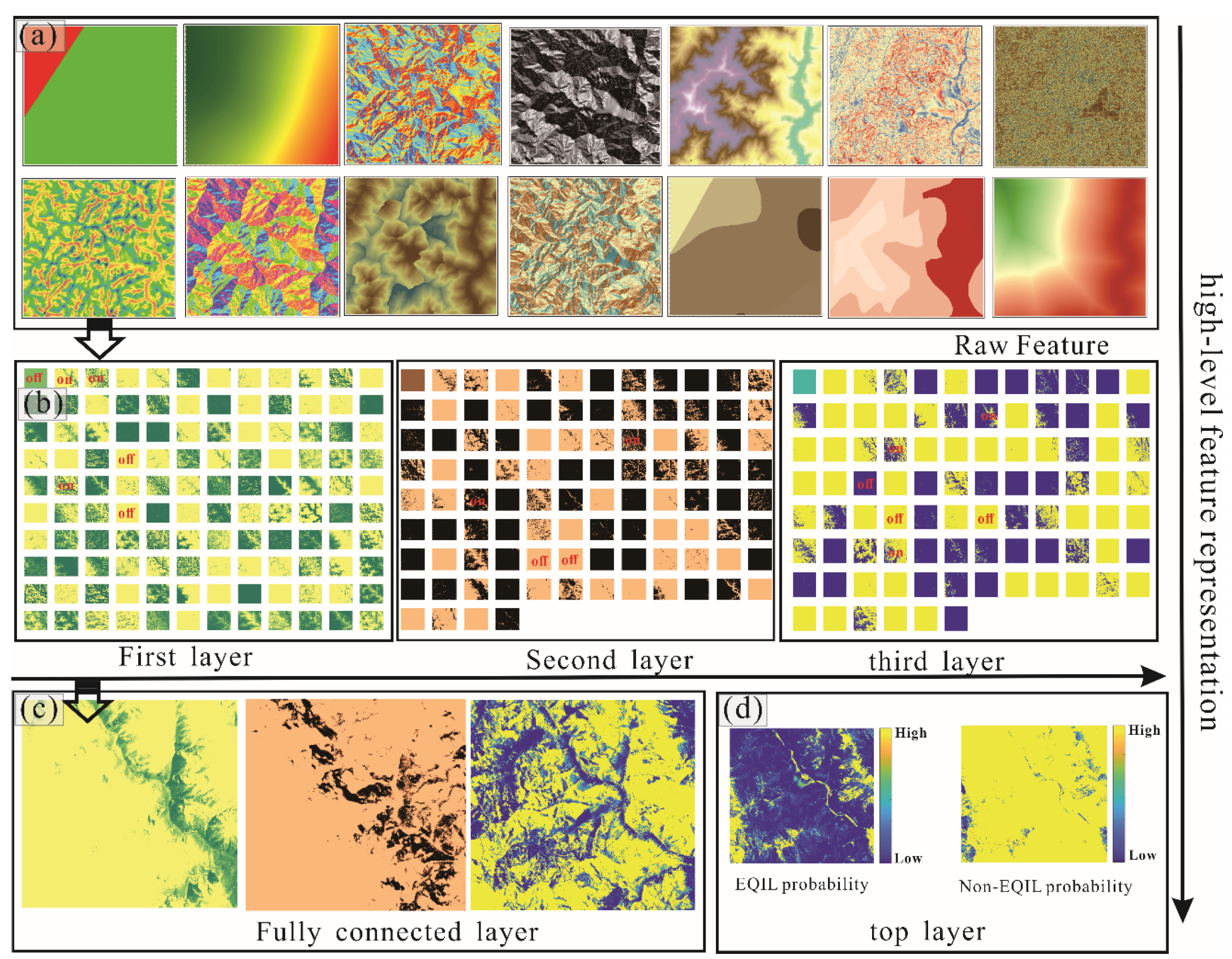
5.1. High-Level Feature Representation
5.2. Performance of Rock Landslide Prediction
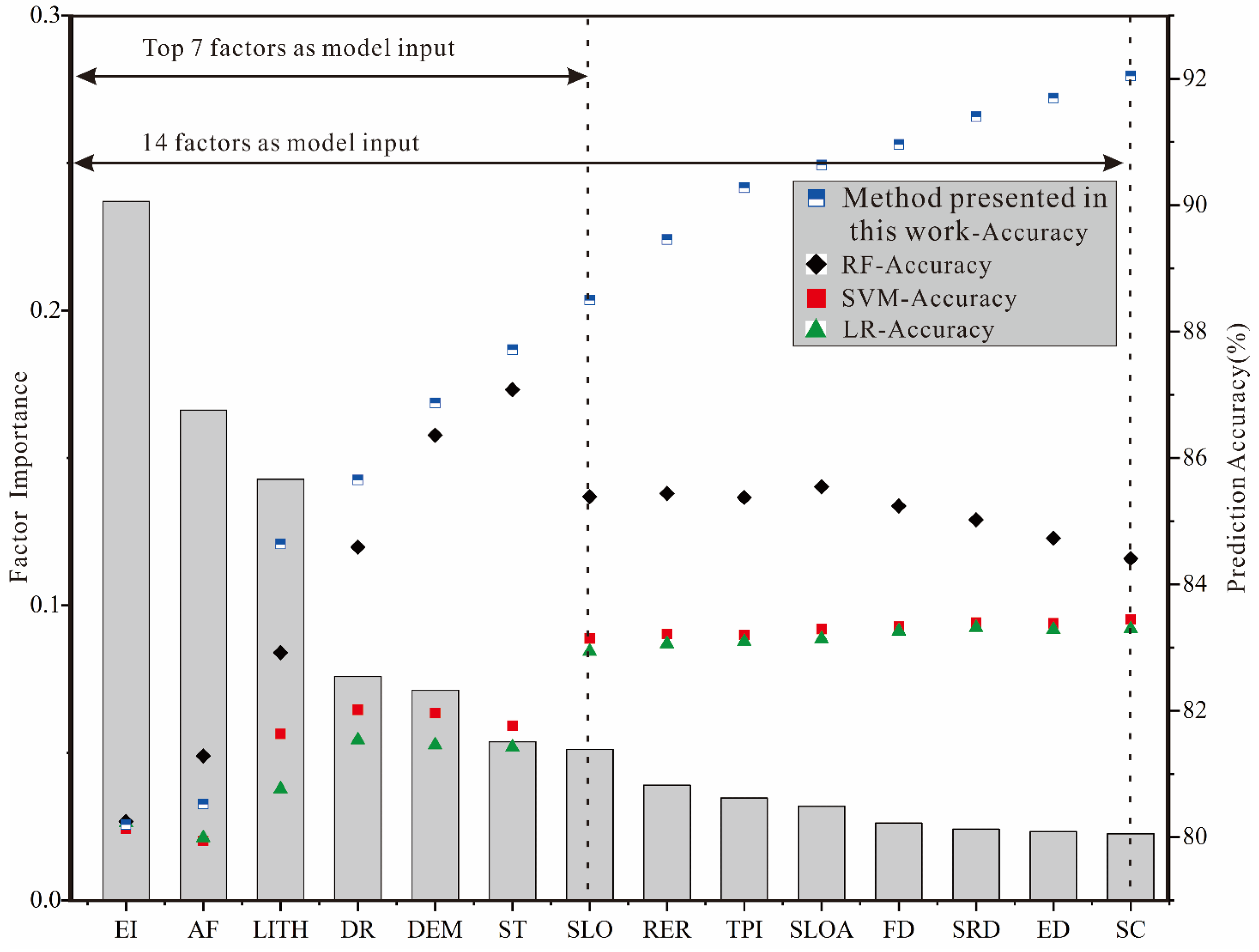
5.3. Influence on Factor Importance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, X.; Scaringi, G.; Korup, O.; West, A.J.; van Westen, C.J.; Tanyas, H.; Hovius, N.; Hales, T.C.; Jibson, R.W.; Allstadt, K.E. Earthquake-induced chains of geologic hazards: Patterns, mechanisms, and impacts. Rev. Geophys. 2019, 57, 421–503. [Google Scholar] [CrossRef] [Green Version]
- Umar, Z.; Pradhan, B.; Ahmad, A.; Jebur, M.N.; Tehrany, M.S. Earthquake induced landslide susceptibility mapping using an integrated ensemble frequency ratio and logistic regression models in West Sumatera Province, Indonesia. Catena 2014, 118, 124–135. [Google Scholar] [CrossRef]
- Alfaro, P.; Delgado, J.; García-Tortosa, F.; Lenti, L.; López, J.; López-Casado, C.; Martino, S.J.E.G. Widespread landslides induced by the Mw 5.1 earthquake of 11 May 2011 in Lorca, SE Spain. Eng. Geol. 2012, 137, 40–52. [Google Scholar] [CrossRef]
- Cui, P.; Zhu, Y.-Y.; Han, Y.-S.; Chen, X.-Q.; Zhuang, J.-Q. The 12 May Wenchuan earthquake-induced landslide lakes: Distribution and preliminary risk evaluation. Landslides 2009, 6, 209–223. [Google Scholar] [CrossRef]
- Gorum, T.; Fan, X.; van Westen, C.J.; Huang, R.Q.; Xu, Q.; Tang, C.; Wang, G. Distribution pattern of earthquake-induced landslides triggered by the 12 May 2008 Wenchuan earthquake. Geomorphology 2011, 133, 152–167. [Google Scholar] [CrossRef]
- Parker, R.N.; Hancox, G.T.; Petley, D.N.; Massey, C.I.; Densmore, A.L.; Rosser, N.J. Spatial distributions of earthquake-induced landslides and hillslope preconditioning in northwest South Island, New Zealand. Earth Surf. Dynam. 2015, 3, 501–525. [Google Scholar] [CrossRef] [Green Version]
- Ye, C.; Li, Y.; Cui, P.; Liang, L.; Pirasteh, S.; Marcato, J.; Goncalves, W.N.; Li, J. Landslide detection of hyperspectral remote sensing data based on deep learning with constrains. IEEE. J. Sel. Top. Appl. 2019, 12, 5047–5060. [Google Scholar] [CrossRef]
- Fan, X.; Scaringi, G.; Xu, Q.; Zhan, W.; Dai, L.; Li, Y.; Pei, X.; Yang, Q.; Huang, R. Coseismic landslides triggered by the 8th August 2017 M s 7.0 Jiuzhaigou earthquake (Sichuan, China): Factors controlling their spatial distribution and implications for the seismogenic blind fault identification. Landslides 2018, 15, 967–983. [Google Scholar] [CrossRef]
- Meunier, P.; Hovius, N.; Haines, J.A. Topographic site effects and the location of earthquake induced landslides. Earth Planet. Sci. Lett. 2008, 275, 221–232. [Google Scholar] [CrossRef]
- Valagussa, A.; Marc, O.; Frattini, P.; Crosta, G.B. Seismic and geological controls on earthquake-induced landslide size. Earth Planet. Sci. Lett. 2019, 506, 268–281. [Google Scholar] [CrossRef]
- Korup, O.; Stolle, A. Landslide prediction from machine learning. Geol. Today 2014, 30, 26–33. [Google Scholar] [CrossRef]
- Mao, Z.; Liu, G.; Huang, Y.; Bao, Y. A conservative and consistent Lagrangian gradient smoothing method for earthquake-induced landslide simulation. Eng. Geol. 2019, 260, 105226. [Google Scholar] [CrossRef]
- Romeo, R. Seismically induced landslide displacements: A predictive model. Eng. Geol. 2000, 58, 337–351. [Google Scholar] [CrossRef]
- Song, J.; Fan, Q.; Feng, T.; Chen, Z.; Chen, J.; Gao, Y. A multi-block sliding approach to calculate the permanent seismic displacement of slopes. Eng. Geol. 2019, 255, 48–58. [Google Scholar] [CrossRef]
- Yiğit, A. Prediction of amount of earthquake-induced slope displacement by using Newmark method. Eng. Geol. 2020, 264, 105385. [Google Scholar] [CrossRef]
- Caccavale, M.; Matano, F.; Sacchi, M. An integrated approach to earthquake-induced landslide hazard zoning based on probabilistic seismic scenario for Phlegrean Islands (Ischia, Procida and Vivara), Italy. Geomorphology 2017, 295, 235–259. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M.B. Hybrid integration of multilayer perceptron neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Jibson, R.W. Methods for assessing the stability of slopes during earthquakes—A retrospective. Eng. Geol. 2011, 122, 43–50. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of earthquakes on dams and embankments. Geotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef] [Green Version]
- Bojadjieva, J.; Sheshov, V.; Bonnard, C. Hazard and risk assessment of earthquake-induced landslides—Case study. Landslides 2018, 15, 161–171. [Google Scholar] [CrossRef]
- Bhandari, T.; Hamad, F.; Moormann, C.; Sharma, K.G.; Westrich, B. Numerical modelling of seismic slope failure using MPM. Comput. Geotech. 2016, 75, 126–134. [Google Scholar] [CrossRef]
- Jibson, R.W. Predicting earthquake-induced landslide displacements using Newmark’s sliding block analysis. Transp. Res. Record. 1993, 1411, 9–17. [Google Scholar]
- García-Rodríguez, M.J.; Malpica, J.A.; Benito, B.; Díaz, M. Susceptibility assessment of earthquake-triggered landslides in El Salvador using logistic regression. Geomorphology 2008, 95, 172–191. [Google Scholar] [CrossRef] [Green Version]
- Yi, Y.; Zhang, Z.; Zhang, W.; Xu, Q.; Deng, C.; Li, Q. GIS-based earthquake-triggered-landslide susceptibility mapping with an integrated weighted index model in Jiuzhaigou region of Sichuan Province, China. Nat. Hazards Earth Syst. Sci. 2019, 19, 1973–1988. [Google Scholar] [CrossRef] [Green Version]
- Huang, F.; Zhang, J.; Zhou, C.; Wang, Y.; Huang, J.; Zhu, L. A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 2020, 17, 217–229. [Google Scholar] [CrossRef]
- Daneshvar, M.R.M. Landslide susceptibility zonation using analytical hierarchy process and GIS for the Bojnurd region, northeast of Iran. Landslides 2014, 11, 1079–1091. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, C.; Hong, H.; Zhou, Q.; Wang, D. Mapping earthquake-triggered landslide susceptibility by use of artificial neural network (ANN) models: An example of the 2013 Minxian (China) Mw 5.9 event. Geomat. Nat. Hazards Risk 2019, 10, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Provost, F.; Hibert, C.; Malet, J.P. Automatic classification of endogenous landslide seismicity using the Random Forest supervised classifier. Geophys. Res. Lett. 2017, 44, 113–120. [Google Scholar] [CrossRef]
- Bui, D.T.; Tsangaratos, P.; Nguyen, V.-T.; Van Liem, N.; Trinh, P.T. Comparing the prediction performance of a deep learning neural network model with conventional machine learning models in landslide susceptibility assessment. Catena 2020, 188, 104426. [Google Scholar] [CrossRef]
- Hinton, G. Where do features come from? Cogn. Sci. 2014, 38, 1078–1101. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Alamri, A.M. Pathways and challenges of the application of artificial intelligence to geohazards modelling. Gondwana Res. 2020, in press. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.-R.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Karpatne, A.; Ebert-Uphoff, I.; Ravela, S.; Babaie, H.A.; Kumar, V. Machine learning for the geosciences: Challenges and opportunities. IEEE Trans. Knowl. Data Eng. 2018, 31, 1544–1554. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Karpouza, M.; Chousianitis, K.; Bathrellos, G.D.; Skilodimou, H.D.; Kaviris, G.; Antonarakou, A. Hazard zonation mapping of earthquake-induced secondary effects using spatial multi-criteria analysis. Nat. Hazards 2021. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H. Comparison of convolutional neural networks for landslide susceptibility mapping in Yanshan County, China. Sci. Total Environ. 2019, 666, 975–993. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.-A.; Bottou, L. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Gold, S.; Rangarajan, A. Softmax to softassign: Neural network algorithms for combinatorial optimization. J. Artif. Neural Netw. 1996, 2, 381–399. [Google Scholar]
- Nowicki Jessee, M.A.; Hamburger, M.W.; Allstadt, K.; Wald, D.J.; Robeson, S.M.; Tanyas, H.; Hearne, M.; Thompson, E.M. A global empirical model for near-real-time assessment of seismically induced landslides. J. Geophys. Res. Earth Surf. 2018, 123, 1835–1859. [Google Scholar] [CrossRef] [Green Version]
- Tanyaş, H.; Van Westen, C.J.; Allstadt, K.E.; Nowicki Jessee, M.A.; Görüm, T.; Jibson, R.W.; Godt, J.W.; Sato, H.P.; Schmitt, R.G.; Marc, O. Presentation and analysis of a worldwide database of earthquake-induced landslide inventories. J. Geophys. Res. Earth Surf. 2017, 122, 1991–2015. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Xu, X.; Yao, X.; Dai, F. Three (nearly) complete inventories of landslides triggered by the May 12, 2008 Wenchuan Mw 7.9 earthquake of China and their spatial distribution statistical analysis. Landslides 2014, 11, 441–461. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Cheng, Y.; Yin, Y.; Lan, H.; Wang, J.; Fu, X. High-position debris flow: A long-term active geohazard after the Wenchuan earthquake. Eng. Geol. 2014, 180, 45–54. [Google Scholar] [CrossRef]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA spatial modeling of plant species distribution. Plant Ecol. 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Sun, D.; Wen, H.; Wang, D.; Xu, J. A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Xu, C. Do buried-rupture earthquakes trigger less landslides than surface-rupture earthquakes for reverse faults? Geomorphology 2014, 216, 53–57. [Google Scholar] [CrossRef]
- Kargel, J.S.; Leonard, G.J.; Shugar, D.H.; Haritashya, U.K.; Bevington, A.; Fielding, E.J.; Fujita, K.; Geertsema, M.; Miles, E.S.; Steiner, J.; et al. Geomorphic and geologic controls of geohazards induced by Nepal’s 2015 Gorkha earthquake. Science 2016, 351, aac8353. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Wang, J.; Li, Y.; Yi, S. Discussions on the transformation conditions of Wangcang landslide-induced debris flow. Landslides 2021, 18, 1833–1843. [Google Scholar] [CrossRef]
- Guo, J.; Yi, S.; Yin, Y.; Cui, Y.; Qin, M.; Li, T.; Wang, C. The effect of topography on landslide kinematics: A case study of the Jichang town landslide in Guizhou, China. Landslides 2020, 17, 959–973. [Google Scholar] [CrossRef]
- Keefer, D.K. Investigating landslides caused by earthquakes–a historical review. Surv. Geophys. 2002, 23, 473–510. [Google Scholar] [CrossRef]
- Lv, Q.; Liu, Y.; Yang, Q. Stability analysis of earthquake-induced rock slope based on back analysis of shear strength parameters of rock mass. Eng. Geol. 2017, 228, 39–49. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef] [PubMed]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef] [Green Version]

| Actually Positive (1) | Actually Negative (0) | |
|---|---|---|
| Predicted Positive (1) | True Positives (TP) | False Positives (FP) |
| Predicted Negative (0) | False Negatives (FN) | True Negatives (TN) |
| Category Name | No. of Pixels | No. of Training Samples | No. of Testing Samples |
|---|---|---|---|
| EQIL | 819,389 | 163,877 | 655,512 |
| Non-EQIL | 819,389 | 163,877 | 655,512 |
| Total | 1,638,778 | 327,754 | 1,211,024 |
| Category | Control Factors | Data Type | Data Source |
|---|---|---|---|
| Seismic property | EI—Earthquake intensity | Polygon | China Earthquake Administration (CEA) |
| ED—Epicenter directivity | Point | ||
| SRD—Surface rupture directivity | Polyline | ||
| AF—Aftershocks | Point | ||
| Topography | DEM (12.5 m resolution) | Raster | Alaska Satellite Facility, USA |
| SLO—Slope gradients | Raster | ||
| SLOA—Slope aspect | Raster | ||
| TPI—Topographic position index [47] | Raster | ||
| SC—Slope curvature | Raster | ||
| RER—Relative relief | Raster | ||
| Geology | LITH—Lithology | Polygon | China Geological Survey |
| FD—Fault direction | Polyline | ||
| Hydrology | DR—Distance to rivers | Polyline | Department of Forestry, Sichuan Province |
| Soil | ST—Soil type | Polygon | Department Natural Resources, Sichuan Province |
| Learning Rate | 0.0001 | 0.001 | 0.01 | 0.1 | 0.8 |
|---|---|---|---|---|---|
| OA (%) | 80.35 ± 0.40 | 83.03 ± 0.05 | 83.84 ± 0.10 | 85.49 ± 0.16 | 86.72 ± 0.23 |
| Precision (%) | 79.85 ± 0.45 | 81.91 ± 0.07 | 82.45 ± 0.13 | 84.14 ± 0.88 | 85.37 ± 0.96 |
| Recall (%) | 81.24 ± 0.65 | 84.83 ± 0.001 | 86.02 ± 0.11 | 87.53 ± 1.25 | 88.68 ± 1.9 |
| Measurements | Logistic Regression | Support Vector Machine | Random Forest | Proposed Method |
|---|---|---|---|---|
| OA (%) | 80.75 ± 0.23 | 82.22 ± 0.15 | 84.16 ± 0.22 | 91.88 ± 0.18 |
| Precision of EQIL (%) | 79.10 ± 0.34 | 80.70 ± 0.23 | 81.93 ± 0.17 | 87.56 ± 0.21 |
| Recall of EQIL (%) | 80.33 ± 0.27 | 82.07 ± 0. 12 | 84.40 ± 0. 15 | 91.40 ± 0. 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Cui, P.; Ye, C.; Junior, J.M.; Zhang, Z.; Guo, J.; Li, J. Accurate Prediction of Earthquake-Induced Landslides Based on Deep Learning Considering Landslide Source Area. Remote Sens. 2021, 13, 3436. https://doi.org/10.3390/rs13173436
Li Y, Cui P, Ye C, Junior JM, Zhang Z, Guo J, Li J. Accurate Prediction of Earthquake-Induced Landslides Based on Deep Learning Considering Landslide Source Area. Remote Sensing. 2021; 13(17):3436. https://doi.org/10.3390/rs13173436
Chicago/Turabian StyleLi, Yao, Peng Cui, Chengming Ye, José Marcato Junior, Zhengtao Zhang, Jian Guo, and Jonathan Li. 2021. "Accurate Prediction of Earthquake-Induced Landslides Based on Deep Learning Considering Landslide Source Area" Remote Sensing 13, no. 17: 3436. https://doi.org/10.3390/rs13173436
APA StyleLi, Y., Cui, P., Ye, C., Junior, J. M., Zhang, Z., Guo, J., & Li, J. (2021). Accurate Prediction of Earthquake-Induced Landslides Based on Deep Learning Considering Landslide Source Area. Remote Sensing, 13(17), 3436. https://doi.org/10.3390/rs13173436







