On the Structure and Kinematics of an Algerian Eddy in the Southwestern Mediterranean Sea
Abstract
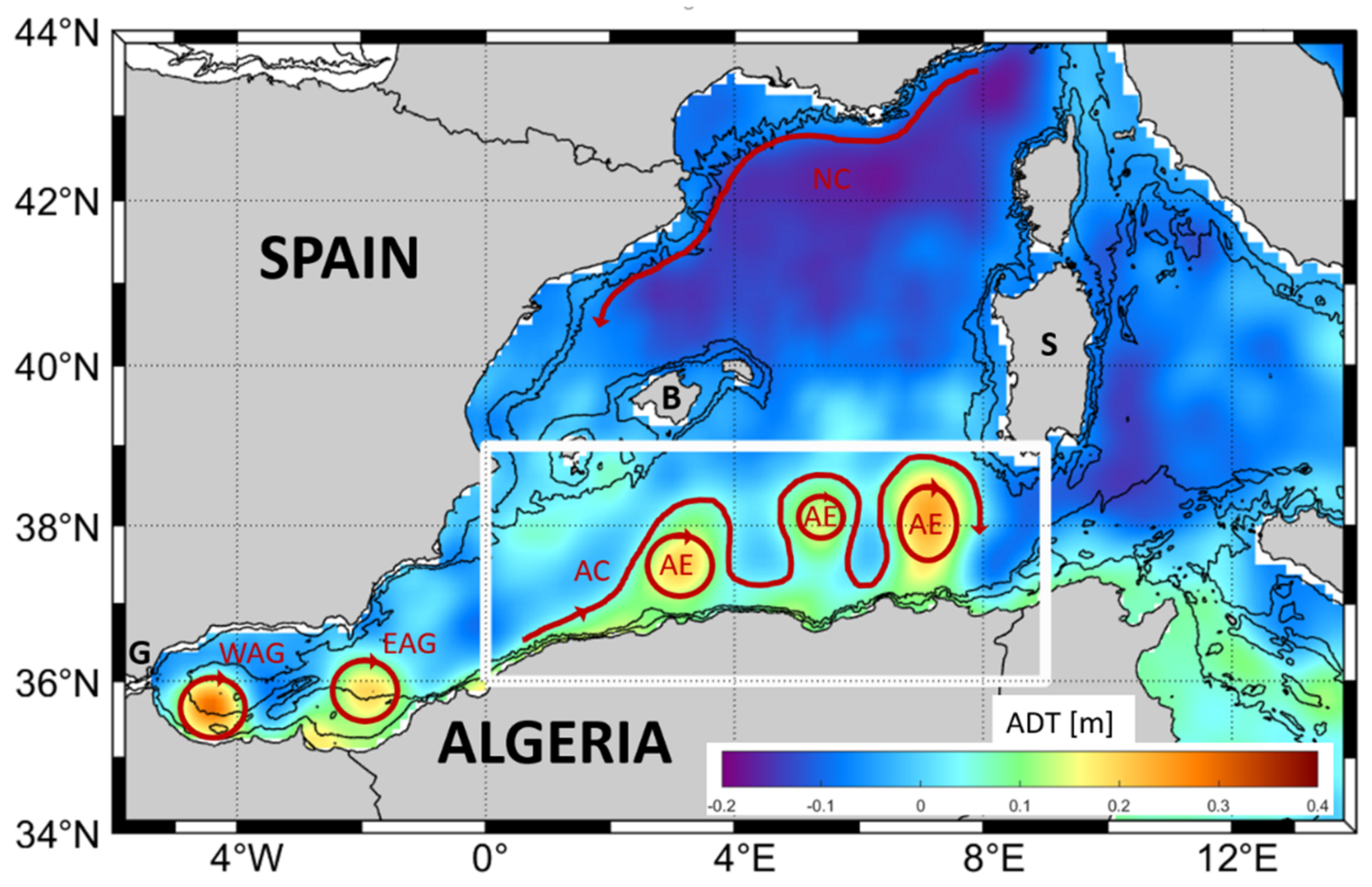
1. Introduction
2. Data and Methods
2.1. Lagrangian Instruments and Data
2.2. Operational Products
2.3. Methods
3. Results
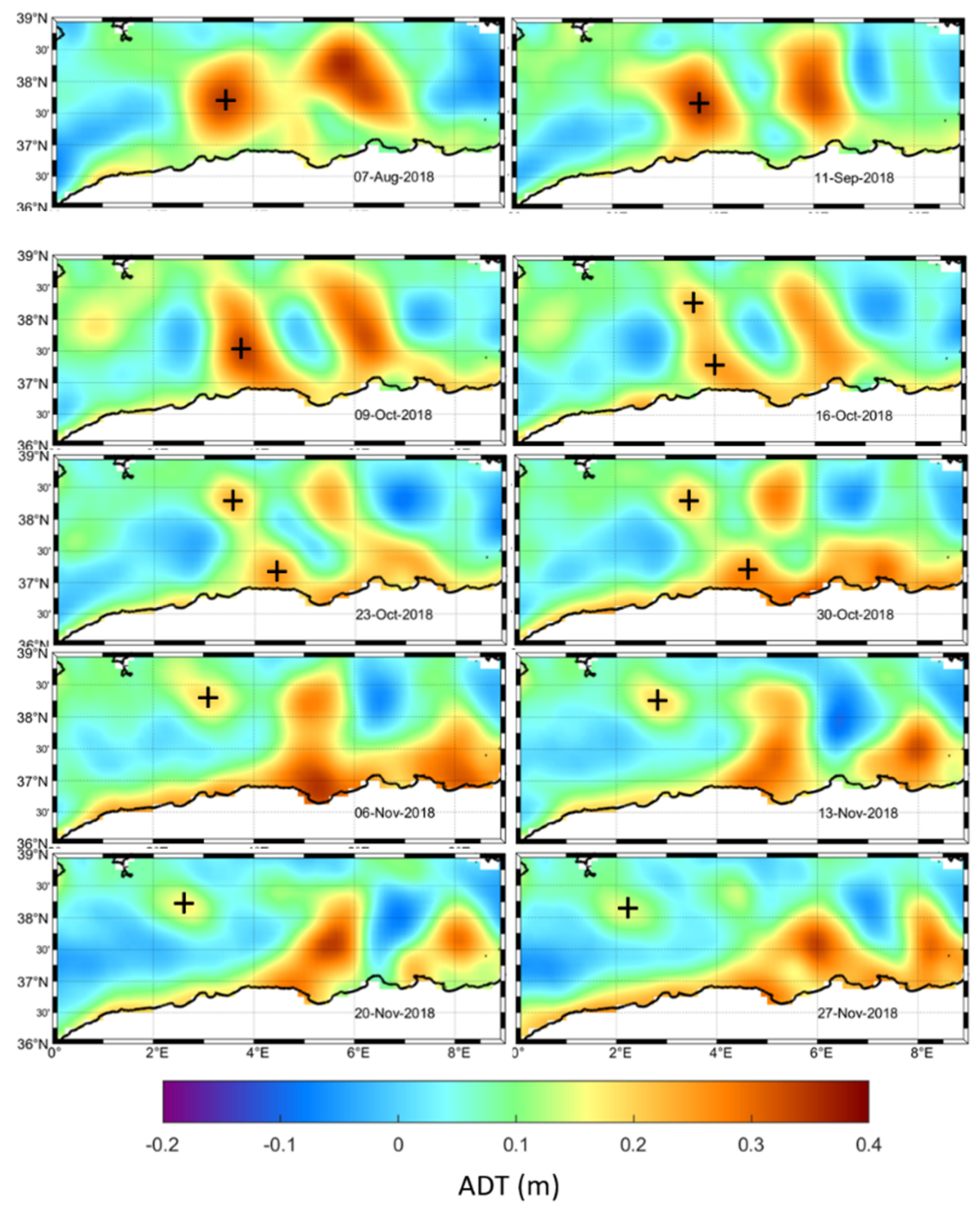
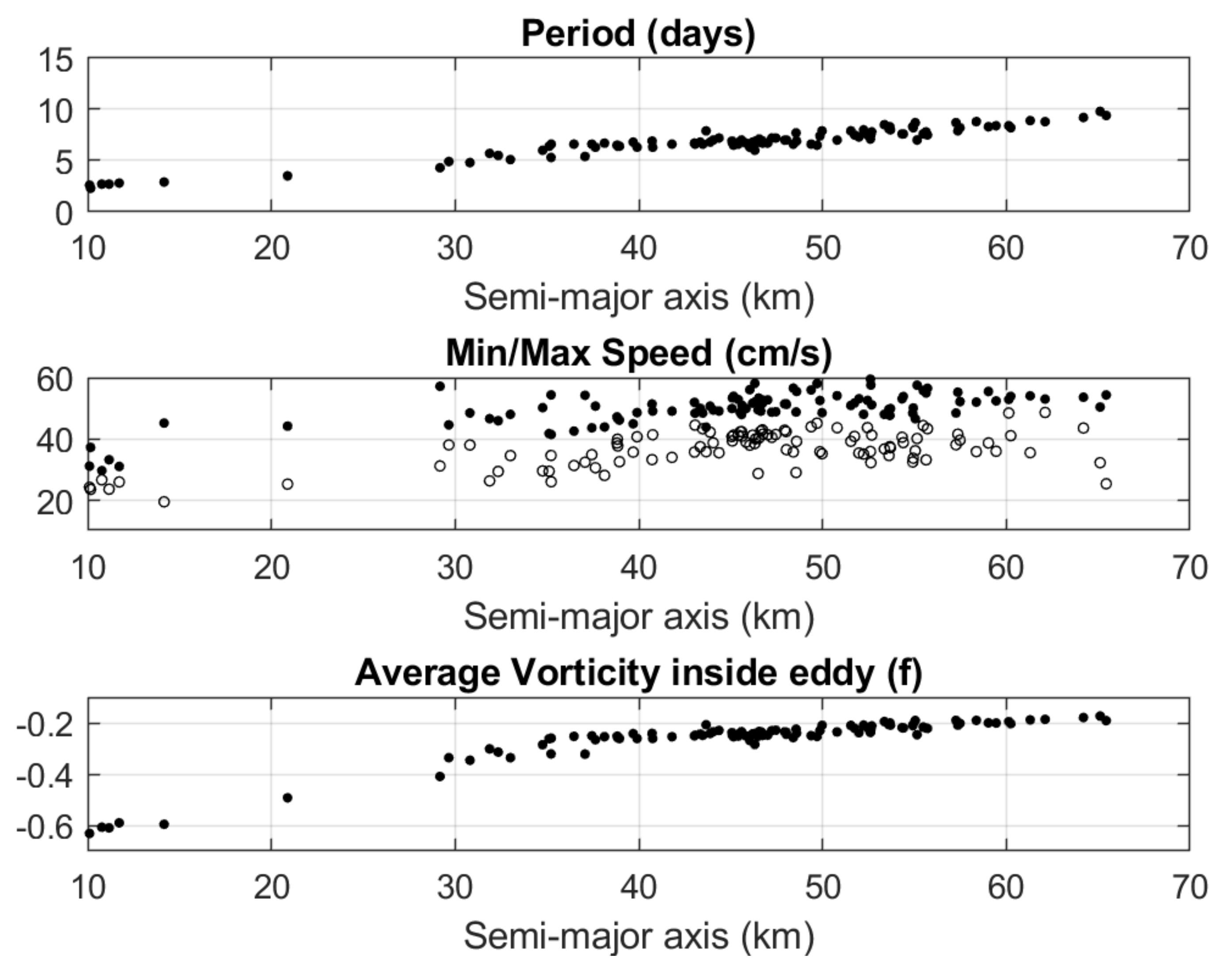
3.1. Long-Term Evolution of the AE
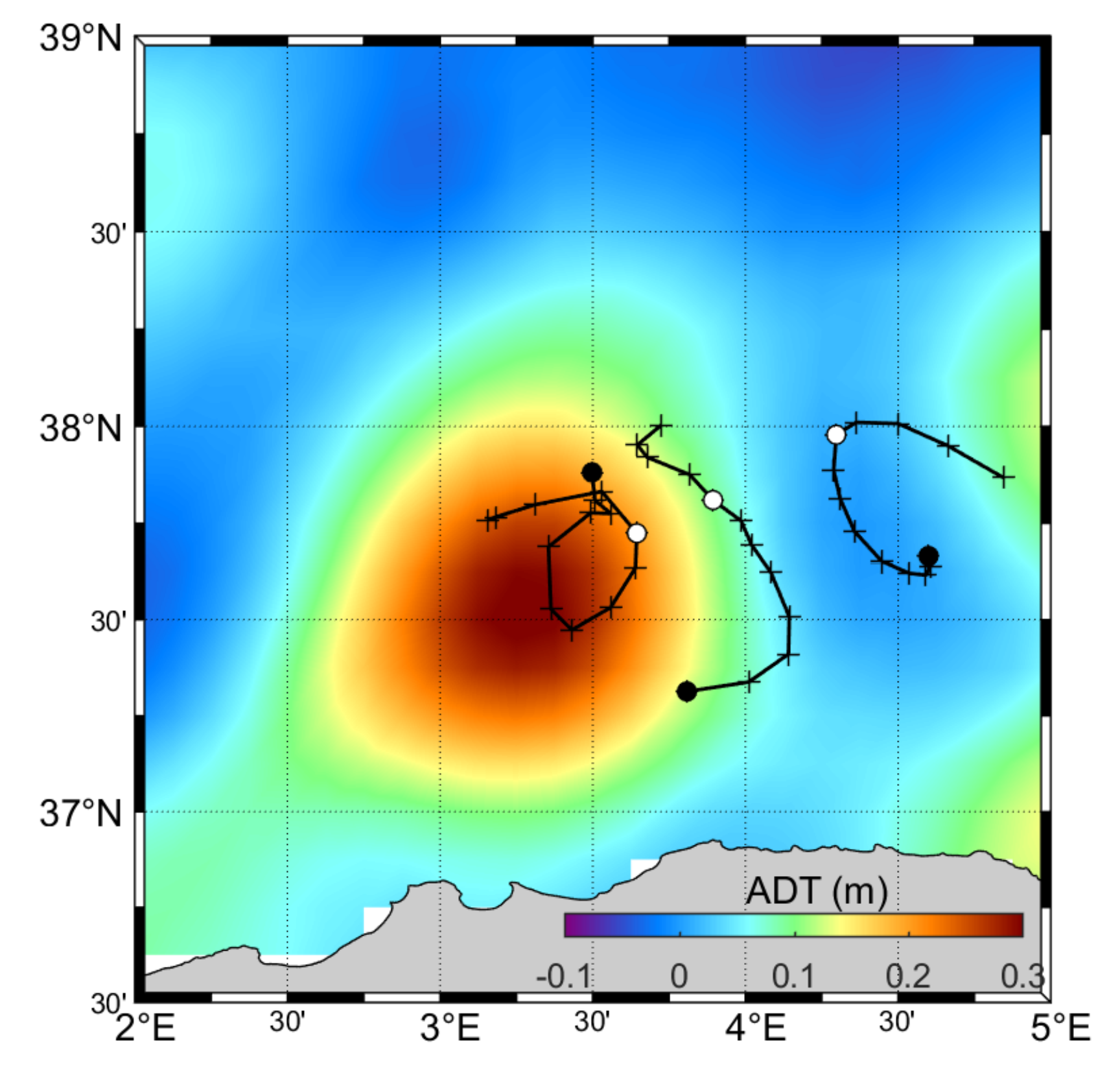
3.2. Evolution, Morphology and Kinematics of the AE in June–July 2018
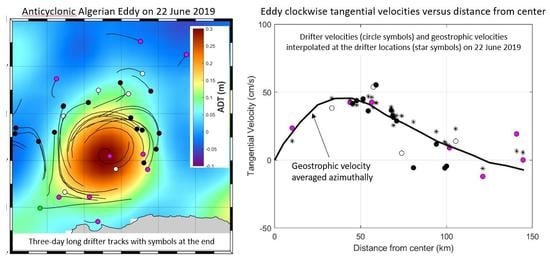
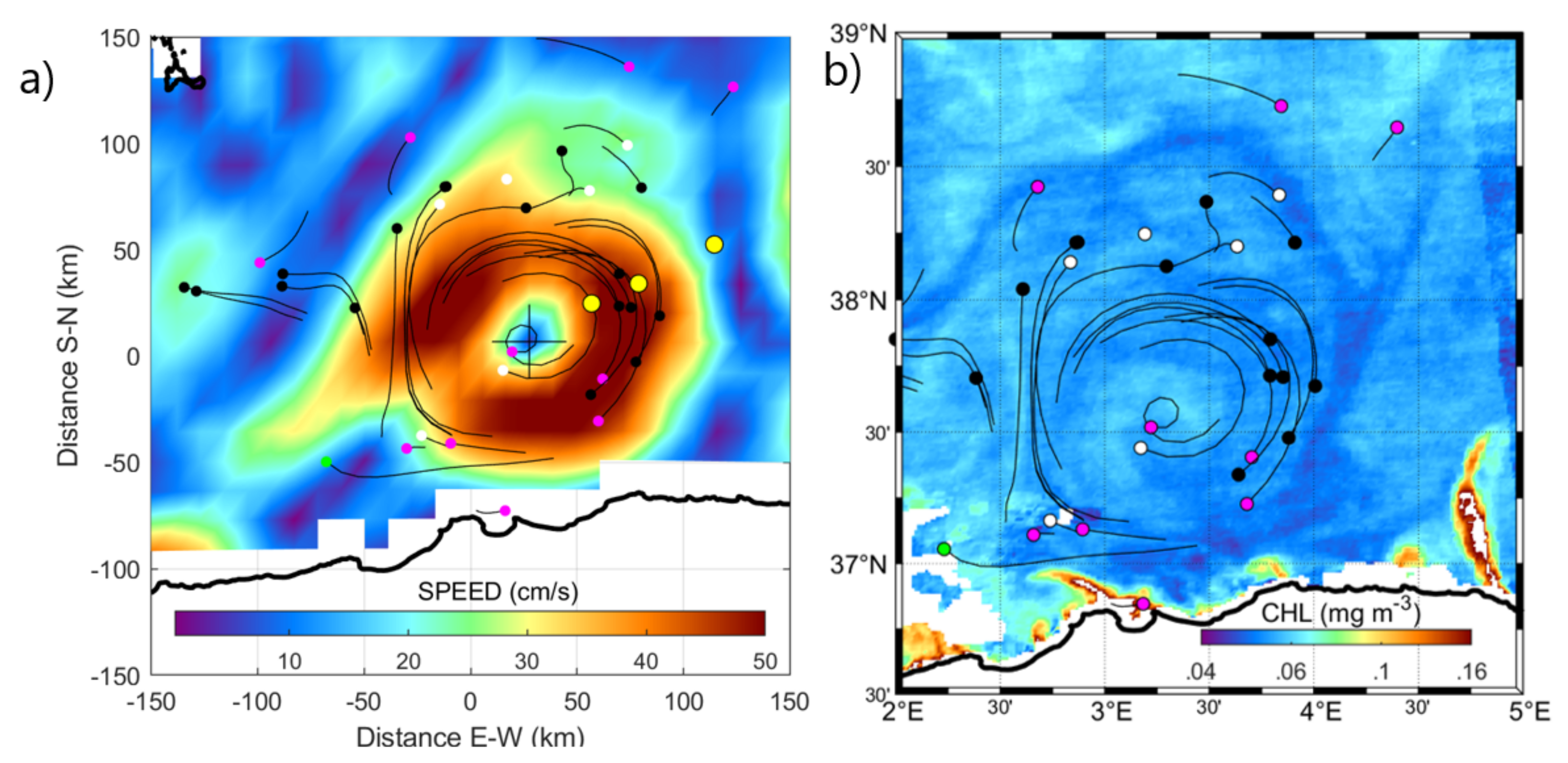
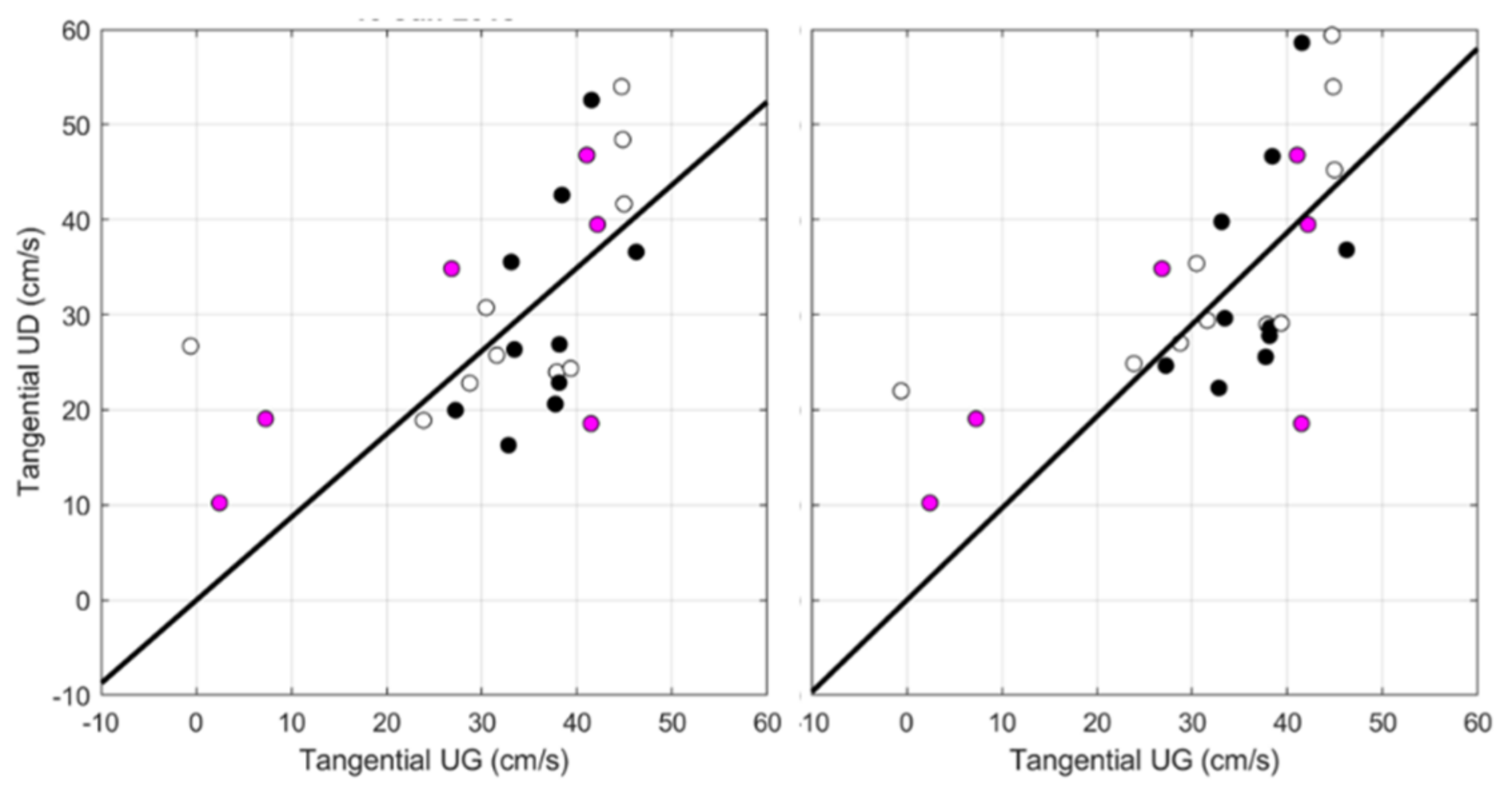
3.2.1. Near-Surface Characteristics
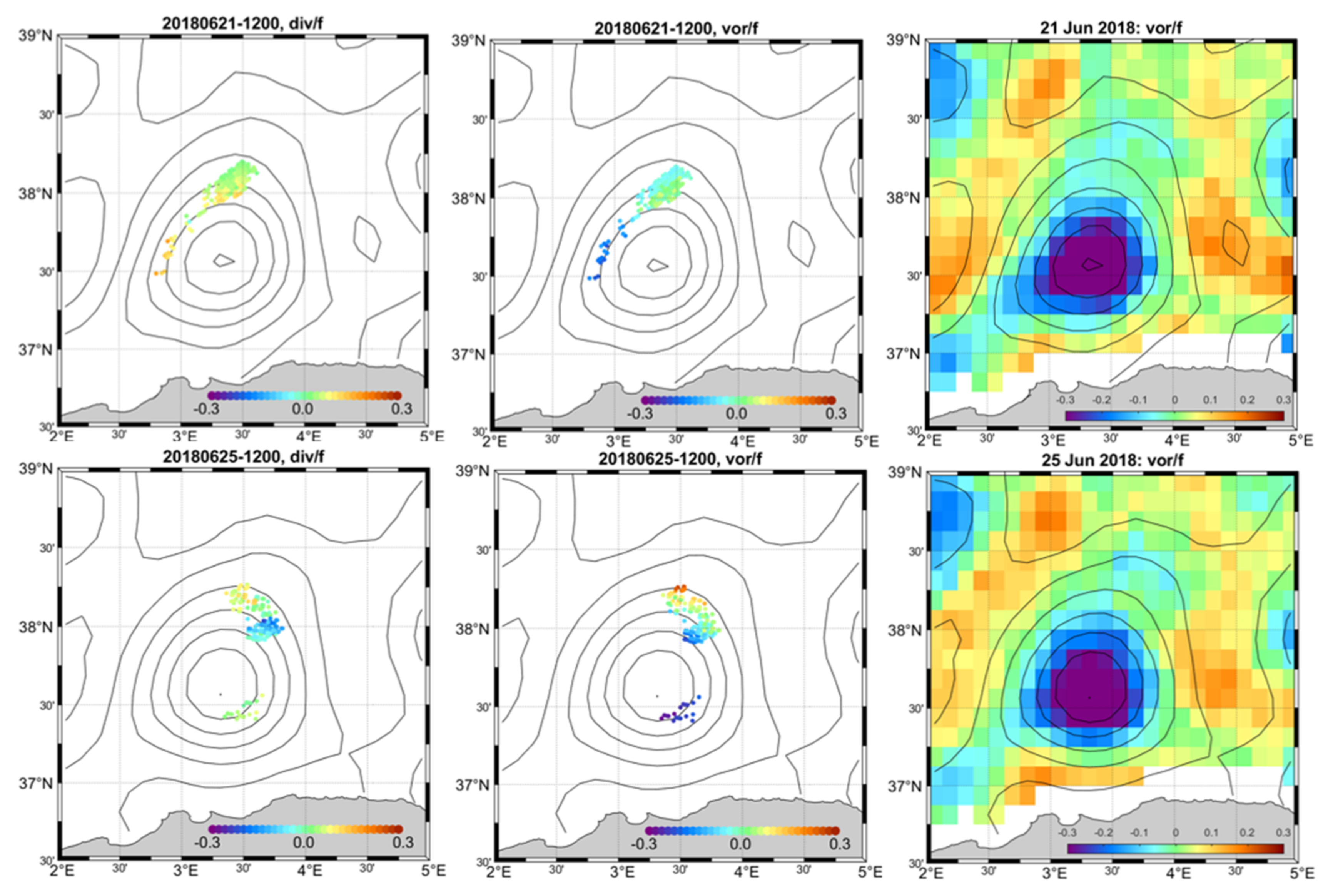
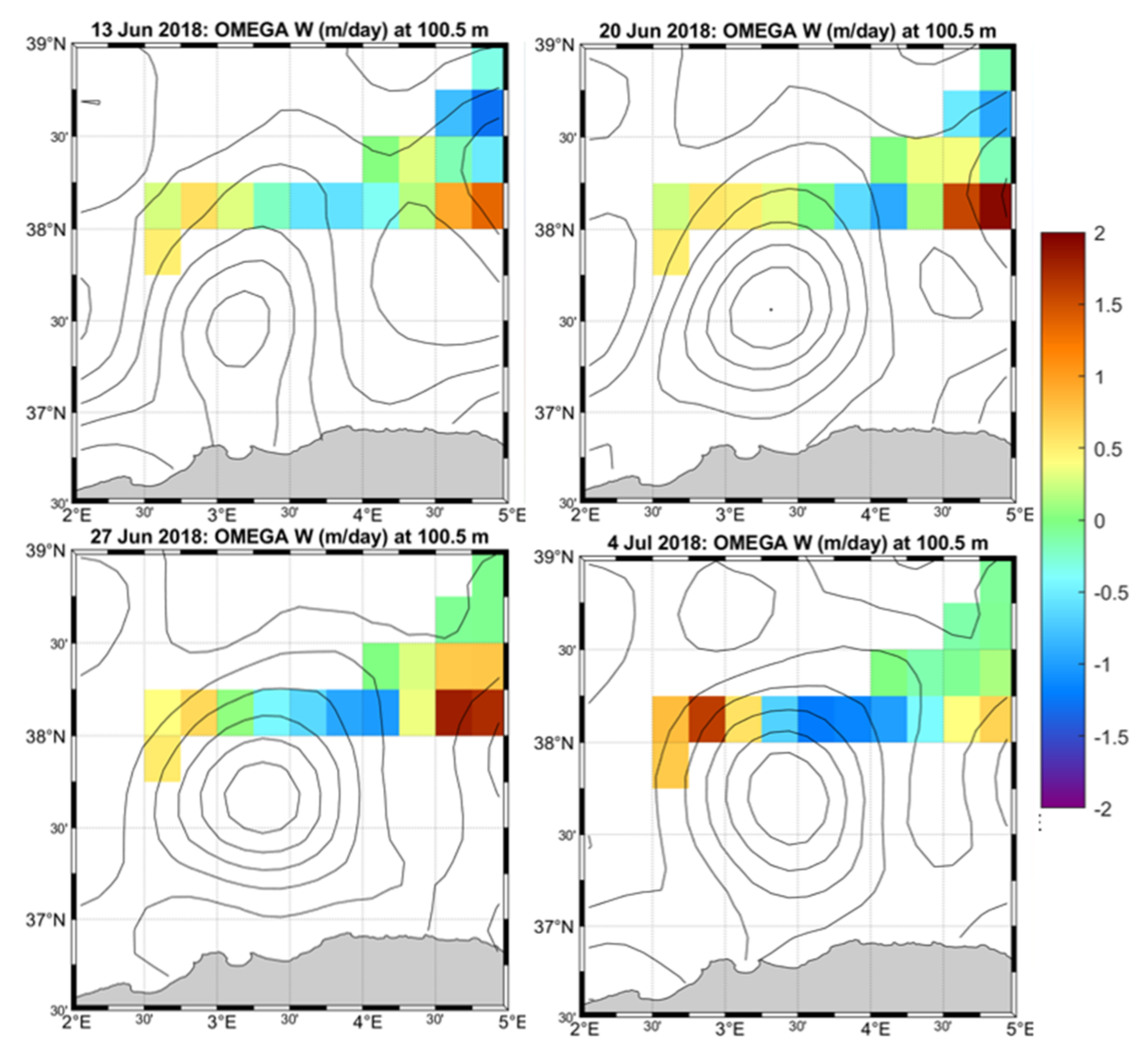
3.2.2. Differential Kinematic Properties and Vertical Velocity in the Vicinity of the AE
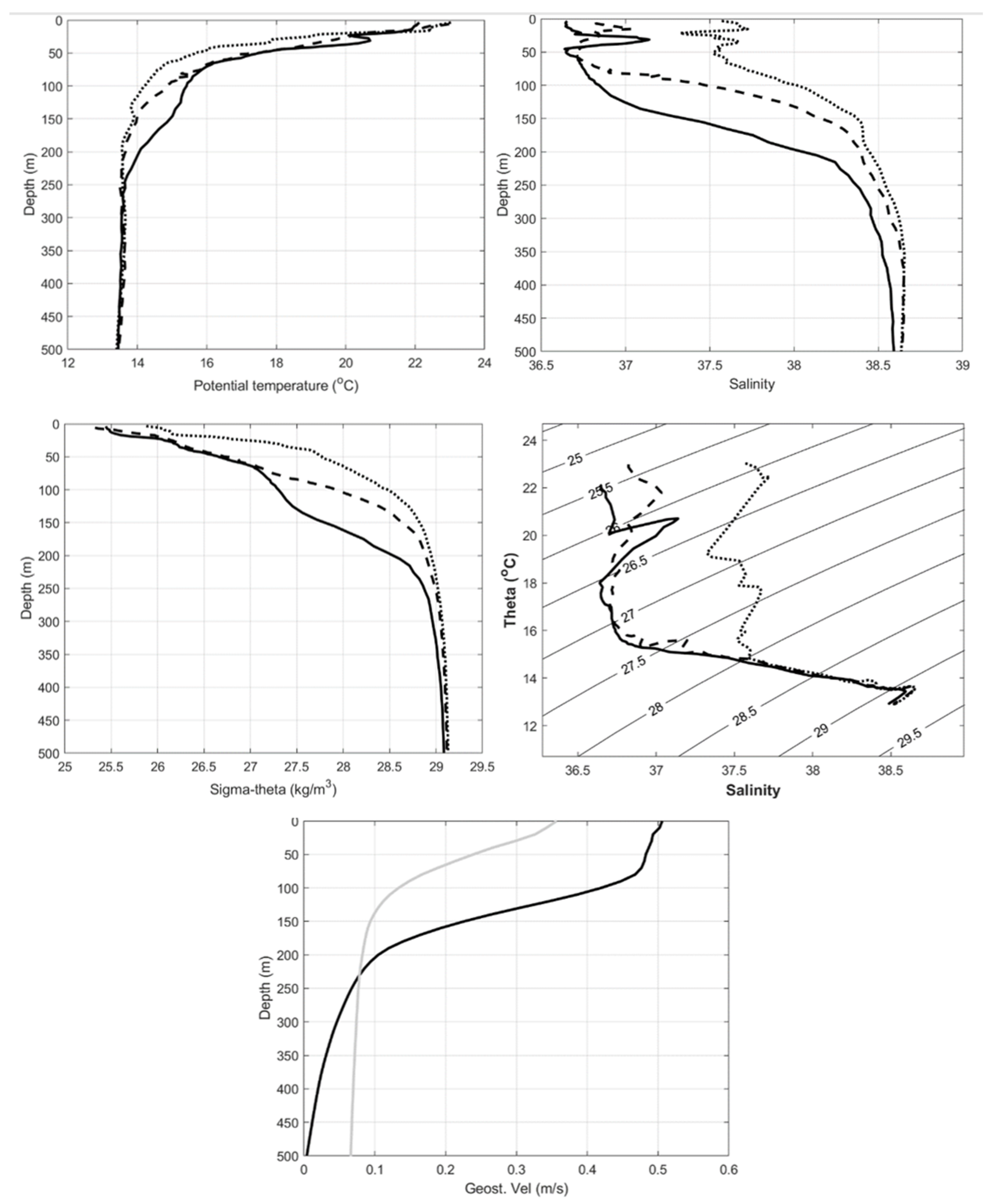
3.2.3. Vertical Structure of the AE
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
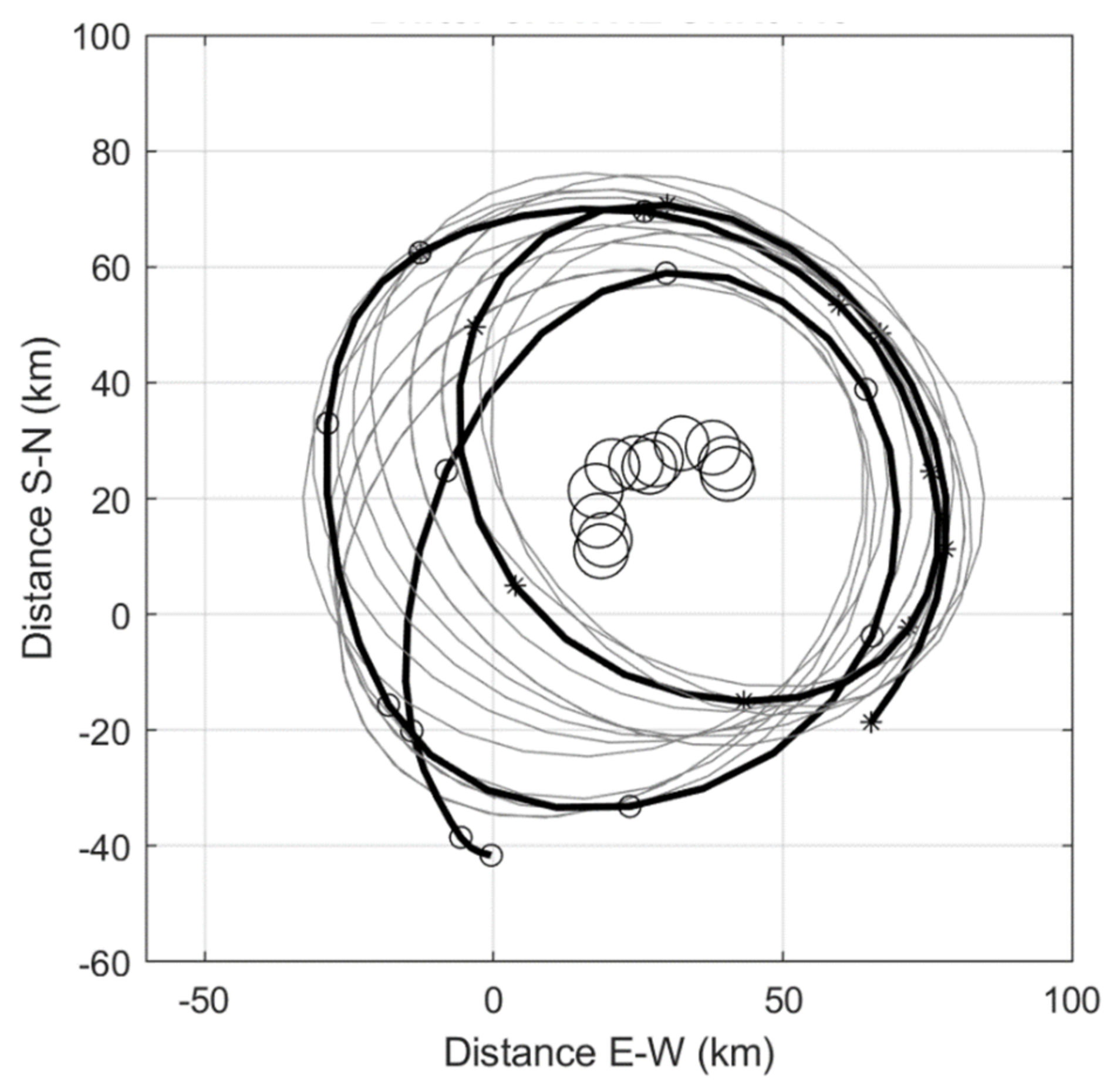
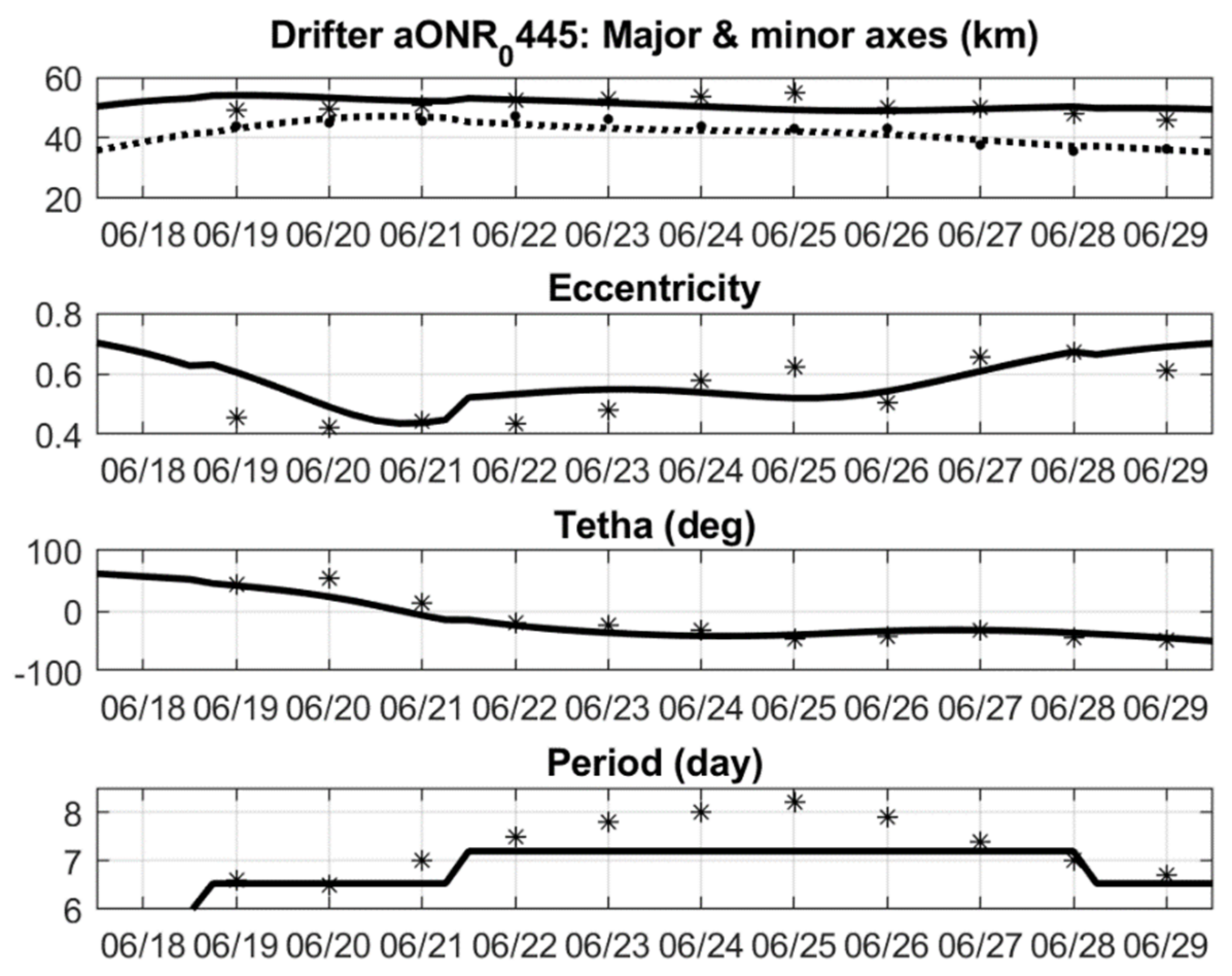
Appendix A. Fitting an Elliptical Path to a Drifter Looping Track
A.1. Least-Squares Fitting of Elliptical Track
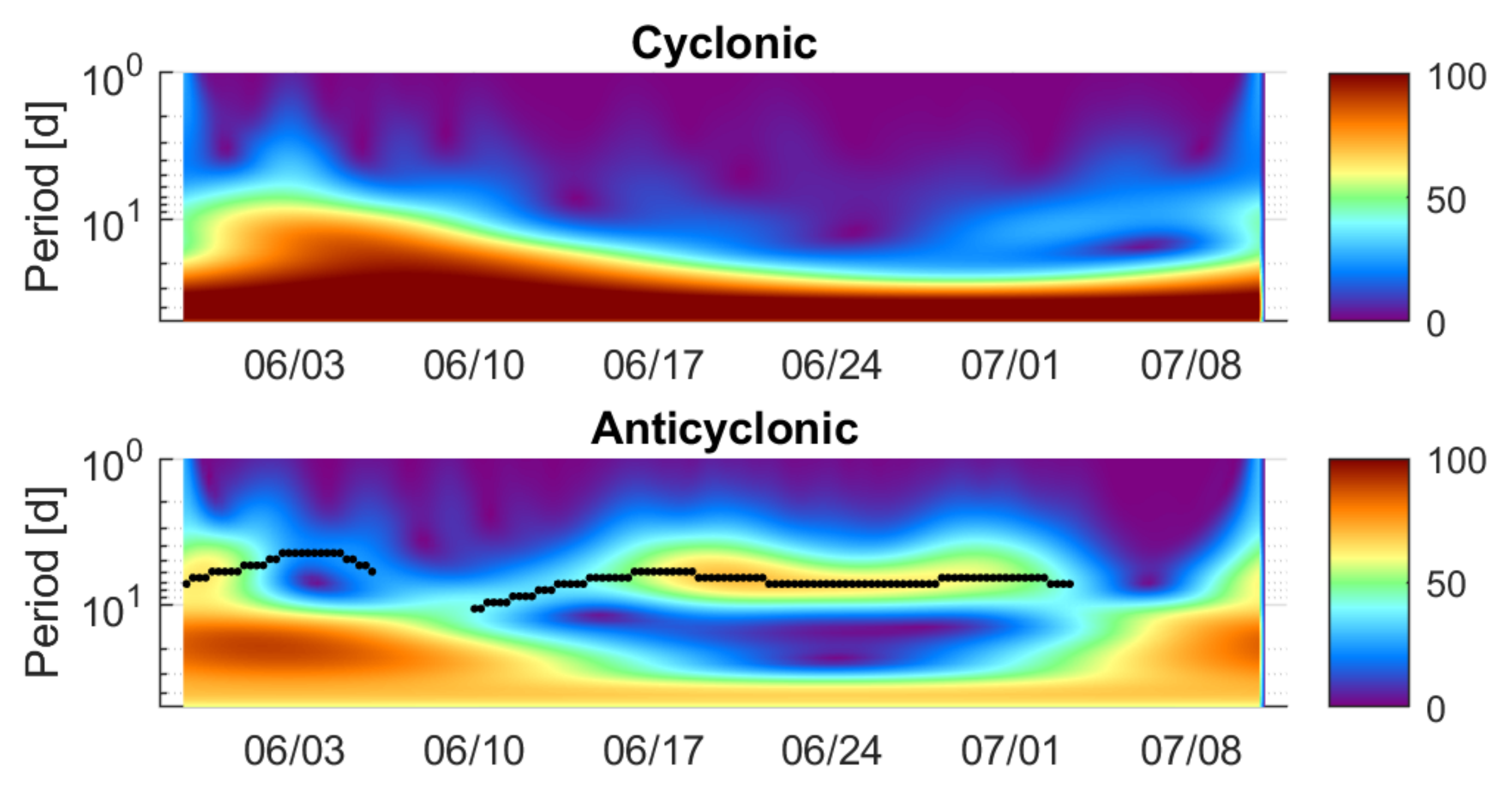
A.2. Wavelet Ridge Analysis
References
- Glenn, S.M.; Ebbesmeyer, C.C. Drifting buoy observations of a loop current anticyclonic eddy. J. Geophys. Res. Space Phys. 1993, 98, 20105–20119. [Google Scholar] [CrossRef]
- Sanderson, B.G. Structure of an eddy measured with drifters. J. Geophys. Res. Space Phys. 1995, 100, 6761–6776. [Google Scholar] [CrossRef]
- Matteoda, A.M.; Glenn, S.M. Observations of recurrent mesoscale eddies in the eastern Mediterranean. J. Geophys. Res. Space Phys. 1996, 101, 20687–20709. [Google Scholar] [CrossRef]
- Brassington, G.B. Estimating Surface Divergence of Ocean Eddies Using Observed Trajectories from a Surface Drifting Buoy. J. Atmos. Ocean. Technol. 2010, 27, 705–720. [Google Scholar] [CrossRef]
- Shapiro, G.; Barton, E.D.; Meschanov, S.L. Capture and release of Lagrangian floats by eddies in shear flow. J. Geophys. Res. Space Phys. 1997, 102, 27887–27902. [Google Scholar] [CrossRef][Green Version]
- Millot, C. Circulation in the Western Mediterranean Sea. J. Mar. Syst. 1999, 20, 423–442. [Google Scholar] [CrossRef]
- Millot, C.; Taupier-Letage, I.; Benzohra, M. The Algerian eddies. Earth Sci. Rev. 1990, 27, 203–219. [Google Scholar] [CrossRef]
- Benzorha, M.; Millot, C. Hydrodynamics of an open sea Algerian eddy. Deep Sea Res. I 1995, 42, 1831–1847. [Google Scholar] [CrossRef]
- Obaton, D.; Millot, C.; Chabert D’Hières, G.; Taupier-Letage, I. The Algerian current: Comparison between in situ and laboratory data sets. Deep Sea Res. I 2000, 47, 2159–2190. [Google Scholar] [CrossRef]
- Ruiz, S.; Font, J.; Emelianov, M.; Isern-Fontanet, J.; Millot, C.; Salas, J.; Taupier-Letage, I. Deep structure of an open sea eddy in the Algerian Basin. J. Mar. Syst. 2002, 33–34, 179–195. [Google Scholar] [CrossRef]
- Cotroneo, Y.; Aulicino, G.; Ruiz, S.; Pascual, A.; Budillon, G.; Fusco, G.; Tintoré, J. Glider and satellite high resolution monitoring of a mesoscale eddy in the algerian basin: Effects on the mixed layer depth and biochemistry. J. Mar. Syst. 2016, 162, 73–88. [Google Scholar] [CrossRef]
- Puillat, I.; Taupier-Letage, I.; Millot, C. Algerian Eddies lifetime can near 3 years. J. Mar. Syst. 2002, 31, 245–259. [Google Scholar] [CrossRef]
- Menna, M.; Gerin, R.; Bussani, A.; Poulain, P.-M. The OGS Mediterranean Drifter Database: 1986–2016; Istituto Nazionale di Oceanografia e di Geofisica Sperimentale: Trieste, Italy, 2017; p. 34. [Google Scholar]
- Mahadevan, A.; Pascual, A.; Rudnick, D.L.; Ruiz, S.; Tintoré, J.; D’Asaro, E. Coherent Pathways for Vertical Transport from the Surface Ocean to Interior. Bull. Am. Meteorol. Soc. 2020, 101, E1996–E2004. [Google Scholar] [CrossRef]
- Poulain, P.-M.; Özgökmen, T.; Guigand, C.; Wirth, N.; Casas, B.; Centurioni, L. CALYPSO Pilot Experiment 2018 27 May–2 June 2018 R/V ALLIANCE & R/V SOCIB: Lagrangian Drifter and Float Deployments; Istituto Nazionale di Oceanografia e di Geofisica Sperimentale: Trieste, Italy, 2018; p. 22. [Google Scholar]
- Niiler, P.P. The World Ocean Surface Circulation. Ocean Circulation and Climate: Observing and Modelling the Global Ocean; Siedler, G., Church, J., Gould, J., Eds.; International Geophysics Series; Academic Press: Cambridge, MA, USA, 2001; Volume 77, pp. 193–204. [Google Scholar]
- Kirwan, J.A.D.; Rossby, T.; Lumpkin, R.; Pazos, M.; Bower, A.; Furey, H.; Grodsky, S.; Carton, J.; Centurioni, L.R.; Niiler, P.P.; et al. Lagrangian Analysis and Prediction of Coastal and Ocean Dynamics. In Lagrangian Analysis and Prediction of Coastal and Ocean Dynamics; Cambridge University Press: Cambridge, UK, 2007; pp. 39–67. [Google Scholar]
- Centurioni, L.R. Drifter Technology and Impacts for Sea Surface Temperature, Sea-Level Pressure, and Ocean Circulation Studies, in Observing the Oceans in Real Time; Venkatesan, R., Tandon, A., D’Asaro, E., Atmanand, M.A., Eds.; Springer: Cham, Switzerland, 2018; pp. 37–57. [Google Scholar]
- Niiler, P.P.; Sybrandy, A.S.; Bi, K.; Poulain, P.-M.; Bitterman, D. Measurements of the water-following capability of holey-sock and TRISTAR drifters. Deep. Sea Res. Part I Oceanogr. Res. Pap. 1995, 42, 1951–1964. [Google Scholar] [CrossRef]
- Poulain, P.-M.; Gerin, R.; Mauri, E.; Pennel, R. Wind Effects on Drogued and Undrogued Drifters in the Eastern Mediterranean. J. Atmos. Ocean. Technol. 2009, 26, 1144–1156. [Google Scholar] [CrossRef]
- Centurioni, L.; Braasch, L.; Di Lauro, E.; Contestabile, P.; De Leo, F.; Casotti, R.; Franco, L.; Vicinanza, D. a New Strategic Wave Measurement Station off Naples Port Main Breakwater. Coast. Eng. Proc. 2017, 1, 36. [Google Scholar] [CrossRef]
- Davis, R.E. Drifter observations of coastal surface currents during CODE: The method and descriptive view. J. Geophys. Res. Space Phys. 1985, 90, 4741–4755. [Google Scholar] [CrossRef]
- Poulain, P.-M. Drifter observations of surface circulation in the Adriatic Sea between December 1994 and March 1996. J. Mar. Syst. 1999, 20, 231–253. [Google Scholar] [CrossRef]
- Poulain, P.-M.; Gerin, R. Assessment of the Water-Following Capabilities of CODE Drifters Based on Direct Relative Flow Measurements. J. Atmos. Ocean. Technol. 2019, 36, 621–633. [Google Scholar] [CrossRef]
- Novelli, G.; Guigand, C.M.; Cousin, C.; Ryan, E.; Laxague, N.J.M.; Dai, H.; Haus, B.K.; Özgökmen, T.M. A Biodegradable Surface Drifter for Ocean Sampling on a Massive Scale. J. Atmos. Ocean. Technol. 2017, 34, 2509–2532. [Google Scholar] [CrossRef]
- Poulain, P.-M.; Centurioni, L.; Özgökmen, T. Comparing the currents measured by CARTHE, CODE and SVP drifters as a function of wind and wave conditions in the southwestern Mediterranean Sea. J. Atmos. Ocean. Technol 2021, Submitted. [Google Scholar]
- Menna, M.; Poulain, P.-M.; Bussani, A.; Gerin, R. Detecting the drogue presence of SVP drifters from wind slippage in the Mediterranean Sea. Measurement 2018, 125, 447–453. [Google Scholar] [CrossRef]
- Argo. Argo Float Data and Metadata from Global Data Assembly Centre (Argo GDAC); SEANOE: Issy-les-Moulineaux, France, 2021. [Google Scholar] [CrossRef]
- Wong, A.L.S.; Johnson, J.M.; Owens, W.B. Delayed-mode calibration of autonomous CTD profiling float salinity data θ-S climatology. J. Atmos. Ocean. Tech. 2003, 20, 308–318. [Google Scholar] [CrossRef]
- Böhme, L.; Send, U. Objective analyses of hydrographic data for referencing profiling float salinities in highly variable environments. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2005, 52, 651–664. [Google Scholar] [CrossRef]
- Owens, W.B.; Wong, A.P. An improved calibration method for the drift of the conductivity sensor on autonomous CTD profiling floats by θ–S climatology. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2009, 56, 450–457. [Google Scholar] [CrossRef]
- Notarstefano, G.; Poulain, P.-M. Delayed Mode Quality Control of Argo Salinity Data in the Mediterranean Sea A Regional Approach; Istituto Nazionale di Oceanografia e di Geofisica Sperimentale: Trieste, Italy, 2012; p. 19. [Google Scholar]
- Cabanes, C.; Thierry, V.; Lagadec, C. Improvement of bias detection in Argo float conductivity sensors and its application in the North Atlantic. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2016, 114, 128–136. [Google Scholar] [CrossRef]
- Rio, M.H.; Pascual, A.; Poulain, P.-M.; Menna, M.; Barceló-Llull, B.; Tintoré, J. Computation of a new mean dynamic topography for the Mediterranean Sea from model outputs, altimeter measurements and oceanographic in situ data. Ocean Sci. 2014, 10, 731–744. [Google Scholar] [CrossRef]
- Nardelli, B.B. A multi-year time series of observation-based 3D horizontal and vertical quasi-geostrophic global ocean currents. Earth Syst. Sci. Data 2020, 12, 1711–1723. [Google Scholar] [CrossRef]
- Guinehut, S.; Dhomps, A.-L.; Larnicol, G.; Le Traon, P.-Y. High resolution 3-D temperature and salinity fields derived from in situ and satellite observations. Ocean Sci. 2012, 8, 845–857. [Google Scholar] [CrossRef]
- Mulet, S.; Rio, M.-H.; Mignot, A.; Guinehut, S.; Morrow, R. A new estimate of the global 3D geostrophic ocean circulation based on satellite data and in-situ measurements. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2012, 77–80, 70–81. [Google Scholar] [CrossRef]
- Molinari, R.; Kirwan, A.D. Calculations of Differential Kinematic Properties from Lagrangian Observations in the Western Caribbean Sea. J. Phys. Oceanogr. 1975, 5, 483–491. [Google Scholar] [CrossRef]
- Essink, S.; Hormann, V.; Centurioni, L.R.; Mahadevan, A. Can We Detect Submesoscale Motions in Drifter Pair Dispersion? J. Phys. Oceanogr. 2019, 49, 2237–2254. [Google Scholar] [CrossRef]
- Tarry, D.R.; Essink, S.; Pascual, A.; Ruiz, S.; Poulain, P.; Özgökmen, T.; Centurioni, L.R.; Farrar, J.T.; Shcherbina, A.; Mahadevan, A.; et al. Frontal Convergence and Vertical Velocity Measured by Drifters in the Alboran Sea. J. Geophys. Res. Oceans 2021, 126. [Google Scholar] [CrossRef]
- Choi, J.; Bracco, A.; Barkan, R.; Shchepetkin, A.F.; McWilliams, J.C.; Molemaker, J.M. Submesoscale Dynamics in the Northern Gulf of Mexico. Part III: Lagrangian Implications. J. Phys. Oceanogr. 2017, 47, 2361–2376. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Heil, W.H.; Nof, D. Oscillations and rotations of elliptical warm-core rings. J. Geophys. Res. Space Phys. 1985, 90, 11756. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B.; Santoleri, R.; Sparnocchia, S. Small mesoscale features at a meandering upper-ocean fron in the western Ionian Sea (Mediterranean Sea): Vertical motion and potential vorticity analysis. J. Phys. Oceanogr. 2001, 31, 227–2250. [Google Scholar]
- Barceló-Llull, B.; Pallàs-Sanz, E.; Sangrà, P.; Martínez-Marrero, A.; Estrada-Allis, S.; Arístegui, J. Ageostrophic Secondary Circulation in a Subtropical Intrathermocline Eddy. J. Phys. Oceanogr. 2017, 47, 1107–1123. [Google Scholar] [CrossRef]
- Pascual, A.; Gomis, D.; Haney, R.L.; Ruiz, S. A quasigeostrophic analysis of a meander in the Palamos Canyon: Vertical velocity, peopotential tendency and relocation technique. J. Phys. Oceanogr. 2004, 34, 2274–2287. [Google Scholar] [CrossRef][Green Version]
- Lilly, J.M.; Gascard, J.-C. Wavelet ridge diagnosis of time-varying elliptical signals with application to an oceanic eddy. Nonlinear Process. Geophys. 2006, 13, 467–483. [Google Scholar] [CrossRef][Green Version]
- Lilly, J.M.; Pérez-Brunius, P. Extracting statistically significant eddy signals from large Lagrangian datasets using wavelet ridge analysis, with application to the Gulf of Mexico. Nonlinear Process. Geophys. 2021, 28, 181–212. [Google Scholar] [CrossRef]




| Day | Number of Points | Number of Points > 100 km | Slope | RMSE (cm/s) |
|---|---|---|---|---|
| 13-Jun-2018 | 37 | 29 | 0.43 ± 0.09 | 14.3 |
| 16-Jun-2018 | 30 | 26 | 0.87 ± 0.06 | 10.9 |
| 16-Jun-2018 * | 30 | 26 | 0.97 ± 0.06 | 10.6 |
| 19-Jun-2018 | 32 | 25 | 1.03 ± 0.06 | 12.5 |
| 22-Jun-2018 | 25 | 20 | 0.94 ± 0.08 | 13.4 |
| 25-Jun-2018 | 22 | 17 | 1.04 ± 0.07 | 11.8 |
| 28-Jun-2018 | 17 | 13 | 1.08 ± 0.06 | 8.3 |
| 1-Jul-2018 | 15 | 11 | 1.04 ± 0.12 | 13.6 |
| 4-Jul-2018 | 11 | 8 | 0.69 ± 0.16 | 14.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poulain, P.-M.; Centurioni, L.; Özgökmen, T.; Tarry, D.; Pascual, A.; Ruiz, S.; Mauri, E.; Menna, M.; Notarstefano, G. On the Structure and Kinematics of an Algerian Eddy in the Southwestern Mediterranean Sea. Remote Sens. 2021, 13, 3039. https://doi.org/10.3390/rs13153039
Poulain P-M, Centurioni L, Özgökmen T, Tarry D, Pascual A, Ruiz S, Mauri E, Menna M, Notarstefano G. On the Structure and Kinematics of an Algerian Eddy in the Southwestern Mediterranean Sea. Remote Sensing. 2021; 13(15):3039. https://doi.org/10.3390/rs13153039
Chicago/Turabian StylePoulain, Pierre-Marie, Luca Centurioni, Tamay Özgökmen, Daniel Tarry, Ananda Pascual, Simon Ruiz, Elena Mauri, Milena Menna, and Giulio Notarstefano. 2021. "On the Structure and Kinematics of an Algerian Eddy in the Southwestern Mediterranean Sea" Remote Sensing 13, no. 15: 3039. https://doi.org/10.3390/rs13153039
APA StylePoulain, P.-M., Centurioni, L., Özgökmen, T., Tarry, D., Pascual, A., Ruiz, S., Mauri, E., Menna, M., & Notarstefano, G. (2021). On the Structure and Kinematics of an Algerian Eddy in the Southwestern Mediterranean Sea. Remote Sensing, 13(15), 3039. https://doi.org/10.3390/rs13153039