Two-Stream Convolutional Long- and Short-Term Memory Model Using Perceptual Loss for Sequence-to-Sequence Arctic Sea Ice Prediction
Abstract
:1. Introduction
2. Datasets
2.1. Sea Ice Data
2.2. ECMWF Reanalysis v5 (ERA5)
2.3. Input Data Compilation
3. Methods
3.1. Prediction Models
3.1.1. Baseline Models: Persistence, LSTM, and ConvLSTM
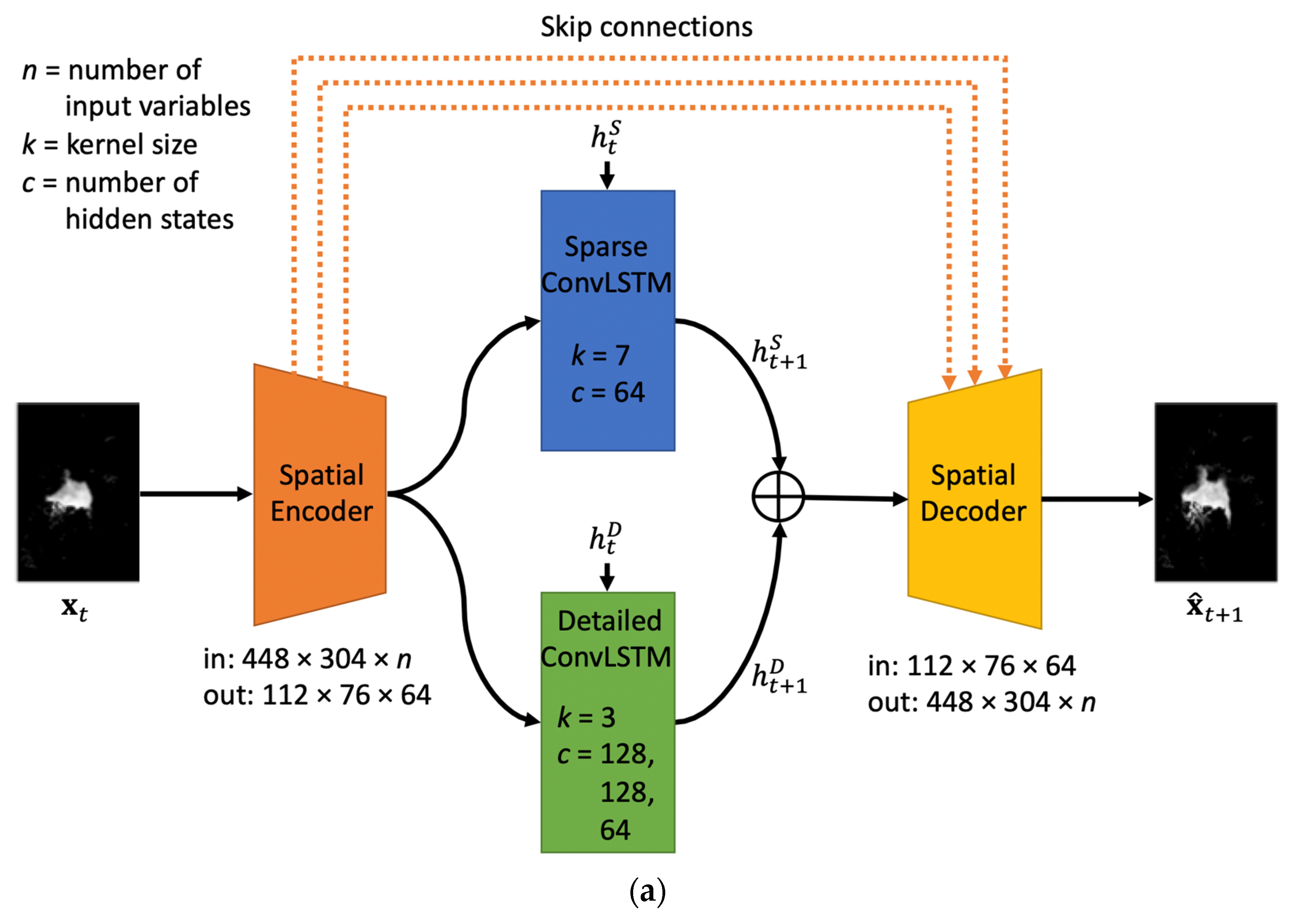
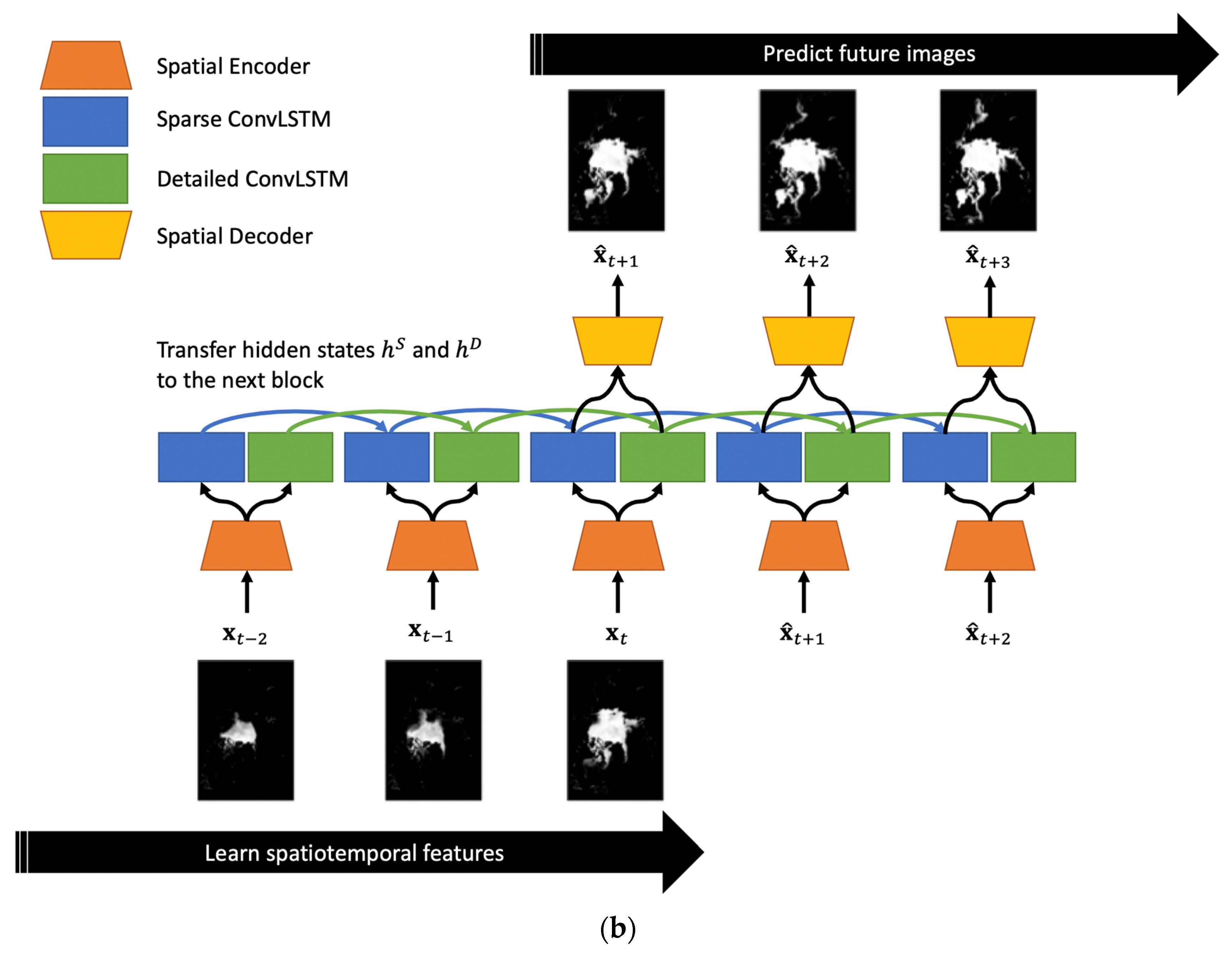
3.1.2. Proposed Model: Two-Stream ConvLSTM
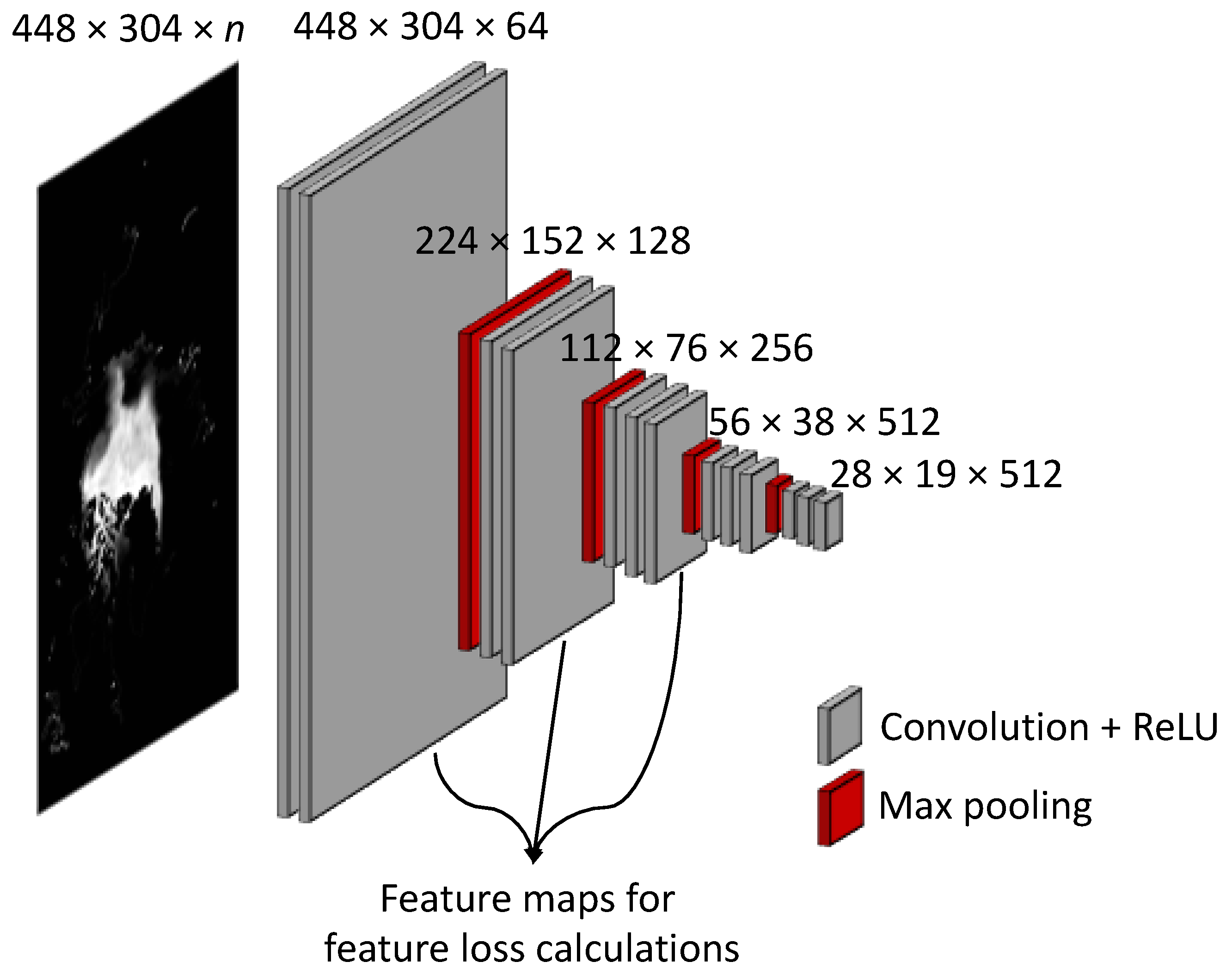
3.2. Loss Functions
3.3. Sensitivity of Input Variables
3.4. Training and Testing of Model
3.5. Evaluation Metrics
4. Experimental Results
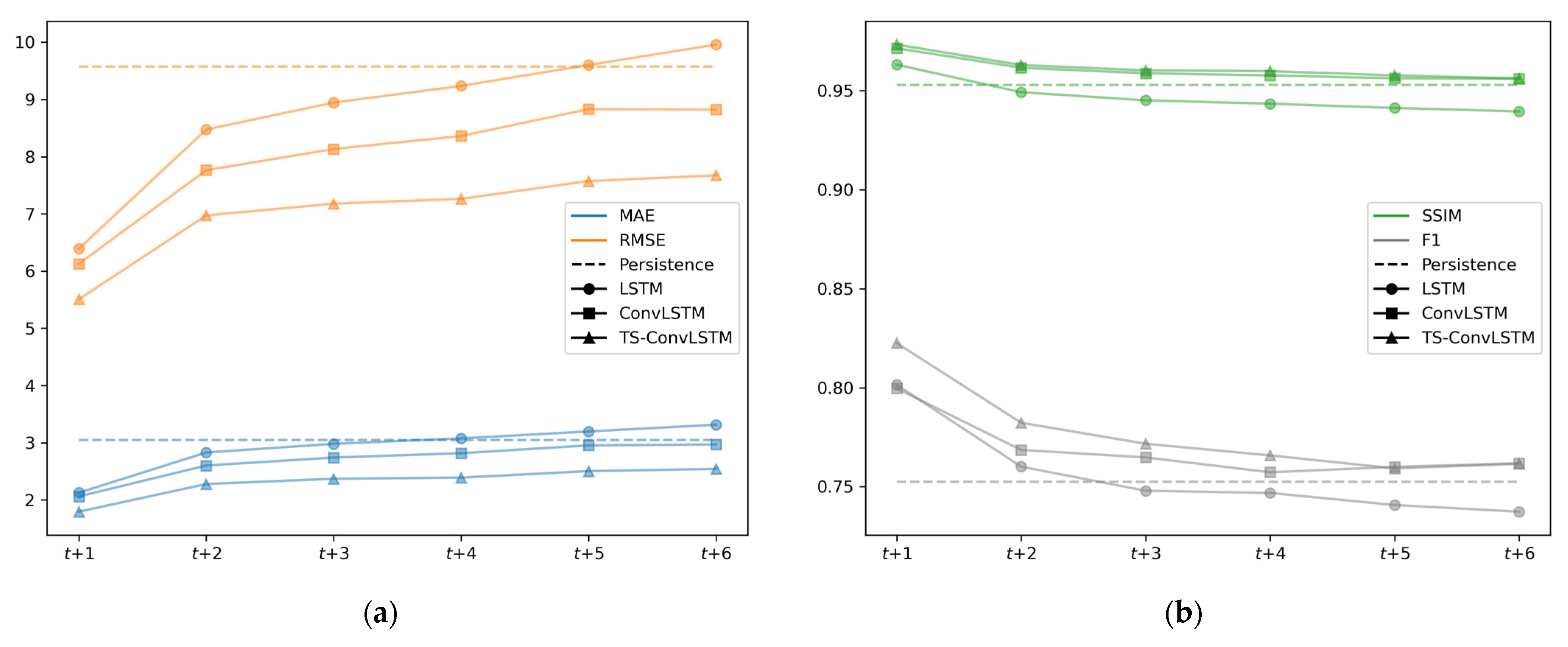
4.1. Comparison of Prediction Models
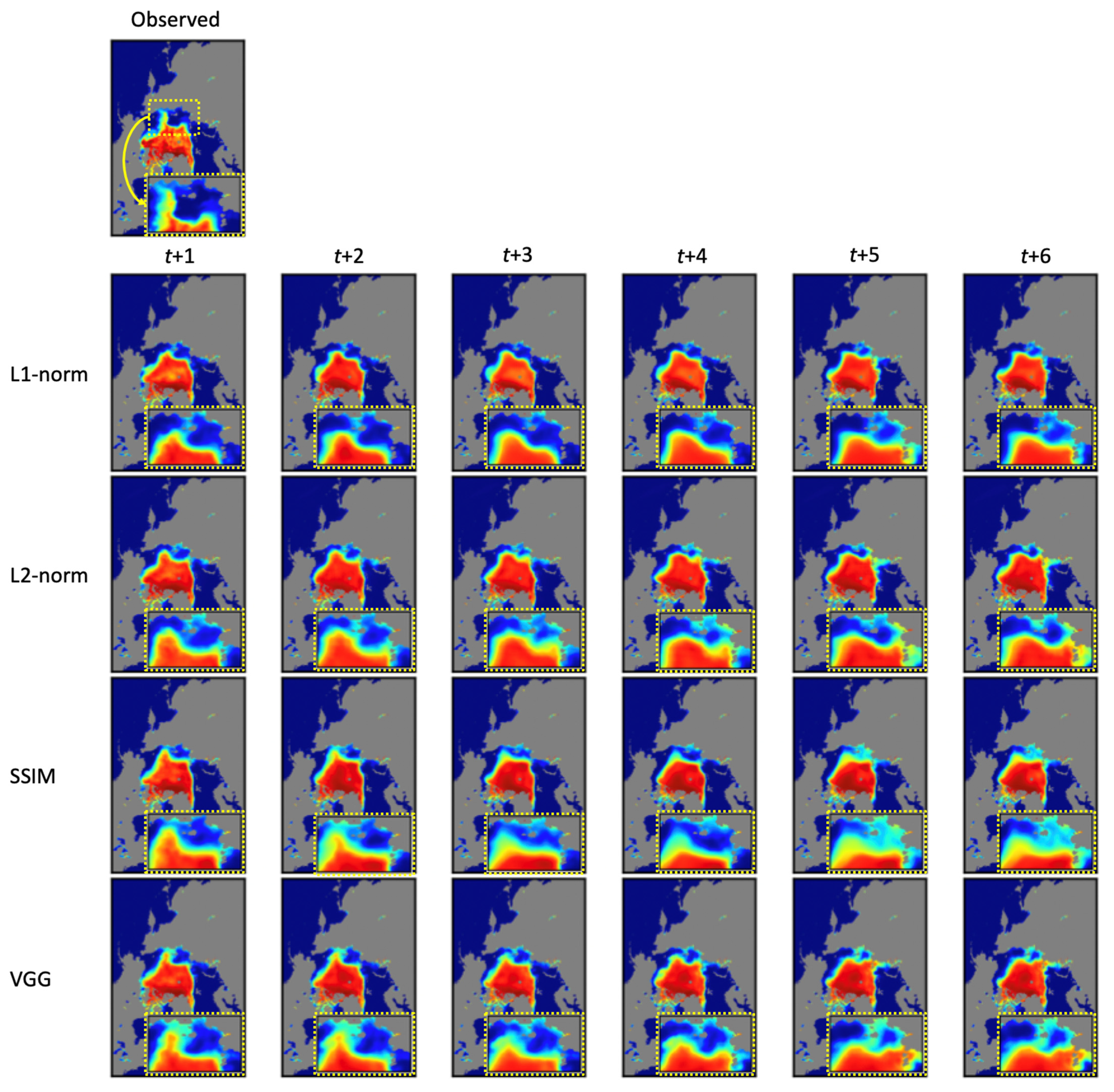
4.2. Loss Comparison
4.3. Input Variable Comparison
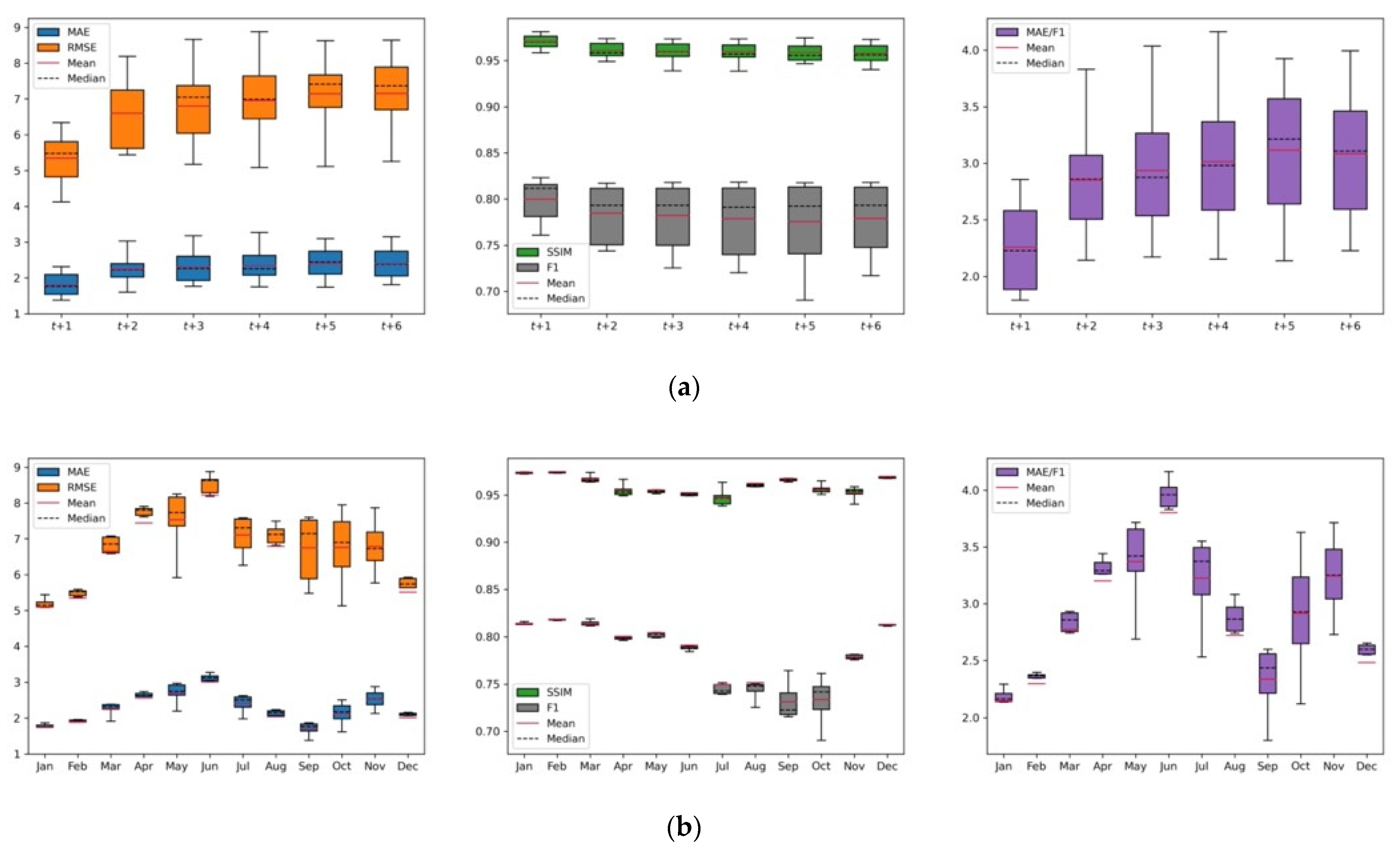
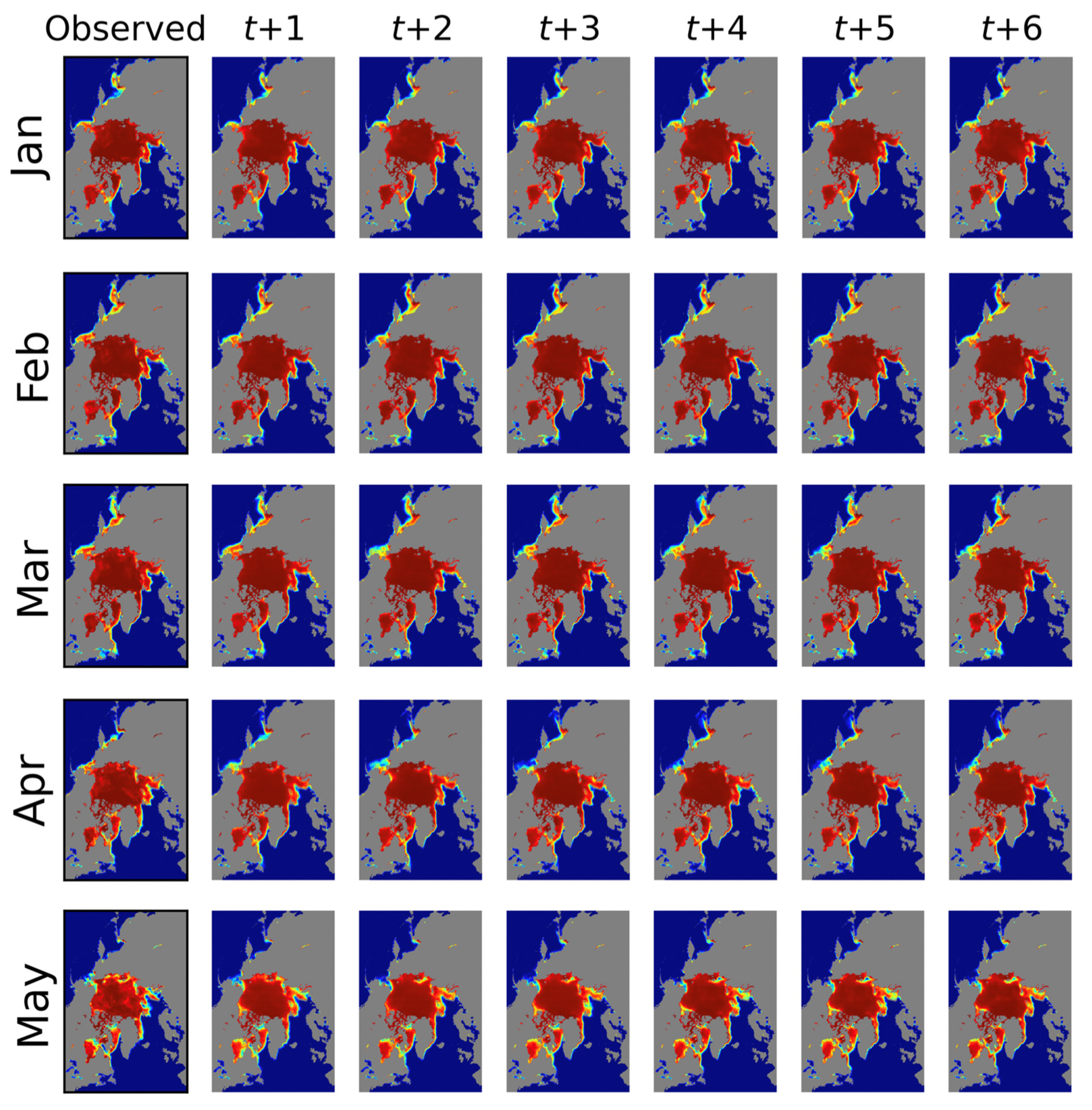
4.4. Experimental Results for 2020
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thackeray, C.W.; Hall, A. An emergent constraint on future Arctic sea-ice albedo feedback. Nat. Clim. Chang. 2019, 9, 972–978. [Google Scholar] [CrossRef]
- Najafi, M.R.; Zwiers, F.W.; Gillett, N.P. Attribution of Arctic temperature change to greenhouse-gas and aerosol influences. Nat. Clim. Chang. 2015, 5, 246–249. [Google Scholar] [CrossRef]
- Stroeve, J.; Holland, M.M.; Meier, W.; Scambos, T.; Serreze, M. Arctic sea ice decline: Faster than forecast. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Vihma, T. Effects of Arctic Sea Ice Decline on Weather and Climate: A Review. Surv. Geophys. 2014, 35, 1175–1214. [Google Scholar] [CrossRef] [Green Version]
- Meier, W.; Bhatt, U.S.; Walsh, J.; Thoman, R.; Bieniek, P.; Bitz, C.M.; Blanchard-Wrigglesworth, E.; Eicken, H.; Hamilton, L.C.; Hardman, M.; et al. 2020 Sea Ice Outlook Post-Season Report; Sea Ice Prediction Network: Fairbanks, AK, USA, 2021. [Google Scholar]
- Screen, J.A.; Simmonds, I. The central role of diminishing sea ice in recent Arctic temperature amplification. Nat. Cell Biol. 2010, 464, 1334–1337. [Google Scholar] [CrossRef] [Green Version]
- Pithan, F.; Mauritsen, T. Arctic amplification dominated by temperature feedbacks in contemporary climate models. Nat. Geosci. 2014, 7, 181–184. [Google Scholar] [CrossRef]
- Mioduszewski, J.R.; Vavrus, S.; Wang, M.; Holland, M.; Landrum, L. Past and future interannual variability in Arctic sea ice in coupled climate models. Cryosphere 2019, 13, 113–124. [Google Scholar] [CrossRef] [Green Version]
- Guemas, V.; Blanchard-Wrigglesworth, E.; Chevallier, M.; Day, J.; Déqué, M.; Doblas-Reyes, F.; Fučkar, N.S.; Germe, A.; Hawkins, E.; Keeley, S.; et al. A review on Arctic sea-ice predictability and prediction on seasonal to decadal time-scales. Q. J. R. Meteorol. Soc. 2016, 142, 546–561. [Google Scholar] [CrossRef]
- Stroeve, J.; Hamilton, L.C.; Bitz, C.M.; Blanchard-Wrigglesworth, E. Predicting September sea ice: Ensemble skill of the SEARCH Sea Ice Outlook 2008–2013. Geophys. Res. Lett. 2014, 41, 2411–2418. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Chen, M.; Kumar, A. Seasonal Prediction of Arctic Sea Ice Extent from a Coupled Dynamical Forecast System. Mon. Weather. Rev. 2013, 141, 1375–1394. [Google Scholar] [CrossRef]
- Sigmond, M.; Fyfe, J.C.; Flato, G.M.; Kharin, V.V.; Merryfield, W.J. Seasonal forecast skill of Arctic sea ice area in a dynamical forecast system. Geophys. Res. Lett. 2013, 40, 529–534. [Google Scholar] [CrossRef]
- Chi, J.; Kim, H.-C. Prediction of Arctic Sea Ice Concentration Using a Fully Data Driven Deep Neural Network. Remote Sens. 2017, 9, 1305. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Kim, K.; Cho, J.; Kang, Y.Q.; Yoon, H.-J.; Lee, Y.-W. Satellite-Based Prediction of Arctic Sea Ice Concentration Using a Deep Neural Network with Multi-Model Ensemble. Remote Sens. 2018, 11, 19. [Google Scholar] [CrossRef] [Green Version]
- Choi, M.; De Silva, L.W.A.; Yamaguchi, H. Artificial Neural Network for the Short-Term Prediction of Arctic Sea Ice Concentration. Remote Sens. 2019, 11, 1071. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.J.; Kim, H.-C.; Han, D.; Lee, S.; Im, J. Prediction of monthly Arctic sea ice concentrations using satellite and reanalysis data based on convolutional neural networks. Cryosphere 2020, 14, 1083–1104. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Zhang, R.; Wang, Y.; Yan, H.; Hong, M. Daily Prediction of the Arctic Sea Ice Concentration Using Reanalysis Data Based on a Convolutional LSTM Network. J. Mar. Sci. Eng. 2021, 9, 330. [Google Scholar] [CrossRef]
- Cho, K.; Naoki, K. Advantages of AMSR2 for Monitoring Sea Ice from Space; Citeseer: University Park, PA, USA, 2015; pp. 19–23. [Google Scholar]
- Ivanova, N.; Johannessen, O.M.; Pedersen, L.T.; Tonboe, R.T. Retrieval of Arctic Sea Ice Parameters by Satellite Passive Microwave Sensors: A Comparison of Eleven Sea Ice Concentration Algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7233–7246. [Google Scholar] [CrossRef]
- Cavalieri, D.; Parkinson, C.; Gloersen, P.; Zwally, H.J. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data; Version 1; NASA Goddard Earth Sciences Data and Information Services Center: Greenbelt, MD, USA, 2020; p. 25.
- Spreen, G.; Kaleschke, L.; Heygster, G. Sea ice remote sensing using AMSR-E 89-GHz channels. J. Geophys. Res. Space Phys. 2008, 113, 113. [Google Scholar] [CrossRef] [Green Version]
- Comiso, J.C. SSM/I Sea Ice Concentrations Using the Bootstrap Algorithm; National Aeronautics and Space Administration, Goddard Space Flight Center: Greenbelt, MD, USA, 1995; Volume 1380.
- Vinnikov, K.Y.; Robock, A.; Stouffer, R.J.; Walsh, J.E.; Parkinson, C.L.; Cavalieri, D.J.; Mitchell, J.F.B.; Garrett, D.; Zakharov, V.F. Global Warming and Northern Hemisphere Sea Ice Extent. Science 1999, 286, 1934–1937. [Google Scholar] [CrossRef] [PubMed]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1979 to Present. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview (accessed on 2 June 2021). [CrossRef]
- Lindsay, R.; Wensnahan, M.; Schweiger, A.; Zhang, J. Evaluation of Seven Different Atmospheric Reanalysis Products in the Arctic. J. Clim. 2014, 27, 2588–2606. [Google Scholar] [CrossRef] [Green Version]
- Graham, R.M.; Hudson, S.R.; Maturilli, M. Improved Performance of ERA5 in Arctic Gateway Relative to Four Global Atmospheric Reanalyses. Geophys. Res. Lett. 2019, 46, 6138–6147. [Google Scholar] [CrossRef] [Green Version]
- Dong, X.; Wang, Y.; Hou, S.; Ding, M.; Yin, B.; Zhang, Y. Robustness of the Recent Global Atmospheric Reanalyses for Antarctic Near-Surface Wind Speed Climatology. J. Clim. 2020, 33, 4027–4043. [Google Scholar] [CrossRef] [Green Version]
- Greff, K.; Srivastava, R.K.; Koutnik, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, S.; Lessmann, S. A comparative study of LSTM neural networks in forecasting day-ahead global horizontal irradiance with satellite data. Sol. Energy 2018, 162, 232–247. [Google Scholar] [CrossRef]
- Rhif, M.; Ben Abbes, A.; Martinez, B.; Farah, I.R. A deep learning approach for forecasting non-stationary big remote sensing time series. Arab. J. Geosci. 2020, 13, 1–11. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.; Woo, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. arXiv 2015, arXiv:1506.04214. [Google Scholar]
- Chen, L.; Cao, Y.; Ma, L.; Zhang, J. A Deep Learning-Based Methodology for Precipitation Nowcasting With Radar. Earth Space Sci. 2020, 7, 7. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Wu, J.; Huang, H.; Wang, R.; Liang, F.; Xinhua, H. Prediction of Short-Time Rainfall Based on Deep Learning. Math. Probl. Eng. 2021, 2021, 1–8. [Google Scholar] [CrossRef]
- Kreuzer, D.; Munz, M.; Schlüter, S. Short-term temperature forecasts using a convolutional neural network—An application to different weather stations in Germany. Mach. Learn. Appl. 2020, 2, 100007. [Google Scholar] [CrossRef]
- Kim, K.-S.; Lee, J.-B.; Roh, M.-I.; Han, K.-M.; Lee, G.-H. Prediction of Ocean Weather Based on Denoising AutoEncoder and Convolutional LSTM. J. Mar. Sci. Eng. 2020, 8, 805. [Google Scholar] [CrossRef]
- Donahue, J.; Hendricks, L.A.; Rohrbach, M.; Venugopalan, S.; Guadarrama, S.; Saenko, K.; Darrell, T. Long-Term Recurrent Convolutional Networks for Visual Recognition and Description. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 677–691. [Google Scholar] [CrossRef]
- Ma, C.-Y.; Chen, M.-H.; Kira, Z.; AlRegib, G. TS-LSTM and temporal-inception: Exploiting spatiotemporal dynamics for activity recognition. Signal Process. Image Commun. 2019, 71, 76–87. [Google Scholar] [CrossRef] [Green Version]
- Ye, W.; Cheng, J.; Yang, F.; Xu, Y. Two-Stream Convolutional Network for Improving Activity Recognition Using Convolutional Long Short-Term Memory Networks. IEEE Access 2019, 7, 67772–67780. [Google Scholar] [CrossRef]
- Chi, J.; Kim, H.-C. Retrieval of daily sea ice thickness from AMSR2 passive microwave data using ensemble convolutional neural networks. GIScience Remote Sens. 2021, 1–19. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. In Computer Vision—ECCV 2016; Springer: Cham, Switzerland, 2016; pp. 694–711. [Google Scholar] [CrossRef] [Green Version]
- Chi, J.; Kim, H.-C.; Lee, S.; Crawford, M.M. Deep learning based retrieval algorithm for Arctic sea ice concentration from AMSR2 passive microwave and MODIS optical data. Remote Sens. Environ. 2019, 231, 111204. [Google Scholar] [CrossRef]
- Perez, L.; Wang, J. The Effectiveness of Data Augmentation in Image Classification Using Deep Learning. arXiv 2017, arXiv:1712.04621v1. [Google Scholar]
- Williams, R.J.; Zipser, D. A Learning Algorithm for Continually Running Fully Recurrent Neural Networks. Neural Comput. 1989, 1, 270–280. [Google Scholar] [CrossRef]
- He, T.; Zhang, J.; Zhou, Z.; Glass, J. Quantifying Exposure Bias for Open-Ended Language Generation. arXiv 2019, arXiv:1905.10617. [Google Scholar]
- Tran, Q.-K.; Song, S.-K. Computer Vision in Precipitation Nowcasting: Applying Image Quality Assessment Metrics for Training Deep Neural Networks. Atmosphere 2019, 10, 244. [Google Scholar] [CrossRef] [Green Version]
- Rigor, I.G.; Colony, R.L.; Martin, S. Variations in Surface Air Temperature Observations in the Arctic, 1979–97. J. Clim. 2000, 13, 896–914. [Google Scholar] [CrossRef]
- Serreze, M.C.; Maslanik, J.A.; Scambos, T.A.; Fetterer, F.; Stroeve, J.; Knowles, K.; Fowler, C.; Drobot, S.; Barry, R.; Haran, T.M. A record minimum arctic sea ice extent and area in 2002. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Morello, L. Summer storms bolster Arctic ice. Nat. Cell Biol. 2013, 500, 512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Webster, M.A.; Parker, C.; Boisvert, L.; Kwok, R. The role of cyclone activity in snow accumulation on Arctic sea ice. Nat. Commun. 2019, 10, 5285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chavas, J.-P.; Grainger, C. On the dynamic instability of Arctic sea ice. Npj Clim. Atmospheric Sci. 2019, 2, 23. [Google Scholar] [CrossRef]
- Kaiming, H.; Xiangyu, Z.; Shaoqing, R.; Jian, S. Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: New York, NY, USA, 2017; pp. 1251–1258. [Google Scholar]
- Tan, M.; Le, Q.V. Efficientnet: Rethinking model scaling for convolutional neural networks. arXiv 2019, arXiv:1905.11946. [Google Scholar]
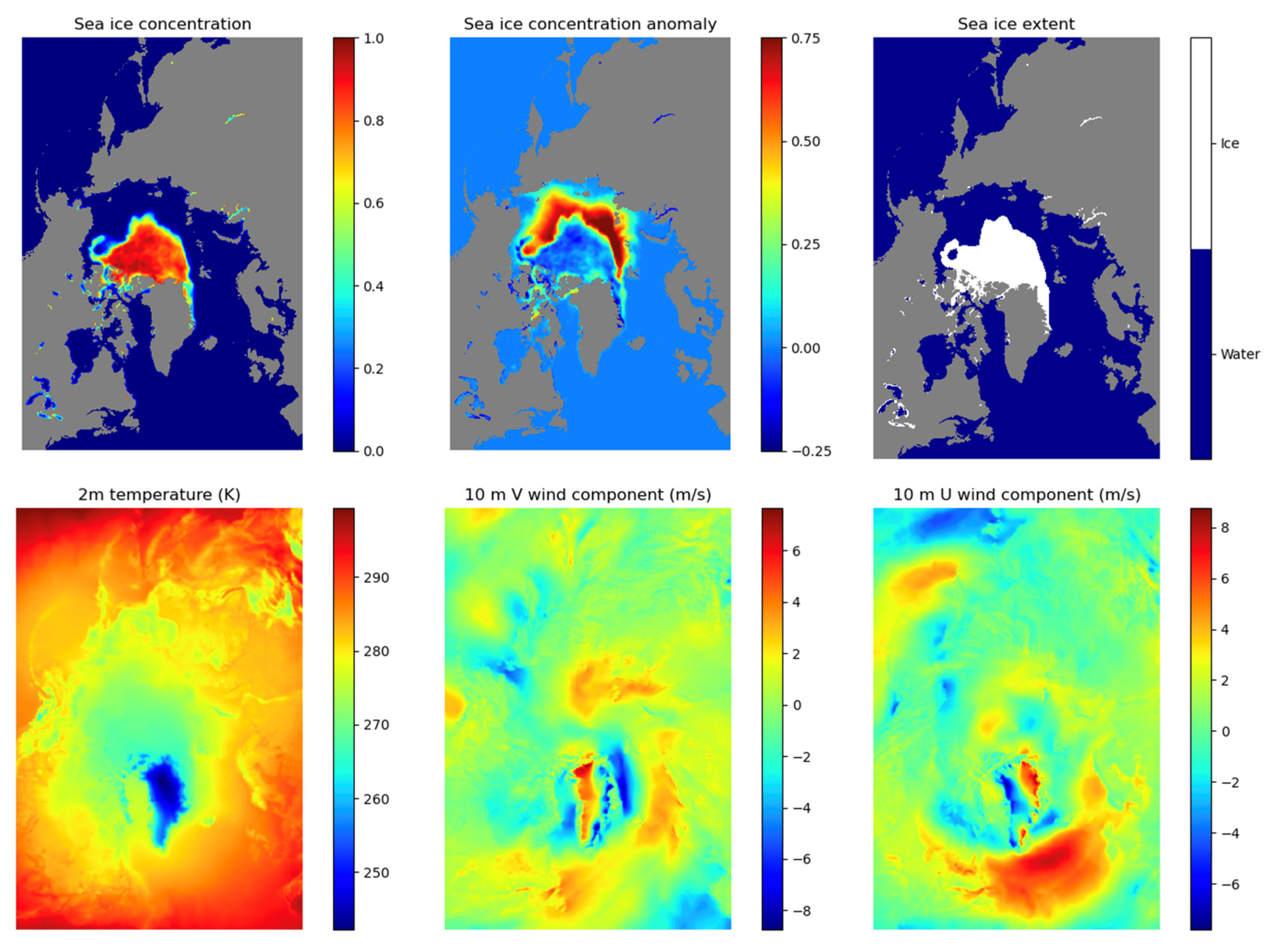

| Group | Variable | Abbreviation | Unit |
|---|---|---|---|
| Sea ice | Sea ice concentration | SIC | % |
| Sea ice concentration anomaly | SICano | % | |
| Sea ice extent | SIE | Binary | |
| ERA5 | 2 m temperature | T2m | K |
| 10 m V wind component | V10m | m/s | |
| 10 m U wind component | U10m | m/s |
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| SIC | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| SICano | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| SIE | ✓ | ✓ | ✓ | ✓ | ||||||
| T2m | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| V10m | ✓ | ✓ | ✓ | |||||||
| U10m | ✓ | ✓ | ✓ |
| MAE | RMSE | SSIM | F1 | MAE/F1 | ||
|---|---|---|---|---|---|---|
| Prediction models | Persistence | 3.0439 | 9.5741 | 0.9528 | 0.7526 | 4.0447 |
| LSTM | 2.9917 | 9.1791 | 0.9501 | 0.7438 | 4.0112 | |
| ConvLSTM | 2.6904 | 8.0059 | 0.9603 | 0.7687 | 3.5209 | |
| TS-ConvLSTM | 2.3130 | 7.0274 | 0.9617 | 0.7772 | 3.0157 |
| MAE | RMSE | SSIM | F1 | MAE/F1 | ||
|---|---|---|---|---|---|---|
| Loss function | L1-norm | 2.3130 | 7.0274 | 0.9617 | 0.7772 | 3.0157 |
| L2-norm | 2.5347 | 7.1096 | 0.9528 | 0.7482 | 3.4337 | |
| SSIM | 2.3764 | 7.2373 | 0.9648 | 0.7852 | 3.0836 | |
| VGG | 2.2480 | 6.8250 | 0.9641 | 0.7864 | 2.8922 |
| Avg. | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| MAE | 2.2480 | 2.2484 | 2.4248 | 2.3048 | 2.3241 | 2.2936 | 2.2768 | 2.2721 | 2.4822 | 2.3946 |
| RMSE | 6.8250 | 6.6659 | 7.1526 | 6.7504 | 6.7499 | 6.6584 | 6.8210 | 7.3290 | 6.8440 | 7.0379 |
| SSIM | 0.9641 | 0.9611 | 0.9583 | 0.9617 | 0.9609 | 0.9607 | 0.9628 | 0.9375 | 0.9460 | 0.9581 |
| F1 | 0.7864 | 0.7833 | 0.7737 | 0.7885 | 0.7808 | 0.7882 | 0.7848 | 0.7734 | 0.7812 | 0.7724 |
| MAE/F1 | 2.8922 | 2.8764 | 3.1992 | 2.9667 | 3.0413 | 2.9456 | 2.9490 | 3.5472 | 3.2053 | 3.1428 |
| Std. Dev. | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| MAE | 0.5601 | 0.4515 | 0.5980 | 0.5186 | 0.4694 | 0.5010 | 0.5427 | 0.5178 | 0.4682 | 0.5248 |
| RMSE | 1.4970 | 1.1525 | 1.6554 | 1.3358 | 1.2441 | 1.1900 | 1.4999 | 1.3183 | 1.1999 | 1.4581 |
| SSIM | 0.0139 | 0.0103 | 0.0148 | 0.0141 | 0.0141 | 0.0130 | 0.0141 | 0.0118 | 0.0125 | 0.0136 |
| F1 | 0.0434 | 0.0342 | 0.0452 | 0.0400 | 0.0466 | 0.0425 | 0.0404 | 0.0346 | 0.0369 | 0.0384 |
| MAE/F1 | 0.7627 | 0.5899 | 0.8787 | 0.6831 | 0.6551 | 0.6515 | 0.7265 | 0.7040 | 0.6352 | 0.7118 |
| MAE | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
| t+1 | 1.5449 | 1.6073 | 1.9119 | 2.0731 | 2.1925 | 2.3110 | 1.9762 | 1.4274 | 1.3749 | 1.6131 | 2.1307 | 1.5121 |
| t+2 | 1.8651 | 1.9391 | 2.2336 | 2.6025 | 2.6588 | 3.0276 | 2.2576 | 2.0488 | 1.5990 | 2.2147 | 2.3257 | 2.0685 |
| t+3 | 1.7661 | 1.9172 | 2.3787 | 2.6064 | 2.6328 | 3.1759 | 2.6029 | 2.1151 | 1.7610 | 1.9262 | 2.5185 | 2.1391 |
| t+4 | 1.7501 | 1.9257 | 2.2756 | 2.6432 | 2.8337 | 3.2640 | 2.6258 | 2.2361 | 1.7602 | 2.1307 | 2.5406 | 2.1382 |
| t+5 | 1.7408 | 1.9589 | 2.3791 | 2.7415 | 2.9673 | 3.0936 | 2.5449 | 2.2148 | 1.8593 | 2.5055 | 2.7582 | 2.1568 |
| t+6 | 1.8103 | 1.9429 | 2.3729 | 2.7009 | 2.9537 | 3.1456 | 2.4645 | 2.1787 | 1.8640 | 2.3840 | 2.8797 | 2.0871 |
| RMSE | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
| t+1 | 4.5148 | 4.4901 | 5.4807 | 5.6759 | 5.9136 | 6.3384 | 6.2614 | 4.9205 | 5.4771 | 5.1247 | 5.7645 | 4.1212 |
| t+2 | 5.4400 | 5.5926 | 6.5878 | 7.8104 | 7.5234 | 8.1855 | 6.6227 | 6.8165 | 5.5151 | 7.1589 | 6.2950 | 5.6306 |
| t+3 | 5.1743 | 5.3749 | 7.0786 | 7.6140 | 7.3080 | 8.6651 | 7.5839 | 7.1062 | 7.0182 | 6.0830 | 6.7504 | 5.9125 |
| t+4 | 5.0823 | 5.5483 | 6.6607 | 7.8540 | 7.9402 | 8.8780 | 7.5768 | 7.4978 | 7.2786 | 6.6463 | 6.7005 | 5.8293 |
| t+5 | 5.1137 | 5.5092 | 7.0488 | 7.9020 | 8.2512 | 8.6228 | 7.4925 | 7.3205 | 7.6022 | 7.5872 | 7.3328 | 5.9219 |
| t+6 | 5.2537 | 5.5314 | 7.0453 | 7.7836 | 8.2356 | 8.6377 | 7.1290 | 7.1325 | 7.6024 | 7.9469 | 7.8677 | 5.6516 |
| SSIM | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
| t+1 | 0.9789 | 0.9811 | 0.9738 | 0.9666 | 0.9650 | 0.9653 | 0.9635 | 0.9757 | 0.9763 | 0.9648 | 0.9585 | 0.9766 |
| t+2 | 0.9720 | 0.9737 | 0.9681 | 0.9567 | 0.9527 | 0.9490 | 0.9500 | 0.9602 | 0.9637 | 0.9559 | 0.9561 | 0.9693 |
| t+3 | 0.9735 | 0.9735 | 0.9636 | 0.9546 | 0.9549 | 0.9490 | 0.9387 | 0.9615 | 0.9675 | 0.9578 | 0.9534 | 0.9689 |
| t+4 | 0.9735 | 0.9734 | 0.9658 | 0.9512 | 0.9554 | 0.9500 | 0.9384 | 0.9586 | 0.9662 | 0.9553 | 0.9546 | 0.9683 |
| t+5 | 0.9745 | 0.9731 | 0.9639 | 0.9491 | 0.9527 | 0.9518 | 0.9466 | 0.9585 | 0.9648 | 0.9505 | 0.9503 | 0.9675 |
| t+6 | 0.9723 | 0.9729 | 0.9651 | 0.9502 | 0.9513 | 0.9499 | 0.9472 | 0.9599 | 0.9654 | 0.9525 | 0.9403 | 0.9673 |
| F1 | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
| t+1 | 0.8161 | 0.8231 | 0.8188 | 0.8143 | 0.8156 | 0.8088 | 0.7811 | 0.7978 | 0.7642 | 0.7610 | 0.7812 | 0.8150 |
| t+2 | 0.8128 | 0.8170 | 0.8147 | 0.7959 | 0.8045 | 0.7902 | 0.7514 | 0.7475 | 0.7459 | 0.7440 | 0.7813 | 0.8113 |
| t+3 | 0.8133 | 0.8179 | 0.8114 | 0.7992 | 0.8030 | 0.7869 | 0.7407 | 0.7502 | 0.7253 | 0.7487 | 0.7770 | 0.8120 |
| t+4 | 0.8130 | 0.8182 | 0.8118 | 0.7985 | 0.8018 | 0.7841 | 0.7393 | 0.7254 | 0.7202 | 0.7399 | 0.7789 | 0.8125 |
| t+5 | 0.8144 | 0.8176 | 0.8142 | 0.7969 | 0.7988 | 0.7879 | 0.7401 | 0.7410 | 0.7156 | 0.6905 | 0.7767 | 0.8129 |
| t+6 | 0.8129 | 0.8180 | 0.8156 | 0.7984 | 0.7987 | 0.7878 | 0.7451 | 0.7484 | 0.7171 | 0.7177 | 0.7755 | 0.8129 |
| MAE/F1 | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
| t+1 | 1.8929 | 1.9527 | 2.3349 | 2.5458 | 2.6883 | 2.8572 | 2.5302 | 1.7891 | 1.7991 | 2.1198 | 2.7274 | 1.8554 |
| t+2 | 2.2946 | 2.3735 | 2.7415 | 3.2699 | 3.3050 | 3.8314 | 3.0046 | 2.7407 | 2.1438 | 2.9765 | 2.9766 | 2.5497 |
| t+3 | 2.1715 | 2.3439 | 2.9314 | 3.2614 | 3.2786 | 4.0360 | 3.5141 | 2.8193 | 2.4279 | 2.5728 | 3.2413 | 2.6344 |
| t+4 | 2.1527 | 2.3537 | 2.8032 | 3.3103 | 3.5343 | 4.1629 | 3.5518 | 3.0824 | 2.4442 | 2.8796 | 3.2619 | 2.6317 |
| t+5 | 2.1377 | 2.3959 | 2.9221 | 3.4401 | 3.7148 | 3.9264 | 3.4387 | 2.9887 | 2.5983 | 3.6285 | 3.5509 | 2.6533 |
| t+6 | 2.2270 | 2.3751 | 2.9093 | 3.3828 | 3.6979 | 3.9929 | 3.3077 | 2.9112 | 2.5995 | 3.3218 | 3.7131 | 2.5673 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, J.; Bae, J.; Kwon, Y.-J. Two-Stream Convolutional Long- and Short-Term Memory Model Using Perceptual Loss for Sequence-to-Sequence Arctic Sea Ice Prediction. Remote Sens. 2021, 13, 3413. https://doi.org/10.3390/rs13173413
Chi J, Bae J, Kwon Y-J. Two-Stream Convolutional Long- and Short-Term Memory Model Using Perceptual Loss for Sequence-to-Sequence Arctic Sea Ice Prediction. Remote Sensing. 2021; 13(17):3413. https://doi.org/10.3390/rs13173413
Chicago/Turabian StyleChi, Junhwa, Jihyun Bae, and Young-Joo Kwon. 2021. "Two-Stream Convolutional Long- and Short-Term Memory Model Using Perceptual Loss for Sequence-to-Sequence Arctic Sea Ice Prediction" Remote Sensing 13, no. 17: 3413. https://doi.org/10.3390/rs13173413
APA StyleChi, J., Bae, J., & Kwon, Y.-J. (2021). Two-Stream Convolutional Long- and Short-Term Memory Model Using Perceptual Loss for Sequence-to-Sequence Arctic Sea Ice Prediction. Remote Sensing, 13(17), 3413. https://doi.org/10.3390/rs13173413








