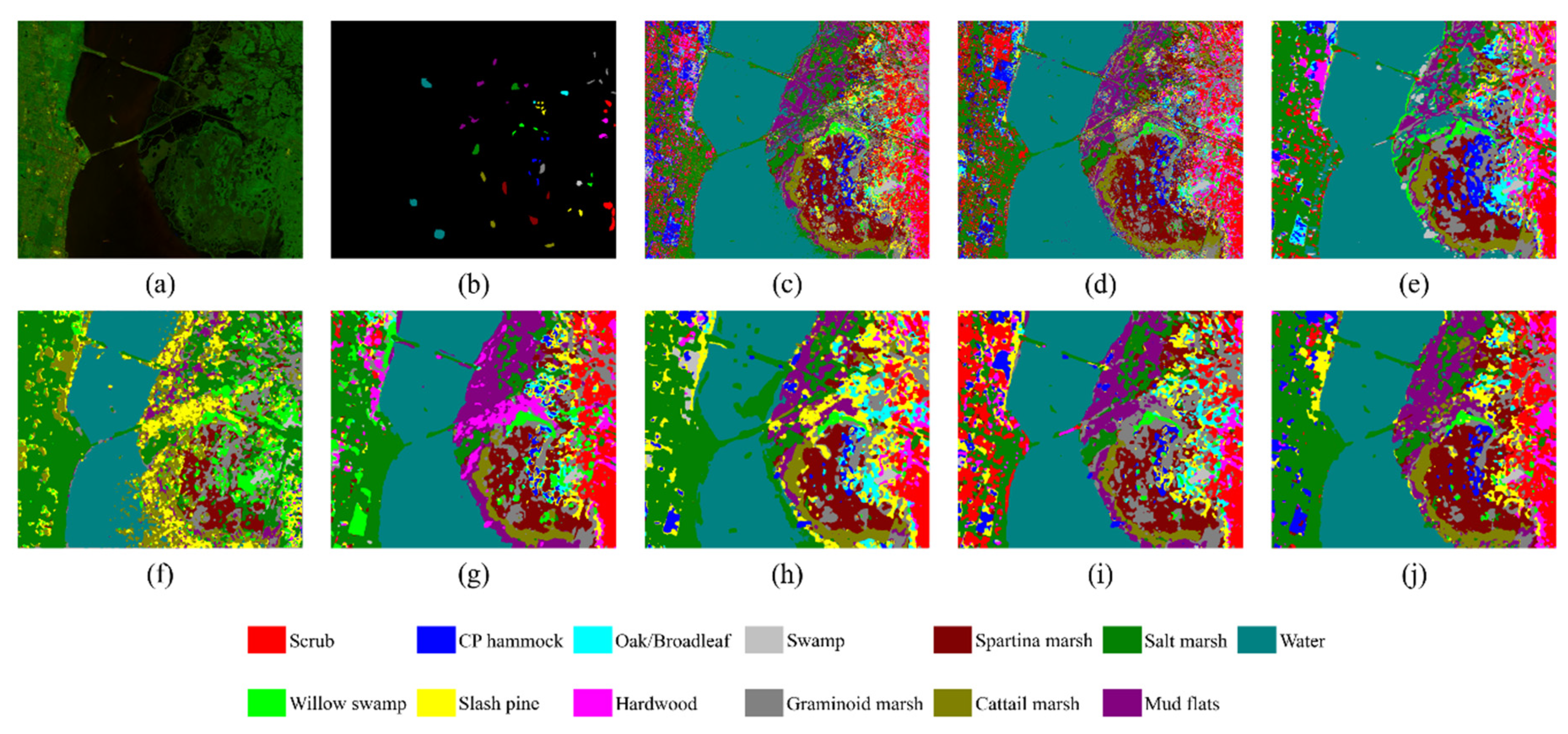
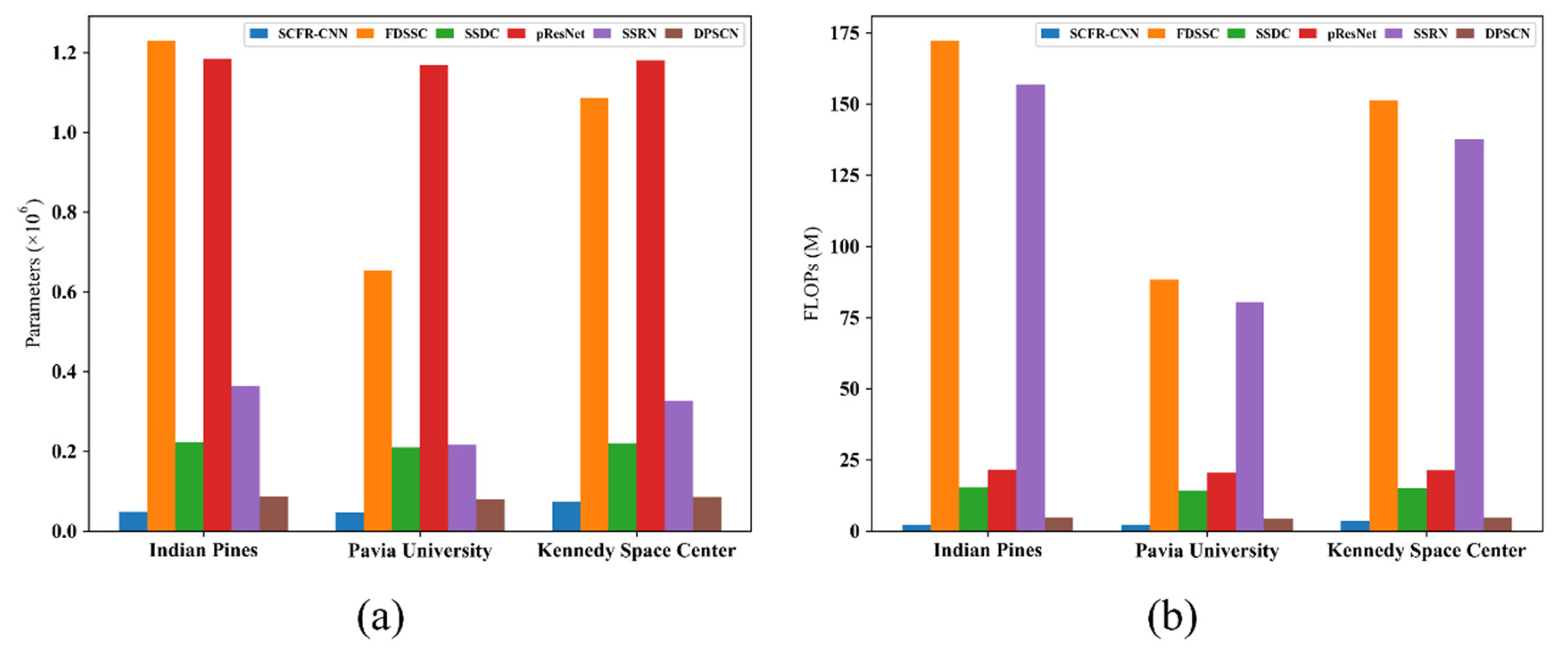
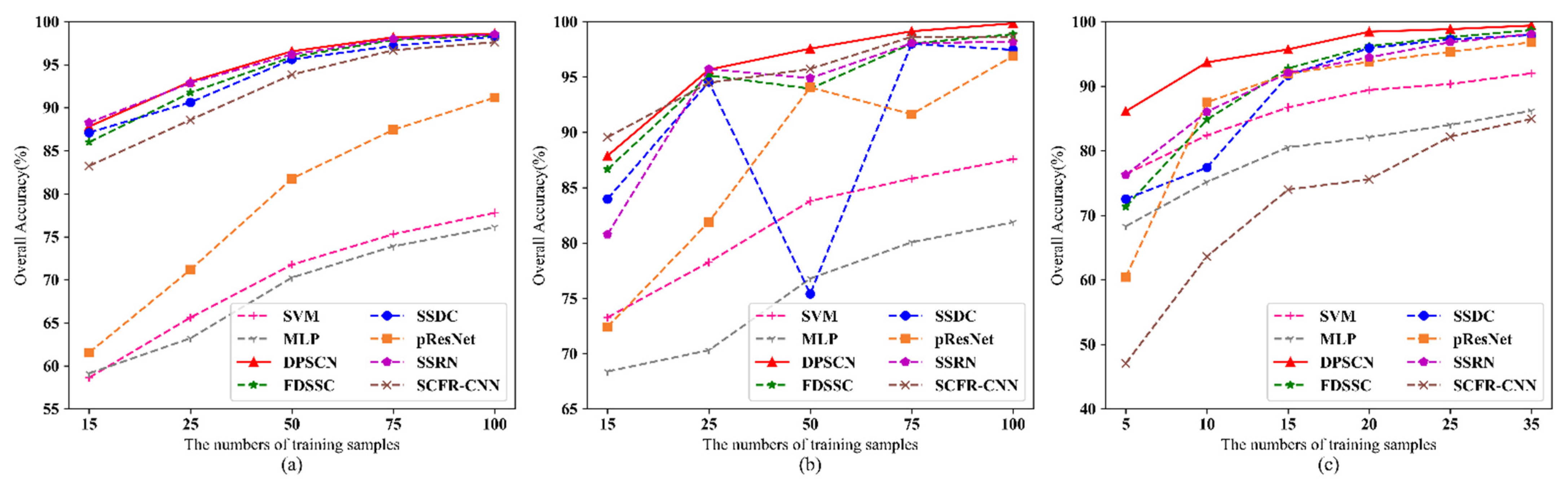
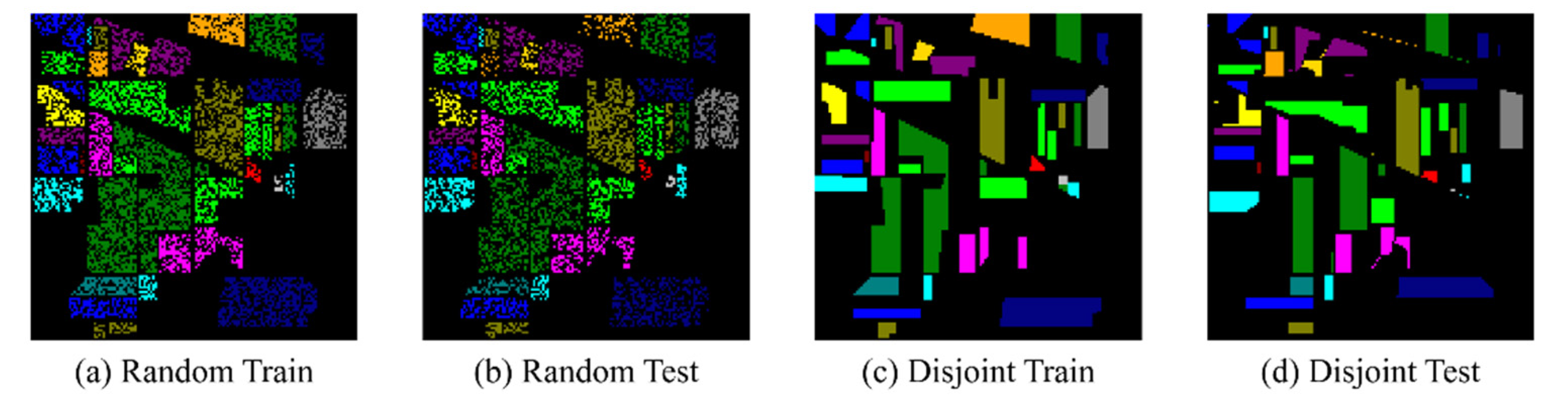
In this section, we introduce the dual-path small convolution (DPSC) module. This section then describes the proposed network model in detail. The model includes two core parts: the data preprocessing in the initial stage and spectral feature fusion and spectral-spatial features fusion in the later stage.
2.1. Small Convolution with Dual-Path
For building a deep CNN model, the introduction of a residual connection can effectively realize feature reuse and alleviate the problem of network degradation [
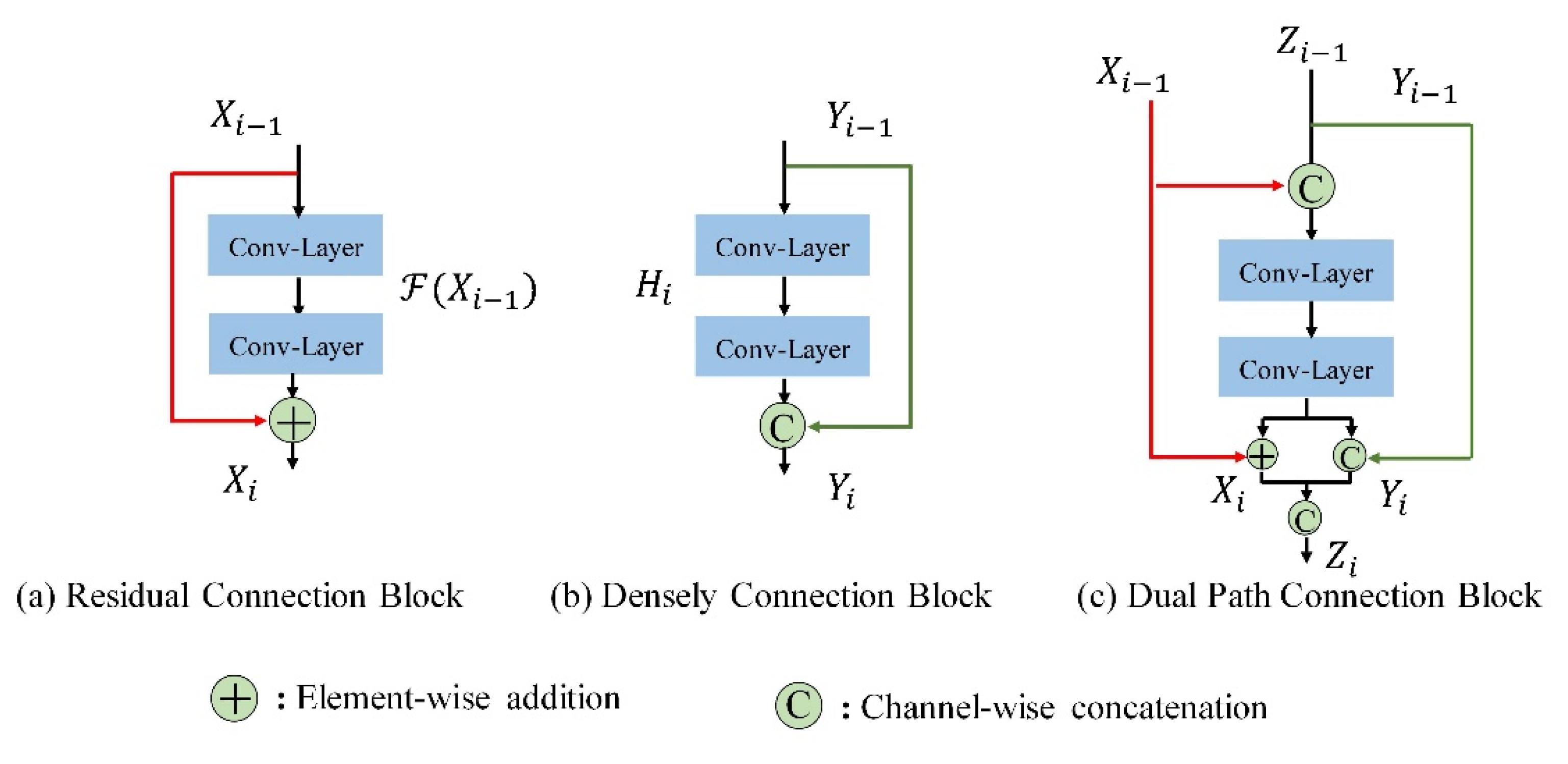
29]. The structure of the basic residual connection is shown in
Figure 1a. Assuming that
Χi is the output of the
i-th layer residual unit,
(*) represents a residual mapping of the current layer. The basic residual structure is expressed as the following formula:
Equation (1) shows that the input and output of each residual structure are added together, which is then used as the input of the next layer.
Different from the residual path, each layer of density connection is connected to all subsequent layers. This way, the model can encourage feature propagation and continuously explore new features to alleviate the problem of vanishing-gradient [
30].
Figure 1b gives an illustration of a basic density connection structure. If
Yi is the output of the
i-th layer, then the basic density path architecture is expressed as follows:
where
denotes the concatenation of all feature maps from the zeroth to the (
i1)-th layers, H(⋅) denotes a nonlinear combination function of the current layer, and Equation (2) indicates that the
i-th layer input of the density structure is formed by concatenating the feature maps of the preceding the (
i1)-th layer.
As a combination of residual connection and density connection, dual-path architecture inherits the advantages of both connections, enabling the network to reuse features while excavating new features at the same time [
28]. The block structure of the dual-path is shown in
Figure 1c. The input of the first layer in each micro-block is divided into two branches, one is element-wise that is added to the residual branch and is represented in red. The other is concatenated with the density branch that is represented in green. After the convolution of the layers, the output is concatenated by the feature maps generated by the dual-path model. Suppose
Zi is the
i-th layer output of a dual-path structure, its basic structure can be described as:
where
Xi and
Yi are the outputs of residual path and density path of the
i-th layer respectively.
In the recent literature on computer vision, 3 × 3 convolution kernels, such as ResNet-34 [
29], {1 × 1, 3 × 3} convolution strategies, DenseNet-169 [
30], {1 × 1, 3 × 3, 1 × 1} (bottleneck layer), ResNet-50, and DPN-98 [
28], have been widely used in the convolution layer of their basic modules. The network constructed with these convolution blocks of different sizes has achieved competitive performance in the application of natural image classification. In particular, small convolution kernels (1 × 1) play an important role in feature representation. Specifically, small convolution kernels have the following advantages. First, multiple channels in the structure could be recombined without changing the size of the space, so the spatial information must be preserved. Second, the nonlinear characteristics of the structure could be increased (ReLU activation function after convolution was used). In this manner, a CNN model that applies small convolution with distinct kernels can strengthen the generalization performance of the model [
31]. Moreover, by stacking small convolution kernels to deepen the model, the abstract features of the image can be extracted without increasing the number of training parameters in the model.
For HSI classification, a considerable number of researchers have applied the large-scale 3D convolution strategy with residual learning, density connection (SSRN, FDSSC), or deeper layer to the classification of HSI. Although high classification accuracy has been achieved this way, most classification models often have complex and redundant structure designs and high computational loads, resulting in an inefficient classification process. Moreover, the training samples of HSI are limited and there is complex contextual spatial information and high spectral correlation in HSI, which is a great challenge to the classification performance.
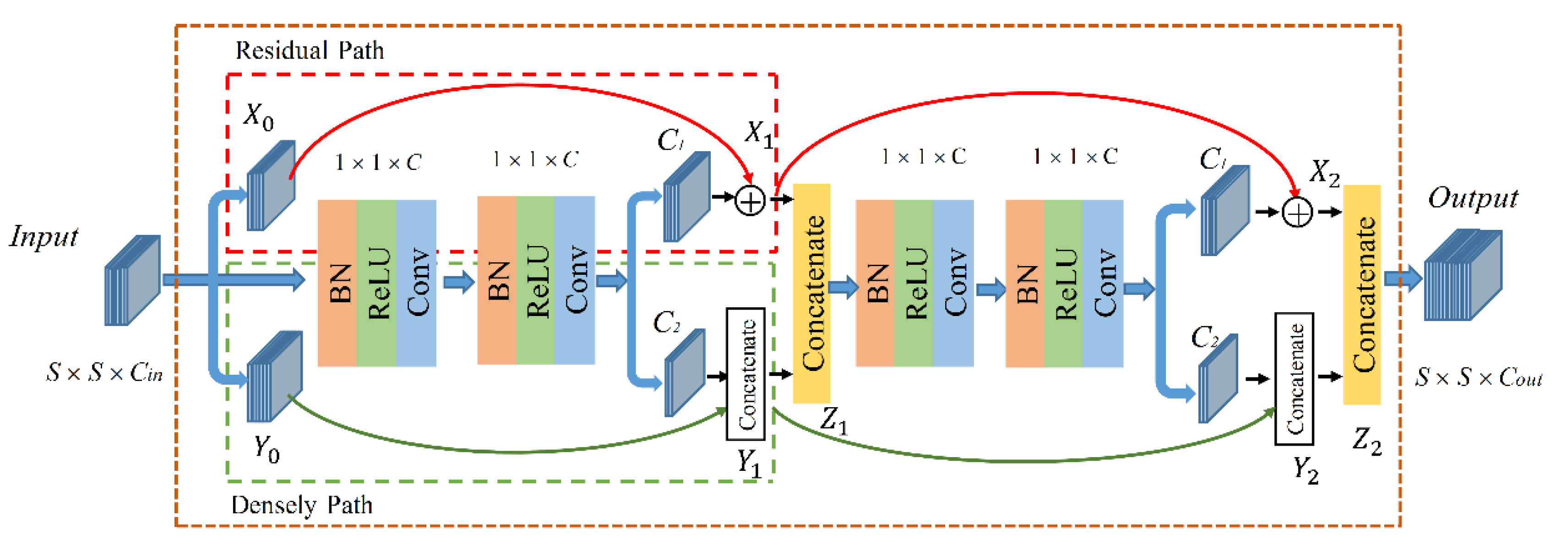
Given all that, and benefiting from the advantages of a dual-path and the small convolution, this article discusses the building of a feature extraction module, namely dual-path small convolution (DPSC). The module structure is shown in
Figure 2. It is composed of two composite layers, each of which is composed of two 1 × 1 small convolution kernels. The output of the last 1 × 1 layer is divided into two groups of channels, which are added by the elements on the residual path (red dashed box in
Figure 2), and the other part is concatenated with the density path. The same number of convolution kernels are set in each layer of DPSC. In addition, the residual connected path serves the dual-path network as the backbone.
In the DPCN module, the Batch Normalization (BN) [
32] strategy was adopted before each convolution layer for enabling the network to make faster and smoother convergence. The BN is represented as:
where
is normalization result of the batch feature maps
Xl of the
l-th layer, E(⋅) and VAR(⋅) represent the mean and variance function of the input tensor of the current layer, respectively. In addition, the BN layer is followed by a rectified linear unit (ReLU) [
33] that is an activation function for nonlinear feature extraction. The ReLU is defined as:
where
x is the input feature tensor. Moreover, suppose
Cl is the number of convolution kernels in the
l-th layer,
denotes the feature tensor of the input of
j-th layer, and * denotes the convolution calculation;
and
, respectively, are the weight and the corresponding bias stored in kernels in layer
l. The output
of convolution can be directly given by:
Succinctly, the execution process of each convolution layers in DPSC is described as BN→ ReLU → Conv.
Furthermore, we analyzed the number of feature maps generated from different stages of the DPSC module to elaborate the details of DPSC processes. Suppose that the channel number of input features is
Cin and the convolution kernel number per layer of the module is
C. The output of 1 × 1 convolution in the last layer of each composite layer is divided into two groups of channels, as seen in
Figure 2, assuming that their numbers are
C1 and
C2, respectively. Specifically, the
C1 of the first part is added to the element-wise residual path and the
C2 of the second part is concatenated with the densely connected path. Here, the identity mapping (represented by the red solid line) that is shortcut connection was considered for the addition of elements.
The advantage of this strategy is that it can effectively realize feature reuse without adding additional training parameters. T residual path in the DPSC module contains
C1 feature maps. The number of feature maps
Y0 used for density connections in the input layer is
Cin −
X0, because
C1 =
X0, so
Y0 =
Cin −
C1, Y1 =
C2 +
Y0. After the first layer of dual-path, the number of output
Z1 of the first composite layer is
C1 +
Y0 + C2, i.e.,
Cin +
C2. In addition, the same is true for the calculation of the second composite layer. From this, the number of feature maps output by the DPSN module can be formulated as:
Here, from the perspective of the residual path, we define a residual channel rate
r and let it represent the ratio of the residual channel number (
C1) to the total channel number at the end of each hybrid layer in the DPSC module, that is,
r = C
1/
C. Then, 1 −
r represents the number of densely connected channels (
C2) occupying the total feature map. therefore,
C2 =
C × (1 −
r). Furthermore, Equation (7) is finally updated as:
When the input channel number Cin is fixed, the output channel number is only related to the convolution kernels C and residual channel rate r in the DPSC module. In this work, C was fixed to 32. Considering that the residual networks are more widely used in practice, the residual connected path serves the dual-path module as the backbone (r was selected as 0.75).
2.2. Overview of Network Architectures
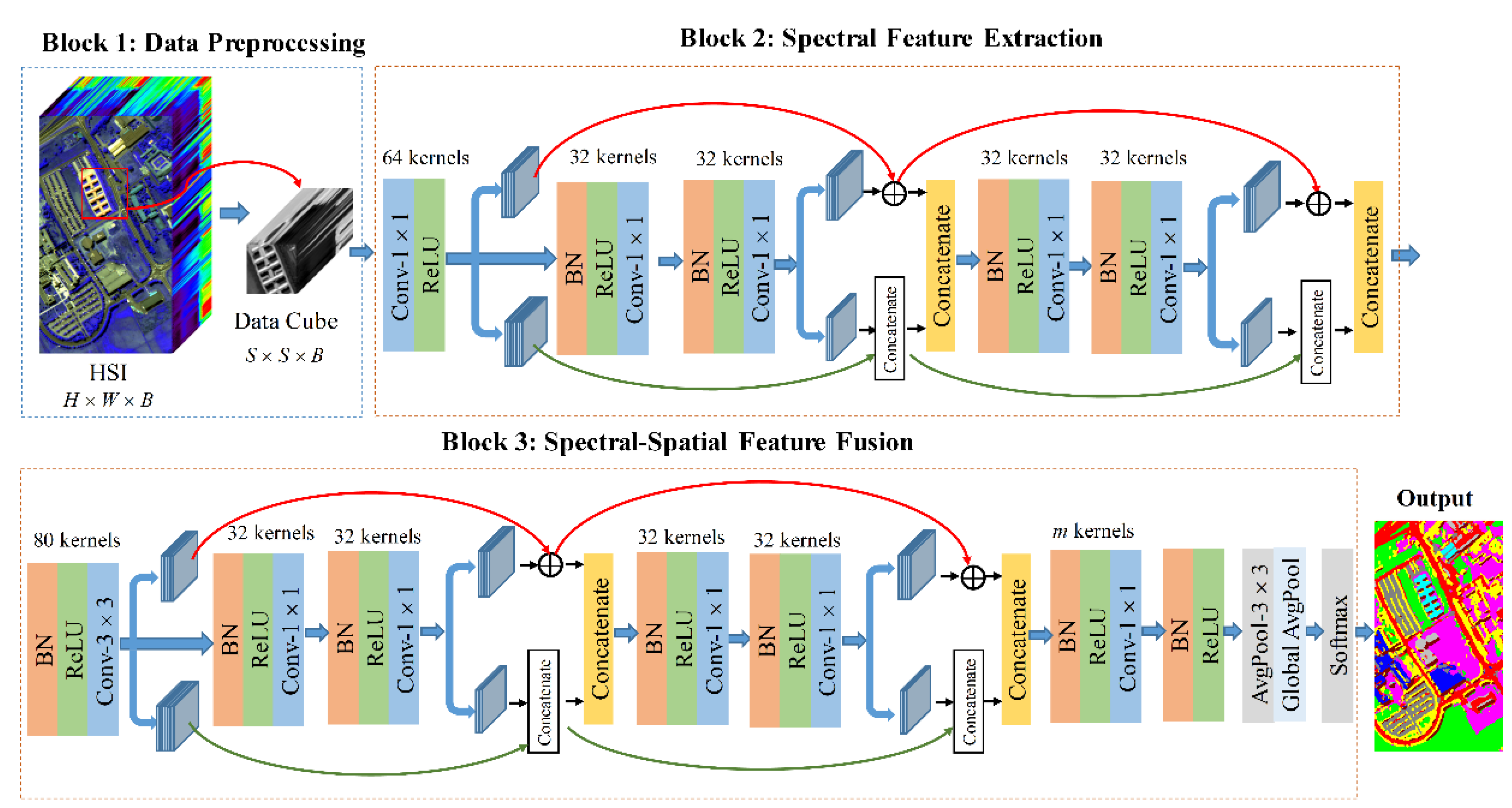
The integral network structure constructed in this article is shown in
Figure 3. The network framework is mainly composed of three cascade parts: data preprocessing, spectral feature extraction, and spectral-spatial feature fusion. The whole hyperspectral data is first normalized to have a zero-mean. Then, the input HSI is preprocessed: each pixel in HSI can be successively taken as the center. Its pixel cube whose neighborhood size is
S ×
S ×
B (i.e.,
S is the length and width of the cube, and
B is the number of bands) can be extracted to be used as the input to the model. Then, Block 2 and Block 3 are the spectral feature extraction module and the spectral-spatial feature fusion module constructed by DPSC, respectively. They are mainly responsible for feature learning at this stage and are also the core of the proposed model. Finally, 1 x 1 convolution combined with global average pooling (GAP) is used to complete the final classification at the end of the network model. The source code of this work can be obtained from
https://github.com/pangpd/DPSCN (accessed on 25 September 2020). The detailed description of the network will be elaborated in the following subsections.
The main differences between the proposed model and the dual-path network [
28] are as follows:
- (1)
In the convolutional layer part of [
28], the bottleneck layer convolution (1 × 1, 3 × 3, 1 × 1) was used. For hyperspectral images, this was not applicable when extracting spectral information. Therefore, we simplified this method and changed it to a multi-layer 1 × 1 convolution. On the one hand, it was used for the extraction of spectral information and the fusion of space-spectrum features, and it also simplified the model.
- (2)
We benefited from the dual-path idea and did not directly adopt the dual-path network. The proposed model in this article was built independently based on the characteristics of the hyperspectral image itself. Our model paid more attention to the improvement of classification results and efficiency.
- (3)
The construction of the proposed network follows the characteristics of hyperspectral images, whereas the dual-path network is used for the classification of natural images, which is the significant difference between the two models.
In the model we built, all convolutional layers used 2D convolution kernels for feature learning. Although the model was based on a 3D convolution kernel that had become a mainstream practice in hyperspectral classification, when the classification precision of 2D network and 3D network was high enough, applying a 3D convolution kernel was indeed a great challenge in terms of computational complexity and classification time. Given these issues, the advantages of the networks constructed by a 3D filter were no longer obvious.
In order to illustrate the proposed model in more detail, we took the Pavia University data set, whose input shape size was 9 × 9 × 103, as an example to illustrate the specific network configuration information. This is given in detail in
Table 1.
In
Section 2.3,
Section 2.4 and
Section 2.5, we elaborate more on the design of each module in the model and explain the reason for the design of this part combining with the characteristics of HSIs.
2.5. Spectral-Spatial Feature Fusion
In an HSI, the pixels within a small neighborhood are usually composed of similar materials whose spectral properties are highly correlated [
34]. Therefore, they show a high probability of being similar. Many network models tend to design multi-scale kernels, such as 3 × 3, 5 × 5, or convolution layers with larger scales for extracting spatial context information. However, this approach has two drawbacks. First, training parameters and computational cost are increased. Second, the larger kernels may learn those test pixels that are mixed into the training samples. Consequently, the generalization ability of the model may be inadequate suffer from unknown samples. For this problem, before entering the DPSC of Block 3, only 3 × 3 convolutions (Stride = 1, Padding = 0) were performed for the subsampling operation that extracts the neighborhood spatial information of the current pixel cube produced by Block 2. After the first layer convolution at Block 3, the element values of index positions (
x,
y) on the
i-th feature map were calculated as follows:
where
and
bi is the weight at the position (
p,
q) of the kernel and bias for this feature map, respectively.
P and
Q are the height and width of the kernel, both of which are 3, and the number of kernels is consistent with the output produced by Block 2. From
Table 1, the output of Block 2 is 9 × 9. After Equation (11), the generated feature size becomes 7 × 7 × 80. As a result, the spatial information of the neighborhood of the central pixel is captured. The spectral data cube with new spatial information (spectral-spatial cube) flows into the next layer. As in block 2, the DPSC module is also adopted for feature extraction, but the DPSC module here is used purely to explore deeper fusion representation in the spectral-spatial domain.
At the end of the existing CNN network models (presented in [
21,
24,
26]) for HSI classification, the FC layer was usually considered for multi-features combination. Such practice makes the parameters of the FC layer take up a higher proportion of the entire network. There is often a great deal of redundant parameters in a network, that can easily lead to overfitting the networks. In order to avoid this problem, the FC layer was replaced by a 1 × 1 convolution combined with a global average pooling layer (GAP) at the end of the model proposed in our model. This greatly simplified the calculation of the parameters in the model and further hastened the convergence trend of the network. Finally, feeding the output feature vector
X generated by the GAP layer into the softmax classifier (a probability function, as Equation (12)) to predict the probability
P that the input pixel belongs to the ground object of class
i:
where
m is the total number of categories and
Xi is the
i-th element of the feature vector. The index of the maximum value in the probability vector
P is the predicted label of the input pixel.
Here, two points needed to be pointed out. First, in the middle of the 1 × 1 convolutional layer and GAP, an average pooling layer (kernel size = 3, stride = 2), as shown in Block 3 of
Figure 3, compresses the size of the feature map, which is to facilitate the GAP that is located in the last layer of the model. Second, the 1 × 1 kernel should be the same quantity as the land-cover categories (
m) of the current data set to ensure that the output from the GAP is a 1 ×
m feature vector to complete classification that the index of the maximum value in the vector is the prediction label.