Multi-Stage Convolutional Broad Learning with Block Diagonal Constraint for Hyperspectral Image Classification
Abstract
:1. Introduction
2. MSCBL-BD for HSI Classification
2.1. Structure of MSCBL-BD
2.2. CNN Pre-Training
2.3. MSCBL-BD
3. Experiments and Analysis
3.1. Parameter Setting
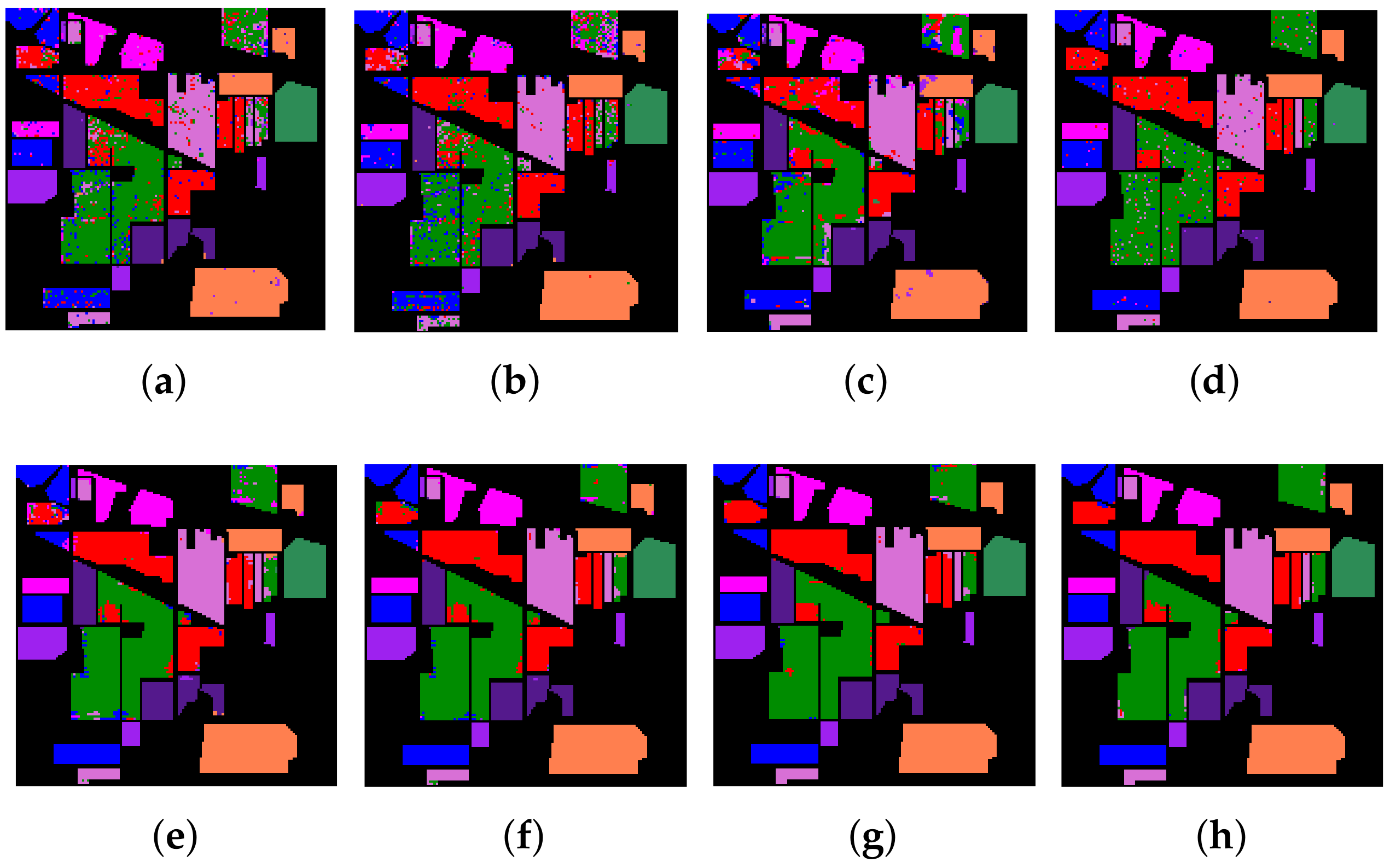
3.2. Comparative Experiments
- (1)
- Traditional classification methods: SVM [8], whose optimal super-parameters are selected through the fivefold cross-validation method;
- (2)
- (3)
- Special cases of MSCBL-BD: CBL (the CBFs of the last stage are connected to the output layer and not constrained with the block diagonal matrix); MSCBL (the MSCBFs are connected to the output layer and not constrained with the block-diagonal matrix).
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADMM | Alternating direction method of multipliers |
| BASS-Net | Band-adaptive spectral-spatial feature learning neural network |
| BF | Broad feature |
| BLS | Broad learning system |
| CBF | Convolutional broad feature |
| CF | Convolutional feature |
| CNN | Convolutional neural network |
| CNN-PPF | Convolutional neural network with pixel-pair features |
| DBN | Deep belief network |
| EN | Enhancement node |
| HSI | Hyperspectral image |
| MF | Mapped feature |
| MSBF | Multi-stage broad feature |
| MSCBF | Multi-stage convolutional broad feature |
| MSCBL-BD | Block-diagonal constrained multi-stage convolutional broad learning |
| MSCF | Multi-stage convolutional feature |
| PCA | Principal component analysis |
| SS-DBN | Spectral-spatial deep belief network |
| SVM | Support vector machine |
References
- Luo, F.; Du, B.; Zhang, L.; Zhang, L.; Tao, D. Feature learning using spatial-spectral hypergraph discriminant analysis for hyperspectral image. IEEE Trans. Cybern. 2019, 49, 2406–2419. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wei, Y. Learning hierarchical spectral-spatial features for hyperspectral image classification. IEEE Trans. Cybern. 2016, 46, 1667–1678. [Google Scholar] [CrossRef] [PubMed]
- Meroni, M.; Fasbender, D.; Balaghi, R.; Dali, M.; Haffani, M.; Haythem, I.; Hooker, J.; Lahlou, M.; Lopez-Lozano, R.; Mahyou, H.; et al. Evaluating NDVI data continuity between SPOT-VEGETATION and PROBA-V missions for operational yield forecasting in North African countries. IEEE Trans. Geosci. Remote Sens. 2016, 54, 795–804. [Google Scholar] [CrossRef]
- Brunet, D.; Sills, D. A generalized distance transform: Theory and applications to weather analysis and forecasting. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1752–1764. [Google Scholar] [CrossRef]
- Islam, T.; Hulley, G.C.; Malakar, N.K.; Radocinski, R.G.; Guillevic, P.C.; Hook, S.J. A Physics-based algorithm for the simultaneous retrieval of land surface temperature and emissivity from VIIRS thermal infrared data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 563–576. [Google Scholar] [CrossRef]
- Matsuki, T.; Yokoya, N.; Iwasaki, A. Hyperspectral tree species classification of Japanese complex mixed forest with the aid of lidar data. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 2177–2187. [Google Scholar] [CrossRef]
- Liu, L.; Huang, W.; Wang, C. Hyperspectral image classification with kernel-based least-squares support vector machines in sum space. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 1144–1157. [Google Scholar] [CrossRef]
- Tan, K.; Zhang, J.; Du, Q.; Wang, X. GPU parallel implementation of support vector machines for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 4647–4656. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.; Tian, J. Local manifold learning-based k-nearest-neighbor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Halevy, A.; Benedetto, J.; Czaja, W.; Liu, C.; Wu, H.; Shi, B.; Li, W. UL-Isomap based nonlinear dimensionality reduction for hyperspectral imagery classification. ISPRS J. Photogramm. Remote Sens. 2014, 89, 25–36. [Google Scholar] [CrossRef]
- Sun, W.; Yang, G.; Du, B.; Zhang, L.; Zhang, L. A sparse and low-rank near-isometric linear embedding method for feature extraction in hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4032–4046. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Du, B.; Huang, X.; Tang, Y.Y.; Tao, D. Simultaneous spectral-spatial feature selection and extraction for hyperspectral images. IEEE Trans. Cybern. 2018, 48, 16–28. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, W.; Liu, J.; Du, Q. Sparse and low-rank graph for discriminant analysis of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4094–4105. [Google Scholar] [CrossRef]
- Huang, H.; Shi, G.; He, H.; Duan, Y.; Luo, F. Dimensionality reduction of hyperspectral imagery based on spatial-spectral manifold learning. IEEE Trans. Cybern. 2020, 50, 2604–2616. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Li, H.; Li, W.; Chen, X.; Wu, G.; Du, Q. Discriminant analysis of hyperspectral imagery using fast kernel sparse and low-rank graph. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6085–6098. [Google Scholar] [CrossRef]
- Pan, L.; Li, H.; Deng, Y.; Zhang, F.; Chen, X.; Du, Q. Hyperspectral dimensionality reduction by tensor sparse and low-rank graph-based discriminant analysis. Remote Sens. 2017, 9, 452. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Du, B.; Zhang, L.; Zhang, L. Dimensionality reduction and classification of hyperspectral images using ensemble discriminative local metric learning. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2509–2524. [Google Scholar] [CrossRef]
- Dong, Y.; Du, B.; Zhang, L.; Zhang, L. Exploring locally adaptive dimensionality reduction for hyperspectral image classification: A maximum margin metric learning aspect. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 1136–1150. [Google Scholar] [CrossRef]
- Kang, X.; Xiang, X.; Li, S.; Benediktsson, J. PCA-based edge-preserving features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Jia, S.; Shen, L.; Zhu, J.; Li, Q. A 3-D Gabor phase-based coding and matching framework for hyperspectral imagery classification. IEEE Trans. Cybern. 2018, 48, 1176–1188. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X. On combining multiple features for hyperspectral remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 879–893. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Gamba, P.; Bioucas-Dias, J.; Zhang, L.; Benediktsson, J.; Plaza, A. Multiple feature learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1592–1606. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Chen, C.L.P. Broad learning system: Structural extensions on single-layer and multi-layer neural networks. In Proceedings of the International Conference on Security, Pattern Analysis, and Cybernetics, Shenzhen, China, 15–18 December 2017; pp. 136–141. [Google Scholar]
- Chen, C.L.P.; Liu, Z. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.L.P.; Liu, Z.; Feng, S. Universal approximation capability of broad learning system and its structural variations. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1191–1204. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Chen, C.L.P. Fuzzy broad learning system: A novel neuro-fuzzy model for regression and classification. IEEE Trans. Cybern. 2020, 50, 414–424. [Google Scholar] [CrossRef] [PubMed]
- Kong, Y.; Wang, X.; Cheng, Y.; Chen, C.L.P. Hyperspectral imagery classification based on semi-supervised broad learning system. Remote Sens. 2018, 10, 685. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.; Tuia, D.; Mou, L.; Xia, G.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Su, G.; Qing, C.; Xu, X.; Cai, B.; Xing, X. Hierarchical lifelong learning by sharing representations and integrating hypothesis. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1004–1014. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral-spatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Ma, X.; Wang, H.; Geng, J. Spectral-spatial classification of hyperspectral image based on deep auto-encoder. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4073–4085. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.B. Learning to diversify deep belief networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Zhou, X.; Li, S.; Tang, F.; Qin, K.; Hu, S.; Liu, S. Deep learning with grouped features for spatial spectral classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 97–101. [Google Scholar] [CrossRef]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised deep feature extraction for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1349–1362. [Google Scholar] [CrossRef] [Green Version]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Du, S. Spectral-spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Ghamisi, P.; Chen, Y.; Zhu, X. A self-improving convolution neural network for the classification of hyperspectral data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1537–1541. [Google Scholar] [CrossRef] [Green Version]
- Santara, A.; Mani, K.; Hatwar, P.; Singh, A.; Garg, A.; Padia, K.; Mitra, P. BASS net: Band-adaptive spectral-spatial feature learning neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5293–5301. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.; Jia, K.; Gao, S.; Lu, J.; Zeng, Z.; Ma, Y. PCANet: A simple deep learning baseline for image classification. IEEE Trans. Image Process. 2015, 24, 5017–5032. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, B.; Shi, Z.; Zhang, N.; Xie, S. Hyperspectral image classification based on nonlinear spectral-spatial network. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1782–1786. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. R-VCANet: A new deep-learning-based hyperspectral image classification method. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2017, 10, 1975–1986. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, X.; Cheng, Y.; Wang, Z. Dimensionality reduction for hyperspectral data based on class-aware tensor neighborhood graph and patch alignment. IEEE Trans. Neural Netw. Learn. Sys. 2015, 26, 1582–1593. [Google Scholar]
- Jin, J.; Fu, K.; Zhang, C. Traffic sign recognition with hinge loss trained convolutional neural networks. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1991–2000. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Shao, L.; Yang, J. Discriminative block-diagonal representation learning for image recognition. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3111–3125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Q.; He, X.; Li, X. Locality and structure regularized low rank representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 911–923. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wang, X.; Tian, F.; Liu, C.H.; Yu, H. Constrained low-rank representation for robust subspace clustering. IEEE Trans. Cybern. 2017, 47, 4534–4546. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, J.-F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Vedaldi, A.; Lenc, K. Matconvnet-convolutional neural networks for matlab. In Proceedings of the ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 689–692. [Google Scholar]





| Layer | Input | Number of Filters | Width of Filters | Height of Filters | Step Size | Output | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Width | Height | Channel | Width | Height | Channel | Dimension | |||||
| I1 | 17 | 17 | 15 | 4335 | |||||||
| C1 | 17 | 17 | 15 | 30 | 4 | 4 | 1 | 14 | 14 | 30 | 5880 |
| P1 | 14 | 14 | 30 | 2 | 2 | 2 | 7 | 7 | 30 | 1470 | |
| N1 | 7 | 7 | 30 | / | / | / | / | 7 | 7 | 30 | 1470 |
| C2 | 7 | 7 | 30 | 30 | 1 | 1 | 1 | 7 | 7 | 30 | 1470 |
| N2 | 7 | 7 | 30 | 30 | 1 | 1 | 1 | 7 | 7 | 30 | 1470 |
| C3 | 7 | 7 | 30 | 30 | 4 | 4 | 1 | 4 | 4 | 30 | 480 |
| P3 | 4 | 4 | 30 | / | 2 | 2 | 2 | 2 | 2 | 30 | 120 |
| N3 | 2 | 2 | 30 | / | / | / | / | 2 | 2 | 30 | 120 |
| C4 | 2 | 2 | 30 | 30 | 1 | 1 | 1 | 2 | 2 | 30 | 120 |
| N4 | 2 | 2 | 30 | / | / | / | / | 2 | 2 | 30 | 120 |
| C5 | 2 | 2 | 30 | 9/16 | 2 | 2 | 1 | 1 | 1 | 9/16 | 9/16 |
| Softmax | 1 | 1 | 9/16 | / | / | / | / | 1 | 1 | 9/16 | 9/16 |
| Number of Iterations | Number of Nodes in EN | ||
|---|---|---|---|
| Indian Pines | 500 | ||
| Pavia University | 110 | 400 | |
| Salinas | 500 |
| SVM [8] | BLS [25] | SS-DBN [34] | CNN-PPF [47] | CNN [39] | CBL | MSCBL | MSCBL-BD | |
|---|---|---|---|---|---|---|---|---|
| A1 (%) | 75.49 | 82.54 | 77.20 | 92.23 | 89.98 | 92.84 | 94.14 | 96.58 |
| A2 (%) | 73.78 | 82.29 | 82.76 | 96.69 | 97.75 | 98.43 | 99.06 | 99.32 |
| A3 (%) | 95.26 | 95.26 | 94.42 | 99.86 | 98.80 | 99.40 | 99.82 | 100 |
| A4 (%) | 98.45 | 99.10 | 98.30 | 99.43 | 99.21 | 99.68 | 99.85 | 99.96 |
| A5 (%) | 99.71 | 99.71 | 99.86 | 99.86 | 99.93 | 100 | 100 | 100 |
| A6 (%) | 78.21 | 86.68 | 87.23 | 95.10 | 94.69 | 96.22 | 97.20 | 99.02 |
| A7 (%) | 66.18 | 69.65 | 76.02 | 89.48 | 89.59 | 92.28 | 94.12 | 95.96 |
| A8 (%) | 83.77 | 93.39 | 90.59 | 97.00 | 98.19 | 98.93 | 99.42 | 99.87 |
| A9 (%) | 98.27 | 98.91 | 94.93 | 99.89 | 99.02 | 99.54 | 99.81 | 99.81 |
| AA (%) | 85.46 | 89.73 | 89.04 | 96.62 | 96.35 | 97.48 | 98.16 | 98.95 |
| OA (%) | 79.80 | 84.26 | 84.61 | 94.51 | 94.10 | 95.78 | 96.80 | 98.01 |
| Kappa | 0.7611 | 0.8142 | 0.8178 | 0.9344 | 0.9296 | 0.9495 | 0.9617 | 0.9762 |
| SVM [8] | BLS [25] | SS-DBN [34] | CNN-PPF [47] | CNN [39] | CBL | MSCBL | MSCBL-BD | |
|---|---|---|---|---|---|---|---|---|
| A1 (%) | 83.35 | 76.32 | 81.46 | 97.40 | 96.68 | 97.21 | 97.78 | 98.25 |
| A2 (%) | 86.12 | 90.13 | 92.96 | 97.40 | 98.93 | 99.10 | 99.27 | 99.39 |
| A3 (%) | 83.23 | 82.59 | 88.37 | 92.29 | 97.91 | 98.40 | 98.78 | 98.79 |
| A4 (%) | 94.66 | 95.49 | 95.55 | 97.63 | 98.54 | 98.62 | 98.80 | 98.80 |
| A5 (%) | 99.55 | 99.62 | 99.91 | 99.93 | 99.89 | 99.97 | 100 | 99.99 |
| A6 (%) | 88.87 | 91.25 | 88.92 | 97.89 | 99.64 | 99.96 | 99.96 | 99.92 |
| A7 (%) | 90.48 | 94.67 | 90.35 | 97.33 | 99.11 | 99.58 | 99.74 | 99.83 |
| A8 (%) | 84.39 | 84.54 | 85.93 | 93.97 | 98.31 | 98.27 | 98.73 | 98.96 |
| A9 (%) | 99.90 | 99.65 | 99.49 | 99.57 | 99.69 | 99.80 | 99.84 | 99.85 |
| AA (%) | 90.06 | 90.47 | 91.44 | 97.05 | 98.74 | 98.99 | 99.21 | 99.31 |
| OA (%) | 87.07 | 88.21 | 90.29 | 97.05 | 98.58 | 98.82 | 99.06 | 99.21 |
| Kappa | 0.8301 | 0.8445 | 0.8708 | 0.9626 | 0.9809 | 0.9842 | 0.9873 | 0.9893 |
| SVM [8] | BLS [25] | SS-DBN [34] | CNN-PPF [47] | CNN [39] | CBL | MSCBL | MSCBL-BD | |
|---|---|---|---|---|---|---|---|---|
| A1 (%) | 99.14 | 99.60 | 98.94 | 99.86 | 99.97 | 99.98 | 100 | 100 |
| A2 (%) | 99.45 | 99.65 | 98.95 | 99.59 | 99.95 | 99.98 | 100 | 100 |
| A3 (%) | 99.46 | 99.46 | 79.60 | 99.83 | 99.46 | 99.85 | 99.93 | 99.90 |
| A4 (%) | 99.58 | 99.43 | 99.58 | 99.68 | 99.51 | 99.92 | 99.91 | 99.93 |
| A5 (%) | 98.79 | 99.28 | 99.71 | 98.41 | 98.94 | 99.40 | 99.53 | 99.76 |
| A6 (%) | 99.79 | 99.81 | 99.91 | 99.78 | 100 | 100 | 100 | 100 |
| A7 (%) | 99.67 | 99.57 | 98.90 | 99.85 | 99.87 | 99.95 | 99.98 | 99.99 |
| A8 (%) | 84.40 | 83.18 | 87.04 | 83.28 | 85.61 | 91.05 | 92.41 | 94.24 |
| A9 (%) | 99.37 | 99.75 | 97.93 | 97.44 | 99.31 | 99.47 | 99.55 | 99.63 |
| A10 (%) | 94.65 | 95.76 | 95.79 | 95.84 | 98.98 | 99.44 | 99.64 | 99.72 |
| A11 (%) | 98.87 | 98.66 | 98.64 | 99.75 | 99.60 | 99.88 | 99.94 | 99.90 |
| A12 (%) | 99.95 | 100 | 99.73 | 100 | 99.90 | 99.95 | 99.94 | 99.98 |
| A13 (%) | 99.52 | 99.16 | 99.50 | 99.38 | 100 | 100 | 100 | 100 |
| A14 (%) | 97.91 | 98.12 | 99.95 | 99.52 | 99.79 | 99.96 | 100 | 100 |
| A15 (%) | 69.35 | 73.82 | 85.92 | 81.18 | 95.12 | 95.02 | 95.90 | 97.17 |
| A16 (%) | 99.02 | 98.94 | 99.75 | 98.51 | 99.84 | 99.89 | 99.91 | 99.97 |
| AA (%) | 96.19 | 96.51 | 96.24 | 96.99 | 98.49 | 98.98 | 99.16 | 99.39 |
| OA (%) | 91.67 | 92.18 | 93.76 | 92.98 | 95.94 | 97.22 | 97.67 | 98.27 |
| Kappa | 0.9067 | 0.9125 | 0.9302 | 0.9215 | 0.9546 | 0.9689 | 0.9740 | 0.9807 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, Y.; Wang, X.; Cheng, Y.; Chen, C.L.P. Multi-Stage Convolutional Broad Learning with Block Diagonal Constraint for Hyperspectral Image Classification. Remote Sens. 2021, 13, 3412. https://doi.org/10.3390/rs13173412
Kong Y, Wang X, Cheng Y, Chen CLP. Multi-Stage Convolutional Broad Learning with Block Diagonal Constraint for Hyperspectral Image Classification. Remote Sensing. 2021; 13(17):3412. https://doi.org/10.3390/rs13173412
Chicago/Turabian StyleKong, Yi, Xuesong Wang, Yuhu Cheng, and C. L. Philip Chen. 2021. "Multi-Stage Convolutional Broad Learning with Block Diagonal Constraint for Hyperspectral Image Classification" Remote Sensing 13, no. 17: 3412. https://doi.org/10.3390/rs13173412
APA StyleKong, Y., Wang, X., Cheng, Y., & Chen, C. L. P. (2021). Multi-Stage Convolutional Broad Learning with Block Diagonal Constraint for Hyperspectral Image Classification. Remote Sensing, 13(17), 3412. https://doi.org/10.3390/rs13173412







