Performance Evaluation of Long NDVI Timeseries from AVHRR, MODIS and Landsat Sensors over Landslide-Prone Locations in Qinghai-Tibetan Plateau
Abstract
:1. Introduction
- i.
- Evaluation of the performances of the five NDVI datasets in different land covers as well as over the predominant land cover types in QTP;
- ii.
- Identification of the most suitable sensor for NDVI time series analysis across QTP.
| No | Topics of NDVI Application | NDVI-Product (Sensor)/Period of Study | Key Findings | Reference |
|---|---|---|---|---|
| 1 | NDVI (Grassland phenology) and climate change relationship | GIMMS NOAA-AVHRR (15-day composite) (1982–2006) | NDVI significantly related to increasing temperatures, precipitation effects less pronounced. | [44] |
| 2 | NPP of Alpine Grassland; effect of topography and human activity | NOAA-AVHRR (10-day composite) MODIS (10-day composite) (1981–2004) | NPP (Net Primary Productivity) showed greater decreasing trend in high-elevation regions with slope 15–30°, aspect having little influence and roads having higher effect than residential areas. | [54] |
| 3 | Grassland vegetation cover and climatic factors | GIMMS NOAA-AVHRR (15-day composite) (1982–1999) | NDVI increase in growing season from both advanced growing season and accelerated vegetation activity. Apart from temperate steppe, NDVI exhibited no significant increase in autumn, corresponded to an increase in temperature in spring, and in summer, it was related to temperature and sensitive to precipitation in the spring. There were significant lagged correlations between precipitation and NDVI for alpine grasslands (alpine meadow, alpine steppe). | [55] |
| 4 | Vegetation greening and elevation | SPOT-VGT (10-day maximum value composite) (1999–2013) | NDVI increased more at lower elevations, but was relatively stable or even decreased at high elevations. Vegetation greening rate is in contrast to the pattern of elevation-dependent warming (EDW) with more significant temperature increases at higher elevations. Decreasing precipitation does not reverse overall increasing trend in NDVI, but it may be a limiting factor. | [56] |
| 5 | Vegetation response to temperature changes | GIMMS NOAA-AVHRR (15-day composite) (1981–1999) | Persistent increase in growing season NDVI and longer active growing season brought about by an early spring and delayed autumn. NDVI decreases possibly due to temperature-induced drought. Meaningful relation between changes in NDVI and land surface temperature. | [30] |
| 6 | Human impact on vegetation dynamics | SPOT-VGT (10-day maximum value composite) (1999–2013) | Impact of human activities in a relatively large area is minor and does not reverse the major trends of vegetation dynamics caused by the warming temperature in recent decades. | [25] |
| 7 | Spatial pattern of soil respiration in Tibetan alpine grasslands | Landsat TM MODIS (8-day composite) (2006) | NDVI exhibits spatial variation in soil respiration better than EVI and MSAVI. At the peak growing season of alpine grasslands, soil respiration was generally much higher in the SE Tibetan Plateau and gradually decreased toward NW part. | [57] |
| 8 | Monitoring vegetation phenology in Tibetan alpine grasslands | MODIS (16-day composite) C5 and C6 (2001–2015) | To evaluate the uncertainty of MODIS C5 and C6 NDVI in monitoring vegetation phenology, higher resolution near-surface remote sensing data and corresponding validation methods needed. | [29] |
| 9 | Vegetation classification | MODIS (16-day composite) (2004) | NDVI time-series curves of coniferous forest, high-cold meadow, high-cold meadow steppe and high-cold steppe all appear a mono-peak model during vegetation growth with the maximum peak occurring in August. | [58] |
| 10 | Sensitivity of NDVI to climate conditions | NOAA AVHRR GVI (1985–1999) | NDVI time series shows increasing trend of vegetation biomass. NDVI is strongly correlated but more sensitive to precipitation than temperature in semiarid climate zone of Lhasa area. | [59] |
| 11 | Variation in NPP | GIMMS NOAA-AVHRR (15-day composite) (1982–1999) | NPP decreases from the SE to the NW TP, consistent with precipitation and temperature patterns. NPP trends for most vegetation types resembled that of the whole plateau with alpine meadows showing the largest annual NPP increase. Changes in solar radiation and temperature significantly influenced NPP variation. | [60] |
| 12 | Vegetation and climate change | GIMMS NOAA-AVHRR (15-day composite) (1982–2012) | NDVI and temperature positively correlated during the growing season, responses to changes in precipitation were complex, particularly for different vegetation types. Growing season NDVI increased in 55% area of TP. | [27] |
| 13 | Vegetation trend | Landsat 5, 7, and 8 MODIS (16-day composite) (1990–2018) | Vegetation trend (NDVI product) for the entire Tibetan Plateau at 30 m spatial resolution for 1990–2018. | [3] |
| 14 | Green-up dates or Start of vegetation growing season (SOS) | GIMMS NOAA-AVHRR (15-day composite) SPOT VGT (10-day composite) MODIS (16-day composite) (1982–2011) | GIMMS NDVI in 2001–2006 differed substantially from SPOT-VGT and MODIS NDVIs and may have severe data quality issues in western TP. Alpine vegetation SOS in experienced continuous advancing trend in 1982–2011, consistent with observed warming in springs and winters. | [61] |
| 15 | Start of vegetation growing season (SGS) | GIMMS NOAA-AVHRR (15-day composite) SPOT VGT (10-day composite) (1982–2012) | SGS values display advancing trend with significant variations in SGS dates related to vegetation cover. Critical to know seasonal change characteristics of the different vegetation types, particularly in areas with sparse grassland or evergreen forest. | [53] |
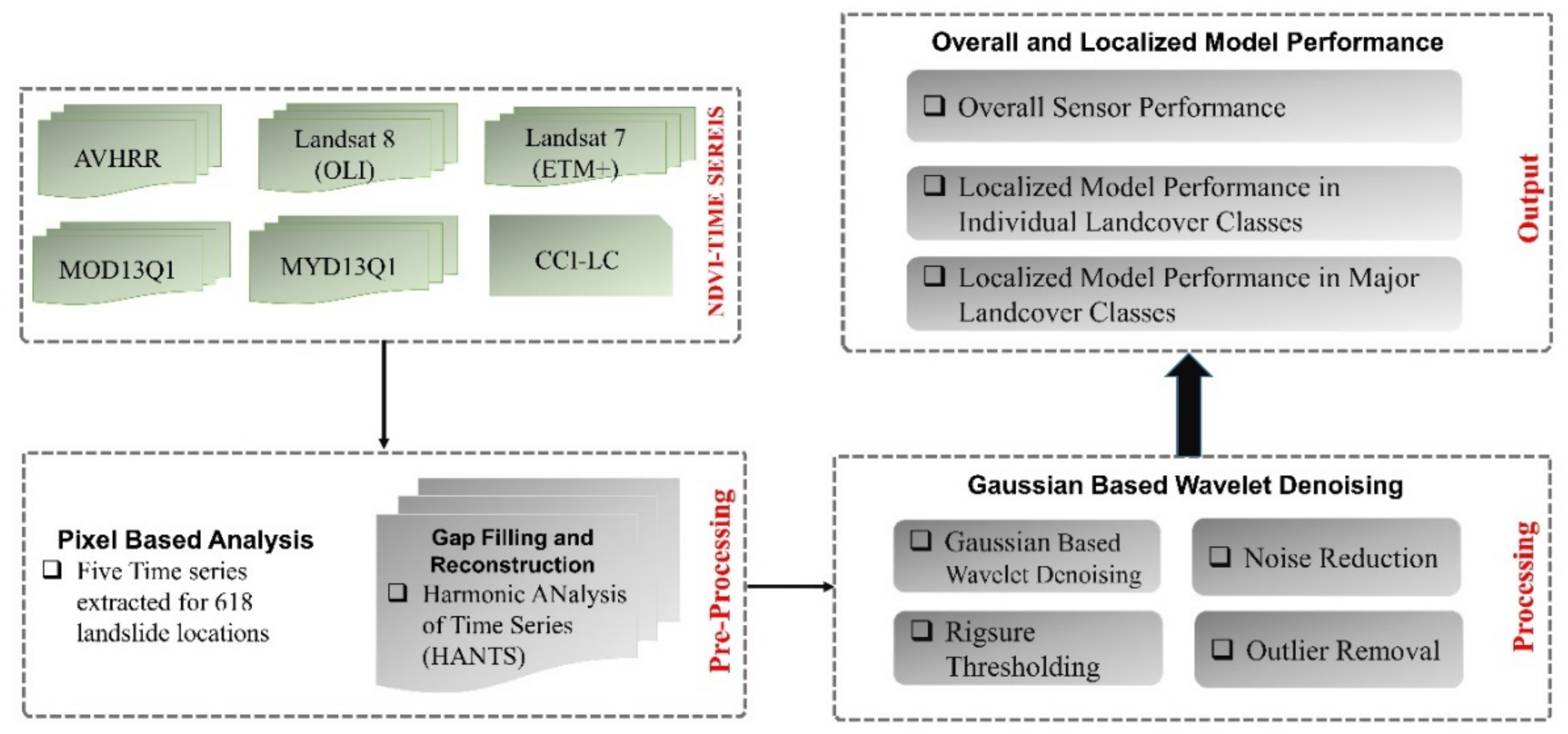
2. Materials and Methods
2.1. Study Area
2.2. Data Used
2.2.1. NOAA-AVHRR-NDVI-V5
2.2.2. MODIS-NDVI (MOD13Q1-MYD13Q1)
2.2.3. Landsat Series (7 and 8)
2.2.4. Land Cover Dataset
2.3. Methods
2.3.1. Harmonic Analysis of Time Series (HANTS) Algorithm
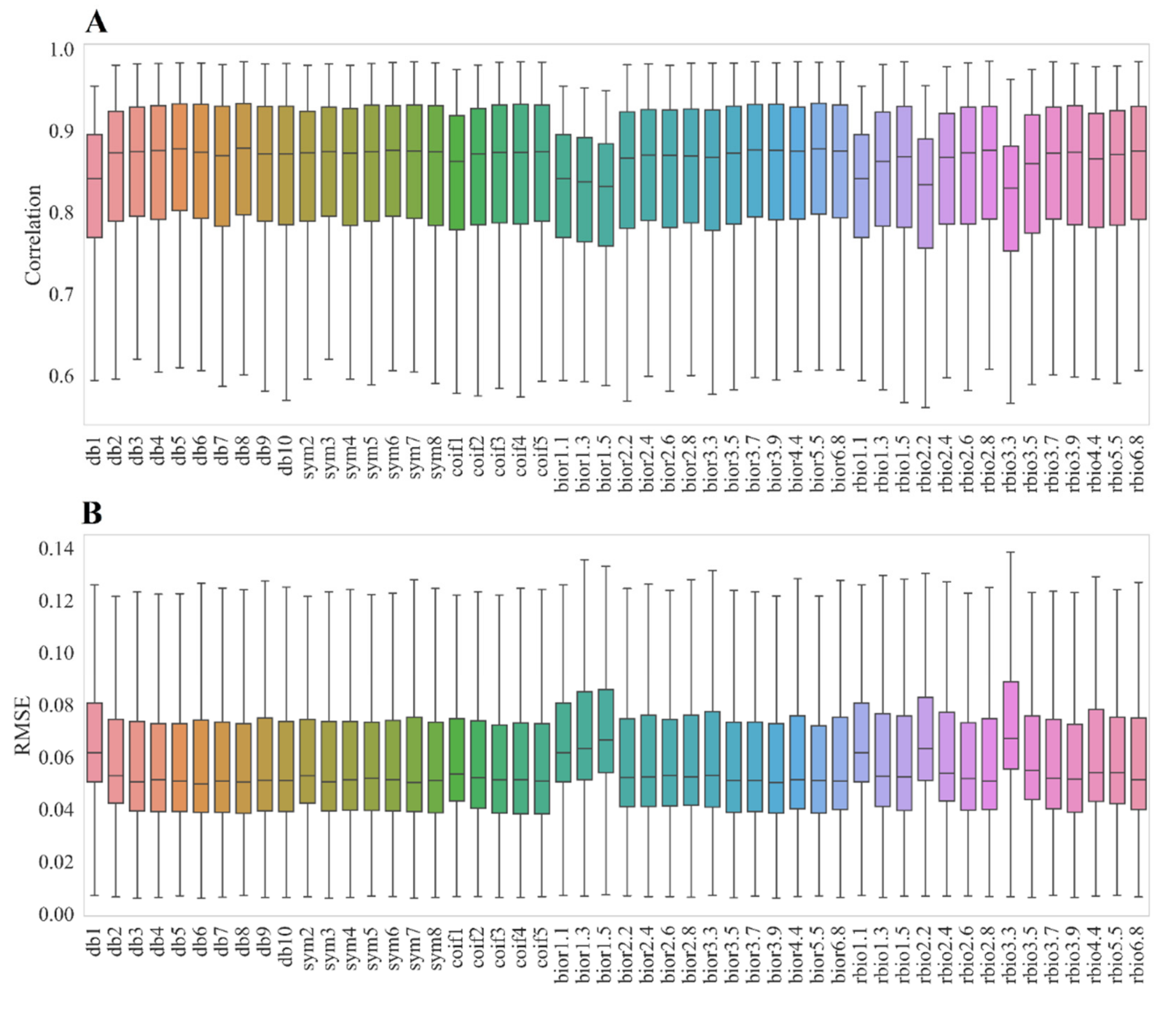
2.3.2. Gaussian-Based Wavelet Threshold Denoising (WTD)
- i.
- Since abrupt changes caused by outliers influence the NDVI time series, it is essential to identify and eliminate these detail coefficients. The Gaussian-based thresholding method was used in this study. Hence, based on the experimental examination, the confidence interval of −σ ~ σ + μ (68.27%, is mean value and is standard deviation) was considered as an outlier, and those detail coefficients outside the confidence interval were removed (i.e., set as 0) [119,120].
- ii.
- Typical wavelet thresholding method “RIGRSURE” was performed to estimate threshold Tj [121] (in Equation (7) (Figure 3). The mathematical equation of the RIGRSURE threshold [122,123,124] can be defined as:where is the standard deviation of the wavelet coefficient at scale j; represents the th coefficient wavelet square (coefficient at minimal risk) at scale j.
2.4. Overall and Localized Model Performance
3. Results
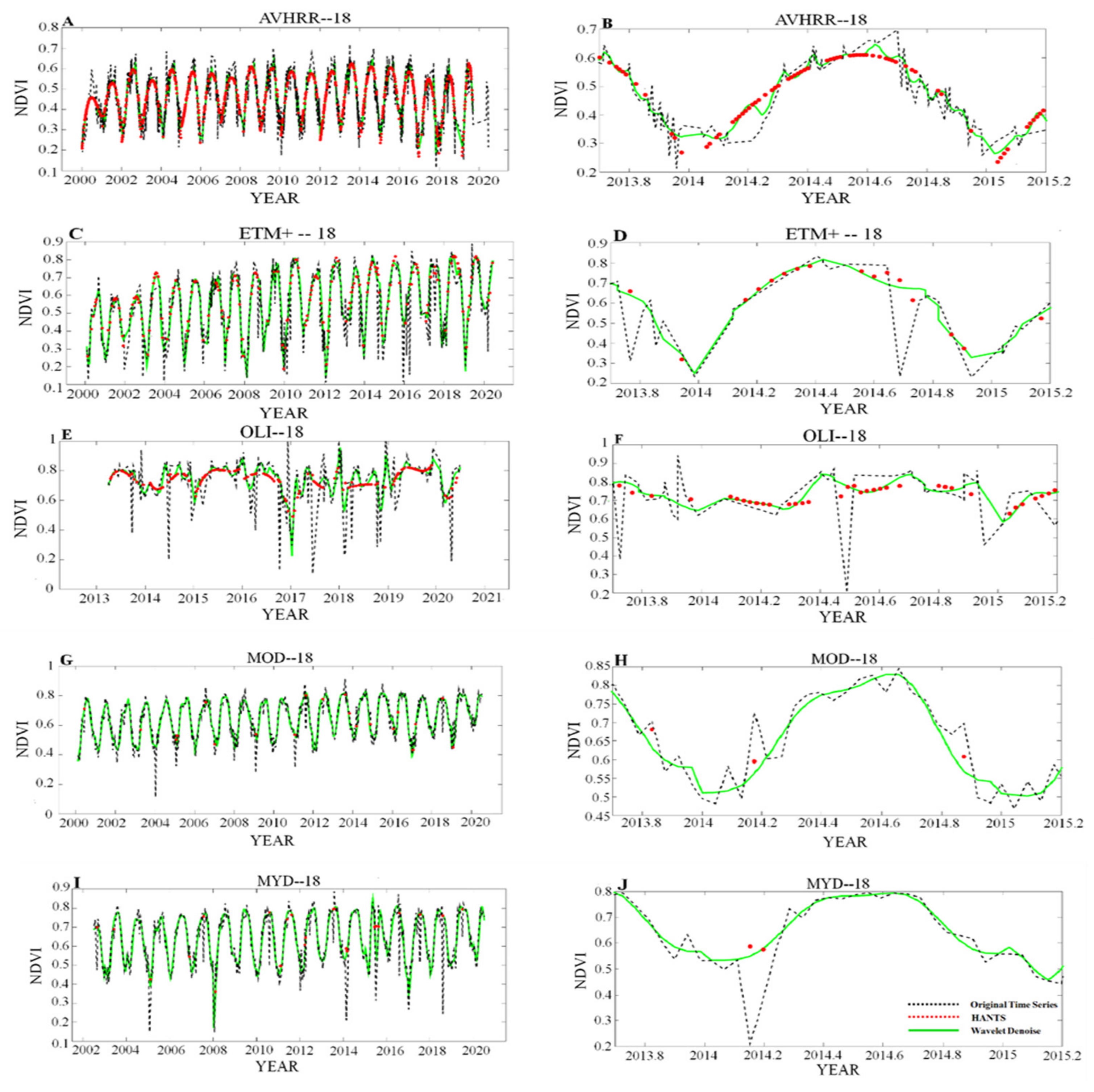
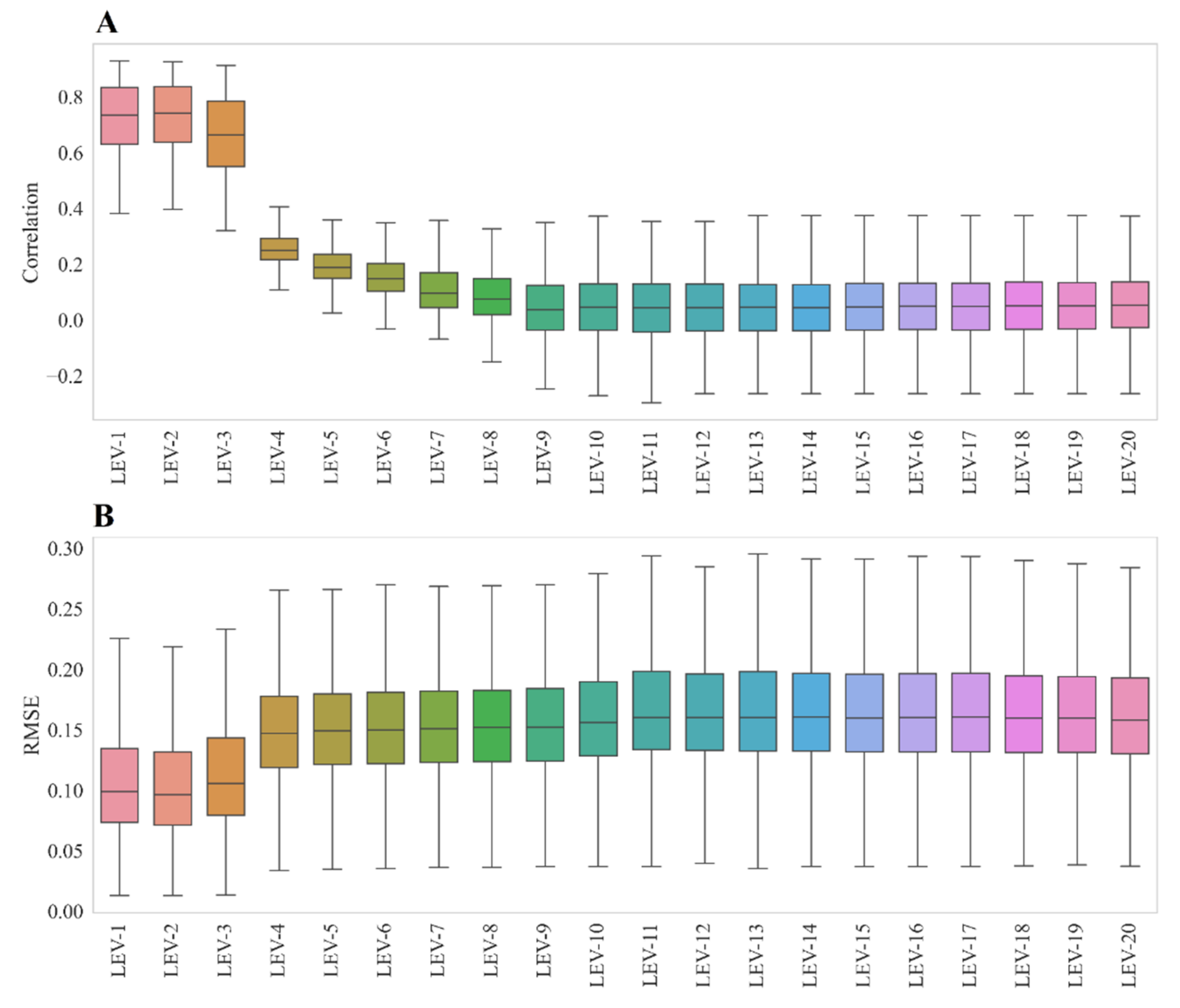
3.1. NDVI Time Series Denoising and Evaluation
3.2. Results of AVHRR Dataset
3.3. Results of Landsat Dataset (ETM+, OLI)
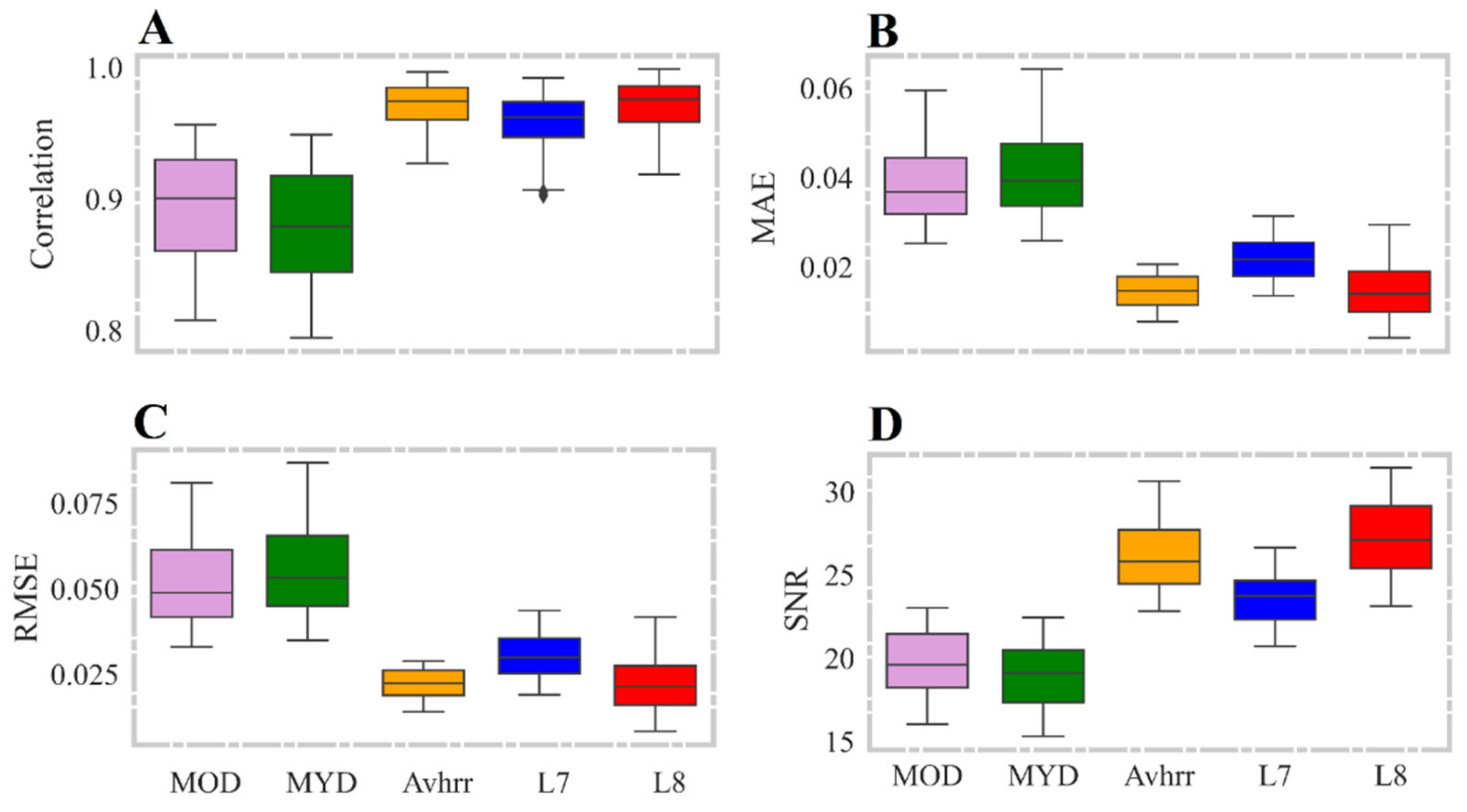
3.4. Results of MODIS Dataset (AQUA, TERRA)
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, D. The vegetation zonation of the Tibetan Plateau. Mt. Res. Dev. 1981, 1, 29–48. [Google Scholar] [CrossRef]
- Hua, W.; Fan, G.; Zhou, D.; Ni, C.; Li, X.; Wang, Y.; Liu, Y.; Huang, X. Preliminary analysis on the relationships between Tibetan Plateau NDVI change and its surface heat source and precipitation of China. Sci. China Ser. D Earth Sci. 2008, 51, 677–685. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Schiller, C.; Kattenborn, T.; Zhao, X.; Qu, J. A Landsat-based vegetation trend product of the Tibetan Plateau for the time-period 1990–2018. Sci. Data 2019, 6, 78. [Google Scholar] [CrossRef]
- Tian, L.; Chen, J.; Zhang, Y. Growing season carries stronger contributions to albedo dynamics on the Tibetan plateau. PLoS ONE 2017, 12, e0180559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, H.; Wu, L.Z.; Huang, R.Q.; Guo, X.G.; He, Q. Formation of the Siwanli ancient landslide in the Dadu River, China. Landslides 2017, 14, 385–394. [Google Scholar] [CrossRef]
- Qi, T.; Meng, X.; Qing, F.; Zhao, Y.; Shi, W.; Chen, G.; Zhang, Y.; Li, Y.; Yue, D.; Su, X.; et al. Distribution and characteristics of large landslides in a fault zone: A case study of the NE Qinghai-Tibet Plateau. Geomorphology 2021, 379, 107592. [Google Scholar] [CrossRef]
- Yao, T.; Xue, Y.; Chen, D.; Chen, F.; Thompson, L.; Cui, P.; Koike, T.; Lau, W.K.M.; Lettenmaier, D.; Mosbrugger, V.; et al. Recent third pole’s rapid warming accompanies cryospheric melt and water cycle intensification and interactions between monsoon and environment: Multidisciplinary approach with observations, modeling, and analysis. Bull. Am. Meteorol. Soc. 2019, 100, 423–444. [Google Scholar] [CrossRef]
- Zhao, B.; Zhao, X.; Zeng, L.; Wang, S.; Du, Y. The mechanisms of complex morphological features of a prehistorical landslide on the eastern margin of the Qinghai-Tibetan Plateau. Bull. Eng. Geol. Environ. 2021, 80, 3423–3437. [Google Scholar] [CrossRef]
- Nadim, F.; Kjekstad, O.; Peduzzi, P.; Herold, C.; Jaedicke, C. Global landslide and avalanche hotspots. Landslides 2006, 3, 159–173. [Google Scholar] [CrossRef]
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Stanley, T.; Kirschbaum, D.B.; Pascale, S.; Kapnick, S. Extreme precipitation in the Himalayan landslide hotspot. Adv. Glob. Chang. Res. 2020, 69, 1087–1111. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kornejady, A.; Kerle, N.; Shabani, F. Investigating the effects of different landslide positioning techniques, landslide partitioning approaches, and presence-absence balances on landslide susceptibility mapping. Catena 2020, 187, 104364. [Google Scholar] [CrossRef]
- Ahmad, H.; Ningsheng, C.; Rahman, M.; Islam, M.M.; Pourghasemi, H.R.; Hussain, S.F.; Habumugisha, J.M.; Liu, E.; Zheng, H.; Ni, H.; et al. Geohazards susceptibility assessment along the upper indus basin using four machine learning and statistical models. ISPRS Int. J. Geo. Inf. 2021, 10, 315. [Google Scholar] [CrossRef]
- Saha, S.; Arabameri, A.; Saha, A.; Blaschke, T.; Ngo, P.T.T.; Nhu, V.H.; Band, S.S. Prediction of landslide susceptibility in Rudraprayag, India using novel ensemble of conditional probability and boosted regression tree-based on cross-validation method. Sci. Total Environ. 2021, 764, 142928. [Google Scholar] [CrossRef]
- Adnan, M.S.G.; Rahman, M.S.; Ahmed, N.; Ahmed, B.; Rabbi, M.F.; Rahman, R.M. Improving spatial agreement in machine learning-based landslide susceptibility mapping. Remote Sens. 2020, 12, 3347. [Google Scholar] [CrossRef]
- Choi, J.; Oh, H.J.; Lee, H.J.; Lee, C.; Lee, S. Combining landslide susceptibility maps obtained from frequency ratio, logistic regression, and artificial neural network models using ASTER images and GIS. Eng. Geol. 2012, 124, 12–23. [Google Scholar] [CrossRef]
- Ozturk, U.; Pittore, M.; Behling, R.; Roessner, S.; Andreani, L.; Korup, O. How robust are landslide susceptibility estimates? Landslides 2020, 18, 681–695. [Google Scholar] [CrossRef]
- Moreiras, S.M. Climatic effect of ENSO associated with landslide occurrence in the Central Andes, Mendoza province, Argentina. Landslides 2005, 2, 53–59. [Google Scholar] [CrossRef]
- Petley, D.; Hearn, G.; Hart, A.; Rosser, N.; Dunning, S.; Oven, K.; Mitchell, W. Trends in landslide occurrence in Nepal. Nat. Hazards 2007, 43, 23–44. [Google Scholar] [CrossRef]
- Bennett, G.L.; Miller, S.R.; Roering, J.J.; Schmidt, D.A. Landslides, threshold slopes, and the survival of relict terrain in the wake of the Mendocino Triple Junction. Geology 2016, 44, 363–366. [Google Scholar] [CrossRef] [Green Version]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Lu, Z. Remote sensing of landslides—A review. Remote Sens. 2018, 10, 279. [Google Scholar] [CrossRef] [Green Version]
- Mattia, C.; Bischetti, G.B.; Gentile, F. Biotechnical characteristics of root systems of typical Mediterranean species. Plant Soil 2005, 278, 23–32. [Google Scholar] [CrossRef]
- Hu, X.-S.; Brierley, G.; Zhu, H.-L.; Li, G.-R.; Fu, J.-T.; Mao, X.-Q.; Yu, Q.-Q.; Qiao, N. An exploratory analysis of vegetation strategies to reduce shallow landslide activity on loess hillslopes, Northeast Qinghai-Tibet Plateau, China. J. Mt. Sci. 2013, 10, 668–686. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Li, Y.; Gao, Y.; Zou, C.; Yan, S.; Gao, J. Human impact on vegetation dynamics around Lhasa, southern Tibetan Plateau, China. Sustainability 2016, 8, 1146. [Google Scholar] [CrossRef] [Green Version]
- Kuang, Q.; Yuan, Q.Z.; Han, J.C. A remote sensing monitoring method for alpine grasslands desertification in the eastern Qinghai-Tibetan plateau. J. Mt. Sci. 2020, 17. [Google Scholar] [CrossRef]
- Pang, G.; Wang, X.; Yang, M. Using the NDVI to identify variations in, and responses of, vegetation to climate change on the Tibetan Plateau from 1982 to 2012. Quat. Int. 2017, 444, 87–96. [Google Scholar] [CrossRef]
- Sun, J.; Cheng, G.; Li, W.; Sha, Y.; Yang, Y. On the variation of NDVI with the principal climatic elements in the Tibetan plateau. Remote Sens. 2013, 5, 1894–1911. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z.; Zhu, W. Uncertainty of remote sensing data in monitoring vegetation phenology: A comparison of MODIS C5 and C6 vegetation index products on the Tibetan plateau. Remote Sens. 2017, 9, 1288. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variations in northern vegetation activity inferred from satellite data of vegetation index during 1981 to 1999. J. Geophys. Res. Atmos. 2001, 106, 20069–20083. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, Y.; Tagesson, T.; Brandt, M.; Wang, L.; Chen, N.; Zu, J.; Jin, H.; Cai, Z.; Tong, X. The confounding effect of snow cover on assessing spring phenology from space: A new look at trends on the Tibetan Plateau. Sci. Total Environ. 2020, 756, 144011. [Google Scholar] [CrossRef]
- Yin, H.; Cao, C.; Xu, M.; Chen, W.; Ni, X.; Chen, X. Long-term snow disasters during 1982–2012 in the Tibetan Plateau using satellite data. Geomat. Nat. Hazards Risk 2017, 8, 466–477. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Liu, S.; Dong, S.; Su, X.; Wang, X.; Wu, X.; Wu, L.; Zhang, X. Analysis of vegetation change associated with human disturbance using MODIS data on the rangelands of the Qinghai-Tibet Plateau. Rangel. J. 2015, 37, 77–87. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Song, C.; Band, L.E.; Sun, G.; Li, J. Reanalysis of global terrestrial vegetation trends from MODIS products: Browning or greening? Remote Sens. Environ. 2017, 191, 145–154. [Google Scholar] [CrossRef] [Green Version]
- Gholamnia, M.; Khandan, R.; Bonafoni, S.; Sadeghi, A. Spatiotemporal analysis of MODIS NDVI in the semi-arid region of Kurdistan (Iran). Remote Sens. 2019, 11, 1723. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.R.; Liu, H.Q.; Batchily, K.V.; Van Leeuwen, W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Peng, J.; Liu, Z.; Liu, Y.; Wu, J.; Han, Y. Trend analysis of vegetation dynamics in Qinghai-Tibet Plateau using Hurst Exponent. Ecol. Indic. 2012, 14, 28–39. [Google Scholar] [CrossRef]
- Cihlar, J.; Ly, H.; Li, Z.; Chen, J.; Pokrant, H.; Huang, F. Multitemporal, multichannel AVHRR data sets for land biosphere studies—Artifacts and corrections. Remote Sens. Environ. 1997, 60, 35–57. [Google Scholar] [CrossRef]
- Hall-Beyer, M. Comparison of single-year and multiyear NDVI time series principal components in cold temperate biomes. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2568–2574. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Yan, F.; Fan, X. The Variability of NDVI over northwest China and its relation to temperature and precipitation. Int. Geosci. Remote Sens. Symp. 2003, 4, 2275–2277. [Google Scholar] [CrossRef]
- Fensholt, R.; Rasmussen, K.; Nielsen, T.T.; Mbow, C. Evaluation of earth observation based long term vegetation trends—Intercomparing NDVI time series trend analysis consistency of Sahel from AVHRR GIMMS, Terra MODIS and SPOT VGT data. Remote Sens. Environ. 2009, 113, 1886–1898. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, H.; Ji, L.; Lei, L.; Wang, C.; Yan, D.; Li, B.; Li, J. Vegetation greenness trend (2000 to 2009) and the climate controls in the Qinghai-Tibetan Plateau. J. Appl. Remote Sens. 2013, 7, 073572. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, J.; Sun, P.; Liu, S.; Liu, W. Inconsistent NDVI trends from AVHRR, MODIS, and SPOT sensors in the Tibetan Plateau. In Proceedings of the 2013 2nd International Conference on Agro-Geoinformatics, Fairfax, VA, USA, 12–16 August 2013; pp. 97–101. [Google Scholar] [CrossRef]
- Wen, J.; Su, Z.; Ma, Y. Reconstruction of a cloud-free vegetation index time series for the Tibetan Plateau. Mt. Res. Dev. 2004, 24, 348–353. [Google Scholar]
- Detsch, F.; Otte, I.; Appelhans, T.; Nauss, T. A comparative study of cross-product NDVI dynamics in the Kilimanjaro region—A matter of sensor, degradation calibration, and significance. Remote Sens. 2016, 8, 159. [Google Scholar] [CrossRef] [Green Version]
- Reed, B.C.; Brown, J.F.; VanderZee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Roy, D.P.; Kovalskyy, V.; Zhang, H.K.; Vermote, E.F.; Yan, L.; Kumar, S.S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 reflective wavelength and normalized difference vegetation index continuity. Remote Sens. Environ. 2016, 185, 57–70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Dijk, A.; Callis, S.L.; Sakamoto, C.M.; Decker, W.L. Smoothing vegetation index profiles: An alternative method for reducing radiometric disturbance in Noaa/Avhrr data. Photogramm. Eng. Remote Sens. 1987, 53, 1059–1067. [Google Scholar]
- Zhang, J.; Yao, F.; Zheng, L.; Yang, L. Evaluation of grassland dynamics in the northern-Tibet plateau of China using remote sensing and climate data. Sensors 2007, 7, 3312–3328. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global MODIS NDVI time series: Performance of Harmonic Analysis of Time Series (HANTS). Remote Sens. Environ. 2015, 163, 217–228. [Google Scholar] [CrossRef]
- Piao, Y.; Yan, B.; Guo, S.; Guan, Y.; Li, J.; Cai, D. Change detection of MODIS time series using a wavelet transform. In Proceedings of the 2012 International Conference on Systems and Informatics (ICSAI2012), Yantai, China, 19–20 May 2012; pp. 2093–2097. [Google Scholar] [CrossRef]
- Ding, M.; Li, L.; Zhang, Y.; Sun, X.; Liu, L.; Gao, J.; Wang, Z.; Li, Y. Start of vegetation growing season on the Tibetan Plateau inferred from multiple methods based on GIMMS and SPOT NDVI data. J. Geogr. Sci. 2015, 25, 131–148. [Google Scholar] [CrossRef]
- Gao, Q.; Wan, Y.; Li, Y.; Guo, Y.; Ganjurjav; Qin, X.; Jiangcun, W.; Wang, B. Effects of topography and human activity on the net primary productivity (NPP) of alpine grassland in northern Tibet from 1981 to 2004. Int. J. Remote Sens. 2013, 34, 2057–2069. [Google Scholar] [CrossRef]
- Yang Yuan-He, P.S.-L. Variations in grassland vegetation cover in relation to climatic factors on the Tibetan plateau. Chin. J. Plant. Ecol. 2006, 30, 1–8. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Shen, W.; Li, Y.; Lin, J.; Lu, X.; Xu, X.; Jiang, J. Elevation-dependent vegetation greening of the Yarlung Zangbo River basin in the Southern Tibetan Plateau, 1999–2013. Remote Sens. 2015, 7, 16672–16687. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.; He, J.S.; Niu, Z. Estimating the spatial pattern of soil respiration in Tibetan alpine grasslands using Landsat TM images and MODIS data. Ecol. Indic. 2013, 26, 117–125. [Google Scholar] [CrossRef]
- Lu, Y.; Yan, Y.; Tao, H. Classification of vegetation in North Tibet Plateau based on MODIS time-series data. Wuhan Univ. J. Nat. Sci. 2008, 13, 273–278. [Google Scholar] [CrossRef]
- Chu, D.; Lu, L.; Zhang, T. Sensitivity of normalized difference vegetation index (NDVI) to seasonal and interannual climate conditions in the Lhasa area, Tibetan Plateau, China. Arct. Antarct. Alp. Res. 2007, 39, 635–641. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; He, J. Variations in vegetation net primary production in the Qinghai-Xizang Plateau, China, from 1982 to 1999. Clim. Chang. 2006, 74, 253–267. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Y.; Dong, J.; Xiao, X. Green-up dates in the Tibetan Plateau have continuously advanced from 1982 to 2011. Proc. Natl. Acad. Sci. USA 2013, 110, 4309–4314. [Google Scholar] [CrossRef] [Green Version]
- Yi-li, Z.; Du, Z.; Bing-yuan, L.I. A discussion on the boundary and area of the Tibetan Plateau in China. Geogr. Res. 2002, 21, 1–8. [Google Scholar]
- Cui, X.; Graf, H.-F. Recent land cover changes on the Tibetan Plateau: A review. Clim. Chang. 2009, 94, 47–61. [Google Scholar] [CrossRef] [Green Version]
- You, Q.; Fraedrich, K.; Ren, G.; Pepin, N.; Kang, S. Variability of temperature in the Tibetan Plateau based on homogenized surface stations and reanalysis data. Int. J. Climatol. 2013, 33, 1337–1347. [Google Scholar] [CrossRef] [Green Version]
- Du, M.; Kawashima, S.; Yonemura, S.; Zhang, X.; Chen, S. Mutual influence between human activities and climate change in the Tibetan Plateau during recent years. Glob. Planet. Chang. 2004, 41, 241–249. [Google Scholar] [CrossRef]
- Gillespie, T.W.; Madson, A.; Cusack, C.F.; Xue, Y. Changes in NDVI and human population in protected areas on the Tibetan Plateau. Arct. Antarct. Alp. Res. 2019, 51, 428–439. [Google Scholar] [CrossRef] [Green Version]
- Li, W.H.; Zhou, X.M. Ecosystems of Qinghai-Xizang (Tibetan) Plateau and Approach for Their Sustainable Management; Guangdong Science and Technology Press: Guangzhou, China, 1998. [Google Scholar]
- Kirschbaum, D.B.; Adler, R.; Hong, Y.; Hill, S.; Lerner-Lam, A. A global landslide catalog for hazard applications: Method, results, and limitations. Nat. Hazards 2010, 52, 561–575. [Google Scholar] [CrossRef] [Green Version]
- Lin, L.; Lin, Q.; Wang, Y. Landslide susceptibility mapping on a global scale using the method of logistic regression. Nat. Hazards Earth Syst. Sci. 2017, 17, 1411–1424. [Google Scholar] [CrossRef] [Green Version]
- Kirschbaum, D.; Stanley, T.; Zhou, Y. Spatial and temporal analysis of a global landslide catalog. Geomorphology 2015, 249, 4–15. [Google Scholar] [CrossRef]
- Kashyap, R.; Pandey, A.C.; Parida, B.R. Spatio-temporal variability of monsoon precipitation and their effect on precipitation triggered landslides in relation to relief in Himalayas. Spat. Inf. Res. 2021, 1–13. [Google Scholar] [CrossRef]
- Kirschbaum, D.; Kapnick, S.B.; Stanley, T.; Pascale, S. Changes in extreme precipitation and landslides over high mountain Asia. Geophys. Res. Lett. 2020, 47, 1–9. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Escuin, S.; Navarro, R.; Fernandez, P. Fire severity assessment by using NBR (Normalized Burn Ratio) and NDVI (Normalized Difference Vegetation Index) derived from LANDSAT TM/ETM images. Int. J. Remote Sens. 2008, 29, 1053–1073. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Csiszar, I.; Eidenshink, J.; Myneni, R.; Baret, F.; Masuoka, E.; Wolfe, R.; Claverie, M. NOAA Climate Data Record (CDR) of Normalized Difference Vegetation Index (NDVI); Version 4; NOAA National Centers for Environmental Information: Silver Spring, MD, USA, 2014. [CrossRef]
- Rogan, J.; Franklin, J.; Roberts, D.A. A comparison of methods for monitoring multitemporal vegetation change using Thematic Mapper imagery. Remote Sens. Environ. 2002, 80, 143–156. [Google Scholar] [CrossRef]
- Pinzon, J.E.; Tucker, C.J. A non-stationary 1981–2012 AVHRR NDVI3g time series. Remote Sens. 2014, 6, 6929–6960. [Google Scholar] [CrossRef] [Green Version]
- Albarakat, R.; Lakshmi, V. Comparison of normalized difference vegetation index derived from landsat, MODIS, and AVHRR for the mesopotamian marshes between 2002 and 2018. Remote Sens. 2019, 11, 1245. [Google Scholar] [CrossRef] [Green Version]
- Steven, M.D.; Malthus, T.J.; Baret, F.; Xu, H.; Chopping, M.J. Intercalibration of vegetation indices from different sensor systems. Remote Sens. Environ. 2003, 88, 412–422. [Google Scholar] [CrossRef]
- Pedelty, J.; Devadiga, S.; Masuoka, E.; Brown, M.; Pinzon, J.; Tucker, C.; Vermote, E.; Prince, S.; Nagol, J.; Justice, C. Generating a long-term land data record from the AVHRR and MODIS instruments. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 1021–1025. [Google Scholar]
- Robinson, N.P.; Allred, B.W.; Jones, M.O.; Moreno, A.; Kimball, J.S.; Naugle, D.E.; Erickson, T.A.; Richardson, A.D. A dynamic landsat derived normalized difference vegetation index (NDVI) product for the conterminous United States. Remote Sens. 2017, 9, 863. [Google Scholar] [CrossRef] [Green Version]
- Solano, R.; Didan, K.; Jacobson, A.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series); University of Arizona, Vegetation Index and Phenology Lab: Tuscon, AZ, USA, 2010; pp. 1–42. [Google Scholar]
- Van Leeuwen, W.J.D.; Huete, A.R.; Laing, T.W. MODIS vegetation index compositing approach: A prototype with AVHRR data. Remote Sens. Environ. 1999, 69, 264–280. [Google Scholar] [CrossRef]
- Kovalskyy, V.; Roy, D.P. The global availability of Landsat 5 TM and Landsat 7 ETM+ land surface observations and implications for global 30 m Landsat data product generation. Remote Sens. Environ. 2013, 130, 280–293. [Google Scholar] [CrossRef] [Green Version]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D., Jr.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Hughes, M.J.; Laue, B. Cloud detection algorithm comparison and validation for operational Landsat data products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef] [Green Version]
- Claverie, M.; Masek, J.G.; Ju, J.; Dungan, J.L. Harmonized Landsat-8 Sentinel-2 (Hls) Product User’s Guide; NASA: Washington, DC, USA, 2017.
- Bontemps, S.; Defourny, P.; Radoux, J.; Van Bogaert, E.; Lamarche, C.; Achard, F.; Mayaux, P.; Boettcher, M.; Brockmann, C.; Kirches, G.; et al. Consistent global land cover maps for climate modeling communities: Current achievements of the ESA’s land cover CCI. In Proceedings of the ESA Living Planet Symposium, Edinburgh, UK, 9–13 September 2013; pp. 9–13. [Google Scholar]
- Li, W.; MacBean, N.; Ciais, P.; Defourny, P.; Lamarche, C.; Bontemps, S.; Houghton, R.A.; Peng, S. Gross and net land cover changes in the main plant functional types derived from the annual ESA CCI land cover maps (1992–2015). Earth Syst. Sci. Data 2018, 10, 219–234. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Ciais, P.; MacBean, N.; Peng, S.; Defourny, P.; Bontemps, S. Major forest changes and land cover transitions based on plant functional types derived from the ESA CCI Land Cover product. Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 30–39. [Google Scholar] [CrossRef]
- Pérez-Hoyos, A.; Rembold, F.; Kerdiles, H.; Gallego, J. Comparison of global land cover datasets for cropland monitoring. Remote Sens. 2017, 9, 1118. [Google Scholar] [CrossRef] [Green Version]
- Defourny, P.; Schouten, L.; Bartalev, S.; Bontemps, S.; Cacetta, P.; De Wit, A.J.W.; Di Bella, C.; Gérard, B.; Giri, C.; Gond, V. Accuracy Assessment of a 300 m Global Land Cover Map: The GlobCover Experience; International Center for Remote Sensing of Environment (ICRSE): Tucson, AZ, USA, 2009. [Google Scholar]
- Liu, X.; Yu, L.; Sia, Y.; Zhang, C.; Lu, H.; Yu, C.; Gong, P. Identifying patterns and hotspots of global land cover transitions using the ESA CCI land cover dataset. Remote Sens. Lett. 2018, 9, 972–981. [Google Scholar] [CrossRef]
- Lau, K.-M.; Weng, H. Climate signal detection using wavelet transform: How to make a time series sing. Bull. Am. Meteorol. Soc. 1995, 76, 2391–2402. [Google Scholar] [CrossRef] [Green Version]
- Azzali, S.; Menenti, M. Mapping vegetation-soil-climate complexes in southern Africa using temporal Fourier analysis of NOAA-AVHRR NDVI data. Int. J. Remote Sens. 2000, 21, 973–996. [Google Scholar] [CrossRef]
- Moody, A.; Johnson, D.M. Land-surface phenologies from AVHRR using the discrete Fourier transform. Remote Sens. Environ. 2001, 75, 305–323. [Google Scholar] [CrossRef]
- Geerken, R.; Zaitchik, B.; Evans, J.P. Classifying rangeland vegetation type and coverage from NDVI time series using Fourier Filtered Cycle Similarity. Int. J. Remote Sens. 2005, 26, 5535–5554. [Google Scholar] [CrossRef]
- Verhegghen, A.; Bontemps, S.; Defourny, P. A global NDVI and EVI reference data set for land-surface phenology using 13 years of daily SPOT-VEGETATION observations. Int. J. Remote Sens. 2014, 35, 2440–2471. [Google Scholar] [CrossRef] [Green Version]
- Sakamoto, T.; Yokozawa, M.; Toritani, H.; Shibayama, M.; Ishitsuka, N.; Ohno, H. A crop phenology detection method using time-series MODIS data. Remote Sens. Environ. 2005, 96, 366–374. [Google Scholar] [CrossRef]
- Bruce, L.M.; Mathur, A.; Byrd, J.D. Denoising and wavelet-based feature extraction of MODIS multi-temporal vegetation signatures. GIScience Remote Sens. 2006, 43, 67–77. [Google Scholar] [CrossRef]
- Galford, G.L.; Mustard, J.F.; Melillo, J.; Gendrin, A.; Cerri, C.C.; Cerri, C.E.P. Wavelet analysis of MODIS time series to detect expansion and intensification of row-crop agriculture in Brazil. Remote Sens. Environ. 2008, 112, 576–587. [Google Scholar] [CrossRef]
- Martínez, B.; Gilabert, M.A. Vegetation dynamics from NDVI time series analysis using the wavelet transform. Remote Sens. Environ. 2009, 113, 1823–1842. [Google Scholar] [CrossRef]
- Mak, M. Orthogonal wavelet analysis: Interannual variability in the sea surface temperature. Bull. Am. Meteorol. Soc. 1995, 76, 2179–2186. [Google Scholar] [CrossRef] [Green Version]
- Castaño, F.A.; Hernández, A.M.; Soto-Romero, G. Assessment of artifacts reduction and denoising techniques in Electrocardiographic signals using Ensemble Average-based method. Comput. Methods Programs Biomed. 2019, 182. [Google Scholar] [CrossRef]
- Sang, Y.F. A Practical guide to discrete wavelet decomposition of hydrologic time series. Water Resour. Manag. 2012, 26, 3345–3365. [Google Scholar] [CrossRef]
- Sang, Y.-F.; Wang, D.; Wu, J.-C.; Zhu, Q.-P.; Wang, L. Entropy-based wavelet de-noising method for time series analysis. Entropy 2009, 11, 1123–1147. [Google Scholar] [CrossRef] [Green Version]
- Daubechies, I. 1. The what, why, and how of wavelets. In Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1992; pp. 1–16. [Google Scholar] [CrossRef]
- Sang, Y.F.; Liu, C.; Wang, Z.; Wen, J.; Shang, L. Energy-based wavelet de-noising of hydrologic time series. PLoS ONE 2014, 9, e0110733. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef] [Green Version]
- Chiann, C.; Morettin, P.A. A wavelet analysis for time series. J. Nonparametr. Stat. 1998, 10, 1–46. [Google Scholar] [CrossRef]
- Sang, Y. A review on the applications of wavelet transform in hydrology time series analysis. Atmos. Res. 2013, 122, 8–15. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L.; Johnstone, I.M. Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 1995, 90, 1200–1224. [Google Scholar] [CrossRef]
- Jansen, M.; Bultheel, A. Asymptotic behavior of the minimum mean squared error threshold for noisy wavelet coefficients of piecewise smooth signals. IEEE Trans. Signal. Process. 2001, 49, 1113–1118. [Google Scholar] [CrossRef]
- Aussem, A. Waveletbased feature extraction and decomposition strategies for financial forecasting. Int. J. Comput. Intell. Financ. 1998, 6, 5–12. [Google Scholar]
- Adamowski, J.; Sun, K. Development of a coupled wavelet transform and neural network method for flow forecasting of non-perennial rivers in semi-arid watersheds. J. Hydrol. 2010, 390, 85–91. [Google Scholar] [CrossRef]
- Kannan, K.; Perumal, A.; Arulmozhi, K. Optimal decomposition level of discrete, stationary and dual tree complex wavelet transform for pixel based fusion of multi-focused images. Serb. J. Electr. Eng. 2010, 7, 81–93. [Google Scholar] [CrossRef]
- Shoaib, M.; Shamseldin, A.Y.; Melville, B.W. Comparative study of different wavelet based neural network models for rainfall–runoff modeling. J. Hydrol. 2014, 515, 47–58. [Google Scholar] [CrossRef]
- Pinto, C.T.; Ponzoni, F.J.; de Castro, R.M. A reference surface uniformity evaluation for sensors absolute calibration. In Proceedings of the 20th IMEKO World Congress 2012, Busan, Korea, 9–12 September 2012. [Google Scholar]
- Hirt, C.; Filmer, M.S.; Featherstone, W.E. Comparison and validation of the recent freely available ASTER-GDEM ver1, SRTM ver4. 1 and GEODATA DEM-9S ver3 digital elevation models over Australia. Aust. J. Earth Sci. 2010, 57, 337–347. [Google Scholar] [CrossRef] [Green Version]
- Moghtased-Azar, K.; Gholamnia, M. Effect of using different types of threshold schemes (in wavelet space) on noise reduction over GPS times series. J. Geomat. Sci. Technol. 2014, 4, 51–66. [Google Scholar]
- Verma, N.; Verma, A.K. Performance analysis of wavelet thresholding methods in denoising of audio signals of some Indian musical instruments. Int. J. Eng. Sci. Technol 2012, 4, 2040–2045. [Google Scholar]
- Üstündağ, M.; Şengür, A.; Gökbulut, M.; Ata, F. Performance comparison of wavelet thresholding techniques on weak ECG signal denoising. Przegląd Elektrotechniczny 2013, 89, 63–66. [Google Scholar]
- Valencia, D.; Orejuela, D.; Salazar, J.; Valencia, J. Comparison analysis between rigrsure, sqtwolog, heursure and minimaxi techniques using hard and soft thresholding methods. In Proceedings of the 2016 XXI Symposium on Signal Processing, Images and Artificial Vision (STSIVA), Bucaramanga, Colombia, 31 August–2 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, L.; Hu, G.; Menenti, M. Evaluation of Harmonic Analysis of Time Series (HANTS): Impact of gaps on time series reconstruction. In Proceedings of the 2012 Second International Workshop on Earth Observation and Remote Sensing Applications, Shanghai, China, 8–11 June 2012; pp. 31–35. [Google Scholar] [CrossRef]
- Hird, J.N.; McDermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ. 2009, 113, 248–258. [Google Scholar] [CrossRef]
- Ma, Q.; Su, Y.; Luo, L.; Li, L.; Kelly, M.; Guo, Q. Evaluating the uncertainty of Landsat-derived vegetation indices in quantifying forest fuel treatments using bi-temporal LiDAR data. Ecol. Indic. 2018, 95, 298–310. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Jia, L.; Menenti, M.; Gorte, B. On the performance of remote sensing time series reconstruction methods—A spatial comparison. Remote Sens. Environ. 2016, 187, 367–384. [Google Scholar] [CrossRef]
- Su, C.H.; Narsey, S.Y.; Gruber, A.; Xaver, A.; Chung, D.; Ryu, D.; Wagner, W. Evaluation of post-retrieval de-noising of active and passive microwave satellite soil moisture. Remote Sens. Environ. 2015, 163, 127–139. [Google Scholar] [CrossRef]
- Joseph, S.M.; Babu Anto, P. Speech coding based on orthogonal and biorthogonal wavelet. Procedia Technol. 2012, 6, 397–404. [Google Scholar] [CrossRef] [Green Version]
- Sundar, A. A comprehensive assessment of the performance of modern algorithms for enhancement of digital volume pulse signals. Int. J. Pharma Med. Biol. Sci. 2016, 5, 91. [Google Scholar] [CrossRef] [Green Version]
- Misiti, M.; Misiti, Y.; Oppenheim, G.; Poggi, J.-M. Wavelet Toolbox; The MathWorks, Inc.: Natick, MA, USA, 1996. [Google Scholar]
- Uyulan, C.; Erguzel, T. Comparison of wavelet families for mental task classification. J. Neurobehav. Sci. 2016, 3, 59. [Google Scholar] [CrossRef]
- Karel, J.; Peeters, R. Orthogonal matched wavelets with vanishing moments: A sparsity design approach. Circuits Syst. Signal. Process. 2018, 37, 3487–3514. [Google Scholar] [CrossRef] [Green Version]
- Dixit, A.; Majumdar, S. Comparative analysis of Coiflet and Daubechies wavelet using global TRhreshold for image de-noising. Int. J. Adv. Eng. Technol. 2013, 6, 2247–2252. [Google Scholar] [CrossRef]
- Keinert, F. Biorthogonal wavelets for fast matrix computations. Appl. Comput. Harmon. Anal. 1994, 1, 147–156. [Google Scholar] [CrossRef] [Green Version]
- Mishra, V.; Kumar, A.; Jaiswal, A. Performance comparison of Daubechies, Biorthogonal and Haar transform for grayscale image compression. Int. J. Comput. Appl. 2015, 126, 975–8887. [Google Scholar] [CrossRef] [Green Version]
- Teillet, P.M.; Staenz, K.; William, D.J. Effects of spectral, spatial, and radiometric characteristics on remote sensing vegetation indices of forested regions. Remote Sens. Environ. 1997, 61, 139–149. [Google Scholar] [CrossRef]
- Miura, T.; Nagai, S. Landslide detection with himawari-8 geostationary satellite data: A case study of a torrential rain event in Kyushu, Japan. Remote Sens. 2020, 12, 1734. [Google Scholar] [CrossRef]
- Lu, P.; Qin, Y.; Li, Z.; Mondini, A.C.; Casagli, N. Landslide mapping from multi-sensor data through improved change detection-based Markov random field. Remote Sens. Environ. 2019, 231, 111235. [Google Scholar] [CrossRef]
- Mondini, A.C.; Guzzetti, F.; Reichenbach, P.; Rossi, M.; Cardinali, M.; Ardizzone, F. Semi-automatic recognition and mapping of rainfall induced shallow landslides using optical satellite images. Remote Sens. Environ. 2011, 115, 1743–1757. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, C.; Meng, Y.; Chen, J.; Yue, A.; Li, Z.; Shi, W.; Lu, P.; Yan, L.; Wang, Q.; et al. Landslide mapping from aerial photographs using change detection-based Markov random field. Remote Sens. Environ. 2016, 187, 76–90. [Google Scholar]
- Julien, Y.; Sobrino, J.A. Optimizing and comparing gap-filling techniques using simulated NDVI time series from remotely sensed global data. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 93–111. [Google Scholar] [CrossRef]
- Padhee, S.K.; Dutta, S. Spatio-temporal reconstruction of MODIS NDVI by regional land surface phenology and harmonic analysis of time-series. GISci. Remote Sens. 2019, 56, 1261–1288. [Google Scholar] [CrossRef]
- Xu, L.; Yang, J.; Li, S.; Li, X. The reconstruction of NDVI time series using spatio-temporal information. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H.; Wu, Z.; Zhao, J.; Zhang, Z. Comparison and evaluation of annual NDVI time series in China derived from the NOAA AVHRR LTDR and terra MODIS MOD13C1 products. Sensors 2017, 17, 1298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buheaosier; Tsuchiya, K.; Kaneko, M.; Sung, S.J. Comparison of image data acquired with AVHRR, MODIS, ETM + and ASTER over Hokkaido, Japan. Adv. Sp. Res. 2003, 32, 2211–2216. [Google Scholar] [CrossRef]
- Gallo, K.; Ji, L.; Reed, B.; Eidenshink, J.; Dwyer, J. Multi-platform comparisons of MODIS and AVHRR normalized difference vegetation index data. Remote Sens. Environ. 2005, 99, 221–231. [Google Scholar] [CrossRef] [Green Version]
- Miura, T.; Huete, A.R.; Didan, K.; van Leeuwen, W.J.D.; Yoshioka, H. An assessment of the MODIS vegetation index compositing algorithm using quality assurance flags and sun/view angles. In Proceedings of the IGARSS 2000: IEEE 2000 International Geoscience and Remote Sensing Symposium, Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment (Cat. No. 00CH37120), Honolulu, HI, USA, 24–28 July 2000; Volume 2, pp. 545–547. [Google Scholar]
- Asner, G.P. Cloud cover in Landsat observations of the Brazilian Amazon. Int. J. Remote Sens. 2001, 22, 3855–3862. [Google Scholar] [CrossRef]
- Ju, J.; Roy, D.P. The availability of cloud-free Landsat ETM + data over the conterminous United States and globally. Remote. Sens. Environ. 2008, 112, 1196–1211. [Google Scholar] [CrossRef]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat data continuity mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Mancino, G.; Ferrara, A.; Padula, A.; Nolè, A. Cross-comparison between Landsat 8 (OLI) and Landsat 7 (ETM+) derived vegetation indices in a Mediterranean Environment. Remote Sens. 2020, 12, 291. [Google Scholar] [CrossRef] [Green Version]
- Thenkabail, P.S. Inter-sensor relationships between IKONOS and Landsat-7 ETM+ NDVI data in three ecoregions of Africa. Int. J. Remote Sens. 2004, 25, 389–408. [Google Scholar] [CrossRef]


| Sensors/Model | Temporal Resolution (day) | Spatial Resolution (m) | Bands | Data Source |
|---|---|---|---|---|
| NOAA-AVHRR-NDVI-V5 | 1 | 0.05° | NDVI | http://ltdr.nascom.nasa.gov (accessed on 10 July 2020 from GEE) |
| MYD13Q1 | 16 | 250 | NDVI | https://lpdaac.usgs.gov/products/myd13q1v006/ (accessed on 10 July 2020 from GEE) |
| MOD13Q1 | 16 | 250 | NDVI | https://lpdaac.usgs.gov/products/mod13q1v006/ (accessed on 10 July 2020 from GEE) |
| Landsat 7 | 16 | 30 | NIR, R | http://landsat.usgs.gov/CDR_LSR (accessed on 10 July 2020 from GEE) |
| Landsat 8 | 16 | 30 | NIR, R | http://landsat.usgs.gov/CDR_LSR (accessed on 10 July 2020 from GEE) |
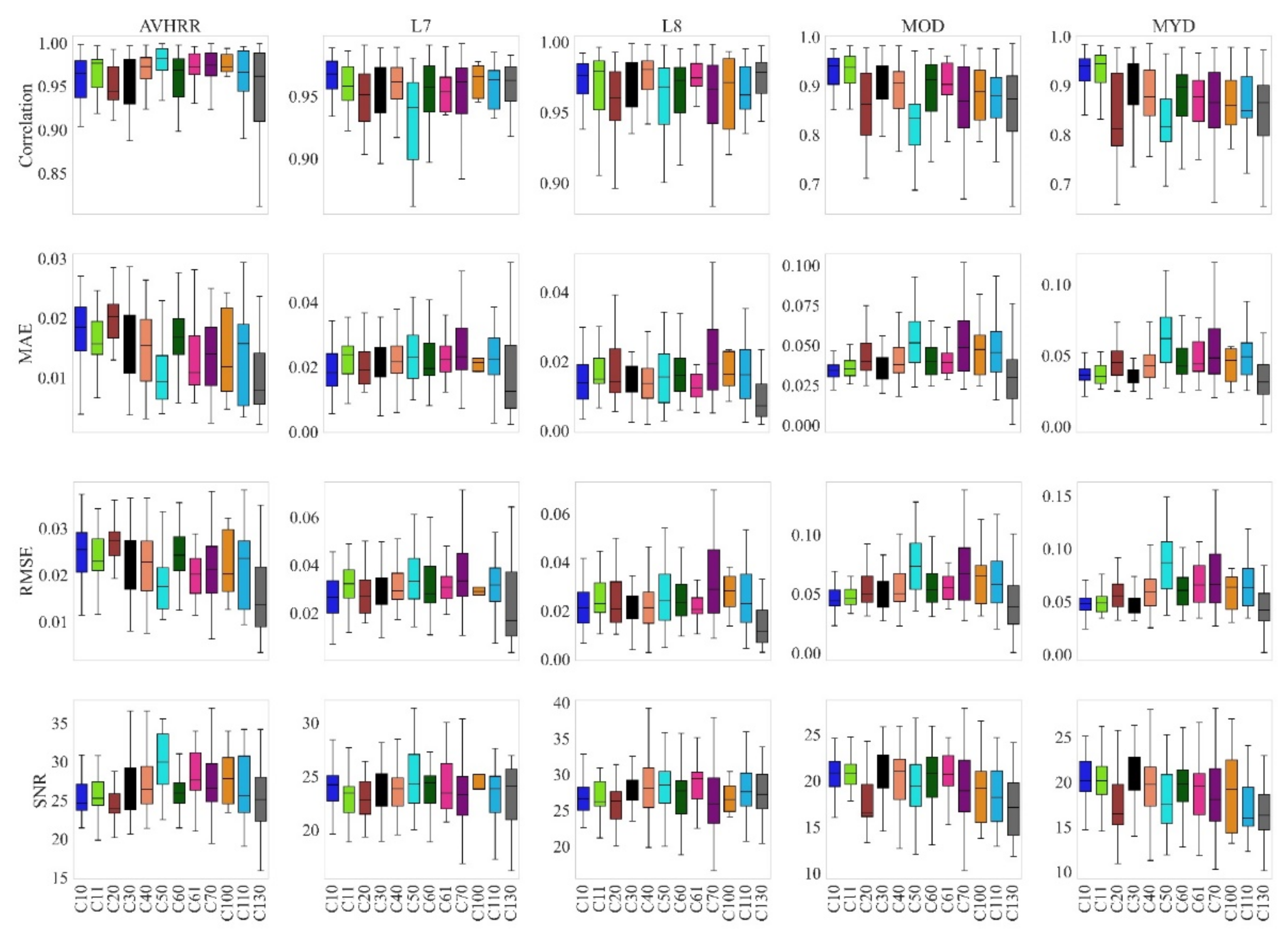
| Landcover Codes (LCC) | LC (%) | MOD13Q1 | MYD13Q1 | AVHRR | ETM+ | OLI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | CC | SNR | RMSE | CC | SNR | RMSE | CC | SNR | RMSE | CC | SNR | RMSE | CC | SNR | ||
| Cropland, rainfed (10) | 8.90 | 0.043 | 0.941 | 20.505 | 0.048 | 0.939 | 20.299 | 0.025 | 0.965 | 25.423 | 0.026 | 0.967 | 24.081 | 0.021 | 0.976 | 27.092 |
| Herbaceous cover (11) | 3.56 | 0.046 | 0.937 | 20.434 | 0.048 | 0.944 | 20.292 | 0.022 | 0.976 | 26.054 | 0.032 | 0.957 | 22.877 | 0.023 | 0.979 | 26.630 |
| Cropland, irrigated (20) | 3.07 | 0.049 | 0.863 | 18.161 | 0.055 | 0.812 | 17.091 | 0.027 | 0.944 | 24.201 | 0.026 | 0.951 | 22.613 | 0.020 | 0.96 | 25.826 |
| Mosaic cropland (30) | 7.28 | 0.048 | 0.919 | 20.634 | 0.047 | 0.913 | 20.210 | 0.022 | 0.966 | 26.448 | 0.025 | 0.958 | 23.717 | 0.021 | 0.971 | 27.839 |
| Mosaic natural vegetation (40) | 15.37 | 0.050 | 0.905 | 20.156 | 0.058 | 0.877 | 19.556 | 0.022 | 0.973 | 27.332 | 0.029 | 0.961 | 23.635 | 0.021 | 0.980 | 28.354 |
| Tree cover, broadleaved, evergreen (50) | 6.95 | 0.073 | 0.834 | 19.402 | 0.086 | 0.816 | 18.170 | 0.017 | 0.982 | 30.075 | 0.033 | 0.94 | 24.721 | 0.024 | 0.968 | 29.142 |
| Deciduous closed to open (60) | 8.09 | 0.053 | 0.912 | 20.368 | 0.060 | 0.898 | 19.618 | 0.024 | 0.969 | 26.265 | 0.028 | 0.957 | 23.898 | 0.023 | 0.972 | 27.202 |
| Broadleaved, deciduous, closed (61) | 3.56 | 0.055 | 0.903 | 20.448 | 0.065 | 0.877 | 19.061 | 0.020 | 0.973 | 28.246 | 0.030 | 0.953 | 24.626 | 0.020 | 0.974 | 29.102 |
| Needle-leaved, evergreen, closed to open (70) | 22.97 | 0.067 | 0.869 | 19.263 | 0.066 | 0.865 | 18.491 | 0.021 | 0.974 | 27.452 | 0.033 | 0.961 | 23.653 | 0.028 | 0.966 | 26.393 |
| Mosaic tree and shrub/herbaceous (100) | 1.45 | 0.065 | 0.888 | 19.100 | 0.063 | 0.86 | 19.107 | 0.020 | 0.972 | 28.112 | 0.029 | 0.965 | 25.330 | 0.028 | 0.971 | 25.821 |
| Mosaic herbaceous/tree and shrub (110) | 5.17 | 0.058 | 0.88 | 18.143 | 0.063 | 0.849 | 17.409 | 0.023 | 0.966 | 26.937 | 0.031 | 0.963 | 23.864 | 0.022 | 0.962 | 27.762 |
| Grassland (130) | 13.26 | 0.039 | 0.873 | 17.581 | 0.042 | 0.865 | 16.763 | 0.013 | 0.961 | 25.350 | 0.016 | 0.962 | 23.216 | 0.011 | 0.978 | 26.855 |
| Overall Performance | 0.052 | 0.894 | 19.724 | 0.055 | 0.879 | 18.955 | 0.021 | 0.972 | 26.236 | 0.030 | 0.96 | 23.562 | 0.022 | 0.973 | 27.220 | |
| Performance Range ** | 0.048 | 0.148 | 7.006 | 0.052 | 0.154 | 7.139 | 0.036 | 0.151 | 7.636 | 0.076 | 0.374 | 5.935 | 0.083 | 0.208 | 8.290 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sajadi, P.; Sang, Y.-F.; Gholamnia, M.; Bonafoni, S.; Brocca, L.; Pradhan, B.; Singh, A. Performance Evaluation of Long NDVI Timeseries from AVHRR, MODIS and Landsat Sensors over Landslide-Prone Locations in Qinghai-Tibetan Plateau. Remote Sens. 2021, 13, 3172. https://doi.org/10.3390/rs13163172
Sajadi P, Sang Y-F, Gholamnia M, Bonafoni S, Brocca L, Pradhan B, Singh A. Performance Evaluation of Long NDVI Timeseries from AVHRR, MODIS and Landsat Sensors over Landslide-Prone Locations in Qinghai-Tibetan Plateau. Remote Sensing. 2021; 13(16):3172. https://doi.org/10.3390/rs13163172
Chicago/Turabian StyleSajadi, Payam, Yan-Fang Sang, Mehdi Gholamnia, Stefania Bonafoni, Luca Brocca, Biswajeet Pradhan, and Amit Singh. 2021. "Performance Evaluation of Long NDVI Timeseries from AVHRR, MODIS and Landsat Sensors over Landslide-Prone Locations in Qinghai-Tibetan Plateau" Remote Sensing 13, no. 16: 3172. https://doi.org/10.3390/rs13163172
APA StyleSajadi, P., Sang, Y.-F., Gholamnia, M., Bonafoni, S., Brocca, L., Pradhan, B., & Singh, A. (2021). Performance Evaluation of Long NDVI Timeseries from AVHRR, MODIS and Landsat Sensors over Landslide-Prone Locations in Qinghai-Tibetan Plateau. Remote Sensing, 13(16), 3172. https://doi.org/10.3390/rs13163172










