Assessment of Empirical Algorithms for Shallow Water Bathymetry Using Multi-Spectral Imagery of Pearl River Delta Coast, China
Abstract
:1. Introduction
2. Study Area and Data
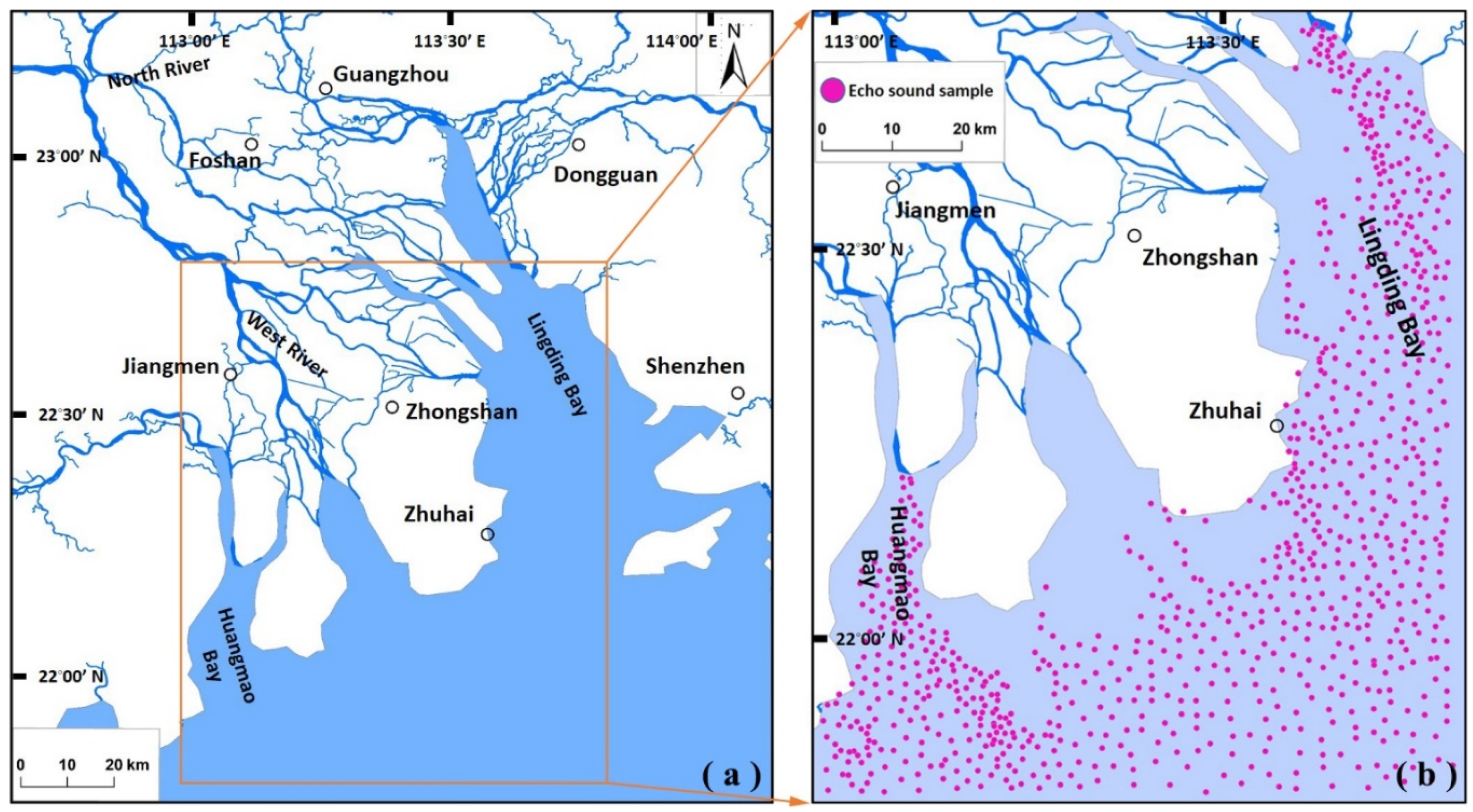
2.1. Study Area
2.2. In Situ Bathymetry Data
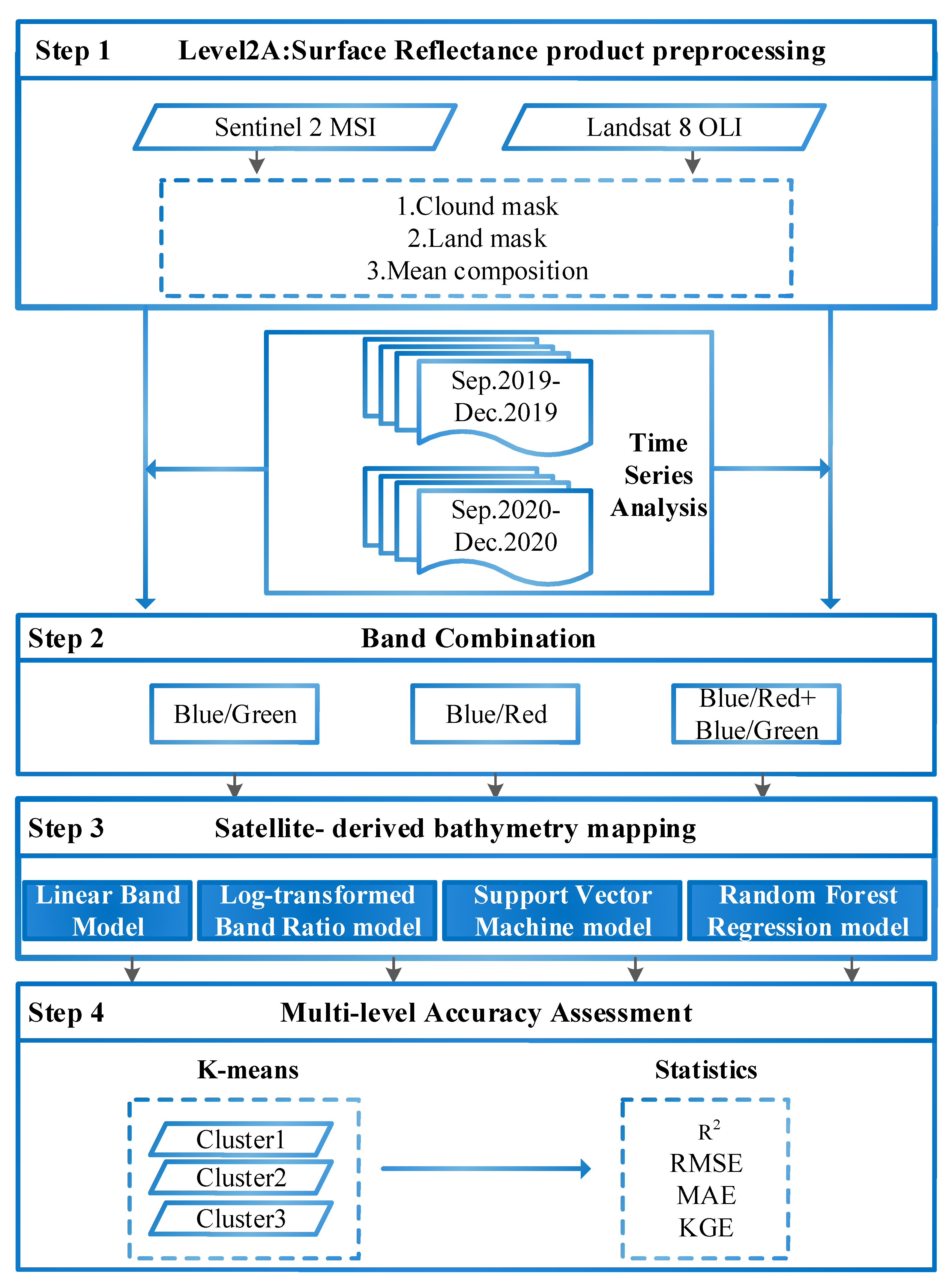
2.3. Satellite Data and Pre-Processing
3. Methodology
3.1. K-Means Clustering
3.2. Linear Band Model (LBM)
3.3. Log-Transformed Band Ratio Model (BRM)
3.4. Non-Linear Regression Model
3.5. Accuracy Assessment
4. Results
4.1. Bathymetry Estimates with/without Clustering
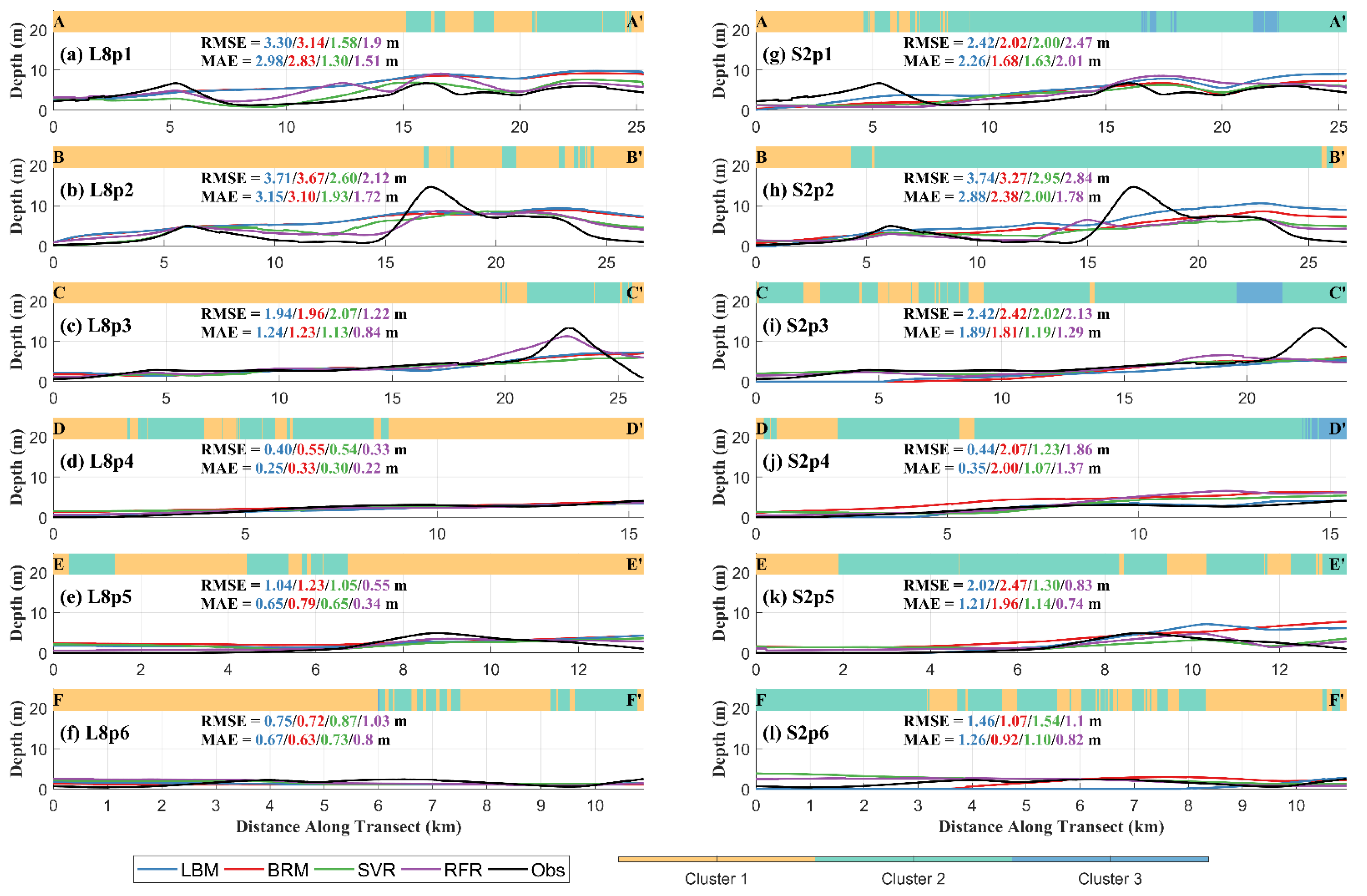
4.2. Bathymetry Estimates in Different Clusters
5. Discussion
5.1. Performance of Different Estimation Strategies
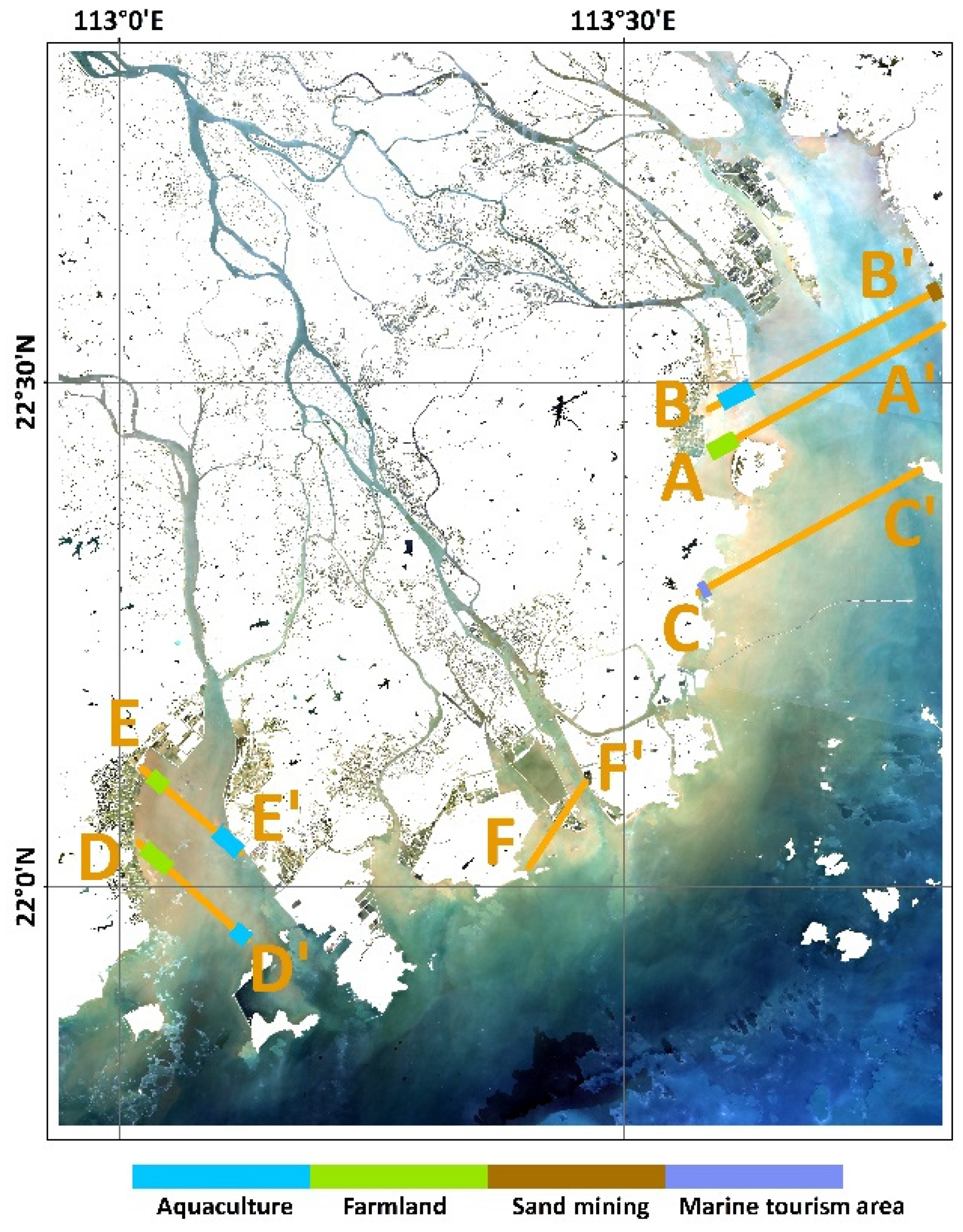
5.2. Influential Factors on the Spectral Information
5.3. Other Sources of Uncertainty
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The state of the world’s beaches. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef]
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geogr. 2009, 33, 103–116. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Zhao, G.; Tseng, K.-H. A high-resolution bathymetry dataset for global reservoirs using multi-source satellite imagery and altimetry. Remote Sens. Environ. 2020, 244, 111831. [Google Scholar] [CrossRef]
- Williams, R.; Brasington, J.; Vericat, D.; Hicks, M.; Labrosse, F.; Nealf, M. Monitoring braided river change using terrestrial laser scanning and optical bathymetric mapping. Dev. Earth Surf. Process. 2011, 15, 507–532. [Google Scholar] [CrossRef]
- Lurton, X. Swath bathymetry using phase difference: Theoretical analysis of acoustical measurement precision. IEEE J. Ocean. Eng. 2000, 25, 351–363. [Google Scholar] [CrossRef]
- Schmitt, T.; Mitchell, N.C.; Ramsay, A.T.S. Characterizing uncertainties for quantifying bathymetry change between time-separated multibeam echo-sounder surveys. Cont. Shelf Res. 2008, 28, 1166–1176. [Google Scholar] [CrossRef]
- Yan, Z.L.; Qin, L.L.; Wang, R.; Li, J.; Wang, X.-M.; Tang, X.-L.; An, R.-D. The application of a multi-beam echo-sounder in the analysis of the sedimentation situation of a large reservoir after an earthquake. Water 2018, 10, 557. [Google Scholar] [CrossRef] [Green Version]
- Calkoen, C.J.; Hesselmans, G.H.F.M.; Wensink, G.J.; Vogelzang, J. The bathymetry assessment system: Efficient depth mapping in shallow seas using radar images. Int. J. Remote Sens. 2001, 22, 2973–2998. [Google Scholar] [CrossRef]
- Eugenio, F.; Marcello, J.; Martin, J. High-resolution maps of bathymetry and benthic habitats in shallow-water environments using multispectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3539–3549. [Google Scholar] [CrossRef]
- Lyons, M.; Phinn, S.; Roelfsema, C. Integrating Quickbird multi-spectral satellite and field data: Mapping bathymetry, seagrass cover, seagrass species and change in Moreton Bay, Australia in 2004 and 2007. Remote Sens. 2011, 3, 42–64. [Google Scholar] [CrossRef] [Green Version]
- Pattanaik, A.; Sahu, K.; Bhutiyani, M.R. Estimation of shallow water bathymetry using IRS-multispectral imagery of Odisha coast, India. Aquat. Procedia 2015, 4, 173–181. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Halls, J.; Costin, K. Submerged and emergent land cover and bathymetric mapping of estuarine habitats using WorldView-2 and LiDAR imagery. Remote Sens. 2016, 8, 718. [Google Scholar] [CrossRef] [Green Version]
- Jawak, S.D.; Vadlamani, S.S.; Luis, A.J. A Synoptic review on deriving bathymetry information using remote sensing technologies: Models, methods and comparisons. Adv. Remote Sens. 2015, 4, 147–162. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Botter, G.; Jawitz, J.W.; Rao, P.S.C. Stochastic modeling of hydrologic variability of geographically isolated wetlands: Effects of hydro-climatic forcing and wetland bathymetry. Adv. Water Resour. 2014, 69, 38–48. [Google Scholar] [CrossRef]
- Lesser, M.P.; Mobley, C.D. Bathymetry, water optical properties, and benthic classification of coral reefs using hyperspectral remote sensing imagery. Coral Reefs 2007, 26, 819–829. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Roberts, D.A. A forward image model for passive optical remote sensing of river bathymetry. Remote Sens. Environ. 2009, 113, 1025–1045. [Google Scholar] [CrossRef]
- Manessa, M.D.M.; Haidar, M.; Hartuti, M.; Kresnawati, D.K. Determination of the best methodology for bathymetry mapping using SPOT 6 imagery: A study of 12 empirical algorithms. Int. J. Remote Sens. Earth Sci. 2018, 14, 127. [Google Scholar] [CrossRef] [Green Version]
- Hamylton, S.; Hedley, J.; Beaman, R. Derivation of high-resolution bathymetry from multispectral satellite imagery: A comparison of empirical and optimisation methods through geographical error analysis. Remote Sens. 2015, 7, 16257–16273. [Google Scholar] [CrossRef] [Green Version]
- Flener, C.; Lotsari, E.; Alho, P.; Käyhkö, J. Comparison of empirical and theoretical remote sensing based bathymetry models in river environments. River Res. Appl. 2012, 28, 118–133. [Google Scholar] [CrossRef]
- Gholamalifard, M.; Kutser, T.; Esmaili-Sari, A.; Abkar, A.A.; Naimi, B. Remotely sensed empirical modeling of bathymetry in the Southeastern Caspian Sea. Remote Sens. 2013, 5, 2746. [Google Scholar] [CrossRef] [Green Version]
- Cahalane, C.; Magee, A.; Monteys, X.; Casal, G.; Hanafin, J.; Harris, P. A comparison of Landsat 8, RapidEye and Pleiades products for improving empirical predictions of satellite-derived bathymetry. Remote Sens. Environ. 2019, 233, 111414. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Traganos, D.; Reinartz, P. Interannual change detection of Mediterranean seagrasses using RapidEye image time series. Front. Plant Sci. 2018, 9, 96. [Google Scholar] [CrossRef] [Green Version]
- Bramante, J.F.; Raju, D.K.; Sin, T.M. Multispectral derivation of bathymetry in Singapore’s shallow, turbid waters. Int. J. Remote Sens. 2013, 34, 2070–2088. [Google Scholar] [CrossRef]
- Mcintyre, M.L.; Naar, D.F.; Carder, K.L.; Donahue, B.T.; Mallinson, D.J. Coastal bathymetry from hyperspectral remote sensing data: Comparisons with high resolution multibeam bathymetry. Mar. Geophys. Res. 2006, 27, 129–136. [Google Scholar] [CrossRef]
- Purkis, S.J.; Gleason, A.C.R.; Purkis, C.R.; Dempsey, A.C.; Renaud, P.G.; Faisal, M.; Saul, S.; Kerr, J.M. High-resolution habitat and bathymetry maps for 65,000 sq. km of Earth’s remotest coral reefs. Coral Reefs. 2019, 38, 467–488. [Google Scholar] [CrossRef] [Green Version]
- Jawak, S.D.; Luis, A.J. High-resolution multispectral satellite imagery for extracting bathymetric information of Antarctic shallow lakes. Remote Sens. 2016, 9878, 987819. [Google Scholar] [CrossRef]
- Misra, A.; Ramakrishnan, B. Assessment of coastal geomorphological changes using multi-temporal satellite-derived bathymetry. Cont. Shelf Res. 2020, 207, 104213. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.; Brando, V.; Giardino, C.; Kutser, T.; Phinn, S.; Mumby, P.J.; Barrilero, O.; Laporte, J.; Koetz, B. Coral reef applications of Sentinel-2: Coverage, characteristics, bathymetry and benthic mapping with comparison to Landsat 8. Remote Sens. Environ. 2018, 216, 598–614. [Google Scholar] [CrossRef]
- Roy, D.P.; Li, J.; Zhang, H.K.; Yan, L.; Huang, H.; Li, Z. Examination of Sentinel-2A multi-spectral instrument (MSI) reflectance anisotropy and the suitability of a general method to normalize MSI reflectance to nadir BRDF adjusted reflectance. Remote Sens. Environ. 2017, 199, 25–38. [Google Scholar] [CrossRef]
- Albright, A.; Glennie, C. Nearshore bathymetry from fusion of Sentinel-2 and ICESat-2 observations. IEEE Geosci. Remote Sens. Lett. 2020, 18, 900–904. [Google Scholar] [CrossRef]
- Evagorou, E.; Mettas, C.; Agapiou, A.; Themistocleous, K.; Hadjimitsis, D. Bathymetric maps from multi-temporal analysis of Sentinel-2 data: The case study of Limassol, Cyprus. Adv. Geosci. 2019, 45, 397–407. [Google Scholar] [CrossRef] [Green Version]
- Giardino, C.; Brando, V.E.; Gege, P.; Pinnel, N.; Hochberg, E.; Knaeps, E.; Reusen, I.; Doerffer, R.; Bresciani, M.; Braga, F.; et al. Dekker Imaging spectrometry of inland and coastal waters: State of the art, achievements and perspectives. Surv. Geophys. 2019, 40, 401–429. [Google Scholar] [CrossRef] [Green Version]
- Caballero, I.; Stumpf, R.P. Retrieval of nearshore bathymetry from Sentinel-2A and 2B satellites in South Florida coastal waters. Estuar. Coast. Shelf Sci. 2019, 226, 106277. [Google Scholar] [CrossRef]
- Mao, Q.; Shi, P.; Yin, K.; Gan, J.; Qi, Y. Tides and tidal currents in the Pearl River Estuary. Cont. Shelf Res. 2004, 24, 1797–1808. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, W.; Zhu, Y. Impact of trends in river discharge and ocean tides on water level dynamics in the Pearl River Delta. Coast. Eng. 2020, 157, 103634. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, P.; Hu, S.; Cai, H.; Fu, L.; Liu, F.; Yang, Q. Tidal regime shift in Lingdingyang Bay, the Pearl River Delta: An identification and assessment of driving factors. Hydrol. Process. 2020, 34, 2878–2894. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, Ó. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef] [Green Version]
- Kerr, J.M.; Purkis, S. An algorithm for optically-deriving water depth from multispectral imagery in coral reef landscapes in the absence of ground-truth data. Remote Sens. Environ. 2018, 210, 307–324. [Google Scholar] [CrossRef]
- Liceaga-Correa, M.A.; Euan-Avila, J.I. Assessment of coral reef bathymetric mapping using visible Landsat thematic mapper data. Int. J. Remote Sens. 2002, 23, 3–14. [Google Scholar] [CrossRef]
- Sagawa, T.; Yamashita, Y.; Okumura, T.; Yamanokuchi, T. Satellite derived bathymetry using machine learning and multi-temporal satellite images. Remote Sens. 2019, 11, 1155. [Google Scholar] [CrossRef] [Green Version]
- Hedley, J.; Roelfsema, C.; Koetz, B.; Phinn, S. Capability of the Sentinel 2 mission for tropical coral reef mapping and coral bleaching detection. Remote Sens. Environ. 2012, 20, 145–155. [Google Scholar] [CrossRef]
- Hodúl, M.; Bird, S.; Knudby, A.; Chénier, R. Satellite derived photogrammetric bathymetry. ISPRS J. Photogramm. Remote Sens. 2018, 142, 268–277. [Google Scholar] [CrossRef]
- Heylen, R.; Parente, M.; Gader, P. A review of nonlinear hyperspectral unmixing methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Drakopoulou, P.; Kapsimalis, V.; Parcharidis, I.; Pavlopoulos, K. Retrieval of nearshore bathymetry in the Gulf of Chania, NW Crete, Greece, from WorldWiew-2 multispectral imagery. Remote Sens. Geoinf. Environ. 2018, 10773, 54. [Google Scholar] [CrossRef]
- Acharya, P.K.; Adler-Golden, S.M.; Berk, A.; Bernstein, L.S. Bathymetry of the littoral zone using hyperspectral images. Imaging Spectrom. VIII 2002, 4816, 164. [Google Scholar] [CrossRef]
- Monteys, X.; Harris, P.; Caloca, S.; Cahalane, C. Spatial prediction of coastal bathymetry based on multispectral satellite imagery and multibeam data. Remote Sens. 2015, 7, 13782–13806. [Google Scholar] [CrossRef] [Green Version]
- Casal, G.; Monteys, X.; Hedley, J.; Harris, P.; Cahalane, C.; McCarthy, T. Assessment of empirical algorithms for bathymetry extraction using Sentinel-2 data. Int. J. Remote Sens. 2019, 40, 2855–2879. [Google Scholar] [CrossRef]
- Lafon, V.; Froidefond, J.M.; Lahet, F.; Castaing, P. SPOT shallow water bathymetry of a moderately turbid tidal inlet based on field measurements. Remote Sens. Environ. 2002, 81, 136–148. [Google Scholar] [CrossRef]
- Goodman, J.A.; Lay, M.; Ramirez, L.; Ustin, S.L.; Haverkamp, P.J. Confidence levels, sensitivity, and the role of bathymetry in coral reef remote sensing. Remote Sens. 2020, 12, 496. [Google Scholar] [CrossRef] [Green Version]


| L8 | S2 | |
|---|---|---|
| Swath width | 185 km | 290 km |
| Spatial resolution | 30 m | 10 m |
| Revisit interval | 8 days | 5 days |
| Temporal coverage | 11/02/2013–present | 23/06/2015–present |
| Spectral bands used | Red (636–673 nm) | Red (664.5–665 nm) |
| Green (533–590 nm) | Green (559–560 nm) | |
| Blue (452–512 nm) | Blue (492.1–496.6 nm) | |
| Image volume processed | 8 images (2019) | 46 images (2019) |
| 8 images (2020) | 26 images (2020) |
| 2019.9–2019.11 | Landsat 8 | Sentinel-2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | Clustering | Bands | R2 | RMSE | MAE | KGE | R2 | RMSE | MAE | KGE |
| LBM | Y | B + G | 0.85 | 3.21 | 2.40 | 0.88 | 0.76 | 3.77 | 2.85 | 0.83 |
| B + R + G | 0.85 | 3.18 | 2.38 | 0.88 | 0.76 | 3.75 | 2.84 | 0.83 | ||
| N | B + G | 0.79 | 3.67 | 2.96 | 0.84 | 0.74 | 4.08 | 3.11 | 0.80 | |
| B + R + G | 0.80 | 3.63 | 2.92 | 0.85 | 0.74 | 4.13 | 3.22 | 0.80 | ||
| BRM | Y | B/G | 0.84 | 3.24 | 2.41 | 0.60 | 0.77 | 3.74 | 2.77 | 0.83 |
| B/R | 0.82 | 3.46 | 2.51 | 0.70 | 0.59 | 4.96 | 3.72 | 0.69 | ||
| B/G + B/R | 0.85 | 3.21 | 2.39 | 0.66 | 0.78 | 3.65 | 2.63 | 0.84 | ||
| N | B/G | 0.76 | 3.92 | 3.10 | 0.84 | 0.71 | 4.29 | 3.25 | 0.80 | |
| B/R | 0.67 | 4.60 | 3.79 | 0.77 | 0.47 | 5.84 | 4.50 | 0.59 | ||
| B/G + B/R | 0.77 | 3.89 | 3.12 | 0.85 | 0.75 | 4.04 | 3.03 | 0.82 | ||
| SVR | Y | B/G | 0.85 | 3.22 | 2.25 | 0.92 | 0.79 | 3.54 | 2.30 | 0.83 |
| B/R | 0.83 | 3.41 | 2.37 | 0.88 | 0.65 | 4.55 | 3.00 | 0.69 | ||
| B/G + B/R | 0.86 | 3.01 | 1.95 | 0.92 | 0.78 | 3.64 | 2.28 | 0.84 | ||
| N | B/G | 0.79 | 3.53 | 2.75 | 0.87 | 0.76 | 3.57 | 2.38 | 0.86 | |
| B/R | 0.79 | 3.55 | 2.62 | 0.87 | 0.62 | 4.48 | 2.92 | 0.64 | ||
| B/G + B/R | 0.80 | 3.48 | 2.64 | 0.90 | 0.77 | 3.48 | 2.32 | 0.89 | ||
| RFR | Y | B/G | 0.92 | 2.39 | 1.54 | 0.95 | 0.88 | 2.70 | 1.83 | 0.89 |
| B/R | 0.91 | 2.46 | 1.67 | 0.94 | 0.80 | 3.46 | 2.38 | 0.84 | ||
| B/G + B/R | 0.92 | 2.27 | 1.45 | 0.95 | 0.91 | 2.35 | 1.54 | 0.91 | ||
| N | B/G | 0.73 | 4.03 | 3.01 | 0.90 | 0.74 | 3.68 | 2.50 | 0.90 | |
| B/R | 0.77 | 3.71 | 2.75 | 0.89 | 0.52 | 5.03 | 3.53 | 0.79 | ||
| B/G + B/R | 0.77 | 3.73 | 2.73 | 0.91 | 0.76 | 3.55 | 2.43 | 0.91 | ||
| 2020.9–2020.11 | Landsat 8 | Sentinel-2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | Clustering | Bands | R2 | RMSE | MAE | KGE | R2 | RMSE | MAE | KGE |
| LBM | Y | B + G | 0.72 | 4.40 | 3.39 | 0.78 | 0.73 | 4.23 | 3.31 | 0.80 |
| B + R + G | 0.74 | 4.26 | 3.32 | 0.79 | 0.77 | 3.89 | 2.98 | 0.83 | ||
| N | B/G | 0.54 | 5.42 | 4.38 | 0.68 | 0.70 | 4.41 | 3.51 | 0.79 | |
| B + R + G | 0.60 | 5.07 | 4.16 | 0.68 | 0.72 | 4.22 | 3.31 | 0.81 | ||
| BRM | Y | B/G | 0.73 | 4.33 | 3.29 | 0.60 | 0.72 | 4.32 | 3.44 | 0.79 |
| B/R | 0.62 | 5.18 | 4.08 | 0.70 | 0.50 | 5.77 | 4.65 | 0.60 | ||
| B/G + B/R | 0.76 | 4.14 | 3.28 | 0.66 | 0.77 | 3.86 | 2.95 | 0.83 | ||
| N | B/G | −0.15 | 8.59 | 6.06 | 0.33 | 0.67 | 4.60 | 3.75 | 0.77 | |
| B/R | 0.56 | 5.29 | 4.13 | 0.70 | 0.43 | 6.04 | 4.68 | 0.57 | ||
| B/G + B/R | 0.44 | 6.03 | 4.32 | 0.72 | 0.72 | 4.23 | 3.49 | 0.80 | ||
| SVR | Y | B/G | 0.75 | 4.15 | 2.94 | 0.85 | 0.75 | 4.11 | 2.89 | 0.79 |
| B/R | 0.64 | 5.06 | 3.75 | 0.69 | 0.51 | 5.72 | 4.04 | 0.59 | ||
| B/G + B/R | 0.81 | 3.64 | 2.66 | 0.86 | 0.76 | 3.96 | 2.77 | 0.82 | ||
| N | B/G | 0.30 | 6.70 | 5.19 | 0.28 | 0.70 | 4.14 | 2.98 | 0.81 | |
| B/R | 0.61 | 4.99 | 3.76 | 0.70 | 0.46 | 5.50 | 4.06 | 0.62 | ||
| B/G + B/R | 0.80 | 3.60 | 2.76 | 0.85 | 0.73 | 3.89 | 2.68 | 0.62 | ||
| RFR | Y | B/G | 0.86 | 3.08 | 2.18 | 0.90 | 0.87 | 2.98 | 2.13 | 0.88 |
| B/R | 0.78 | 3.91 | 2.75 | 0.82 | 0.70 | 4.43 | 3.08 | 0.77 | ||
| B/G + B/R | 0.91 | 2.44 | 1.70 | 0.93 | 0.91 | 2.49 | 1.66 | 0.90 | ||
| N | B/G | 0.17 | 7.30 | 5.51 | 0.56 | 0.71 | 4.08 | 3.02 | 0.88 | |
| B/R | 0.58 | 5.17 | 3.89 | 0.78 | 0.40 | 5.84 | 4.24 | 0.75 | ||
| B/G + B/R | 0.79 | 3.70 | 2.84 | 0.89 | 0.76 | 3.66 | 2.63 | 0.91 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, C.; Zhao, Q.; Lu, Y.; Fu, D. Assessment of Empirical Algorithms for Shallow Water Bathymetry Using Multi-Spectral Imagery of Pearl River Delta Coast, China. Remote Sens. 2021, 13, 3123. https://doi.org/10.3390/rs13163123
Wei C, Zhao Q, Lu Y, Fu D. Assessment of Empirical Algorithms for Shallow Water Bathymetry Using Multi-Spectral Imagery of Pearl River Delta Coast, China. Remote Sensing. 2021; 13(16):3123. https://doi.org/10.3390/rs13163123
Chicago/Turabian StyleWei, Chunzhu, Qianying Zhao, Yang Lu, and Dongjie Fu. 2021. "Assessment of Empirical Algorithms for Shallow Water Bathymetry Using Multi-Spectral Imagery of Pearl River Delta Coast, China" Remote Sensing 13, no. 16: 3123. https://doi.org/10.3390/rs13163123
APA StyleWei, C., Zhao, Q., Lu, Y., & Fu, D. (2021). Assessment of Empirical Algorithms for Shallow Water Bathymetry Using Multi-Spectral Imagery of Pearl River Delta Coast, China. Remote Sensing, 13(16), 3123. https://doi.org/10.3390/rs13163123







