Semantic Segmentation of Large-Scale Outdoor Point Clouds by Encoder–Decoder Shared MLPs with Multiple Losses
Abstract
:1. Introduction
- We propose a simple, and yet effective, strategy of the above aforementioned mechanisms, such as a random point sampling, attention-based pooling, and multiple losses summation integrated with the encoder–decoder shared MLPs method, for the large-scale outdoor point clouds semantic segmentation;
- We proof that our method performs good results and has a lower computational cost than PointNet++ [11].
2. Related Works
2.1. Point-Wise MLPs Method
2.2. Point Convolution Method
2.3. Graph-Based Method
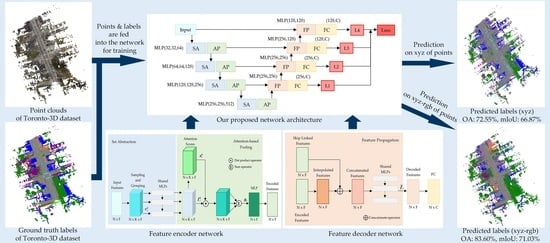
3. Methodology
3.1. Network Architecture
3.2. Feature Encoding Network
3.2.1. Sampling Layer
3.2.2. Grouping Layer
3.2.3. Shared MLPs Layer
3.2.4. Attention-Based Pooling Layer
3.3. Feature Decoding Network
3.4. Multiple Loss Scores
4. Experiments
4.1. Experimental Setup
4.2. Datasets
4.2.1. Toronto-3D Dataset
4.2.2. DALES Dataset
4.3. Data Pre-Processing
5. Results
5.1. Evaluation Metrics
5.2. Results on Toronto-3D Dataset
5.3. Results on DALES Dataset
6. Discussion
6.1. Discussion on Toronto-3D Dataset
6.2. Discussion on DALES Dataset
6.3. Discussion on Computational Cost
6.4. Effect of Our Proposed Mechanism
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A-CNN | Annular convolution neural network |
| AFA | Adaptive feature adjustment |
| AP | Attention-based pooling |
| CNN | Convolutional neural network |
| ConvPoint | Convolutional point |
| DGCNN | Dynamic graph convolutional neural network |
| DL | Deep learning |
| DPAM | Dynamic point agglomeration |
| DPC | Dilated point convolution |
| FC | Fully connected layer |
| FN | False negative |
| FP | Feature propagation |
| FP | False positive |
| FPS | Farthest point sampling |
| GACNet | Graph attention convolution network |
| GRU | Gated recurrent unit |
| GSA | Group shuffle attention |
| HDGCN | Hierarchical depth-wise graph convolution network |
| InterpCNN | Interpolated convolutional neural network |
| KPConv | Kernel point convolution |
| LSANet | Local spatial awareness network |
| mIoU | mean intersection over union |
| MLPs | Multi-layer perceptrons |
| OA | Overall accuracy |
| PAG | Point atrous graph |
| PCCN | Point continuous convolution network |
| PointCNN | Point convolutional neural network |
| RandLA-net | Random and Large-scale network |
| RPS | Random point sampling |
| SA | Set abstraction |
| SPG | Super point graph |
| TP | True positive |
References
- Bello, S.A.; Yu, S.; Wang, C.; Adam, J.M.; Li, J. Review: Deep Learning on 3D point clouds. Remote. Sens. 2020, 12, 1729. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep Learning for 3D point clouds: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020. [Google Scholar] [CrossRef] [PubMed]
- Gwak, J.; Jung, J.; Oh, R.; Park, M.; Rakhimov, M.A.K.; Ahn, J. A review of intelligent self-driving vehicle software research. KSII Trans. Internet Inf. Syst. 2019, 13, 5299–5320. [Google Scholar] [CrossRef] [Green Version]
- Mu, R.; Zeng, X. A Review of Deep Learning research. KSII Trans. Internet Inf. Syst. 2019, 13, 1738–1764. [Google Scholar] [CrossRef]
- Jung, J.; Park, M.; Cho, K.; Mun, C.; Ahn, J. Intelligent hybrid fusion algorithm with vision patterns for generation of precise digital road maps in self-driving vehicles. KSII Trans. Internet Inf. Syst. 2020, 14, 3955–3971. [Google Scholar] [CrossRef]
- Yin, J.; Qu, J.; Huang, W.; Chen, Q. Road damage detection and classification based on multi-level feature pyramids. KSII Trans. Internet Inf. Syst. 2021, 15, 786–799. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, W.; Xing, W.; Wei, X. DA-Res2Net: A novel Densely connected residual attention network for image semantic segmentation. KSII Trans. Internet Inf. Syst. 2020, 14, 4426–4442. [Google Scholar] [CrossRef]
- Lawin, F.J.; Danelljan, M.; Tosteberg, P.; Bhat, G.; Khan, F.S.; Felsberg, M. Deep projective 3D semantic segmentation. In Computer Analysis of Images and Patterns; Felsberg, M., Heyden, A., Krüger, N., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 95–107. [Google Scholar]
- Meng, H.; Gao, L.; Lai, Y.; Manocha, D. VV-net: Voxel VAE net with group convolutions for point cloud segmentation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 8500–8508. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on point sets for 3D classification and segmentation. arXiv 2017, arXiv:1612.00593v2. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4 December 2017; pp. 5105–5114. [Google Scholar]
- Jiang, M.; Wu, Y.; Zhao, T.; Zhao, Z.; Lu, C. Pointsift: A sift-like network module for 3D point cloud semantic segmentation. arXiv 2018, arXiv:1807.00652. [Google Scholar]
- Engelmann, F.; Kontogianni, T.; Schult, J.; Leibe, B. Know What Your Neighbors Do: 3D Semantic Segmentation of Point Clouds. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8 September 2018. [Google Scholar]
- Zeng, W.; Gevers, T. 3DContextNet: Kd tree guided hierarchical learning of point clouds using local and global contextual cues. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8 September 2018. [Google Scholar]
- Xie, S.; Liu, S.; Chen, Z.; Tu, Z. Attentional ShapeContextNet for point cloud recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4606–4615. [Google Scholar]
- Zhao, H.; Jiang, L.; Fu, C.W.; Jia, J. Pointweb: Enhancing local neighborhood features for point cloud processing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 5565–5573. [Google Scholar]
- Yang, J.; Zhang, Q.; Ni, B.; Li, L.; Liu, J.; Zhou, M.; Tian, Q. Modeling Point Clouds with Self-Attention and Gumbel Subset Sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 3323–3332. [Google Scholar]
- Chen, L.Z.; Li, X.Y.; Fan, D.P.; Wang, K.; Lu, S.P.; Cheng, M.M. LSANet: Feature learning on point sets by local spatial aware layer. arXiv 2019, arXiv:1905.05442. [Google Scholar]
- Zhang, Z.; Hua, B.S.; Yeung, S.K. ShellNet: Efficient point cloud convolutional neural networks using concentric shells statistics. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 1607–1616. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual Conference, Seattle, WA, USA, 14–19 June 2020; pp. 11108–11117. Available online: https://www.youtube.com/channel/UC0n76gicaarsN_Y9YShWwhw (accessed on 18 June 2020).
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution on x-transformed points. Adv. Neural Inf. Process. Syst. 2018, 31, 820–830. [Google Scholar]
- Wang, S.; Suo, S.; Ma, W.C.; Pokrovsky, A.; Urtasun, R. Deep parametric continuous convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2589–2597. [Google Scholar]
- Komarichev, A.; Zhong, Z.; Hua, J. A-CNN: Annularly Convolutional Neural Networks on Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 7421–7430. [Google Scholar]
- Boulch, A. ConvPoint: Continuous convolutions for point cloud processing. Comput. Graph. 2020, 88, 24–34. [Google Scholar] [CrossRef] [Green Version]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. KPConv: Flexible and Deformable Convolution for Point Clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 6411–6420. [Google Scholar]
- Engelmann, F.; Kontogianni, T.; Leibe, B. Dilated point convolutions: On the receptive field size of point convolutions on 3D point clouds. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Virtual Conference, Paris, France, 31 May–31 August 2020; pp. 9463–9469. [Google Scholar]
- Mao, J.; Wang, X.; Li, H. Interpolated Convolutional Networks for 3D Point Cloud Understanding. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 1578–1587. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J. Dynamic graph CNN for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Landrieu, L.; Simonovsky, M. Large-scale point cloud semantic segmentation with superpoint graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4558–4567. [Google Scholar]
- Landrieu, L.; Boussaha, M. Point Cloud Oversegmentation with Graph-Structured Deep Metric Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 7440–7449. [Google Scholar]
- Wang, L.; Huang, Y.; Hou, Y.; Zhang, S.; Shan, J. Graph attention convolution for point cloud semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 10296–10305. [Google Scholar]
- Pan, L.; Chew, C.M.; Lee, G.H. PointAtrousGraph: Deep hierarchical encoder-decoder with point atrous convolution for unorganized 3D points. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Virtual Conference, Paris, France, 31 May—31 August 2020; pp. 1113–1120. Available online: https://www.ieee-ras.org/students/events/event/1144-icra-2020-ieee-international-conference-on-robotics-and-automation-icra/ (accessed on 30 June 2020).
- Liang, Z.; Yang, M.; Deng, L.; Wang, C.; Wang, B. Hierarchical depthwise graph convolutional neural network for 3D semantic segmentation of point clouds. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8152–8158. [Google Scholar]
- Jiang, L.; Zhao, H.; Liu, S.; Shen, X.; Fu, C.W.; Jia, J. Hierarchical Point-edge interaction network for point cloud semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 10433–10441. [Google Scholar]
- Lei, H.; Akhtar, N.; Mian, A. Spherical convolutional neural network for 3D point clouds. arXiv 2018, arXiv:1805.07872. [Google Scholar]
- Liu, J.; Ni, B.; Li, C.; Yang, J.; Tian, Q. Dynamic points agglomeration for hierarchical point sets learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 7546–7555. [Google Scholar]
- Tan, W.; Qin, N.; Ma, L.; Li, Y.; Du, J.; Cai, G.; Yang, K.; Li, J. Toronto-3D: A large-scale mobile lidar dataset for semantic segmentation of urban roadways. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPR), Virtual Conference, Seattle, WA, USA, 14–19 June 2020; pp. 202–203. Available online: https://www.youtube.com/channel/UC0n76gicaarsN_Y9YShWwhw (accessed on 18 June 2020).
- Varney, N.; Asari, V.K.; Graehling, Q. DALES: A large-scale aerial LiDAR data set for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPR), Virtual Conference, Seattle, WA, USA, 14–19 June 2020; pp. 186–187. Available online: https://www.youtube.com/channel/UC0n76gicaarsN_Y9YShWwhw (accessed on 18 June 2020).
- Yang, B.; Wang, S.; Markham, A.; Trigoni, N. Robust attentional aggregation of deep feature sets for multi-view 3D reconstruction. Int. J. Comput. Vis. 2020, 128, 53–73. [Google Scholar] [CrossRef] [Green Version]




| Set | Road | Road Marking | Natural | Building | Utility Line | Pole | Car | Fence | Unclassified | Total |
|---|---|---|---|---|---|---|---|---|---|---|
| Training | 35,503 | 1500 | 4626 | 18,234 | 579 | 742 | 3733 | 387 | 2733 | 68,037 |
| Testing | 6353 | 301 | 1942 | 866 | 84 | 155 | 199 | 24 | 360 | 10,284 |
| Total | 41,856 | 1801 | 6568 | 19,100 | 663 | 897 | 3932 | 411 | 3093 | 78,321 |
| Set | Ground | Vegetation | Cars | Trucks | Power Lines | Poles | Fences | Buildings | Unclassified | Total |
|---|---|---|---|---|---|---|---|---|---|---|
| Training | 178 | 121 | 3 | 0.75 | 0.80 | 0.28 | 2 | 57 | 7 | 369.83 |
| Testing | 69 | 41 | 1 | 0.15 | 0.23 | 0.09 | 0.62 | 23 | 0.68 | 135.77 |
| Total | 247 | 162 | 4 | 0.90 | 1.03 | 0.37 | 2.62 | 80 | 7.68 | 505.6 |
| Dataset | Properties | Input Points | Selected Points |
|---|---|---|---|
| Toronto-3D [37] | xyz | 8192 × 3 | 1024 × 3 |
| xyz + rgb | 8192 × 6 | 1024 × 6 | |
| DALES [38] | xyz | 8192 × 3 | 1024 × 3 |
| Method | OA | mIoU | Road | Road Marking | Natural | Building | Utility Line | Pole | Car | Fence |
|---|---|---|---|---|---|---|---|---|---|---|
| Ours (xyz) | 72.55 | 66.87 | 92.74 | 14.75 | 88.66 | 93.52 | 81.03 | 67.71 | 39.65 | 56.90 |
| Ours (xyz + rgb) | 83.601 | 71.03 | 92.84 | 27.43 | 89.90 | 95.27 | 85.59 | 74.50 | 44.41 | 58.30 |
| Method | OA | mIoU | Ground | Vegetation | Cars | Trucks | Power Lines | Poles | Fences | Buildings |
|---|---|---|---|---|---|---|---|---|---|---|
| Ours (xyz) | 76.43 | 59.52 | 86.78 | 85.40 | 50.63 | 32.59 | 67.47 | 50.76 | 84.89 | 17.66 |
| Method | OA | mIoU | Road | Road Marking | Natural | Building | Utility Line | Pole | Car | Fence |
|---|---|---|---|---|---|---|---|---|---|---|
| PointNet++ [11] | 91.21 | 56.55 | 91.44 | 7.59 | 89.80 | 74.00 | 68.60 | 59.53 | 53.97 | 7.54 |
| RandLA-Net [20] | 92.95 1 | 77.71 | 94.61 | 42.62 | 96.89 | 93.01 | 86.51 | 78.07 | 92.85 | 37.12 |
| KPConv [25] | 91.71 2 | 60.30 | 90.20 | 0.00 | 86.79 | 86.83 | 81.08 | 73.06 | 42.85 | 21.57 |
| DGCNN [28] | 89.00 | 49.60 | 90.63 | 0.44 | 81.25 | 63.95 | 47.05 | 56.86 | 49.26 | 7.32 |
| Ours (xyz) | 72.55 | 66.87 | 92.74 | 14.75 | 88.66 | 93.52 | 81.03 | 67.71 | 39.65 | 56.90 |
| Method | OA | mIoU | Ground | Vegetation | Cars | Trucks | Power Lines | Poles | Fences | Buildings |
|---|---|---|---|---|---|---|---|---|---|---|
| PointNet++ [11] | 95.70 2 | 68.30 | 94.10 | 91.20 | 75.40 | 30.30 | 79.90 | 40.00 | 46.20 | 89.10 |
| KPConv [25] | 97.80 1 | 81.10 | 97.10 | 94.10 | 85.30 | 41.90 | 95.50 | 75.00 | 63.50 | 96.60 |
| SPG [29] | 95.50 | 60.60 | 94.70 | 87.90 | 62.90 | 18.70 | 65.20 | 28.50 | 33.60 | 93.40 |
| Ours (xyz) | 76.43 | 59.52 | 86.78 | 85.40 | 50.63 | 32.59 | 67.47 | 50.76 | 84.89 | 17.66 |
| Method | Neighboring | Complexity | No. of Parameters | Inference Time |
|---|---|---|---|---|
| PointNet++ [11] | FPS | 8.70 M | 370.37 ms | |
| RandLA-Net [20] | RPS | 1.24 M | - 1 | |
| KPConv [25] | Kd-tree | 14.90 M | - | |
| DGCNN [28] | - | - | 21 M | - |
| Ours | RPS | 1.98 M | 102.45 ms 2 |
| Mechanism | ||
|---|---|---|
| FPS + AP + ML | 70.88 | 65.67 |
| RPS + MP + ML | 64.79 | 65.37 |
| RPS + AP + SL | 61.42 | 60.12 |
| PRS + AP + ML | 72.55 1 | 66.87 |
| Mechanism | ||
|---|---|---|
| FPS + AP + ML | 81.19 1 | 51.94 |
| RPS + MP + ML | 62.80 | 39.52 |
| RPS + AP + SL | 57.77 | 48.65 |
| PRS + AP + ML | 76.43 | 59.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rim, B.; Lee, A.; Hong, M. Semantic Segmentation of Large-Scale Outdoor Point Clouds by Encoder–Decoder Shared MLPs with Multiple Losses. Remote Sens. 2021, 13, 3121. https://doi.org/10.3390/rs13163121
Rim B, Lee A, Hong M. Semantic Segmentation of Large-Scale Outdoor Point Clouds by Encoder–Decoder Shared MLPs with Multiple Losses. Remote Sensing. 2021; 13(16):3121. https://doi.org/10.3390/rs13163121
Chicago/Turabian StyleRim, Beanbonyka, Ahyoung Lee, and Min Hong. 2021. "Semantic Segmentation of Large-Scale Outdoor Point Clouds by Encoder–Decoder Shared MLPs with Multiple Losses" Remote Sensing 13, no. 16: 3121. https://doi.org/10.3390/rs13163121
APA StyleRim, B., Lee, A., & Hong, M. (2021). Semantic Segmentation of Large-Scale Outdoor Point Clouds by Encoder–Decoder Shared MLPs with Multiple Losses. Remote Sensing, 13(16), 3121. https://doi.org/10.3390/rs13163121