The Importance of Subsurface Processes in Land Surface Modeling over a Temperate Region: An Analysis with SMAP, Cosmic Ray Neutron Sensing and Triple Collocation Analysis
Abstract
:1. Introduction
2. Materials and Methods
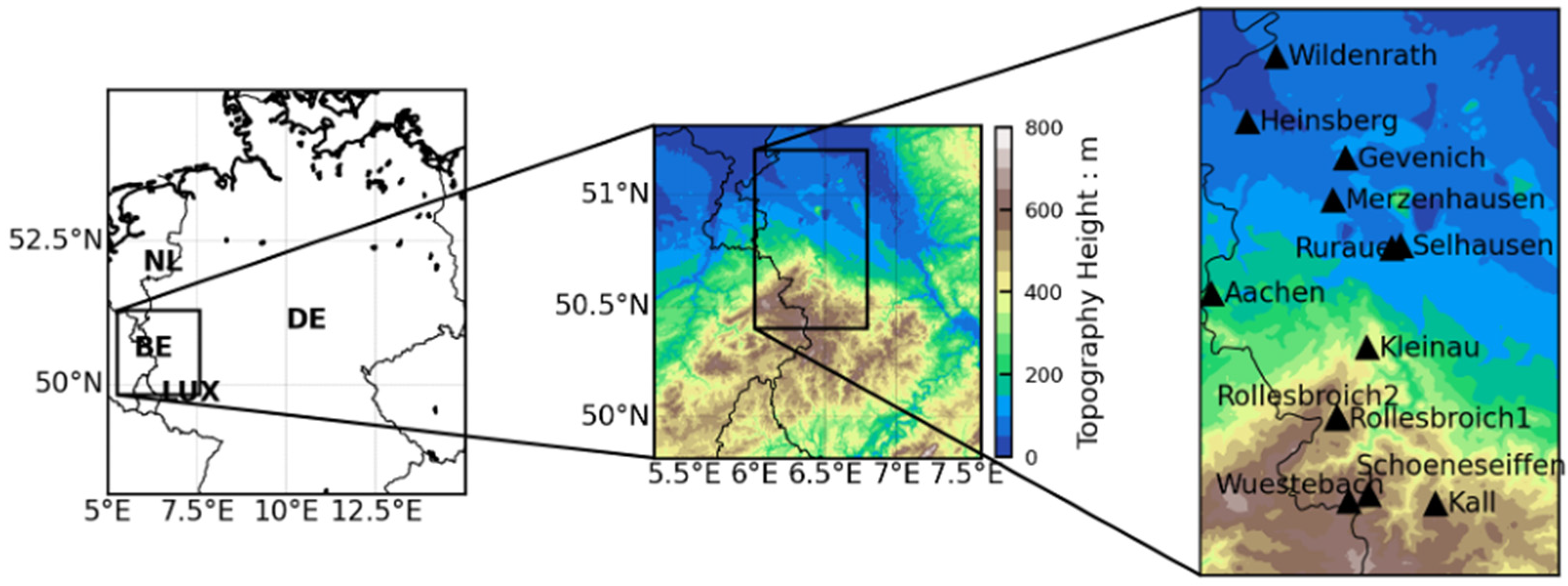
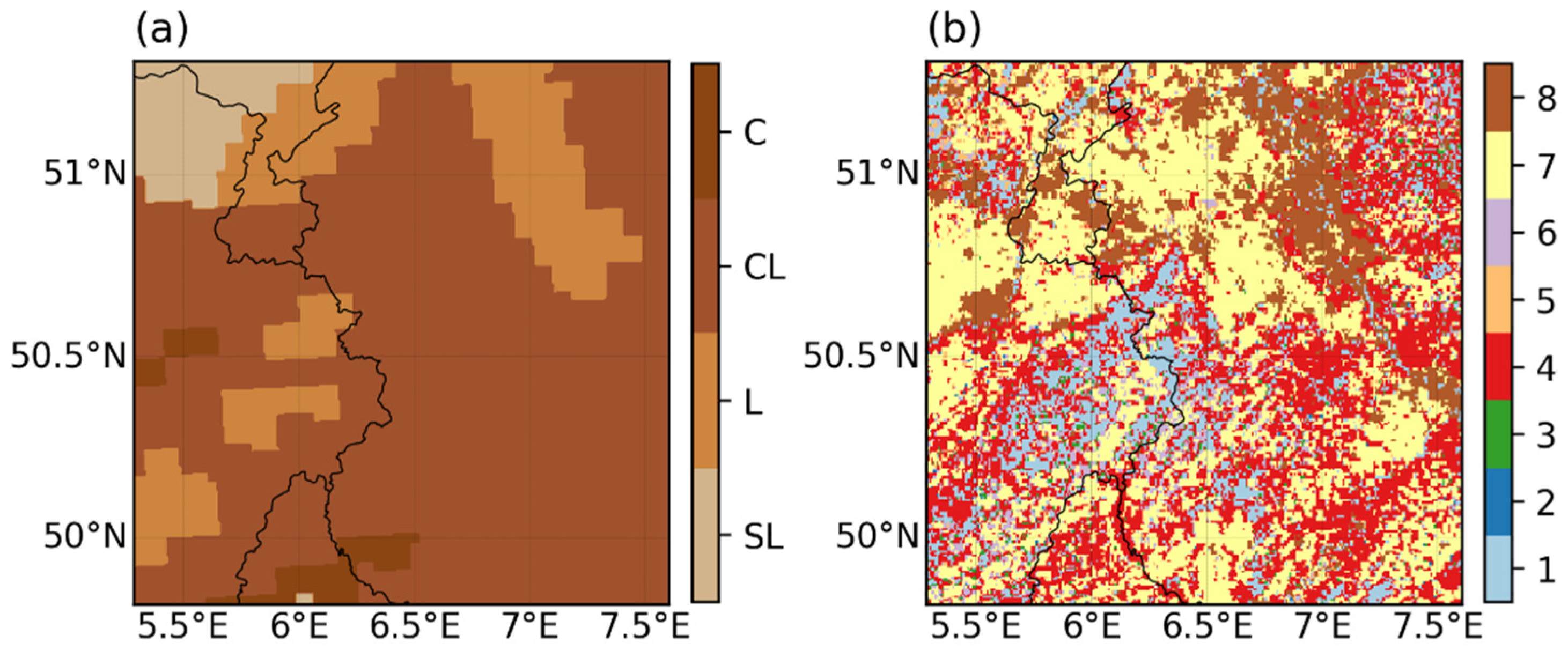
2.1. Study Area
2.2. Data
2.2.1. Land Surface Modeling
2.2.2. CRNS Observations
2.2.3. SMAP Enhanced Soil Moisture Product
2.3. Methods
2.3.1. Data Processing
2.3.2. Standard Evaluation Metrics
2.3.3. Triple Collocation
3. Results and Discussions
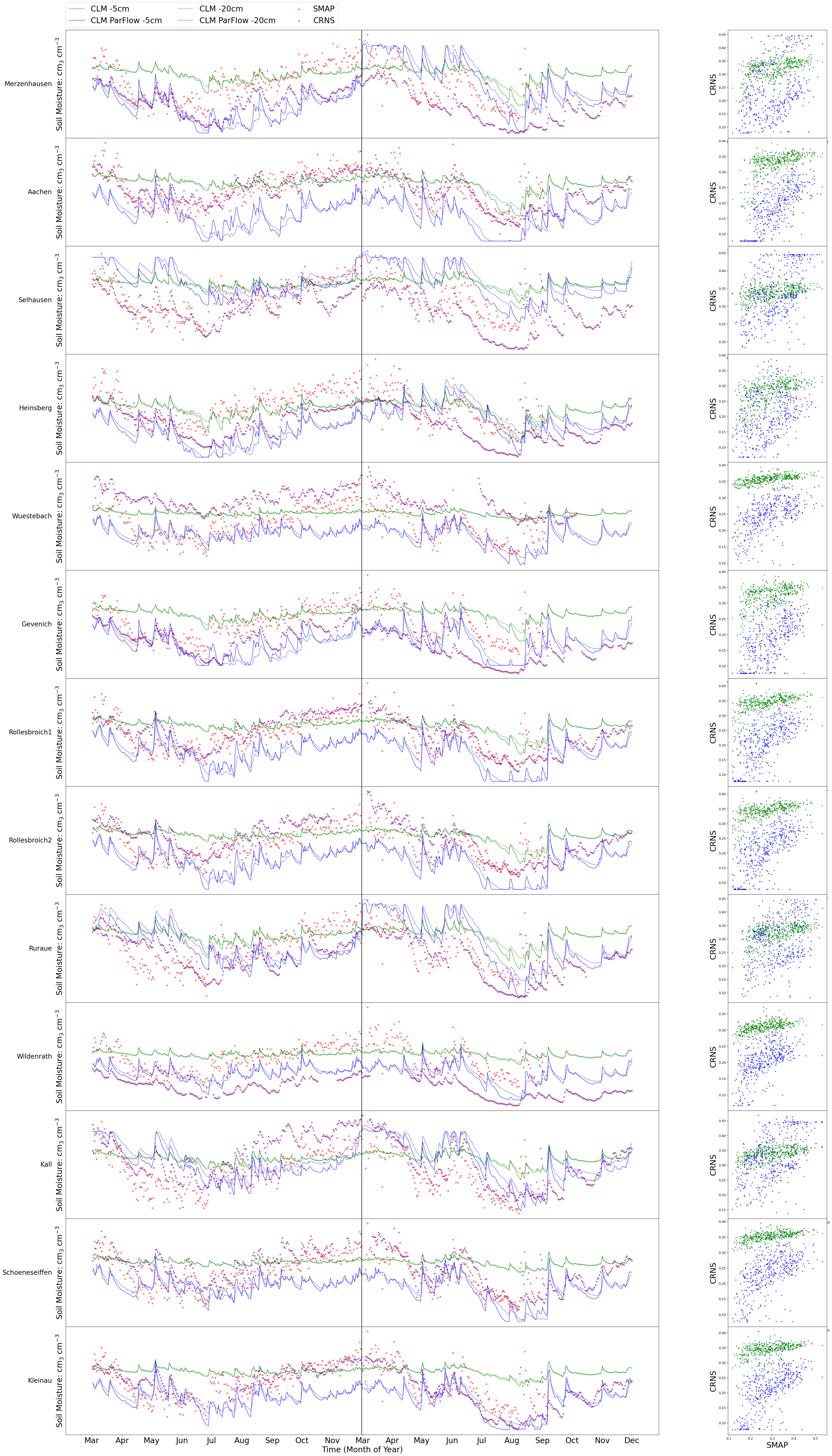
3.1. Agreement between Spaceborne and In Situ Observations
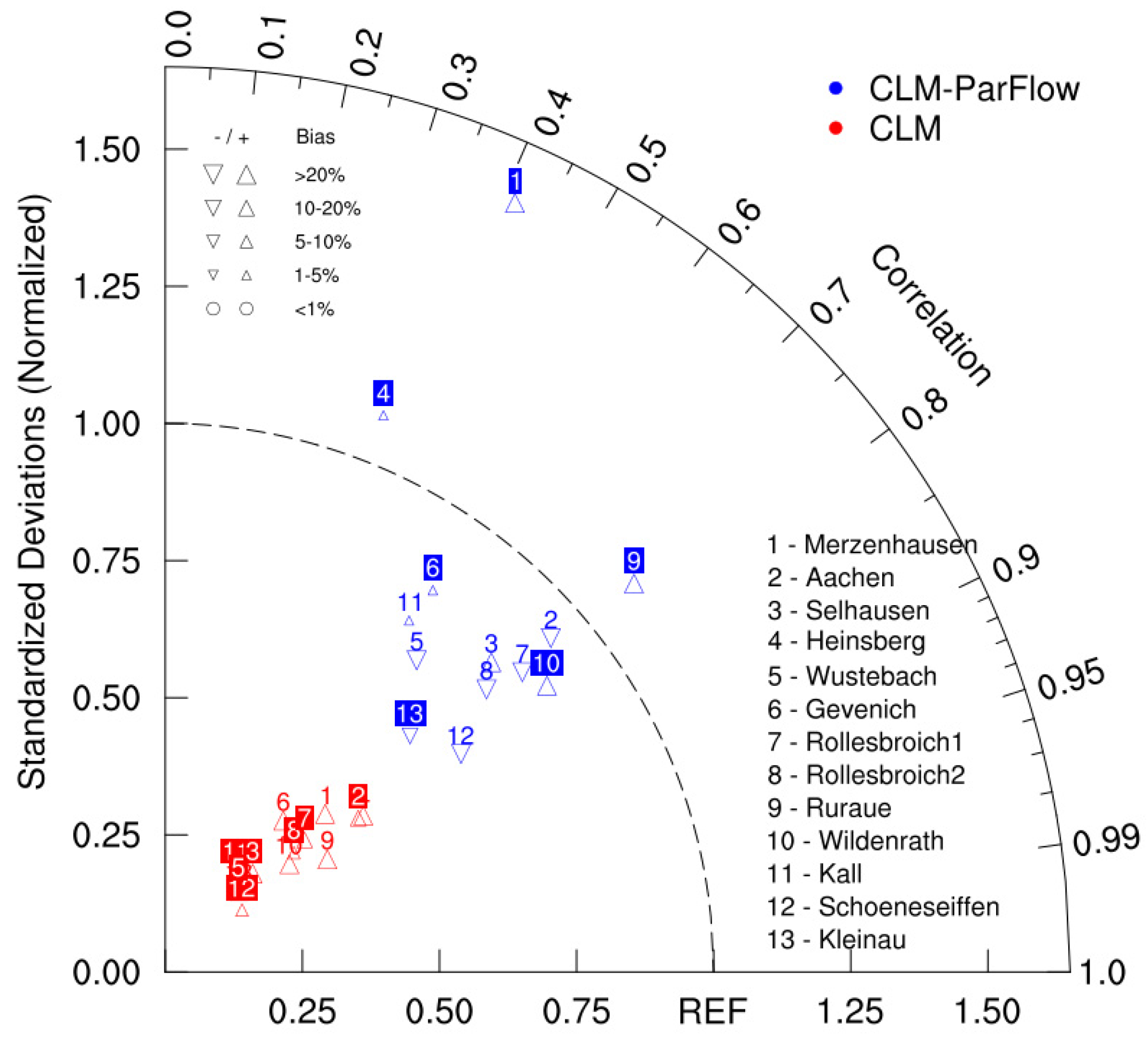
3.2. Comparison of Model Simulation and CRNS Measurements
3.3. Temporal and Spatial Correlation between Model Simulations and the SMAP L3_SM_P_E Product
3.4. Triple Collocation
3.5. Effect of Lateral Water Flow on Soil Moisture
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Miguez-Macho, G.; Fan, Y. The Role of Groundwater in the Amazon Water Cycle: 1. Influence on Seasonal Streamflow, Flooding and Wetlands. J. Geophys. Res. Atmos. 2012, 117, 15113. [Google Scholar] [CrossRef]
- Sulis, M.; Keune, J.; Shrestha, P.; Simmer, C.; Kollet, S.J. Quantifying the Impact of Subsurface-Land Surface Physical Processes on the Predictive Skill of Subseasonal Mesoscale Atmospheric Simulations. J. Geophys. Res. Atmos. 2018, 123, 9131–9151. [Google Scholar] [CrossRef]
- Chen, X.; Hu, Q. Groundwater Influences on Soil Moisture and Surface Evaporation. J. Hydrol. 2004, 297, 285–300. [Google Scholar] [CrossRef] [Green Version]
- Ochoa, C.G.; Fernald, A.G.; Guldan, S.J.; Shukla, M.K. Water Movement through a Shallow Vadose Zone: A Field Irrigation Experiment. Vadose Zone J. 2009, 8, 414–425. [Google Scholar] [CrossRef] [Green Version]
- Zipper, S.C.; Soylu, M.E.; Booth, E.G.; Loheide, S.P. Untangling the Effects of Shallow Groundwater and Soil Texture as Drivers of Subfield-Scale Yield Variability. Water Resour. Res. 2015, 51, 6338–6358. [Google Scholar] [CrossRef] [Green Version]
- Appels, W.M.; Bogaart, P.W.; van der Zee, S.E.A.T.M. Feedbacks Between Shallow Groundwater Dynamics and Surface Topography on Runoff Generation in Flat Fields. Water Resour. Res. 2017, 53, 10336–10353. [Google Scholar] [CrossRef] [Green Version]
- Johnson, E.; Yáñez, J.; Ortiz, C.; Muñoz, J. Evaporation from Shallow Groundwater in Closed Basins in the Chilean Altiplano. Hydrol. Sci. J. 2010, 55, 624–635. [Google Scholar] [CrossRef] [Green Version]
- Alkhaier, F.; Flerchinger, G.N.; Su, Z. Shallow Groundwater Effect on Land Surface Temperature and Surface Energy Balance under Bare Soil Conditions: Modeling and Description. Hydrol. Earth Syst. Sci. 2012, 16, 1817–1831. [Google Scholar] [CrossRef] [Green Version]
- Martínez-De La Torre, A.; Miguez-Macho, G. Groundwater Influence on Soil Moisture Memory and Land-Atmosphere Fluxes in the Iberian Peninsula. Hydrol. Earth Syst. Sci. 2019, 23, 4909–4932. [Google Scholar] [CrossRef] [Green Version]
- Alkhaier, F.; Schotting, R.J.; Su, Z. A Qualitative Description of Shallow Groundwater Effect on Surface Temperature of Bare Soil. Hydrol. Earth Syst. Sci. 2009, 13, 1749–1756. [Google Scholar] [CrossRef] [Green Version]
- Niu, G.-Y.; Paniconi, C.; Troch, P.A.; Scott, R.L.; Durcik, M.; Zeng, X.; Huxman, T.; Goodrich, D.C. An Integrated Modelling Framework of Catchment-Scale Ecohydrological Processes: 1. Model Description and Tests over an Energy-Limited Watershed. Ecohydrology 2014, 7, 427–439. [Google Scholar] [CrossRef]
- Sridhar, V.; Billah, M.M.; Hildreth, J.W. Coupled Surface and Groundwater Hydrological Modeling in a Changing Climate. Groundwater 2018, 56, 618–635. [Google Scholar] [CrossRef] [PubMed]
- Kollet, S.J.; Maxwell, R.M. Capturing the Influence of Groundwater Dynamics on Land Surface Processes Using an Integrated, Distributed Watershed Model. Water Resour. Res. 2008, 44, 2402. [Google Scholar] [CrossRef]
- Dumedah, G.; Walker, J.P. Assessment of Land Surface Model Uncertainty: A Crucial Step towards the Identification of Model Weaknesses. J. Hydrol. 2014, 519, 1474–1484. [Google Scholar] [CrossRef]
- Cuntz, M.; Mai, J.; Samaniego, L.; Clark, M.; Wulfmeyer, V.; Branch, O.; Attinger, S.; Thober, S. The Impact of Standard and Hard-Coded Parameters on the Hydrologic Fluxes in the Noah-MP Land Surface Model. J. Geophys. Res. Atmos. 2016, 121, 10,676–10,700. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. In Situ Measurement of Soil Moisture: A Comparison of Techniques. J. Hydrol. 2004, 293, 85–99. [Google Scholar] [CrossRef]
- Hanson, B. Field Estimation of Soil Water Content: A Practical Guide to Methods, Instrumentation and Sensor Technology. Vadose Zone J. 2009, 8, 628. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, Proximal, and Satellite Remote Sensing of Soil Moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef] [Green Version]
- Montzka, C.; Bogena, H.R.; Herbst, M.; Cosh, M.H.; Jagdhuber, T.; Vereecken, H. Estimating the Number of Reference Sites Necessary for the Validation of Global Soil Moisture Products. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Franz, T.E.; Zreda, M.; Rosolem, R.; Ferre, T.P.A. Field Validation of a Cosmic-Ray Neutron Sensor Using a Distributed Sensor Network. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef] [Green Version]
- Zreda, M.; Shuttleworth, W.J.; Zeng, X.; Zweck, C.; Desilets, D.; Franz, T.; Rosolem, R. Corrigendum to “COSMOS: The COsmic-ray Soil Moisture Observing System” published in Hydrol. Earth Syst. Sci., 16, 4079–4099, 2012. Hydrol. Earth Syst. Sci. 2013, 17, 1065–1066. [Google Scholar] [CrossRef]
- Zreda, M.; Desilets, D.; Ferré, T.P.A.; Scott, R.L. Measuring Soil Moisture Content Non-Invasively at Intermediate Spatial Scale Using Cosmic-Ray Neutrons. Geophys. Res. Lett. 2008, 35, L21402. [Google Scholar] [CrossRef] [Green Version]
- Montzka, C.; Bogena, H.R.; Zreda, M.; Monerris, A.; Morrison, R.; Muddu, S.; Vereecken, H. Validation of Spaceborne and Modelled Surface Soil Moisture Products with Cosmic-Ray Neutron Probes. Remote Sens. 2017, 9, 103. [Google Scholar] [CrossRef] [Green Version]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements Ofthe Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Chan, S.; Bindlish, R.; O’Neill, P.; Jackson, T.; Chaubell, J.; Piepmeier, J.; Dunbar, S.; Colliander, A.; Chen, F.; Entekhabi, D.; et al. Development and Validation of the SMAP Enhanced Passive Soil Moisture Product. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: New York, NY, USA, 2017; pp. 2539–2542. [Google Scholar]
- Zhang, R.; Kim, S.; Sharma, A. A Comprehensive Validation of the SMAP Enhanced Level-3 Soil Moisture Product Using Ground Measurements over Varied Climates and Landscapes. Remote Sens. Environ. 2019, 223, 82–94. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP Surface Soil Moisture Products with Core Validation Sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Colliander, A.; Reichle, R.H.; Crow, W.T.; Cosh, M.H.; Chen, F.; Chan, S.; Das, N.; Bindlish, R.; Chaubell, J.; Kim, S.B.; et al. Preprint-Submitted to IEEE JSTARS CC BY-NC-SA 4.0 Validation of the Most Recent SMAP Level 2 and 3 SM Retrieval Products (R17000) Validation of Soil Moisture Data Products from the NASA SMAP Mission; TechRxiv: Piscataway, NY, USA, 2021. [Google Scholar]
- el Hajj, M.; Baghdadi, N.; Zribi, M.; Rodríguez-Fernández, N.; Wigneron, J.; Al-Yaari, A.; al Bitar, A.; Albergel, C.; Calvet, J.-C. Evaluation of SMOS, SMAP, ASCAT and Sentinel-1 Soil Moisture Products at Sites in Southwestern France. Remote Sens. 2018, 10, 569. [Google Scholar] [CrossRef] [Green Version]
- Walker, V.A.; Hornbuckle, B.K.; Cosh, M.H.; Prueger, J.H. Seasonal Evaluation of SMAP Soil Moisture in the U.S. Corn Belt. Remote Sens. 2019, 11, 2488. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Parinussa, R.; Konings, A.G.; Wagner, W.; Cosh, M.H.; Lakshmi, V.; Zohaib, M.; Choi, M. Global-Scale Assessment and Combination of SMAP with ASCAT (Active) and AMSR2 (Passive) Soil Moisture Products. Remote. Sens. Environ. 2018, 204, 260–275. [Google Scholar] [CrossRef]
- Bayat, B.; Camacho, F.; Nickeson, J.; Cosh, M.; Bolten, J.; Vereecken, H.; Montzka, C. Toward Operational Validation Systems for Global Satellite-Based Terrestrial Essential Climate Variables. Int. J. Appl. Earth Obs. Geoinf. 2021, 95, 102240. [Google Scholar] [CrossRef]
- Pan, M.; Cai, X.; Chaney, N.W.; Entekhabi, D.; Wood, E.F. An Initial Assessment of SMAP Soil Moisture Retrievals Using High-Resolution Model Simulations and in Situ Observations. Geophys. Res. Lett. 2016, 43, 9662–9668. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Lu, H.; Yang, K.; Han, M.; Wright, J.S.; Chen, Y.; Yu, L.; Xu, S.; Huang, X.; Gong, W. The Evaluation of SMAP Enhanced Soil Moisture Products Using High-Resolution Model Simulations and In-Situ Observations on the Tibetan Plateau. Remote Sens. 2018, 10, 535. [Google Scholar] [CrossRef] [Green Version]
- Bi, H.; Ma, J.; Zheng, W.; Zeng, J. Comparison of Soil Moisture in GLDAS Model Simulations and in Situ Observations over the Tibetan Plateau. J. Geophys. Res. Atmos. 2016, 121, 2658–2678. [Google Scholar] [CrossRef] [Green Version]
- Soulis, E.D.; Snelgrove, K.R.; Kouwen, N.; Seglenieks, F.; Verseghy, D.L. Towards Closing the Vertical Water Balance in Canadian Atmospheric Models: Coupling of the Land Surface Scheme Class with the Distributed Hydrological Model Watflood. Atmos. Ocean 2000, 38, 251–269. [Google Scholar] [CrossRef]
- Forrester, M.M.; Maxwell, R.M. Impact of Lateral Groundwater Flow and Subsurface Lower Boundary Conditions on Atmospheric Boundary Layer Development over Complex Terrain. J. Hydrometeorol. 2020, 21, 1133–1160. [Google Scholar] [CrossRef] [Green Version]
- Duygu, M.B.; Akyürek, Z. Using Cosmic-Ray Neutron Probes in Validating Satellite Soil Moisture Products and Land Surface Models. Water 2019, 11, 1362. [Google Scholar] [CrossRef] [Green Version]
- Albergel, C.; de Rosnay, P.; Gruhier, C.; Muñoz-Sabater, J.; Hasenauer, S.; Isaksen, L.; Kerr, Y.; Wagner, W. Evaluation of Remotely Sensed and Modelled Soil Moisture Products Using Global Ground-Based in Situ Observations. Remote Sens. Environ. 2012, 118, 215–226. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the True Near-Surface Wind Speed: Error Modeling and Calibration Using Triple Collocation. J. Geophys. Res. Ocean. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Caires, S.; Sterl, A. Validation of Ocean Wind and Wave Data Using Triple Collocation. J. Geophys. Res. Ocean. 2003, 108. [Google Scholar] [CrossRef]
- Roebeling, R.A.; Wolters, E.L.A.; Meirink, J.F.; Leijnse, H. Triple Collocation of Summer Precipitation Retrievals from SEVIRI over Europe with Gridded Rain Gauge and Weather Radar Data. J. Hydrometeorol. 2012, 13, 1552–1566. [Google Scholar] [CrossRef]
- McColl, K.A.; Vogelzang, J.; Konings, A.G.; Entekhabi, D.; Piles, M.; Stoffelen, A. Extended Triple Collocation: Estimating Errors and Correlation Coefficients with Respect to an Unknown Target. Geophys. Res. Lett. 2014, 41, 6229–6236. [Google Scholar] [CrossRef] [Green Version]
- Gruber, A.; Su, C.-H.; Zwieback, S.; Crow, W.; Dorigo, W.; Wagner, W. Recent Advances in (Soil Moisture) Triple Collocation Analysis. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 200–211. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.A.; Crow, W.; Wagner, W. Triple Collocation-Based Merging of Satellite Soil Moisture Retrievals. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6780–6792. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Colliander, A.; Cosh, M.H.; Jackson, T.J.; Bindlish, R.; Reichle, R.H.; Chan, S.K.; Bosch, D.D.; Starks, P.J.; et al. Application of Triple Collocation in Ground-Based Validation of Soil Moisture Active/Passive (SMAP) Level 2 Data Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 489–502. [Google Scholar] [CrossRef]
- Tugrul Yilmaz, M.; Crow, W.T. Evaluation of Assumptions in Soil Moisture Triple Collocation Analysis. J. Hydrometeorol. 2014, 15, 1293–1302. [Google Scholar] [CrossRef]
- Kreklow, J.; Tetzlaff, B.; Burkhard, B.; Kuhnt, G. Radar-Based Precipitation Climatology in Germany—Developments, Uncertainties and Potentials. Atmosphere 2020, 11, 217. [Google Scholar] [CrossRef] [Green Version]
- Klimaatlas NRW. Available online: https://www.klimaatlas.nrw.de/Niederschlag-Artikel (accessed on 26 July 2021).
- Batjes, N.H. A World Dataset of Derived Soil Properties by FAO-UNESCO Soil Unit for Global Modelling. Soil Use Manag. 1997, 13, 9–16. [Google Scholar] [CrossRef]
- Herrmann, F.; Keller, L.; Kunkel, R.; Vereecken, H.; Wendland, F. Determination of Spatially Differentiated Water Balance Components Including Groundwater Recharge on the Federal State Level—A Case Study Using the MGROWA Model in North Rhine-Westphalia (Germany). J. Hydrol. Reg. Stud. 2015, 4, 294–312. [Google Scholar] [CrossRef] [Green Version]
- Montzka, C.; Grant, J.P.; Moradkhani, H.; Franssen, H.-J.H.; Weihermüller, L.; Drusch, M.; Vereecken, H. Estimation of Radiative Transfer Parameters from L-Band Passive Microwave Brightness Temperatures Using Advanced Data Assimilation. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef] [Green Version]
- Hasan, S.; Montzka, C.; Rüdiger, C.; Ali, M.; Bogena, H.R.; Vereecken, H. Soil Moisture Retrieval from Airborne L-Band Passive Microwave Using High Resolution Multispectral Data. ISPRS J. Photogramm. Remote Sens. 2014, 91, 59–71. [Google Scholar] [CrossRef]
- Montzka, C.; Jagdhuber, T.; Horn, R.; Bogena, H.R.; Hajnsek, I.; Reigber, A.; Vereecken, H. Investigation of SMAP Fusion Algorithms with Airborne Active and Passive L-Band Microwave Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3878–3889. [Google Scholar] [CrossRef]
- Rötzer, K.; Montzka, C.; Bogena, H.; Wagner, W.; Kerr, Y.H.; Kidd, R.; Vereecken, H. Catchment Scale Validation of SMOS and ASCAT Soil Moisture Products Using Hydrological Modeling and Temporal Stability Analysis. J. Hydrol. 2014, 519, 934–946. [Google Scholar] [CrossRef]
- Han, X.; Hendricks Franssen, H.-J.; Li, X.; Zhang, Y.; Montzka, C.; Vereecken, H. Joint Assimilation of Surface Temperature and L-Band Microwave Brightness Temperature in Land Data Assimilation. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Han, X.; Franssen, H.-J.H.; Montzka, C.; Vereecken, H. Soil Moisture and Soil Properties Estimation in the Community Land Model with Synthetic Brightness Temperature Observations. Water Resour. Res. 2014, 50, 6081–6105. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, P.; Sulis, M.; Masbou, M.; Kollet, S.; Simmer, C.; Masbou, M.; Kollet, S.; Shrestha, P. A Scale-Consistent Terrestrial Systems Modeling Platform Based on COSMO, CLM, and ParFlow. Mon. Weather. Rev. 2014, 142, 3466–3483. [Google Scholar] [CrossRef]
- Baatz, R.; Hendricks Franssen, H.-J.; Han, X.; Hoar, T.; Bogena, H.R.; Vereecken, H. Evaluation of a Cosmic-Ray Neutron Sensor Network for Improved Land Surface Model Prediction. Hydrol. Earth Syst. Sci. 2017, 21, 2509–2530. [Google Scholar] [CrossRef] [Green Version]
- Clapp, R.B.; Hornberger, G.M. Empirical Equations for Some Soil Hydraulic Properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef] [Green Version]
- Cosby, B.J.; Hornberger, G.M.; Clapp, R.B.; Ginn, T.R. A Statistical Exploration of the Relationships of Soil Moisture Characteristics to the Physical Properties of Soils. Water Resour. Res. 1984, 20, 682–690. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, R.M.; Miller, N.L.; Maxwell, R.M.; Miller, N.L. Development of a Coupled Land Surface and Groundwater Model. J. Hydrometeorol. 2005, 6, 233–247. [Google Scholar] [CrossRef] [Green Version]
- Van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. Rosetta: A Computer Program for Estimating Soil Hydraulic Parameters with Hierarchical Pedotransfer Functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Bollmeyer, C.; Keller, J.D.; Ohlwein, C.; Wahl, S.; Crewell, S.; Friederichs, P.; Hense, A.; Keune, J.; Kneifel, S.; Pscheidt, I.; et al. Towards a High-Resolution Regional Reanalysis for the European CORDEX Domain. Q. J. R. Meteorol. Soc. 2015, 141, 1–15. [Google Scholar] [CrossRef]
- Baldauf, M.; Seifert, A.; Förstner, J.; Majewski, D.; Raschendorfer, M.; Reinhardt, T. Operational Convective-Scale Numerical Weather Prediction with the COSMO Model: Description and Sensitivities. Mon. Weather. Rev. 2011, 139, 3887–3905. [Google Scholar] [CrossRef]
- Köhli, M.; Schrön, M.; Zreda, M.; Schmidt, U.; Dietrich, P.; Zacharias, S. Footprint Characteristics Revised for Field-Scale Soil Moisture Monitoring with Cosmic-Ray Neutrons. Water Resour. Res. 2015, 51, 5772–5790. [Google Scholar] [CrossRef] [Green Version]
- Schrön, M.; Köhli, M.; Scheiffele, L.; Iwema, J.; Bogena, H.R.; Lv, L.; Martini, E.; Baroni, G.; Rosolem, R.; Weimar, J.; et al. Improving Calibration and Validation of Cosmic-Ray Neutron Sensors in the Light of Spatial Sensitivity. Hydrol. Earth Syst. Sci. 2017, 21, 5009–5030. [Google Scholar] [CrossRef] [Green Version]
- Baatz, R.; Bogena, H.R.; Hendricks Franssen, H.-J.; Huisman, J.A.; Montzka, C.; Vereecken, H. An Empirical Vegetation Correction for Soil Water Content Quantification Using Cosmic Ray Probes. Water Resour. Res. 2015, 51, 2030–2046. [Google Scholar] [CrossRef] [Green Version]
- Jakobi, J.; Huisman, J.A.; Vereecken, H.; Diekkrüger, B.; Bogena, H.R. Cosmic Ray Neutron Sensing for Simultaneous Soil Water Content and Biomass Quantification in Drought Conditions. Water Resour. Res. 2018, 54, 7383–7402. [Google Scholar] [CrossRef] [Green Version]
- Tian, Z.; Li, Z.; Liu, G.; Li, B.; Ren, T. Soil Water Content Determination with Cosmic-Ray Neutron Sensor: Correcting Aboveground Hydrogen Effects with Thermal/Fast Neutron Ratio. J. Hydrol. 2016, 540, 923–933. [Google Scholar] [CrossRef]
- Zhu, X.; Shao, M.; Zeng, C.; Jia, X.; Huang, L.; Zhang, Y.; Zhu, J. Application of Cosmic-Ray Neutron Sensing to Monitor Soil Water Content in an Alpine Meadow Ecosystem on the Northern Tibetan Plateau. J. Hydrol. 2016, 536, 247–254. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Baatz, R.; Hendricks Franssen, H.-J.; Vereecken, H. Accuracy of the Cosmic-Ray Soil Water Content Probe in Humid Forest Ecosystems: The Worst Case Scenario. Water Resour. Res. 2013, 49, 5778–5791. [Google Scholar] [CrossRef] [Green Version]
- Bogena, H.R.; Montzka, C.; Huisman, J.A.; Graf, A.; Schmidt, M.; Stockinger, M.; von Hebel, C.; Hendricks-Franssen, H.J.; van der Kruk, J.; Tappe, W.; et al. The TERENO-Rur Hydrological Observatory: A Multiscale Multi-Compartment Research Platform for the Advancement of Hydrological Science. Vadose Zone J. 2018, 17, 180055. [Google Scholar] [CrossRef]
- Franz, T.E.; Zreda, M.; Rosolem, R.; Ferre, T.P.A. A Universal Calibration Function for Determination of Soil Moisture with Cosmic-Ray Neutrons. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 10303–10322. [Google Scholar] [CrossRef]
- Gruber, A.; de Lannoy, G.; Albergel, C.; Al-Yaari, A.; Brocca, L.; Calvet, J.C.; Colliander, A.; Cosh, M.; Crow, W.; Dorigo, W.; et al. Validation Practices for Satellite Soil Moisture Retrievals: What Are (the) Errors? Remote Sens. Environ. 2020, 244, 111806. [Google Scholar] [CrossRef]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance Metrics for Soil Moisture Retrievals and Application Requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- Scipal, K.; Holmes, T.; de Jeu, R.; Naeimi, V.; Wagner, W. A Possible Solution for the Problem of Estimating the Error Structure of Global Soil Moisture Data Sets. Geophys. Res. Lett. 2008, 35, 24403. [Google Scholar] [CrossRef] [Green Version]
- Su, C.-H.; Ryu, D.; Crow, W.T.; Western, A.W. Beyond Triple Collocation: Applications to Soil Moisture Monitoring. J. Geophys. Res. Atmos. 2014, 119, 6419–6439. [Google Scholar] [CrossRef]
- Dubois, P.C.; Engman, T. Measuring Soil Moisture with Imaging Radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Kelly, R.; Leppanen, L.; Vehvilainen, J.; Kontu, A.; Lemmetyinen, J.; Pulliainen, J. The Influence of Thermal Properties and Canopy-Intercepted Snow on Passive Microwave Transmissivity of a Scots Pine. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5424–5433. [Google Scholar] [CrossRef]
- Mialon, A.; Coret, L.; Kerr, Y.H.; Sécherre, F.; Wigneron, J.P. Flagging the Topographic Impact on the SMOS Signal. IEEE Trans. Geosci. Remote Sens. 2008, 46, 689–694. [Google Scholar] [CrossRef]
- Talone, M.; Camps, A.; Monerris, A.; Vall-llossera, M.; Ferrazzoli, P.; Piles, M. Surface Topography and Mixed-Pixel Effects on the Simulated L-Band Brightness Temperatures. IEEE MicroRad. 2006, 181–186. [Google Scholar] [CrossRef] [Green Version]
- Park, C.; Montzka, C.; Jagdhuber, T.; Jonard, F.; de Lannoy, G.; Hong, J.; Jackson, T.J.; Wulfmeyer, V. A Dielectric Mixing Model Accounting for Soil Organic Matter. Vadose Zone J. 2019, 18, 190036. [Google Scholar] [CrossRef]
- Shellito, P.J.; Small, E.E.; Colliander, A.; Bindlish, R.; Cosh, M.H.; Berg, A.A.; Bosch, D.D.; Caldwell, T.G.; Goodrich, D.C.; McNairn, H.; et al. SMAP Soil Moisture Drying More Rapid than Observed in Situ Following Rainfall Events. Geophys. Res. Lett. 2016, 43, 8068–8075. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Zeng, J.; Cui, C.; Li, Z.; Chen, K.S.; Bai, X.; Xu, J. Soil Moisture Retrieval from SMAP: A Validation and Error Analysis Study Using Ground-Based Observations over the Little Washita Watershed. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1398–1408. [Google Scholar] [CrossRef]
- O’Neill, P.; Chan, S.; Bindlish, R.; Jackson, T.; Colliander, A.; Dunbar, S.; Chen, F.; Piepmeier, J.; Yueh, S.; Entekhabi, D.; et al. Assessment of Version 4 of the SMAP Passive Soil Moisture Standard Product. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: New York, NY, USA, 2017; pp. 3941–3944. [Google Scholar]
- Escorihuela, M.J.; Chanzy, A.; Wigneron, J.P.; Kerr, Y.H. Effective Soil Moisture Sampling Depth of L-Band Radiometry: A Case Study. Remote Sens. Environ. 2010, 114, 995–1001. [Google Scholar] [CrossRef] [Green Version]
- Bierkens, M.F.P.; Bell, V.A.; Burek, P.; Chaney, N.; Condon, L.E.; David, C.H.; de Roo, A.; Döll, P.; Drost, N.; Famiglietti, J.S.; et al. Hyper-Resolution Global Hydrological Modelling: What Is next?: “Everywhere and Locally Relevant” M. F. P. Bierkens et al. Invited Commentary. Hydrol. Process. 2015, 29, 310–320. [Google Scholar] [CrossRef]
- Yair, A. Effects of Surface Runoff and Subsurface Flow on the Spatial Variability of Water Resources in Longitudinal Dunes; Springer: Berlin/Heidelberg, Germany, 2008; pp. 251–269. [Google Scholar]
- Senatore, A.; Mendicino, G.; Gochis, D.J.; Yu, W.; Yates, D.N.; Kunstmann, H. Fully Coupled Atmosphere-Hydrology Simulations for the Central Mediterranean: Impact of Enhanced Hydrological Parameterization for Short and Long Time Scales. J. Adv. Model. Earth Syst. 2015, 7, 1693–1715. [Google Scholar] [CrossRef]
- Albergel, C.; Calvet, J.C.; de Rosnay, P.; Balsamo, G.; Wagner, W.; Hasenauer, S.; Naeimi, V.; Martin, E.; Bazile, E.; Bouyssel, F.; et al. Cross-Evaluation of Modelled and Remotely Sensed Surface Soil Moisture with in Situ Data in Southwestern France. Hydrol. Earth Syst. Sci. 2010, 14, 2177–2191. [Google Scholar] [CrossRef] [Green Version]
- Ford, T.W.; Quiring, S.M. Comparison of Contemporary In Situ, Model, and Satellite Remote Sensing Soil Moisture With a Focus on Drought Monitoring. Water Resour. Res. 2019, 55, 1565–1582. [Google Scholar] [CrossRef]
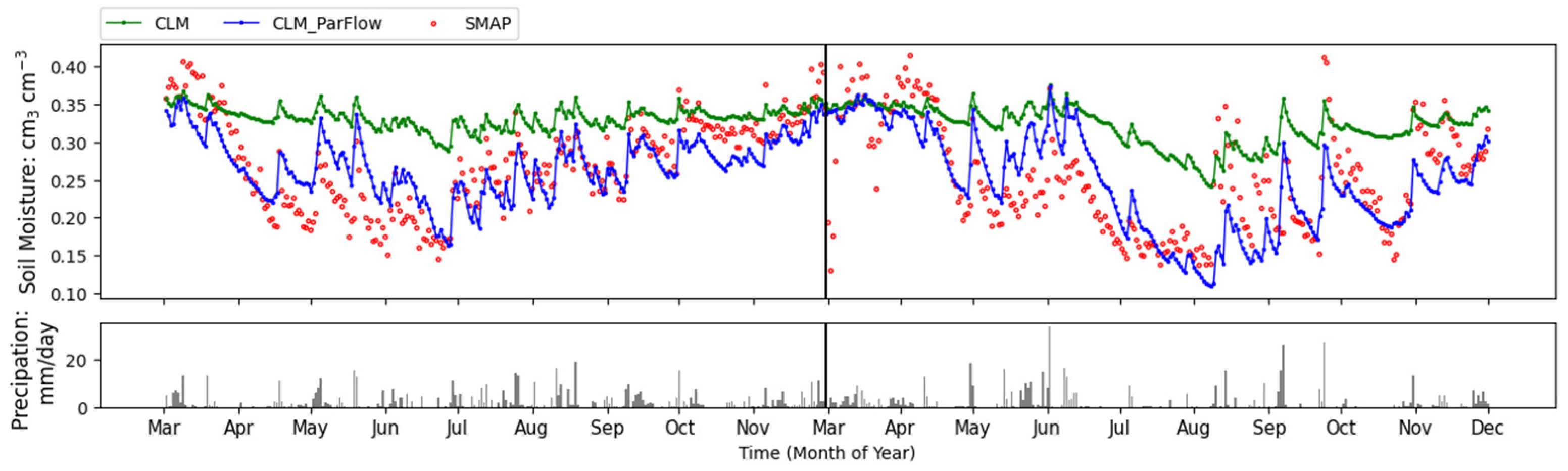
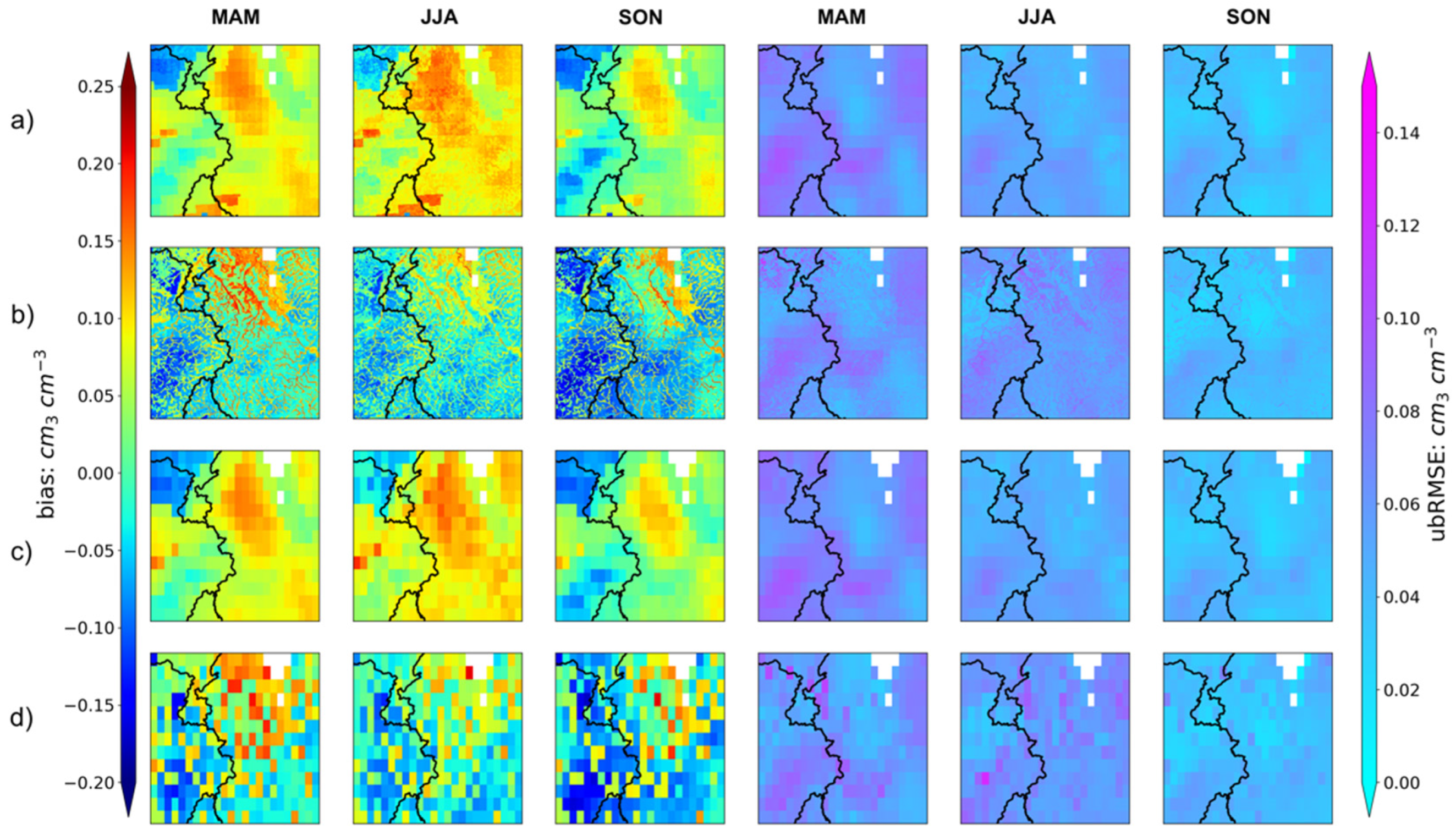
| Soil Layer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Depth (m) | 0.010 | 0.035 | 0.075 | 0.135 | 0.235 | 0.400 | 0.650 | 1.050 | 1.650 | 2.500 |
| Soil Type | Clay | Clay Loam | Loam | Sandy Loam |
|---|---|---|---|---|
| (m hr−1) | 0.0062 | 0.0034 | 0.0050 | 0.0158 |
| (m−1) | 2.1 | 2.1 | 2.0 | 2.7 |
| n | 2.0 | 2.0 | 2.0 | 2.0 |
| 1 | 0.4701 | 0.4449 | 0.4386 | 0.4071 |
| 1 | 0.21 | 0.17 | 0.15 | 0.1 |
| Name | Latitude | Longitude | Altitude | Precip. | Land Use | Clay % | Sand % | Bulk g cm−3 |
|---|---|---|---|---|---|---|---|---|
| Merzenhausen | 50.9303 | 6.29747 | 94 | 825 | crop | 22 | 21 | 1.39 |
| Aachen | 50.7986 | 6.02472 | 232 | 952 | crop | 23 | 22 | 1.20 |
| Selhausen | 50.8659 | 6.44719 | − | − | crop | 24 | 16 | 1.26 |
| Heinsberg | 51.0411 | 6.10424 | 57 | 814 | grassland, crop | 19 | 18 | 1.27 |
| Wüstebach | 50.5049 | 6.33092 | 605 | 1401 | spruce | 23 | 19 | 0.83 |
| Gevenich | 50.9892 | 6.32355 | 108 | 884 | crop | 20 | 22 | 1.31 |
| Rollesbroich1 | 50.6219 | 6.30424 | 515 | 1307 | grassland | 23 | 22 | 1.09 |
| Rollesbroich2 | 50.6242 | 6.30514 | − | − | grassland | - | - | 1.09 |
| Ruraue | 50.8623 | 6.42734 | 102 | 743 | grassland | 26 | 19 | 1.12 |
| Wildenrath | 51.1327 | 6.16918 | 76 | 856 | needleleaf | 12 | 65 | 1.15 |
| Kall | 50.5013 | 6.52645 | 504 | 935 | grassland | 22 | 20 | 1.31 |
| Schoeneseiffen | 50.5149 | 6.37559 | − | − | grassland | 24 | 16 | 1.11 |
| Kleinhau | 50.7224 | 6.37204 | − | − | grassland | 25 | 15 | 1.12 |
| Name | Bias: cm3 cm−3 | RMSD: cm3 cm−3 | ubRMSD: cm3 cm−3 | |
|---|---|---|---|---|
| Merzenhausen | 0.076 | 0.096 | 0.059 | 0.674 |
| Aachen | −0.003 | 0.049 | 0.049 | 0.768 |
| Selhausen | 0.031 | 0.066 | 0.059 | 0.653 |
| Heinsberg | 0.070 | 0.091 | 0.057 | 0.668 |
| Wüstebach | −0.120 | 0.133 | 0.057 | 0.752 |
| Gevenich | 0.067 | 0.088 | 0.058 | 0.684 |
| Rollesbroich1 | −0.023 | 0.060 | 0.055 | 0.741 |
| Rollesbroich2 | −0.053 | 0.077 | 0.055 | 0.708 |
| Ruraue | 0.030 | 0.080 | 0.075 | 0.452 |
| Wildenrath | 0.133 | 0.143 | 0.053 | 0.654 |
| Kall | −0.072 | 0.086 | 0.047 | 0.825 |
| Schoeneseiffen | −0.055 | 0.079 | 0.056 | 0.718 |
| Kleinhau | −0.018 | 0.051 | 0.048 | 0.789 |
| Average | 0.005 | 0.085 | 0.056 | 0.699 |
| Name | DEM (m) | IGBP | Clay% | Sand% | Bulk Density (g cm−3) |
|---|---|---|---|---|---|
| Merzenhausen | 79 | 12: Croplands | 21 | 39 | 1.40 |
| Aachen | 209 | 12: Croplands | 22 | 41 | 1.40 |
| Selhausen | 105 | 13: Urban and built-up lands | 23 | 37 | 1.40 |
| Heinsberg | 45 | 13: Urban and built-up lands | 21 | 39 | 1.40 |
| Wüstebach | 610 | 1: Evergreen needleleaf forests | 20 | 42 | 1.30 |
| Gevenich | 99 | 12: Croplands | 22 | 41 | 1.40 |
| Rollesbroich1 | 520 | 14: Cropland /natural vegetation mosaics | 20 | 42 | 1.30 |
| Rollesbroich2 | 520 | 14: Cropland /natural vegetation mosaics | 20 | 42 | 1.30 |
| Ruraue | 98 | 12: Croplands | 22 | 39 | 1.40 |
| Wildenrath | 79 | 5: Mixed forests | 22 | 41 | 1.40 |
| Kall | 510 | 14: Cropland /natural vegetation mosaics | 20 | 40 | 1.30 |
| Schoeneseiffen | 567 | 5: Mixed forests | 20 | 42 | 1.30 |
| Kleinhau | 347 | 5: Mixed forests | 20 | 42 | 1.30 |
| Name | CLM Simulations | CLM-ParFlow Simulations | ||||||
|---|---|---|---|---|---|---|---|---|
| Bias: cm3 cm−3 | RMSD: cm3 cm−3 | ubRMSD: cm3 cm−3 | Bias: cm3 cm−3 | RMSD: cm3 cm−3 | ubRMSD: cm3 cm−3 | |||
| Merzenhausen | 0.108 | 0.136 | 0.050 | 0.711 | 0.045 | 0.105 | 0.094 | 0.414 |
| Aachen | 0.126 | 0.058 | 0.047 | 0.782 | −0.106 | 0.115 | 0.045 | 0.756 |
| Selhausen | 0.035 | 0.127 | 0.063 | 0.664 | 0.131 | 0.141 | 0.050 | 0.725 |
| Heinsberg | 0.111 | 0.088 | 0.049 | 0.785 | 0.005 | 0.083 | 0.083 | 0.365 |
| Wüstebach | 0.073 | 0.079 | 0.052 | 0.665 | −0.169 | 0.175 | 0.047 | 0.628 |
| Gevenich | −0.060 | 0.160 | 0.062 | 0.615 | 0.002 | 0.065 | 0.065 | 0.574 |
| Rollesbroich1 | 0.148 | 0.071 | 0.062 | 0.726 | −0.091 | 0.104 | 0.051 | 0.766 |
| Rollesbroich2 | 0.036 | 0.070 | 0.068 | 0.733 | −0.112 | 0.126 | 0.056 | 0.751 |
| Ruraue | 0.016 | 0.105 | 0.054 | 0.821 | 0.068 | 0.087 | 0.053 | 0.770 |
| Wildenrath | 0.090 | 0.186 | 0.039 | 0.755 | 0.078 | 0.083 | 0.029 | 0.800 |
| Kall | 0.182 | 0.079 | 0.079 | 0.576 | 0.007 | 0.075 | 0.075 | 0.570 |
| Schoeneseiffen | 0.008 | 0.077 | 0.070 | 0.778 | −0.088 | 0.101 | 0.050 | 0.805 |
| Kleinhau | 0.031 | 0.103 | 0.076 | 0.675 | −0.049 | 0.078 | 0.061 | 0.720 |
| Average | 0.070 | 0.103 | 0.059 | 0.714 | −0.021 | 0.103 | 0.058 | 0.665 |
| Name | Z: CLM | Z: CLM-ParFlow | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Merzenhausen | 0.016 | 0.024 | 0.061 | 3.015 | 1.285 | −1.397 | 0.021 | 0.080 | 0.056 | 1.134 | 1.088 | −7.456 |
| Aachen | 0.020 | 0.025 | 0.057 | 2.610 | 1.270 | 1.485 | 0.023 | 0.037 | 0.050 | 1.199 | 1.025 | 6.576 |
| Selhausen | 0.017 | 0.015 | 0.061 | 5.669 | 1.556 | −2.082 | 0.011 | 0.045 | 0.059 | 1.415 | 1.441 | 2.622 |
| Heinsberg | 0.013 | 0.026 | 0.056 | 2.346 | 1.391 | 3.351 | 0.015 | 0.060 | 0.054 | 1.980 | 1.283 | −11.020 |
| Wüstebach | 0.028 | 0.008 | 0.055 | 5.941 | 0.783 | 1.330 | 0.028 | 0.036 | 0.055 | 1.526 | 0.780 | −1.414 |
| Gevenich | 0.020 | 0.024 | 0.060 | 3.520 | 1.376 | −3.166 | 0.040 | 0.041 | 0.052 | 1.257 | 1.052 | 4.035 |
| Rollesbroich1 | 0.023 | 0.024 | 0.058 | 3.698 | 1.455 | −1.250 | 0.030 | 0.038 | 0.050 | 1.267 | 1.144 | 8.143 |
| Rollesbroich2 | 0.019 | 0.023 | 0.059 | 3.858 | 1.579 | −0.489 | 0.039 | 0.038 | 0.050 | 1.322 | 1.192 | 8.099 |
| Ruraue | 0.008 | 0.019 | 0.065 | 2.806 | 1.691 | 6.315 | 0.038 | 0.058 | 0.068 | 1.383 | 2.164 | 0.826 |
| Wildenrath | 0.018 | 0.010 | 0.057 | 3.689 | 0.889 | 4.258 | 0.021 | 0.028 | 0.056 | 1.072 | 0.831 | 7.878 |
| Kall | 0.006 | 0.017 | 0.049 | 7.141 | 1.443 | −6.570 | 0.023 | 0.058 | 0.046 | 1.825 | 1.337 | −4.374 |
| Schoeneseiffen | 0.011 | 0.010 | 0.061 | 7.090 | 1.429 | 2.879 | 0.010 | 0.036 | 0.060 | 1.774 | 1.383 | 4.907 |
| Kleinhau | 0.026 | 0.014 | 0.061 | 7.607 | 1.664 | −2.779 | 0.023 | 0.040 | 0.057 | 1.730 | 1.424 | 3.800 |
| Average | 0.017 | 0.018 | 0.058 | 4.538 | 1.370 | 0.145 | 0.025 | 0.046 | 0.055 | 1.453 | 1.242 | 1.740 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Montzka, C.; Baatz, R.; Vereecken, H.; Franssen, H.-J.H. The Importance of Subsurface Processes in Land Surface Modeling over a Temperate Region: An Analysis with SMAP, Cosmic Ray Neutron Sensing and Triple Collocation Analysis. Remote Sens. 2021, 13, 3068. https://doi.org/10.3390/rs13163068
Zhao H, Montzka C, Baatz R, Vereecken H, Franssen H-JH. The Importance of Subsurface Processes in Land Surface Modeling over a Temperate Region: An Analysis with SMAP, Cosmic Ray Neutron Sensing and Triple Collocation Analysis. Remote Sensing. 2021; 13(16):3068. https://doi.org/10.3390/rs13163068
Chicago/Turabian StyleZhao, Haojin, Carsten Montzka, Roland Baatz, Harry Vereecken, and Harrie-Jan Hendricks Franssen. 2021. "The Importance of Subsurface Processes in Land Surface Modeling over a Temperate Region: An Analysis with SMAP, Cosmic Ray Neutron Sensing and Triple Collocation Analysis" Remote Sensing 13, no. 16: 3068. https://doi.org/10.3390/rs13163068
APA StyleZhao, H., Montzka, C., Baatz, R., Vereecken, H., & Franssen, H.-J. H. (2021). The Importance of Subsurface Processes in Land Surface Modeling over a Temperate Region: An Analysis with SMAP, Cosmic Ray Neutron Sensing and Triple Collocation Analysis. Remote Sensing, 13(16), 3068. https://doi.org/10.3390/rs13163068







