Spreading of Lagrangian Particles in the Black Sea: A Comparison between Drifters and a High-Resolution Ocean Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Drifters
2.1.2. Satellite Altimetry
2.1.3. Models
2.2. Methods
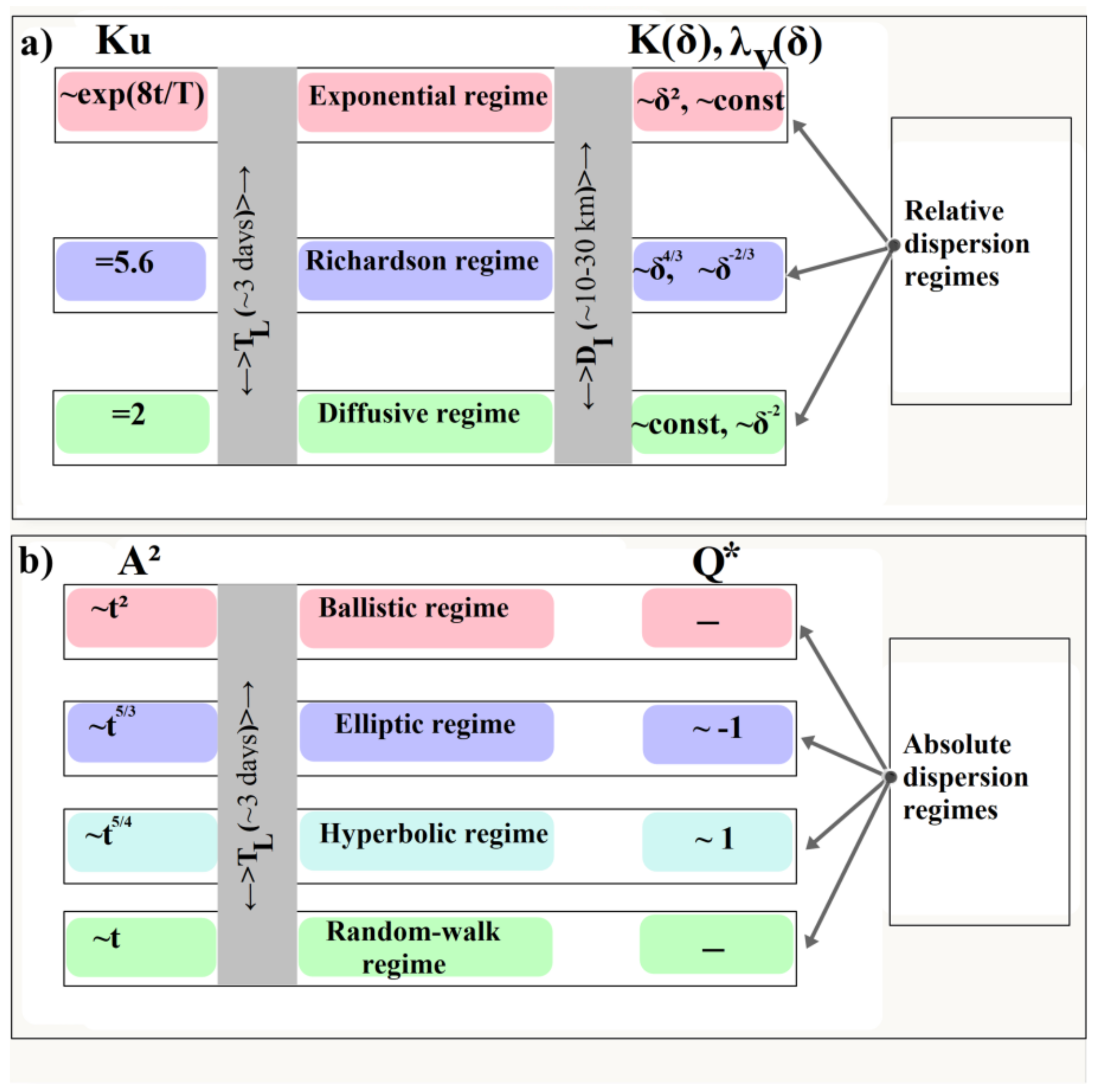
2.2.1. The Turbulent Relative Dispersion Statistics
2.2.2. The Turbulent Absolute Dispersion Statistics
3. Results
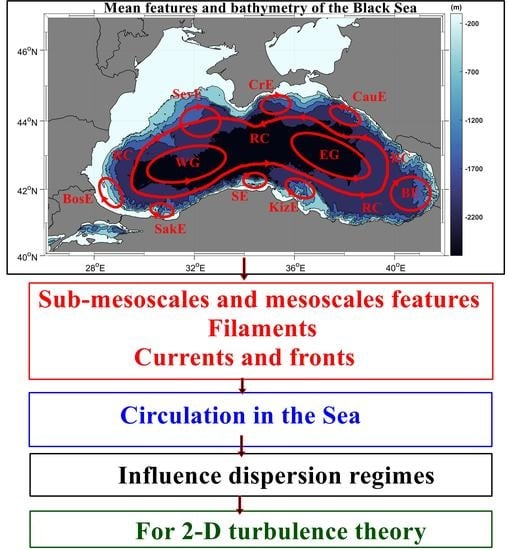
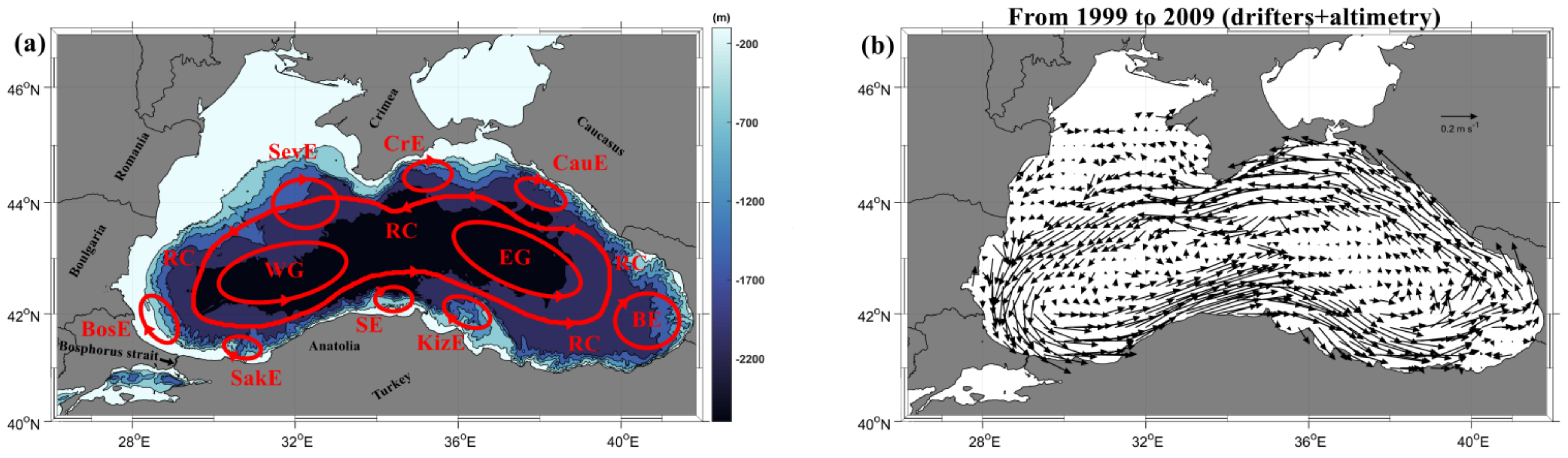
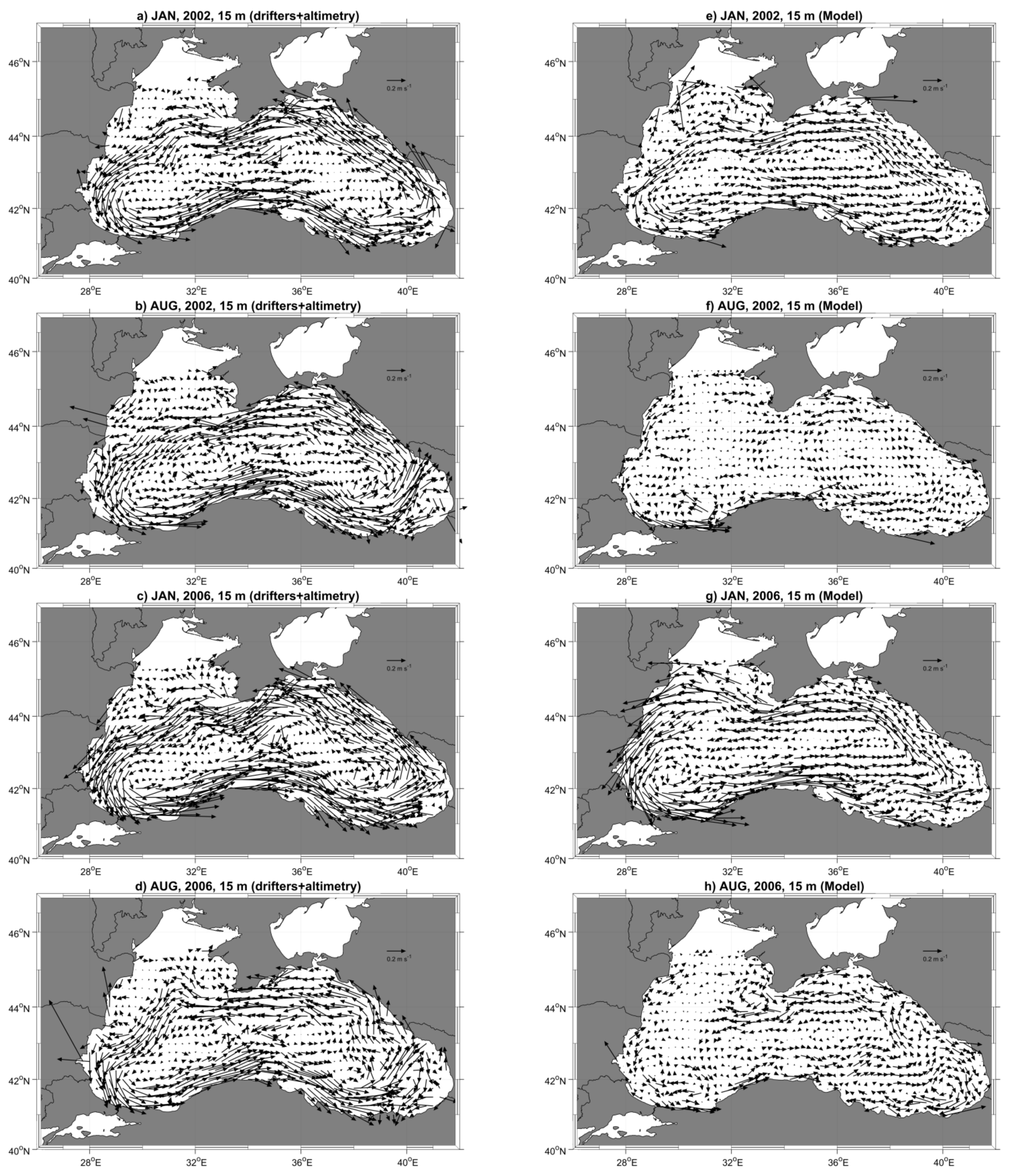
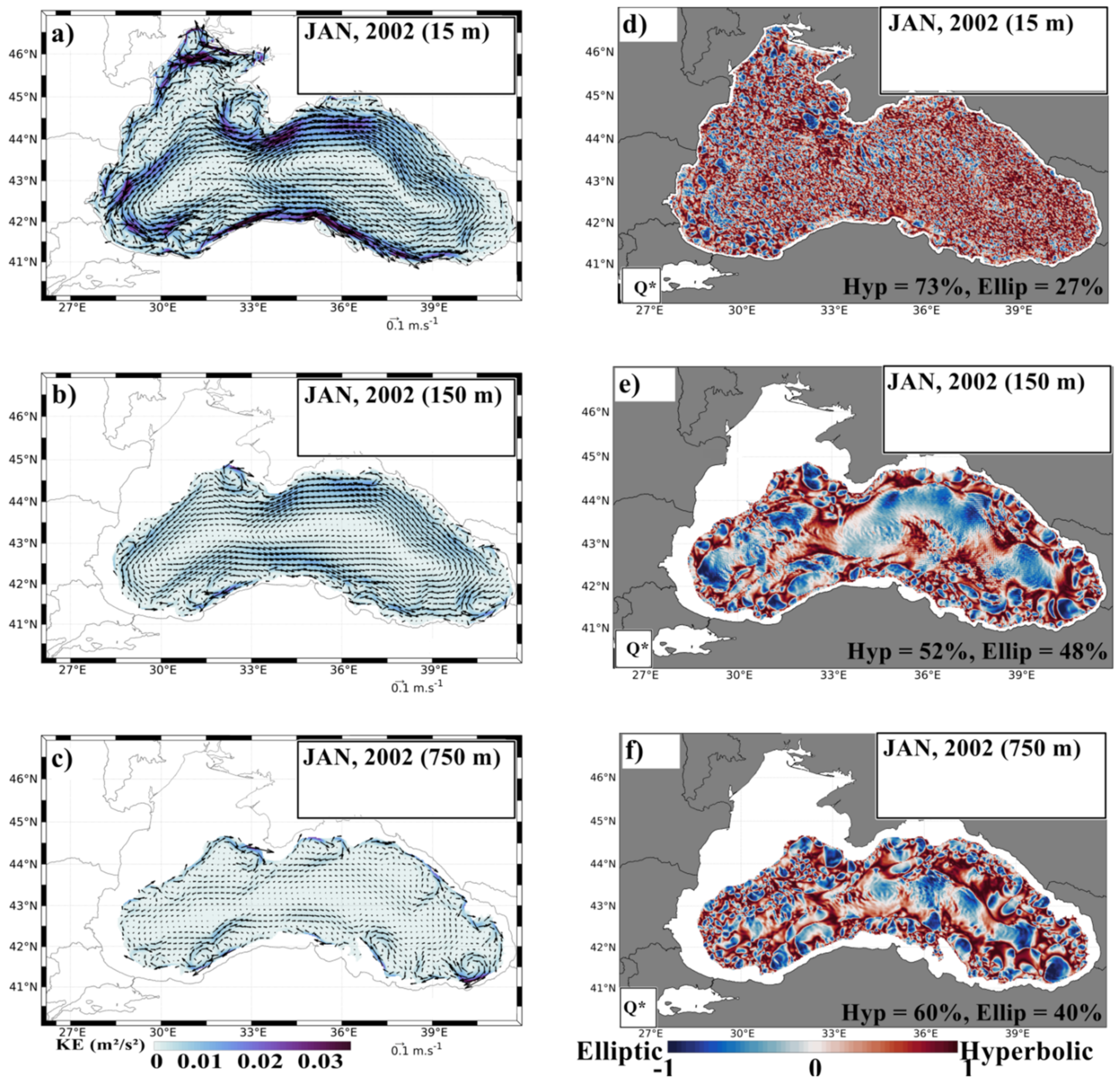
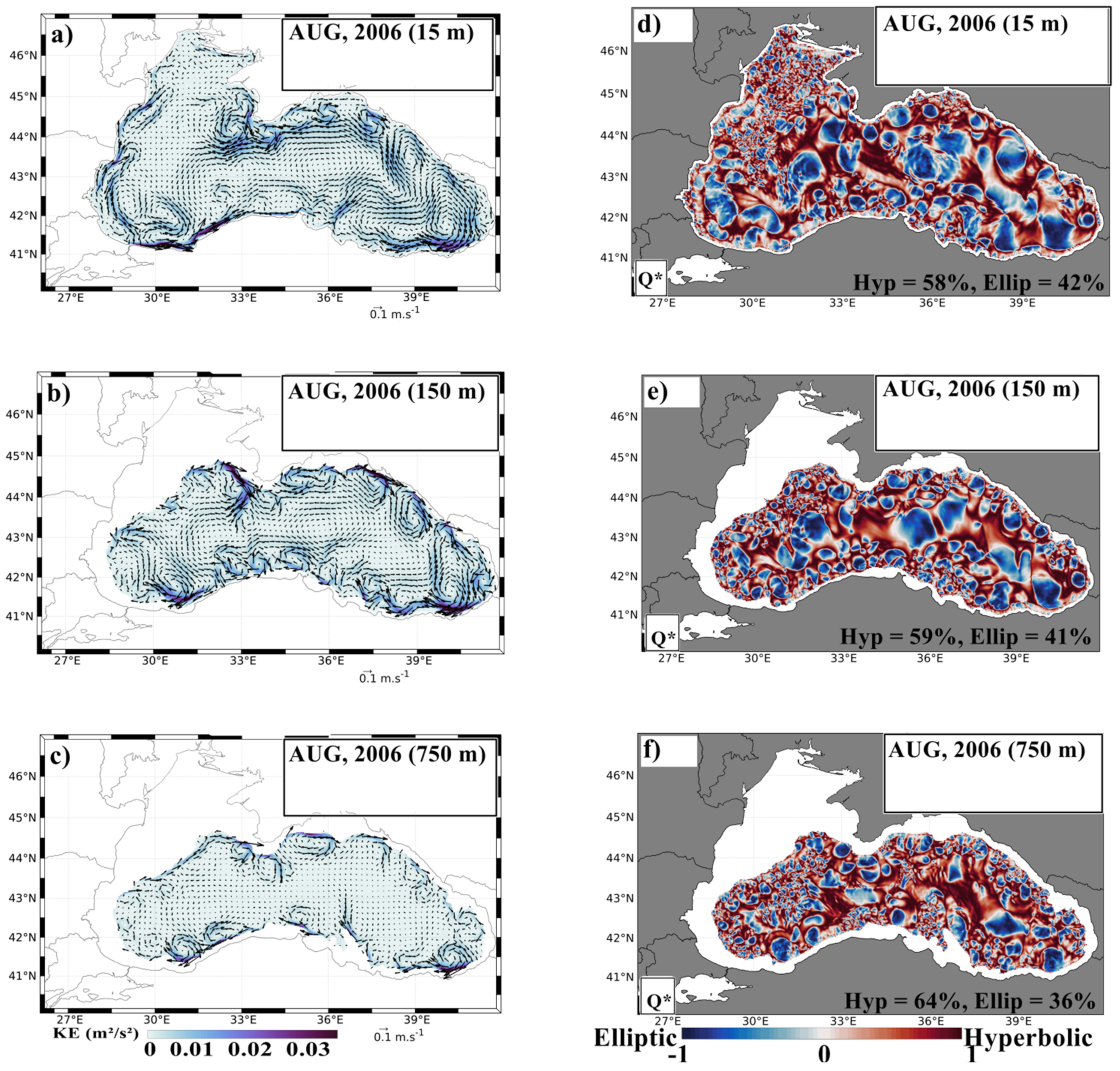
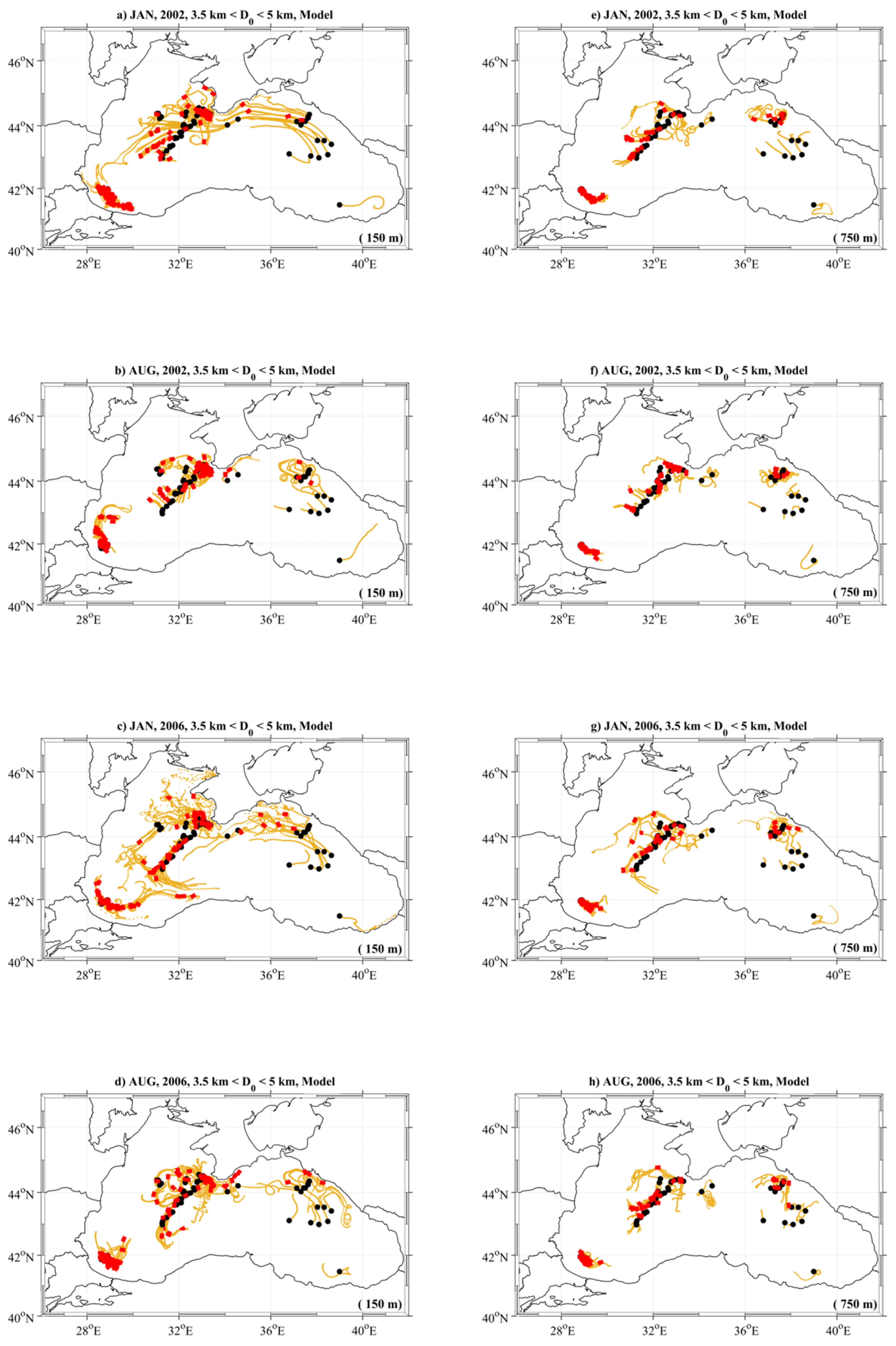
3.1. Circulation of the BS
3.2. Dispersion
3.2.1. Relative Dispersion
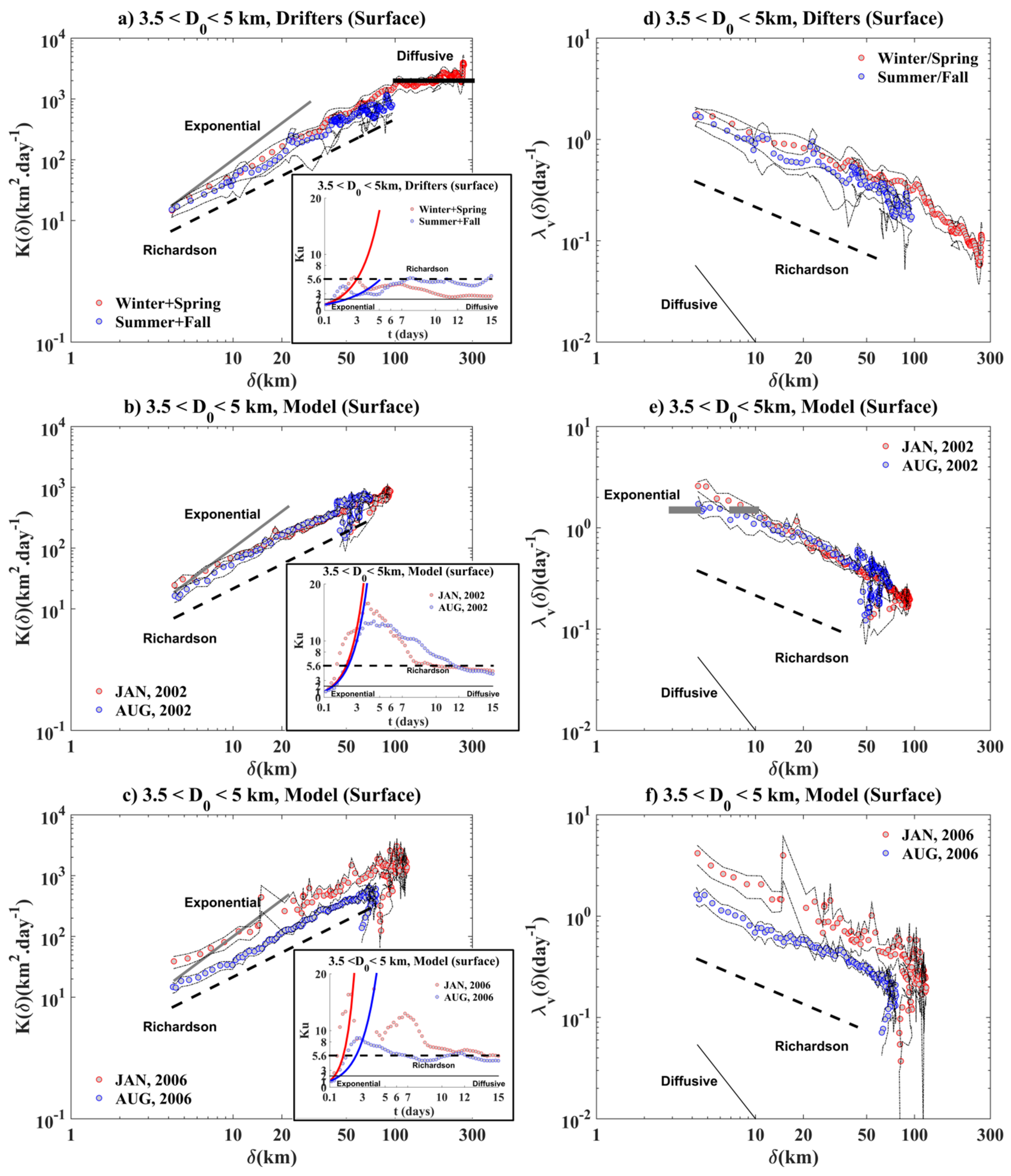
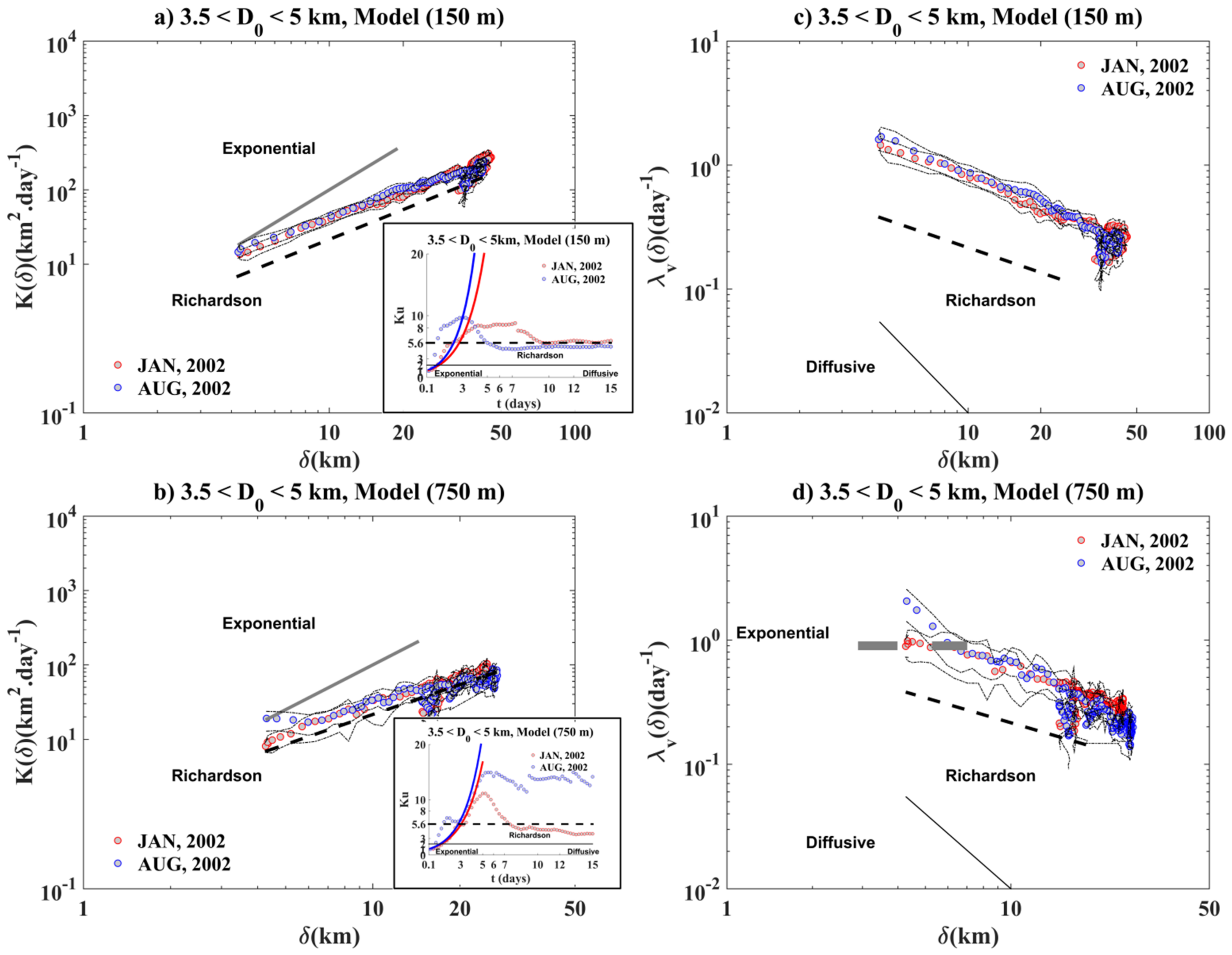
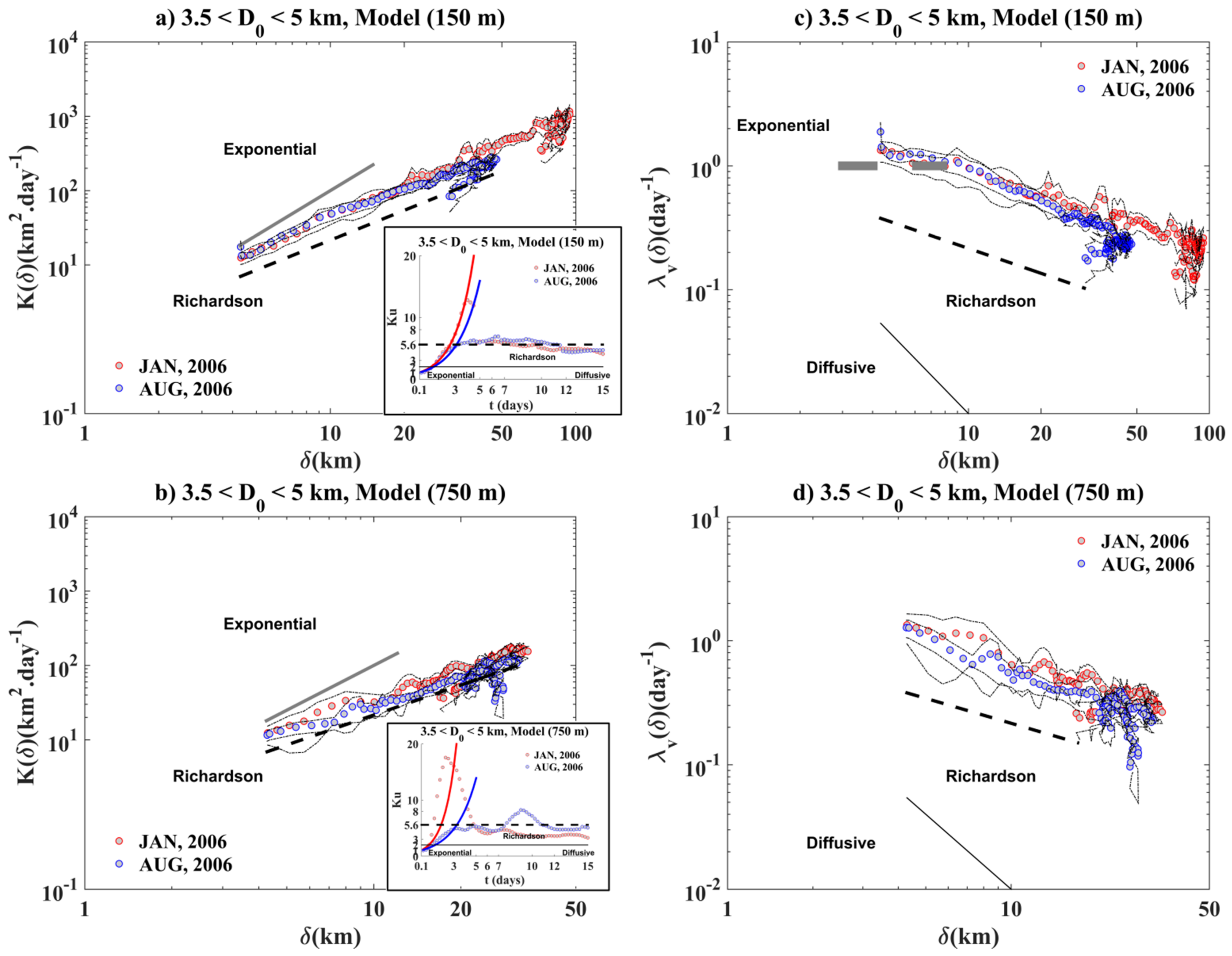
Surface Relative Dispersion
Intermediate and Deep Relative Dispersion
3.2.2. Absolute Dispersion
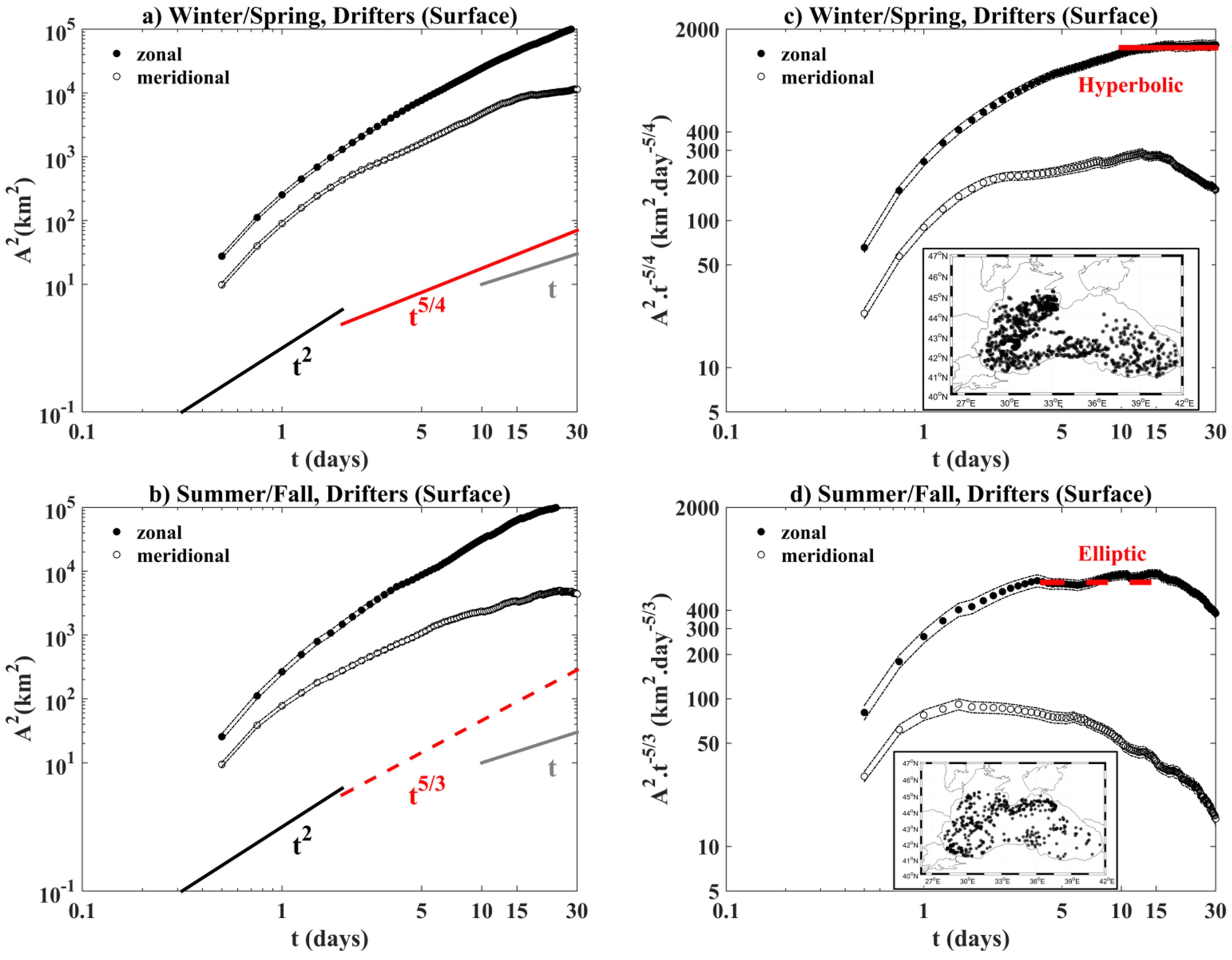
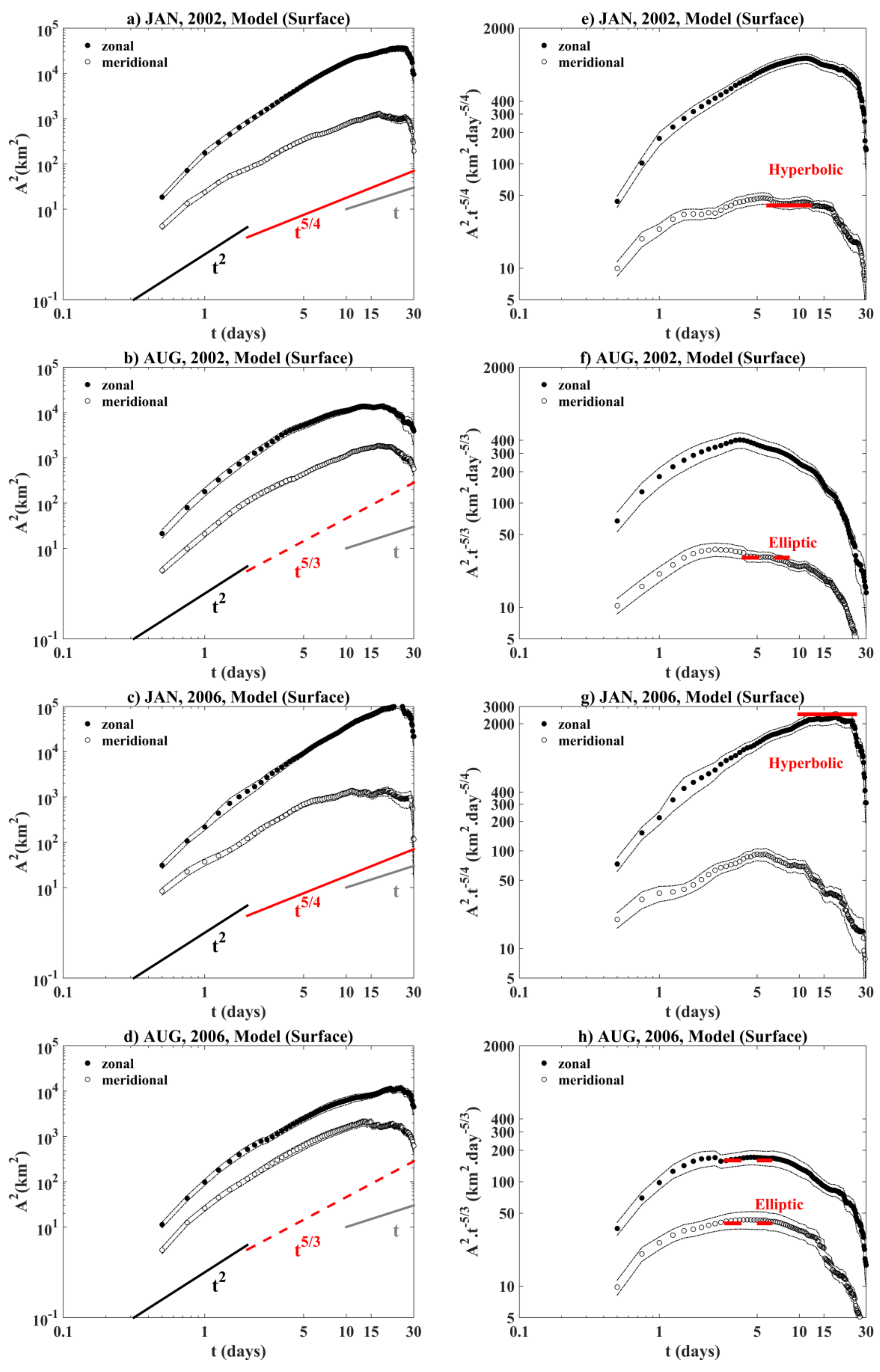
Surface Absolute Dispersion
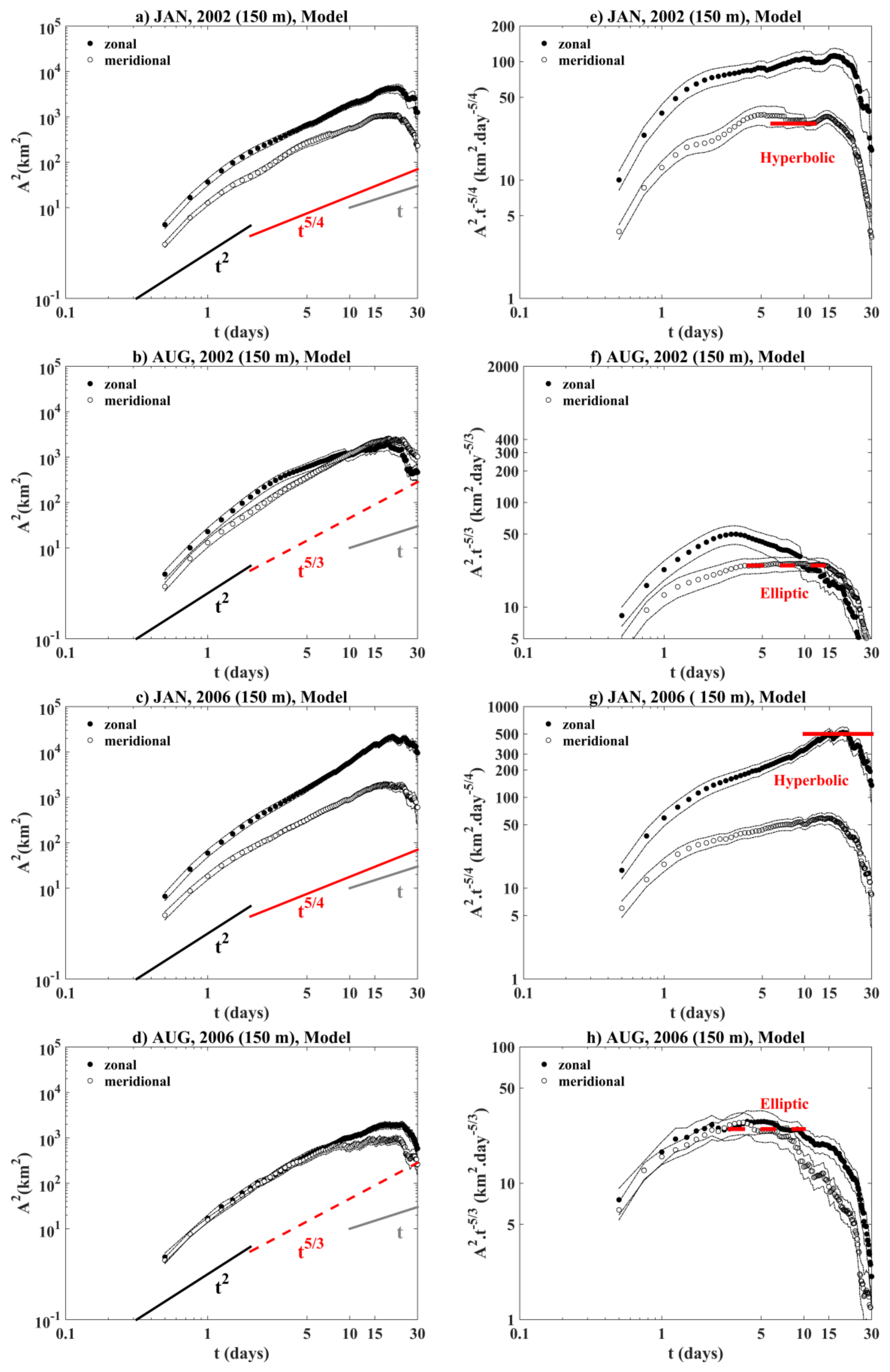
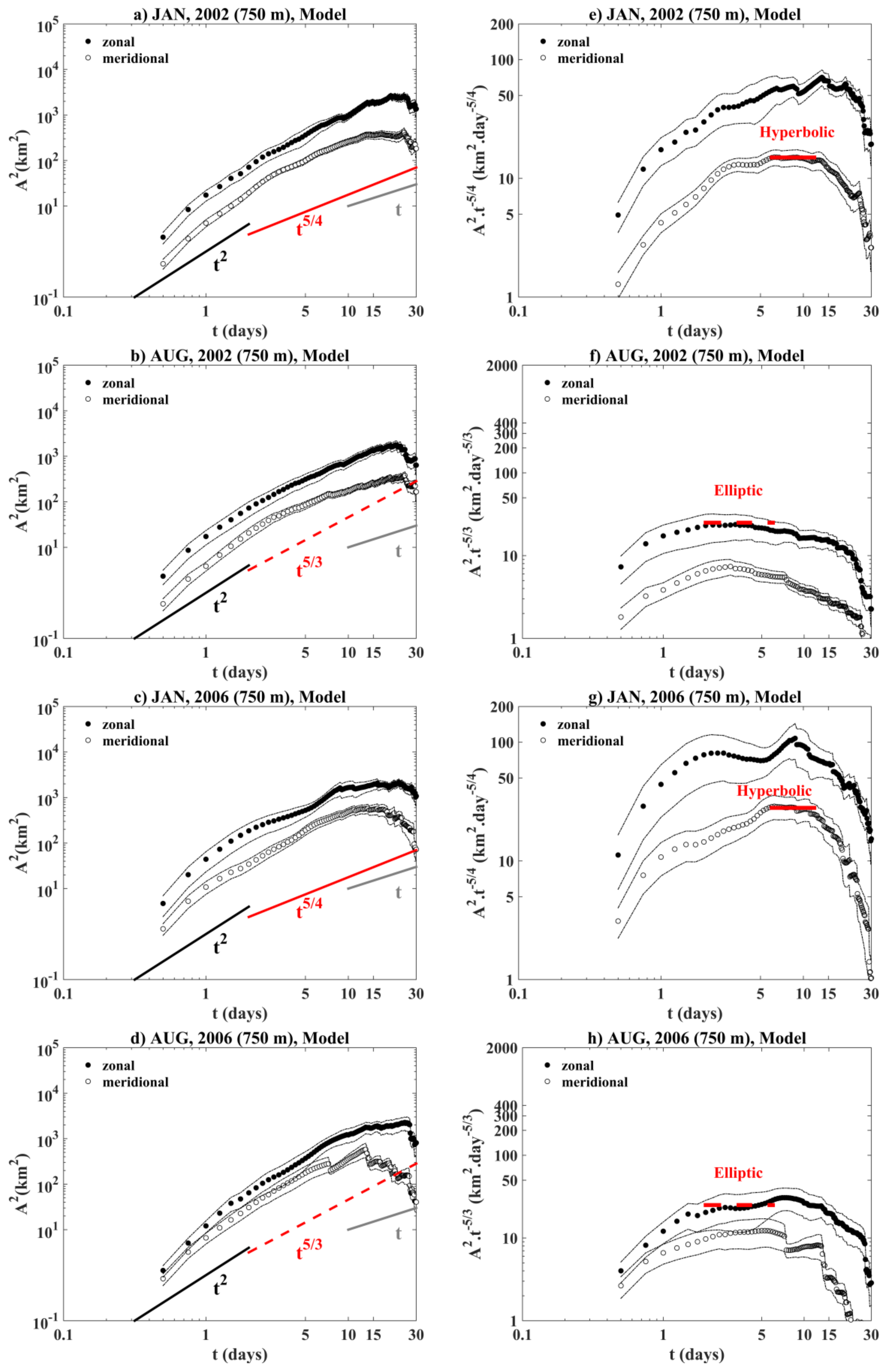
Intermediate and Deep Absolute Dispersion
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gunduz, M.; Özsoy, E.; Hordoir, R.A. Model of Black Sea circulation with strait exchange (2008–2018). Geosci. Model Dev. 2020, 13, 121–138. [Google Scholar] [CrossRef] [Green Version]
- Poulain, P.-M.; Barbanti, R.; Motyzhev, S.; Zatsepin, A. Statistical description of the Black Sea near-surface circulation using drifter in 1999–2003. Deep Sea Res. Part I Oceanogr. Res. Pap. 2005, 52, 2250–2274. [Google Scholar] [CrossRef]
- Kubryakov, A.; Plotnikov, E.; Stanichny, S. Reconstructing large and mesoscale dynamics in the Black Sea region from satellite imagery and altimetry data a comparison of two methods. Remote Sens. 2018, 10, 239. [Google Scholar] [CrossRef] [Green Version]
- Korotenko, K.; Bowman, M.; Dietrich, D. High-resolution numerical model for predicting the transport and dispersal of oil spilled in the Black Sea. Terr. Atmos. Ocean. Sci. 2010, 21, 123–136. [Google Scholar] [CrossRef] [Green Version]
- Tuzhilkin, V.S. General Circulation in the Black Sea Environment. In The Handbook of Environmental Chemistry; Kostianoy, A.G., Kosarev, A.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 5. [Google Scholar] [CrossRef]
- Stanev, E.V. On the mechanisms of the Black Sea circulation. Earth Sci. Rev. 1990, 28, 285–319. [Google Scholar] [CrossRef]
- Oguz, T.; Malanotte-Rizzoli, P.; Aubrey, D. Wind and thermohaline circulation of the Black Sea driven by yearly mean climatological forcing. J. Geophys. Res. 1995, 100, 6846–6865. [Google Scholar] [CrossRef]
- Korotaev, G.K. A reason of seasonal changes of the Black Sea circulation. Mar. Hydrophys. J. 2002, 6, 14–20. (In Russian) [Google Scholar]
- Zatsepin, A.G.; Kremenetskii, V.V.; Poyarkov, S.G.; Poulain, P.-M.; Ratner, Y.B.; Stanichny, S.V. Influence of wind field on the water dynamics of the Black Sea. In Multidisciplinary Investigations of the North-East Part of the Black Sea; Zatsepin, A., Flint, M., Eds.; Nauka: Moscow, Russia, 2002; pp. 91–105. (In Russian) [Google Scholar]
- Capet, A.; Barth, A.; Beckers, J.-M.; Grégoire, M. Interannual variability of Black Sea’s hydrodynamics and conection to atmospheric patterns. Deep Sea Res. Part II Top. Stud. Oceanogr. 2012, 77, 128–142. [Google Scholar] [CrossRef] [Green Version]
- Kubryakov, A.A.; Stanichny, S.V.; Zatsepin, A.G.; Kremenetskiy, V.V. Long-term variations of the Black Sea dynamics and their impact on the marine ecosystem. J. Mar. Syst. 2016, 163, 80–94. [Google Scholar] [CrossRef]
- Oguz, T.; La Violette, P.E.; Unluata, U. Upper layer circulation of the southern Black Sea: Its variability as inferred from hydrographic and satellite observations. J. Geophys. Res. 1992, 97, 12569–12584. [Google Scholar] [CrossRef]
- Toderascu, R.; Rusu, E. Evaluation of the Circulation Patterns in the Black Sea Using Remotely Sensed and in Situ Measurements. Intern. J. Geosci. 2013, 4, 1009–1017. [Google Scholar] [CrossRef] [Green Version]
- Filippov, D.M. The cold intermediate layer in the Black Sea. Oceanology 1965, 5, 47–52. [Google Scholar]
- Ovchinnikov, I.M.; Popov, Y.I. Formation of cold intermediate layer in the Black Sea. Okeanologiya 1987, 27, 739–746. [Google Scholar]
- Menna, M.; Poulain, P.-M. Geostrophic currents and kinetic energies in the Black Sea estimated from merged drifter and satellite altimetry data. Ocean Sci. 2014, 10, 155–165. [Google Scholar] [CrossRef] [Green Version]
- Mariano, A.J.; Griffa, A.; Özgökmen, T.M.; Zambianchi, E. Lagrangian analysis and predictability of coastal and ocean dynamics. J. Atmos. Ocean. Tech. 2002, 19, 1114–1126. [Google Scholar] [CrossRef] [Green Version]
- Griffa, A.; Haza, A.; Oezgoekmen, T.M.; Molcard, A.; Taillandier, V.; Schroeder, K.; Poulain, P.M. Investigating transport pathways in the ocean. Deep Sea Res. Part II Top. Stud. Oceanogr. 2013, 85, 81–95. [Google Scholar] [CrossRef]
- LaCasce, J.H.; Ohlmann, C. Relative dispersion at the surface of the Gulf of Mexico. J. Mar. Res. 2003, 61, 285–312. [Google Scholar] [CrossRef]
- Lumpkin, R.; Elipot, S. Surface drifter pair spreading in the North Atlantic. J. Geophys. Res. 2010, 115, C12017. [Google Scholar] [CrossRef] [Green Version]
- Haza, A.C.; Özgökmen, T.M.; Griffa, A.; Molcard, A.; Poulain, P.-M.; Peggion, G. Transport properties in small-scale coastal flows: Relative dispersion from VHF radar measurements in theGulf of La Spezia. J. Ocean. Dyn. 2010, 60, 861–882. [Google Scholar] [CrossRef]
- Schroeder, K.; Haza, A.C.; Griffa, A.; Ozgoekmen, T.M.; Poulain, P.-M.; Gerrin, R.; Rixen, M. Relative dispersion in the Ligure-Provençal basin: From sub-mescoscale to mesoscale. Deep Sea Res. Part I Oceanogr. Res. Pap. 2011, 58, 209–228. [Google Scholar] [CrossRef]
- Bouzaiene, M.; Menna, M.; Poulain, P.-M.; Elhmaidi, D. Lagrangian dispersion characteristics in the Western Mediterranean. J. Mar. Res. 2018, 76, 139–161. [Google Scholar] [CrossRef]
- Bouzaiene, M.; Menna, M.; Poulain, P.-M.; Bussani, A.; Elhmaidi, D. Analysis of the Surface Dispersion in the Mediterranean Sub-Basins. Front. Mar. Sci. 2020, 7, 486. [Google Scholar] [CrossRef]
- Carratelli, E.P.; Dentale, F.; Reale, F. On the effects of wave-induced drift and dispersion in the deepwater horizon oil spill. Monit. Modeling Deep. Horiz. Oil Spill Rec. Break. Enterp. Geophys. Monogr. Ser. 2011, 195, 197–204. [Google Scholar]
- Weichman, P.B.; Glazman, R.E. Passive scalar transport by travelling wave fields. J. Fluid Mech. 2000, 420, 147–200. [Google Scholar] [CrossRef] [Green Version]
- Meyerjürgens, J.; Ricker, M.; Schakau, V.; Badewien, T.H.; Stanev, E.V. Relative dispersion of surface drifters in the North Sea: The effect of tides on mesoscale diffusivity. J.Geophys. Res. Ocean. 2020, 124, e2019JC015925. [Google Scholar] [CrossRef]
- Oguz, T.; Aubrey, D.G.; Latun, V.S.; Demirov, E.; Koveshnikov, L.; Sur, H.I.; Diacanu, V.; Besiktepe, S.; Duman, M.; Limeburner, R.; et al. Mesoscale circulation and thermohaline structure of the Black sea observed during Hydro Black’91. Deep Sea Res. Part I Oceanogr. Res. Pap. 2014, 41, 603–628. [Google Scholar] [CrossRef]
- Stanev, E.V.; Staneva, J.V. The sensitivity of the heat exchange at sea surface to meso and sub-basin scale eddies. Model study for the Black Sea. Dyn. Atmos. Ocean. 2001, 33, 163–189. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (roms): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Dilmahamod, A.F.; Penven, P.; Aguiar-González, B.; Reason, C.J.C.; Hermes, J.C.A. Model investigation of the influences of the South-East Madagascar Current on the South-East Madagascar Bloom. J. Geophys. Res. Ocean. 2020, 125, e2019JC015761. [Google Scholar] [CrossRef]
- Enriquez, C.E.; Shapiro, G.I.; Souza, A.J.; Zatsepin, A.G. Hydrodynamic modelling of mesoscale eddies in the Black Sea. Ocean Dyn. 2005, 55, 476–489. [Google Scholar] [CrossRef] [Green Version]
- Chawla, A.; Spindler, D.; Tolman, H.L. A Thirty Year Wave Hind Cast Using the Latest NCEP Climate Forecast System Reanalysis Winds. In Proceedings of the 12th International Workshop on Wave Hind Casting and Forecasting, MMAB Contribution, Kona, HI, USA, 30 October–4 November 2011; p. 296. [Google Scholar]
- Chawla, A.; Spindler, D.; Tolman, H. 30 Year Wave Hind Casts Using WAVEWATCH III with CFSR Winds—Phase I; MMAB Contribution NCEP/NOAA: College Park, MD, USA, 2012; p. 12. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Godfrey, J.S.; Wick, G.A.; Edson, J.B.; Young, G.S. Cool-skin and warm-layer effects on sea surface temperature. J. Geophys. Res. 1996, 101, 1295–1308. [Google Scholar] [CrossRef]
- Carton, J.A.; Giese, B.S. A reanalysis of ocean climate using simple ocean data assimilation (SODA). Mon. Weat. Rev. 2008, 136, 2999–3017. [Google Scholar] [CrossRef]
- Renault, L.; McWilliams, J.C.; Kessouri, F.; Alexandre, J.; Frenzel, H.; Chen, R.; Deutsch, C. Evaluation of high-resolution atmospheric and oceanic simulations of the California Current System. Prog. Oceanog. 2021, 195, 102564. [Google Scholar] [CrossRef]
- Medvedev, I.P. Tides in the Black Sea: Observations and Numerical Modelling. Pure Appl. Geophys. 2018, 175, 1951–1969. [Google Scholar] [CrossRef]
- Arabelos, D.N.; Papazachariou, D.Z.; Contadakis, M.E.; Spatalas, S.D. A new tide model for the Mediterranean Sea based on altimetry and tide gauge assimilation. Ocean Sci. 2011, 7, 429–444. [Google Scholar] [CrossRef] [Green Version]
- Lett, C.; Verley, P.; Mullon, C.; Parada, C.; Brochier, T.; Penven, P.; Blanke, B.A. Lagrangian tool for modelling ichthyoplankton dynamics. Environ. Model. Soft. 2008, 23, 1210–1214. [Google Scholar] [CrossRef] [Green Version]
- Miladinova, S.; Macias, D.; Stips, A.; Garcia-Gorriz, E. Identifying distribution and accumulation patterns of floating marine debris in the Black Sea. Mar. Pollut. Bull. 2020, 153, 110964. [Google Scholar] [CrossRef]
- Amemou, H.; Koné, V.; Aman, A.; Lett, C. Assessment of a Lagrangian model using trajectories of oceanographic drifters and fishing devices in the Tropical Atlantic Ocean. Prog. Oceanogr. 2020, 188, 102426. [Google Scholar] [CrossRef]
- Sansón, L.Z.; Perez-Brunius, P.; Sheinbaum, J. Surface relative dispersion in the southwestern Gulf of Mexico. J. Phys. Oceanogr. 2017, 47, 387–403. [Google Scholar] [CrossRef]
- Babiano, A.; Basdevant, C.; LeRoy, P.; Sadourny, R. Relative dispersion in two-dimensional turbulence. J. Fluid Mech. 1990, 214, 535–557. [Google Scholar] [CrossRef]
- Berti, S.; dos Santos, F.A. Relative dispersion and turbulence in the Southwestern Atlantic Ocean from drifter’s data. Chao. Mod. Sim. 2016, 1, 9–20. [Google Scholar]
- Poje, A.C.; Özgökmen, T.M.; Lipphardt, B.L., Jr.; Haus, B.K.; Ryan, E.H.; Haza, A.C.; Mariano, A.J. Submesoscale dispersion in the vicinity of the Deepwater Horizon spill. Proc. Nat. Acad. Sci. USA 2014, 111, 12693–12698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elhmaidi, D.; Provenzale, A.; Babiano, A. Elementary topology of the two-dimensional turbulence from a Lagrangian view-point and single particle dispersion. J. Fluid Mech. 1993, 257, 533–558. [Google Scholar] [CrossRef]
- Okubo, A. Horizontal dispersion of floating particles in the vicinity of velocity singularities such as convergence. Deep Sea Res. Oceanogr. Abstr. 1970, 17, 445–454. [Google Scholar] [CrossRef]
- Weiss, J. The dynamics of the enstrophy transfer in two dimensional turbulence. Phys. D 1991, 48, 273–294. [Google Scholar] [CrossRef]
- Castilla, G.; Hay, G.J. Uncertainties in Land Use Data. Hydrology and Earth System Sciences Discussions; European Geosciences Union: Munich, Germany, 2007; Volume 11, pp. 1857–1868. [Google Scholar] [CrossRef] [Green Version]
- Poulain, P.M.; Menna, M.; Mauri, E. Surface geostrophic circulation of the Mediterranean Sea derived from drifter and satellite altimeter data. J. Phy. Oceanog. 2012, 42, 973–990. [Google Scholar] [CrossRef]
- Kubryakov, A.A.; Stanichny, S.V. Seasonal and interannual variability of the Black Sea eddies and its dependence on characteristics of the large-scale circulation. Deep Sea Res. Part I Oceanogr. Res. Pap. 2015, 97, 80–91. [Google Scholar] [CrossRef]
- LaCasce, J.H.; Bower, A. Relative dispersion in the subsurface North Atlantic. J. Mar. Res. 2000, 58, 863–894. [Google Scholar] [CrossRef]
- Roach, C.J.; Balwada, D.; Speer, K. Horizontal mixing in the Southern Ocean from Argo float trajectories. J. Geophys. Res. Ocean. 2016, 121, 5570–5586. [Google Scholar] [CrossRef] [Green Version]
- Roach, C.J.; Balwada, D.; Speer, K. Global observations of horizontal mixing from Argo float and surface drifter trajectories. J. Geophys. Res. Ocean. 2018, 123, 4560–4575. [Google Scholar] [CrossRef]
- Balwada, D.; LaCasce, J.H.; Speer, K.G.; Ferrari, R. Relative dispersion in the Antarctic Circumpolar Current. J. Phys. Oceanogr. 2020, 51, 553. [Google Scholar] [CrossRef]
- Oguz, T.; Latun, V.S.; Latif, M.A.; Vladimirov, V.V.; Sur, H.I.; Markov, A.A.; Özsoy, E.; Kotovshchikov, B.B.; Eremeev, V.V.; Ünlüata, Ü. Circulation in the surface and intermediate layers of the Black Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 1993, 40, 1597–1612. [Google Scholar] [CrossRef]
- Korotaev, G.; Oguz, T.; Nikiforov, A.; Koblinsky, C. Seasonal, interannual, and mesoscale variability of the Black Sea upper layer circulation derived from altimeter data. J. Geophy. Res. Ocean. 2003, 108. [Google Scholar] [CrossRef]
- Staneva, J.V.; Dietrich, D.E.; Stanev, E.V.; Bowman, M.J. Rim current and coastal eddy mechanisms in an eddy-resolving Black Sea general circulation model. J. Mar. Syst. 2001, 31, 137–157. [Google Scholar] [CrossRef] [Green Version]
- Dymova, O.A.; Miklashevskaya, N.A. Accuracy Estimation of the Black Sea Circulation Modeling Results Obtained at Different Bottom Topography. Phys. Oceanogr. 2019, 26, 304–315. [Google Scholar] [CrossRef] [Green Version]
- Dymova, O.A. Modeling of the Meso- and Submesoscale Dynamic Processes in the Black Sea Coastal Zones. Trans. Kar RC RAS 2017, 21–30. (In Russian) [Google Scholar] [CrossRef] [Green Version]
- Corrado, R.; Lacorata, G.; Palatella, L.; Santoleri, R.; Zambianchi, E. General characteristics of relative dispersion in the ocean. J. Sci. Rep. 2017, 7, 46291. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouzaiene, M.; Menna, M.; Elhmaidi, D.; Dilmahamod, A.F.; Poulain, P.-M. Spreading of Lagrangian Particles in the Black Sea: A Comparison between Drifters and a High-Resolution Ocean Model. Remote Sens. 2021, 13, 2603. https://doi.org/10.3390/rs13132603
Bouzaiene M, Menna M, Elhmaidi D, Dilmahamod AF, Poulain P-M. Spreading of Lagrangian Particles in the Black Sea: A Comparison between Drifters and a High-Resolution Ocean Model. Remote Sensing. 2021; 13(13):2603. https://doi.org/10.3390/rs13132603
Chicago/Turabian StyleBouzaiene, Maher, Milena Menna, Dalila Elhmaidi, Ahmad Fehmi Dilmahamod, and Pierre-Marie Poulain. 2021. "Spreading of Lagrangian Particles in the Black Sea: A Comparison between Drifters and a High-Resolution Ocean Model" Remote Sensing 13, no. 13: 2603. https://doi.org/10.3390/rs13132603
APA StyleBouzaiene, M., Menna, M., Elhmaidi, D., Dilmahamod, A. F., & Poulain, P.-M. (2021). Spreading of Lagrangian Particles in the Black Sea: A Comparison between Drifters and a High-Resolution Ocean Model. Remote Sensing, 13(13), 2603. https://doi.org/10.3390/rs13132603