Abstract
To combat main lobe jamming, preventive measures can be applied to radar in advance based on the concept of active antagonism, and efficient antijamming strategies can be designed through reinforcement learning. However, uncertainties in the radar and the jammer, which will result in a mismatch between the test and training environments, are not considered. Therefore, a robust antijamming strategy design method is proposed in this paper, in which frequency-agile radar and a main lobe jammer are considered. This problem is first formulated under the framework of Wasserstein robust reinforcement learning. Then, the method of imitation learning-based jamming strategy parameterization is presented to express the given jamming strategy mathematically. To reduce the number of parameters that require optimization, a perturbation method inspired by NoisyNet is also proposed. Finally, robust antijamming strategies are designed by incorporating jamming strategy parameterization and jamming strategy perturbation into Wasserstein robust reinforcement learning. The simulation results show that the robust antijamming strategy leads to improved radar performance compared with the nonrobust antijamming strategy when uncertainties exist in the radar and the jammer.
1. Introduction
Main lobe jamming is one of the most challenging jamming types because the jammer and the target are close enough that both are in the main beam of the radar. Common strategies to combat main lobe jamming involve identifying and eliminating jamming signals after the radar is jammed [1,2,3], which can be regarded as passive suppression methods. However, these methods usually require the jammer and the direction-of-look to be separable in angular space. Generally, the smaller the angular separation between the jammer and the direction-of-look, the worse the antijamming performance of the radar is. As a result, these passive suppression methods do not work well (or do not work at all) if the angular separation is small. In this paper, we focus on a situation in which the directions-of-arrival of the received signals incident from the target and the jamming signals are the same, which is common for a target equipped with a self-protection jamming system [4].
The principle of electronic counter-countermeasure (ECCM) techniques is to identify a domain in which the received target signals and the jamming signals can be separated from each other. In fact, such a domain may exist since it is difficult for the jammer to effectively and simultaneously jam both the time and frequency domains. Therefore, in contrast to passive suppression methods, active antagonism requires the radar to actively sense possible unjammed domains and agilely take actions in such domains to avoid being jammed. Specifically, these agile actions include frequency agility in transmission [5], pulse repetition interval agility [6], pulse diversity [7], and so on. Among the above-mentioned agile actions, frequency agility in transmission is considered one effective way to combat main lobe jamming because frequency-agile (FA) radar can actively change its carrier frequency in a random manner. This makes it difficult for the jammer to intercept and jam the radar [5,8,9].
To design FA radar antijamming strategies (hereafter, strategy and policy are used interchangeably), the works in [10,11,12,13] considered a specific jamming strategy situation, and the antijamming strategy design problems were formulated within the framework of the Markov decision process (MDP), which is solved through reinforcement learning (RL) algorithms. The use of RL algorithms to design antijamming strategies has received much attention in the domain of communication [14,15], but its potentiality for radar antijamming requires further exploration. In [10], an RL-based approach was proposed in which FA radar learns the dynamics of the jammer and avoids being jammed. In contrast to the signal-to-noise ratio (SNR) reward signal used in [10], the authors in [11] proposed utilizing the probability of detection as the reward signal, and a similar deep RL-based antijamming scheme for FA radar was proposed. In contrast to the pulse-level FA radar in [10,11], subpulse-level FA radar and a jammer that works in a transmit/receive time-sharing mode were considered in [16], which is more similar to real electronic warfare than the scenarios in [10,11]. In addition, a policy gradient-based RL algorithm known as proximal policy optimization (PPO) [12] was used in [16] to further facilitate the stability of the learning process and improve convergence performance. In [13], the antijamming strategy design was investigated under a partially observable condition, and the authors highlighted that antijamming performance depends on the random nature of the jammer.
As discussed in [10,11,16], FA radar can learn antijamming strategies offline in the training environment and then utilize the learned strategies to combat the jammer in the test environment. At every time step, the jammer will intercept the action of the radar, and the radar will also sense the whole electronic spectrum to infer the action of the jammer. The sensing in these procedures was assumed to be accurate and perfect in the training environment in [10,11,16]. This assumption is not always true in practice because uncertainties exist in both the radar and jammer. For example, if the interception occurs in the frequency domain, then the jammer cannot intercept each radar pulse if it is equipped with a scanning superheterodyne receiver. This is because such a receiver is time multiplexed, and the number of bandwidths that can be scanned [17] is based on a preprogrammed scanning strategy. Even if the jammer is equipped with receivers that have a large instantaneous bandwidth, such as channelized receivers, measurement errors cannot be excluded [17]. Similarly, due to noise and hardware system errors, the radar cannot acquire perfect information about the jammer, even if it can sense the entire electronic spectrum through spectrum sensing [18].
The existence of uncertainties in both the radar and jammer will lead to a mismatch between the presumed and true environment. If uncertainties in the environment are not considered, then radar antijamming performance will be heavily degraded. Therefore, it is of vital importance to design robust antijamming strategies to maintain good performance when uncertainties exist. It should be noted that uncertainties in the jammer were considered in [13], but the best approach to designing robust antijamming strategies remains unknown.
To overcome the uncertainties in both the radar and jammer, a robust antijamming strategy design method for FA radar is proposed in this paper. FA radar and main lobe jamming with a transmit/receive time-sharing jammer are considered and modeled within the framework of RL. The proposed robust method was based on imitation learning [19] and Wasserstein robust reinforcement learning () [20], where imitation learning was used to learn the jammer’s strategy, and was utilized to design a radar strategy that was robust against uncertainties in the jammer’s strategy and itself. The main contributions of this paper are summarized as follows:
- To express the jamming strategy mathematically, a jamming strategy parameterization method based on imitation learning is proposed, where the jammer is assumed to be an expert making decisions in an MDP. Through the proposed method, we can transform the jamming strategy from a “text description” to a neural network consisting of a series of parameters that can be optimized and perturbed;
- To reduce the computational burden of designing robust antijamming strategies, a jamming strategy perturbation method is presented, where only some of the weights of the neural network need to be optimized and perturbed;
- By incorporating jamming strategy parameterization and jamming strategy perturbation into , a robust antijamming strategy design method is proposed to obtain robust antijamming strategies.
The remainder of this paper is organized as follows. The backgrounds of RL, robust RL, and imitation learning are briefly introduced in Section 2. In Section 3, the signal models of the FA radar and the main lobe jammer are presented, and then, the RL framework for the FA radar antijamming strategy design is described. The proposed robust antijamming strategy design method, which incorporates jamming strategy parameterization and jamming strategy perturbation into , is explored in Section 4. Simulation results are shown in Section 5, and Section 6 concludes the paper.
2. Background
2.1. Reinforcement Learning
An RL problem can be formulated within the framework of the MDP, which consists of a five-tuple [21], where S is the set of states, A is the set of actions, describes the probability of transition from the current state to the next state with the chosen action , provides a scalar reward given a state and action , and is a discount factor.
RL emphasizes the interaction between the agent and its environment, and the procedure can be described as follows. At each discrete time step t, the agent is in the state and chooses the action according to the specified policy , which is a function mapping states to a probability distribution over all possible actions. With the obtained state and action , the environment and the agent transition to the next state according to . After that, the agent receives a scalar reward . Finally, the agent collects a trajectory , and the objective of the agent is to find an optimal policy to maximize the cumulative reward, which can be expressed as follows:
where is the cumulative reward of and is a probability density function of trajectory . can be expressed by the transition probability and the policy, which is defined below:
where denotes the initial state distribution.
2.2. Robust Reinforcement Learning
To train an efficient policy for a real-world task, one practical approach is to let the agent interact with the environment in a simulator and then transfer the learned policy to the real world [22]. However, there is a discrepancy between the training environment in a simulator and the real world. Therefore, robust policies are needed to alleviate this discrepancy.
Robust RL is usually based on the idea of the “maxmin” criterion [20,22,23], which aims to maximize the performance of the agent in the worst case. In [23], a softer version of the maxmin objective, the conditional value at risk, was used, and the agent maximized the long-term return for the worst eth percentile of MDPs. Similar to [23], an adversarial agent was introduced to model the uncertainties, and the original agent maximized the long-term reward, while the adversarial agent minimized it [22].
In addition to the methods mentioned above, directly optimizing a maxmin objective can also be used to design robust policies. In [20], a model-free robust policy design method called was proposed. In , the agent formulates robust reinforcement learning as a minmax game, where the agent aims to improve the performance by optimizing its policy, while the environment tries to worsen the performance by changing the dynamic parameters.
Note that the method in [23] requires knowledge of the distribution of environmental parameters that determine the environmental dynamics. Although the method in [22] overcame this problem, a carefully designed adversarial agent was needed, which was difficult to obtain in our problem. In contrast to the methods in [22,23], is model-free and does not require knowledge of the dynamics of the environment. Furthermore, it was based on mathematical optimization and thus more reliable. As a result, was considered in this paper.
2.3. Imitation Learning
Imitation learning aims to derive a policy from demonstration data that are generated by an underlying policy [19]. The demonstration data consist of a series of states and their corresponding actions, which can be expressed as . Note that the states and actions in d are generated by the expert who executes the underlying policy and are different from those in described for RL.
Imitation learning can be accomplished through three main approaches, which are the behavior cloning [19], inverse reinforcement learning (IRL) [24], and generative adversarial imitation learning (GAIL) methods [25].
Behavior cloning regards imitation learning as a supervised learning problem, where a supervised model is trained with training data and labels, which are the states and actions in d, respectively. After the training process ends, the model is capable of predicting an appropriate action for a given state. Behavior cloning is simple and easy to implement. However, each action in the demonstration data d depends on the previous part, which violates the “iid” assumption in supervised learning and results in poor generalization [26].
In IRL, the expert is assumed to make decisions in an MDP/R, which is an MDP without the reward function. In contrast to behavior cloning, IRL can be regarded as a type of indirect imitation learning method, and it aims to recover the reward function on which the expert decisions are based [24]. IRL does not fit single-time-step decisions, so the problem encountered in behavior cloning can be avoided [25].
GAIL extracts a policy from the demonstration data directly and does not need to recover the reward function. Combining imitation learning with generative adversarial networks (GANs), GAIL also trains a generator and a discriminator [25]. The generator is used to produce trajectories whose distribution is close to the distribution of the demonstration data, while the discriminator is used to distinguish them. GAIL has been shown to outperform most existing methods [25]. Based on the above analysis, GAIL was considered in this paper.
3. Problem Statement
3.1. Signal Models of FA Radar and Jammer
Pulse-level FA radar has the capability of changing carrier frequency randomly from pulse to pulse, which imparts the radar with a good ECCM capability [27]. However, if the jammer can react to the current intercepted radar pulse, then the ECCM performance of the pulse-level FA radar will degrade [16]. To improve the ECCM performance against the jammer mentioned above, a subpulse-level frequency-agile waveform [9] was adopted in this paper. For a subpulse-level frequency-agile waveform, one pulse consists of several subpulses, and the radar can change the carrier frequency of each subpulse randomly. It was assumed that a deception subpulse can be chosen for transmission in each pulse. Compared with regular subpulses, less transmitted power can be allocated to the deception subpulse in order to mislead the jammer and protect the regular subpulses from being jammed.
The expression of the subpulse-level frequency-agile waveform in a single pulse at time instant k is provided in (3).
where is the complex envelope, M denotes the number of subpulses, denotes the duration of each subpulse, can have values between 0 and 1, representing how much transmitted power is distributed to this subpulse, and denotes the subcarrier of the subpulse. can be expressed as , where denotes the step size between two subcarriers, represents the initial carrier frequency, and denotes an integer varying from 0 to , with N denoting the number of frequencies available for the radar. The subpulse of is the deception subpulse. Here, represents the rectangle function:
The received signal that includes the target return, the noise signal, and the main lobe suppression jamming signal at time instant k can be expressed as follows:
where is the complex amplitude with respect to subcarrier , is the time delay of the target, is the Doppler frequency with respect to subcarrier , is the noise signal, and is the main lobe suppression jamming signal. Here, is white Gaussian noise, whose mean is zero and variance is . The suppression jamming signal can be regarded as having the same statistical characteristics as the noise signal and can also be modeled as a complex Gaussian distribution [4].
In this paper, it was assumed that the jammer works in a transmit/receive time-sharing mode, which means that the jammer cannot transmit jamming signals and intercept radar signals simultaneously. To jam the radar efficiently, the jammer cannot transmit jamming signals continuously because of the agility of the carrier frequency of the FA radar, and it will interrupt jamming to allow time for the jammer to catch up with the current radar parameters, which is referred to as “look-through” [28].
The jammer was assumed to adopt spot jamming and barrage jamming, which are two typical active suppression jamming types [4]. It should be emphasized that spot jamming is a narrowband signal and barrage jamming is a wideband signal. Although the bandwidth of barrage jamming is wide enough to cover all carrier frequencies of the radar, its power density is much lower than that of spot jamming given the same jammer transmitter power, which greatly weakens the jamming performance. Therefore, it was assumed that the jammer prefers spot jamming to barrage jamming and only adopts the latter under certain conditions due to its limited transmitter power.
For one radar pulse at time step t (the time step is equivalent to the pulse index in the radar scenario), we considered three possible jammer choices, which are stated as follows and depicted in Figure 1:
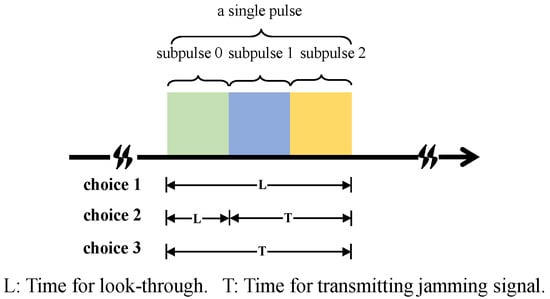
Figure 1.
Three possible jammer choices.
- Choice 1: The jammer performs the look-through operation throughout the whole pulse, which means that the jammer does not transmit a jamming signal and just intercepts the radar waveform;
- Choice 2: The jammer performs the look-through operation for a short period, and then, the jammer transmits a spot jamming signal with a central carrier frequency of or a barrage jamming signal;
- Choice 3: The jammer does not perform the look-through operation and just transmits a spot jamming signal with a central carrier frequency of or a barrage jamming signal.
3.2. RL Formulation of the Anti-Jamming Strategy Problem
As in [10,11], the MDP was used to describe the interaction between the FA radar and the jammer, which were regarded as the agent and the environment, respectively. Here, is used to denote this MDP.
At time step t, the FA radar is in state and then takes action . The jammer performs look-through and/or transmits jamming signals according to predefined rules, and as a result, the state transitions to and the radar receives a scalar reward . The basic elements, including actions, states, and rewards, in our RL problem were previously defined in [16], and we apply these definitions herein. These definitions are briefly reviewed below.
Actions: There are M subpulses in one pulse, including the deception subpulse and regular subpulses. For each regular subpulse, the radar can select one frequency from N available frequencies. For the deception subpulse, the radar can not only decide whether it is transmitted or not, but also determine its subcarrier if it is transmitted.
Here, the radar action at time step t is encoded into a vector with size . All elements except for the first one in are within 0 and , which corresponds to the subcarriers of regular subpulses varying from to . For the deception subpulse, the first element in is within 0 and N, in which N means that the deception subpulse is not transmitted. Taking as an example, means that the radar does not transmit the deception subpulse, and the subcarriers of the other two subpulses are and , respectively.
The action of the jammer can also be encoded into a vector with the size , which is described as follows. If Choice 1 is selected, then can be expressed as , where ⌀ is just used to ensure that the lengths of are equal. For Choices 2 and 3, if the jammer transmits a barrage jamming signal, then is denoted as ; if the jammer transmits a spot jamming signal, then is denoted as with , corresponding to the central carrier frequency of the spot jamming signal.
States: The -order history [21] is used to approximate the state to alleviate the problem of partial observability, and state can be expressed as follows:
where is the observation of the radar and is actually the action of the jammer at time step t.
Reward: The proposed method still applies the probability of detection as the reward signal [11,16], and the goal of the FA radar is to find an optimal strategy to maximize in one coherent processing interval (CPI). If the frequency step between two frequencies is greater than , with c denoting the speed of light and l denoting the target along the radar boresight, then their corresponding target returns will be decorrelated [29]. If the frequency step is less than , then their corresponding target returns are partially correlated.
To simplify the analysis, we assumed that the frequency step was large enough to decorrelate the target returns. In one CPI, the target returns with the same subcarriers can be first integrated coherently, and then, all coherent integration results of all subcarriers can be processed by the SNR weighting-based detection (SWD) algorithm [30]. This procedure is illustrated in Figure 2, and the detailed calculation procedure of is given in Appendix A.
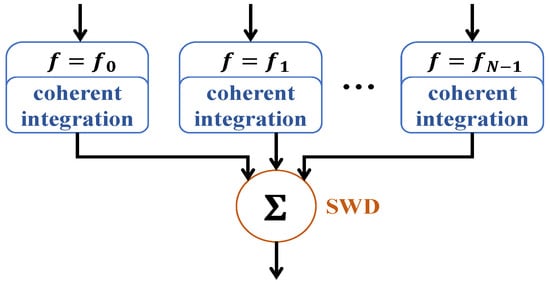
Figure 2.
Signal processing procedure for the FA radar.
In practice, the radar will make use of all pulses in one CPI to detect the target, meaning that it only receives the reward at the end of one CPI. This will result in a sparse reward problem, which hinders the learning of the radar. To address this problem, an additional negative reward v, which is proportional to the signal-to-interference-plus-noise ratio (SINR) of that pulse, is given. The overall reward signal can be expressed as follows.
4. Radar Robust Antijamming Strategy Design
4.1. Robust Formulation
Given a predefined jamming strategy, an optimal antijamming strategy can be obtained by using a large number of RL algorithms in the training environment based on the perfect sensing and interception assumption. As mentioned previously, if this antijamming strategy is used in a test environment in which uncertainties exist in the radar and the jammer, then antijamming performance may degrade because of the mismatch between the training and test environments.
From an RL perspective, uncertainties in the radar and the jammer will result in a discrepancy in the transition probability between the training and test environments. A detailed explanation is given as follows. In Figure 3, the left and right images illustrate the transition probability in the training and test environments, respectively. When the radar is in the training environment, the current state of the radar is , and it will choose an action according to the policy , as shown in the left image in Figure 3. Based on the perfect sensing and interception assumption, the observation of the radar is , and the next state will transition to . When the radar is in the test environment, it is assumed that it is also in and chooses an action , which is the same as the radar in the training environment. The difference is that the observation of the radar may not be the same as due to errors caused by the jammer. In the right-hand image in Figure 3, we use a circle filled with dotted lines to distinguish it from the observation in the training environment. As a result, the next state will not be . Given the same current state and action , the resultant next state is different. Therefore, there exists a discrepancy between the transition probability in the training and test environments. Thus, we considered a robust antijamming strategy design problem, where the transition probability of the test environment deviates from that of the training environment.
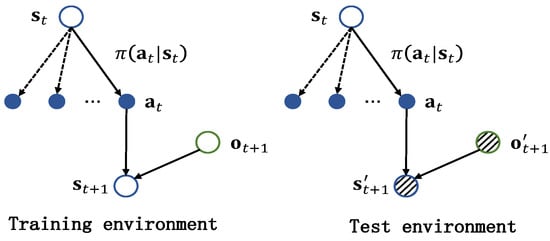
Figure 3.
Illustration of the transition probability in the training and test environments.
Based on the above analysis, [20] is used to solve the radar robust antijamming strategy design problem. As reported in [20], the transition probability of the environment is determined by dynamic parameters. Taking the CartPole [31] task as an example, the length of the pole is the dynamic parameter, and the transition probability varies with the length of the pole. Given the reference dynamic parameters of a task, perturbs the dynamic parameters to determine the worst-case scenarios within an -Wasserstein ball and identifies a policy with parameters to maximize the worst-case performance. With the help of zeroth-order optimization [32], is able to handle high-dimensional tasks.
The objective function of can be expressed as follows:
where is the Wasserstein distance of order 2 [20] between and , is the radius of the -Wasserstein ball, is a policy with a uniform distribution over actions given the state , and follows a uniform distribution over states . For notational convenience, the term in (8) is ignored in the rest of the paper.
As discussed previously, the uncertainties in the radar and those in the jammer have the same effect on the change in the transition probability. As a result, only the uncertainties in the jammer are considered in this paper. In the radar and the jammer scenario, the reference dynamic parameters can be regarded as the jamming strategy in the training environment with the perfect interception assumption. The dynamic parameters can be regarded as jamming strategies with the existence of uncertainties. However, cannot be applied directly. The reasons and their corresponding solutions are given below:
- (1)
- The dynamic parameters remain unknown for a given jamming strategy, and we can only describe it using predefined rules. For example, a jamming strategy can be expressed by the following rule: the jammer transmits a spot jamming signal whose central frequency is based on the last intercepted radar pulse. Therefore, we proposed a method of imitation learning-based jamming strategy parameterization, as presented in Section 4.2, which aims to express the jamming strategy mathematically;
- (2)
- After jamming strategy parameterization, the jamming strategy can be expressed in a neural network consisting of a series of parameters. As is shown later, the number of parameters of this neural network is large, which will lead to a heavy computational burden. Thus, a jamming parameter perturbation method is provided in Section 4.3 to alleviate this problem.
The final robust radar antijamming strategy design method is described in Section 4 and incorporates jamming strategy parameterization and jamming parameter perturbation into .
4.2. Jamming Strategy Parameterization
Dynamic parameters can be easily acquired from a gym environment and perturbed to determine the worst-case scenarios to design a robust RL strategy [20]. Intuitively, the jamming strategy was perturbed in this way in [20]. However, how to characterize or describe the jamming strategy remains unsolved. To this end, a method of imitation learning-based jamming strategy parameterization was proposed to express jamming strategies in a neural network that consists of a series of parameters.
To realize the target mentioned above, a basic assumption about the jammer was made and can be stated as follows.
Assumption: During the interaction between the radar and the jammer, the jammer is also an agent described by MDP with an optimal policy , meaning that its action at every time step is optimal and maximizes its long-term expected reward.
It should be emphasized that is different from the mentioned in Section 3, and a superscript is used to distinguish between them. Note that may not exist in practice; however, this assumption is indeed reasonable because there is always an internal motivation for the jammer’s decisions, which it views as optimal. As a consequence, the jammer can be regarded as an expert whose actions are optimal, and we can learn its implicit policy from the expert trajectories using a series of parameters, which is referred to as jamming strategy parameterization in this paper.
Jamming strategy parameterization can be segmented into two phases: gathering expert trajectories and deriving a policy from these expert data [33]. The first phase is easy to implement. Given a predefined jamming strategy, the trajectories can be collected through the interaction between the radar and the jammer, as shown in Figure 4, with denoting the number of trajectories to be collected. Note that this predefined jamming strategy cannot be expressed mathematically and thus can be regarded as a given rule that instructs the jammer how to choose actions to jam the radar. The trajectory can be expressed as , where and are the states and actions of the jammer, respectively.
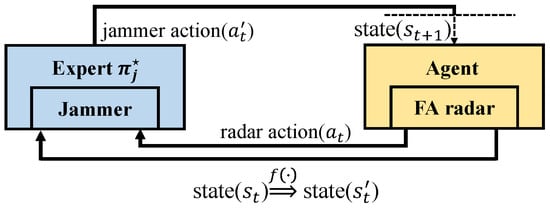
Figure 4.
Trajectory collection of the given jamming strategy.
As shown in Figure 4, gathering the expert trajectories can be achieved based on of the radar antijamming strategy design. At time step t, the jammer action is actually the observation in , and the state can be obtained from , with the input being the state in . Here, is a function that maps from to and is designed to extract useful features for the jammer. Once the trajectories are obtained, imitation learning methods can be used to derive its policy.
The derivation of the policy can be regarded as an IRL problem based on the aforementioned assumption, which can be described as a unified objective function:
where is the implicit reward function of , is a convex cost function regularizer to avoid overfitting, is the set of all stationary stochastic policies, and is the entropy of the policy. Note that (9) looks slightly different from the function given in [25]; the difference is that, here, the agent is assumed to maximize the long-term reward rather than minimize it.
As shown in (9), IRL aims to find a reward function that assigns high reward to the expert policy and low reward to other policies. If IRL methods, such as [24,34], are used to derive the jamming strategy, two steps are needed: recovering the reward function and finding the optimal policy under that obtained reward function. Let the recovered implicit reward function be and its corresponding optimal policy be , which can be considered the derived jamming strategy.
In this paper, we applied an alternative method called GAIL, which stems from the basic concept of IRL in (9), but the step of recovering the reward function is not necessary. More specifically, it can be proven that the final policy mentioned above can be obtained directly by solving in (10) [25].
In (10), is a discriminative classifier that maps the input to a real number ranging from 0 to 1, and is a real number controlling the entropy regularizer.
The policy and the classifier can be parameterized with and , where the solution to (10) is the derived jamming strategy, and is its corresponding jamming parameters. In fact, (10) satisfies the definition of the GAN [35], where the policy can be regarded as the generator and the classifier D is the discriminator.
Algorithm 1 is the overall algorithm of jamming strategy parameterization. Before the algorithm starts, a predefined jamming strategy and a mapping function are needed. Note that was specifically designed for this given jamming strategy. The predefined radar policy is used in the expert trajectory collection phase, which can be a random policy. The first phase is gathering the expert trajectories. In the second phase, a fixed number of trajectories of are first collected, and then, the gradient of the discriminator can be estimated based on Monte Carlo estimation, which is given below.
The update procedure of the generator can be achieved through any RL algorithms with a reward function . Here, TRPO [36] was adopted. The termination condition can be the convergence of the cumulative reward of the generator. Once the termination condition is satisfied, the jamming strategy parameterization is complete.
4.3. Jamming Parameter Perturbation
Through jamming strategy parameterization, the reference jamming parameters and the jamming parameters that need to be optimized and perturbed can both be expressed by neural networks. Let and be the weights of the layer of and , respectively, with and denoting the input and output sizes of this layer. If there are H layers in total, they can be denoted as and , respectively (here, we ignore the biases in and ).
As shown later, a frequent matrix inversion operation is needed during the procedure of robust antijamming strategies, and the dimension of that matrix is related to the dimension of . The dimension of may be high, and an example is described in the following. For a three-layer neural network with and , the number of parameters is 1200. For certain complicated jamming strategies, networks with more parameters are always needed. As a result, there will be a heavy computational burden if the minimization problem in (8) is solved directly.
| Algorithm 1: Jamming strategy parameterization. |
| Input: Predefined jamming strategy, mapping function , the number of pulses in one CPI T, the number of trajectories to be collected , the initial parameters of and as , , predefined radar policy , an empty list Output: The parameters of when GAIL is convergent |
 |
To alleviate the problem mentioned above, we propose an alternating procedure, inspired by NoisyNet, to perturb the jamming parameters [37]. More specifically, can be expressed by the combination of two terms, the reference jamming parameters and an extra term that can be expressed as . To reduce the number of parameters that need to be perturbed, the elements in each column of were set to be the same, which means that only variables need to be perturbed. The relationship between the hth element in , the hth element in and the hth element in is displayed in Figure 5, and the mathematical expression is as follows:
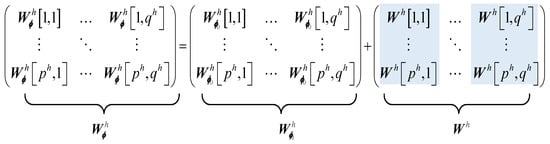
Figure 5.
Jamming parameter perturbation. In , the elements in each column are the same, and their background color is blue.
If the proposed perturbation method is adopted, only needs to be perturbed and optimized in (8), and a new objective function can be obtained, as shown in (13).
where . Clearly, the computational burden greatly decreases. With respect to the example mentioned above, there are only 60 parameters in total.
4.4. -Based Robust Anti-Jamming Strategy Design
In the above subsections, the imitation learning-based jamming strategy parameterization is first proposed, and its corresponding perturbation method is then presented. Incorporating them into , the robust radar antijamming strategy design is presented in this subsection.
As described above in (13), a “maxmin” objective function with respect to and needs to be solved to design a robust strategy, which is slightly different from the original objective function of . However, we can still use the method proposed in [20] to solve it. More specifically, that problem can be solved through an alternating procedure that interchangeably updates one variable while the other remains fixed. This procedure is described briefly in the following.
Let the jamming parameters be at the iteration. The policy parameter is updated to find the optimal policy as follows.
In fact, this is just an RL problem and can be solved by any type of RL algorithm. In this paper, TRPO [36] was used to obtain the current policy, which can be denoted as . After that, the jamming parameter is updated to determine the worst case with respect to , which is expressed as follows:
where .
To solve this minimization problem with a constraint, first-order and second-order Taylor expansions of the objective function and the constraint, respectively, are performed to simplify the analysis. Consider a pair of parameters and . The result is given below, and the detailed derivation can be found in [20].
where , is the Hessian matrix of the constraint in (13) at (), and its expression is given in (17).
The closed-form solution to (16) given below can be easily obtained through the Lagrange multiplier method [20]:
where is the gradient of the expected cumulative reward with respect to at , i.e., . Thus, the jamming parameters can be expressed as .
The estimation of and can be achieved via a zero-order optimization method [32,38]. According to the two propositions in [20], and can be expressed as follows.
As shown in (19) and (20), a random variable with the same size as is sampled from the given Gaussian distribution to perturb .
The procedure mentioned above can be repeated until the maximum number of iterations is reached.
5. Simulation Results
In this section, the performance of jamming strategy parameterization and the robust antijamming strategy design is verified. The basic parameters of the FA radar and the main lobe jammer are given in Table 1.

Table 1.
Parameters of the FA radar and the jammer.
Given the length of the target along the radar boresight l, the frequency step required to decorrelate the target can be calculated by MHz. Therefore, the frequency step size needs to be larger than . In addition, if is just comparable to , then the power density of barrage jamming may still be high because its power is distributed over a narrow bandwidth. Thus, the frequency step size was set to 100 MHz, which was large enough to decorrelate the target and reduce the power density of barrage jamming. It was assumed that the radar cross-section (RCS) of the target does not fluctuate at the same frequency, but the RCS may differ among different frequencies. Without loss of generality, the RCS with respect to these three frequencies was set to σRCS = [3 m2, 3 m2, 3 m2].
If the jammer adopts spot jamming, it was assumed that its jamming power would be distributed over a frequency band whose bandwidth is , which is wider than B. If the jammer adopts barrage jamming, its jamming power was assumed to be distributed over a frequency band whose bandwidth is MHz to cover all possible frequencies of the FA radar. The last observations and actions were used to approximate the history . In addition, , , and in (3) were predefined and set to [0,1,1] or [0.2,0.9,0.9], depending on whether the deception subpulse was transmitted.
According to the radar equation [29], the SINR used to calculate the probability of detection in (A2) and (A3) can be easily calculated based on these basic simulation parameters. More specifically, the received power scattered by the target with respect to different RCSs, the received jamming power , and the noise power can be calculated as follows:
where is the wavelength. The power of the thermal noise in the radar receiver can be calculated by , where J/K is Boltzmann’s constant, K is the system noise temperature, and is the noise bandwidth. With all parameters of the radar and the jammer given, the received power , the noise power , and the received jamming power can be obtained; therefore, the SNR (when the radar is not jammed) and the SINRs (when the radar is jammed) can be easily calculated.
Figure 6 shows three different jamming strategies that were used to verify the effectiveness of the proposed method. Jamming Strategy 1 selects Choice 2, while Jamming Strategies 2 and 3 select Choices 1 and 3 simultaneously. To simplify the analysis, it was assumed that the duration of look-through and jamming signal transmission was an integer multiple of the duration of each subpulse, as shown in Figure 6. These three different jamming strategies are described as follows.
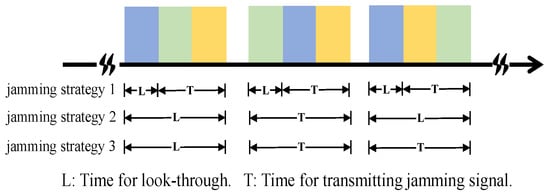
Figure 6.
Three different jamming strategies.
Jamming Strategy 1: The duration of look-through for Jamming Strategy 1 is short, and the jammer transmits spot jamming once the radar signal is intercepted. The central frequency of spot jamming is the same as the subcarrier of the intercepted radar signal, meaning that the jammer will be misled if the deception subpulse is transmitted.
Jamming Strategy 2: For Jamming Strategy 2, the jammer performs the look-through operation for the first pulse to intercept the whole pulse. For the next pulse, the jammer only transmits the jamming signal. The jammer will ignore the deception subpulse and jam the regular subpulses. If there are two different subcarriers in this intercepted pulse, the jammer will adopt barrage jamming. If not, the jammer will adopt spot jamming, whose central frequency is the same as that of the intercepted subpulse.
Jamming Strategy 3: Jamming Strategy 3 is similar to Jamming Strategy 2. The only difference is that the jammer will jam the next two pulses based on the last intercepted pulse.
5.1. Performance of Jamming Strategy Parameterization
In this subsection, the performance of jamming strategy parameterization is tested. Some details are first provided.
As mentioned above, a mapping function is needed when the expert trajectories are collected. For the three different jamming strategies, different mapping functions were designed to enhance learning performance.
With respect to Jamming Strategies 1 and 2, can be expressed as follows.
The state of Jamming Strategies 1 and 2 at time step t only extracts the most recent action of the radar since this information is sufficient for GAIL to derive the strategy of the jammer. With respect to Jamming Strategy 3, can be expressed as in (23):
where is the operation for calculating the remainder and is an indicator function that equals one if the subcarriers and in are the same. The state of Jamming Strategy 3 not only contains the most recent action of the radar, but also includes the time and frequency information about the radar.
Fully connected neural networks with four layers and thirty-two hidden units in each layer were used to parameterize the generator and the discriminator in GAIL. expert trajectories were generated to train GAIL to parameterize the jamming strategy. The parameterization performance with respect to three jamming strategies is given in Figure 7. The Wasserstein distance was used to evaluate how close the distance was between the derived jamming strategies and the predefined jamming strategies, and the y-axis in Figure 7 denotes their Wasserstein distance after each training epoch. As shown in Figure 7, their Wasserstein distance converged to zero. This means that the predefined jamming strategy can be expressed by the derived jamming strategy, which consists of a series of parameters .
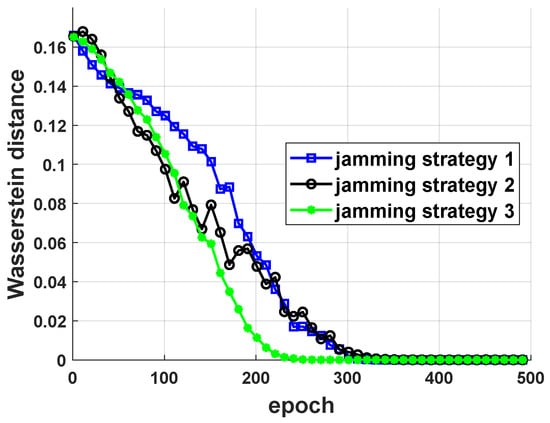
Figure 7.
Parameterization performance with respect to three different jamming strategies.
For a better understanding, Figure 8 presents the learning results of the derived jamming strategy for Jamming Strategy 1 in multiple phases. Here, the radar adopted a random strategy to select subcarriers. The derived jamming strategies were used to jam the random radar when their Wasserstein distance was 0.17, 0.025, and 0. The actions of the jammer induced by the derived jamming strategies and predefined Jamming Strategy 1 are plotted in Figure 8, which are denoted as “parameterization” and “ground truth”, respectively. It can be seen that the difference between the actions induced by the derived jamming strategies and predefined Jamming Strategy 1 became smaller as the Wasserstein distance decreased.
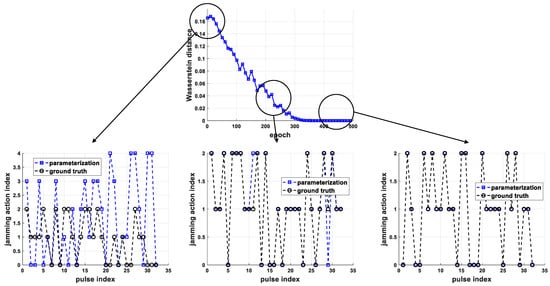
Figure 8.
Illustration of the derived jamming strategy in multiple phases.
For jamming strategy parameterization, the number of expert trajectories is of critical importance. For an imitation learning task, more expert trajectories mean that the agent can collect more information about the expert, which will result in better performance. For the problem considered here, as increased, the performance of jamming strategy parameterization improved.
In Figure 9, Jamming Strategy 1 is used as an example to show the influence of on the performance of jamming strategy parameterization. Three different cases were considered, where was set to 10, 100, and 200, respectively. As shown in Figure 9, when , the performance of jamming strategy parameterization was the worst. It can be seen in Figure 9 that the performance of jamming strategy parameterization was similar when and . Therefore, was set to 100 in this paper.
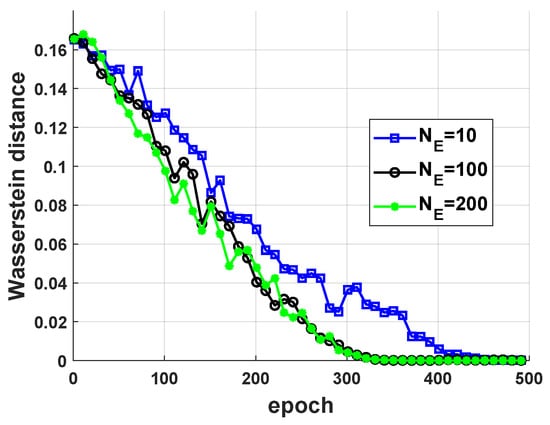
Figure 9.
The influence of on jamming strategy parameterization performance.
5.2. Performance of Robust Antijamming Strategy Design
Before presenting the results of the robust antijamming strategy design, we first present the training performance against three different jamming strategies under the perfect interception assumption. As shown in Figure 10, the performance obtained through the RL algorithm (TRPO was used here) was compared with the performance of a random strategy to show its effectiveness (random strategy means that the radar chooses actions randomly at each pulse).
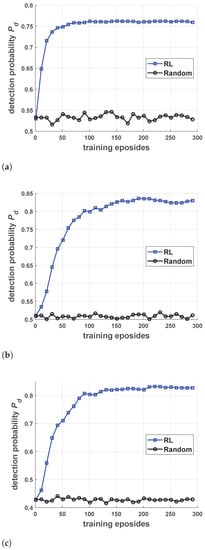
Figure 10.
The training performance against three different jamming strategies with the perfect interception assumption. (a–c) presents the training performance against Jamming Strategy 1, 2 and 3, respectively.
As shown in Figure 8, the magnitude of the uncertainties in the jammer was equivalent to the magnitude of the Wasserstein distance between a jamming strategy and its corresponding reference jamming strategy. As a consequence, numerous random jamming strategies were generated to test the robustness of the obtained antijamming strategies. Note that the Wasserstein distance between these random jamming strategies and their corresponding reference jamming strategies varied in a given range to model the magnitude variation in uncertainties in the jammer. The three different jamming strategies described previously were regarded as the reference jamming strategies, and their parameters, which can be parameterized by the proposed method, were the reference dynamic parameters. Taking Jamming Strategy 1 as an example, the following describes how to generate test samples.
Let the parameters of Jamming Strategy 1 be . The proposed jamming parameter perturbation method was used to perturb to generate test samples. More specifically, we sampled a large number of independently, which followed a Gaussian distribution with mean and variance . According to jamming parameter perturbation, was added to to generate the parameters of random jamming strategies. Then, the Wasserstein distance between these random strategies and Jamming Strategy 1 was calculated, and each random jamming strategy was labeled with its Wasserstein distance. We collected the random jamming strategies whose Wasserstein distance varied from 0 to 0.2 and divide them uniformly into ten groups. The Wasserstein distance between the random strategies in the ith group and Jamming Strategy 1 was within . In this analysis, there were 100 random jamming strategies in each group.
The performance of the robust antijamming strategies against three different jamming strategies is given in Figure 11. With respect to each jamming strategy, the antijamming strategy with , which was actually a nonrobust design, was compared with two other robust antijamming strategies. It should be emphasized that does not determine the exact radius of the -Wasserstein ball because there are some approximations of the objective function and the constraint of .
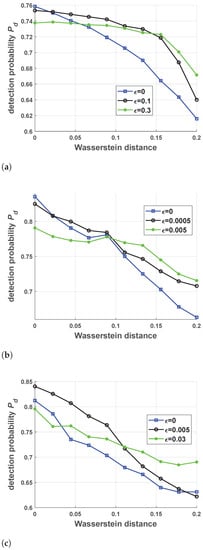
Figure 11.
The probability of detection for three different jamming strategies with respect to different magnitudes of the Wasserstein distance. The x-axis is the Wasserstein distance between the test jamming strategies and the reference jamming strategies, and the y-axis is the final probability of detection. (a–c) presents the detection probability for Jamming Strategy 1, 2 and 3 respectively with respect to different magnitudes of the Wasserstein distance.
For all three jamming strategies, the performance of nonrobust and robust antijamming strategies decreased as the uncertainty increased, which was caused by the mismatch between the test and training jamming strategies. However, it can be seen in Figure 11 that the robust antijamming strategies outperformed the nonrobust antijamming strategies if the uncertainty reached a certain level. Here, “nonrobust” indicates that the antijamming strategies were directly designed by TRPO [36] with the perfect interception assumption. The training performance of nonrobust antijamming strategies is given in Figure 10.
Taking the performance of the robust antijamming strategies against Jamming Strategy 1 as an example, a detailed explanation of the simulation results in Figure 11a is provided (the simulation results in Figure 11 are similar, so only one result is explained). To describe the simulation results more clearly, the x-axis, which ranges from 0 to 0.2, was divided into four stages, as shown in Figure 12, and each stage was analyzed.
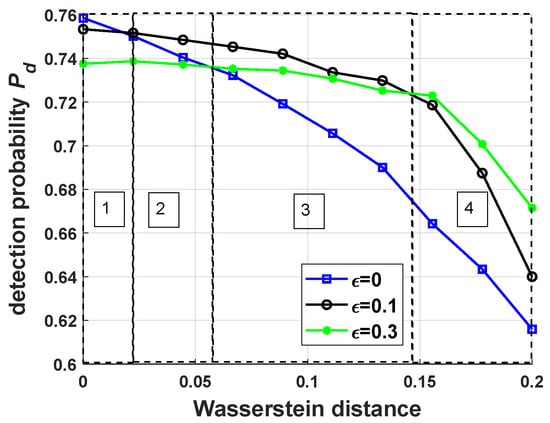
Figure 12.
The probability of detection for Jamming Strategy 1 with respect to different magnitudes of the Wasserstein distance. The four rectangles with dotted lines correspond to different stages.
In Stage 1, the performance of the nonrobust antijamming strategy was the best, and the performance of the robust antijamming strategy with was the worst. In this stage, the mismatch between the training and test environments was so small that it could be ignored. Therefore, the performance of the nonrobust antijamming strategy was the best.
In Stage 2, the performance of the robust antijamming strategy with was the best, and the performance of the robust antijamming strategy with was the worst. In this stage, although the mismatch could not be ignored, the nonrobust antijamming strategy against Jamming Strategy 1 could still outperform the robust antijamming strategy with .
In Stage 3, the performance of the robust antijamming strategy with was still the best, and the performance of the nonrobust antijamming strategy was the worst. The mismatch in this stage was so large that the nonrobust antijamming strategy achieved the worst performance.
In Stage 4, the performance of the robust antijamming strategy with was the best, and the performance of the nonrobust antijamming strategy was the worst. Not surprisingly, the performance of the nonrobust antijamming strategy was still the worst. The mismatch in this stage was large enough that it could not be covered by the -Wasserstein ball with , so the performance of the robust antijamming strategy with was no longer the best.
In theory, the performance of nonrobust antijamming strategies was the best if the Wasserstein distance between the test jamming strategies and the reference jamming strategies was zero. It should be emphasized that the tick label of the x-axis in Figure 11 actually indicates that the Wasserstein distance varied in a given range. Therefore, it is possible that the performance of nonrobust antijamming strategies was worse than that of robust antijamming strategies when the tick label of the x-axis was zero, as shown in Figure 11c.
To test the robustness of the radar under adversarial circumstances, we assumed that the jammer was capable of learning to design an adversarial jamming strategy to combat the nonrobust antijamming strategy.
For a jammer with a predefined jamming strategy, a nonrobust antijamming strategy could be obtained through RL algorithms such as TRPO. Therefore, three nonrobust antijamming strategies with parameters , and against Jamming Strategies 1, 2, and 3 could be obtained, as shown in Figure 13. Given different radii of the -Wasserstein ball, robust antijamming strategies against Jamming Strategies 1, 2 and 3 could also be obtained through the proposed robust antijamming strategy design method in this paper.
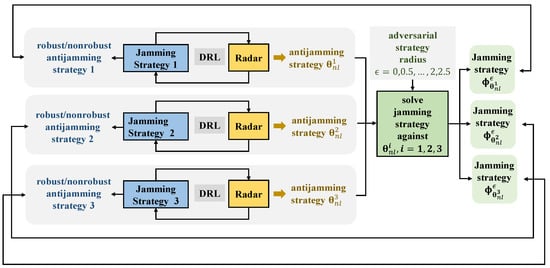
Figure 13.
The competition between the adversarial jamming strategies and the nonrobust/robust antijamming strategies.
As shown in Figure 13, the adversarial jamming strategy against each nonrobust antijamming strategy could be obtained by solving (15), and the parameters of the resultant adversarial jamming strategies are denoted by , , and , respectively.
Different values in (15), which is referred to as the adversarial strategy radius, were chosen to design adversarial jamming strategies. As shown in Figure 13, we let the nonrobust and robust antijamming strategies combat their corresponding adversarial jamming strategies with different adversarial strategy radii, and the results are given in Figure 14. Figure 14a–c shows the results related to Jamming Strategies 1, 2 and 3, respectively.
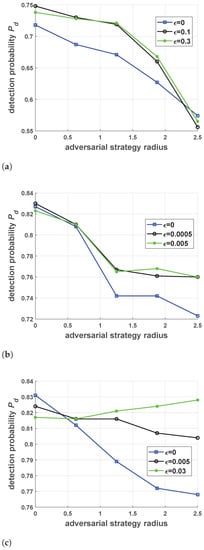
Figure 14.
The probability of detection for three different jamming strategies with respect to different adversarial strategy radii. The x-axis is the radius of the -Wasserstein ball when the adversarial strategies were generated. (a–c) presents the detection probability for Jamming Strategy 1, 2 and 3 respectively with respect to different adversarial strategy radii.
As shown in Figure 14, a larger adversarial strategy radius would usually lead to worse performance, and robust antijamming strategies outperformed nonrobust antijamming strategies in most instances. This can be easily explained by the fact that jamming is more efficient in a larger -Wasserstein ball.
6. Conclusions
In this paper, we proposed a robust antijamming strategy design method that was designed to combat main lobe jamming for FA radar when uncertainties exist in the environment. The proposed method incorporated jamming strategy parameterization and jamming parameter perturbation into . We showed that, by regarding the jammer as an expert and applying imitation learning, a given jamming strategy can be represented by a series of parameters. Simulation results showed that the obtained jamming parameters can replace the given jamming strategy with minor errors. It can be seen that jamming parameter perturbation is capable of reducing the dimensions of the parameters and generating random jamming strategies to test the proposed method. Most importantly, the results showed that the robust antijamming strategies outperformed the nonrobust antijamming strategies when the uncertainties in jamming strategies reached a certain level. In addition, it should be pointed out that the proposed method can also be used in the antijamming strategy design in the domain of communication [15,39].
It should be emphasized that the proposed method only addresses how to design robust antijamming strategies against known jamming strategies. If the jamming strategy is unknown, then the radar needs to perform jamming strategy parameterization in an online fashion, and the collected expert trajectories are not accurate since uncertainties exist in the jammer. As a result, the performance of the proposed method will worsen. This problem will be investigated in the future.
Author Contributions
Conceptualization, K.L.; methodology, B.J. and K.L.; software, K.L.; validation, K.L. and W.P.; investigation, B.J. and H.L.; writing—original draft preparation, K.L.; writing—review and editing, B.J., H.L., and W.P.; supervision, B.J. All authors read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the National Natural Science Foundation of China, the Fund for Foreign Scholars in University Research and Teaching Programs (the 111 project) (No. B18039), Shaanxi Innovation Team Project.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Calculation of the Probability of Detection
As mentioned previously, there are N available frequencies for the radar, which are denoted as . Assume that subpulses with subcarrier are transmitted in one CPI. Let , and be the coherent integration results of the target returns, the noise signal, and the jamming signals for different subcarriers, respectively. Taking the radar received signals of the subcarrier as an example, coherent integration results can be obtained by collecting all received signals of and summing them directly [29]. The overall coherent integration results can be expressed as . Let denote the coherent integration results of subcarrier , and is actually .
In contrast to the conventional noncoherent integration, the SWD assigns different weights to the received echoes according to their different SNRs [30]. Let be the SINR of the received signal of subcarrier . According to the SWD, the test statistic can be expressed as follows.
Under the hypothesis (the target is absent), follows a weighted Chi-squared distribution with weights and degrees of freedom , which is denoted as [30]. Therefore, the false-alarm rate can be expressed as follows:
where is the decision threshold, is the probability operator, and is the cumulative distribution function (CDF) of the weighted Chi-squared distribution variable .
Under the hypothesis (the target is present), also follows a weighted Chi-squared distribution with weights and degrees of freedoms , which is denoted as [30]. Similarly, the probability of detection can be expressed as follows:
References
- Su, B.; Wang, Y.; Zhou, L. A main lobe interference cancelling method. In Proceedings of the 2005 IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Beijing, China, 8–12 August 2005; Volume 1, pp. 23–26. [Google Scholar]
- Luo, Z.; Wang, H.; Lv, W.; Tian, H. Main lobe Anti-Jamming via Eigen-Projection Processing and Covariance Matrix Reconstruction. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2017, E100.A, 1055–1059. [Google Scholar]
- Ge, M.; Cui, G.; Yu, X.; Huang, D.; Kong, L. Main lobe jamming suppression via blind source separation. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 914–918. [Google Scholar]
- Neri, F. Introduction to Electronic Defense Systems; SciTech Publishing: Boston, MA, USA, 2006. [Google Scholar]
- Axelsson, S.R.J. Analysis of Random Step Frequency Radar and Comparison With Experiments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 890–904. [Google Scholar]
- Quan, Y.; Wu, Y.; Li, Y.; Sun, G.; Xing, M. Range-Doppler reconstruction for frequency agile and PRF-jittering radar. IET Radar Sonar Navig. 2018, 12, 348–352. [Google Scholar]
- Akhtar, J. Orthogonal Block Coded ECCM Schemes Against Repeat Radar Jammers. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1218–1226. [Google Scholar]
- Zhou, R.; Xia, G.; Zhao, Y.; Liu, H. Coherent signal processing method for frequency-agile radar. In Proceedings of the 2015 12th IEEE International Conference on Electronic Measurement Instruments (ICEMI), Qingdao, China, 16–18 July 2015; Volume 1, pp. 431–434. [Google Scholar]
- Bică, M.; Koivunen, V. Generalized multicarrier radar: Models and performance. IEEE Trans. Signal Process. 2016, 64, 4389–4402. [Google Scholar]
- Kang, L.; Bo, J.; Hongwei, L.; Siyuan, L. Reinforcement Learning based Anti-jamming Frequency Hopping Strategies Design for Cognitive Radar. In Proceedings of the 2018 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Qingdao, China, 14–16 September 2018; pp. 1–5. [Google Scholar]
- Li, K.; Jiu, B.; Liu, H. Deep Q-Network based Anti-Jamming Strategy Design for Frequency Agile Radar. In Proceedings of the 2019 International Radar Conference (RADAR), Toulon, France, 23–27 September 2019; pp. 1–5. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Ak, S.; Brüggenwirth, S. Avoiding Jammers: A Reinforcement Learning Approach. In Proceedings of the 2020 IEEE International Radar Conference (RADAR), Florence, Italy, 21–25 September 2020; pp. 321–326. [Google Scholar]
- Naparstek, O.; Cohen, K. Deep Multi-User Reinforcement Learning for Dynamic Spectrum Access in Multichannel Wireless Networks. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar]
- Xiao, L.; Jiang, D.; Xu, D.; Zhu, H.; Zhang, Y.; Poor, H.V. Two-Dimensional Antijamming Mobile Communication Based on Reinforcement Learning. IEEE Trans. Veh. Technol. 2018, 67, 9499–9512. [Google Scholar]
- Li, K.; Jiu, B.; Wang, P.; Liu, H.; Shi, Y. Radar Active Antagonism through Deep Reinforcement Learning: A Way to Address the Challenge of Main lobe Jamming. Signal Process. 2021, 2021, 108130. [Google Scholar]
- De Martino, A. Introduction to Modern EW Systems; Artech House: Norwood, MA, USA, 2018. [Google Scholar]
- Stinco, P.; Greco, M.; Gini, F.; Himed, B. Cognitive radars in spectrally dense environments. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 20–27. [Google Scholar]
- Hussein, A.; Gaber, M.M.; Elyan, E.; Jayne, C. Imitation learning: A survey of learning methods. ACM Comput. Surv. 2017, 50, 1–35. [Google Scholar]
- Abdullah, M.A.; Ren, H.; Ammar, H.B.; Milenkovic, V.; Luo, R.; Zhang, M.; Wang, J. Wasserstein robust reinforcement learning. arXiv 2019, arXiv:1907.13196. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Pinto, L.; Davidson, J.; Sukthankar, R.; Gupta, A. Robust Adversarial Reinforcement Learning. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2817–2826. [Google Scholar]
- Rajeswaran, A.; Ghotra, S.; Ravindran, B.; Levine, S. EPOpt: Learning Robust Neural Network Policies Using Model Ensembles. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Abbeel, P.; Ng, A.Y. Apprenticeship learning via inverse reinforcement learning. In Proceedings of the Twenty-First International Conference on Machine learning, Banff, AB, Canada, 4–8 July 2004. [Google Scholar]
- Ho, J.; Ermon, S. Generative adversarial imitation learning. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2016; pp. 4565–4573. [Google Scholar]
- Ross, S.; Bagnell, D. Efficient Reductions for Imitation Learning. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics; Teh, Y.W., Titterington, M., Eds.; Proceedings of Machine Learning Research; PMLR: Sardinia, Italy, 2010; Volume 9, pp. 661–668. [Google Scholar]
- Huang, T.; Liu, Y.; Meng, H.; Wang, X. Cognitive random stepped frequency radar with sparse recovery. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 858–870. [Google Scholar]
- Adamy, D. EW 101: A First Course in Electronic Warfare; Artech House: Norwood, MA, USA, 2001; Volume 101. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing; Tata McGraw-Hill Education: New Delhi, India, 2005. [Google Scholar]
- Liu, H.; Zhou, S.; Su, H.; Yu, Y. Detection performance of spatial-frequency diversity MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3137–3155. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Nesterov, Y.; Spokoiny, V. Random gradient-free minimization of convex functions. Found. Comput. Math. 2017, 17, 527–566. [Google Scholar]
- Argall, B.D.; Chernova, S.; Veloso, M.; Browning, B. A survey of robot learning from demonstration. Robot. Auton. Syst. 2009, 57, 469–483. [Google Scholar]
- Ng, A.Y.; Russell, S.J. Algorithms for inverse reinforcement learning. Icml 2000, 1, 2. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–11 December 2014; pp. 2672–2680. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
- Fortunato, M.; Azar, M.G.; Piot, B.; Menick, J.; Hessel, M.; Osband, I.; Graves, A.; Mnih, V.; Munos, R.; Hassabis, D.; et al. Noisy Networks For Exploration. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Salimans, T.; Ho, J.; Chen, X.; Sidor, S.; Sutskever, I. Evolution strategies as a scalable alternative to reinforcement learning. arXiv 2017, arXiv:1703.03864. [Google Scholar]
- Chen, T.; Liu, J.; Xiao, L.; Huang, L. Anti-jamming transmissions with learning in heterogenous cognitive radio networks. In Proceedings of the 2015 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), New Orleans, LA, USA, 9–12 March 2015; pp. 293–298. [Google Scholar]
- Castano-Martinez, A.; Lopez-Blazquez, F. Distribution of a sum of weighted central chi-square variables. Commun. Stat. Theory Methods 2005, 34, 515–524. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).