Abstract
The availability of aerial and satellite imageries has greatly reduced the costs and time associated with gully mapping, especially in remote locations. Regardless, accurate identification of gullies from satellite images remains an open issue despite the amount of literature addressing this problem. The main objective of this work was to investigate the performance of support vector machines (SVM) and random forest (RF) algorithms in extracting gullies based on two resampling methods: bootstrapping and k-fold cross-validation (CV). In order to achieve this objective, we used PlanetScope data, acquired during the wet and dry seasons. Using the Normalized Difference Vegetation Index (NDVI) and multispectral bands, we also explored the potential of the PlanetScope image in discriminating gullies from the surrounding land cover. Results revealed that gullies had significantly different (p < 0.001) spectral profiles from any other land cover class regarding all bands of the PlanetScope image, both in the wet and dry seasons. However, NDVI was not efficient in gully discrimination. Based on the overall accuracies, RF’s performance was better with CV, particularly in the dry season, where its performance was up to 4% better than the SVM’s. Nevertheless, class level metrics (omission error: 11.8%; commission error: 19%) showed that SVM combined with CV was more successful in gully extraction in the wet season. On the contrary, RF combined with bootstrapping had relatively low omission (16.4%) and commission errors (10.4%), making it the most efficient algorithm in the dry season. The estimated gully area was 88 ± 14.4 ha in the dry season and 57.2 ± 18.8 ha in the wet season. Based on the standard error (8.2 ha), the wet season was more appropriate in gully identification than the dry season, which had a slightly higher standard error (8.6 ha). For the first time, this study sheds light on the influence of these resampling techniques on the accuracy of satellite-based gully mapping. More importantly, this study provides the basis for further investigations into the accuracy of such resampling techniques, especially when using different satellite images other than the PlanetScope data.
1. Introduction
Defined as the detachment, transportation, and deposition of soil particles by the erosive forces of raindrop and runoff [1,2], soil erosion by water represents one of the most typical forms of land degradation affecting many countries around the world [3]. While soil erosion has many negative effects, the most concerning one include the decline in soil fertility, resulting in limited food production [4,5]. This, in turn, contributes to food insecurity in several developing countries, particularly in those ones where a considerable segment of their population strongly relies on agriculture for their survival [6]. South Africa, with approximately six million people deriving a livelihood from agriculture [7], is extremely exposed to soil erosion. Formal agriculture provides employment to about 930,000 farm workers, including seasonal and contract workers [7]. Given the geomorphological conditions coupled with the strongly seasonal nature of rainfall across South Africa, it is not surprising that the country is predisposed to soil erosion, a serious threat to sustainable agriculture and natural environments [8]. Soil erosion in South Africa, especially in rural communities, has been further aggravated by human activities such as inappropriate agricultural practices and overstocking [9,10,11,12].
Although various types of water-borne erosion exist in the country, gully formation has been recognized as the major form of erosion in South Africa, accounting for considerable volumes of soil loss [13,14]. Accordingly, the Department of Agriculture, Forestry, and Fisheries (DAFF) in South Africa has identified the need to determine the spatial extent of gullies and their severity at a national scale [15]. Gullies occur when the soil and its parent material are scored and destroyed by surface runoff, resulting in the formation of v-shaped incised channels [16]. Gullies can either be classified as ephemeral or classical (also called permanent) based mainly on their depth. Unlike ephemeral gullies, classical gullies are deeper than 0.5 m and cannot be easily filled in by normal tillage [17], especially in highly dissected terrains [18]. Gullies also result from piping and tunneling due to the influence of soil chemistry on hydrological pathways [19]. The prevalence of erodible duplex and dispersive soils in certain parts of South Africa, especially the Eastern Cape where the subsurface (piping) erosion mostly occur, considerably facilities the formation and development of gullies [9,14]. Land use type and changes also trigger gully initiation [19]. In the context of South Africa, gullies are more prominent on gently sloping lands suitable for cultivation [15]. The spatial extent and severity of gully erosion vary from one province to another because of the differences in land use, soil types, vegetation, rainfall, and topography existing in different provinces. The Eastern Cape is one of the most gully-affected provinces in South Africa, with about 161,500 ha of land covered by gullies [15]. For this reason, most gully erosion studies in the country have been conducted in this province [9,14,20,21,22].
Accurate mapping of gullies is essential for monitoring gully erosion and understanding the associated environmental and socio-economic impacts [23], thereby supporting the implementation of practical erosion control measures [24,25]. Manual field-based assessments using tapes, rulers, and topographic profilers have been used for years to obtain gully information [26], but over the last few decades, rapid developments had been witnessed in digital aerial photography, and more recently, satellite images with different imaging capabilities [23]. Following the availability of such remotely sensed data, gully information has either been obtained through visual interpretation or automatic classification of remotely sensed data. Remote sensing related mapping, either based on visual interpretation or automatic method, is presently the only practical approach for mapping gully features over large areas, in arid or semi-arid regions, given the complexity of gully appearance (i.e., variability in size, shape, and occurrence) [27]. Although nowadays visual interpretation is regarded as the most traditional and time consuming method, some researchers still prefer it over the automatic method [15,28] because automatically-classified results are still subject to the characteristics of the selected training samples, algorithms, and satellite image, among other factors [29]. However, the low efficiency, uncertainty and high subjectivity associated with visual interpretation have made most researchers to investigate automatic methods [29].
The automatic extraction of gully information from satellite earth observation data takes two forms: pixel-based and object-based analysis [23,30]. The pixel-based analysis is relatively simple, and is the most frequently used and direct approach for image classification, using only the spectral information [31]. Such spectral information can be extracted using various image classification algorithms such as random forest (RF) and support vector machines (SVM), which thus far, are arguably the most commonly used algorithms due to their classification efficiency in relation to other algorithms, including k-nearest neighbor (kNN), maximum likelihood (ML), artificial Neural Network (ANN), convolutional neural networks (CNN), discriminant analysis (DA), and minimum distance (MD). One study mapped the areas susceptible to gully erosion using RF and ANN [32], and found that RF performed better than ANN. Noi and Kappas [33] compared SVM, RF, and kNN in land cover classification, and found that SVM, followed by RF, were better than kNN. Phinzi et al. [34] reported that both SVM and RF outperformed linear discriminant analyst (LDA) in a study on gully detection. Although deep learning methods such as CNNs have shown better performance over SVM and RF [35], like most deep learning methods, CNNs also strongly rely on the availability of abundant high-quality training/ground truth data [36]. While CNNs perform well in detecting and differentiating active gullies from other forms of surface erosion (e.g., sheet and rills), they have errors in detecting complex gully systems [37]. For these reasons, SVM and RF still attract most researchers’ attention, because of their low computational complexity and higher interpretability capabilities compared to deep learning algorithms [36].
The wide usage of these machine learning algorithms in remote sensing proved that learning features from dataset is more efficient and practical than merely defining the features [38]. Although the application of machine learning in soil erosion research is not new, previous investigations commonly use coarser spatial imagery such as Landsat, ASTER and Sentinel/Sentinel-SAR (Synthetic Aperture Radar), which from an economic point of view makes sense, given that such images are obtainable at no cost. Besides, these sensors are good for wide area mapping of soil erosion. However, what has become apparent from previous studies, is that such sensors cannot identify individual gullies (especially small discontinuous gullies) with sufficient detail, this limitation is attributable to their low spatial resolution [15]. Whereas other optical sensors such as IKONOS, WorldView, and RapidEye with relatively higher spatial resolution exist for gully mapping, these sensors are not readily or freely available, as such, their high acquisition costs limit their application for gully mapping. Similarly, the use of LiDAR-derived elevation data from airborne surveys including Unmanned Aerial Vehicles (UAVs) is limited by a lack of financial resources. Depending on the availability of data and objective of a given study, multi-source and multi-sensor data fusion are common in remote sensing since this provides synthetic data that have the combined advantages of different sensors [39]. Multi-sensor or pixel level data fusion are mainly applied to optical images, for example, the fusion of high resolution panchromatic and low resolution multi-spectral images [40], was successfully applied in gully feature extraction [34]. Multi-source data fusion concerns feature level and decision level fusion of data from various sources such as SAR, optical images, LiDAR, geographic information system (GIS) data, and in-situ data [40]. In our case, we did not perform any data fusion due to lack of data (including the panchromatic band) with suitable spatial resolution necessary for detecting individual gullies.
Despite the unavailability of a higher spatial resolution panchromatic band, the 3 m PlanetScope image, which is available free of charge for research purposes, offers a great potential for detecting individual gullies. However, the capability of PlanetScope image in classifying gullies in different seasons (dry and wet) in an arid or semi-arid environment had been investigated only in areas of large forms (1–5 km length, 100–600 m width) [41]. While machine learning algorithms such as the SVM and RF have been frequently applied, little efforts have been made to investigate the influence of resampling techniques, particularly, bootstrapping and k-fold cross-validation (CV), on the accuracy relations. We identified gullies from PlanetScope images based on these resampling methods. Our aim was (i) to compare the satellite’s bands reflectance values from the aspect of gullies, (ii) to reveal which classifier (RF or SVM) and resampling technique (CV or bootstrapping) perform better regarding the overall and class level accuracy metrics, and (iii) which season is more appropriate to identify the gullies.
2. Materials and Methods
2.1. Study Area
The study area was located in the rural part of eastern South Africa, characterized by extensive erosion where permanent gully erosion was the most prominent erosion type [42]. Geographically, the study area lies between 30°42′30″–30°43′55″S 28°46′22″–28°48′47″E, covering a surface of about 10 km2 (Figure 1). Subsistence agriculture (e.g., crop farming and livestock rearing) and settlement were the main land use types. Grassland was the most common vegetation type throughout the area, with some forest patches found in the north-western section of the study area. The topography ranges from 1213 m–1658 m, with the north-western and south-western sections being steeper than other parts of the area. Steep mountain slopes with gently undulating footslopes characterize the geomorphology of the area [14]. The climate is semi-arid with temperatures ranging from 7–30 °C. Winters are cold and dry, with less vegetation due to limited rainfall. Rainfall mostly occurs during the summer season reaching approximately 670 mm on average per year. Although the study area has limited annual rainfall, it experiences high-intensity rainfall events. Gully development in the area was further fostered by the predominance of highly erodible soils such as duplex and dispersive soils [9,43], predominantly underlain by mudstone and sandstone of the Beaufort Group [44]. Although vegetation exists in the wet season, its effectiveness in protecting soil against erosion and inappropriate land-use practices such as overgrazing usually reduces vegetation cover, making the area susceptible to soil erosion. The study area features both continuous and discontinuous gully networks with distinct occurrences and appearances, i.e., narrow, wide, vegetated, shallow, deep with shadows, etc. [14,42]. Additionally, some gullies resemble the unpaved road network in appearance. Such complexity of gullies within the area makes the area particularly suitable for study.
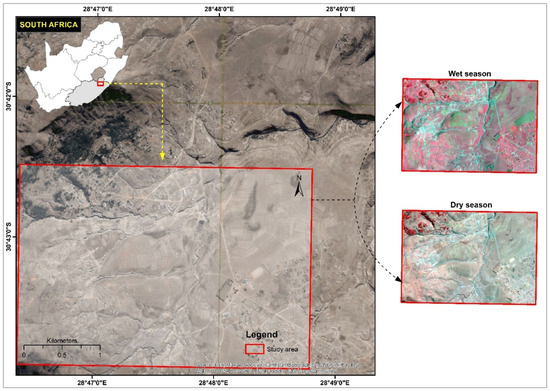
Figure 1.
Location of the study area (PlanetScope false-color images).
2.2. Data Acquisition and Pre-Processing
Two cloud-free PlanetScope orthorectified products (Level 3B) for the wet and dry seasons acquired on 23 January 2017 and 25 June 2017, respectively, were used in this study. The images were downloaded from the Planet explorer website (https://www.planet.com/explorer (accessed on 30 July 2020)). The orthorectified scenes had already been radiometrically and geometrically corrected and projected to the Universal Traverse Mercator (UTM) projection, referenced to the world geodetic system (WGS84) datum. With a spatial resolution of 3 m and temporal resolution of 1 day, the PlanetScope image is comprised of 4 spectral bands: red, green, blue (RGB), and near-infrared (NIR). The flowchart summarizing the workflow followed in this study is presented in Figure 2.
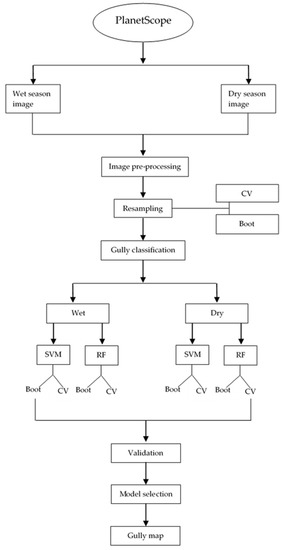
Figure 2.
Workflow followed in this study (CV: cross-validation; boot: bootstrapping; SVM: support vector machines; RF: random forest).
2.3. Gully Classification
Classification of gullies from the PlanetScope image was conducted in Python software using random forest (RF) and support vector machines (SVM). These were the most widely applied algorithms and their detailed description has been provided in the literature [10,34,36,45,46,47]. The RF, developed by Breiman [48], is a robust machine learning algorithm that is increasingly becoming more popular in remote sensing of soil erosion. The algorithm has several parameters that need to be tuned, amongst which the ntree (number of trees) and mtry (number of features in each split) are the most important that should be considered when training the algorithm [49]. The models were built using only 4 variables (e.g., four multispectral bands of the PlanetScope image), thus we tested all possible values of the mtry parameter. For the ntree parameter, we tested different values ranging from 50 to 1000. After ntree = 100, the accuracies stagnated while the computational time kept increasing [50]; thus, the final model was trained with 100 individual decision trees, selecting 2 random variables at each split.
The support vector machine (SVM) model was capable of overcoming both classification and regression problems [51,52]. To achieve this, SVM searched for the flat boundary (hyperplane) in some feature space that best separated the classes into homogeneous partitions where each partition contained only data points of a given class [34,49]. In reality, however, it was difficult to find a hyperplane that perfectly separated the classes using just the original features [49]. SVM overcomes this problem in 2 ways: first, loosen what is meant by “perfectly separates,” and second, use the so-called kernel trick to expand the feature space to the extent that perfect separation of classes is more likely [49]. The radial basis function (RBF) was chosen for the kernel type. For RBF, a C penalty parameter against misclassifications and a kernel coefficient (γ) as a decision boundary have to be specified, which greatly affects the performance of the model [53]. Hyperparameter tuning was performed with the grid search method.
2.4. Reference Data Collection and Accuracy Assessment
The reference data were collected through field surveys and visual interpretation of high-resolution Google Earth images. We delineated the study area into 7 land cover classes, of which all were identifiable both in the field and in images (Google Earth and PanetScope): forest, built-up, agriculture, gully, bare soil, and mixed bare soil (i.e., exposed rocks, unpaved roads/dirty roads, and exposed soil mostly in ploughed fields). A total of 966 points were collected using stratified random sampling in ArcMap. Each land cover class was assigned a number of points proportional to its size.
We evaluated the overall performance of the RF and SVM algorithms using CV and bootstrapping. Kappa coefficients and overall accuracy (OA) were among the most commonly used metrics to evaluate classification accuracy [54]. However, the use of kappa in remote sensing classification accuracy is becoming less common [33,55]. Pontius and Millones [56], Flight and Julious [57], and more recently, Delgado and Tibau [58], recommend against using kappa because of its inherent limitations. A major limitation of kappa was that it is highly sensitive to the distribution of the marginal totals, potentially producing unreliable results [57]. Thus, we used OA to assess the overall performance of the models. Contrary to the conventional error matrix, which used all of the available data to test the model, CV splits the reference dataset into training and testing data. It used the majority of the data for training and the remainder, often called the holdout sample, was used to test the model, ensuring that the model was robust [49]. In total, we used 17,757 pixels for the wet season and 30,597 pixels for the dry season, generated from PlanetScope. We repeated the 5-fold CV 20 times, meaning that final accuracies were computed from 100 models. Before each repetition, the dataset was randomly shuffled and new folds were generated to increase the robustness of the models. Unlike CV, in bootstrapping, the original data were randomly sampled with replacement, meaning that, after a data point (bootstrap sample) was selected for inclusion in the subset, it was still available for further selection [49]. Two parameters must be chosen before running bootstrapping: sample size and the number of repetitions. In our case, the sample size was the same as the original dataset [59], and we applied 100 repetitions. The models were validated on the samples that were not included in the bootstrap sample.
We used the traditional error matrix to assess the model performance at class level as bootstrapping and CV do not provide class accuracies. An error matrix compared reference data to the classified map using various accuracy indices [54], but in this study, we only focused on class level accuracies/errors: producer’s accuracy (PA) and user’s accuracy (UA); PA was also known as sensitivity or recall while UA was sometimes referred to as precision. The difference of the possible 100% accuracy and the PA represented the omission error, which occurred when a pixel was excluded from the class to which it belonged. A difference of 100% and UA represented a commission error, which occurred when a pixel was incorrectly included in the class where it did not belong. We computed unbiased area-based PAs and UAs, following “good practice” recommendations for accuracy assessment [60]. The F1-score was also reported as the harmonic mean of UA and PA [61]. Additionally, we computed unbiased areal coverages (ha) of gullies along with their standard errors (ha) and associated ± 95% confidence intervals (ha). We generated 6 algorithms based on the combination of the classifiers: svm and rf, seasons: dry (d) and wet (w), and resampling methods: bootstrapping (b) and cross validation (cv), i.e., rf-d-b, rf-d-cv, rf-w-cv, rf-w-b, svm-d-cv, svm-d-b, svm-w-cv, and svm-w-b.
2.5. Statistical Analysis
NDVI values of the images, and specifically focusing on the gullies, were compared by the 2 seasons with the robust Mann–Whitney test using the Monte Carlo p (pMC) with 9999 permutations. We applied the General Linear Model (GLM) to determine the effects of spectral bands (4 bands; RGB + NIR), seasons (wet and dry), and the LULC classes (7 classes). Furthermore, we also determined the statistical interactions to reveal if factorial variables had a common effect (e.g., effects of spectral bands differed by LULC classes or were different in the dry or wet seasons). Besides, we also determined the effect size (ω2) as a standardized measure of the variables’ contribution in the model (higher values indicate larger contribution, ω2 > 0.14 was considered as a large effect [62].
The Dunnett test [63] was used to determine if gullies had significant differences from other land cover types (H0: mean reflectance values of gullies was identical with the other land cover types). The Dunnett test was developed to perform multiple comparisons against 1 control group; in this case, gullies’ land cover type was chosen as the control. As in the Dunnett test, the number of comparisons was limited (related to a full factorial approach; i.e., 6 instead of 21). Furthermore, the test compared the factor groups’ means with the control group’s mean (unlike other tests, which compare group means to the grand mean); thus, it can reveal small significant differences [64], and our intent was to find all overlaps in the reflectance with the gullies.
3. Results
3.1. Spectral Bands, Land Cover Classes and Seasons as Determinants of Reflectance
The difference of NDVI values was significant between the two seasons (U = 35303, z = 19.102, pMC < 0.0001). The NDVI for the wet season had relatively higher values ranging from −0.36 to 0.81, while the values for the dry season lay in the range −0.41 to 0.59. The dry season had bimodal distribution while the wet season had multimodal distribution (Figure 3). Such bimodal distribution in the dry season represents non-vegetation (first mode) and vegetation pixels (second mode). Like in the dry season, the first mode in the wet season was indicative of non-vegetation pixels denoted by lower NDVI values compared to the last two modes, represented by relatively higher NDVI values. These last two modes represent vegetated areas: vegetation and forest pixels, respectively.
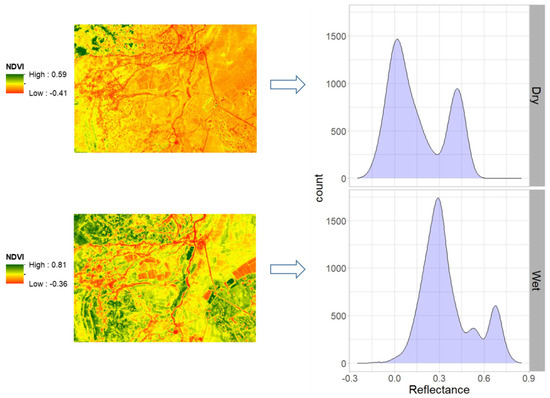
Figure 3.
Distribution of NDVI reflectance values in the dry and wet season.
We also compared the NDVIs’ of the gullies in the dry and wet seasons. Accordingly, the difference was significant (U = 162, z = 9.5534, p < 0.0001). The mean difference was 0.08 in the wet season, green vegetation was also present in gullies, thus, NDVI was larger. According to the results of the GLM we found that the spectral bands, LULC classes, and the seasons, as factorial variables and the interactions, were significant (p < 0.001) and explained 92.3% of the variance. Among the factors, the difference of dry and wet seasons had the largest effect on the reflectance (0.868). The bands and LULC classes had almost the same effect with a bit lower value (~0.6), however, also indicating a large effect. Regarding the interactions, we confirmed that reflectance by the band was different by LULC classes and seasons. The contribution of these interactions was large (Table 1). Furthermore, the effect size of the interaction between the seasons and the LULC classes was the lowest, being only third related to the interactions with the bands (0.141), but it still indicated a large effect. The interaction of all factors (spectral bands, seasons, LULC classes) also had a large effect but only with a smaller value (0.185).

Table 1.
Results of General Linear Modelling (GLM) performed with reflectance as an independent variable (SS: Sum of Squares, df: degree of freedom, F: F-statistic, p: significance, ω2p: effect size; p < 0.05: significance level).
The post hoc test performed with the Dunnett test revealed significant differences (p < 0.001) between the gullies and other LULC classes in the dry season (Figure 4). The difference was not significant between the gullies and the agricultural areas (blue band), the vegetation and agricultural areas (green band and red band) in the wet season. Table 2 ranks the original band’s importance in terms of discriminating gullies. We also studied the differences of NDVI and found that this spectral index was not as successful in discriminating the gullies as the original bands. It did not differ from the mixed bare soil and the vegetation in the dry season. Although NDVI performed better in the wet season, the difference was not significant with the built-up class.
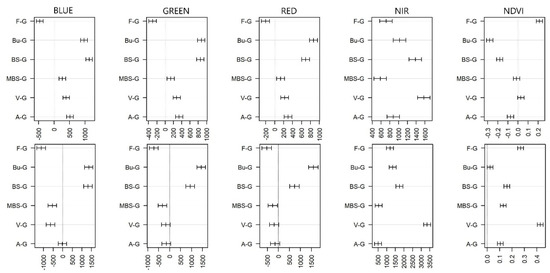
Figure 4.
Differences of gullies and other land cover types’ reflectance by bands and seasons (G: gully; F: forest; Bu: built-up; BS: bare soil; MBS: mixed bare soil; V: vegetation; A: agriculture; mean ± 95% confidence intervals; the difference was not significant if confidence range intersects the dashed line).

Table 2.
PlanetScope bands ranking in discriminating gullies against the surrounding land cover.
3.2. Accuracy Assessment of Gully Mapping
Using machine learning algorithms (RF and SVM), the cross-validation (CV) resampling method yielded better OA compared to bootstrapping for both the wet and dry seasons (Figure 5). Two apparent trends can be observed from these results based on OA: (i) RF consistently performed better than SVM irrespective of the season or resampling methods: bootstrapping and cross-validation; (ii) dry season had better OAs than the wet season, but this was not reflected in class level accuracy indices for gully classification. Based on the unbiased UA, all algorithms showed good performance in gully classification, recording UA above 70% (Figure 6). In particular, the best performance belonged to the svm-d-b (93.4%), whereas the worst UA belonged to the rf-w-b model (77%). For most models, PA was generally low relative to UA. Only half of the models recorded a PA greater than 70%, with the best performance belonging to svm-w-cv (89.2%), while the other half fell below 70%, with the svm-d-b model recording the lowest PA (32.5%).
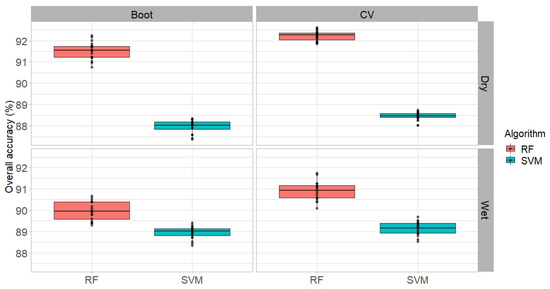
Figure 5.
Accuracy assessment based on overall accuracy (OA) by the classification algorithm (RF: random forest, SVM: support vector machine), resampling method (boot: bootstrapping, CV: cross-validation), and season (wet and dry).
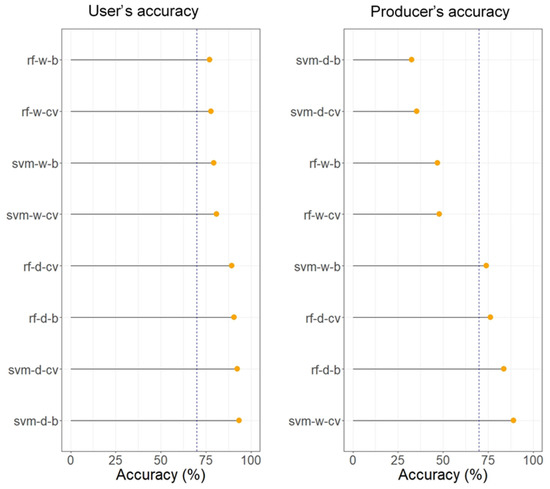
Figure 6.
Unbiased user’s accuracy and producer’s accuracy (rf: random forest, svm: support vector machine, w: wet season, d: dry season, cv: cross-validation, b: bootstrapping, blue dashed line is 70% accuracy benchmark).
An unbiased area estimate of gullies (ha) is presented in Table 3. With the highest PA (89.2%) and lowest standard error (3.7 ha), svm-w-cv provided the most accurate gully areal coverage (57.2ha). The highest standard error (11.5 ha) belonged to rf-w-b model, which had a gully area of 55.2 ± 25ha. However, in the F1-score ranking, rf-d-b and rf-d-cv algorithms achieved the best results (>0.90), but RF algorithms belonging to the wet season had relatively low score (0.82). On the other hand, all SVM algorithms (svm-d-cv, svm-d-b, svm-w-cv, and svm-w-b) recorded lower F1-scores, ranging 0.85–0.88. The two resampling techniques recorded the same omission error (85.1%), but slightly different commission errors, e.g., bootstrapping had 40.8% error of commission compared to 37.8% error for k-fold CV (Table 4).

Table 3.
Estimated gully area (ha) with associated standard error (ha) at ± 95% CI (ha) for each algorithm (rf: random forest, svm: support vector machine, d: dry, w: wet, b: bootstrapping, cv: cross-validation, CI: confidence interval).

Table 4.
Summary of average error for resampling techniques, classifier, and season (RF: random forest, svm: support vector machine, CV: cross-validation).
The two resampling techniques recorded the same omission error (85.1%), but slightly different commission errors, e.g., bootstrapping had 40.8% error of commission compared to 37.8% error for k-fold CV.
3.3. Gully Distribution
Results indicated that gullies can be spectrally discriminated from other land cover classes, both in the dry and wet season; although there were observable differences in the distribution of the extracted gullies in these two seasons (Figure 7). In the wet season, there seem to be more gullies than there are in the dry season. This difference in gully areal coverage between the two seasons is more pronounced in Figure 7a, corresponding to rf-d-b and Figure 7b, representing the svm-w-cv model.

Figure 7.
Spatial distribution of gullies: (a) rf-d-b and (b) svm-w-cv correspond to the best models for gully mapping in the dry and wet seasons, respectively (rf: random forest, svm: support vector machine, w: wet season, d: dry season, cv: cross-validation, b: bootstrapping).
Differences in gully reflectance among the two seasons also had a bearing on gully classification. The underlying statistical test revealed that the difference was significant (U = 162, z = 9.5534, p < 0.0001), and the mean difference was 0.08. The wet season had more vegetation covering bare surfaces, and because of this, spectral differences were more pronounced during the wet season (Figure 8). On the contrary, in the dry season, most gullies spectrally resembled the bare surfaces they dissect. Consequently, the algorithms were less efficient in extracting gullies occurring on bare soil surfaces in the dry season. This probably explains the high commission error (43.1%) and standard error (8.6 ha) in the dry season.
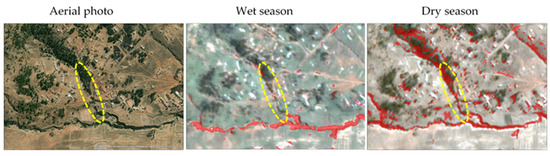
Figure 8.
An example of a vegetated gully (dashed yellow ellipse) in the dry and wet seasons.
4. Discussion
Remotely sensed data are inherently subject to errors, hence, error assessment is essential for data assimilation, one of the primary uses of satellite data products [65]. In this section, we discuss errors associated with the derived gully maps, offering a possible explanation for such error sources. Different resampling methods undoubtedly play an important role in classification accuracy, hence, the final model selection. Specifically, we explored the influence of bootstrapping and k-fold cross-validation techniques in gully classification, considering different seasons (dry and wet) and classifiers (SVM and RF). Results revealed that k-fold CV performs slightly better than bootstrapping in terms of commission error. Kohavi et al. [66], in his study of CV and bootstrap for accuracy estimation and model selection, also reported k-fold CV as the best method to use over bootstrapping. Kim [67] estimated classification error rate, comparing repeated k-fold CV, repeated hold-out and bootstrap, and found that the repeated k-fold CV was better than bootstrap. The author further reported that bootstrapping had bias problems for both large and small samples, despite its small variance, hence, the expectation for better performance for small samples.
Although the results of our study are generally in agreement with previous studies, it is worth noting that the performance of the bootstrapping and k-fold CV varied considerably at class level with algorithm and season. There are instances where bootstrapping performed better than k-fold CV in gully classification. For instance, the best model, namely, svm-d-b, based on UA, belonged to bootstrapping. Such results are important because most studies using either bootstrapping or k-fold CV rarely focus on class level accuracy when evaluating the performance of these resampling techniques. More importantly, even at the class level, different accuracy metrics ought to be considered. This increases the robustness and reliability of the accuracy results, making it possible for researchers to draw correct deductions on the behavior of the algorithms under investigation [61]. However, various class accuracy metrics (UA, PA, standard error, and F1-score) used in the current study, all derived from the confusion matrix, disagreed with one another in some instances. For example, some algorithms that obtained high PA values had low corresponding UA values or vice-versa. This is also true with F1-score vs. either PA or UA. Based on the F1-score, the best algorithms belonged to RF (e.g., rf-d-b and rf-d-cv). Given the disagreement amongst various accuracy metrics, we relied on the standard error as a reliable measure to judge the accuracy of the algorithms.
In the wet season, the algorithms proved to be more efficient in gully classification on bare soil surfaces due to the existence of vegetation cover in bare soil surfaces, making it possible to discriminate gullies. Such findings are comparable or similar to those of previous studies. For example, one study automatically identified gullies based on ASTER images acquired during the dry and wet seasons [68]. The study concluded that the wet season-acquired image performed better than the dry season one. It is worth noting that the wet season is not always appropriate for gully identification in all situations. The success of gully identification depends on the complexity of gully appearance as influenced by their morphological characteristics (shape, size, length, depth, etc.) [42], sensor type and/or resolution, and classification algorithms [69], amongst other factors. For example, Sentinel and Landsat images performed relatively well in the dry season than in the wet season [70]. Although gully classification was successful in the wet season relative to the dry season, there were few locations where gullies were filled up with vegetation. Such gullies could not be automatically classified, in which case we relied on visual interpretation of high-resolution aerial photographs and/or dry season PlanetScope images.
Gully appearance also played an important role in gully classification. Consistent with previous studies [42,71], the classification algorithms were efficient in detecting continuous gullies mostly in linear shape. Conversely, the algorithms proved to be less efficient in areas with high gully density, often surrounded by transitional zones to non-gully [71], but these areas form a relatively small portion of the study area and had negligible influence on the accuracy. The SVM combined with CV (e.g., svm-w-cv) reflected the best performance in the wet season with the least standard error (3.7 ha) and highest PA (89.2%), followed by a RF model (rf-d-b), recording slightly different standard error (6.1 ha) and PA (83.6%). Nevertheless, 50% of the models obtained a PA that is below 70%. Despite this discrepancy, the estimated gully areas (ha), based on area-weighted metrics, are unbiased and can be relied upon.
From a practical point of view, the identification of gullies from satellite images with reasonable accuracies is of paramount importance to gully rehabilitation. Like all remote sensing-derived products, gully maps are subject to errors, and hence, accuracy assessment is a prerequisite [54]. However, most remote sensing-based gully studies tend to rely on accuracy indices, such as PA and UA, without taking into account the uncertainty of the estimated gully areas. Although it is not a requirement, it is often recommended to provide not only PA and UA but also unbiased quantitative area estimates such as the area-weighted metrics and confidence intervals [60]. In this study, we quantified gullied areas (ha) together with their associated levels of uncertainties, such as standard errors (ha) and confidence intervals (ha).
RF combined with bootstrapping resampling provided the best gully area (88 ± 14.4 ha) estimate with the least standard error (6.1 ha) in the dry season. In the wet season, SVM combined with CV resampling estimated gully area (57.2 ± 18.8 ha) with the lowest standard error (3.7 ha). These findings shed light on the influence of these resampling techniques on the accuracy of satellite-based gully mapping but also provides the basis for further investigations into the accuracy of such resampling techniques, especially when using different satellite images other than the PlanetScope data, preferable, freely available ones, with higher spatial resolution. Initially, we planned to use both PlanetScope and SPOT-7 images, also obtainable free of charge for the test area, but SPOT-7 image scenes acquired in the wet and dry season months were not available for the test area. Nevertheless, given that we only mapped gullies in a small part of the problem area, we are planning to test the method in other areas with wider spatial coverage. However, mapping gullies over large areas, particularly using automatic methods, is still a challenge due to the complexity of gullies over such large areas [14]. Thus far, even advanced methods such as CNNs have errors in detecting complex gully systems [37]. It is worth noting that the detection of gullies mainly depends on the spatial resolution of the image used. For example, at larger scales, gullies have only been mapped at a spatial resolution of up to 2.5 m in South Africa [14,15]. To overcome this challenge, the future implementation of our method, will in part, require the use of a high spatial resolution (<2 m) image, for instance, pansharpened SPOT-7 image (1.5 m) or WorldView (0.5 m), which can detect individual gullies. Another limitation of this method relates to climate. The method is suitable for application in arid/semi-arid regions where gullies are often not covered by trees [42]. Our study demonstrated that gullies could be better identified in the dry season with RF combined with bootstrapping, whereas SVM combined with k-fold CV is best for identifying gullies in the wet season. Therefore, we recommend the use of RF and SVM for mapping gullies in the dry and wet seasons, respectively. Provided that PlanetScope provides global spatial coverage with daily revisit time, we particularly recommend it for continuous monitoring of gullies at any location.
5. Conclusions
The aim of this study was to assess the efficacy of cross-validation and bootstrapping in gully classification and also to reveal how well the PlanetScope images perform in gully extraction in the dry and wet seasons of a semi-arid climate. We found the following outcomes.
- Gullies were spectrally different in all bands of the PlanetScope images, both in the dry and the wet seasons.
- NDVI values did not differ from all land cover classes regarding the reflectance values; thus, it was not involved in gully classification.
- Dry and wet seasons ensured different classification accuracy, but gully extraction was successful. RF outperformed the SVM algorithm in terms of OA, but the differences of the OAs were < 4%. Differences were larger in the dry season (3.5%) and smaller in the wet season (~1%).
- Generally, based on the OAs, CV performed better with the RF algorithm than the bootstrapping (with ~1.0–1.5% differences), but on a class level, bootstrapping provided the most accurate gully extraction with the RF in the dry season, whereas CV was efficient with SVM in the wet season.
Accordingly, both resampling techniques were efficient, but RF with bootstrapping resampling technique in the dry season can be suggested to map gullies. In the future, we plan to extend the mapping in larger areas to help landowners and managers to fight against erosion and to plan the interventions at the hot spot areas.
Author Contributions
Conceptualization, K.P. and S.S.; methodology, K.P.; software, K.P. and D.A.; validation, K.P. and D.A., formal analysis, K.P.; investigation, K.P.; resources, S.S.; data curation, K.P. and D.A.; writing—original draft preparation, K.P.; writing—review and editing, K.P. and S.S.; visualization, K.P., D.A., and S.S.; supervision, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Thematic Excellence Programme (TKP2020-NKA-04) of the Ministry for Innovation and Technology in Hungary projects and Department of Higher Education and Training (DHET) of South Africa.
Data Availability Statement
PlanetScope images can be purchased from the PlanetLabs Inc. Limited, non-commercial access to PlanetScope imagery can also be gained through the Education and Research Program (https://www.planet.com/markets/education-and-research/ (accessed on 30 July 2020)). Reference data can be provided by the authors on demand.
Acknowledgments
The first author (K.P.) greatly acknowledges the Tempus Public Foundation for funding his Ph.D. studies through the Stipendium Hungaricum Scholarship Programme. The author is equally grateful to the Department of Higher Education and Training (DHET) of South Africa for the supplementary support.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Meyer, L.D.; Wischmeier, W.H. Mathematical simulation of the process of soil erosion by water. Trans. ASAE 1969, 12, 754–758. [Google Scholar]
- Morgan, R.P.C. Soil Erosion and Conservation; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 140514467X. [Google Scholar]
- Borrelli, P.; Robinson, D.A.; Fleischer, L.R.; Lugato, E.; Ballabio, C.; Alewell, C.; Meusburger, K.; Modugno, S.; Schütt, B.; Ferro, V.; et al. An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 2017, 8, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Omuto, C.; Nachtergaele, F.; Rojas, R.V. State of the Art Report on Global and Regional Soil Information: Where Are We? Where To Go? Food and Agriculture Organization of the United Nations: Rome, Italy, 2013; ISBN 9251074496. [Google Scholar]
- Kertész, A.; Křeček, J. Landscape degradation in the world and in Hungary. Hung. Geogr. Bull. 2019, 68, 201–221. [Google Scholar] [CrossRef] [Green Version]
- Phinzi, K.; Ngetar, N.S.; Ebhuoma, O. Soil erosion risk assessment in the Umzintlava catchment (T32E), Eastern Cape, South Africa, using RUSLE and random forest algorithm. S. Afr. Geogr. J. 2020, 103, 139–162. [Google Scholar] [CrossRef]
- Strategic Plan for the Department of Agriculture, Pretoria, South Africa. 2007. Available online: https://www.gov.za/sites/default/files/gcis_document/201409/agricstratplan2007.pdf (accessed on 16 July 2020).
- Meadows, M.E.; Hoffman, M.T. The nature, extent and causes of land degradation in South Africa: Legacy of the past, lessons for the future? Area 2002, 34, 428–437. [Google Scholar] [CrossRef]
- Beckedahl, H.R.; de Villiers, A.B. Accelerated erosion by piping in the Eastern Cape Province, South Africa. S. Afr. Geogr. J. 2000, 82, 157–162. [Google Scholar] [CrossRef]
- Kakembo, V.; Rowntree, K.M. The relationship between land use and soil erosion in the communal lands near Peddie town, Eastern Cape, South Africa. Land Degrad. Dev. 2003, 14, 39–49. [Google Scholar] [CrossRef]
- Mhangara, P.; Kakembo, V.; Lim, K.J. Soil erosion risk assessment of the Keiskamma catchment, South Africa using GIS and remote sensing. Environ. Earth Sci. 2012, 65, 2087–2102. [Google Scholar] [CrossRef]
- Phinzi, K.; Ngetar, N.S. Land use/land cover dynamics and soil erosion in the Umzintlava catchment (T32E), Eastern Cape, South Africa. Trans. R. Soc. S. Afr. 2019, 74, 223–237. [Google Scholar] [CrossRef]
- Kakembo, V.; Xanga, W.W.; Rowntree, K. Topographic thresholds in gully development on the hillslopes of communal areas in Ngqushwa Local Municipality, Eastern Cape, South Africa. Geomorphology 2009, 110, 188–194. [Google Scholar] [CrossRef]
- Le Roux, J.J.; Sumner, P.D. Factors controlling gully development: Comparing continuous and discontinuous gullies. Land Degrad. Dev. 2012, 23, 440–449. [Google Scholar] [CrossRef] [Green Version]
- Mararakanye, N.; Le Roux, J.J. Gully location mapping at a national scale for South Africa. S. Afr. Geogr. J. 2012, 94, 208–218. [Google Scholar] [CrossRef]
- Poesen, J.; Nachtergaele, J.; Verstraeten, G.; Valentin, C. Gully erosion and environmental change: Importance and research needs. Catena 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, G.; Duan, X.; Wilson, G.V. Spatial distribution and morphologic characteristics of gullies in the Black Soil Region of Northeast China: Hebei watershed. Phys. Geogr. 2016, 37, 228–250. [Google Scholar] [CrossRef]
- Zgłobicki, W.; Poesen, J.; Cohen, M.; Del Monte, M.; García-Ruiz, J.M.; Ionita, I.; Niacsu, L.; Machová, Z.; Martín-Duque, J.F.; Nadal-Romero, E.; et al. The potential of permanent gullies in Europe as geomorphosites. Geoheritage 2019, 11, 217–239. [Google Scholar] [CrossRef]
- Valentin, C.; Poesen, J.; Li, Y. Gully erosion: Impacts, factors and control. Catena 2005, 63, 132–153. [Google Scholar] [CrossRef]
- Phinzi, K.; Ngetar, N.S. Mapping soil erosion in a quaternary catchment in Eastern Cape using geographic information system and remote sensing. S. Afr. J. Geomat. 2017, 6, 11. [Google Scholar] [CrossRef] [Green Version]
- Seutloali, K.E.; Dube, T.; Mutanga, O. Assessing and mapping the severity of soil erosion using the 30-m Landsat multispectral satellite data in the former South African homelands of Transkei. Phys. Chem. Earth 2017, 100, 296–304. [Google Scholar] [CrossRef]
- Phinzi, K.; Ngetar, N.S.; Ebhuoma, O.; Szabó, S. Comparison of rusle and supervised classification algorithms for identifying erosion-prone areas in a mountainous rural landscape. Carpathian J. Earth Environ. Sci. 2020, 15, 405–413. [Google Scholar] [CrossRef]
- Shruthi, R.B.V.; Kerle, N.; Jetten, V. Object-based gully feature extraction using high spatial resolution imagery. Geomorphology 2011, 134, 260–268. [Google Scholar] [CrossRef]
- Seutloali, K.E.; Beckedahl, H.R.; Dube, T.; Sibanda, M. An assessment of gully erosion along major armoured roads in south-eastern region of South Africa: A remote sensing and GIS approach. Geocarto Int. 2016, 31, 225–239. [Google Scholar] [CrossRef]
- Phinzi, K.; Ngetar, N.S. The assessment of water-borne erosion at catchment level using GIS-based RUSLE and remote sensing: A review. Int. Soil Water Conserv. Res. 2019, 7, 27–46. [Google Scholar] [CrossRef]
- Casalí, J.; López, J.J.; Giráldez, J.V. Ephemeral gully erosion in southern Navarra (Spain). Catena 1999, 36, 65–84. [Google Scholar] [CrossRef]
- Knight, J.; Spencer, J.; Brooks, A.; Phinn, S. Large-area, high-resolution remote sensing based mapping of alluvial gully erosion in Australia’s tropical rivers. In Proceedings of the 5th Australian Stream Management Conference, Thurgoona, Australia, 21–25 May 2007; Institute for Land, Water and Society, Charles Sturt University: Bathurst, Australia, 2007; Volume 2, pp. 199–204. [Google Scholar] [CrossRef]
- Karydas, C.; Panagos, P. Towards an assessment of the ephemeral gully erosion potential in Greece using google earth. Water 2020, 12, 603. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Ding, H.; Tang, G.; Zhu, A.X.; Yang, X.; Jiang, S.; Cao, J. An object-based approach for two-level gully feature mapping using high-resolution DEM and imagery: A case study on hilly loess plateau region, China. Chin. Geogr. Sci. 2017, 27, 415–430. [Google Scholar] [CrossRef]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Shahabi, H.; Mirchooli, F.; Valizadeh Kamran, K.; Lim, S.; Aryal, J.; Jarihani, B.; Blaschke, T. Gully erosion susceptibility mapping (GESM) using machine learning methods optimized by the multi-collinearity analysis and K-fold cross-validation. Geomat. Nat. Hazards Risk 2020, 11, 1653–1678. [Google Scholar] [CrossRef]
- Thanh Noi, P.; Kappas, M. Comparison of Random Forest, k-Nearest Neighbor, and Support Vector Machine Classifiers for Land Cover Classification Using Sentinel-2 Imagery. Sensors 2017, 18, 18. [Google Scholar] [CrossRef] [Green Version]
- Phinzi, K.; Abriha, D.; Bertalan, L.; Holb, I.; Szabó, S. Machine learning for gully feature extraction based on a pan-sharpened multispectral image: Multiclass vs. Binary approach. ISPRS Int. J. Geo Inf. 2020, 9, 252. [Google Scholar] [CrossRef] [Green Version]
- Heydari, S.S.; Mountrakis, G. Meta-analysis of deep neural networks in remote sensing: A comparative study of mono-temporal classification to support vector machines. ISPRS J. Photogramm. Remote Sens. 2019, 152, 192–210. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support Vector Machine Versus Random Forest for Remote Sensing Image Classification: A Meta-Analysis and Systematic Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- Gafurov, A.M.; Yermolayev, O.P. Automatic gully detection: Neural networks and computer vision. Remote Sens. 2020, 12, 1743. [Google Scholar] [CrossRef]
- Dong, L.; Xing, L.; Liu, T.; Du, H.; Mao, F.; Han, N.; Li, X.; Zhou, G.; Zhu, D.; Zheng, J.; et al. Very High Resolution Remote Sensing Imagery Classification Using a Fusion of Random Forest and Deep Learning Technique-Subtropical Area for Example. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 113–128. [Google Scholar] [CrossRef]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.; Anders, K.; Gloaguen, R. Multisource and multitemporal data fusion in remote sensing: A comprehensive review of the state of the art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J. Multi-source remote sensing data fusion: Status and trends. Int. J. Image Data Fusion 2010, 1, 5–24. [Google Scholar] [CrossRef] [Green Version]
- Shahabi, H.; Jarihani, B.; Tavakkoli Piralilou, S.; Chittleborough, D.; Avand, M.; Ghorbanzadeh, O. A Semi-Automated Object-Based Gully Networks Detection Using Different Machine Learning Models: A Case Study of Bowen Catchment, Queensland, Australia. Sensors 2019, 19, 4893. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phinzi, K.; Holb, I.; Szabó, S. Mapping Permanent Gullies in an Agricultural Area Using Satellite Images: Efficacy of Machine Learning Algorithms. Agronomy 2021, 11, 333. [Google Scholar] [CrossRef]
- van Breda Weaver, A. The distribution of soil erosion as a function of slope aspect and parent material in Ciskei, Southern Africa. GeoJournal 1991, 23, 29–34. [Google Scholar] [CrossRef]
- Hilbich, C.; Daut, G.; Mäusbacher, R.; Helmschrot, J. A landscape-based model to characterize the evolution and recent dynamics of wetlands in the Umzimvubu headwaters, Eastern Cape, South Africa. In Wetlands: Modelling, Monitoring, Management; Kotkowski, W., Maltby, E., Miroslaw–Swiatek, D., Okruszko, T., Szatylowicz, J., Eds.; Taylor & Francis: Abingdon, UK, 2007; pp. 61–69. [Google Scholar]
- Adam, E.; Mutanga, O.; Odindi, J.; Abdel-Rahman, E.M. Land-use/cover classification in a heterogeneous coastal landscape using RapidEye imagery: Evaluating the performance of random forest and support vector machines classifiers. Int. J. Remote Sens. 2014, 35, 3440–3458. [Google Scholar] [CrossRef]
- Sabat-Tomala, A.; Raczko, E. Comparison of Support Vector Machine and Random Forest Algorithms for Invasive and Expansive Species Classification Using Airborne Hyperspectral Data. Remote Sens. 2020, 12, 516. [Google Scholar] [CrossRef] [Green Version]
- Papp, L.; van Leeuwen, B.; Szilassi, P.; Tobak, Z.; Szatmári, J.; Árvai, M.; Mészáros, J.; Pásztor, L. Monitoring invasive plant species using hyperspectral remote sensing data. Land 2021, 10, 29. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Boehmke, B.; Greenwell, B.M. Hands-On Machine Learning with R; CRC Press: Boca Raton, FL, USA, 2019; ISBN 1000730190. [Google Scholar]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How many trees in a random forest? In Proceedings of the 8th International Workshop on Machine Learning and Data Mining in Pattern Recognition, Berlin, Germany, 13–20 July 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 154–168. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; ISBN 1475732643. [Google Scholar]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Heydari, S.S.; Mountrakis, G. Effect of classifier selection, reference sample size, reference class distribution and scene heterogeneity in per-pixel classification accuracy using 26 Landsat sites. Remote Sens. Environ. 2018, 204, 648–658. [Google Scholar] [CrossRef]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Flight, L.; Julious, S.A. The disagreeable behaviour of the kappa statistic. Pharm. Stat. 2015, 14, 74–78. [Google Scholar] [CrossRef] [PubMed]
- Delgado, R.; Tibau, X.-A. Why Cohen’s Kappa should be avoided as performance measure in classification. PLoS ONE 2019, 14, e0222916. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Field, A. Discovering Statistics Using IBM SPSS Statistics; Sage: Newcastle upon Tyne, UK, 2013; ISBN 1446274586. [Google Scholar]
- Lee, S.; Lee, D.K. What is the proper way to apply the multiple comparison test? Korean J. Anesth. 2018, 71, 353. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McHugh, M.L. Multiple comparison analysis testing in ANOVA. Biochem. Med. 2011, 21, 203–209. [Google Scholar] [CrossRef] [PubMed]
- Povey, A.C.; Grainger, R.G. Known and unknown unknowns: Uncertainty estimation in satellite remote sensing. Atmos. Meas. Tech. 2015, 8, 4699–4718. [Google Scholar] [CrossRef] [Green Version]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI), Montreal, QC, Canada, 20 August 1995; Volume 14, pp. 1137–1145. [Google Scholar]
- Kim, J.-H. Estimating classification error rate: Repeated cross-validation, repeated hold-out and bootstrap. Comput. Stat. Data Anal. 2009, 53, 3735–3745. [Google Scholar] [CrossRef]
- Vrieling, A.; Rodrigues, S.C.; Bartholomeus, H.; Sterk, G. Automatic identification of erosion gullies with ASTER imagery in the Brazilian Cerrados. Int. J. Remote Sens. 2007, 28, 2723–2738. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Sepuru, T.K.; Dube, T. Understanding the spatial distribution of eroded areas in the former rural homelands of South Africa: Comparative evidence from two new non-commercial multispectral sensors. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 119–132. [Google Scholar] [CrossRef]
- Orti, M.V.; Winiwarter, L.; Corral-Pazos-de-Provens, E.; Williams, J.G.; Bubenzer, O.; Höfle, B. Use of TanDEM-X and Sentinel products to derive gully activity maps in Kunene Region (Namibia) based on automatic iterative Random Forest approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 607–623. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).