Tracking of Multiple Maneuvering Random Hypersurface Extended Objects Using High Resolution Sensors
Abstract
:1. Introduction
2. Problem Formulation
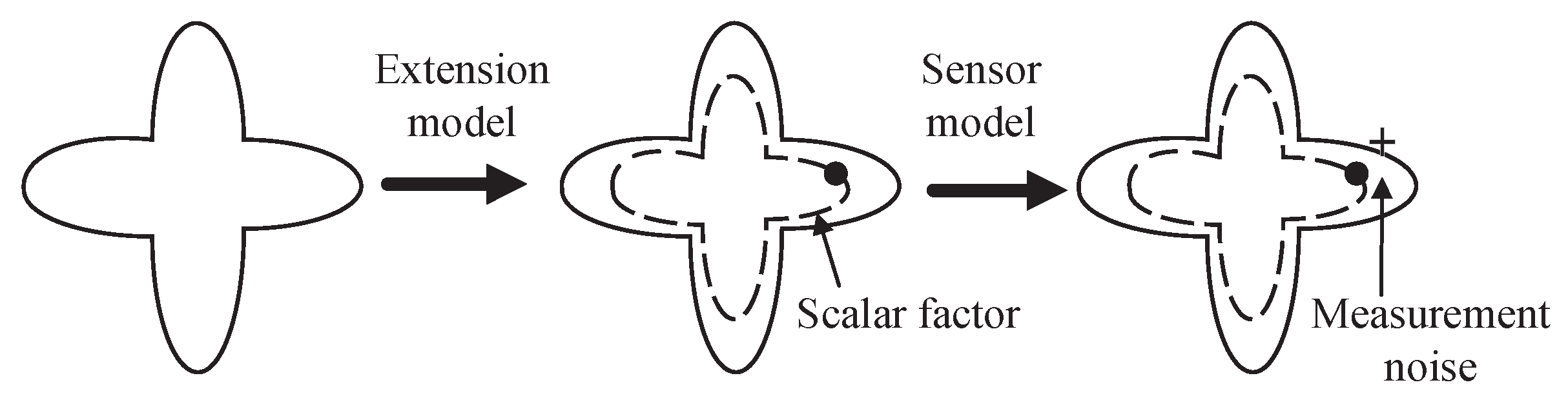
2.1. System Models of A Star-Convex Extended Object
2.2. Multiple Extended Object Tracking Framework
- the number of predicted Gaussian mixture components;
- the weight of the predicted Gaussian mixture component;
- the predicted mean and covariance of the predicted Gaussian mixture component, respectively.
- the intensity updated by the measurement subset W;
- the expected measurement number of a single extended object, which obeys the Poisson distribution;
- the probability of object detection;
- the mean number of measurements from clutters;
- the spatial distribution of clutters;
- the partition in which the measurement set is partitioned into several non-empty subsets;
- non-negative coefficients for the partition P and the subset W, respectively;
- the likelihood function for the measurement .
3. An IMM-GMPHD Filter For Tracking Multiple Maneuvering Extended Objects Using RHMs
3.1. Maneuver Models for Star-Convex Extended Objects Using RHMs
3.2. Model Probability Update for Maneuvering Extended Object Tracking
3.3. The IMM-GMPHD Filtering Recursion
4. Simulation Results and Performance Evaluation
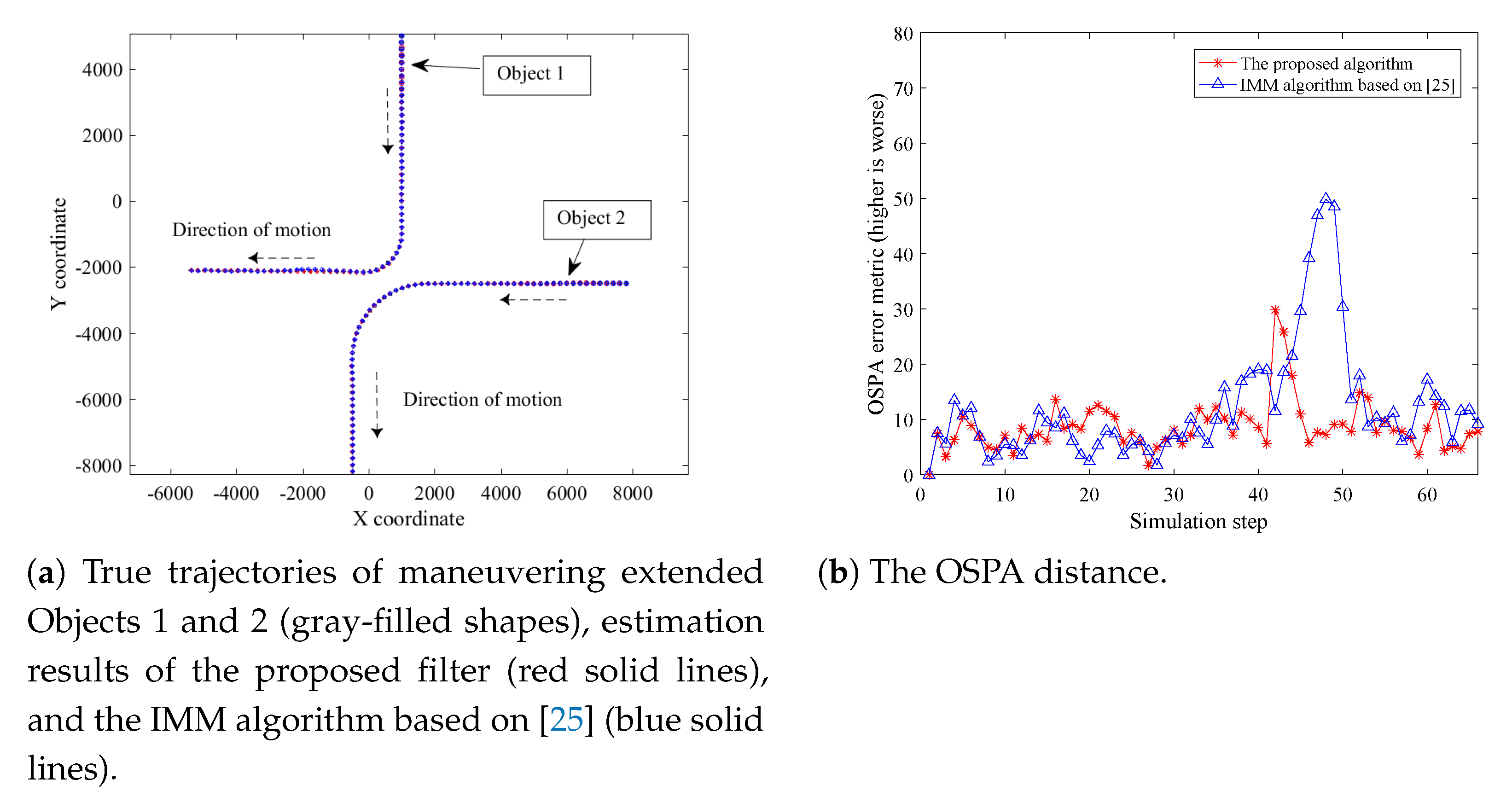
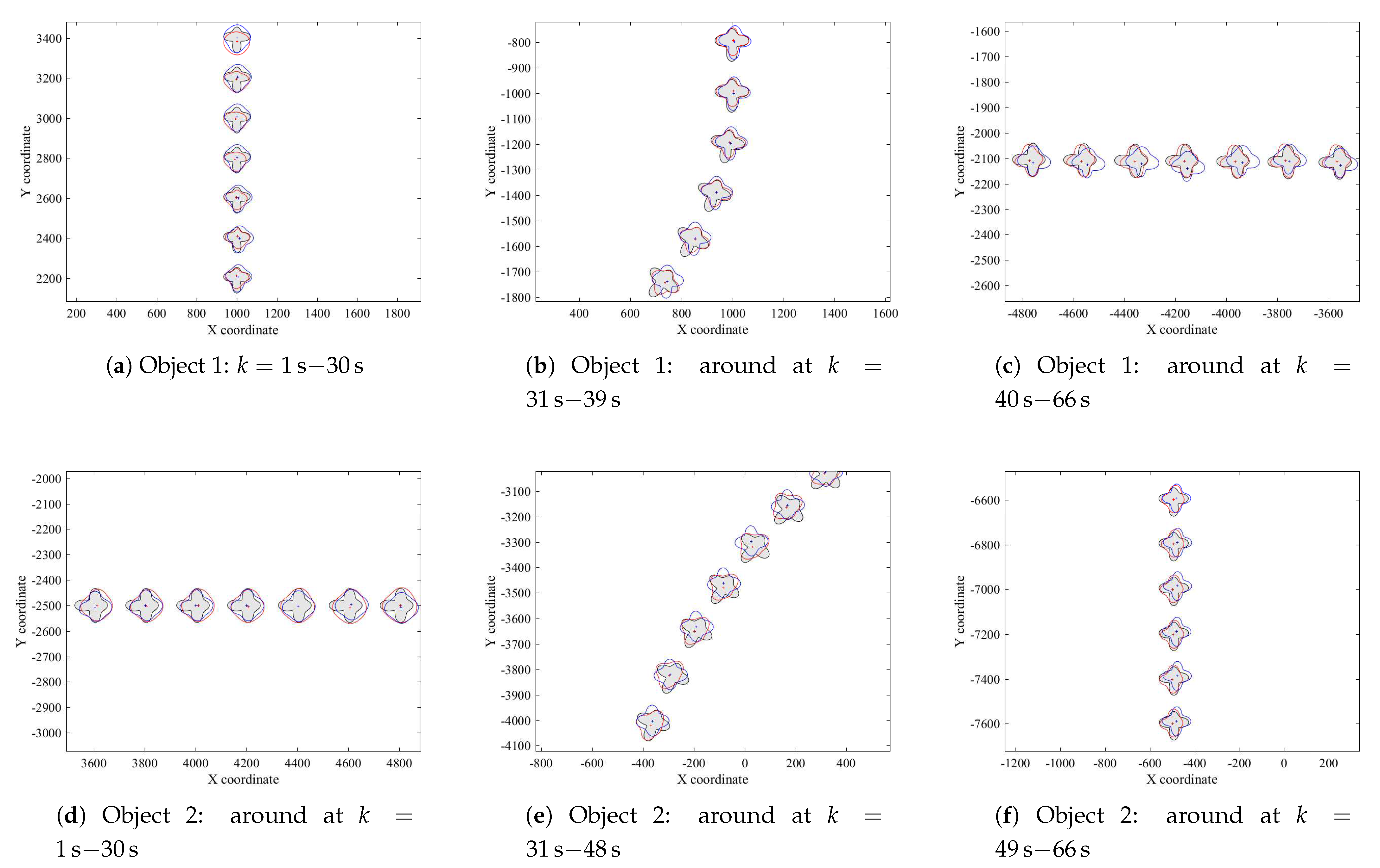
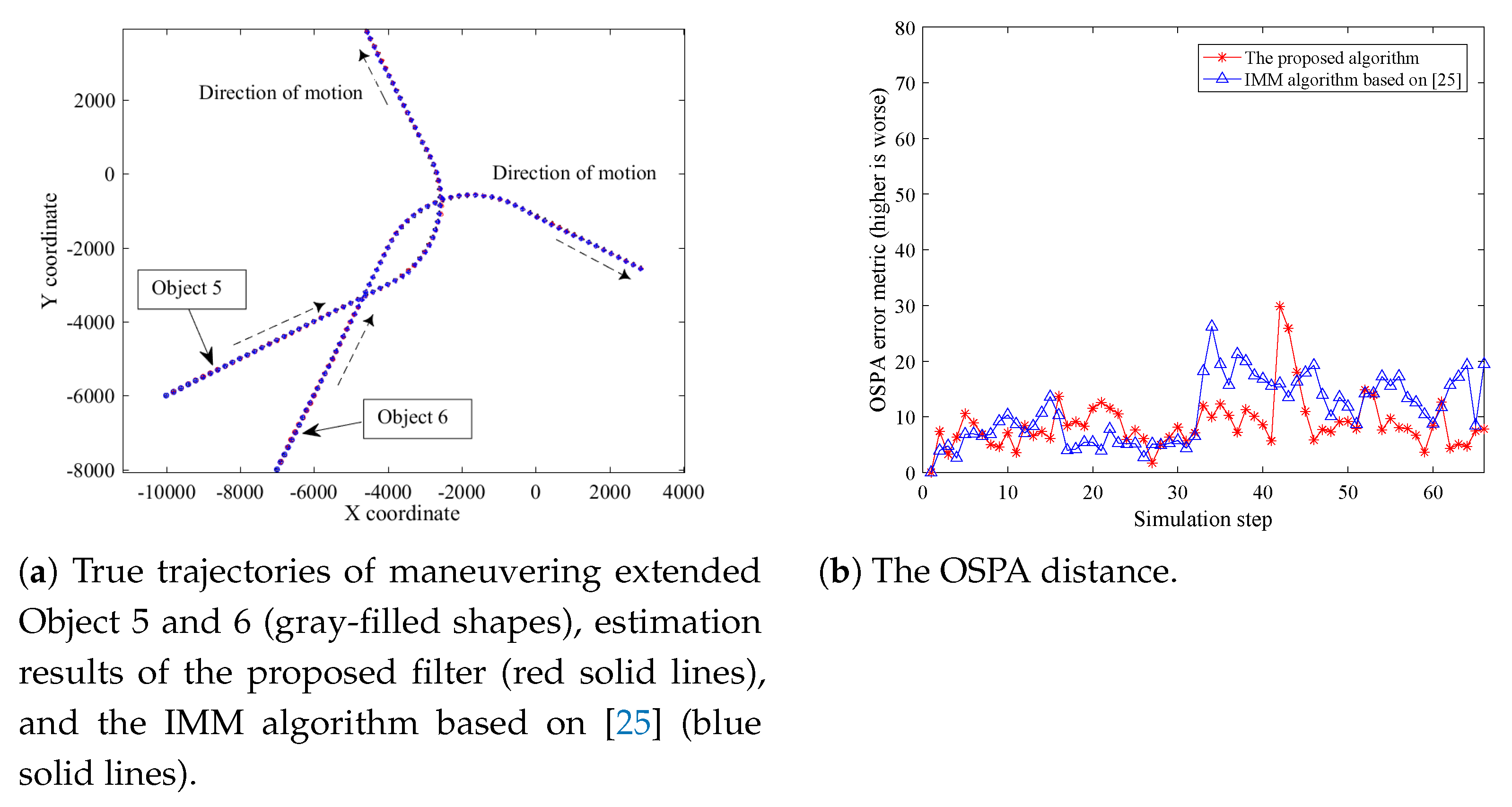
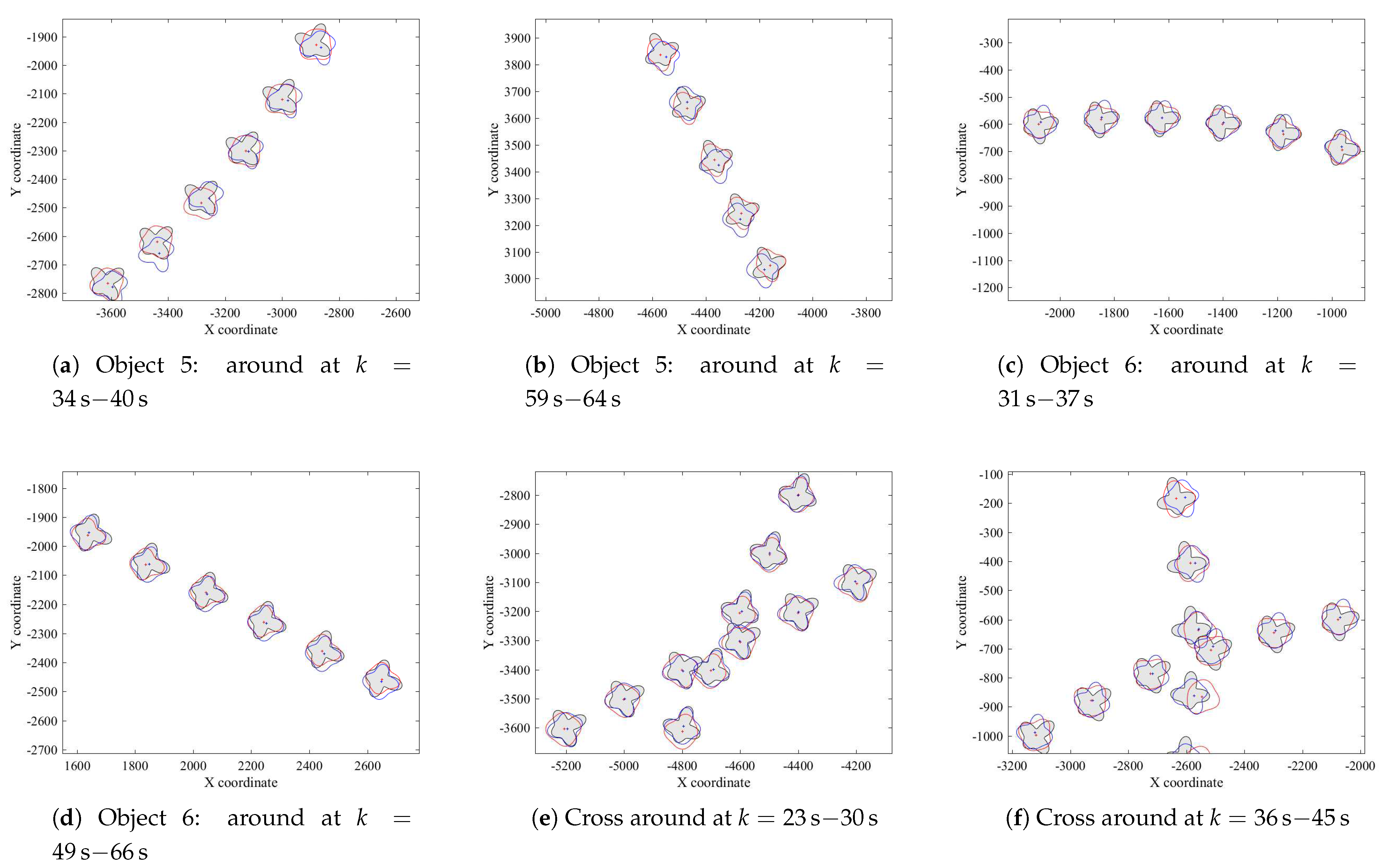
4.1. Tracking Performance in Scenario A
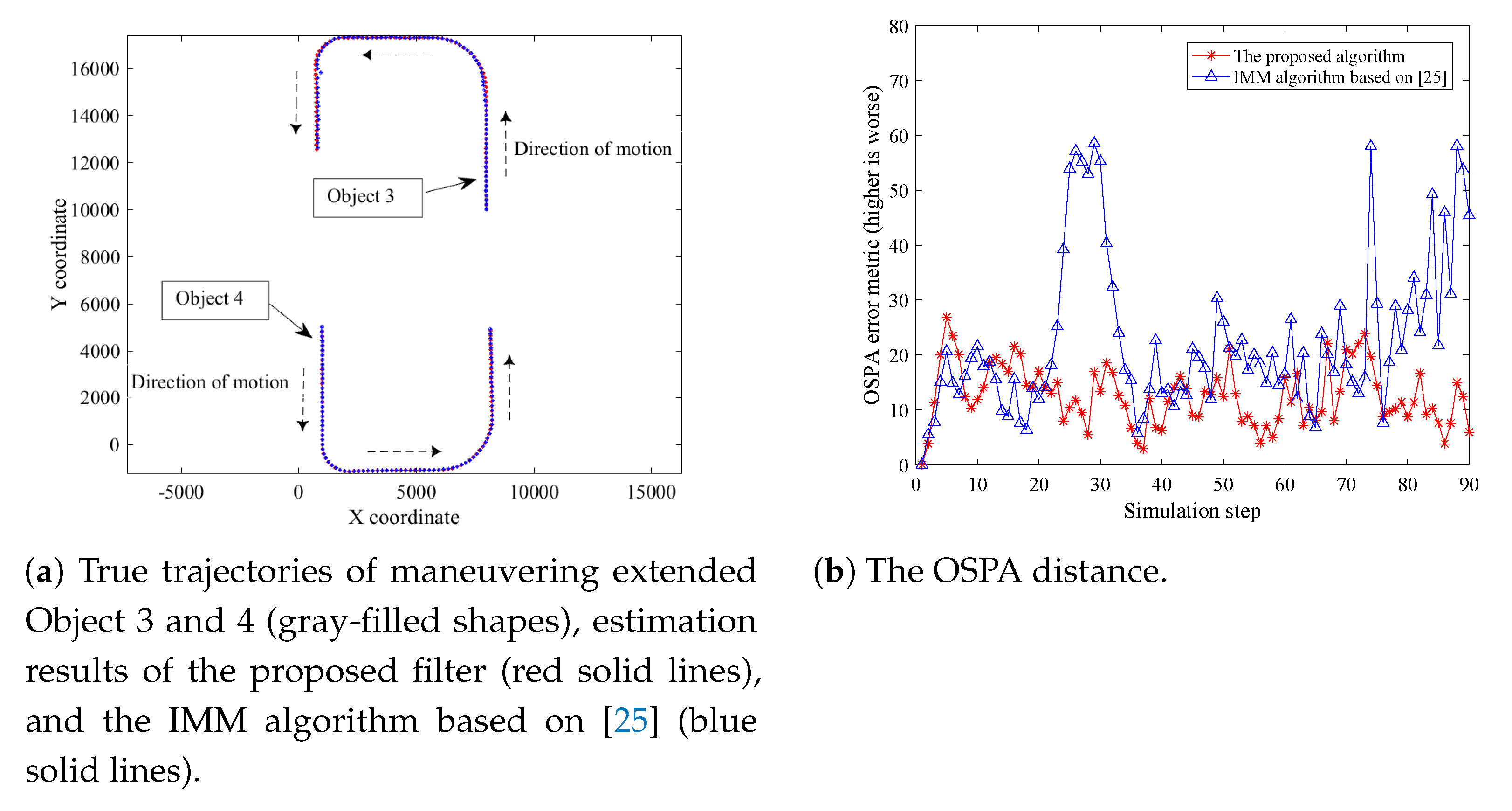
4.2. Tracking Performance in Scenario B
4.3. Tracking Performance in Scenario C
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, L.; Mao, D.; Niu, J.; Wu, Q.M.; Ji, Y. Continuous Tracking of Targets for Stereoscopic HFSWR Based on IMM Filtering Combined with ELM. Remote Sens. 2020, 12, 272. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.; Zhang, X.; Yang, Q. Modified Multi-Mode Target Tracker for High-Frequency Surface Wave Radar. Remote Sens. 2018, 10, 1061. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Huang, H.; Zhao, H.; Zhao, X.; Yin, X. Adaptive Unscented Kalman Filter for Target Tracking in the Presence of Nonlinear Systems Involving Model Mismatches. Remote Sens. 2017, 9, 657. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.; Yan, X.; Tang, S.; Wu, M.; Li, C. An adaptive non-zero mean damping model for trajectory tracking of hypersonic glide vehicles. Aerosp. Sci. Technol. 2021, 111, 106529. [Google Scholar] [CrossRef]
- Blackman, S. Multiple hypothesis tracking for multiple target tracking. IEEE Aerosp. Electr. Syst. Mag. 2004, 19, 5–18. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Shan, Y.; Cui, N. Quantized genetic resampling particle filtering for vision-based ground moving target tracking. Aerosp. Sci. Technol. 2020, 103, 105925. [Google Scholar] [CrossRef]
- Mahler, R. Multitarget bayes filtering via firstorder multi target moments. IEEE Trans. Aerosp. Electr. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Mahler, R. Statistical multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007. [Google Scholar]
- Kim, D.; Kwon, C.; Hwang, I. Gaussian mixture probability hypothesis density filter against measurement origin uncertainty. Signal Process. 2020, 171, 107448. [Google Scholar] [CrossRef]
- Vo, B.N.; Singh, S.; Doucet, A. Sequential monte carlo implementation of the PHD filter for multi-target tracking. In Proceedings of the International Conference Information Fusion, 2003; pp. 792–799. Available online: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=24BC893EC3158E28FD9689520CF57E64?doi=10.1.1.9.5930&rep=rep1&type=pdf (accessed on 24 May 2021).
- Clark, D.E.; Panta, K.; Vo, B.N. The GM-PHD filter multiple target tracker. In Proceedings of the 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; pp. 1–8. [Google Scholar]
- Mahler, R. CPHD and PHD filters for unknown backgrounds, II: Multitarget filtering in dynamic clutter. In Proceedings of the Sensors and Systems for Space Applications III, Orlando, FA, USA, 6 May 2009; International Society for Optics and Photonics, 2009; Volume 7330, p. 73300L. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/7330/73300L/CPHD-and-PHD-filters-for-unknown-backgrounds-II--multitarget/10.1117/12.818023.full?SSO=1 (accessed on 24 May 2021).
- Li, P.; Ge, H.W.; Yang, J.L.; Wang, W. Modified Gaussian inverse Wishart PHD filter for tracking multiple non-ellipsoidal extended targets. Signal Process. 2018, 150, 191–203. [Google Scholar] [CrossRef]
- Hu, Q.; Ji, H.; Zhang, Y. A standard PHD filter for joint tracking and classification of maneuvering extended targets using random matrix. Signal Process. 2018, 144, 352–363. [Google Scholar] [CrossRef]
- Gilholm, K.; Salmon, D. Spatial distribution model for tracking extended objects. IEEE Proc. Radar Sonar Navig. 2005, 152, 364–371. [Google Scholar] [CrossRef]
- Gilholm, K.; Godsill, S.; Maskell, S.; Salmond, D. Poisson models for extended target and group tracking. In Signal and Data Processing of Small Targets; International Society for Optics and Photonics: San Diego, CA, USA, 2005; Volume 5913, p. 59130R. [Google Scholar]
- Mahler, R. PHD filters for nonstandard targets, I: Extended targets. In Proceedings of the IEEE 12th International Conference on Information Fusion, Seattle, WA, USA, 6–9 July 2009; pp. 915–921. [Google Scholar]
- Granstrom, K.; Lundquist, C.; Orguner, O. Extended target tracking using a gaussian mixture PHD filter. IEEE Trans. Aerosp. Electr. Syst. 2012, 48, 3268–3286. [Google Scholar] [CrossRef] [Green Version]
- Feldmann, M.; Fränken, D.; Koch, W. Tracking of extended objects and group targets using random matrices. IEEE Trans. Signal Process. 2011, 59, 1409–1420. [Google Scholar] [CrossRef]
- Zong, P.; Barbary, M. Improved multi-bernoulli filter for extended stealth targets tracking based on sub-random matrices. IEEE Sens. J. 2015, 16, 1428–1447. [Google Scholar] [CrossRef]
- Vivone, G.; Granström, K.; Braca, P.; Willett, P. Multiple sensor measurement updates for the extended target tracking random matrix model. IEEE Trans. Aerosp. Electr. Syst. 2017, 53, 2544–2558. [Google Scholar] [CrossRef]
- Hassan, M.; Bermak, A. Robust bayesian inference for gas identification in electronic nose applications by using random matrix theory. IEEE Sens. J. 2016, 16, 2036–2045. [Google Scholar] [CrossRef]
- Baum, M.; Hanebeck, U.D. Shape tracking of extended objects and group targets with star-convex RHMs. In Proceedings of the IEEE 14th International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011; pp. 338–345. [Google Scholar]
- Baum, M.; Hanebeck, U.D. Extended object tracking with random hypersurface models. IEEE Trans. Aerosp. Electr. Syst. 2014, 50, 149–159. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Zhu, H.; Han, C. A gaussian-mixture PHD Filter Based on random hypersurface model for multiple extended targets. In Proceedings of the IEEE Proceedings of the 16th International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; pp. 1752–1759. [Google Scholar]
- Wood, T.M. Interacting methods for manoeuvre handling in the GM-PHD filter. IEEE Trans. Aerosp. Electr. Syst. 2011, 47, 3021–3025. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking Part I: Dynamic models. IEEE Trans. Aerosp. Electr. Syst. 2003, 39, 1333–1364. [Google Scholar]
- Vo, B.N.; Pasha, A.; Tuan, H.D. A gaussian mixture PHD filter for nonlinear jump markov models. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 3162–3167. [Google Scholar]
- Punithakumar, K.; Kirubarajan, T.; Sinha, A. Multiple-model probability hypothesis density filter for tracking maneuvering targets. IEEE Trans. Aerosp. Electr. Syst. 2008, 44, 87–98. [Google Scholar] [CrossRef]
- Dong, P.; Jing, Z.; Gong, D.; Tang, B. Maneuvering multi-target tracking based on variable structure multiple model GMCPHD filter. Signal Process. 2017, 141, 158–167. [Google Scholar] [CrossRef]
- Wang, C.; Wu, P.; He, S.; Yun, P. Robust CPHD algorithm for maneuvering targets tracking via airborne pulsed Doppler radar. Optik 2019, 178, 285–296. [Google Scholar] [CrossRef]
- Hirscher, T.; Scheel, A.; Reuter, S.; Dietmayer, K. Multiple extended object tracking using Gaussian processes. In Proceedings of the IEEE 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; pp. 868–875. [Google Scholar]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef] [Green Version]


| Input: the mixed posterior intensity , |
| each posterior intensity (), |
| and model probabilities corresponding to . |
| Repeat |
| merging Gaussian mixture components of the mixed posterior intensity: |
| , |
| merging model probabilities: |
| merging Gaussian mixture components of each posterior intensity: |
| , |
| until |
| Output: the final mixed posterior intensity , |
| each posterior intensity (), |
| and model probabilities corresponding to . |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Yu, H.; Lan, J.; Fu, Z.; He, Z.; Pu, J. Tracking of Multiple Maneuvering Random Hypersurface Extended Objects Using High Resolution Sensors. Remote Sens. 2021, 13, 2963. https://doi.org/10.3390/rs13152963
Sun L, Yu H, Lan J, Fu Z, He Z, Pu J. Tracking of Multiple Maneuvering Random Hypersurface Extended Objects Using High Resolution Sensors. Remote Sensing. 2021; 13(15):2963. https://doi.org/10.3390/rs13152963
Chicago/Turabian StyleSun, Lifan, Haofang Yu, Jian Lan, Zhumu Fu, Zishu He, and Jiexin Pu. 2021. "Tracking of Multiple Maneuvering Random Hypersurface Extended Objects Using High Resolution Sensors" Remote Sensing 13, no. 15: 2963. https://doi.org/10.3390/rs13152963
APA StyleSun, L., Yu, H., Lan, J., Fu, Z., He, Z., & Pu, J. (2021). Tracking of Multiple Maneuvering Random Hypersurface Extended Objects Using High Resolution Sensors. Remote Sensing, 13(15), 2963. https://doi.org/10.3390/rs13152963





