Remote Sensing Image Super-Resolution Based on Dense Channel Attention Network

Abstract

In the recent years, convolutional neural networks (CNN)-based super resolution (SR) methods are widely used in the field of remote sensing. However, complicated remote sensing images contain abundant high-frequency details, which are difficult to capture and reconstruct effectively. To address this problem, we propose a dense channel attention network (DCAN) to reconstruct high-resolution (HR) remote sensing images. The proposed method learns multi-level feature information and pays more attention to the important and useful regions in order to better reconstruct the final image. Specifically, we construct a dense channel attention mechanism (DCAM), which densely uses the feature maps from the channel attention block via skip connection. This mechanism makes better use of multi-level feature maps which contain abundant high-frequency information. Further, we add a spatial attention block, which makes the network have more flexible discriminative ability. Experimental results demonstrate that the proposed DCAN method outperforms several state-of-the-art methods in both quantitative evaluation and visual quality.

1. Introduction

High-resolution (HR) remote sensing images provide detailed geometric information about land cover. Thus, HR remote sensing images are essential for many applications, such as object detection [1,2], urban planning [3], building extraction [4,5,6] and so on [7,8,9,10,11,12,13,14,15]. However, the spatial resolution of remote sensing images are influenced by the limitations of hardware and environmental factors [16,17,18]. Compared to current physical imaging technology, super resolution (SR) which recovers HR images from low-resolution (LR) images is more convenient and low cost. Thus, SR becomes an alternative method in the remote sensing field.

SR can be classified into single image super resolution (SISR) and multiple image super resolution (MISR) [19] by the number of input images. MISR methods utilize multiple LR images of the same area, to provide more information, to better reconstruct high spatial-frequency details and texture [20]. Nevertheless, it is difficult to obtain multiple remote sensing images of the same scene. Thus, this paper considers a study of SISR methods. The traditional SISR methods [21] are mainly grouped into interpolation-based methods and reconstruction-based methods [22]. The interpolation-based methods predict the unknown pixel using a simple linear or non-linear interpolation [23] operation. Although interpolation-based methods are convenient, they have limited performance for images which contain more details. The reconstruction-based methods utilize a certain kind of prior information to produce better results, such as local, nonlocal and sparse priors [23,24]. Although reconstruction-based methods [25] are flexible and allow consideration of different prior constraints [26,27,28,29,30,31], they also have difficulties with complicated remote sensing images. Recently, deep learning-based methods attracted a lot of attention in the remote sensing images super resolution task. In 2015, a super resolution convolutional neural network (SRCNN) [32] was first proposed by Dong et al. to achieve the natural images super resolution. As the poineer, SRCNN learned the mapping between the HR images and the corresponding LR images using a three layers network. While SRCNN had outperformed traditional-based methods, bicubic LR images made the network to operate in a high-dimensional space and largely increased the computational cost. To alleviate the problem, a fast super resolution convolutional neural netork (FSRCNN) [33] and an efficient subpixel convolutional network (ESPCN) [34] were proposed which used a deconvolutional layer and a subpixel convolutional layer to achieve direct reconstruction in a low-dimensional space and save the computational cost, respectively. These networks were shallow and their performance were limited by the network depth. However, increasing the network depth leads to a vanishing gradient and an exploding gradient. To handle the problem, the skip connection operation [35] was proposed by He et al., which combined the low-level features and high-level features to effectively alleviate the gradient vanishing. Thus, the skip connection operation was gradually used in the SR networks. Among these networks, the very deep super resolution convolutional network (VDSR) [36] which used a global residual connection was proposed by Kim et al. to spread the LR information to the network end. It was the first network which introduced the residual learning to SR and succeeded training a 20-layer network. Besides, enhanced deep super resolution (EDSR) [37] and SRResNet [38] also used global residual connection. In addition, EDSR and SRResNet employed residual blocks as basic network module, which introduced local residual connection to ease the deep network training difficulty. Later, Zhang et al. [39] constructed a residual in residual structure where residual blocks compose residual groups using short and long skip connections. Further, cascading residual network (CARN) [40], dense deep back-projection network (D-DBPN) [41], SRDenseNet [42], residual dense network (RDN) [43], employed the dense skip connections or multiple skip connections to increase the training effect.

Deep learning-based SR methods in the field of remote sensing also developed fast in recent years. In 2017, a local-global combined network (LGC) [19] was first proposed by Lei et al. to enhance the spatial resolution of remote sensing images. LGC learns multi-level information including local details and global priors using the skip connection operation. In 2018, a residual dense backprojection network (RDBPN) [22] was proposed by Pan et al., which consists of several residual dense backprojection blocks that contain the upprojection module and the downprojection module. In 2020, Zhang et al. proposed a scene adaptive method [44] via a multi-scale attention network to enhance the SR reconstruction details under the different remote sensing scenes. Recently, an approach named dense-sampling super resolution network (DSSR) [45] presented a dense sampling mechanism which reuses an upscaler to upsample and overcome the large-scale remote sensing images SR reconstruction problem. However, the complex spatial distribution of remote sensing images need more attention. In 2020, a second-order multi-scale super resolution network (SMSR) [46] was proposed by Dong et al. to reuse the learned multi-level information to the high-frequency regions of remote sensing images. The multi-perception attention network (MPSR) [47] and the multi-scale residual neural network (MRNN) [48] are also doing some related work about using multi-scale information. In addition, the generative adversarial network (GAN)-based SR method is used to generate visually pleasing remote sensing images. In 2019, Jiang et al. presented an edge-enhancement generative adversarial network (EEGAN) [49], which introduces an edge enhancement module to improve the remote sensing images SR performance. In 2020, Lei et al. proposed a coupled-discriminated generative adversarial network (CDGAN) [50] for solving the discrimination-ambiguity problem for the low-frequency regions in the remote sensing images.

Although the above-mentioned methods have good performance, their results can be further improved. First, the distributions of remote sensing images are very complex; therefore, we need more high-frequency details and texture to better reconstruct HR images. Secondly, redundancy feature information are not beneficial to recover details and increase computation cost. So, we propose a dense channel attention network (DCAN) which learns multi-level feature information and pays more attention to the important and useful regions in order to better reconstruct the final image. The major contributions are as follows:

(1)

We propose a DCAN for SR of the single remote sensing image, which makes full use of the features learned at different depths through densely using multi-level feature information and pay more attention to high-frequency regions. Both quantitative and qualitative evaluations demonstrate the superiority of DCAN over the state-of-the-art methods.

(2)

A dense channel attention mechanism (DCAM) is proposed to utilize the channel attention block through the dense skip connection manner. This mechanism can increase the flow of information through the network and improve the representation capacity of the network.

(3)

A spatial attention block (SAB) is added to the network. This helps the network have more flexible discriminative ability for different local regions. It contributes to reconstruct the final image. In addition, this helps the network have more flexible discriminative ability for global structure and focus on high-frequency information from the spatial dimension.

2. Method

2.1. Network Architecture

The architecture of our proposed DCAN is illustrated in Figure 1, which consists of three parts: shallow feature extraction, deep feature extraction, and reconstruction. The network first extracts the shallow features from the input LR image. Then, the second part extracts the deep features and increase the weights of important feature maps. Finally, the features which contain abundant useful information are sent to the third part of network for reconstruction. The network details will be introduced in the next part.

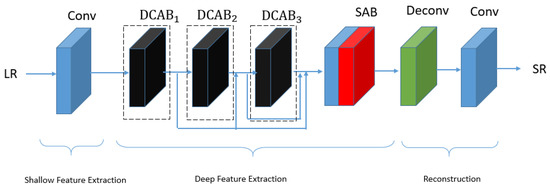
Figure 1. The structure of the proposed dense channel attention network (DCAN).

(1)

Shallow Feature Extraction: Let Conv(k, f, c) be a convolutional layer, where k, f, c represent the filter kernel size, the number of filters, and the number of filter channels, respectively. We use a $3\times 3$ convolutional layer to extract the shallow feature $F_0$ from the input image $I^{LR}$, which contributes to the next feature extraction. The shallow feature extraction $f_{SF}(.)$ operation can be formulated as follows:

$$F_0=f_{SF}\left(I^{LR}\right)=Conv(k,f,c)\left(I^{LR}\right)$$

(1)

(2)

Deep Feature Extraction: After the shallow feature extraction, the backbone part which contains a series of Dense Channel Attention blocks (${\mathrm{DCAB}}_s$) and a Spatial Attention Block (SAB) is designed to extract deep features. The main block DCAB receives the feature maps from each single DCAB as input, the structure of which will be given in Section 2.2. Then, the feature $F_G$ which is the sum of output features of G ${\mathrm{DCAB}}_s$ is sent to a convolutional layer:

$$F_{G^{{}^{\prime }}}=Conv(k,f,c)\left(F_G\right)$$

(2)

where $F_{G^{\prime }}$ is generated by the convolution operation, G denotes the number of ${\mathrm{DCAB}}_s$. Then, the $F_{G^{\prime }}$ is sent to a SAB as follows:

$$F_{\mathrm{SAB}}=H_{\mathrm{SAB}}\left(F_{G^{\prime }}\right)$$

(3)

where $H_{\mathrm{SAB}}$ denotes the operation of the SAB. The operational details will be described in Section 2.3.

(3)

Reconstruction: The reconstruction part contains two convolutional layers and a deconvolution layer. The SR image $I^{SR}$ is generated as follows:

$$I^{SR}=Conv(k,f,c)\left(H_{Up}\left(Conv(k,f,c)\left(F_{\mathrm{SAB}}\right)\right)\right)$$

(4)

where $H_{up}$ denotes the operation of the deconvolution layer.

2.2. Dense Channel Attention Mechanism

As discussed in Section 1, most existing super-resolution models do not make full use of the information from the input LR image. So, we propose a novel dense channel attention mechanism to solve the problem. It concentrates on the high-frequency information and weakens the useless information. Figure 2 shows DCAM, which can be described that the $G_{th}$ DCAB computes the feature map $F_G$ from the outputs of the ${\mathrm{DCAB}}_{G-1},{\mathrm{DCAB}}_{G-2},...,{\mathrm{DCAB}}_1$ as follows:

$$F_G=H_{{\mathrm{DCAB}}_G}(F_{G-1}+F_{G-2}+\dots +F_1)$$

(5)

where $H_{{\mathrm{DCAB}}_G}$ denotes the operation of the $G_{th}$ DCAB, $F_{G-1},F_{G-2},\dots ,F_1$ denote the outputs of the ${\mathrm{DCAB}}_{G-1},{\mathrm{DCAB}}_{G-2},\dots ,{\mathrm{DCAB}}_1$. The purpose of DCAM is to focus on high-frequency components and make better use of the information.

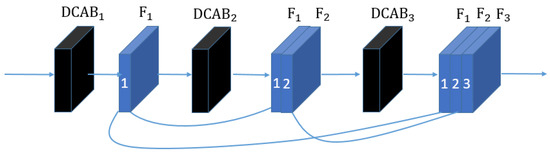
Figure 2. The structure of dense channel attention mechanism (DCAM).

As shown in Figure 2, the DCAB is the basic block of the proposed DCAM. It mainly contains two convolutional layers and a CA (Channel Attention) block. To be specific, in Figure 3, the first convolutional layer before Relu consists of $n_f$ filters of size $n_c\times 3\times 3$. The second convolutional layer after Relu contains $n_f$ filters of size $n_f\times 3\times 3$. Let $F_{i-1}$ be the input of ${\mathrm{DCAB}}_i$ (the i-th DCAB in the ${\mathrm{DCAB}}_s$), there is

$$X_i=W^{(3,n_f,n_f)}\ast \sigma (W^{(3,n_f,n_c)}\ast F_{i-1})$$

(6)

where $X_i$ is an intermediate feature contaninting $n_f$ feature maps. $W^{(3,n_f,n_f)}$ and $W^{(3,n_f,n_c)}$ denote the weight matrix of $n_f$ filters of size $n_f\times 3\times 3$ and $n_f$ filters of size $n_c\times 3\times 3$. $\sigma (.)=max(0,x)$ indicates the Relu activation.

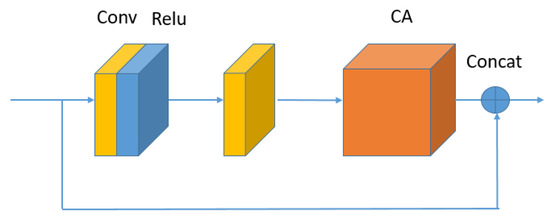
Figure 3. The structure of dense channel attention block (DCAB).

Then, CA is used to improve the discriminative learning ability. As shown in Figure 4, the mechanism of CA can be formulated as follows:

$$X_i^{\prime }=X_i\otimes S_i=[X_1^i,\dots ,X_{n_f}^i]\otimes [S_1^i,\dots ,S_{n_f}^i]$$

(7)

where $X_i^{\prime }$ is the output of $X_i$, $X_1^i,\dots ,X_{n_f}^i$ is the feature map of $X_i$, $S_1^i,\dots ,S_{n_f}^i$ are the elements of $S_i$, ⊗ indicates the elementwise product. $S_i$ is a $n_f$ dimensional channel statistical descriptor, which is used to update $X_i$. $S_i$ is obtained by

$$S_i=f_{sigmoid}\left(f_{up}\left(\sigma \left(f_{down}\left(f_{gap}\left(X_i\right)\right)\right)\right)\right)$$

(8)

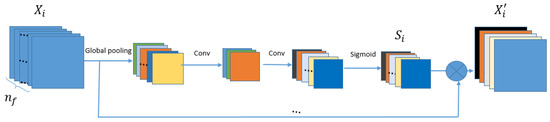
Figure 4. The structure of Channel Attention Block (CA).

It contains several operations, including global average pooling $f_{gap}\left(\right)$, channel-down $f_{down}=Conv(1,n_f/r,n_f)$, Relu activation $\sigma \left(\right)$, channel-up $f_{up}=Conv(1,n_f,n_f/r)$, and sigmoid function $f_{sigmoid}$, on $X_i$ (r is set to 16). The channel statistical descriptor can help express the different information among the feature maps of $X_i$.

As shown in Figure 3, the input of the $i_{th}$ DCAB is from the output of $i_1,\dots ,i_{th-1}{\mathrm{DCAB}}_s$. In general, the complete operation of DCAB can be formulated as follows:

$$F_i=S_i\otimes (W^{(3,n_f,n_f)}\ast \sigma (W^{(3,n_f,n_c)}\ast F_{i-1}))+F_{i-1}$$

(9)

This operation increases the flow of information through the network and the representation capacity of the network.

2.3. Spatial Attention Block

Considering the complicated spatial information and distribution of the remote sensing images, we add a SAB to increase the discriminative ability of the network. It helps the network have discriminative ability for different local regions and pay more attention to the regions which are more important and more difficult to reconstruct. As shown in Figure 5, the operation of SAB can be formulated as follows:

$$F_{\mathrm{SAB}}=F_{input}\otimes f_{sigmoid}\left(f_{conv}\left(f_{concat}(f_{Avgpooling}\left(F_{input}\right),f_{Maxpooling}\left(F_{input}\right))\right)\right)$$

(10)

where $F_{\mathrm{SAB}}$ is obtained by several operations, including average pooling $f_{Avgpooling}\left(\right)$, $f_{Maxpooling\left(\right)}$, concat $f_{concat}\left(\right)$, channel-down $f_{conv}\left(\right)=Conv(1,1,2)$, sigmoid function $f_{sigmoid}\left(\right)$, and element-wise product $\sigma$. The operation of SAB can focus on the local regions of $F_{input}$ which are useful to reconstruct.

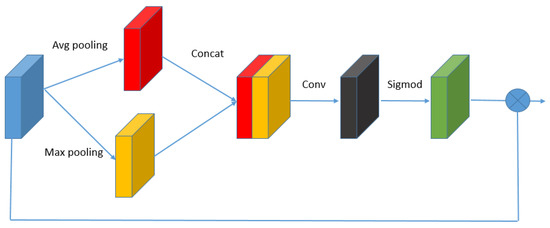
Figure 5. The structure of Spatial Attention Block (SAB).

2.4. Loss Function

We use the $L_1$ loss as the total loss because the $L_1$ loss can support better convergence. In addition, the $L_1$ loss can be described as follows:

$$L_1\left(\theta \right)=\frac{1}{n}\sum _{i=1}^n\parallel f_{\mathrm{DCAN}}(I_i^{LR};\theta )-I_i^{HR}\parallel$$

(11)

where $\theta$ represents the whole parameter of the DCAN network, n represents the number of training images. The purpose of the $L_1$ loss function is that the reconstructed HR image $I_i^{SR}=f_{\mathrm{DCAN}}(I_i^{LR};\theta )$ can be similar to its corresponding ground truth image $I_i^{HR}$.

3. Results

3.1. Experimental Settings

The relevant experimental settings on the experimental datasets, degradation method, and evaluation metrics are detailed in this section.

(1) Datasets: We use UC Merced dataset and RSSCN7 dataset for qualitative and quantitative analysis. The UC Merced dataset [51] is a classification dataset of remote sensing images containing 21 land use classes, and each class contains 100 images with size $256\times 256$ and RGB channels. Figure 6 shows some images. The UC Merced dataset is mainly used as the experimental data and divided into two sections. The first section includes images in 21 classes of agricultural, baseball diamond, beach, building and so on. For each category, 90 images are taken to create the training set. Therefore, the second section includes the remaining ten images for each class which are taken to construct the test set. We can validate the performance of our model for each class. The results are discussed in Section 3.2.

Figure 6. Some images in the UC Merced dataset: 21 land use classes, including buildings, agricultural, airplane, baseball diamond, beach, chaparral, dense residential, forest, freeway, golf course, harbor, intersection, medium residential, mobile home park, overpass, parking lot, river, runway, sparse residential, storage tanks, and tennis court. The above images correspond to the above categories respectively.

In addition, the other dataset named RSSCN7 [52] is also used to train our method and verify the effectiveness of our method. The RSSCN7 dataset is a classification dataset of remote sensing images containing 7 land use classes, and each class contains 400 images with size $400\times 400$ and RGB channels. Figure 7 shows some images. This dataset is divided into two sections. The first section contains images in 7 classes. For each class, 360 images are used to train the model. Thus, the second section includes the remaining 40 images for each class which are used to construct the test set. The test results are discussed in Section 3.2.

Figure 7. Some images in the RSSCN7 dataset: 7 land use classes, including grass, filed, industry, river lake, forest, resident and parking. The above images correspond to the above categories respectively.

To validate the robustness of the proposed method, the real world data from GaoFen-2 in Ningxia, China, are used to test our model in Section 3.4. Experiments are designed by the $\times 4$ scale factor and the $\times 8$ scale factor, respectively. We obtain LR images by down sampling HR images using the bicubic operation.

All the parameter settings are same on the UC Merced dataset and RSSCN7 dataset. The training step is performed on the three channels of the RGB space. The channel number of the input image $n_c$ is 3, the filter size k is set as 3. The Adam [53] optimizer with ${\beta }_1=0.9$ and ${\beta }_2=0.999$ is used to train the proposed models under the batchsize of 16. The weights of the model are initialized using the method in [54]. We initialize the learning rate as ${10}^{-4}$ and halve it at every $2\times {10}^5$ batches updates. We implement the proposed algorithm with the PyTorch [55] framework, and we train the DCAN model using one NVIDIA Tesla V100 GPU.

(2) Evaluation Metrics: Two widely used image quality assessment metrics, the peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) are used as evaluation metrics. They are used as the criteria for evaluating the quality of reconstructed HR images. Given the ground truth HR image x and its corresponding super-resolved image y, the PSNR of the super-resolved image y is computed as follows:

$$\mathrm{MSE}(x,y)=\frac{1}{n_s}\sum _{i=1}^{n_s}{(x_i-y_i)}^2$$

(12)

$$\mathrm{PSNR}(x,y)=10lo{g}_{10}\frac{{255}^2}{\mathrm{MSE}(x,y)}$$

(13)

where $x_i$ and $y_i$ denote the ith pixel in x and y values, respectively. $n_s$ represents the image pixel number. The higher PSNR indicates that the quality of the SR image is better. In addition to using PSNR to measure image quality, we also use SSIM as the image quality assessment, the SSIM of the super-resolved image y is defined as follows:

$$\mathrm{SSIM}(x,y)=\frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\sigma }_x^2+{\sigma }_y^2+C_2)}$$

(14)

where ${\mu }_x$ and ${\mu }_y$ denote the mean values of x and y, and ${\sigma }_x$ and ${\sigma }_y$ denote the standard deviation values of x and y, and $C_1$ and $C_2$ are constants. The higher SSIM indicates that the quality of the SR image is better.

3.2. Comparisons with the Other Methods

The proposed DCAN method is compared with four state-of-the-art methods: Bicubic, SRCNN [32], VDSR [36], SRResNet [38]. In this experiment, we use the same training datasets and test datasets to compare these methods fairly. In addition, these models are trained well to test under the suitable conditions. Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 show some reconstructed images of the UC Merced test set using the corresponding algorithm and the ground truth HR images in the visual quality.

Figure 8. $\times 4$ super resolved-images of “airplane89.jpg” on the UC Merced dataset via different algorithms, and the numbers under these images represent the PSNR and SSIM values. (a) represent HR image, (b–f) represent the super-resolved image of Bicubic, SRCNN, VDSR, SRResNet, DCAN.

Figure 9. $\times 4$ super-resolved images of “overpass18.jpg” on the UC Merced dataset via different algorithms, and the numbers under these images represent the PSNR and SSIM values. (a) represent HR image, (b–f) represent the super-resolved image of Bicubic, SRCNN, VDSR, SRResNet, DCAN.

Figure 10. $\times 8$ super-resolved images of “harbor32.jpg” on the UC Merced dataset via different algorithms, and the numbers under these images represent the PSNR and SSIM values. (a) represent HR image, (b–f) represent the super-resolved image of Bicubic, SRCNN, VDSR, SRResNet, DCAN.

Figure 11. The detail of super-resolved “harbor32.jpg” region with a scale factor of $\times 8$. (a) represent HR image, (b–e) represent the super-resolved image patch of SRCNN, VDSR, SRResNet, DCAN.

Figure 12. $\times 4$ super-resolved images of “storagetanks68.jpg” on the UC Merced dataset via different algorithms, and the numbers under these images represent the PSNR and SSIM values. (a) represent HR image, (b–f) represent the super-resolved image of Bicubic, SRCNN, VDSR, SRResNet, DCAN.

Figure 13. $\times 8$ super-resolved images of “mediumresidential34.jpg” on the UC Merced dataset via different algorithms, and the numbers under these images represent the PSNR and SSIM values. (a) represent HR image, (b–f) represent the super-resolved image of Bicubic, SRCNN, VDSR, SRResNet, DCAN.

Figure 14. $\times 8$ super-resolved images of “runway39.jpg” on the UC Merced dataset via different algorithms, and the numbers under these images represent the PSNR and SSIM values. (a) represent HR image, (b–f) represent the super-resolved image of Bicubic, SRCNN, VDSR, SRResNet, DCAN.

Figure 15. The detail of super-resolved “runway39.jpg” region with a scale factor of $\times 8$. (a) represent HR image, (b–e) represent the super-resolved image patch of SRCNN, VDSR, SRResNet, DCAN.

Figure 8 shows the super-resolved HR images obtained through different models for “airplane89.jpg” with a scale factor of $\times 4$. The figure demonstrates that the reconstructed result of our DCAN model is better than those of the other algorithms, such as the edge of the plane. The reconstructed images for “overpass18.jpg” with a scale factor of $\times 4$ are shown in Figure 9. It is obvious that DCAN reconstructed more details and recovered sharper edges, such as the traffic index line of the road and the car. Comparison results for “harbor32.jpg” of a $\times 8$ scale factor are shown in Figure 10. We can get the conclusion that our method successfully reconstructed the main part of the bridge. The reconstructed HR images of “storagetanks68.jpg” are compared in Figure 12. The results demonstrate that the DCAN method provided more enhanced textures and recovered more details in comparison with other algorithms. Figure 13 shows the reconstructed images of “mediumresidential34.jpg” of a $\times 4$ scale factor. It can be seen that the result of our proposed method reconstructed the edges sharper than the other methods. Figure 14 compares the reconstructed images of “runway39.jpg” with other methods. It is obvious that the proposed methods reconstructed the details better than the other algorithms, such as the thin strip lines at the right of the image. As shown in Figure 11 and Figure 15, we enlarge some regions of super-resolved images to better compare the textures and details. The texture and details of our proposed method are superior than those of other methods. The above results show that our method achieves better results compared with other methods in terms of the visual quality.

Table 1 and Table 2 show the PSNR and SSIM of the reconstructed HR images of the UC Merced test set on the $\times 4$ and $\times 8$ enlargement, respectively.

Table 1. The PSNR and SSIM of UC Merced test dataset with a scale factor of 4.

Data	Scale	Bicubic	SRCNN	VDSR	SRResNet	DCAN
Agricultural	$\times 4$	25.24/0.4526	25.66/0.4728	25.87/0.0.4753	25.74/0.4811	26.20/0.5332
Airplane	$\times 4$	25.83/0.7524	26.40/0.7654	27.93/0.8311	27.95/0.8192	28.57/0.8627
Baseball diamond	$\times 4$	30.32/0.7754	30.73/0.8003	31.48/0.8166	31.78/0.8195	32.37/0.8314
Beach	$\times 4$	33.16/0.8375	33.47/0.8507	33.85/0.8611	34.05/0.8665	34.26/0.8678
Buildings	$\times 4$	21.44/0.6602	22.11/0.6687	22.55/0.7449	23.62/0.7814	24.12/0.8217
Chaparral	$\times 4$	24.15/0.6512	24.78/0.6978	24.86/0.7146	25.21/0.7431	25.54/0.7438
Dense residential	$\times 4$	23.34/0.6721	23.85/0.6742	24.27/0.7211	25.43/0.7785	25.92/0.8014
Forest	$\times 4$	26.28/0.6010	26.47/0.6413	26.63/0.6572	26.89/0.6723	27.11/0.6914
Freeway	$\times 4$	26.23/0.6773	26.69/0.6914	27.11/0.7411	27.91/0.7708	28.46/0.7928
Golf course	$\times 4$	30.76/0.7711	31.22/0.7834	31.24/0.7912	31.53/0.8003	32.31/0.8077
Harbor	$\times 4$	17.38/0.6906	17.90/0.6991	18.58/0.8064	19.79/0.8453	21.03/0.8603
Intersection	$\times 4$	24.37/0.6951	24.81/0.6983	24.89/0.7437	25.82/0.7763	26.11/0.7883
Medium residential	$\times 4$	23.47/0.6534	23.96/0.6864	24.51/0.7281	25.42/0.7533	25.63/0.7682
Mobile homepark	$\times 4$	21.83/0.6631	22.45/0.6943	23.19/0.7516	24.31/0.7815	24.93/0.8006
Overpass	$\times 4$	23.14/0.6417	23.51/0.6463	24.06/0.6944	25.41/0.7469	25.94/0.7664
Parking lot	$\times 4$	19.21/0.6011	19.83/0.6213	19.52/0.6617	20.04/0.7148	21.08/0.7760
River	$\times 4$	26.41/0.6551	26.82/0.6904	26.99/0.7038	27.07/0.7109	27.37/0.7162
Runway	$\times 4$	26.56/0.7177	27.24/0.7401	28.21/0.7753	29.64/0.7962	30.53/0.8093
Sparse residential	$\times 4$	26.15/0.6704	26.64/0.7038	27.08/0.7263	27.65/0.7384	27.81/0.7463
Storage tanks	$\times 4$	23.57/0.6970	24.01/0.6998	24.43/0.7607	25.26/0.7875	25.53/0.8211
Tennis court	$\times 4$	28.03/0.7812	28.67/0.7816	28.99/0.8324	30.02/0.8514	30.46/0.8601

Table 2. The PSNR and SSIM of UC Merced test dataset with a scale factor of 8.

Data	Scale	Bicubic	SRCNN	VDSR	SRResNet	DCAN
Agricultural	$\times 8$	23.62/0.2711	23.74/0.2813	23.78/0.2817	23.61/0.2806	23.77/0.2874
Airplane	$\times 8$	22.98/0.6152	23.45/0.6321	23.89/0.6564	24.02/0.6583	24.33/0.6759
Baseball diamond	$\times 8$	27.15/0.6514	27.87/0.6661	27.98/0.6825	28.17/0.6856	28.41/0.6933
Beach	$\times 8$	30.31/0.7385	30.56/0.7383	30.94/0.7524	30.68/0.7574	31.02/0.7614
Buildings	$\times 8$	18.74/0.4497	/19.14/0.4623	19.45/0.5209	19.92/0.5497	20.11/0.5687
Chaparral	$\times 8$	20.61/0.3165	20.53/0.3395	20.68/0.3567	20.93/0.3741	20.99/0.3977
Dense residential	$\times 8$	20.44/0.4617	20.92/0.4775	21.03/0.5236	21.55/0.5491	21.73/0.5702
Forest	$\times 8$	23.97/0.3741	24.14/0.4011	24.21/0.4018	24.13/0.4019	24.27/0.4147
Freeway	$\times 8$	23.84/0.4946	24.27/0.5271	24.59/0.5497	24.71/0.5533	24.95/0.5841
Golf course	$\times 8$	27.65/0.6491	28.15/0.6601	28.56/0.6753	28.63/0.6817	28.96/0.6893
Harbor	$\times 8$	14.84/0.5089	15.16/0.4997	15.29/0.5849	15.72/0.6243	15.91/0.6704
Intersection	$\times 8$	21.46/0.4880	21.89/0.5112	21.82/0.5194	22.36/0.5437	22.63/0.5722
Medium residential	$\times 8$	20.40/0.4227	20.77/0.4416	20.84/0.4663	21.36/0.4999	21.55/0.5208
Mobile homepark	$\times 8$	18.27/0.4143	18.59/0.4361	18.78/0.4698	19.42/0.5068	19.61/0.5301
Overpass	$\times 8$	20.72/0.4182	20.97/0.4424	21.25/0.4659	21.67/0.4932	22.86/0.5321
Parking lot	$\times 8$	16.98/0.3771	17.21/0.3889	16.95/0.4057	17.19/0.4187	17.29/0.4416
River	$\times 8$	24.41/0.5025	24.75/0.5269	24.74/0.5311	24.77/0.5335	24.94/0.5435
Runway	$\times 8$	23.25/0.5567	23.51/0.5498	24.03/0.5849	24.84/0.6136	25.63/0.6371
Sparse residential	$\times 8$	22.93/0.4678	23.28/0.4915	23.41/0.5022	23.72/0.5168	23.95/0.5298
Storage tanks	$\times 8$	21.22/0.5356	21.68/0.5439	21.87/0.5835	22.16/0.6008	22.79/0.6451
Tennis court	$\times 8$	24.43/0.5968	25.13/0.6194	25.41/0.6456	25.63/0.6542	26.13/0.8078

Our proposed method is also better than other methods in the quantitative evaluation. Table 3 and Table 4 show the PSNR and SSIM of the reconstructed HR images of RSSCN7 test set on the $\times 4$ enlargement and $\times 8$ enlargement, respectively. Experimental results demonstrate the effectiveness of our method.

Table 3. The PSNR and SSIM of RSSCN7 test dataset with a scale factor of 4.

Data	Scale	Bicubic	SRCNN	VDSR	SRResNet	DCAN
Grass	$\times 4$	32.69/0.8073	33.48/0.8132	34.04/0.8231	34.27/0.8294	34.39/0.8342
Industry	$\times 4$	24.42/0.6617	24.85/0.6651	25.76/0.7185	26.39/0.7414	26.61/0.7536
River lake	$\times 4$	29.89/0.8014	30.33/0.8062	30.91/0.8231	31.17/0.8294	31.35/0.8346
Filed	$\times 4$	31.83/0.7228	32.59/0.7332	33.10/0.7527	33.37/0.7528	33.51/0.7683
Forest	$\times 4$	27.79/0.5996	28.06/0.6072	28.27/0.6271	28.38/0.6403	28.53/0.6421
Resident	$\times 4$	23.82/0.6431	24.11/0.6453	24.87/0.6931	25.39/0.7182	25.59/0.7287
Parking	$\times 4$	23.76/0.6187	24.34/0.6332	25.12/0.6761	25.57/0.7064	25.82/0.7138

Table 4. The PSNR and SSIM of RSSCN7 test dataset with a scale factor of 8.

Data	Scale	Bicubic	SRCNN	VDSR	SRResNet	DCAN
Grass	$\times 8$	29.67/0.7214	31.07/0.7361	31.41/0.7513	31.55/0.7496	31.76/0.7552
Industry	$\times 8$	21.85/0.4853	22.04/0.4872	22.44/0.5131	22.58/0.5164	22.69/0.5273
River lake	$\times 8$	27.42/0.7011	27.91/0.7154	28.23/0.7263	28.35/0.7295	28.51/0.7353
Filed	$\times 8$	30.04/0.6771	30.97/0.6841	31.25/0.6874	31.36/0.6893	31.44/0.6936
Forest	$\times 8$	25.56/0.4418	25.91/0.4433	26.11/0.4554	26.17/0.4585	26.31/0.4615
Resident	$\times 8$	20.78/0.4239	21.13/0.4251	21.44/0.4482	21.54/0.4563	21.70/0.4624
Parking	$\times 8$	21.77/0.4531	22.05/0.4681	22.35/0.4873	22.46/0.4942	22.59/0.4998

3.3. Model Analysis

In this section, we use three groups of experiments to analyze the proposed method using the UC Merced dataset, including the number of DCAB, the dense channel attention mechanism, and the SAB. In addition, we use PSNR as quantitative evaluation.

(1)

DCAB: A small DCAN which contains four DCAB_s was used to learn the effect of $n_f$. The experimental results about the effect of $n_f$ are presented in Table 5. We use three widely used values, including 32, 64 and 128. When $n_f=64$, the average PSNR values on the test dataset are 0.27 dB higher than $n_f=32$, and it also are 0.16 dB higher than $n_f=128$. So, we set the $n_f=64$ in the rest of the experiments.

Table 5. The PSNR of DCAN with a scale factor of 4 under different $n_f$ on the UC Merced dataset.

${\mathit{n}}_{\mathit{f}}$	PSNR
32	28.41
64	28.68
128	28.52

(2)

Dense Channel Attention Mechanism: We use several DCAN which contain different ${\mathrm{DCAB}}_s$ to study the effect of the number of DCAB_s. The experimental results about the effect of ${\mathrm{DCAB}}_s$ are provided in Table 6. We set the number of DCAB_s to 4, 8 and 10, respectively. As shown in the table, we conclude that the PSNR of ten DCAB_s are higher than 4 and 8.

Table 6. The PSNR of DCAN which have different ${\mathrm{DCAB}}_s$ with a scale factor of 4 on the UC Merced dataset.

${\mathbf{DCAB}}_{\mathit{s}}$	PSNR
4	28.68
8	28.70
10	28.71

(3)

SAB: To study the effect of the SAB, we compare the DCAN-s which contain a SAB and the DCAN without SAB. The experimental results are provided in Table 7. It can be seen that the PSNR of DCAN-s is higher than DCAN. It demonstrates that SAB improves the network performance.

Table 7. The PSNR of DCAN and DCAN-s with a scale factor of 4 on the UC Merced dataset.

Model	PSNR
DCAN	28.63
DCAN-S	28.70

In addition, we explore the relationship between PSNR and epochs of network training. As shown in Figure 16, it can be seen that the PSNR of around 350 epochs begins to converge with a scale factor of ×4. As shown in Figure 17, at around 50 epochs, it begins to converge with a scale factor of ×8. We can draw the conclusion that, with our model, it is easy to achieve high performance.

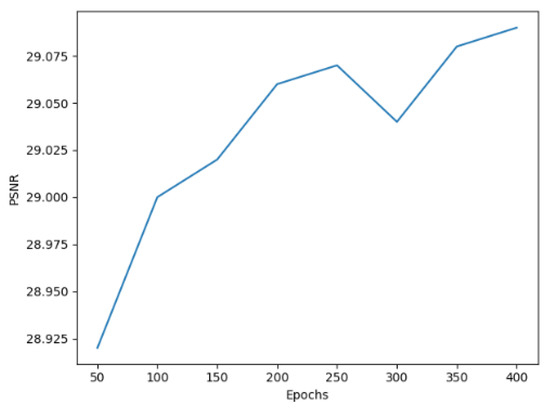
Figure 16. PSNR of DCAN with a scale factor of ×4 on the UC Merced dataset.

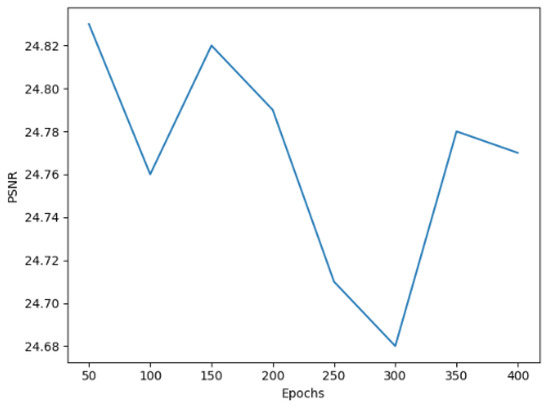
Figure 17. PSNR of DCAN with a scale factor of ×8 on the UC Merced dataset.

3.4. Super-Resolving the Real-World Data

In this section, we use the real data to validate the robustness of our proposed method. The model is trained by UC Merced dataset and tested by some remote sensing images from GaoFen-2 in Ningxia, China, as the real-world data. The size and band number of real-word images are $400\times 400$ and 3, respectively. Figure 18 and Figure 19 show one LR image on the $\times 4$ and $\times 8$ enlargement, respectively. The reconstructed results show that the DCAN method achieves good results in terms of the visual quality.

Figure 18. SR results of real data of $\times 4$ and $\times 8$ scale factor. (a–d) represent the result of Bicubic $\times 4$, DCAN $\times 4$, Bicubic $\times 8$, DCAN $\times 8$, respectively.

Figure 19. SR results of real data of $\times 4$ and $\times 8$ scale factor. (a–d) represent the result of Bicubic $\times 4$, DCAN $\times 4$, Bicubic $\times 8$, DCAN $\times 8$, respectively.

4. Discussion

The proposed DCAN method is proven to have a good performance with experimental results. In Section 3.2, our method outperforms several state-of-the-art methods in both quantitative evaluation and visual quality. In Section 3.3, the increase of PSNR after adding DCAB and SAB demonstrates the effectiveness of our approch. In Section 3.4, we deal with real satellite images from GaoFen-2 using the DCAN model and obtain satisfactory SR results. In addition, we discussed the experimental results in combination with theoretical analysis.

(1)

Effect of Dense Channel Attention Block: As shown in Table 6, the PSNR of super-resolved images increases after we add the DCAB. It can be seen that when the number of ${\mathrm{DCAB}}_s$ increases from 4 to 10, it improves the performance of network. It proves that when we increase appropriately the number of ${\mathrm{DCAB}}_s$, the capacity of the network can be improved.

(2)

Effect of Spatial Attention Block: As shown in Table 7, it can be seen that the PSNR value ranges from 28.63 to 28.70 after we add the SAB. Thus, we conclude that SAB can improve the performance of network and help the network have more flexible discriminative ability for global structure and focus on high-frequency information from spatial dimension.

(3)

Effect of Scale Factor: As shown in Table 1 and Table 2, due to the increasing scale factor, the improvement of our proposed DCAN method reduces. It indicates that the large-scale super resolution is still a hard problem.

5. Conclusions

This article develops a DCAN network which achieves good performance in super-resolving the remote sensing images with complicated spatial distribution. Specifically, we design a network which densely uses the multi-level feature information and strengthens the effective information. In addition, we propose a dense channel attention mechanism which makes better use of multi-level feature maps which contain abundant high-frequency information. Further, we add a spatial attention block to pay more attention to the regions which are more important and more difficult to reconstruct. Results of the extensive experiments demonstrate the superiority of our method over the other compared algorithms.