Remote Sensing Estimation of Bamboo Forest Aboveground Biomass Based on Geographically Weighted Regression
Abstract
:1. Introduction
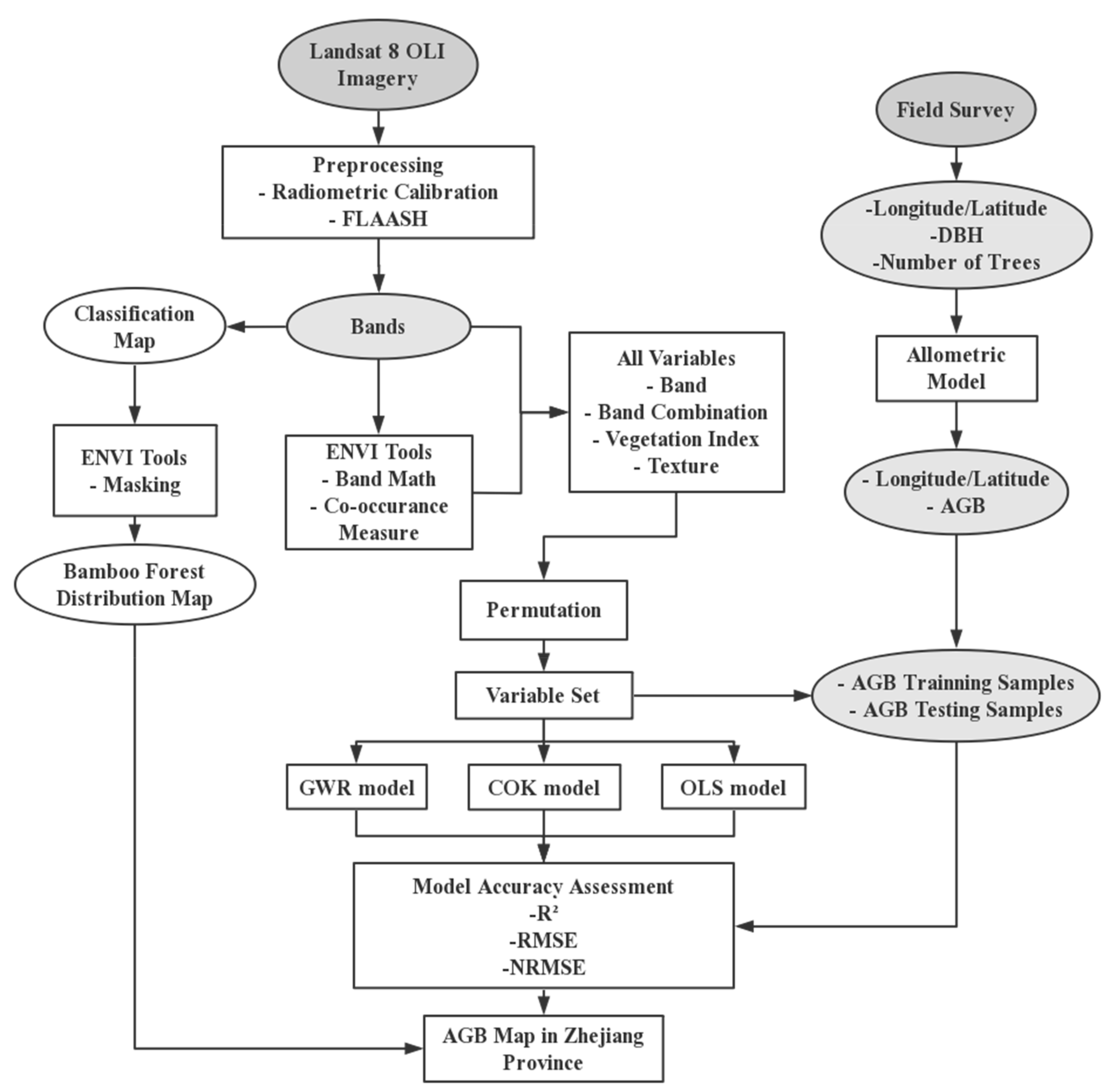
2. Materials and Methods
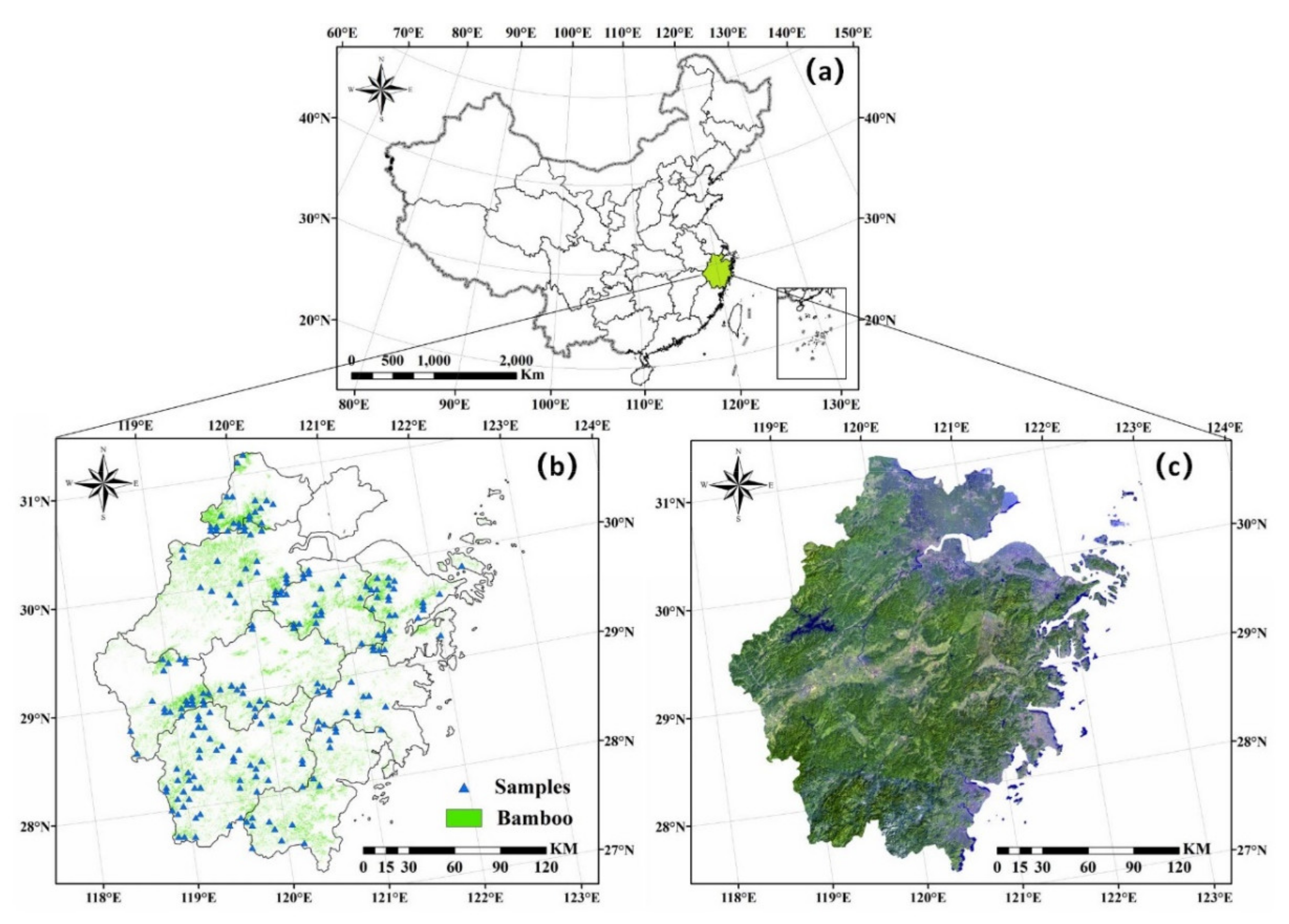
2.1. Study Area
2.2. Datasets and Processing
2.2.1. Landsat 8 OLI Satellite Data
2.2.2. AGB Observed Data of Bamboo Forests
2.3. Extraction of Variables
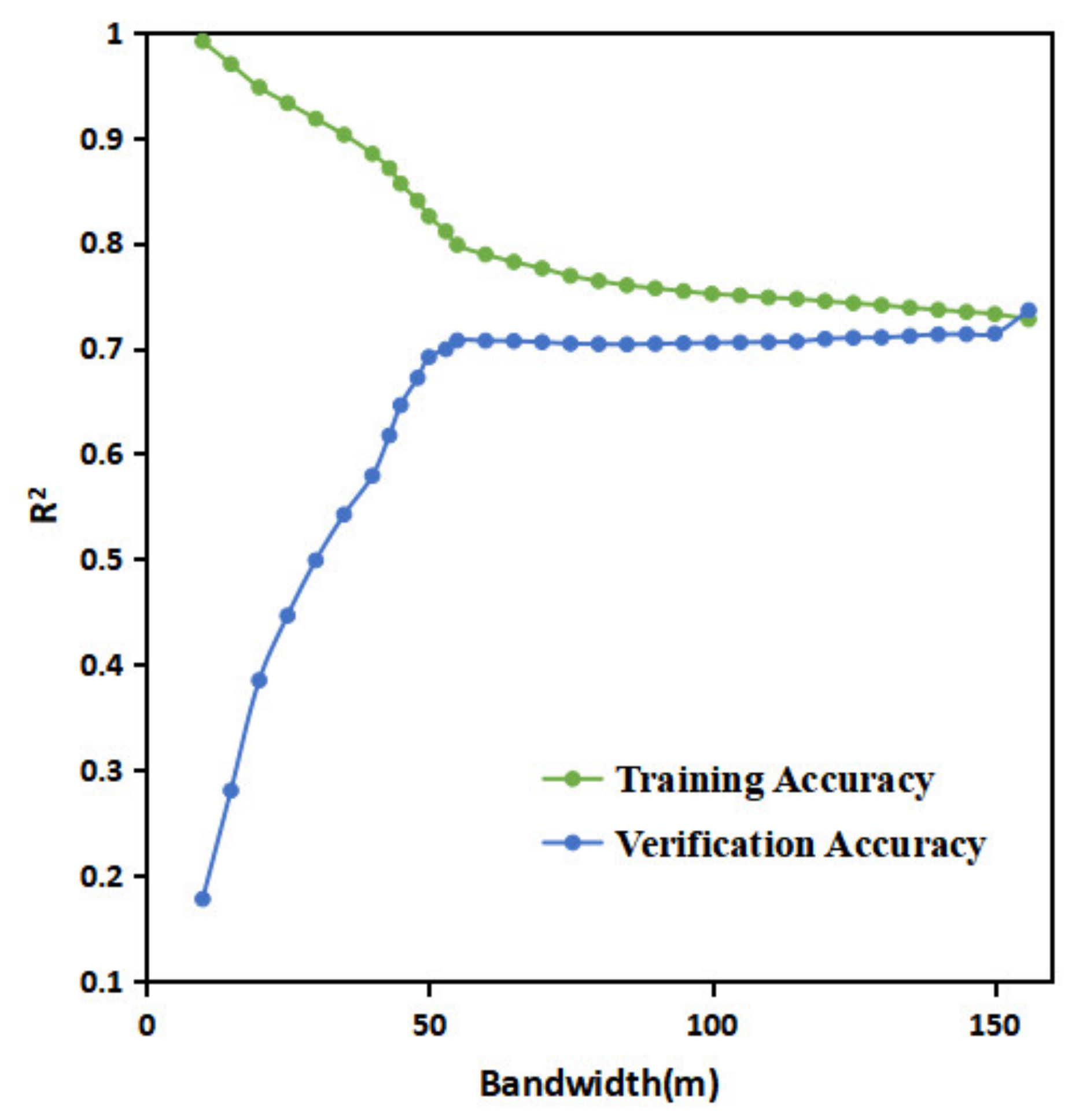
2.4. GWR Model
2.5. Accuracy Assessment
2.6. Experiment Design
3. Results
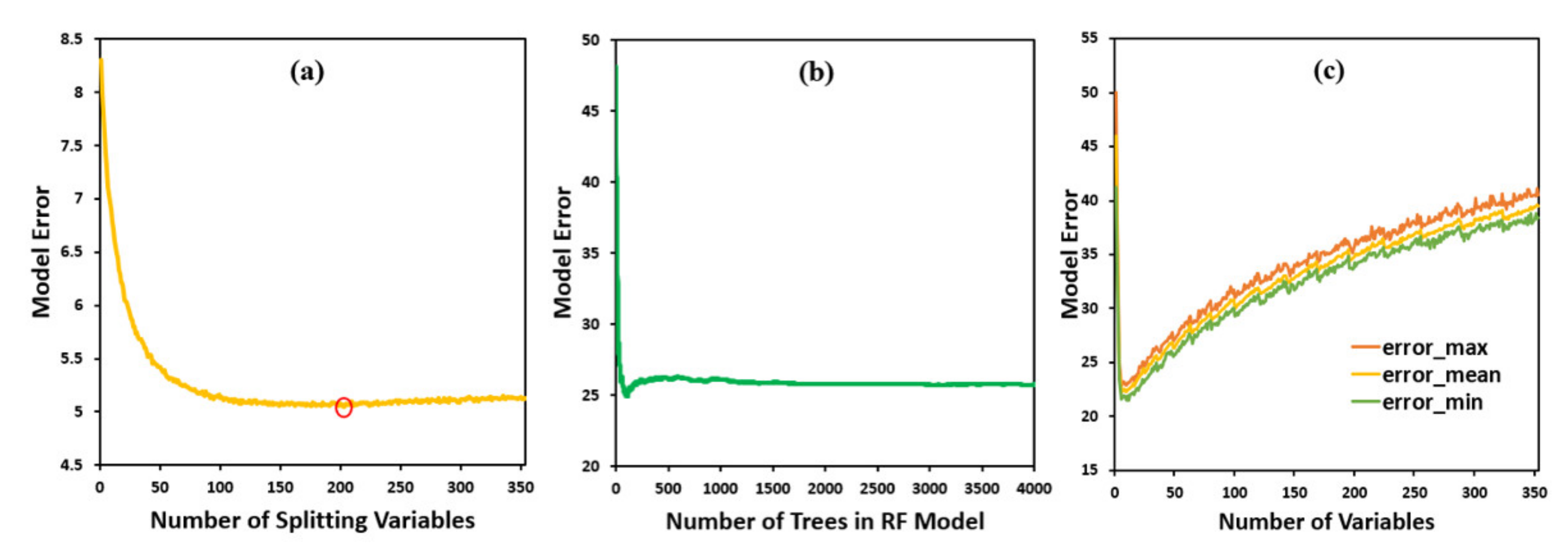
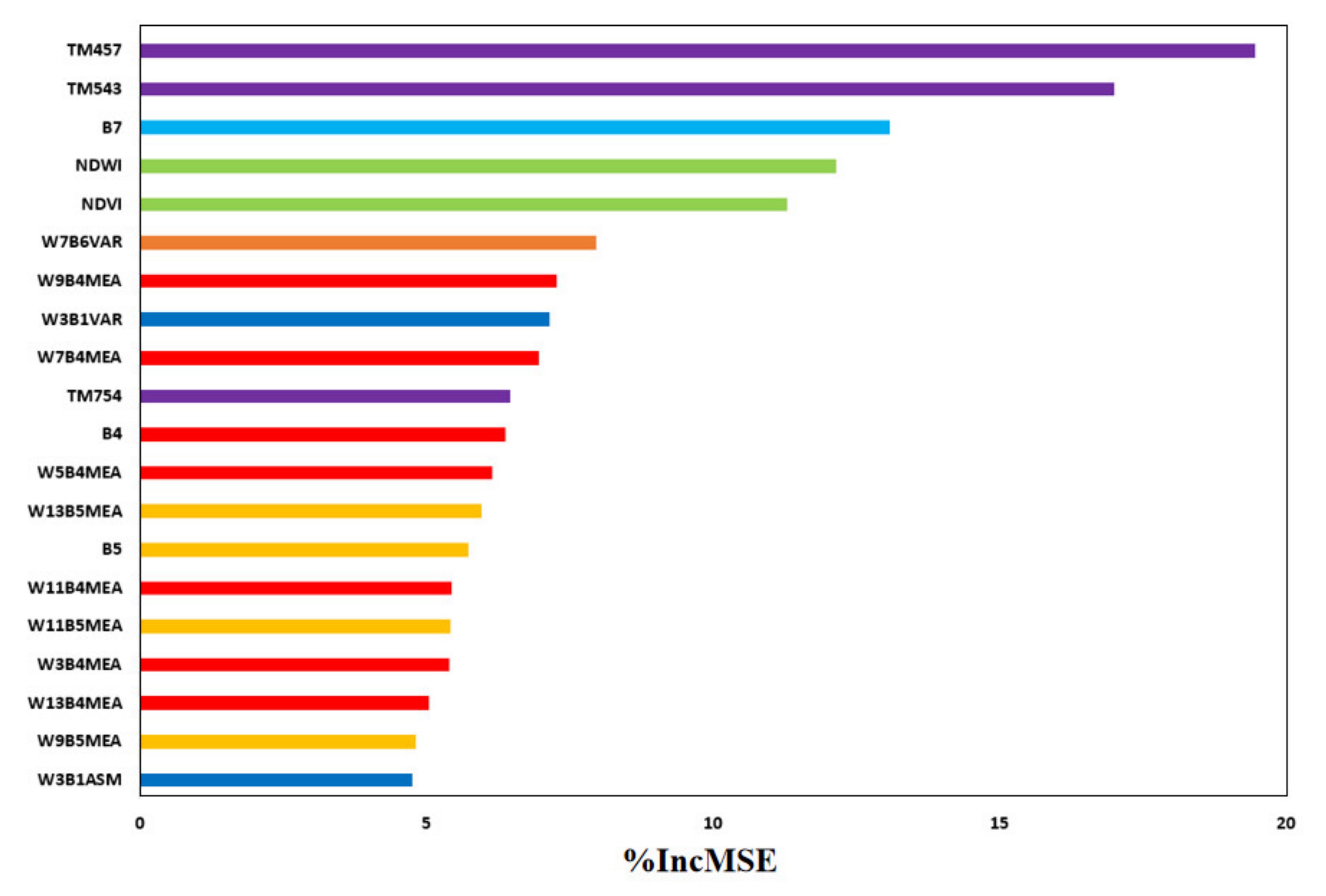
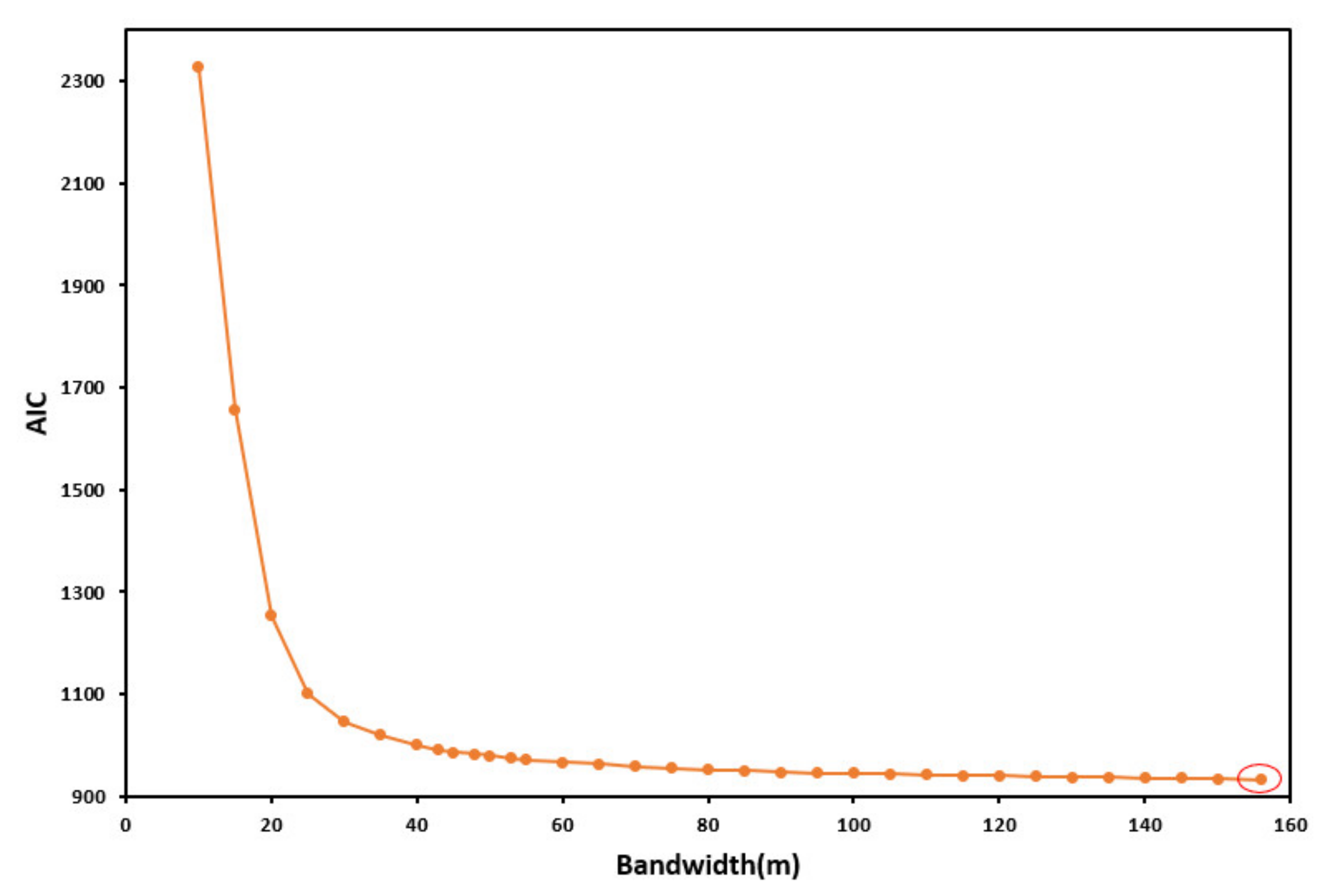
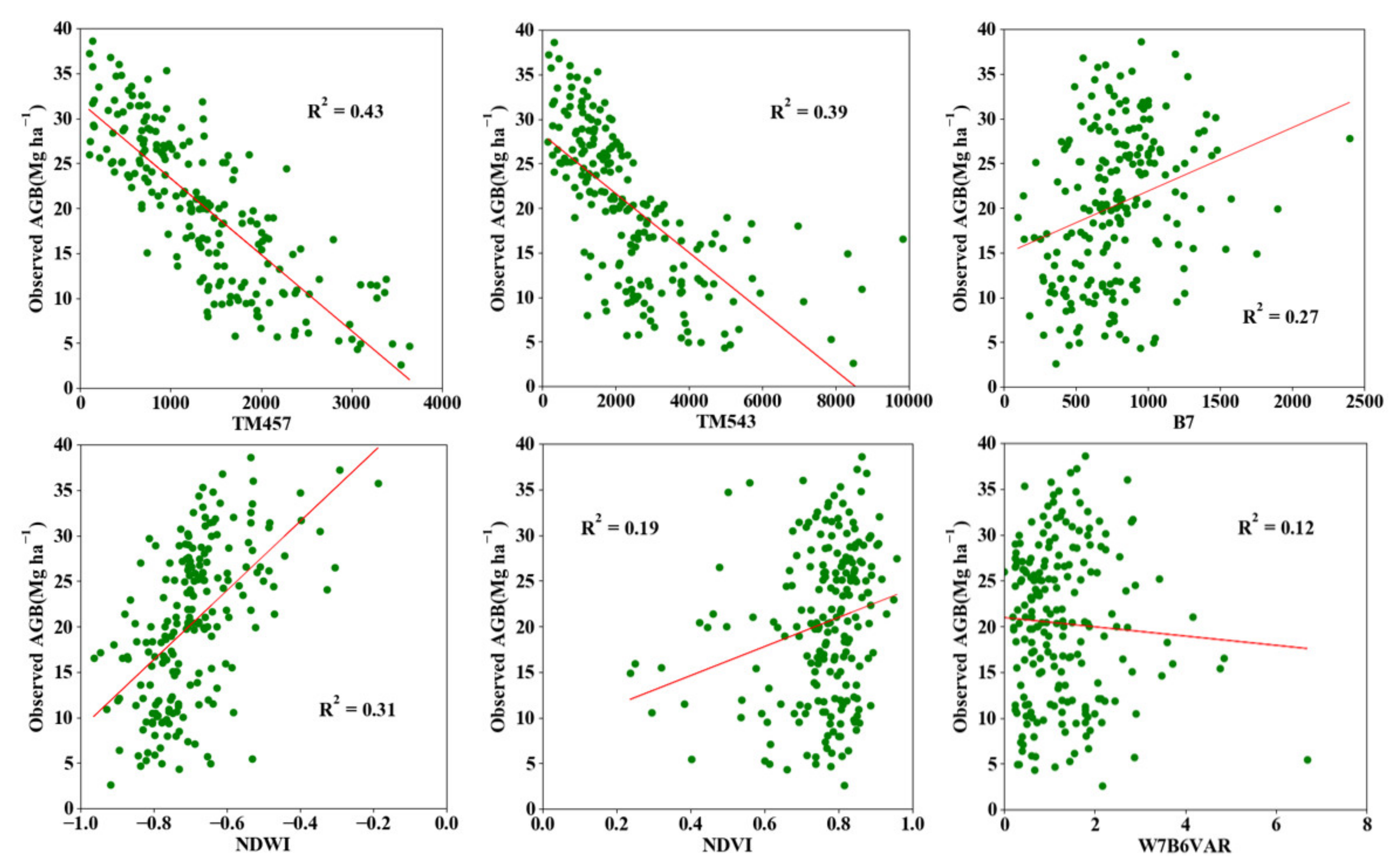
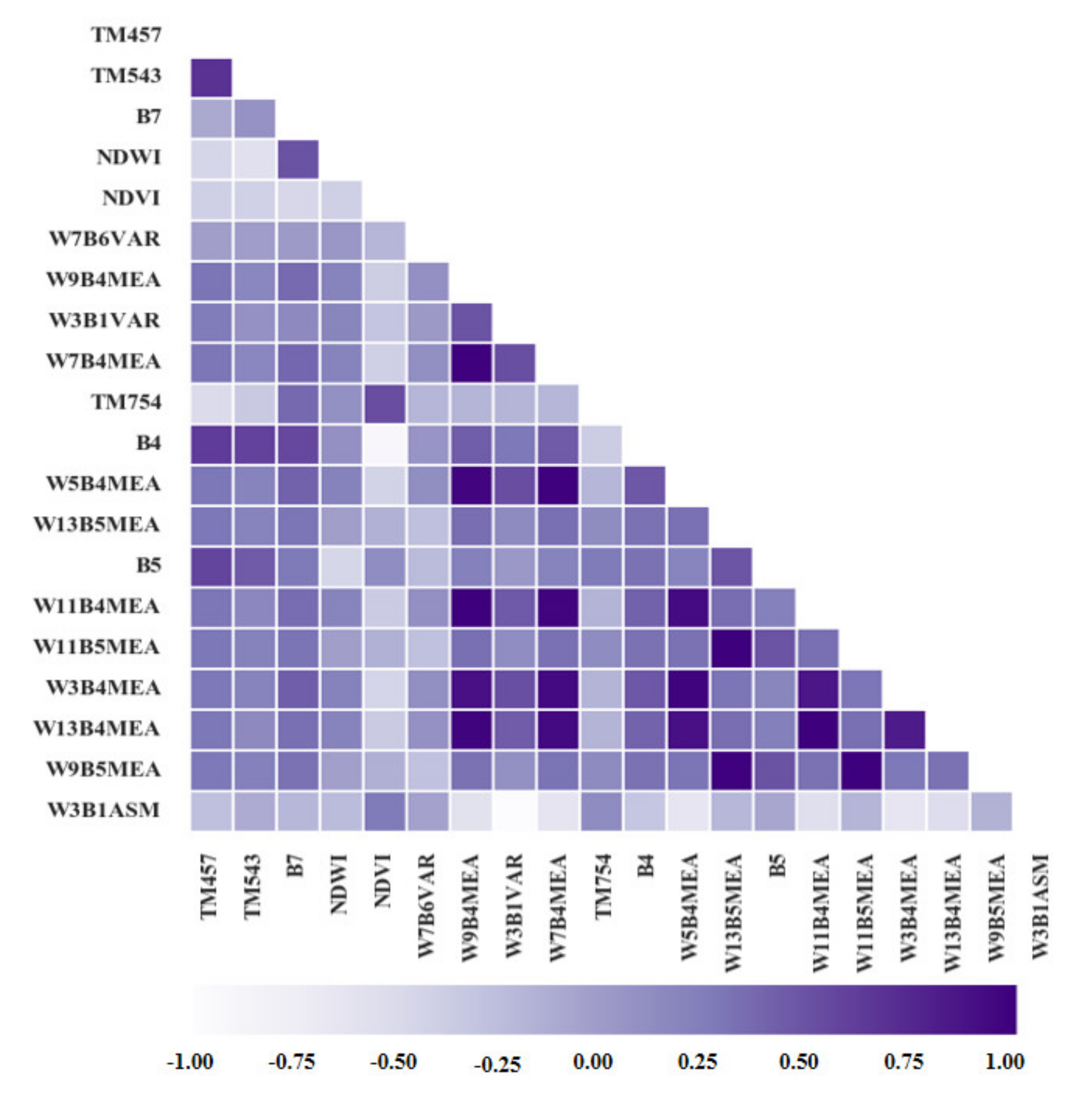
3.1. Selected Variables
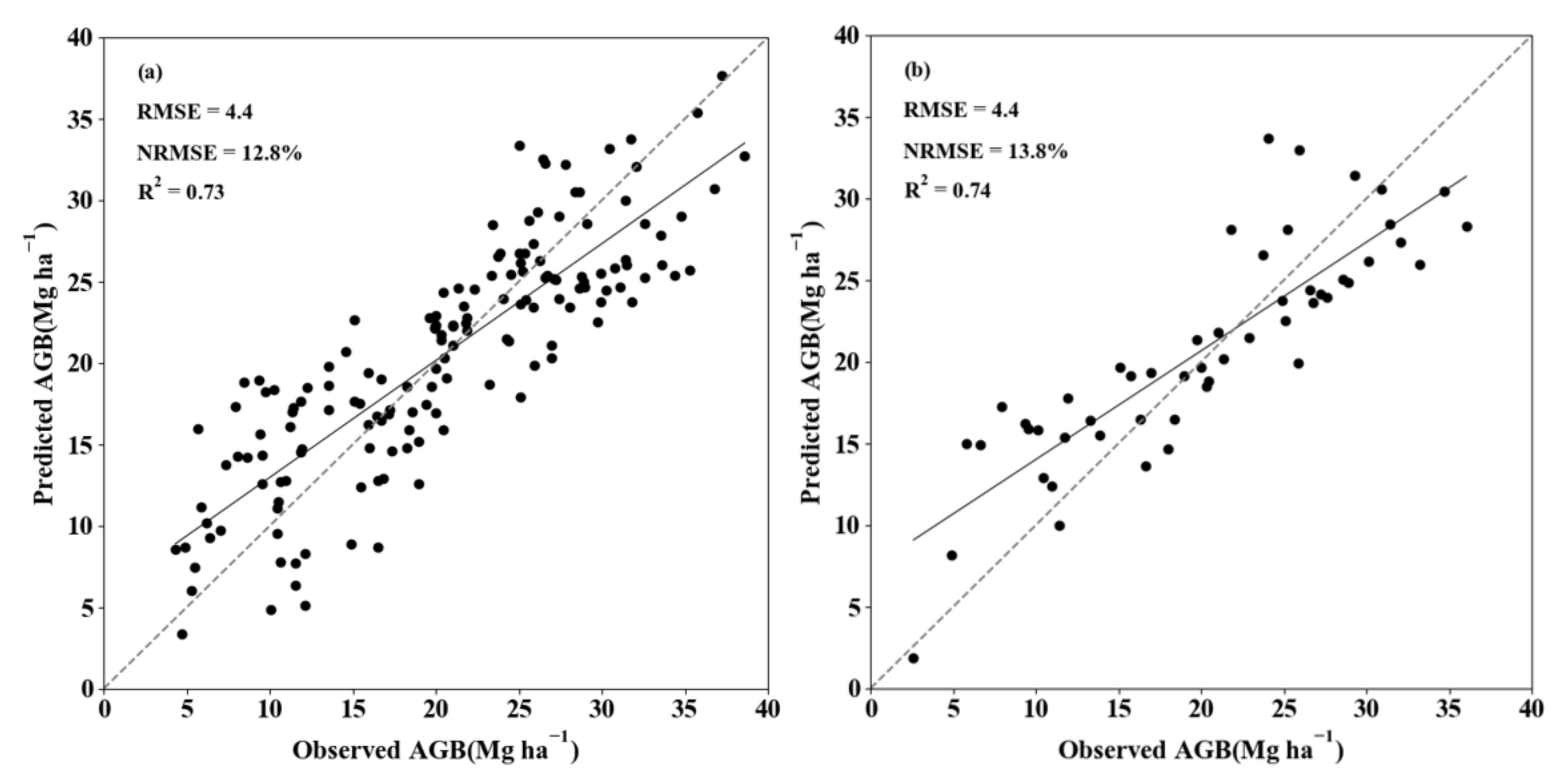
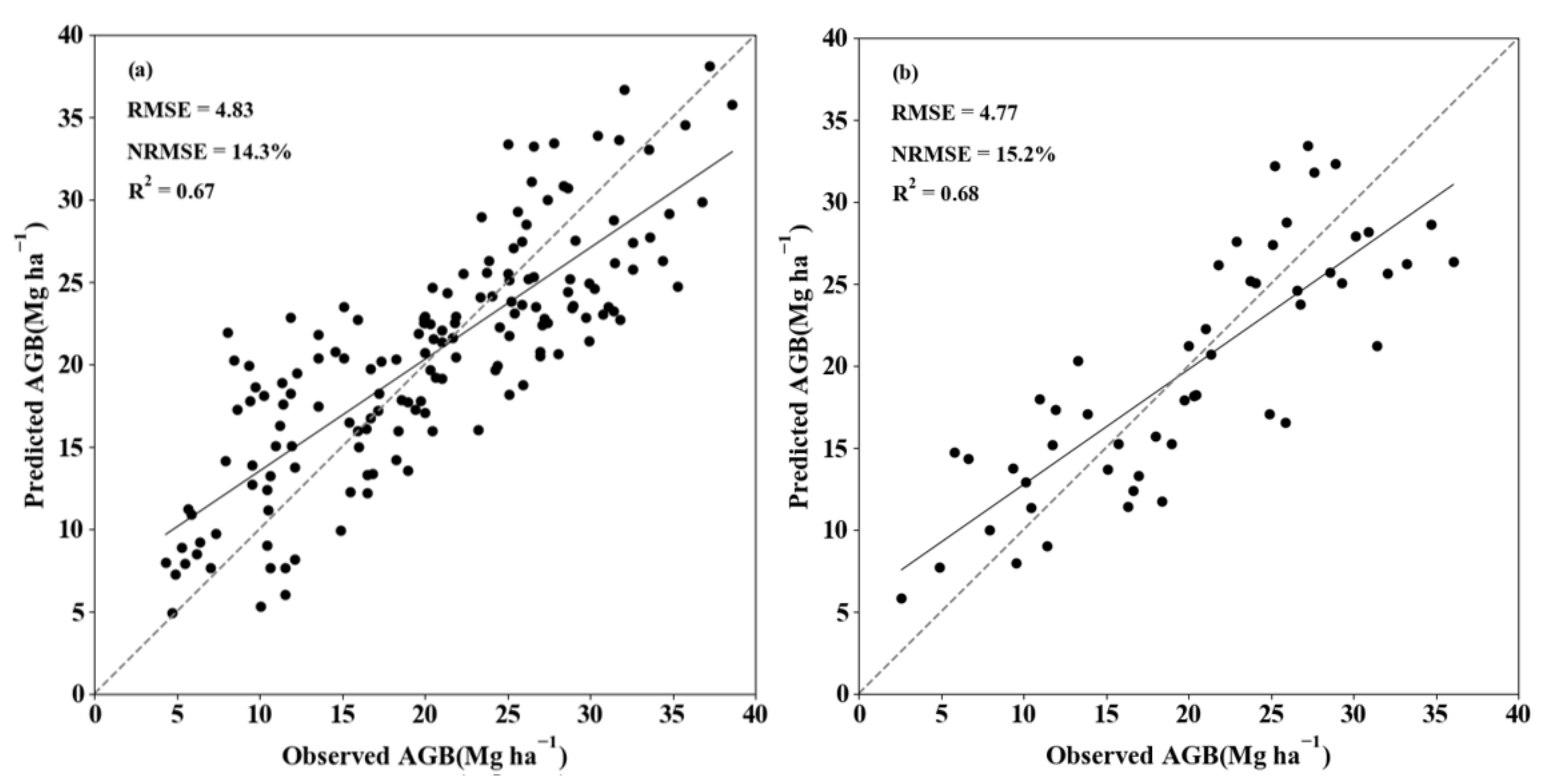
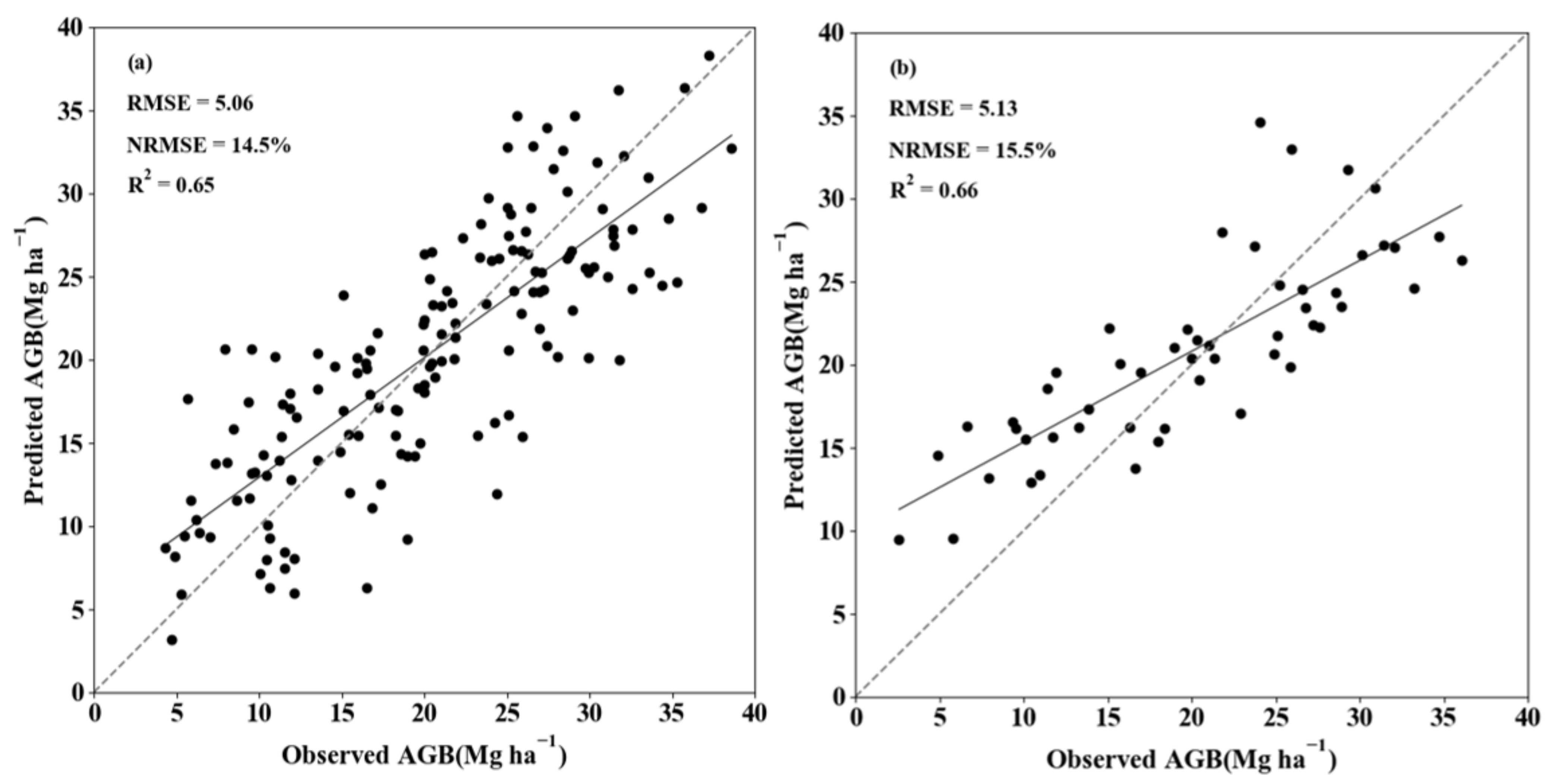
3.2. AGB Estimation Based on GWR
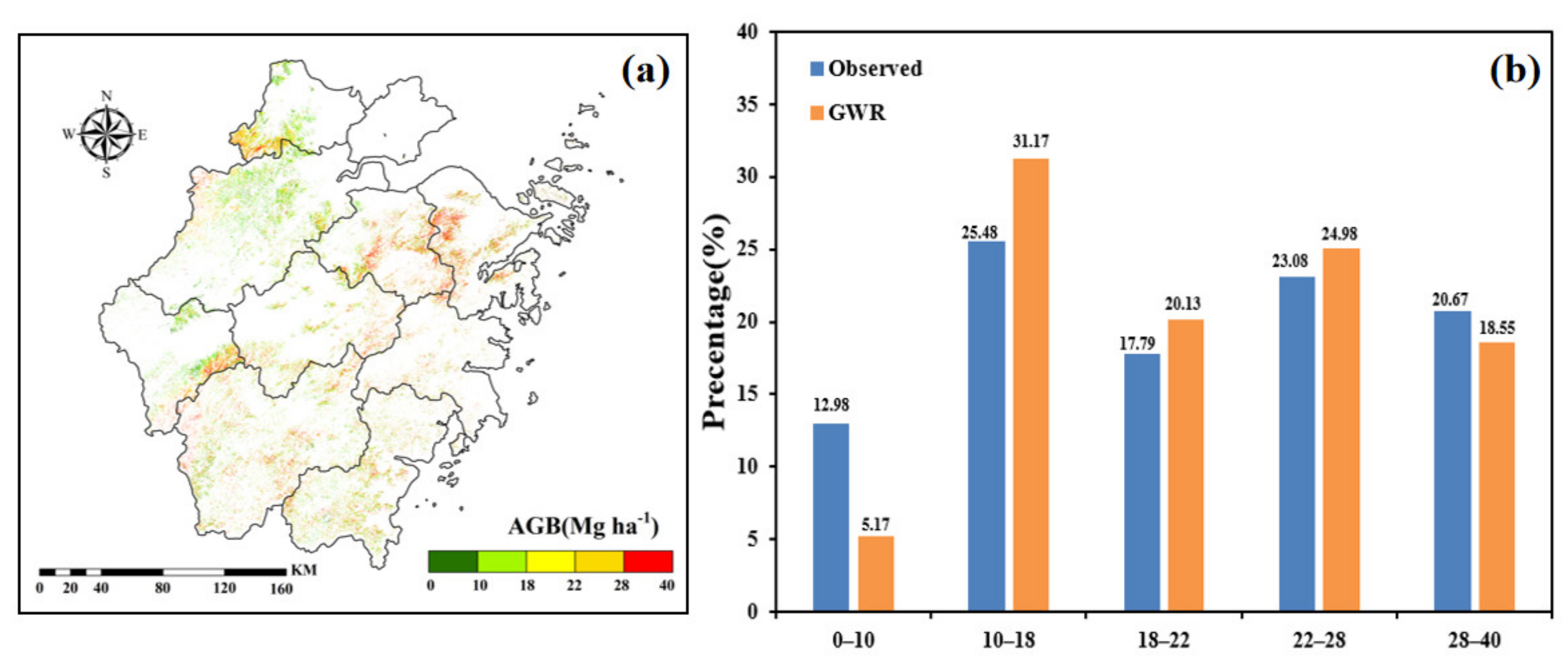
3.3. AGB Spatial Estimation of Bamboo Forest
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nichol, J.E.; Sarker, M.L.R. Improved biomass estimation using the texture parameters of two high-resolution optical sensors. IEEE Trans. Geosci. Remote Sens. 2011, 49, 930–948. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Du, H.; Han, N.; Li, X.; He, S. Application of Convolutional Neural Network on Lei Bamboo Above-Ground-Biomass (AGB) Estimation Using Worldview-2. Remote Sens. 2020, 12, 958. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Du, H.; Zhou, G.; Fan, W. Review on Correlation Analysis of Independent Variables in Estimation Models of Vegetation Biomass Based on Remote Sensing. Remote Sens. Technol. Appl. 2008, 23, 239–247. [Google Scholar]
- Brown, S. Aboveground biomass estimates for tropical moist forests of Brazilian Amazon. Interciencia 1992, 17, 8–18. [Google Scholar]
- Fang, J.Y. Forest Biomass of China: An estimate based on the Biomass-Volume Relationship. Ecol. Appl. 1998, 8, 1084–1091. [Google Scholar]
- Fang, J.Y. Forest biomass estimation at regional and global levels, with special reference to China’s forest biomass. Ecol. Res. 2010, 16, 587–592. [Google Scholar] [CrossRef]
- Li, D.; Wang, C.; Hu, Y.; Liu, S. General Review on Remote Sensing-Based Biomass Estimation. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 631–635. [Google Scholar]
- Wang, C.; Jia, X.; Zhao, Y.; Jin, H.; Liu, L.; Yin, H.; Wang, Z. Review of Methods on Estimation Forest Biomass. J. Beihua Univ. (Nat. Sci.) 2019, 20, 116–119. [Google Scholar]
- Zhu, X.; Liu, D. Improving forest aboveground biomass estimation using seasonal Landsat NDVI time-series. Isprs J. Photogramm. Remote Sens. 2015, 102, 222–231. [Google Scholar] [CrossRef]
- Tian, X.; Yan, M.; van der Tol, C.; Li, Z.; Su, Z.; Chen, E.; Li, X.; Li, L.; Wang, X.; Pan, X.; et al. Modeling forest above-ground biomass dynamics using multi-source data and incorporated models: A case study over the qilian mountains. Agric. For. Meteorol. 2017, 246, 1–14. [Google Scholar] [CrossRef]
- Sasan, V.; Javad, S.; Kamran, A.; Hadi, F.; Hamed, N.; Tien, P.; Dieu, T.B. Improving Accuracy Estimation of Forest Aboveground Biomass Based on Incorporation of ALOS-2 PALSAR-2 and Sentinel-2A Imagery and Machine Learning: A Case Study of the Hyrcanian Forest Area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar]
- Ojoatre, S.; Zhang, C.; Hussin, Y.; Kloosterman, H.; Ismail, M.H. Assessing the Uncertainty of Tree Height and Aboveground Biomass From Terrestrial Laser Scanner and Hypsometer Using Airborne LiDAR Data in Tropical Rainforests. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4149–4159. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Zhou, X.; Ouyang, Z.; Avitabile, V.; Giannico, V. Estimating aboveground biomass in subtropical forests of China by integrating multisource remote sensing and ground data. Remote Sens. Environ. 2019, 232, 111341. [Google Scholar] [CrossRef]
- Puliti, S.; Breidenbach, J.; Schumacher, J.; Hauglin, M.; Astrup, R. Above-ground biomass change estimation using national forest inventory data with Sentinel-2 and Landsat 8. arXiv 2020, arXiv:2010.14262. [Google Scholar]
- Huaqiang, D.U.; Zhou, G.; Hongli, G.E.; Fan, W.; Xiaojun, X.U.; Fan, W.; Shi, Y. Satellite-based carbon stock estimation for bamboo forest with a non-linear partial least square regression technique. Int. J. Remote Sens. 2012, 33, 1917–1933. [Google Scholar]
- Duan, Z.; Zhao, D.; Zeng, Y.; Zhao, Y.; Wu, B.; Zhu, J. Estimation of the Forest Aboveground Biomass at Regional Scale Based on Remote Sensing. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 1400–1408. [Google Scholar]
- Li, Y.; Ning, H.; Li, X.; Du, H.; Xing, L. Spatiotemporal Estimation of Bamboo Forest Aboveground Carbon Storage Based on Landsat Data in Zhejiang, China. Remote Sens. 2018, 10, 898. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Du, H.; Mao, F.; Zhou, G.; Chen, L.; Xing, L.; Fan, W.; Xu, X.; Liu, Y.; Cui, L. Estimating bamboo forest aboveground biomass using EnKF-assimilated MODIS LAI spatiotemporal data and machine learning algorithms—ScienceDirect. Agric. For. Meteorol. 2018, 256–257, 445–457. [Google Scholar] [CrossRef]
- Rasel, S.; Chang, H.C.; Ralph, T.J.; Saintilan, N.; Diti, I.J. Application of feature selection methods and machine learning algorithms for saltmarsh biomass estimation using Worldview-2 imagery. Geocarto Int. 2019, 1–25. [Google Scholar] [CrossRef]
- Zhang, M.; Du, H.; Zhou, G.; Li, X.; He, S. Estimating Forest Aboveground Carbon Storage in Hang-Jia-Hu Using Landsat TM/OLI Data and Random Forest Model. Forests 2019, 10, 1004. [Google Scholar] [CrossRef] [Green Version]
- He, P.; Zhang, H.; Lei, X.; Xu, G.; Gao, X. Estimation of Forest Above-Ground Biomass Based on Geostatistics. Sci. Silvae Sin. 2013, 49, 101–109. [Google Scholar]
- Guo, H. Geographically Weighted Regression based Estimation of Regional Forest Carbon Storage; Zhejiang A&F Universuty: Hangzhou, China, 2015. [Google Scholar]
- Zhou, L.; Ou, G.; Wang, J.; Xu, H. Light Saturation Point Determination and Biomass Remote Sensing Estimation of Pinus kesiya var. langbianensis Forest Based on Spatial Regression Models. Sci. Silvae Sin. 2020, 56, 38–47. [Google Scholar]
- Izadi, s.; Sohrabi, H. Estimating the Spatial Distribution of Above-ground Carbon of Zagros Forests using Regression Kriging, Geographically Weighted Regression Kriging and Landsat 8 imagery. J. Environ. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Izadi, S.; Sohrabi, H.; Jafari Khaledi, M. Comparison of Geographically Weighted Regression and Regression Kriging to Estimate the Spatial Distribution of Aboveground Biomass of Zagros Forests. J. Geomat. Sci. Technol. 2020, 9, 113–124. [Google Scholar]
- Zhang, B.; Ou, G. Application of Spatial Effect and Regression Model on Forestry Research. J. Southwest For. Univ. 2016, 144–152. [Google Scholar]
- Zhang, L.; Shi, H. Local Modeling of Tree Growth by Geographically Weighted Regression. Forest Sci. 2004, 50, 225–244. [Google Scholar]
- Foody, G.M. Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI–rainfall relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Kupfer, J.A.; Farris, C.A. Incorporating spatial non-stationarity of regression coefficients into predictive vegetation models. Landsc. Ecol. 2006, 22, 837–852. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, M. Spatial Variations in School Performance: A Local Analysis Using Geographically Weighted Regression. Geogr. Environ. Model. 2001, 5, 43–66. [Google Scholar] [CrossRef]
- Dong, L.; Xing, L.; Liu, T.; Du, H.; Zhang, M. Very High Resolution Remote Sensing Imagery Classification Using a Fusion of Random Forest and Deep Learning Technique—Subtropical Area for Example. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 13, 113–128. [Google Scholar] [CrossRef]
- Tian, Q.; Zheng, L. Image-Based atmospheric radiation correction and reflectance retrieval methods. Q. J. Appl. Meteorol. 1998, 9, 456–461. [Google Scholar]
- Kaufman, Y.J.; Tanré, D. Strategy for direct and indirect methods for correcting the aerosol effect on remote sensing: From AVHRR to EOS-MODIS. Remote Sens. Environ. 1996, 55, 65–79. [Google Scholar] [CrossRef]
- Tang, J.; Nie, Z. Geometric Correction of Remote Sensing Image. Geomat. Spat. Inf. Technol. 2007, 30, 100–102. [Google Scholar]
- Zhou, G. Carbon Storage, Fixation and Distribution in Mao Bamboo(Phyllostachys Pubescens) Stands Ecosystem. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2006. [Google Scholar]
- Tian, Q.; Min, X. Advances in study on vegetation indices. Adv. Earth Sci. 1998, 13, 327–333. [Google Scholar]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Kaufman, Y.J.; Tanre, D.; Holben, B.N.; Markham, B.; Gitelson, A. Atmospheric effects on the NDVI—Strategies for its removal. In Proceedings of the International Geoscience & Remote Sensing Symposium, Houston, TX, USA, 26–29 May 1992; IEEE: Piscataway, NJ, USA, 1992. [Google Scholar]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 2005, 67, 786–804. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, W.; Li, G. Spatial distribution of forest carbon storage in Maoershan region, Northeast China based on geographically weighted regression kriging model. Chin. J. Appl. Ecol. 2019, 30, 1642–1650. [Google Scholar]
- Lv, Y.; Li, C.; Ou, G.; Xiong, H.; Wei, A.; Zhang, B.; Xu, H. Remote Sensing Estimation of Biomass of Pinus kesiya var. langbianensis by Geographically Weighted Regression Models. For. Resour. Manag. 2017. [Google Scholar] [CrossRef]
- Akaike, H.T. A new look at the statistical model identification. Autom. Control IEEE Trans. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Liu, C. Spatial Distribution of Forest Carbon Storage in Heilongjiang Province. Ying Yong Sheng Tai Xue Bao 2014, 25, 2779–2786. [Google Scholar]
- Han, N.; Du, H.; Zhou, G.; Xiaojun, X.; Cui, R.; Gu, C. Spatiotemporal heterogeneity of Moso bamboo aboveground carbon storage with Landsat Thematic Mapper images: A case study from Anji County, China. Int. J. Remote Sens 2013, 34, 4917–4932. [Google Scholar] [CrossRef]
- Wang, H.; Hou, R.; Zheng, D.; Gao, X.; Xia, C.; Peng, D. Biomass Estimation of Arbor Forest in Subtropical Region Based on Geographically Weighted Regression Model. Trans. Chin. Soc. Agric. Mach. 2018, 49, 184–190. [Google Scholar]
- Propastin, P. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 82–90. [Google Scholar] [CrossRef]
- Du, H.; Zhou, G.; Fan, W.; Ge, H.; Fan, W. Spatial heterogeneity and carbon contribution of aboveground biomass of moso bamboo by using geostatistical theory. Plant Ecol. 2010, 207, 131–139. [Google Scholar] [CrossRef]

| Data Identification | Row/Column Number | Date | Cloudage |
|---|---|---|---|
| LC81180392014164LGN00 | 118,039 | 13 June 2014 | 10.03 |
| LC81180402014164LGN00 | 118,040 | 13 June 2014 | 6.05 |
| LC81180412014164LGN00 | 118,041 | 13 June 2014 | 7.94 |
| LC81190392014203LGN00 | 119,039 | 22 July 2014 | 2.31 |
| LC81190402014203LGN01 | 119,040 | 22 July 2014 | 3.09 |
| LC81190412014203LGN00 | 119,041 | 22 July 2014 | 4.02 |
| LC81200392014162LGN01 | 120,039 | 11 June 2014 | 1.03 |
| LC81200402014162LGN01 | 120,040 | 11 June 2014 | 0.09 |
| Type | Name | Details | References |
|---|---|---|---|
| Bands | Band 1 Coastal (B1) | / | |
| Band 2 Blue (B2) | / | ||
| Band 3 Green (B3) | / | ||
| Band 4 Red (B4) | / | ||
| Band 5 NIR (B5) | / | ||
| Band 6 SWIR 1 (B6) | / | ||
| Band 7 SWIR 2 (B7) | / | ||
| Band Combinations | TM754 | [17] | |
| TM563 | |||
| TM457 | |||
| TM432 | . | ||
| TM543 | |||
| Vegetation Indices | Difference Vegetation Index (DVI) | [37] | |
| Normalized Difference Vegetation Index (NDVI) | [38] | ||
| Normalized Difference Water Index (NDWI) | [39] | ||
| Ratio Vegetation Index (RVI) | (Pearson, 1972) | ||
| Solid-Adjusted Vegetation Index (SAVI) | (Huete, 1988) | ||
| Gray-Level Co-Occurrence Matrices | Mean (MEA) | [40] | |
| Variance (VAR) | |||
| Homogeneity (HOM) | |||
| Contrast (CON) | |||
| Dissimilarity (DIS) | |||
| Entropy (ENT) | |||
| Augular Second Moment (ASM) | |||
| Correlation (COR) | |||
| Notes: | |||
| Variables | Min | Max | Mean | StdDev |
|---|---|---|---|---|
| Intercept | 29.887076 | 36.211161 | 32.830443 | 1.933700 |
| TM457 | −0.006452 | −0.005701 | −0.006129 | 0.000224 |
| TM543 | −0.000883 | −0.000303 | −0.000564 | 0.000188 |
| B7 | 0.002119 | 0.004565 | 0.003407 | 0.000633 |
| NDWI | 12.2544 | 19.2605 | 16.537775 | 2.102416 |
| NDVI | 6.13575 | 10.815 | 8.027686 | 1.299880 |
| W7B6VAR | −0.535064 | 0.396925 | −0.078334 | 0.282045 |
| Model | R2 | Residual SS | Nugget | Still | Structural Ratio | Range |
|---|---|---|---|---|---|---|
| Spherical | 0.6711 | 3384.70 | 0.0312 | 1.1789 | 0.9735 | 7978.455 |
| Exponential | 0.6759 | 3460.67 | 0.0102 | 1.1569 | 0.9911 | 8989.212 |
| Gaussian | 0.5689 | 3734.11 | 0.0012 | 1.1905 | 0.9869 | 8373.171 |
| Rational Quadratic | 0.6771 | 3371.19 | 0.0011 | 1.1092 | 0.999 | 7983.505 |
| Hole Effect | 0.6809 | 3551.67 | 0.0221 | 1.018 | 0.9782 | 7983.505 |
| K-Bessel | 0.6807 | 3291.64 | 0.0083 | 1.0811 | 0.9998 | 39,449.225 |
| J-Bessel | 0.6826 | 3275.97 | 0.0217 | 1.0926 | 0.98 | 10,357.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Du, H.; Li, X.; Mao, F.; Zhang, M.; Liu, E.; Ji, J.; Kang, F. Remote Sensing Estimation of Bamboo Forest Aboveground Biomass Based on Geographically Weighted Regression. Remote Sens. 2021, 13, 2962. https://doi.org/10.3390/rs13152962
Wang J, Du H, Li X, Mao F, Zhang M, Liu E, Ji J, Kang F. Remote Sensing Estimation of Bamboo Forest Aboveground Biomass Based on Geographically Weighted Regression. Remote Sensing. 2021; 13(15):2962. https://doi.org/10.3390/rs13152962
Chicago/Turabian StyleWang, Jingyi, Huaqiang Du, Xuejian Li, Fangjie Mao, Meng Zhang, Enbin Liu, Jiayi Ji, and Fangfang Kang. 2021. "Remote Sensing Estimation of Bamboo Forest Aboveground Biomass Based on Geographically Weighted Regression" Remote Sensing 13, no. 15: 2962. https://doi.org/10.3390/rs13152962
APA StyleWang, J., Du, H., Li, X., Mao, F., Zhang, M., Liu, E., Ji, J., & Kang, F. (2021). Remote Sensing Estimation of Bamboo Forest Aboveground Biomass Based on Geographically Weighted Regression. Remote Sensing, 13(15), 2962. https://doi.org/10.3390/rs13152962







